A General State-Space Formulation for Online Scheduling
Abstract
:1. Introduction
2. Background
2.1. Chemical Production Scheduling
2.1.1. General Problem Statement
- (i)
- Production facility data (e.g., unit capacities and connectivity),
- (ii)
- Production recipes (e.g., processing times and mixing rules),
- (iii)
- Production costs (e.g., material holding costs),
- (iv)
- Material availability (e.g., raw materials delivery amounts and dates),
- (v)
- Resource availability (e.g., maintenance schedule and utility levels), and
- (vi)
- Production targets or orders with due-times;
- (i)
- Number and the associated processing-sizes of the needed tasks,
- (ii)
- Assignment of these tasks to processing units, and
- (iii)
- Timing (or just the sequence) of these tasks on the assigned units;
2.1.2. Problem Representation
2.1.3. Model Classification
2.1.4. Solution Methods
2.2. Scheduling MILP Model
2.3. Standard form of State-Space Models
2.4. Scheduling State-Space Model
3. Modeling Generalizations
3.1. New Basic Formulation
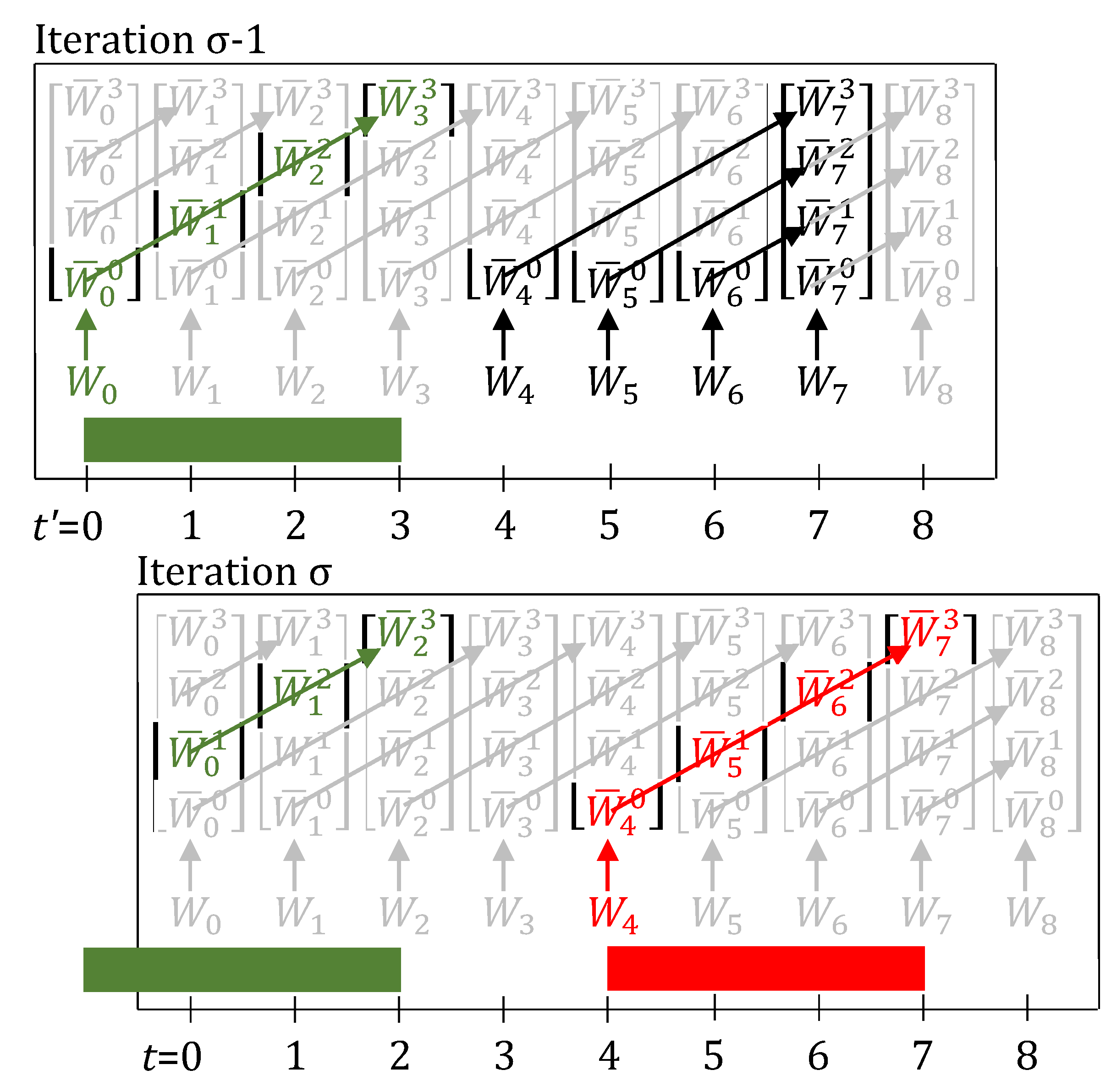
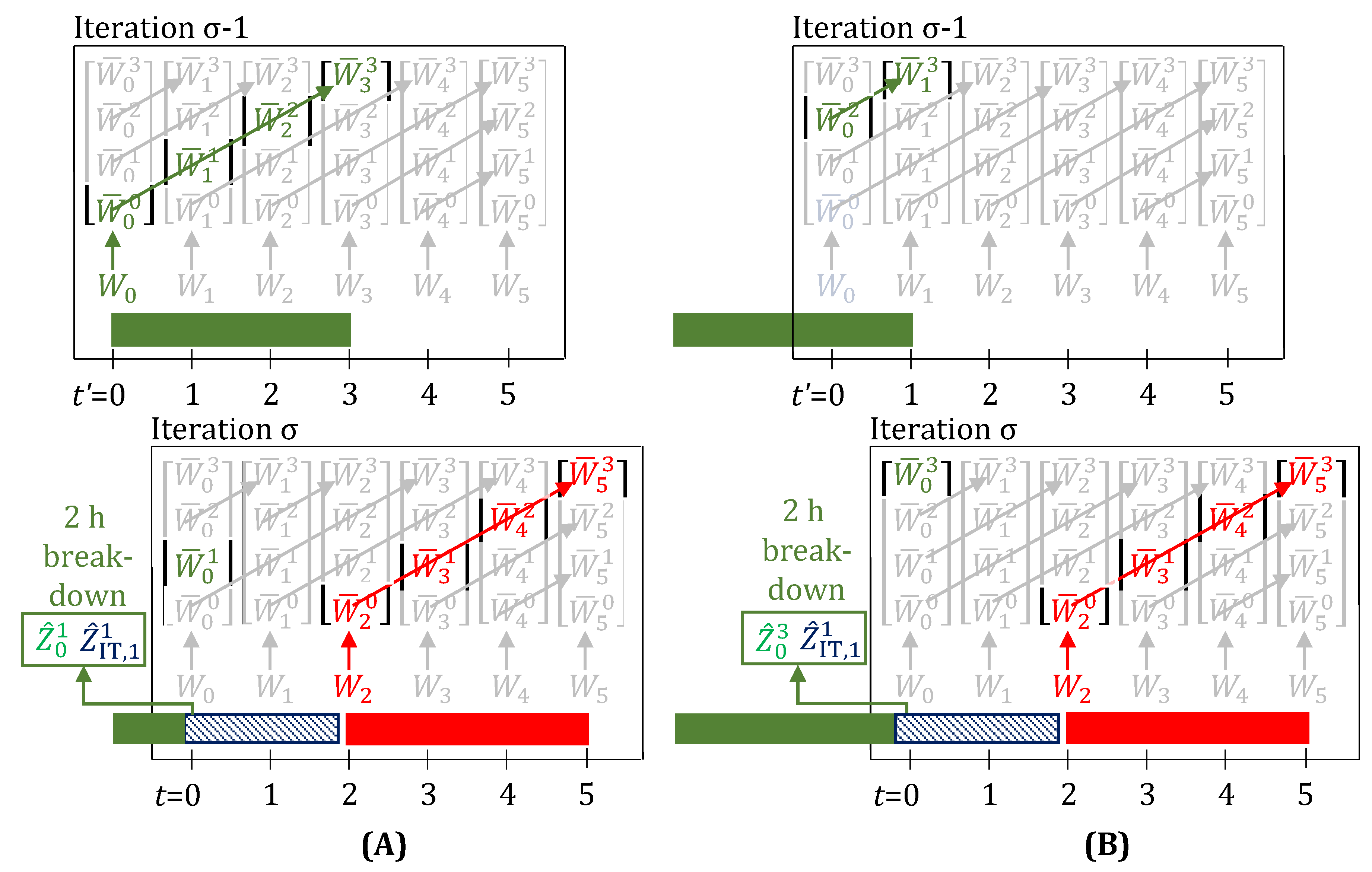
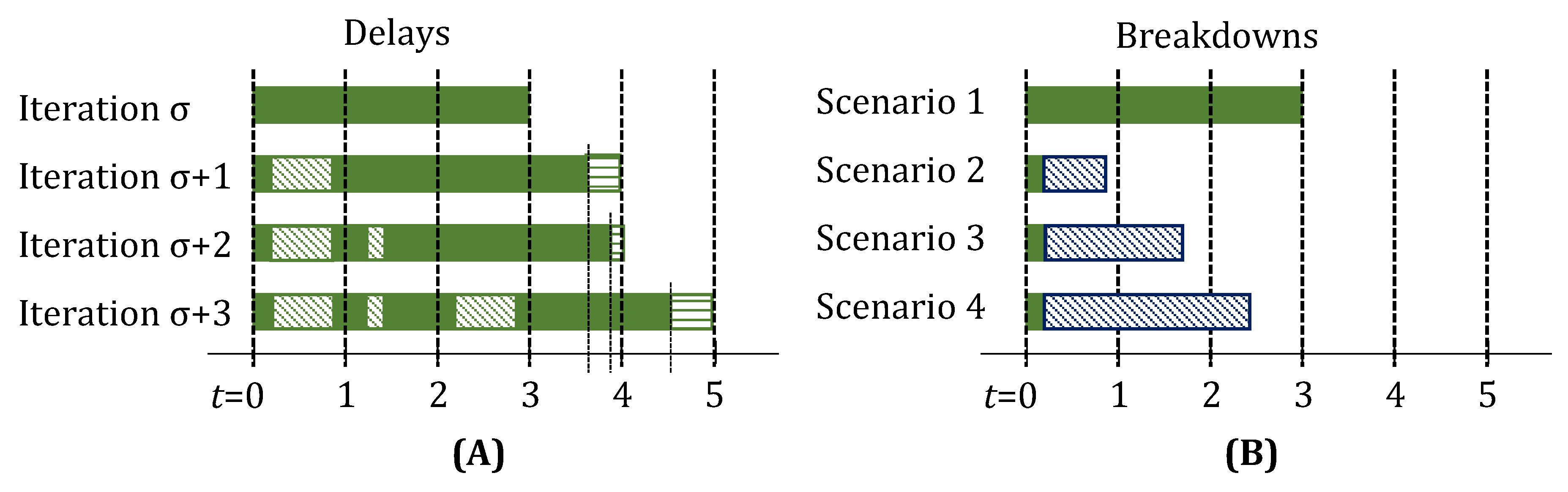
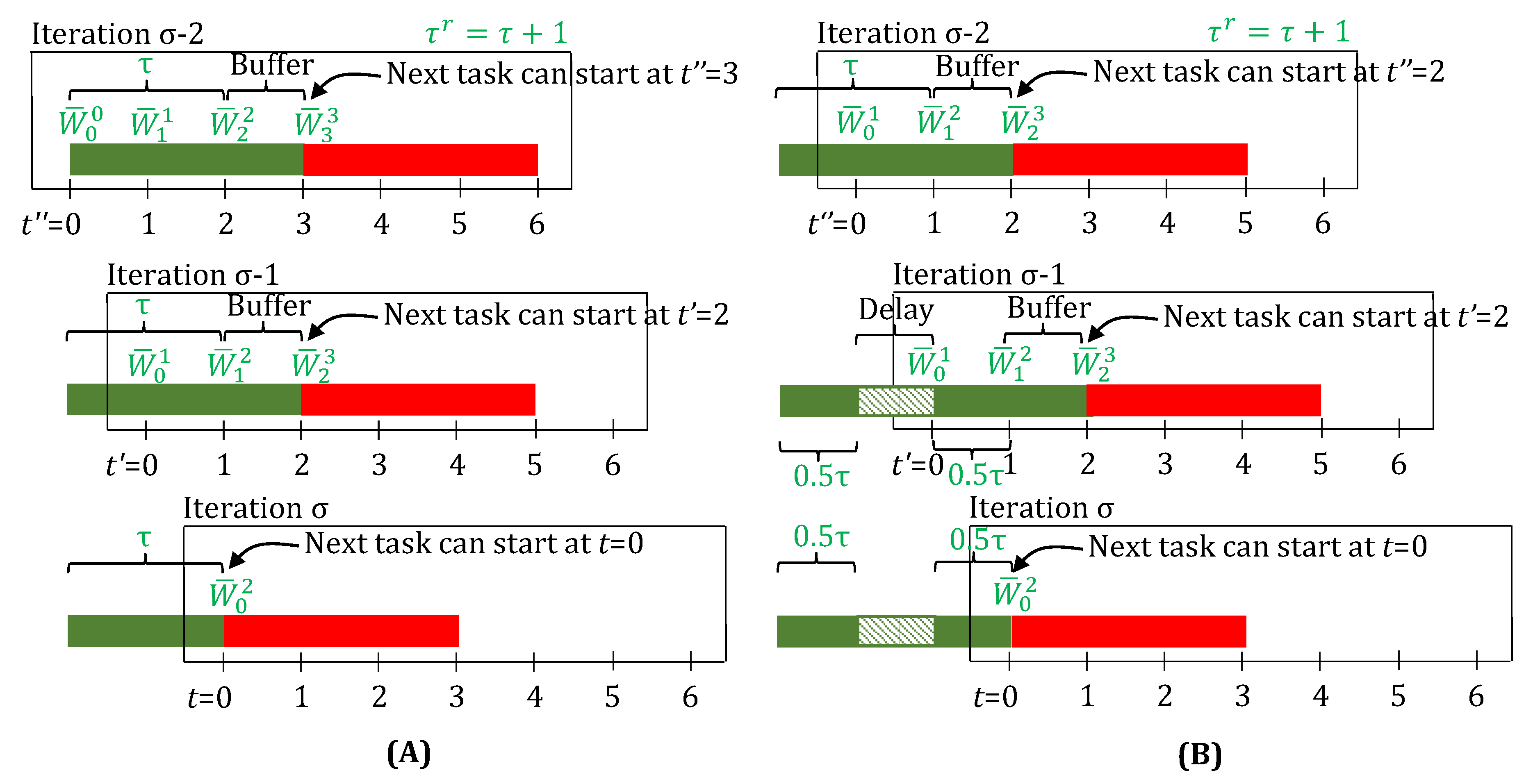
3.2. Fractional Delays and Unit Downtimes
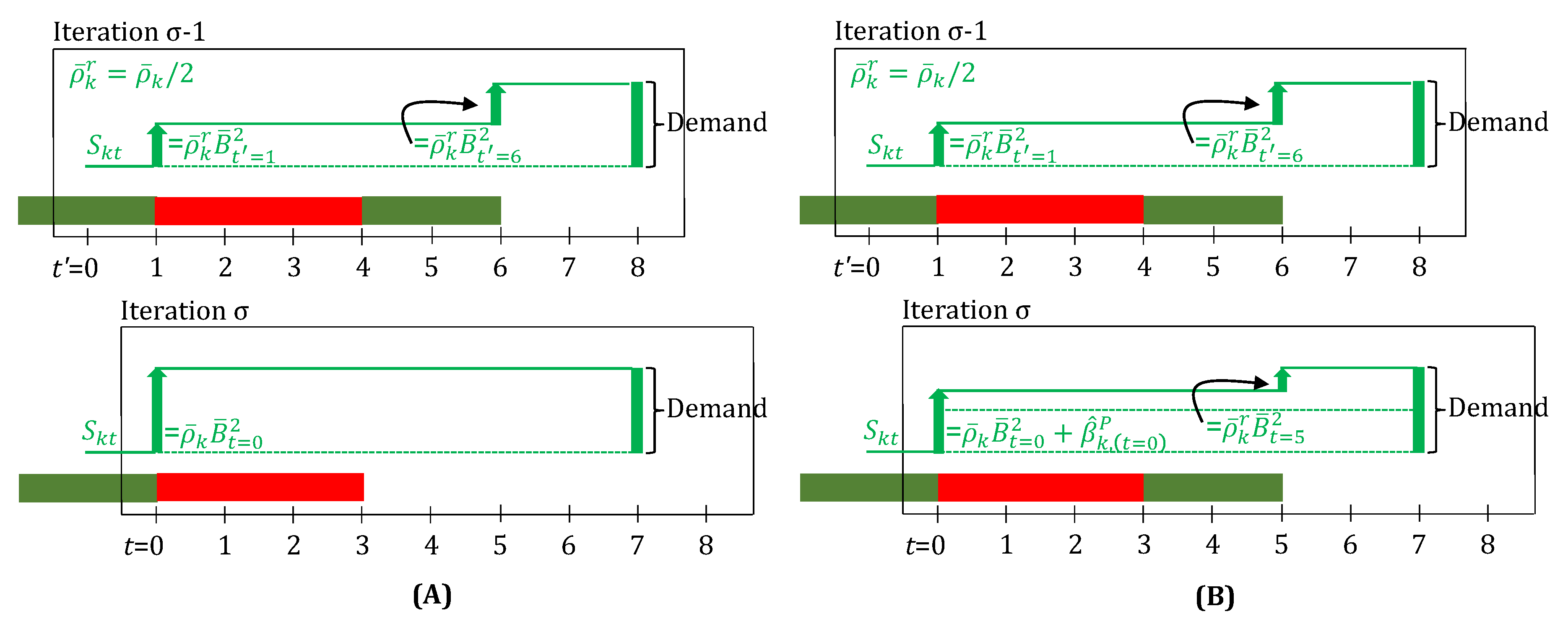
3.3. Variable Batch-Sizes
3.4. Robust Scheduling: Batch-Sizes
3.5. Robust Scheduling: Processing Times
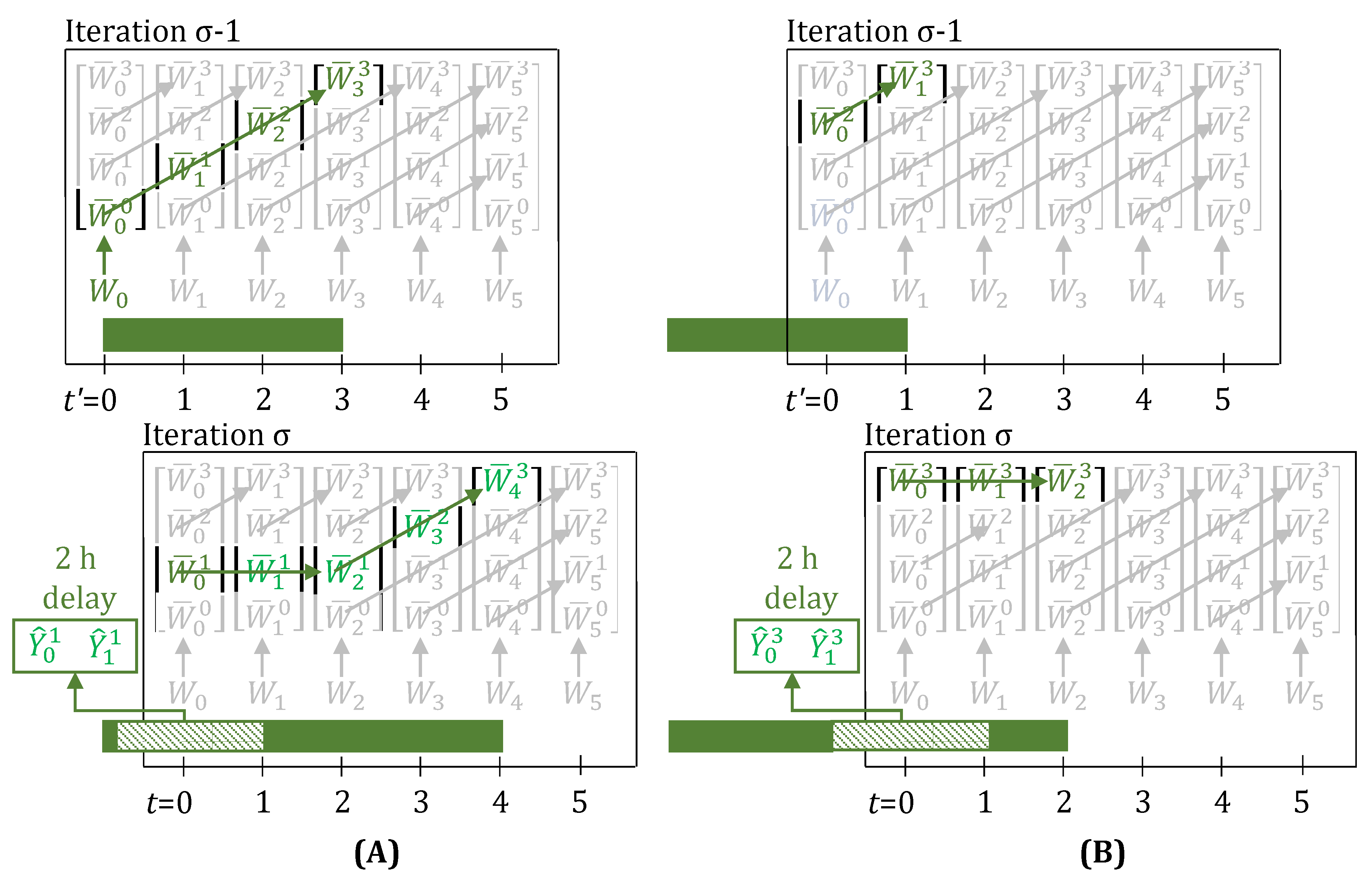
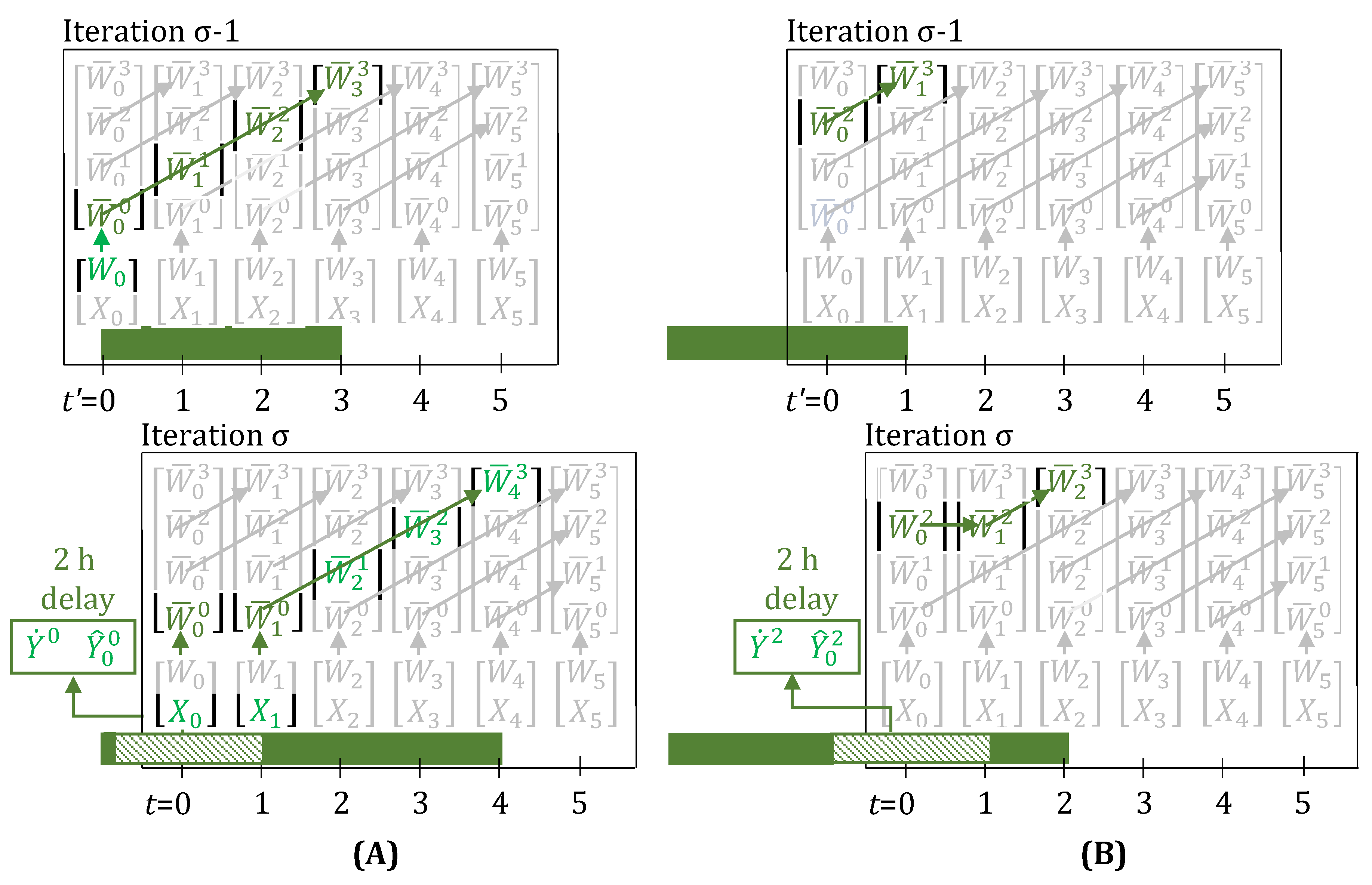
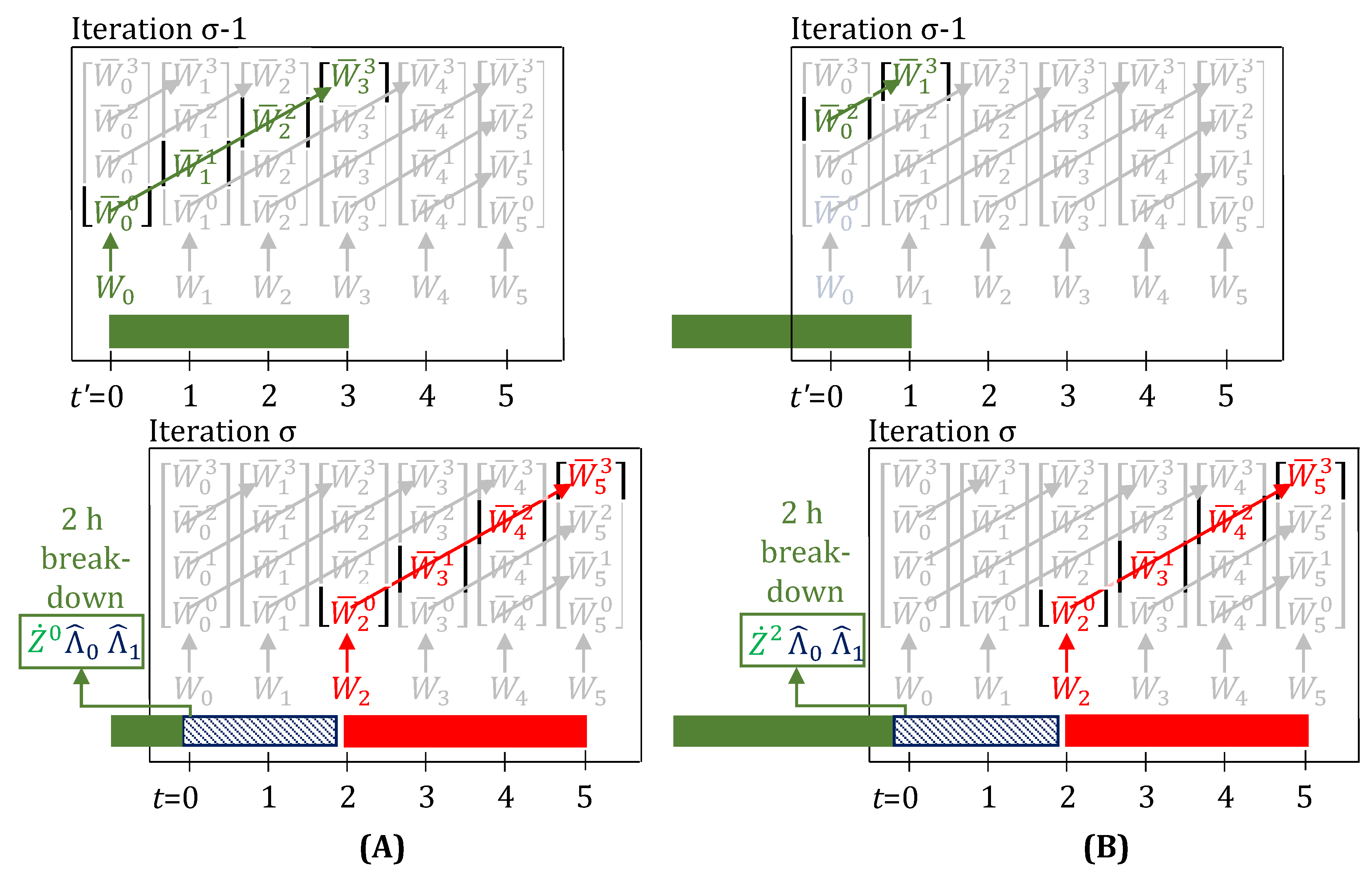
3.6. Feedback on Yield Estimates
3.7. Task Termination
3.8. Post-Production Storage in Unit
3.9. Unit Capacity Degradation and Maintenance
4. Integrated Model
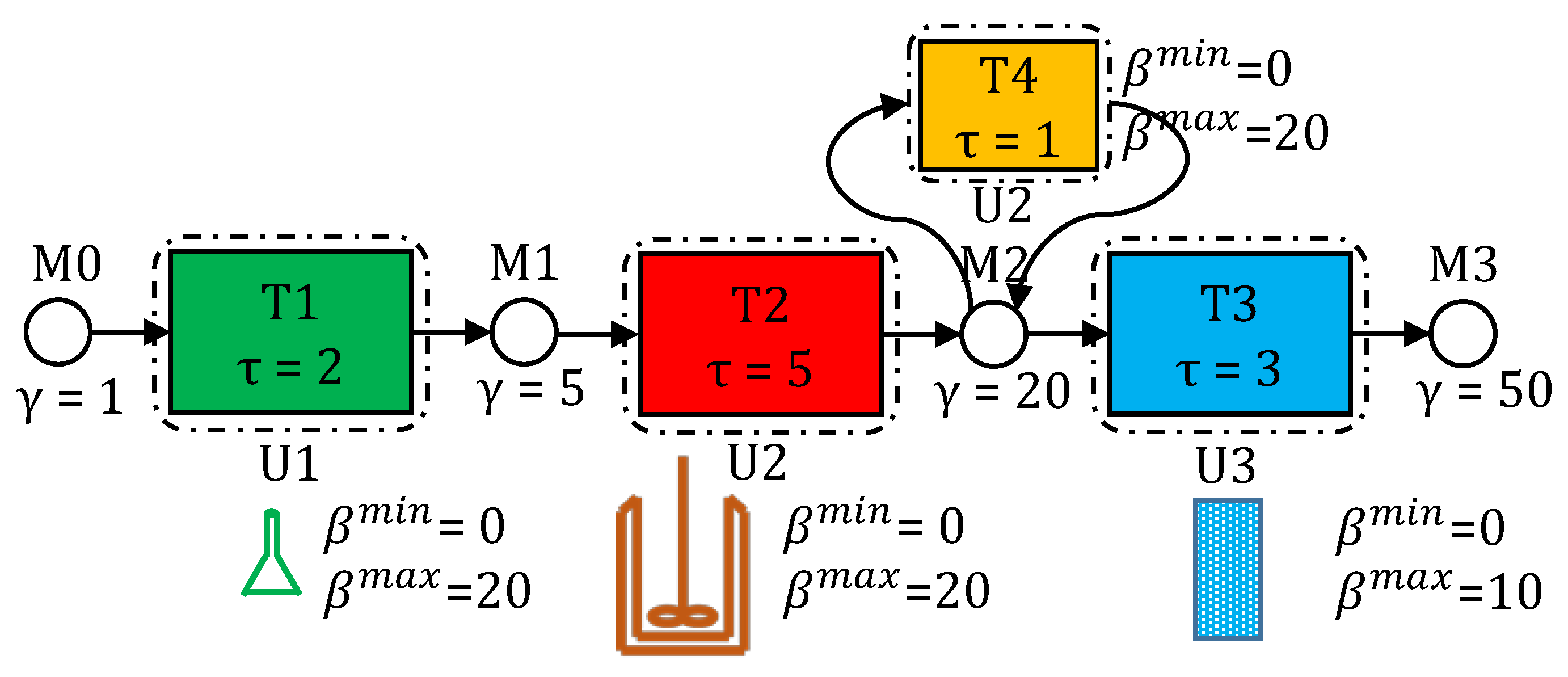
5. Case Study
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| MILP | mixed integer linear program |
| MPC | model predictive control |
| RTN | resource task network |
| STN | state task network |
| HOLD | hold (storage) task |
| MT | maintenance (cleaning) task |
Nomenclature
| Indices/sets | |
| tasks | |
| units (equipment) | |
| materials | |
| time-points/periods | |
| tasks that can be carried out in unit j | |
| tasks producing material k | |
| tasks consuming material k | |
| hold (storage) tasks | |
| maintenance tasks | |
| units suitable for carrying out task i | |
| units which can degrade, and consequently, need a corresponding maintenance task | |
| feed (raw) materials | |
| intermediates | |
| final products | |
| Parameters | |
| fixed cost of running task i on unit j | |
| proportional cost of running task i on unit j | |
| cost of terminating task i on unit j | |
| proportional cost of maintenance task i on unit j | |
| fixed batch-size of task i executed on unit j | |
| min/max capacity on batch-size of task i executed on unit j | |
| material unloading/loading loss during production/consumption of material k | |
| selling price of material k | |
| inventory cost of material k | |
| backlog cost of material k | |
| discretization of time-grid; length of time-periods | |
| incoming shipment of material k at time t | |
| disturbance parameter denoting unit breakdown | |
| batch-size of task suspended due to unit breakdown | |
| yield-loss size of task suspended due to unit breakdown | |
| maintenance-size of maintenance task suspended due to unit breakdown | |
| dummy parameter as defined in Equation (46) | |
| dummy parameter as defined in Equation (37) | |
| dummy parameter as defined in Equation (63) | |
| yield loss in task i running on unit j, with run status n | |
| binary parameter, when 1, denotes unit j unavailable during time | |
| when negative, represents extent of sudden partial loss in unit capacity | |
| demand for material k at time t | |
| demand disturbance for material k at time t | |
| actual (fractional) time at which a unit breaks down | |
| fractional downtime in a unit | |
| fractional delay in a task | |
| rth delay in a task | |
| mass-conversion coefficient (material consumption) | |
| mass-conversion coefficient (material production) | |
| conservative mass-conversion coefficient for production () | |
| deterioration in unit capacity to perform task i, due to performing task on that unit j. | |
| online iteration number | |
| processing time of task i on unit j | |
| conservative processing time of task i () on unit j | |
| task independent unit j downtime after terminating a task | |
| task dependent unit j downtime after terminating task i | |
| , | single-/multi-period disturbance parameters denoting delay |
| , | single-/multi-period disturbance parameters denoting batch-size of a delayed task |
| , | single-/multi-period disturbance parameters denoting yield-loss size of a delayed task |
| , | single-/multi-period disturbance parameters denoting maintenance-size of delayed maintenance task |
| duration of delay or breakdown, in multiples of | |
| recurrence count of delay for a task | |
| Variables | |
| batch-size of task i on unit j | |
| lifted batch-size | |
| backlog level of material k during period | |
| capacity of unit j to perform task i during period | |
| lifted yield-loss variables | |
| maintenance-size of the maintenance task | |
| lifted maintenance-size | |
| inventory level of material k during period | |
| binary variable, when 1, denotes termination of task i, with run-status n, on unit j | |
| outgoing shipment to meet demand for material k at time t | |
| binary variable, when 1, denotes task i starts on unit j at time-point t | |
| lifted task-start variables | |
| when 1, captures the information about delays in a task with progress status | |
| the batch-size of delayed task with progress status | |
| yield-loss of delayed task with progress status | |
| maintenance-size of delayed maintenance task with progress status | |
References
- Harjunkoski, I.; Maravelias, C.T.; Bongers, P.; Castro, P.M.; Engell, S.; Grossmann, I.E.; Hooker, J.; Méndez, C.A.; Sand, G.; Wassick, J.M. Scope for industrial applications of production scheduling models and solution methods. Comput. Chem. Eng. 2014, 62, 161–193. [Google Scholar] [CrossRef]
- Kelly, J.D.; Mann, J. Crude oil blend scheduling optimization: An application with multimillion dollar benefits. Hydrocarb. Process. 2003, 82, 47–54. [Google Scholar]
- Méndez, C.A.; Cerdá, J.; Grossmann, I.E.; Harjunkoski, I.; Fahl, M. State-of-the-art review of optimization methods for short-term scheduling of batch processes. Comput. Chem. Eng. 2006, 30, 913–946. [Google Scholar] [CrossRef]
- Maravelias, C.T. General framework and modeling approach classification for chemical production scheduling. AIChE J. 2012, 58, 1812–1828. [Google Scholar] [CrossRef]
- Velez, S.; Maravelias, C.T. Reformulations and branching methods for mixed-integer programming chemical production scheduling models. Ind. Eng. Chem. Res. 2013, 52, 3832–3841. [Google Scholar] [CrossRef]
- Wassick, J.M.; Ferrio, J. Extending the resource task network for industrial applications. Comput. Chem. Eng. 2011, 35, 2124–2140. [Google Scholar] [CrossRef]
- Nie, Y.; Biegler, L.T.; Villa, C.M.; Wassick, J.M. Discrete Time Formulation for the Integration of Scheduling and Dynamic Optimization. Ind. Eng. Chem. Res. 2015, 54, 4303–4315. [Google Scholar] [CrossRef]
- Gupta, D.; Maravelias, C.T.; Wassick, J.M. From rescheduling to online scheduling. Chem. Eng. Res. Des. 2016, 116, 83–97. [Google Scholar] [CrossRef]
- Cott, B.J.; Macchietto, S. Minimizing the effects of batch process variability using online schedule modification. Comput. Chem. Eng. 1989, 13, 105–113. [Google Scholar] [CrossRef]
- Kanakamedala, K.B.; Reklaitis, G.V.; Venkatasubramanian, V. Reactive schedule modification in multipurpose batch chemical plants. Ind. Eng. Chem. Res. 1994, 33, 77–90. [Google Scholar] [CrossRef]
- Huercio, A.; Espuña, A.; Puigjaner, L. Incorporating on-line scheduling strategies in integrated batch productioncontrol. Comput. Chem. Eng. 1995, 19, 609–614. [Google Scholar] [CrossRef]
- Kim, M.; Lee, I.B. Rule-based reactive rescheduling system for multi-purpose batch processes. Comput. Chem. Eng. 1997, 21, S1197–S1202. [Google Scholar] [CrossRef]
- Ko, D.; Na, S.; Moon, I.; Oh, M.; Dong-Gu Samsung, T.S. Development of a Rescheduling System for the Optimal Operation of Pipeless Plants. Comput. Chem. Eng. 1999, 23, S523–S526. [Google Scholar] [CrossRef]
- Huang, W.; Chung, P.W.H. A constraint approach for rescheduling batch processing plants including pipeless plants. Comput. Aided Chem. Eng. 2003, 14, 161–166. [Google Scholar]
- Henning, G.P.; Cerdá, J. Knowledge-based predictive and reactive scheduling in industrial environments. Comput. Chem. Eng. 2000, 24, 2315–2338. [Google Scholar] [CrossRef]
- Palombarini, J.; Martínez, E. SmartGantt—An interactive system for generating and updating rescheduling knowledge using relational abstractions. Comput. Chem. Eng. 2012, 47, 202–216. [Google Scholar] [CrossRef]
- Elkamel, A.; Mohindra, A. A rolling horizon heuristic for reactive scheduling of batch process operations. Eng. Optim. 1999, 31, 763–792. [Google Scholar] [CrossRef]
- Vin, J.; Ierapetritou, M.G. A new approach for efficient rescheduling of multiproduct batch plants. Ind. Eng. Chem. Res. 2000, 39, 4228–4238. [Google Scholar] [CrossRef]
- Méndez, C.A.; Cerdá, J. Dynamic scheduling in multiproduct batch plants. Comput. Chem. Eng. 2003, 27, 1247–1259. [Google Scholar] [CrossRef]
- Ferrer-Nadal, S.; Méndez, C.A.; Graells, M.; Puigjaner, L. Optimal reactive scheduling of manufacturing plants with flexible batch recipes. Ind. Eng. Chem. Res. 2007, 46, 6273–6283. [Google Scholar] [CrossRef]
- Janak, S.L.; Floudas, C.A.; Kallrath, J.; Vormbrock, N. Production scheduling of a large-scale industrial batch plant. II. Reactive scheduling. Ind. Eng. Chem. Res. 2006, 45, 8253–8269. [Google Scholar] [CrossRef]
- Novas, J.M.; Henning, G.P. Reactive scheduling framework based on domain knowledge and constraint programming. Comput. Chem. Eng. 2010, 34, 2129–2148. [Google Scholar] [CrossRef]
- Honkomp, S.; Mockus, L.; Reklaitis, G.V. A framework for schedule evaluation with processing uncertainty. Comput. Chem. Eng. 1999, 23, 595–609. [Google Scholar] [CrossRef]
- Subramanian, K.; Maravelias, C.T.; Rawlings, J.B. A state-space model for chemical production scheduling. Comput. Chem. Eng. 2012, 47, 97–110. [Google Scholar] [CrossRef]
- Gupta, D.; Maravelias, C.T. On deterministic online scheduling: Major considerations, paradoxes and remedies. Comput. Chem. Eng. 2016, 94, 312–330. [Google Scholar] [CrossRef]
- Velez, S.; Maravelias, C.T. Advances in Mixed-Integer Programming Methods for Chemical Production Scheduling. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 97–121. [Google Scholar] [CrossRef] [PubMed]
- Subramanian, K.; Rawlings, J.B.; Maravelias, C.T.; Flores-Cerrillo, J.; Megan, L. Integration of control theory and scheduling methods for supply chain management. Comput. Chem. Eng. 2013, 51, 4–20. [Google Scholar] [CrossRef]
- Subramanian, K.; Rawlings, J.B.; Maravelias, C.T. Economic model predictive control for inventory management in supply chains. Comput. Chem. Eng. 2014, 64, 71–80. [Google Scholar] [CrossRef]
- Kondili, E.; Pantelides, C.C.; Sargent, R.W.H. A general algorithm for short-term scheduling of batch operations-I. MILP formulation. Comput. Chem. Eng. 1993, 17, 211–227. [Google Scholar] [CrossRef]
- Pantelides, C.C. Unified frameworks for optimal process planning and scheduling. In Proceedings of the Second Conference on Foundations of Computer Aided Operations; Cache: New York, NY, USA, 1994; pp. 253–274. [Google Scholar]
- Sundaramoorthy, A.; Maravelias, C.T. Computational Study of Network-Based Mixed-Integer Programming Approaches for Chemical Production Scheduling. Ind. Eng. Chem. Res. 2011, 50, 5023–5040. [Google Scholar] [CrossRef]
- Pinto, J.M.; Grossmann, I.E. A Continuous Time Mixed Integer Linear Programming Model for Short Term Scheduling of Multistage Batch Plants. Ind. Eng. Chem. Res. 1995, 34, 3037–3051. [Google Scholar] [CrossRef]
- Blomer, F.; Gunther, H.O. LP-based heuristics for scheduling chemical batch processes. Ind. Eng. Chem. Res. 2000, 38, 1029–1051. [Google Scholar] [CrossRef]
- Velez, S.; Maravelias, C.T. Mixed-integer programming model and tightening methods for scheduling in general chemical production environments. Ind. Eng. Chem. Res. 2013, 52, 3407–3423. [Google Scholar] [CrossRef]
- Merchan, A.F.; Maravelias, C.T. Reformulations of Mixed-Integer Programming Continuous-Time Models for Chemical Production Scheduling. Ind. Eng. Chem. Res. 2014, 53, 10155–10165. [Google Scholar] [CrossRef]
- Burkard, R.; Hatzl, J. Review, extensions and computational comparison of MILP formulations for scheduling of batch processes. Comput. Chem. Eng. 2005, 29, 1752–1769. [Google Scholar] [CrossRef]
- Janak, S.L.; Floudas, C.A. Improving unit-specific event based continuous-time approaches for batch processes: Integrality gap and task splitting. Comput. Chem. Eng. 2008, 32, 913–955. [Google Scholar] [CrossRef]
- Lee, H.; Maravelias, C.T. Discrete-time mixed-integer programming models for short-term scheduling in multipurpose environments. Comput. Chem. Eng. 2017, 107, 171–183. [Google Scholar] [CrossRef]
- Sahinidis, N.; Grossmann, I. Reformulation of multiperiod MILP models for planning and scheduling of chemical processes. Comput. Chem. Eng. 1991, 15, 255–272. [Google Scholar] [CrossRef]
- Yee, K.; Shah, N. Improving the efficiency of discrete time scheduling formulation. Comput. Chem. Eng. 1998, 22, S403–S410. [Google Scholar] [CrossRef]
- Lee, H.; Maravelias, C.T. Mixed-integer programming models for simultaneous batching and scheduling in multipurpose batch plants. Comput. Chem. Eng. 2017, 106, 621–644. [Google Scholar] [CrossRef]
- Papageorgiou, L.G.; Pantelides, C.C. Optimal campaign planning/scheduling of multipurpose batch/semicontinuous plants. 2. A mathematical decomposition approach. Ind. Eng. Chem. Res. 1996, 35, 510–529. [Google Scholar] [CrossRef]
- Bassett, M.H.; Pekny, J.F.; Reklaitis, G.V. Decomposition techniques for the solution of large-scale scheduling problems. AIChE J. 1996, 42, 3373–3387. [Google Scholar] [CrossRef]
- Kelly, J.D.; Zyngier, D. Hierarchical decomposition heuristic for scheduling: Coordinated reasoning for decentralized and distributed decision-making problems. Comput. Chem. Eng. 2008, 32, 2684–2705. [Google Scholar] [CrossRef]
- Wu, D.; Ierapetritou, M.G. Decomposition approaches for the efficient solution of short-term scheduling problems. Comput. Chem. Eng. 2003, 27, 1261–1276. [Google Scholar] [CrossRef]
- Calfa, B.A.; Agarwal, A.; Grossmann, I.E.; Wassick, J.M. Hybrid Bilevel-Lagrangean Decomposition Scheme for the Integration of Planning and Scheduling of a Network of Batch Plants. Ind. Eng. Chem. Res. 2013, 52, 2152–2167. [Google Scholar] [CrossRef]
- Castro, P.M.; Harjunkoski, I.; Grossmann, I.E. Greedy algorithm for scheduling batch plants with sequence-dependent changeovers. AIChE J. 2011, 57, 373–387. [Google Scholar] [CrossRef]
- Roslöf, J.; Harjunkoski, I.; Björkqvist, J.; Karlsson, S.; Westerlund, T. An MILP-based reordering algorithm for complex industrial scheduling and rescheduling. Comput. Chem. Eng. 2001, 25, 821–828. [Google Scholar] [CrossRef]
- Kopanos, G.M.; Méndez, C.A.; Puigjaner, L. MIP-based decomposition strategies for large-scale scheduling problems in multiproduct multistage batch plants: A benchmark scheduling problem of the pharmaceutical industry. Eur. J. Oper. Res. 2010, 207, 644–655. [Google Scholar] [CrossRef]
- Relvas, S.; Barbosa-Póvoa, A.P.F.; Matos, H.A. Heuristic batch sequencing on a multiproduct oil distribution system. Comput. Chem. Eng. 2009, 33, 712–730. [Google Scholar] [CrossRef]
- Jain, V.; Grossmann, I.E. Algorithms for Hybrid MILP/CP Models for a Class of Optimization Problems. INFORMS J. Comput. 2001, 13, 258–276. [Google Scholar] [CrossRef]
- Harjunkoski, I.; Grossmann, I.E. Decomposition techniques for multistage scheduling problems using mixed-integer and constraint programming methods. Comput. Chem. Eng. 2002, 26, 1533–1552. [Google Scholar] [CrossRef]
- Maravelias, C.T.; Grossmann, I.E. A hybrid MILP/CP decomposition approach for the continuous time scheduling of multipurpose batch plants. Comput. Chem. Eng. 2004, 28, 1921–1949. [Google Scholar] [CrossRef]
- Roe, B.; Papageorgiou, L.G.; Shah, N. A hybrid MILP/CLP algorithm for multipurpose batch process scheduling. Comput. Chem. Eng. 2005, 29, 1277–1291. [Google Scholar] [CrossRef]
- Maravelias, C.T. A decomposition framework for the scheduling of single- and multi-stage processes. Comput. Chem. Eng. 2006, 30, 407–420. [Google Scholar] [CrossRef]
- Subrahmanyam, S.; Kudva, G.K.; Bassett, M.H.; Pekny, J.F. Application of distributed computing to batch plant design and scheduling. AIChE J. 1996, 42, 1648–1661. [Google Scholar] [CrossRef]
- Ferris, M.C.; Maravelias, C.T.; Sundaramoorthy, A. Simultaneous Batching and Scheduling Using Dynamic Decomposition on a Grid. INFORMS J. Comput. 2009, 21, 398–410. [Google Scholar] [CrossRef]
- Velez, S.; Maravelias, C.T. A branch-and-bound algorithm for the solution of chemical production scheduling MIP models using parallel computing. Comput. Chem. Eng. 2013, 55, 28–39. [Google Scholar] [CrossRef]
- Shah, N.; Pantelides, C.C.; Sargent, R.W.H. A general algorithm for short-term scheduling of batch operations-II. Computational issues. Comput. Chem. Eng. 1993, 17, 229–244. [Google Scholar] [CrossRef]
- Stephanopoulos, G. Chemical Process Control: An Introduction to Theory and Practice; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984; p. 696. [Google Scholar]
- Ogunnaike, B.A.; Ray, W.H. Process Dynamics, Modeling, and Control; Oxford University Press: New York, NY, USA, 1994; p. 1260. [Google Scholar]
- Bequette, B.W. Process Control: Modeling, Design, and Simulation; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2003; p. 769. [Google Scholar]
- Rawlings, J.B.; Mayne, D. Model Predictive Control: Theory and Design; Nob Hill Pub: Madison, WI, USA, 2009; p. 669. [Google Scholar]
- Seborg, D.E.; Edgar, T.F.; Duncan, M.A.; Doyle, F.J., III. Process Dynamics and Control; Wiley: Hoboken, NJ, USA, 2016; p. 502. [Google Scholar]
- Amrit, R.; Rawlings, J.B.; Biegler, L.T. Optimizing process economics online using model predictive control. Comput. Chem. Eng. 2013, 58, 334–343. [Google Scholar] [CrossRef]
- Ellis, M.; Durand, H.; Christofides, P.D. A tutorial review of economic model predictive control methods. J. Process Control 2014, 24, 1156–1178. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Risbeck, M.J. Model predictive control with discrete actuators: Theory and application. Automatica 2017, 78, 258–265. [Google Scholar] [CrossRef]
- Baldea, M.; Harjunkoski, I. Integrated production scheduling and process control: A systematic review. Comput. Chem. Eng. 2014, 71, 377–390. [Google Scholar] [CrossRef]
- Li, Z.; Ierapetritou, M.G. Process scheduling under uncertainty: Review and challenges. Comput. Chem. Eng. 2008, 32, 715–727. [Google Scholar] [CrossRef]
- Janak, S.L.; Lin, X.; Floudas, C.A. A new robust optimization approach for scheduling under uncertainty. II. Uncertainty with known probability distribution. Comput. Chem. Eng. 2007, 31, 171–195. [Google Scholar] [CrossRef]
- Sand, G.; Engell, S. Modeling and solving real-time scheduling problems by stochastic integer programming. Comput. Chem. Eng. 2004, 28, 1087–1103. [Google Scholar] [CrossRef]
- Sabuncuoglu, I.; Karabuk, S. Rescheduling frequency in an fms with uncertain processing times and unreliable machines. J. Manuf. Syst. 1999, 18, 268–283. [Google Scholar] [CrossRef]
- Chaari, T.; Chaabane, S.; Aissani, N.; Trentesaux, D. Scheduling under uncertainty: Survey and research directions. In Proceedings of the 2014 International Conference on Advanced Logistics and Transport, Hammamet, Tunisia, 1–3 May 2014; pp. 229–234. [Google Scholar]
- Martagan, T.; Krishnamurthy, A. Control and Optimization of Bioprocesses Using Markov Decision Process. In Proceedings of the 2012 Industrial and Systems Engineering Research Conference, Orlando, FL, USA, 19–23 May 2012; pp. 1–8. [Google Scholar]
- Martagan, T.; Krishnamurthy, A.; Maravelias, C.T. Optimal condition-based harvesting policies for biomanufacturing operations with failure risks. IIE Trans. 2016, 48, 440–461. [Google Scholar] [CrossRef]
- Dedopoulos, I.T.; Shah, N. Optimal Short-Term Scheduling of Maintenance and Production for Multipurpose Plants. Ind. Eng. Chem. Res. 1995, 34, 192–201. [Google Scholar] [CrossRef]
- Sanmartí, E.; Espuña, A.; Puigjaner, L. Batch production and preventive maintenance scheduling under equipment failure uncertainty. Comput. Chem. Eng. 1997, 21, 1157–1168. [Google Scholar] [CrossRef]
- Vassiliadis, C.; Pistikopoulos, E. Maintenance scheduling and process optimization under uncertainty. Comput. Chem. Eng. 2001, 25, 217–236. [Google Scholar] [CrossRef]
- Kopanos, G.M.; Xenos, D.P.; Cicciotti, M.; Pistikopoulos, E.N.; Thornhill, N.F. Optimization of a network of compressors in parallel: Operational and maintenance planning – The air separation plant case. Appl. Energy 2015, 146, 453–470. [Google Scholar] [CrossRef]
- Xenos, D.P.; Kopanos, G.M.; Cicciotti, M.; Thornhill, N.F. Operational optimization of networks of compressors considering condition-based maintenance. Comput. Chem. Eng. 2016, 84, 117–131. [Google Scholar] [CrossRef]
- Biondi, M.; Sand, G.; Harjunkoski, I. Optimization of multipurpose process plant operations: A multi-time-scale maintenance and production scheduling approach. Comput. Chem. Eng. 2017, 99, 325–339. [Google Scholar] [CrossRef]
- Zhang, Y.H.P.; Sun, J.; Ma, Y. Biomanufacturing: History and perspective. J. Ind. Microbiol. Biotechnol. 2017, 44, 773–784. [Google Scholar] [CrossRef] [PubMed]
- Clomburg, J.M.; Crumbley, A.M.; Gonzalez, R. Industrial biomanufacturing: The future of chemical production. Science 2017, 355. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, D.; Maravelias, C.T. A General State-Space Formulation for Online Scheduling. Processes 2017, 5, 69. https://doi.org/10.3390/pr5040069
Gupta D, Maravelias CT. A General State-Space Formulation for Online Scheduling. Processes. 2017; 5(4):69. https://doi.org/10.3390/pr5040069
Chicago/Turabian StyleGupta, Dhruv, and Christos T. Maravelias. 2017. "A General State-Space Formulation for Online Scheduling" Processes 5, no. 4: 69. https://doi.org/10.3390/pr5040069
APA StyleGupta, D., & Maravelias, C. T. (2017). A General State-Space Formulation for Online Scheduling. Processes, 5(4), 69. https://doi.org/10.3390/pr5040069






