Dispersal-Based Microbial Community Assembly Decreases Biogeochemical Function
Abstract
1. Introduction
2. Materials and Methods
2.1. Regional Species Pool Simulation
2.2. Community Assembly
2.3. Ecological Inferences Using Null Models
2.4. Statistical Analysis
3. Results and Discussion
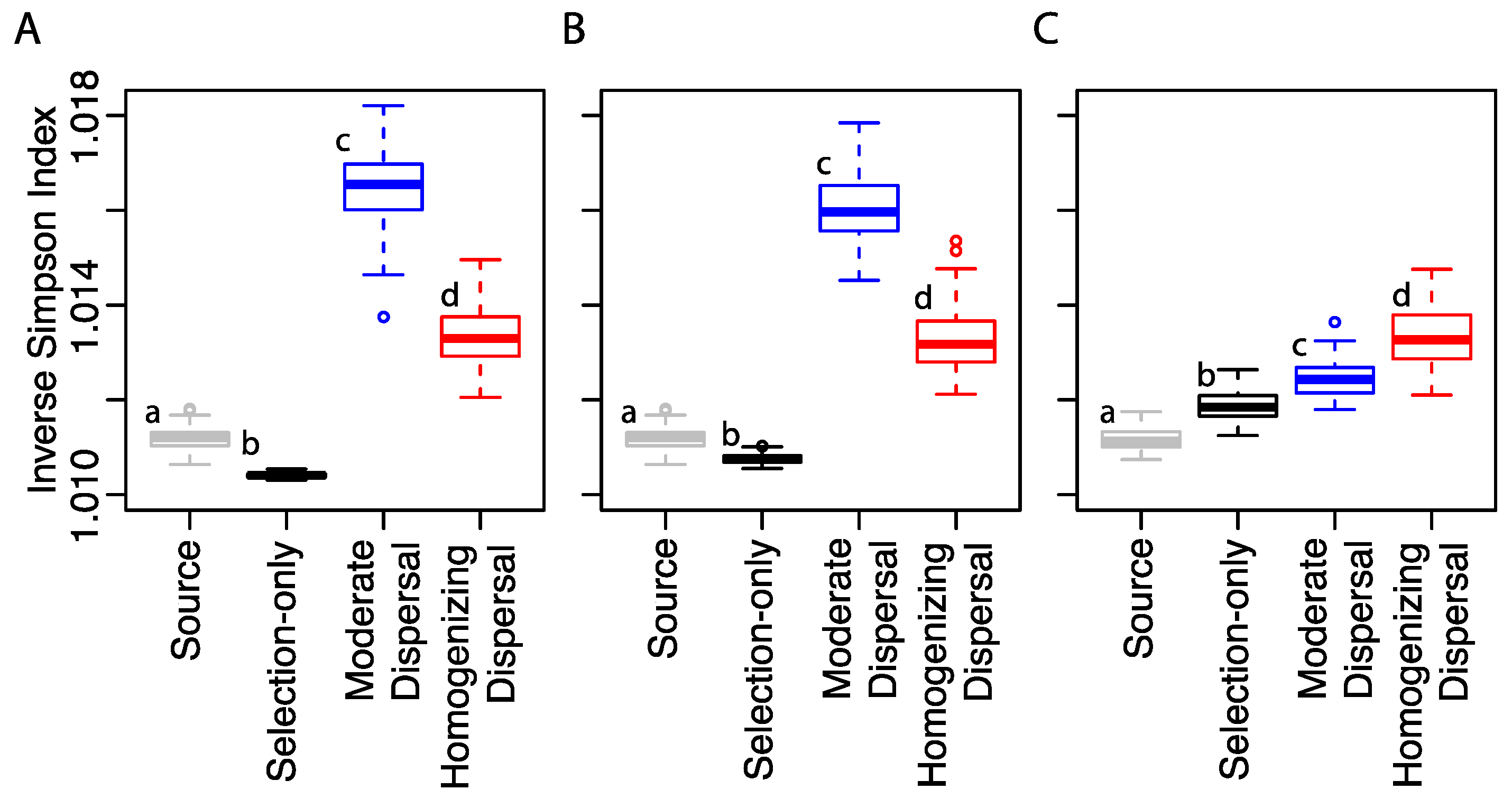
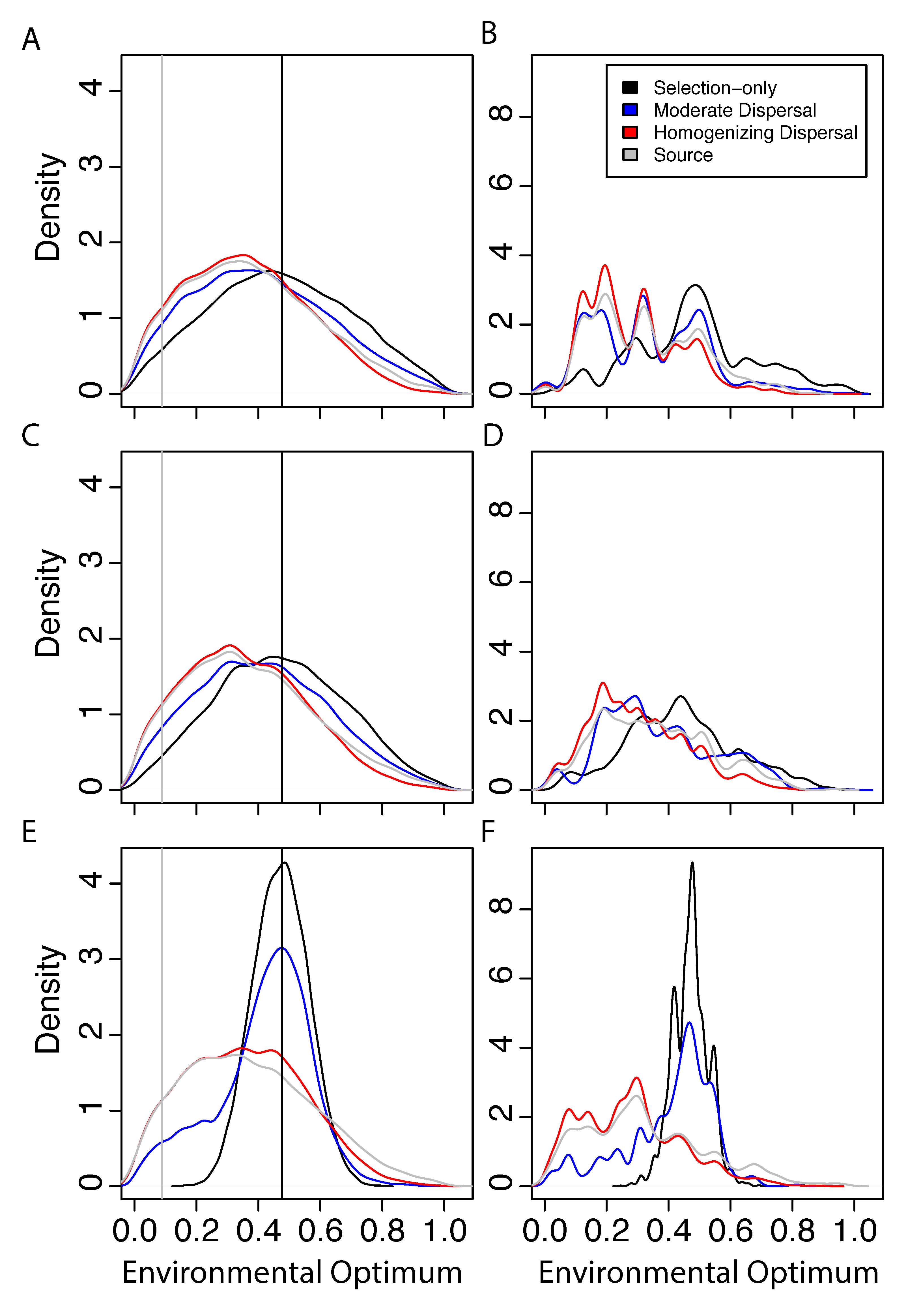
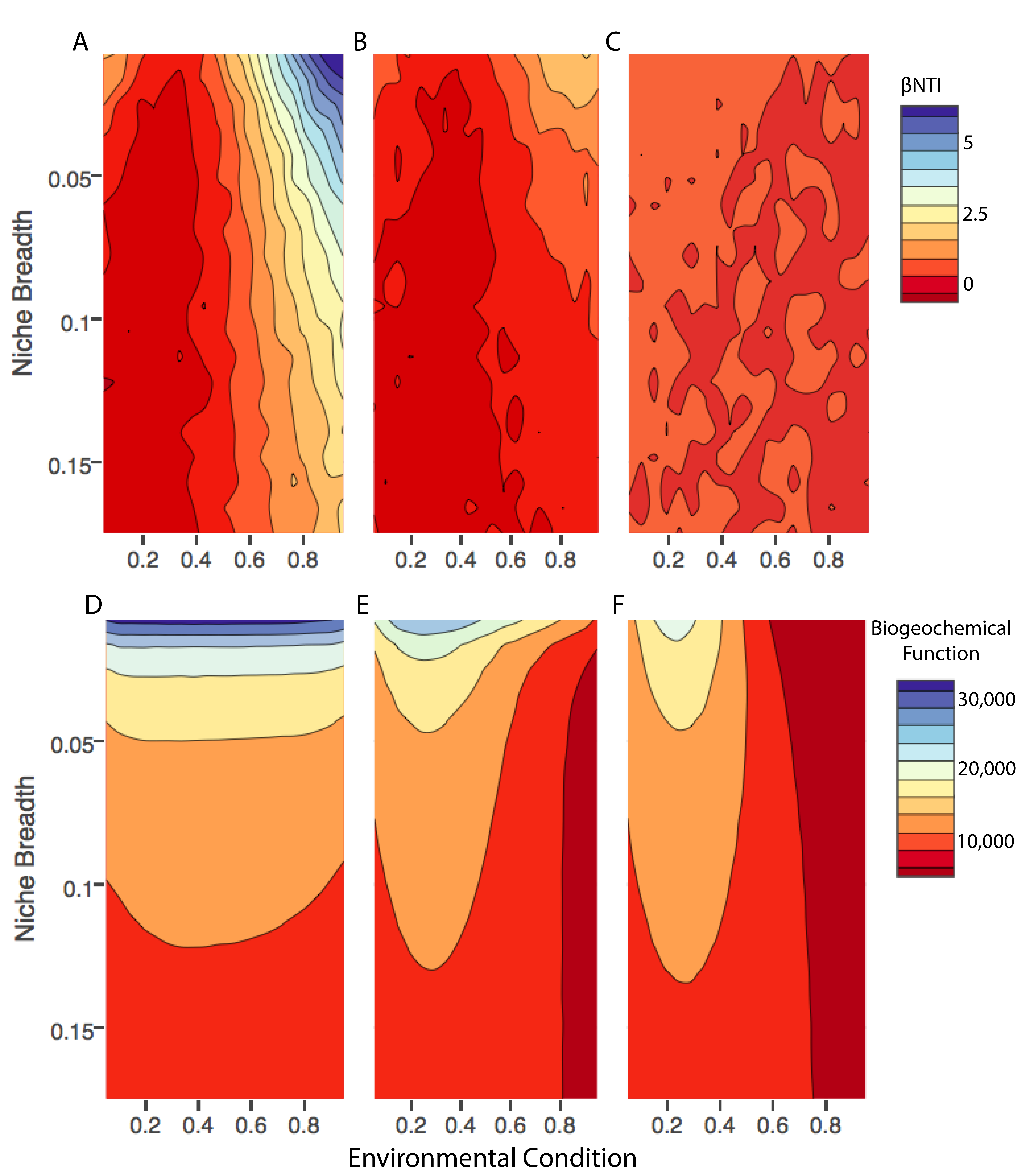
3.1. Microbial Community Composition in Response to Dispersal
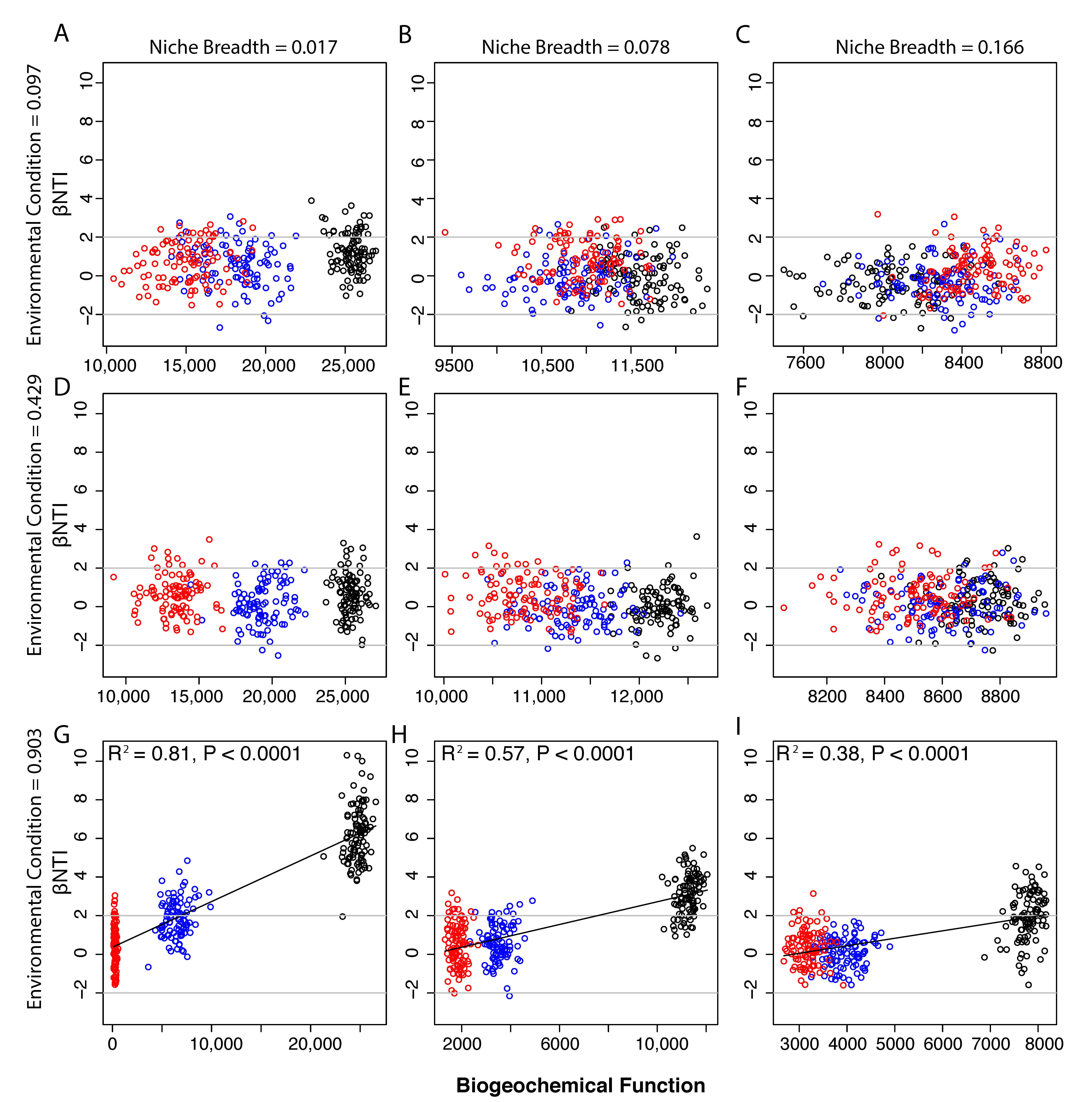
3.2. Dispersal, Microbial Community Composition, and Biogeochemical Function
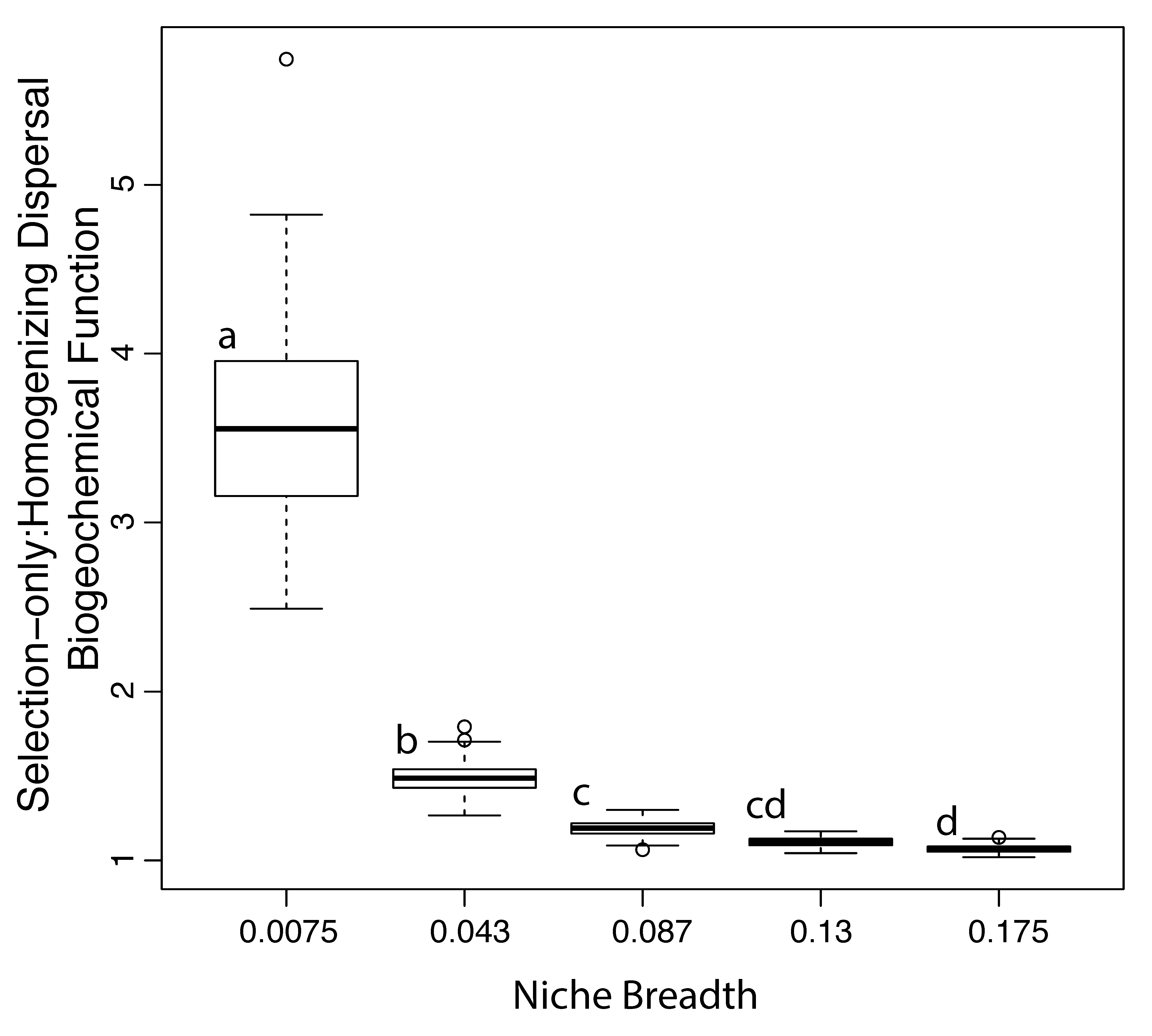
3.3. Impact of Assembly Processes on Biogeochemical Function
3.4. Implications for Ecosystem Models
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wallenstein, M.D.; Hall, E.K. A trait-based framework for predicting when and where microbial adaptation to climate change will affect ecosystem functioning. Biogeochemistry 2012, 109, 35–47. [Google Scholar] [CrossRef]
- Graham, E.B.; Crump, A.R.; Resch, C.T.; Fansler, S.; Arntzen, E.; Kennedy, D.W.; Fredrickson, J.K.; Stegen, J.C. Coupling spatiotemporal community assembly processes to changes in microbial metabolism. Front. Microbiol. 2016, 7, 1949. [Google Scholar] [CrossRef] [PubMed]
- Graham, E.B.; Knelman, J.E.; Schindlbacher, A.; Siciliano, S.; Breulmann, M.; Yannarell, A.; Beman, J.; Abell, G.; Philippot, L.; Prosser, J. Microbes as engines of ecosystem function: When does community structure enhance predictions of ecosystem processes? Front. Microbiol. 2016, 7, 214. [Google Scholar] [CrossRef] [PubMed]
- Martiny, J.B.; Jones, S.E.; Lennon, J.T.; Martiny, A.C. Microbiomes in light of traits: A phylogenetic perspective. Science 2015, 350, aac9323. [Google Scholar] [CrossRef] [PubMed]
- Bier, R.L.; Bernhardt, E.S.; Boot, C.M.; Graham, E.B.; Hall, E.K.; Lennon, J.T.; Nemergut, D.R.; Osborne, B.B.; Ruiz-González, C.; Schimel, J.P. Linking microbial community structure and microbial processes: An empirical and conceptual overview. FEMS Microbiol. Ecol. 2015, 91. [Google Scholar] [CrossRef] [PubMed]
- Rocca, J.D.; Hall, E.K.; Lennon, J.T.; Evans, S.E.; Waldrop, M.P.; Cotner, J.B.; Nemergut, D.R.; Graham, E.B.; Wallenstein, M.D. Relationships between protein-encoding gene abundance and corresponding process are commonly assumed yet rarely observed. ISME J. 2015, 9, 1693. [Google Scholar] [CrossRef] [PubMed]
- Nemergut, D.R.; Schmidt, S.K.; Fukami, T.; O'Neill, S.P.; Bilinski, T.M.; Stanish, L.F.; Knelman, J.E.; Darcy, J.L.; Lynch, R.C.; Wickey, P. Patterns and processes of microbial community assembly. Microbiol. Mol. Biol. Rev. 2013, 77, 342–356. [Google Scholar] [CrossRef] [PubMed]
- Nemergut, D.R.; Shade, A.; Violle, C. When, where and how does microbial community composition matter? Front. Microbiol. 2014, 5, 497. [Google Scholar] [CrossRef] [PubMed]
- Pholchan, M.K.; Baptista, J.D.C.; Davenport, R.J.; Sloan, W.T.; Curtis, T.P. Microbial community assembly, theory and rare functions. Front. Microbiol. 2013, 4, 68. [Google Scholar] [CrossRef] [PubMed]
- Cardinale, B.J.; Wright, J.P.; Cadotte, M.W.; Carroll, I.T.; Hector, A.; Srivastava, D.S.; Loreau, M.; Weis, J.J. Impacts of plant diversity on biomass production increase through time because of species complementarity. Proc. Natl. Acad. Sci. USA 2007, 104, 18123–18128. [Google Scholar] [CrossRef] [PubMed]
- Cadotte, M.W.; Carscadden, K.; Mirotchnick, N. Beyond species: Functional diversity and the maintenance of ecological processes and services. J. Appl. Ecol. 2011, 48, 1079–1087. [Google Scholar] [CrossRef]
- Cadotte, M.W. Dispersal and species diversity: A meta-analysis. Am. Nat. 2006, 167, 913–924. [Google Scholar] [PubMed]
- Cardinale, B.J. Biodiversity improves water quality through niche partitioning. Nature 2011, 472, 86. [Google Scholar] [CrossRef] [PubMed]
- Graham, E.B.; Crump, A.R.; Resch, C.T.; Fansler, S.; Arntzen, E.; Kennedy, D.W.; Fredrickson, J.K.; Stegen, J.C. Deterministic influences exceed dispersal effects on hydrologically-connected microbiomes. Environ. Microbiol. 2017, 19, 1552–1567. [Google Scholar] [CrossRef] [PubMed]
- Stegen, J.C.; Lin, X.; Fredrickson, J.K.; Konopka, A.E. Estimating and mapping ecological processes influencing microbial community assembly. Front. Microbiol. 2015, 6, 370. [Google Scholar] [CrossRef] [PubMed]
- Vellend, M. Conceptual synthesis in community ecology. Q. Rev. Biol. 2010, 85, 183–206. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Ning, D. Stochastic community assembly: Does it matter in microbial ecology? Microbiol. Mol. Biol. Rev. 2017, 81, e00002–e00017. [Google Scholar] [CrossRef] [PubMed]
- Leibold, M.A.; Holyoak, M.; Mouquet, N.; Amarasekare, P.; Chase, J.M.; Hoopes, M.F.; Holt, R.D.; Shurin, J.B.; Law, R.; Tilman, D. The metacommunity concept: A framework for multi-scale community ecology. Ecol. Lett. 2004, 7, 601–613. [Google Scholar] [CrossRef]
- Tilman, D.; Lehman, C.L.; Bristow, C.E. Diversity-stability relationships: Statistical inevitability or ecological consequence? Am. Nat. 1998, 151, 277–282. [Google Scholar] [PubMed]
- Doak, D.F.; Bigger, D.; Harding, E.; Marvier, M.; O'malley, R.; Thomson, D. The statistical inevitability of stability-diversity relationships in community ecology. Am. Nat. 1998, 151, 264–276. [Google Scholar] [PubMed]
- Tilman, D. The ecological consequences of changes in biodiversity: A search for general principles. Ecology 1999, 80, 1455–1474. [Google Scholar] [CrossRef]
- Strickland, M.S.; Lauber, C.; Fierer, N.; Bradford, M.A. Testing the functional significance of microbial community composition. Ecology 2009, 90, 441–451. [Google Scholar] [CrossRef] [PubMed]
- Pulliam, H.R. Sources, sinks, and population regulation. Am. Nat. 1988, 132, 652–661. [Google Scholar] [CrossRef]
- Shmida, A.; Wilson, M.V. Biological determinants of species diversity. J. Biogeogr. 1985, 12, 1–20. [Google Scholar] [CrossRef]
- Fierer, N.; Jackson, R.B. The diversity and biogeography of soil bacterial communities. Proc. Natl. Acad. Sci. USA 2006, 103, 626–631. [Google Scholar] [CrossRef] [PubMed]
- Hollister, E.B.; Engledow, A.S.; Hammett, A.J.M.; Provin, T.L.; Wilkinson, H.H.; Gentry, T.J. Shifts in microbial community structure along an ecological gradient of hypersaline soils and sediments. ISME J. 2010, 4, 829. [Google Scholar] [CrossRef] [PubMed]
- Casamayor, E.O.; Massana, R.; Benlloch, S.; Øvreås, L.; Díez, B.; Goddard, V.J.; Gasol, J.M.; Joint, I.; Rodríguez-Valera, F.; Pedrós-Alió, C. Changes in archaeal, bacterial and eukaryal assemblages along a salinity gradient by comparison of genetic fingerprinting methods in a multipond solar saltern. Environ. Microbiol. 2002, 4, 338–348. [Google Scholar] [CrossRef] [PubMed]
- Gotelli, N.J.; Graves, G.R. Null models in ecology. Ecology 1996, 78, 189–211. [Google Scholar]
- Cadotte, M.W.; Tucker, C.M. Should environmental filtering be abandoned? Trends Ecol. Evol. 2017, 32, 429–437. [Google Scholar] [CrossRef] [PubMed]
- Hurlbert, A.H.; Stegen, J.C. When should species richness be energy limited, and how would we know? Ecol. Lett. 2014, 17, 401–413. [Google Scholar] [CrossRef] [PubMed]
- Stegen, J.C.; Lin, X.; Fredrickson, J.K.; Chen, X.; Kennedy, D.W.; Murray, C.J.; Rockhold, M.L.; Konopka, A. Quantifying community assembly processes and identifying features that impose them. ISME J. 2013, 7, 2069. [Google Scholar] [CrossRef] [PubMed]
- Stegen, J.C.; Lin, X.; Konopka, A.E.; Fredrickson, J.K. Stochastic and deterministic assembly processes in subsurface microbial communities. ISME J. 2012, 6, 1653. [Google Scholar] [CrossRef] [PubMed]
- Stegen, J.C.; Hurlbert, A.H. Inferring ecological processes from taxonomic, phylogenetic and functional trait β-diversity. PLoS ONE 2011, 6, e20906. [Google Scholar] [CrossRef] [PubMed]
- Chase, J.M.; Leibold, M.A. Ecological Niches: Linking Classical and Contemporary Approaches; University of Chicago Press: Chicago, IL, USA, 2003. [Google Scholar]
- Webb, C.O.; Ackerly, D.D.; Kembel, S.W. Phylocom: Software for the analysis of phylogenetic community structure and trait evolution. Bioinformatics 2008, 24, 2098–2100. [Google Scholar] [CrossRef] [PubMed]
- Fine, P.V.; Kembel, S.W. Phylogenetic community structure and phylogenetic turnover across space and edaphic gradients in western amazonian tree communities. Ecography 2011, 34, 552–565. [Google Scholar] [CrossRef]
- Dini-Andreote, F.; Stegen, J.C.; van Elsas, J.D.; Salles, J.F. Disentangling mechanisms that mediate the balance between stochastic and deterministic processes in microbial succession. Proc. Natl. Acad. Sci. USA 2015, 112, E1326–E1332. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Shen, J.; Wu, Y.; Tu, C.; Soininen, J.; Stegen, J.C.; He, J.; Liu, X.; Zhang, L.; Zhang, E. Phylogenetic beta diversity in bacterial assemblages across ecosystems: Deterministic versus stochastic processes. ISME J. 2013, 7, 1310. [Google Scholar] [CrossRef] [PubMed]
- Jurburg, S.D.; Nunes, I.; Stegen, J.C.; Le Roux, X.; Priemé, A.; Sørensen, S.J.; Salles, J.F. Autogenic succession and deterministic recovery following disturbance in soil bacterial communities. Sci. Rep. 2017, 7, 45691. [Google Scholar] [CrossRef] [PubMed]
- Veach, A.M.; Stegen, J.C.; Brown, S.P.; Dodds, W.K.; Jumpponen, A. Spatial and successional dynamics of microbial biofilm communities in a grassland stream ecosystem. Mol. Ecol. 2016, 25, 4674–4688. [Google Scholar] [CrossRef] [PubMed]
- Hill, M.O. Diversity and evenness: A unifying notation and its consequences. Ecology 1973, 54, 427–432. [Google Scholar] [CrossRef]
- Morris, E.K.; Caruso, T.; Buscot, F.; Fischer, M.; Hancock, C.; Maier, T.S.; Meiners, T.; Müller, C.; Obermaier, E.; Prati, D. Choosing and using diversity indices: Insights for ecological applications from the german biodiversity exploratories. Ecol. Evol. 2014, 4, 3514–3524. [Google Scholar] [CrossRef] [PubMed]
- Oksanen, J.; Blanchet, F.G.; Kindt, R.; Legendre, P.; Minchin, P.R.; O’hara, R.; Simpson, G.L.; Solymos, P.; Stevens, M.H.H.; Wagner, H.; et al. Package ‘vegan’. Community ecology package, version 2.4-4. Available online: https://cran.r-project.org/web/packages/vegan/index.html (accessed on 24 August 2017).
- Buchkowski, R.W.; Bradford, M.A.; Grandy, A.S.; Schmitz, O.J.; Wieder, W.R. Applying population and community ecology theory to advance understanding of belowground biogeochemistry. Ecol. Lett. 2017, 20, 231–245. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Jagadamma, S.; Mayes, M.A.; Schadt, C.W.; Steinweg, J.M.; Gu, L.; Post, W.M. Microbial dormancy improves development and experimental validation of ecosystem model. ISME J. 2015, 9, 226. [Google Scholar] [CrossRef] [PubMed]
- Wieder, W.; Grandy, A.; Kallenbach, C.; Taylor, P.; Bonan, G. Representing life in the earth system with soil microbial functional traits in the mimics model. Geosci. Model Dev. 2015, 8, 1789–1808. [Google Scholar] [CrossRef]
- Connell, J.H. Diversity in tropical rain forests and coral reefs. Science 1978, 199, 1302–1310. [Google Scholar] [CrossRef] [PubMed]
- DeAngelis, K.M.; Silver, W.L.; Thompson, A.W.; Firestone, M.K. Microbial communities acclimate to recurring changes in soil redox potential status. Environ. Microbiol. 2010, 12, 3137–3149. [Google Scholar] [CrossRef] [PubMed]
- Cregger, M.A.; Schadt, C.W.; McDowell, N.G.; Pockman, W.T.; Classen, A.T. Response of the soil microbial community to changes in precipitation in a semiarid ecosystem. Appl. Environ. Microbiol. 2012, 78, 8587–8594. [Google Scholar] [CrossRef] [PubMed]
- Green, J.; Bohannan, B.J. Spatial scaling of microbial biodiversity. Trends Ecol. Evol. 2006, 21, 501–507. [Google Scholar] [CrossRef] [PubMed]
- Schimel, D.S.; Braswell, B.; McKeown, R.; Ojima, D.S.; Parton, W.; Pulliam, W. Climate and nitrogen controls on the geography and timescales of terrestrial biogeochemical cycling. Glob. Biogeochem. Cycles 1996, 10, 677–692. [Google Scholar] [CrossRef]
- Hawkes, C.V.; Keitt, T.H. Resilience vs. Historical contingency in microbial responses to environmental change. Ecol. Lett. 2015, 18, 612–625. [Google Scholar] [CrossRef] [PubMed]
- Wilson, D.S.; Yoshimura, J. On the coexistence of specialists and generalists. Am. Nat. 1994, 144, 692–707. [Google Scholar] [CrossRef]
- Kassen, R. The experimental evolution of specialists, generalists, and the maintenance of diversity. J. Evolut. Biol. 2002, 15, 173–190. [Google Scholar] [CrossRef]
- Lennon, J.T.; Aanderud, Z.T.; Lehmkuhl, B.; Schoolmaster, D.R. Mapping the niche space of soil microorganisms using taxonomy and traits. Ecology 2012, 93, 1867–1879. [Google Scholar] [CrossRef] [PubMed]
- Shade, A.; Peter, H.; Allison, S.D.; Baho, D.L.; Berga, M.; Bürgmann, H.; Huber, D.H.; Langenheder, S.; Lennon, J.T.; Martiny, J.B. Fundamentals of microbial community resistance and resilience. Front. Microbiol. 2012, 3, 417. [Google Scholar] [CrossRef] [PubMed]
- Mou, X.; Sun, S.; Edwards, R.A.; Hodson, R.E.; Moran, M.A. Bacterial carbon processing by generalist species in the coastal ocean. Nature 2008, 451, 708. [Google Scholar] [CrossRef] [PubMed]
- Langenheder, S.; Lindström, E.S.; Tranvik, L.J. Weak coupling between community composition and functioning of aquatic bacteria. Limnol. Oceanogr. 2005, 50, 957–967. [Google Scholar] [CrossRef]
- Allison, S.D.; Martiny, J.B. Resistance, resilience, and redundancy in microbial communities. Proc. Natl. Acad. Sci. USA 2008, 105, 11512–11519. [Google Scholar] [CrossRef] [PubMed]
- Stegen, J.C.; Fredrickson, J.K.; Wilkins, M.J.; Konopka, A.E.; Nelson, W.C.; Arntzen, E.V.; Chrisler, W.B.; Chu, R.K.; Danczak, R.E.; Fansler, S.J. Groundwater–surface water mixing shifts ecological assembly processes and stimulates organic carbon turnover. Nat. Commun. 2016, 7, 11237. [Google Scholar] [CrossRef] [PubMed]
- Cardinale, B.J.; Matulich, K.L.; Hooper, D.U.; Byrnes, J.E.; Duffy, E.; Gamfeldt, L.; Balvanera, P.; O’Connor, M.I.; Gonzalez, A. The functional role of producer diversity in ecosystems. Am. J. Bot. 2011, 98, 572–592. [Google Scholar] [CrossRef] [PubMed]
- Hooper, D.U.; Adair, E.C.; Cardinale, B.J.; Byrnes, J.E.; Hungate, B.A.; Matulich, K.L.; Gonzalez, A.; Duffy, J.E.; Gamfeldt, L.; O’Connor, M.I. A global synthesis reveals biodiversity loss as a major driver of ecosystem change. Nature 2012, 486, 105–108. [Google Scholar] [CrossRef] [PubMed]
- Bell, T.; Newman, J.A.; Silverman, B.W.; Turner, S.L.; Lilley, A.K. The contribution of species richness and composition to bacterial services. Nature 2005, 436, 1157. [Google Scholar] [CrossRef] [PubMed]
- Langenheder, S.; Bulling, M.T.; Solan, M.; Prosser, J.I. Bacterial biodiversity-ecosystem functioning relations are modified by environmental complexity. PLoS ONE 2010, 5, e10834. [Google Scholar] [CrossRef] [PubMed]
- Levine, U.Y.; Teal, T.K.; Robertson, G.P.; Schmidt, T.M. Agriculture’s impact on microbial diversity and associated fluxes of carbon dioxide and methane. ISME J. 2011, 5, 1683. [Google Scholar] [CrossRef] [PubMed]
- Knelman, J.E.; Nemergut, D.R. Changes in community assembly may shift the relationship between biodiversity and ecosystem function. Front. Microbiol. 2014, 5, 424. [Google Scholar] [CrossRef] [PubMed]
- Tilman, D.; Reich, P.B.; Knops, J.; Wedin, D.; Mielke, T.; Lehman, C. Diversity and productivity in a long-term grassland experiment. Science 2001, 294, 843–845. [Google Scholar] [CrossRef] [PubMed]
- Evans, S.E.; Wallenstein, M.D. Soil microbial community response to drying and rewetting stress: Does historical precipitation regime matter? Biogeochemistry 2012, 109, 101–116. [Google Scholar] [CrossRef]
- Fukami, T. Historical contingency in community assembly: Integrating niches, species pools, and priority effects. Annu. Rev. Ecol. Evol. Syst. 2015, 46, 1–23. [Google Scholar] [CrossRef]
- Wang, G.; Post, W.M.; Mayes, M.A. Development of microbial-enzyme-mediated decomposition model parameters through steady-state and dynamic analyses. Ecol. Appl. 2013, 23, 255–272. [Google Scholar] [CrossRef] [PubMed]
- Wieder, W.; Grandy, A.; Kallenbach, C.; Bonan, G. Integrating microbial physiology and physio-chemical principles in soils with the microbial-mineral carbon stabilization (mimics) model. Biogeosciences 2014, 11, 3899–3917. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Graham, E.B.; Stegen, J.C. Dispersal-Based Microbial Community Assembly Decreases Biogeochemical Function. Processes 2017, 5, 65. https://doi.org/10.3390/pr5040065
Graham EB, Stegen JC. Dispersal-Based Microbial Community Assembly Decreases Biogeochemical Function. Processes. 2017; 5(4):65. https://doi.org/10.3390/pr5040065
Chicago/Turabian StyleGraham, Emily B., and James C. Stegen. 2017. "Dispersal-Based Microbial Community Assembly Decreases Biogeochemical Function" Processes 5, no. 4: 65. https://doi.org/10.3390/pr5040065
APA StyleGraham, E. B., & Stegen, J. C. (2017). Dispersal-Based Microbial Community Assembly Decreases Biogeochemical Function. Processes, 5(4), 65. https://doi.org/10.3390/pr5040065




