Development of Molecular Distillation Based Simulation and Optimization of Refined Palm Oil Process Based on Response Surface Methodology
Abstract
1. Introduction
2. Molecular Distillation Process: Modeling and Validation
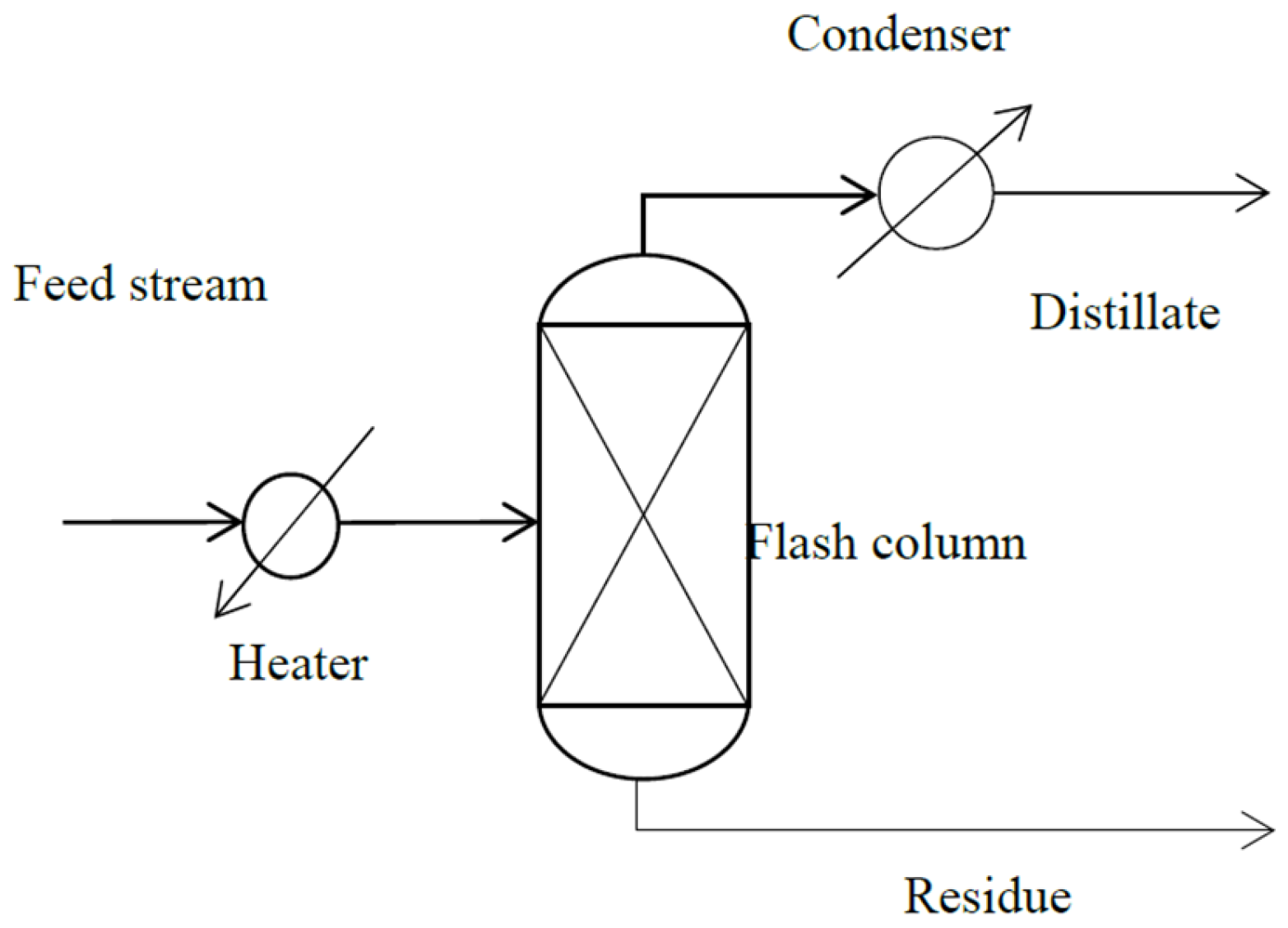
3. Refined Palm Oil Deodorization Process Simulation by ASPEN HYSYS
3.1. Vapor Pressure Estimation
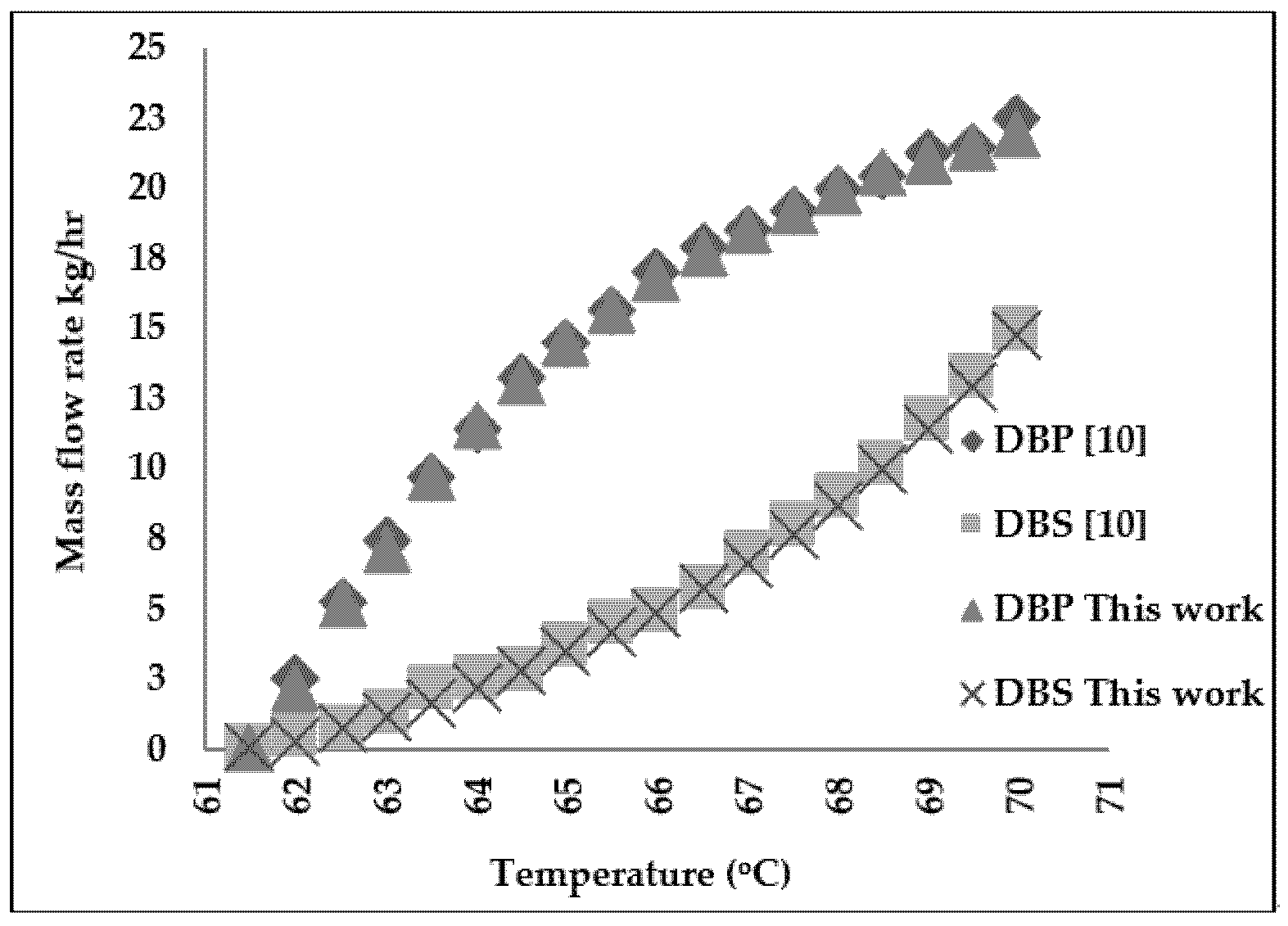
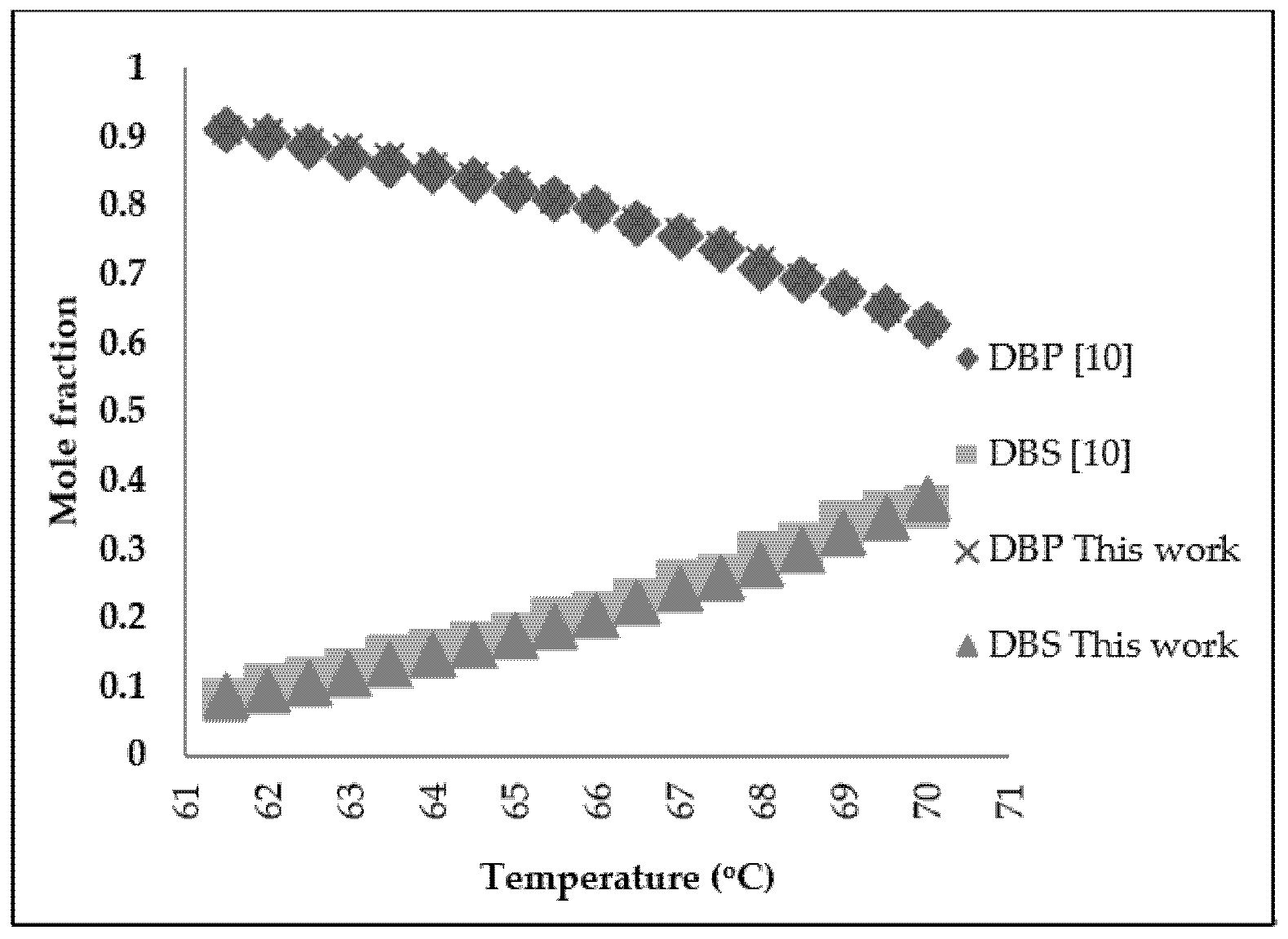
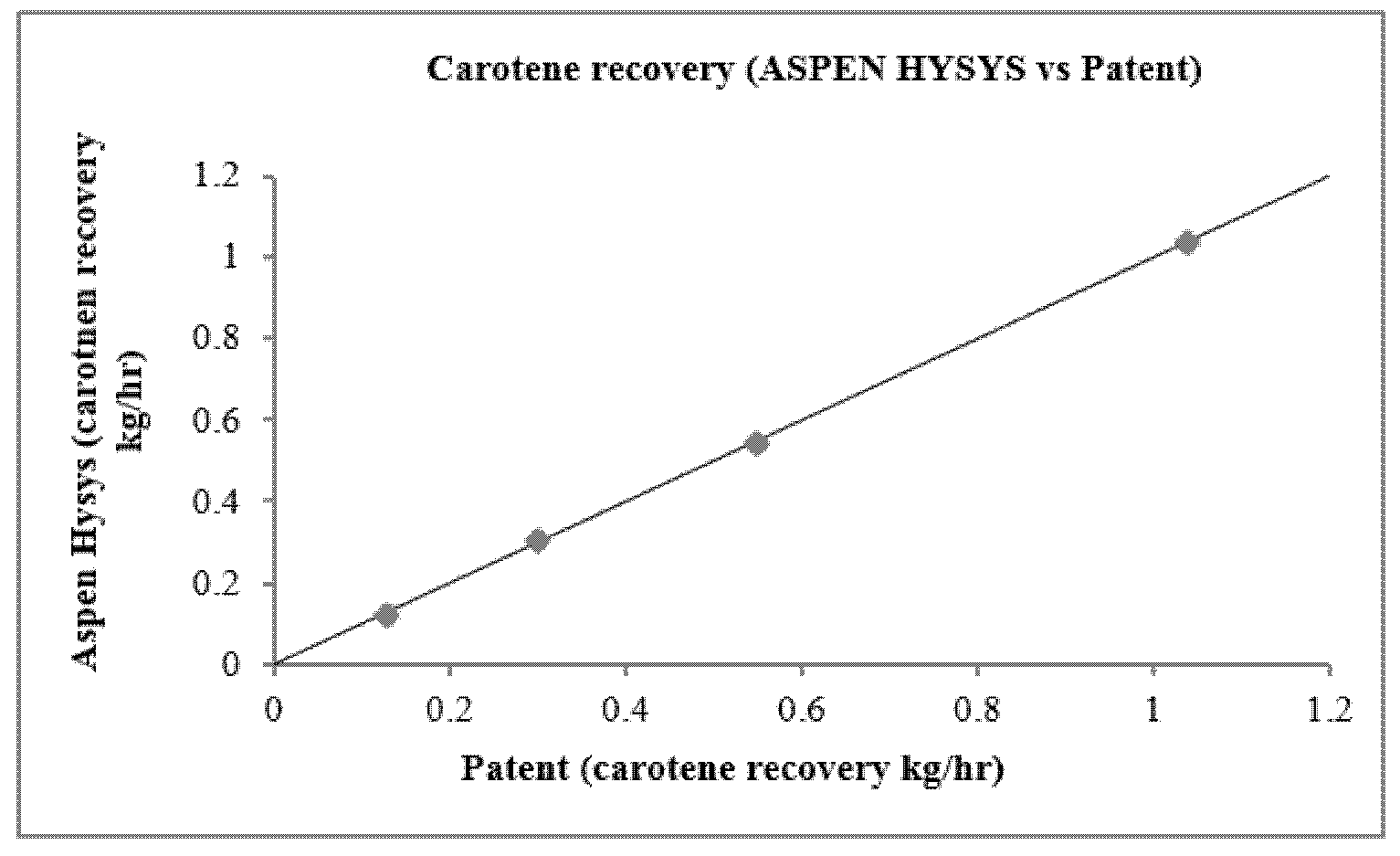
3.2. Refined Palm Oil Deodorization Process Simulation and Validation
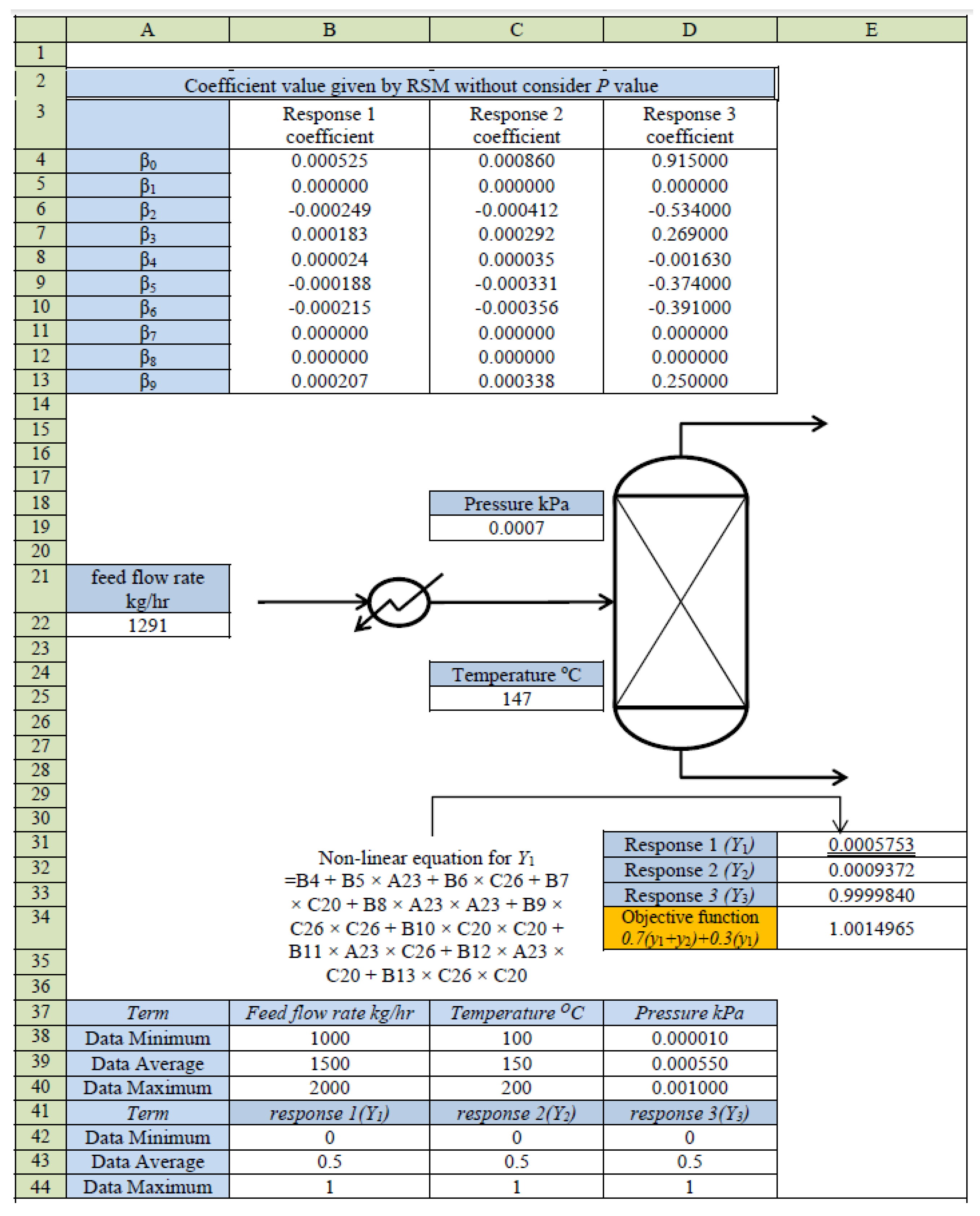
4. RSM-Based Process Model
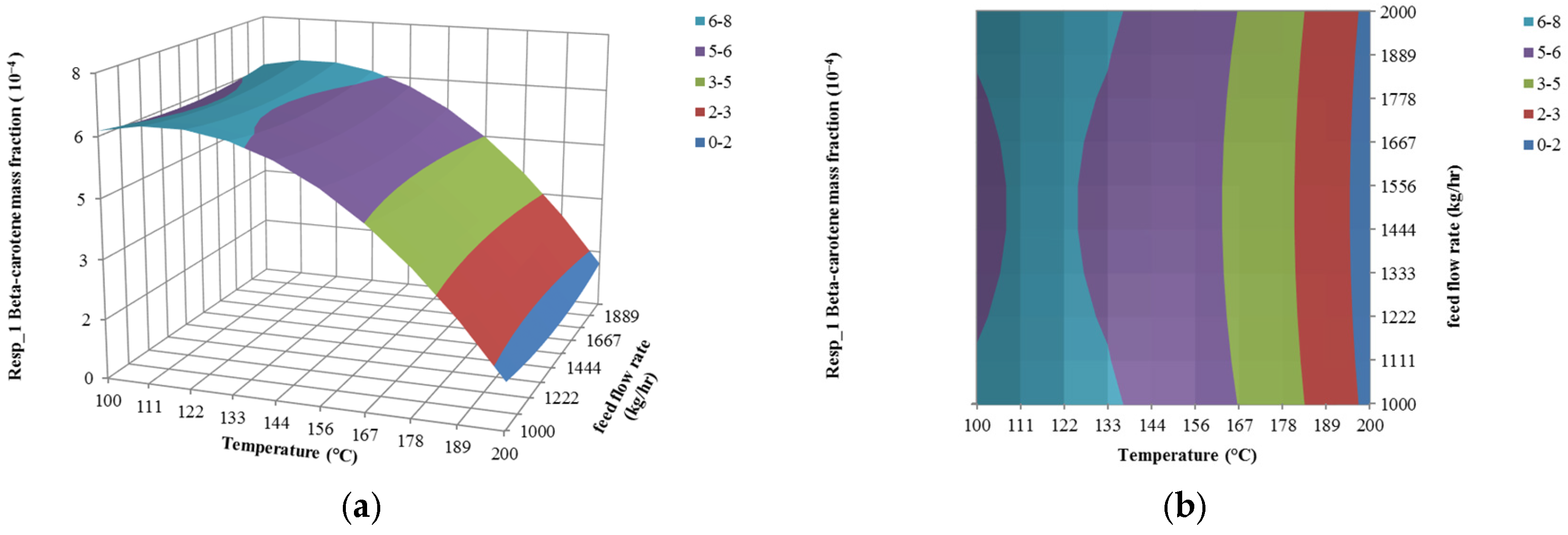
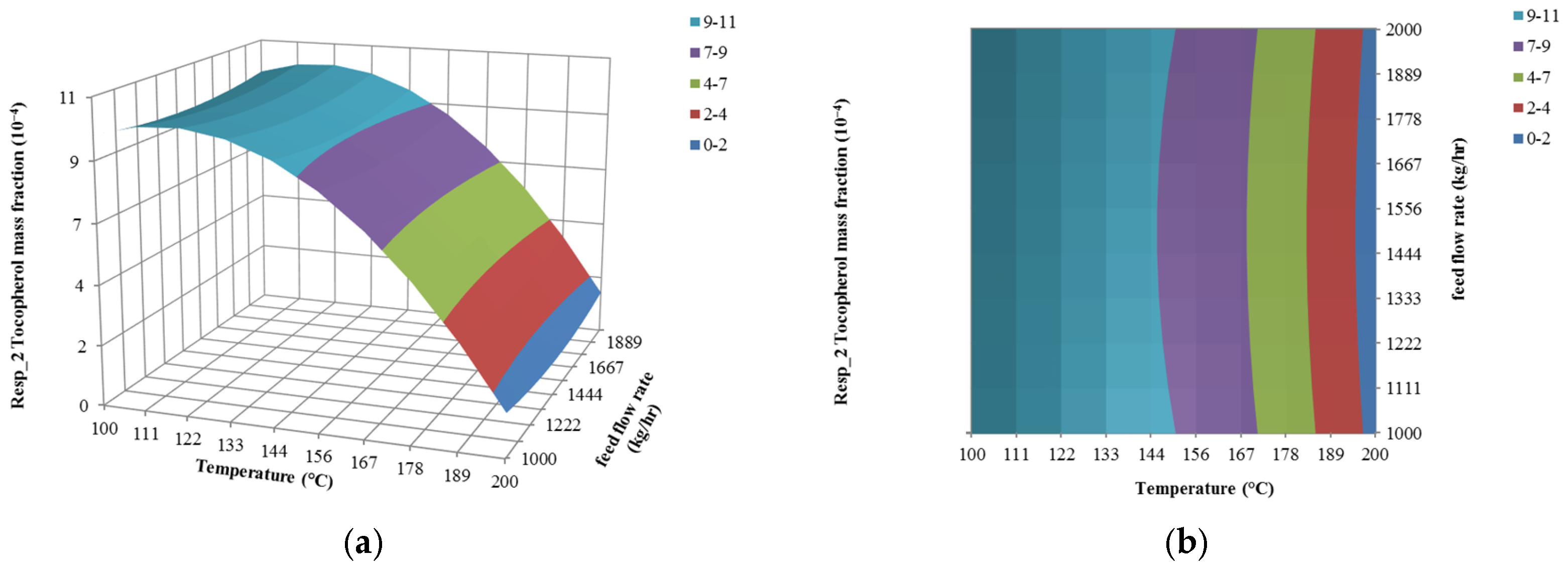
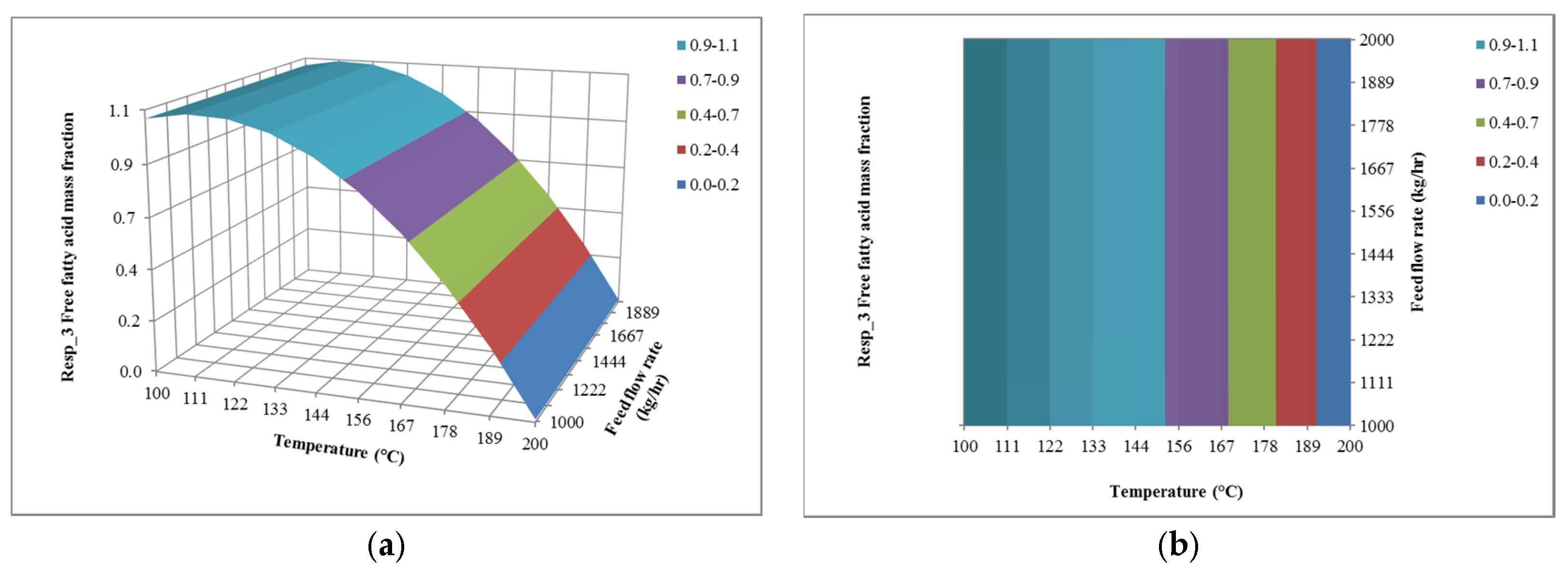
4.1. The Effect of Feed Flow Rate on Responses
4.2. The Effect of Temperature on Responses
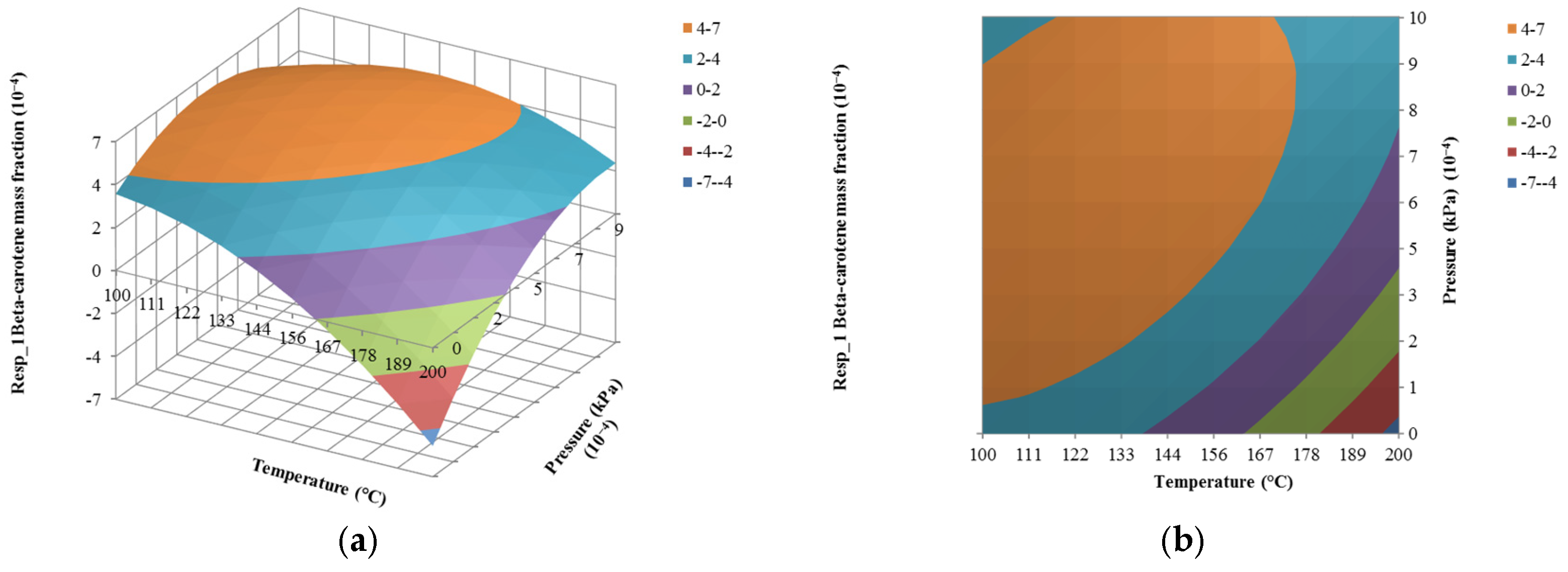
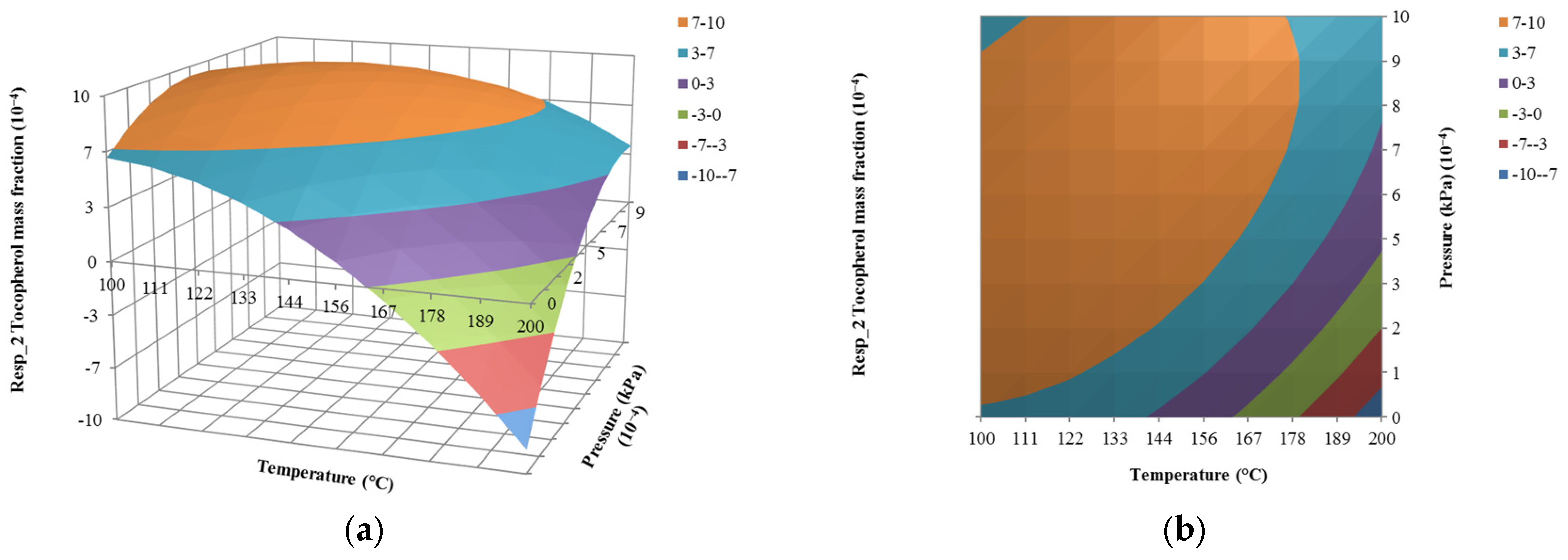
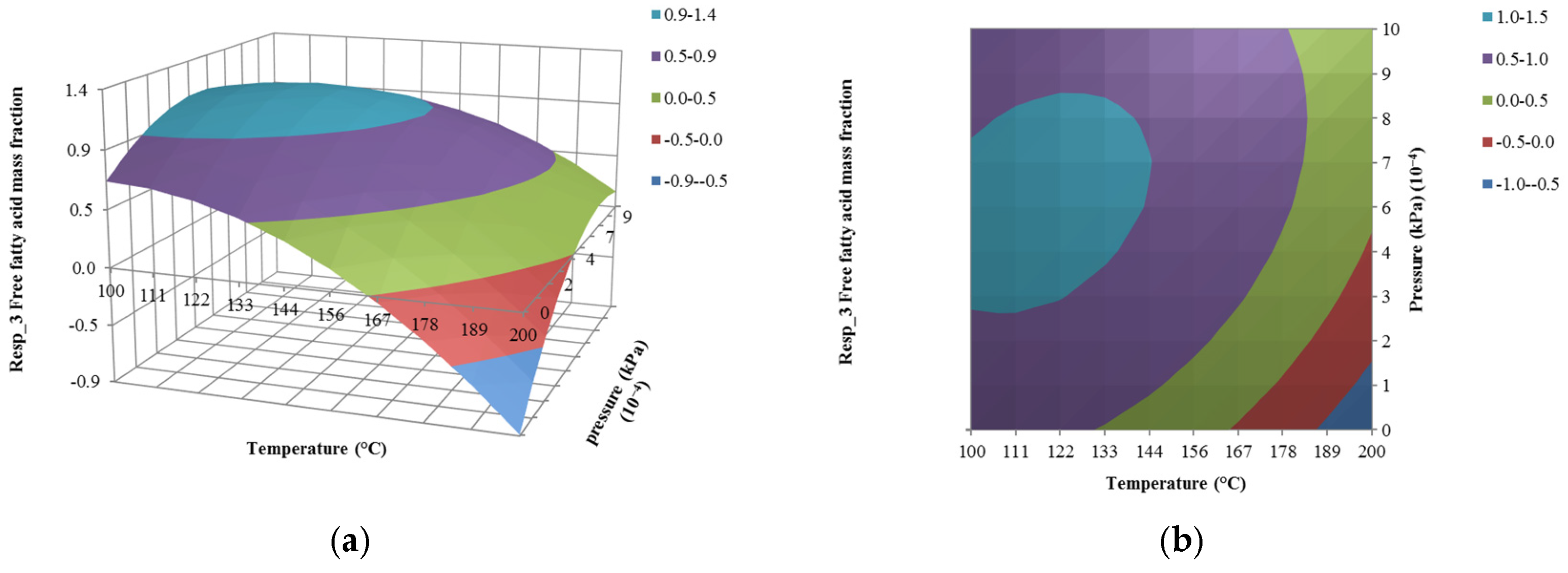
4.3. The Effect of Pressure on Responses
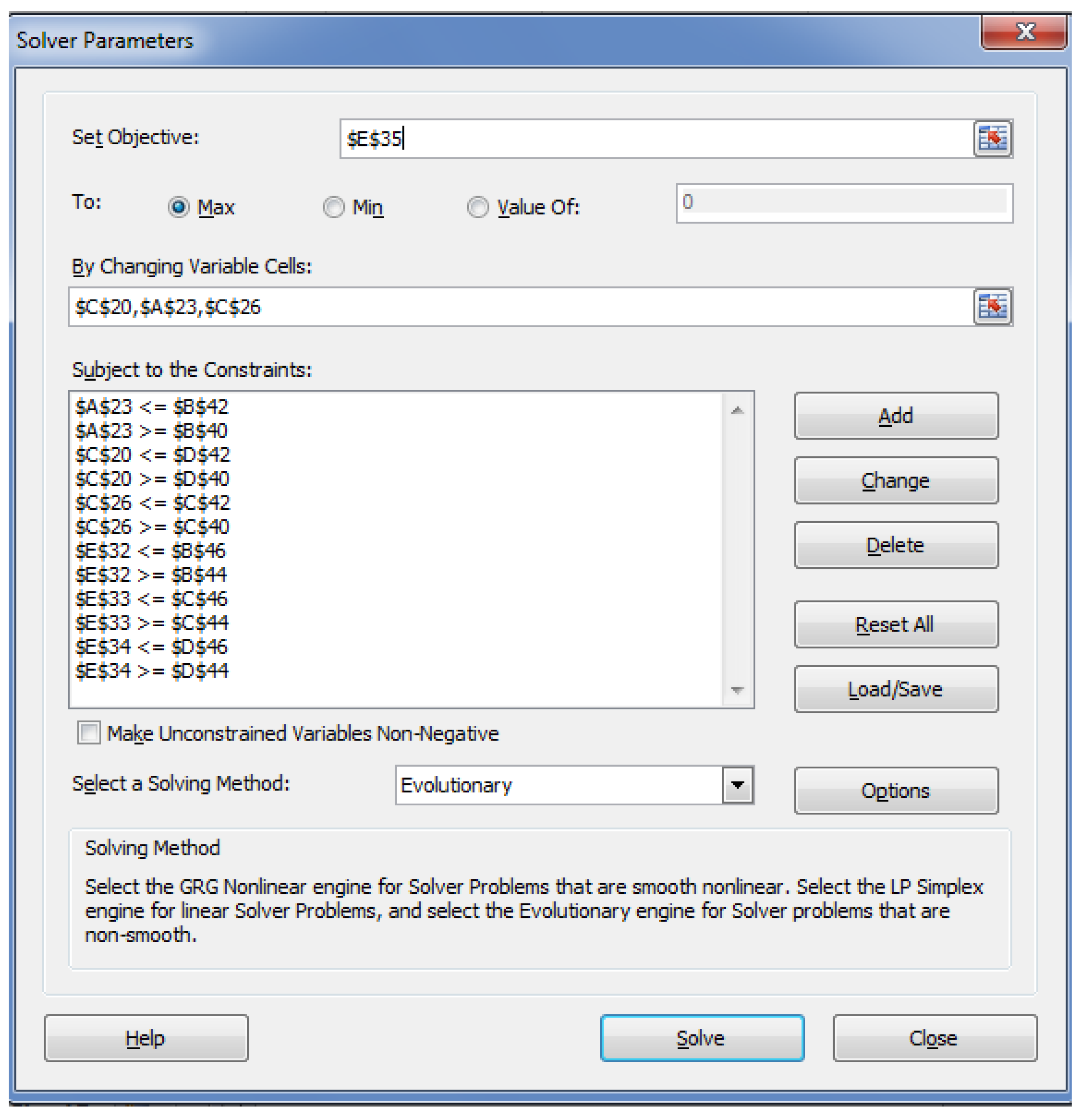
5. Optimization of MD for Refined Palm Oil Process
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
| Component | TB (K) | TC (K) | PC (kPa) | ω | Vl20 (m3/kmol) |
|---|---|---|---|---|---|
| Tripalmitin | 864.21 | 947.10 | 396.82 | 1.6500 | 0.8906 |
| Triolein | 879.92 | 954.10 | 360.15 | 1.8004 | 0.9717 |
| Oleic acid | 646.52 | 813.56 | 1250.2 | 0.8104 | 0.3172 |
| Tocopherol | 794.52 | 936.93 | 838.45 | 1.1946 | 0.4533 |
| Beta-carotene | 908.58 | 1031.1 | 678.41 | 1.6255 | 0.5348 |
References
- Nagendran, B.; Unnithan, U.R.; Choo, Y.M.; Sundram, K. Characteristics of red palm oil, a carotene and vitamin E rich refined oil for food uses. Food Nutr. Bull. 2000, 21, 189–194. [Google Scholar] [CrossRef]
- Rohani, O.; Sharifah, S.A.; MohdRafii, Y.; Ong, M.; Tarmizi, A.H.; Zamzuri, I. Advances in oil palm Research. Adv. oil palm res. 2000, 1, 238–331. [Google Scholar]
- Batistella, C.B.; Maciel, M.R.W. Recovery of caroteniods from palm oil by molecular distillation. Comput. Chem. Eng. 1998, 22, 53–60. [Google Scholar] [CrossRef]
- Huang, H.-J.; Ramaswamy, S.; Tschirner, U.W.; Ramarao, B.V. A review of separation technologies in current and future bio refineries. Sep. Purif. Technol. 2008, 62, 1–21. [Google Scholar] [CrossRef]
- Casilio, D.; Dunford, N.T. Nutritionally Enhanced Edible Oil and Oilseed Processing; AOCS Press: Champaign, IL, USA, 2004; pp. 178–192. [Google Scholar]
- Chen, F.; Cai, T.; Zhao, G.; Liao, X.; Guo, L.; Hu, X. Optimization conditions for the purification of crude octacosanol extract from rice bran wax by molecular distillation analyzed using response surface methodology. J. Food Eng. 2004, 70, 47–53. [Google Scholar] [CrossRef]
- Jiang, S.T.; Shao, P.; Pan, L.J.; Zhao, Y.Y. Molecular distillation for recovering tocopherol and fatty acid methyl ester from rapeseed oil deodorizer distillate. Biosyst. Eng. 2006, 93, 383–391. [Google Scholar] [CrossRef]
- Wu, W.; Wang, C.; Zheng, J. Optimization of deacidification of low calorie cocoa butter by molecular distillation. Food Sci. Technol. 2011, 46, 563–570. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, J.; Liu, Y. Concentraton of omega 3 polyunsaturated fatty acid from oil of schizochytrium limacinum by molecular distillation: Optimization of techonological condition. Ind. Eng. Chem. Res. 2013, 52, 3918–3925. [Google Scholar]
- Mallmann, E.S.; Costa, C.B.B.; Maciel, M.R.W.; Filho, M.R. Development of a Computational Tool for simulating falling film molecular design. Comput. Aided Chem. Eng. 2009, 26, 743–748. [Google Scholar]
- Unnikrishnan, R. Refining of Edible Oil Rich in Natural Carotenes and Vitamin E. United State Patent 6,177,114 B1, 23 January 2001. [Google Scholar]
- Aspen Technology Aspen Plus User Guide. Available online: https://web.ist.utl.pt/ist11038/acad/Aspen/AspUserGuide10.pdf (accessed on 7 July 2017).
- Lim, C.S.; Manan, Z.A.; Sarmidi, M.R. Simulation Modeling of the Phase Behavior of Palm Oil-Supercritical Carbon Dioxide. JAOCS 2003, 80, 1147–1156. [Google Scholar] [CrossRef]
- Kalil, S.J.; Mauger, F.; Rodrigues, M.I. Response Surface Analysis and Simulation as a Tool for Bioprocess Design and Optimization. Process Biochem. 1999, 35, 539–550. [Google Scholar]
- Wang, H.; Cui, X. Response Surface Optimization of the Operating Parameters for a Complex Distillation Column Based on Process Simulation. Energy Procedia 2012, 16, 571–578. [Google Scholar] [CrossRef][Green Version]
- Khuri, A.I.; Siuli, M. Response Surface Methodology; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- Elhameh, N. Optimal of Gasoline Vacuum Layer Using Response Surface Methodology. Chem. Eng. Technol. 2013, 37, 229–239. [Google Scholar]
- Arora, J.S. Chapter 6 Optimum Design with Excel solve. In Introduction to Optimum Design; Elsevier Inc.: Amsterdam, The Netherlands, 2012; pp. 213–273. [Google Scholar]
| Parameters | DIMSOL | ASPEN PLUS [10] | ASPEN HYSYS (This Work) |
|---|---|---|---|
| Operating temperature (K) | 369 | 336 | 336 |
| Distillation mass ratio | 0.212 | 0.212 | 0.212 |
| Distillation DBP molar fraction | 0.775 | 0.790 | 0.793 |
| Residue DBP molar fraction | 0.429 | 0.409 | 0.420 |
| Components | Mass Fraction | MW | Formula | CAS No. |
|---|---|---|---|---|
| Tripalmitin | 0.493682 | 807.320 | C51H98O6 | 555-44-2 |
| Triolein | 0.470891 | 885.449 | C57H104O6 | 122-32-7 |
| Oleic acid | 0.033899 | 282.467 | C18H34O2 | 112-80-1 |
| Tocopherol | 0.000886 | 430.706 | C29H50O2 | 59-02-9 |
| Beta-carotene | 0.000552 | 536.873 | C40H56 | 7235-40-7 |
| Component | Antoine Parameters | ||||
|---|---|---|---|---|---|
| A1 | B1 | C1 | D1 | E1 | |
| Tripalmitin | 108,841 | −4,098,952 | 19.96 | −17,792 | −3.6 × 10−15 |
| Triolein | −514,215 | 19,737,838 | −91.13 | 83,685 | 1.4 × 10−15 |
| Oleic acid | 136.45 | −19,702 | −0.01 | −14.87 | 7.2 × 10−19 |
| Tocopherol | −15.90 | −5118 | 0.05 | 0 | 0.00 |
| β-carotene | −91.32 | −15.90 | 0.239 | 0 | 0.00 |
| Component | Antoine Parameters | R2 | ||||
|---|---|---|---|---|---|---|
| A2 | B2 | C2 | D2 | E2 | ||
| Tripalmitin | 1.509 × 105 | 1.196 × 105 | −0.074 × 105 | −0.21 × 105 | 0.00 | 0.99 |
| Triolein | −0.013 × 107 | −3.170 × 107 | 0.000 | 0.000 | 0.00 | 0.99 |
| Oleic acid | 519.688 | −0.106 | −399.010 | −71.37 | 0.00 | 0.99 |
| Tocopherol | −64.849 | 594.994 | −219.253 | 13.052 | 0.00 | 0.99 |
| β-carotene | 24.079 | −16,160 | −100.623 | 5.191 | 0.00 | 0.99 |
| Condition | Distillation Mass Ratio | Patent Recovery | Simulation Recovery | Prediction Error | ||
|---|---|---|---|---|---|---|
| kg/h | Percent (%) | kg/h | Percent (%) | (%) | ||
| Simulation 1 | 0.036 | 1.0395 | 95.98% | 1.0351 | 98.96% | 3.1% |
| Simulation 2 | 0.036 | 0.5449 | 98.73% | 0.5467 | 99.03% | 0.3% |
| Simulation 3 | 0.036 | 0.1249 | 98.03% | 0.1266 | 99.29% | 1.218% |
| Simulation 4 | 0.036 | 0.2969 | 97.38% | 0.3258 | 99.25% | 1.87% |
| Coded Variables | |||
|---|---|---|---|
| Run | X1 | X2 | X3 |
| 1 | 0 | 0 | −1 |
| 2 | 0 | 0 | 0 |
| 3 | −1 | 0 | 0 |
| 4 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 |
| 6 | −0.59 | 0.59 | −0.59 |
| 7 | 0 | 0 | 0 |
| 8 | 0.59 | −0.59 | 0.59 |
| 9 | −0.59 | −0.59 | −0.59 |
| 10 | 0.59 | 0.59 | 0.59 |
| 11 | 0 | −1 | 0 |
| 12 | 0.59 | 0.59 | −0.59 |
| 13 | -0.59 | 0.59 | 0.59 |
| 14 | 0.59 | −0.59 | −0.59 |
| 15 | 0 | 0 | 1 |
| 16 | 1 | 0 | 0 |
| 17 | −0.59 | −0.59 | 0.59 |
| Variables | Coded Variables and Design Range | ||||
|---|---|---|---|---|---|
| Feed flow rate (kg/h) | 1000 (−1) | 1203 (−0.59) | 1500 (0) | 1797 (0.59) | 2000 (1) |
| Temperature (°C) | 100 (−1) | 120 (−0.59) | 150 (0) | 180 (0.59) | 200 (1) |
| Pressure (kPa) | 1.00 × 10−5 (−1) | 2.11 × 10−4 (−0.59) | 5.05 × 10−4 (0) | 7.99 × 10−4 (0.59) | 1.00 × 10−3 (1) |
| Run | Input Variables | Composition Mass Fraction (Responses) | ||||
|---|---|---|---|---|---|---|
| x1 (kg/h) | x2 (°C) | x3 (10−4 kPa) | y1 (10−4) | y2 (10−4) | y3 | |
| 1 | 1500 | 150 | 0.10 | 0.28 | 0.54 | 0.09 |
| 2 | 1500 | 150 | 5.05 | 5.27 | 8.62 | 0.91 |
| 3 | 1000 | 150 | 5.05 | 5.27 | 8.62 | 0.91 |
| 4 | 1500 | 150 | 5.05 | 5.27 | 8.62 | 0.91 |
| 5 | 1500 | 200 | 5.05 | 7.27 | 9.63 | 0.08 |
| 6 | 1203 | 180 | 2.11 | 1.13 | 1.73 | 0.12 |
| 7 | 1500 | 150 | 5.05 | 5.27 | 8.62 | 0.91 |
| 8 | 1797 | 120 | 7.99 | 5.64 | 9.07 | 1.00 |
| 9 | 1203 | 120 | 2.11 | 5.57 | 9.04 | 0.99 |
| 10 | 1797 | 180 | 7.99 | 4.07 | 6.45 | 0.48 |
| 11 | 1500 | 100 | 5.05 | 5.57 | 8.95 | 1.00 |
| 12 | 1797 | 180 | 2.11 | 1.13 | 1.73 | 0.12 |
| 13 | 1203 | 180 | 7.99 | 4.07 | 6.45 | 0.48 |
| 14 | 1797 | 120 | 2.11 | 5.57 | 9.04 | 0.99 |
| 15 | 1500 | 150 | 1.00 | 5.48 | 8.89 | 0.96 |
| 16 | 2000 | 150 | 5.05 | 5.27 | 8.62 | 0.91 |
| 17 | 1203 | 120 | 7.99 | 5.64 | 9.07 | 1.00 |
| Term | Coefficient | Coefficient | Coefficient |
|---|---|---|---|
| Constant | 5.25 × 10−4 | 8.60 × 10−4 | 9.15 × 10−1 |
| x1 | 1.35 × 10−20 | 3.49 × 10−20 | −1.27x10−18 |
| x2 | −2.49 × 10−4 | −4.12 × 10−4 | −5.34 × 10−1 |
| x3 | 1.83 × 10−4 | 2.92 × 10−4 | 2.69 × 10−1 |
| x1x1 | 2.42 × 10−5 | 3.54 × 10−5 | −1.63 × 10−3 |
| x2x2 | −1.88 × 10−4 | −3.31 × 10−4 | −3.74 × 10−1 |
| x3x3 | −2.15 × 10−4 | −3.56 × 10−4 | −3.91 × 10−1 |
| x1x2 | 6.88 × 10−21 | −1.38 × 10−20 | 2.82 × 10−17 |
| x1x3 | −1.38 × 10−20 | 9.01 × 10−21 | 2.73 × 10−17 |
| x2x3 | 2.07 × 10−4 | 3.38 × 10−4 | 2.50 × 10−1 |
| Variable Description | Low Bound | High Bound |
|---|---|---|
| Inlet Mass flow rate (kg/h) | 1000 | 2000 |
| Temperature (°C) | 100 | 200 |
| Pressure (kPa) | 0.001 | 0.00001 |
| Components | Responses Result from RSM Model | Responses Result from ASPEN HYSYS Simulation |
|---|---|---|
| Beta-carotene | 0.000554 | 0.000545 |
| Tocopherol | 0.000896 | 0.000890 |
| FFA | 0.999000 | 0.953000 |
| Parameters | Regression Statistics |
|---|---|
| Multiple R | 1 |
| R Square | 1 |
| Adjusted R Square | 1 |
| Standard Error | 3.18 × 10−6 |
| Observations | 3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tehlah, N.; Kaewpradit, P.; Mujtaba, I.M. Development of Molecular Distillation Based Simulation and Optimization of Refined Palm Oil Process Based on Response Surface Methodology. Processes 2017, 5, 40. https://doi.org/10.3390/pr5030040
Tehlah N, Kaewpradit P, Mujtaba IM. Development of Molecular Distillation Based Simulation and Optimization of Refined Palm Oil Process Based on Response Surface Methodology. Processes. 2017; 5(3):40. https://doi.org/10.3390/pr5030040
Chicago/Turabian StyleTehlah, Noree, Pornsiri Kaewpradit, and Iqbal M. Mujtaba. 2017. "Development of Molecular Distillation Based Simulation and Optimization of Refined Palm Oil Process Based on Response Surface Methodology" Processes 5, no. 3: 40. https://doi.org/10.3390/pr5030040
APA StyleTehlah, N., Kaewpradit, P., & Mujtaba, I. M. (2017). Development of Molecular Distillation Based Simulation and Optimization of Refined Palm Oil Process Based on Response Surface Methodology. Processes, 5(3), 40. https://doi.org/10.3390/pr5030040






