1. Introduction
In the last few decades, an increased focus has been given to the membrane technology, which is used both in production and down-stream processing. Membrane technologies are exploited in a variety of processes, such as in membrane reactors, membrane distillation, diafiltration, dialysis, electrolysis, etc. All of these employ principles of membrane separation [
1]. There are, however, certain limitations for the application. The major obstacle is the membrane fouling, which refers to the blockage of membrane pores during filtration, causing a decrease in the production rate. Although membrane fouling is an inevitable phenomenon occurring during the filtration process, it can be controlled and its influence alleviated [
2].
There are several operational approaches to deal with membrane fouling. These mainly include scheduling of membrane cleaning cycles and on-line fouling control strategies [
2]. These techniques usually require mathematical models for predicting the fouling behavior. The first attempt to describe the fouling behavior in a unified model was presented by Hermia [
3] who developed four types of fouling behavior. Few works have then been devoted to model-based optimal control of membrane-assisted processes [
4,
5] and membrane fouling and cleaning [
6,
7]. However, optimal control requires knowledge of process model parameters. Thus, in the case of unknown parameters in the model, on-line parameter estimation may be performed in order to improve the process control performance. For this purpose, several methods can be applied, such as common least-squares or some more advanced methods. In Charfi et al. [
8], an estimation of the fouling mechanism model proposed by Hermia was conducted for microfiltration and ultrafiltration in a membrane bioreactor using experimental data reported in the literature.
Parameter identifiability has to be addressed before the actual estimation step. If a model is non-identifiable, the estimated parameters will lead to errors in subsequent model predictions [
9]. The identifiability test also provides a guideline for how to simplify the model structure or indicates when more measurements are needed to allow for unique identifiability [
10].
Recently, the optimal control of a diafiltration process in the presence of fouling was proposed [
11]. The obtained control law depends mainly on the parameters of membrane flux and fouling. In the subsequent work, an on-line control strategy was considered that incorporated parameter estimation using the extended Kalman filter (EKF) [
12]. In this paper, we focus more broadly on the optimal operation of a diafiltration process under fouling where parameter estimation is used to determine the parameters of the fouling model. Compared to the work [
12], in this paper, we provide a comparison of the estimation of the unknown parameters using several optimization-based (least-squares and moving-horizon estimation), as well as recursive (recursive least-squares estimation and extended Kalman filter) methods by considering also measurement and process noise, and we assess their performance on the highly non-linear estimation problem that arises from the nature of the employed process model. In addition, the identifiability test is also performed in order to reveal whether the model parameters can be estimated based on available measurements.
The paper is organized as follows. In the next section, the general formulation of a batch diafiltration process is introduced. In
Section 3, we provide a detailed analysis of the membrane fouling phenomena, and we also discuss the modeling of the membrane fouling.
Section 4 provides the definition of the problem of the optimal operation of the diafiltration process. In
Section 5, a review of identifiability detection methods is given with the main focus on non-linear models described by ordinary differential equations (ODEs). The results and implications of the performed identifiability tests are presented. An introduction is then given to the considered parameter estimation problem, and four different estimation methods are briefly presented. Finally, a simulation study is provided in
Section 6 with a detailed discussion and analysis of the obtained results.
2. Process Description
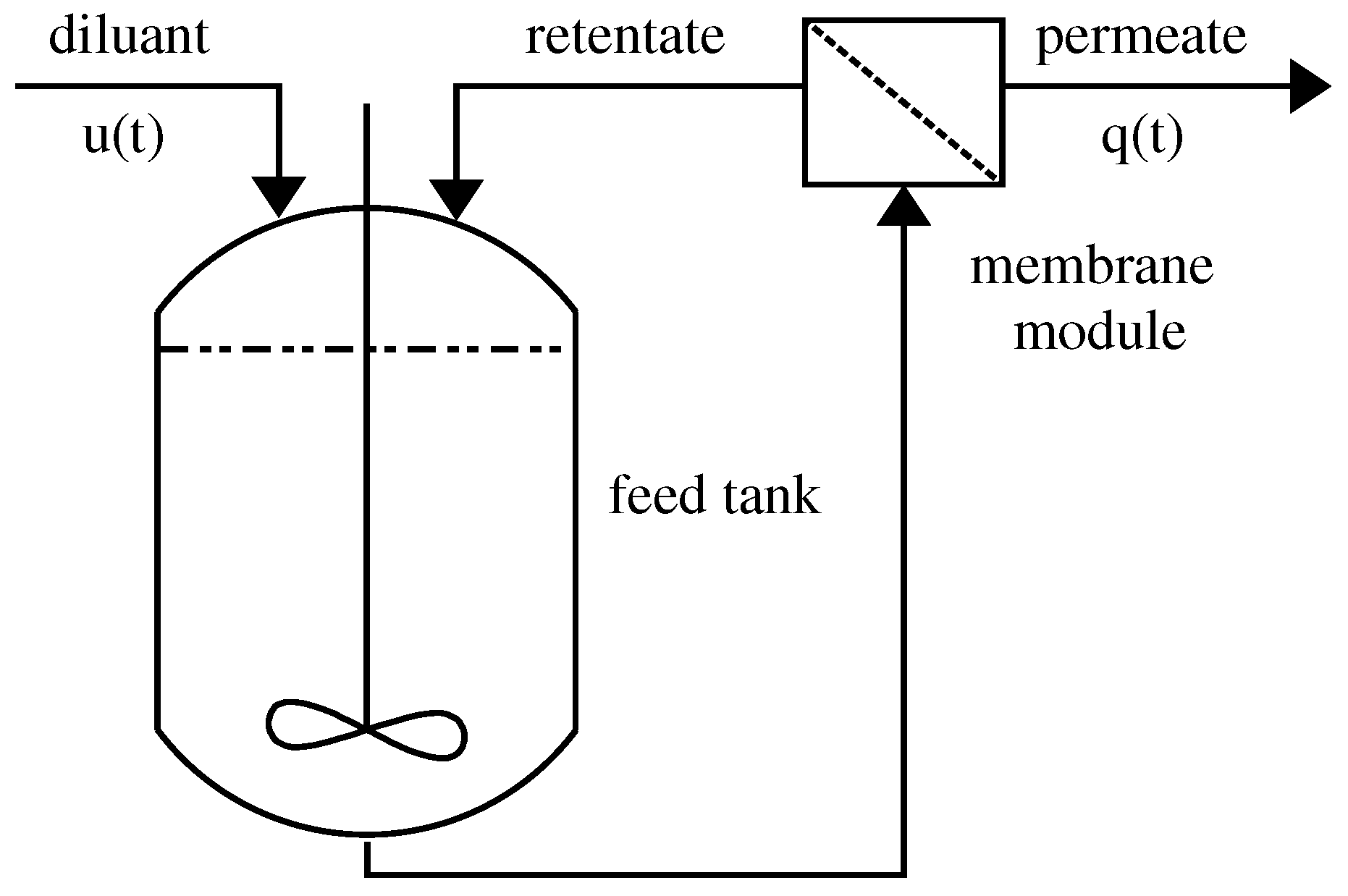
In this paper, we consider the batch diafiltration process shown in
Figure 1. The batch process operates under constant pressure and temperature. The overall batch process consists of a feed tank and a membrane module. We consider that the process solution consist of a solvent (water), macro-solute (high molecular weight component) and micro-solute (low molecular weight component). The process solution is brought from the feed tank to the membrane by means of mechanical energy (e.g., pump). The membrane is designed to retain the macro-solute, while the micro-solute can easily pass through the membrane pores. The stream rejected by the membrane is called the retentate and is taken back into the feed tank. The stream that leaves the system is called the permeate, and its flow-rate is defined as
, where
A is the membrane area and
J is the permeate flux per unit area of the membrane. The flow rate of the permeate stream is a function of both concentrations of the individual solutes and of time, in the case of the occurrence of fouling phenomena.
The control of the batch diafiltration process can be achieved by adjusting the flow-rate of the solvent (diluent) into the feed tank. Then, the control variable
α is defined as the ratio between the inflow into the feed tank and the outflow from the membrane module. Traditional approaches to the operation of the diafiltration process consider sequences of operating regimes, which differ in the rate of diluent addition:
Concentration mode: During this mode, no diluent is added into the feed tank, i.e., .
Constant-volume diafiltration mode: Here, the rate of inflow of the diluent is kept the same as the rate of permeate outflow, i.e., .
(Pure) Dilution mode: In this mode, a certain amount of diluent can be added instantaneously into the feed tank. This can be represented as .
Regarding the practical applicability of the pure dilution mode, as will be shown further, the optimal operation would involve the pure dilution mode as an initial or a final step. In both of these cases, the pure dilution step can be performed out of the batch as a pre-/post-treatment of the separated solution.
The process model [
13] is constituted by the solutes mass balance equations, which have the following form:
where
V is the volume in the feed tank and
denotes the concentration of the
i-th solute;
for macro-solute; and
for micro-solute.
is the observed rejection coefficient of the
i-th solute, which describes the ability of the membrane to retain the solute. The total mass balance is defined as follows:
where
is the initial volume of the process solution.
In many cases, the rejection coefficient
is a function of concentrations. In this paper, we will consider that the rejections are ideal, given and constant for both solutes (
and
). This means that the membrane is perfectly impermeable to macro-solute and that only the micro-solute can pass through the membrane. Moreover, since only the micro-solute can pass through the membrane, the mass of macro-solute in the system will not change and remains constant, such that
. Based on these assumptions, we can eliminate the differential equation for the volume (
2), and the model has now the following form:
3. Membrane Fouling
One of the major obstacles in the field of membrane-assisted processing is the membrane fouling. The membrane fouling is caused by the deposit of the solutes in/on the membrane pores. The main consequence of the membrane fouling is the decrease in the permeate outflow due to the blockage of the pores. The most important factors that cause the membrane fouling are the feed properties and membrane material. Moreover, membrane fouling can increase when the concentration polarization effect takes place. In [
14], the authors have shown that during the membrane filtration, the retained macro-solute can form a gel layer over the membrane surface. The formation of such a gel layer can increase the interactions between the solutes and the membrane surface, which eventually lead to membrane fouling. Further, the process variables, such as temperature and pressure, may also contribute to membrane fouling [
15].
As mentioned above, the main consequence of the membrane fouling is the decrease in the permeate flow rate, which results in the increase of the overall processing time. If the membrane becomes heavily fouled, cleaning must be performed. In some cases, even replacement of the membrane module must be carried out, which leads to the increase of the production costs.
In the past three decades, the modeling of membrane fouling became very important. In 1982, Hermia [
3] derived a unified fouling model for dead-end filtration in terms of total permeate flux and time, which has the following form:
where
is the permeate volume,
t is time and
K represents the fouling rate constant. From the above unified fouling model, four classical fouling models can be derived for different values of the fouling parameter
n. The four models are cake filtration (
), intermediate blocking (
), internal blocking (
) and the complete blocking model (
). By integration of (
5), we obtain the differential equation for the permeate flux [
16,
17], which is expressed as:
This equation can be solved to give an explicit solution if the parameters A, K and n are constant and is the initial flux at time . However, this model holds only for dead-end filtration mode. In order to account for the dynamics of the cross-flow system, which is considered in this paper, we propose to substitute the initial flux with the flux of an unfouled membrane .
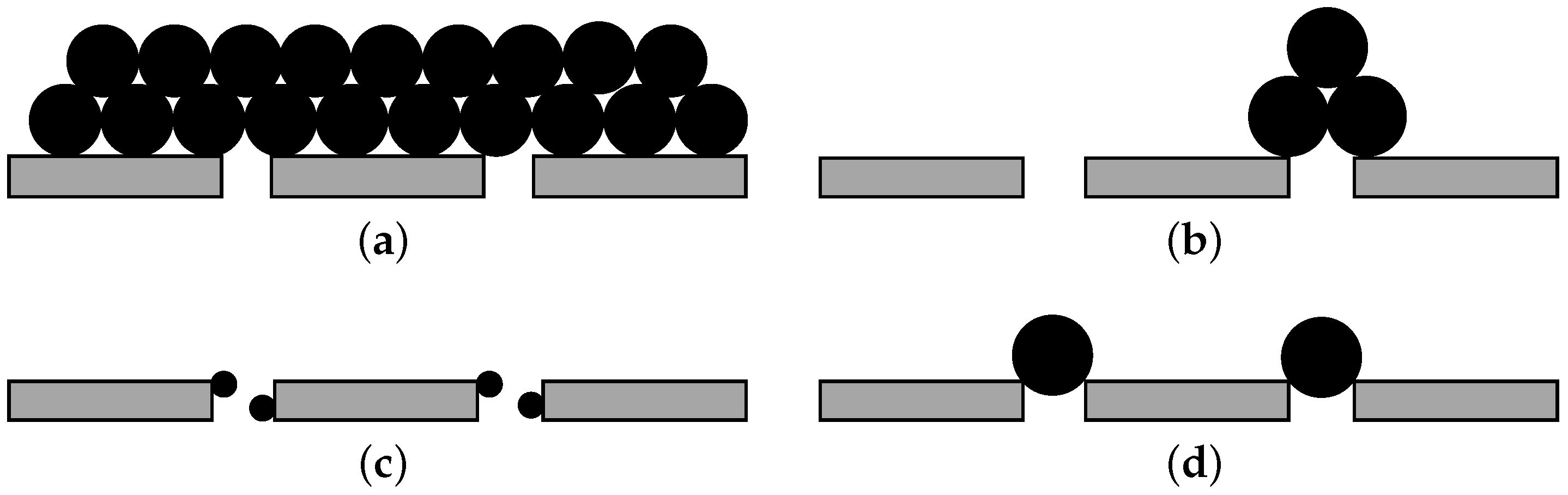
In
Figure 2, we show the graphical representation of the four standard fouling models. The models differ in the way that the solutes deposit on/in the membrane surface. In the following subsections, we will briefly discuss the individual fouling models.
3.1. Cake Filtration Model
The cake filtration model considers that the solutes brought to the membrane surface will form a multi-layered cake formation shown in
Figure 2a. The multi-layered formation is caused by the repeating deposit of the solutes on the membrane surface. The parameter
n is set to zero, and the permeate flux has the following form:
where
J in
is the permeate flow per unit area of the membrane and
is the flux of an unfouled membrane.
3.2. Intermediate Blocking Model
The intermediate fouling model also considers that the solute will block all of the pores. However, in this case, the solutes can also deposit on each other, as illustrated in
Figure 2b. To derive the model, the parameter
n is equal to one, and the permeate flux is of the form:
3.3. Internal Blocking Model
The aforementioned fouling models do not consider the fouling to take place inside the membrane pores. This is not the case with an internal blocking model (
Figure 2c). This type of fouling results in the decrease of the diameter of the membrane pores, which leads to the decrease of the permeate flow. For the internal blocking model, the parameter
n is equal to 3/2, and the permeate flux is derived as:
3.4. Complete Pore Blocking Model
The complete pore blocking model considers that all of the solutes brought to the membrane surface will block the membrane pores (
Figure 2d). Therefore, the permeate flow will be reduced. Moreover, the blockage of the pores is caused only if the molecules of the solutes are larger than the membrane pores. The complete blocking model can be derived from (
5) if
and is of the following form:
Note that unlike in the previous cases, the permeate flux does not depend on the membrane area.
6. Case Study
Here, we present the simulation results obtained with different estimation techniques presented above. We will consider the batch diafiltration process that operates under limiting flux conditions, and the permeate flux for the unfouled membrane reads as:
where
k is the mass transfer coefficient and
is the limiting concentration for the macro-solute. Note that the permeate flux depends only on the concentration of the macro-solute. The overall separation goal is to drive the system from the initial
to the final point
in the minimum time described by (
11) to (
15). The initial process volume is considered to be
. The parameters for the limiting flux model are
,
and the membrane area 1 m
2. The a priori unknown fouling rate is
. As the degree of nonlinearity of the model is strongly dependent on the nature of the fouling behavior, represented by the a priori unknown parameter
n (see
Section 3), we will study the cases when
.
We first study the case where
and
. The time-optimal operation, as stated above, follows a three-step strategy. In the first step, the concentration mode is applied, followed with a singular arc:
and in the last step, pure dilution mode is performed. The switching times between the individual control arcs are determined by the fine precision of the numerical integration around the roots of the singular surface equation. The on-line estimation of the unknown parameters is performed where the samples of the measured process outputs (
25) are assumed to be available with the sampling time (
). This means that the optimal control is updated at each sampling time based on the considered measured outputs. Based on our observations, the chosen sampling time did not pose any computational challenges in the estimation of the parameters. However, in the case of the application on a real process, this sampling time can pose computational difficulties for optimization-based estimation (WLS and WLSMH) since an optimization problem needs to be solved in each sampling time. In the case of the WLSMH method, the initial computing time for one estimation was observed to be approximately 10 s, and once the true values were reached, the computational time decreased to 2 s. For this reason, such a low sampling time is more adequate for recursive methods (RLS and EKF) where no non-linear optimization problem is needed to be solved.
For each studied estimation method (WLS, WLSMH, RLS and EKF), three simulations were performed, with
. For the WLSMH method, the moving horizon was set to
. The length of the horizon is traditionally defined using the sampling instants (steps) as its units. The covariance matrices were tuned for all of the considered simulations as follows
For the WLSMH method, the covariance matrix was updated using the EKF run in parallel. In our simulations with the RLS method, a different matrix had to be chosen for a different value of n; otherwise, a divergent behavior was observed. We attribute this behavior to the strong non-linearities of the process model. Further, due to the non-linear behavior, the choice of was very sensitive to the overall estimation. The noise in the measured data was simulated as a random normally-distributed Gaussian with the covariance matrix (the noise covariance of the approximation of the flux derivative is determined empirically from the simulation data). The same evolution of the random noise is used in all presented simulations. According to our observations, the estimation performance is significantly influenced by the choice of . A small change in the covariance matrix can cause a big difference in the rate of estimation convergence. The chosen variances represent 1% standard deviations of the measurement noise. The actual magnitudes depend on the employed units of the process variables. Hence, the flux varies in the range [0, 0.06] m/h.
The parameter estimation methods discussed in
Section 5.4 were implemented in the MATLAB R2016a environment. For the optimization-based (WLS, WLSMH) methods, the built-in NLP solver fmincon was chosen. The tolerances for the optimized variables and the objective function were both set to
. The ordinary differential equations describing the process model and sensitivity equations were solved using the MATLAB subroutine ode45. The values for the relative and absolute tolerances were set to
and
, respectively. The precision on detecting the switching times by numerical integration was determined with the same tolerances as set by the subroutine ode45. All of the reported results were obtained on the workstation Intel Xeon CPU X5660 with 2.80 GHz and 16 GB RAM.
Table 1 presents a comparison of the rate of suboptimality of the processing time (
) achieved for the on-line control strategy with different estimation methods for different fouling models. We also show the values of normalized root mean squared error (NRMSE) for the estimated parameters (
) and for the concentrations and flux (
) and the cumulative computational time (
) needed for the used estimators. We can observe that the optimality loss for the different estimation techniques is negligible, and the same loss is achieved with all employed estimators. The highest optimality loss occurs in the case of
. The increased optimality loss could be caused here because the value
is used as the lower bound for the estimated parameters, and thus, at least, local convergence problems could occur due to this hard constraint. We can observe that the NRMSE for the estimated parameters for the WLS and WLSMH is higher compared to the recursive methods (RLS and EKF). This was caused due to the high oscillations in the beginning of the estimation of the parameters. The NRMSEs for the concentrations and flux (
) indicate that the difference in the trajectories’ profile in the case of ideal and estimated concentrations and flux is small. The highest difference in all cases was observed only in the EKF method. A possible explanation is that the estimated parameters using the rest of the methods (WLS, WLSMH and RLS) converged exactly or reasonably close with negligible difference to the true values of the parameters on the second interval. If we compare the WLS and WLSMH methods, we can notice a significant decrease in the computational time. This was expected since in the case of the WLS method, every new measurement increases the complexity of the optimization problem that needs to be solved, whereas the complexity remains the same for WLSMH, since only a constant amount of measurements is considered. Simulations with a larger horizon were also performed for WLSMH (
). Although the convergence of the estimated parameters was slightly faster and smoother when compared to the case with
, the computational time increased significantly.
In the case of recursive methods, the computational time was low, since no NLP problem had to be solved and only the current measurements were considered. Overall, we can conclude that all of the estimation methods discussed in this paper were able to estimate the unknown fouling parameters either exactly or with only minor differences. This eventually resulted also in minor differences in the concentration and control trajectories. Further, based on the results, we can also conclude that the best method for on-line estimation is the EKF method. This is due to the fact that no NLP problem has to be solved at each sampling time, and the cumulative computational time is the lowest of all of the proposed methods. Moreover, compared to the RLS method, the EKF does not require different covariance matrices for the individual fouling models as discussed previously. Finally, the EKF method has a satisfactory convergence on the second interval, which leads to accurate information about the singular control.
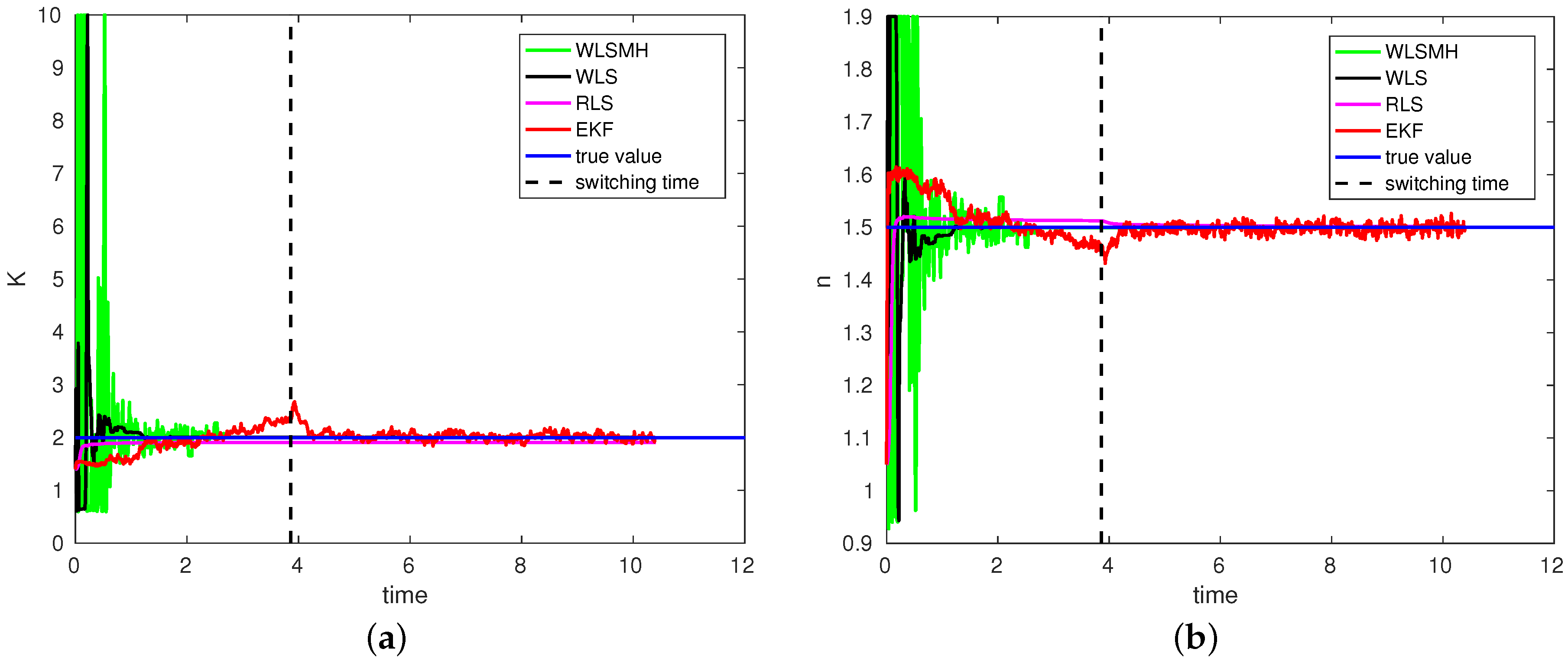
The time-varying profiles of the unknown fouling parameters (
) are shown in
Figure 3. We can observe that in the case of the WLS and WLSMH methods, the parameters converged quickly to a close neighborhood of the true values of the parameters (
and
) prior to the switching time (vertical black dashed line) of the optimal control to the singular arc. The WLS method was able to estimate the true values of the parameters in the first few samples. However, in the case of WLSMH, the estimation needed more time, and we can observe that the parameter values were oscillating for the first two hours. This was due to the NLP solver falling into local minima. This can also be attributed to the chosen length of the moving horizon and the possibly imperfect choice of the initial covariance matrix
. To overcome the issue of NLP solver falling into local minima, one can employ global optimizers. However, based on our observations, the local minima were only hit in the first samples of the estimation when only a few measured outputs were considered. When the recursive methods (RLS, EKF) were used, we can observe that the parameters converged almost to the true values of the parameters. The difference in the estimated and true values of the parameters is attributed to the strong nonlinearity of the process model. Moreover, the performance of these methods also strongly depends on the choice of the covariance matrices. Overall, we can conclude that all of the estimation methods were able to estimate the unknown fouling parameters or converge almost to true values of the parameters even before switching to the singular surface where singular control is applied. As a result, the theoretical optimality of the diafiltration process was almost restored when using the proposed estimators and coupling them within the feedback control law. Similar behavior for parameter estimation was also observed for other fouling models.
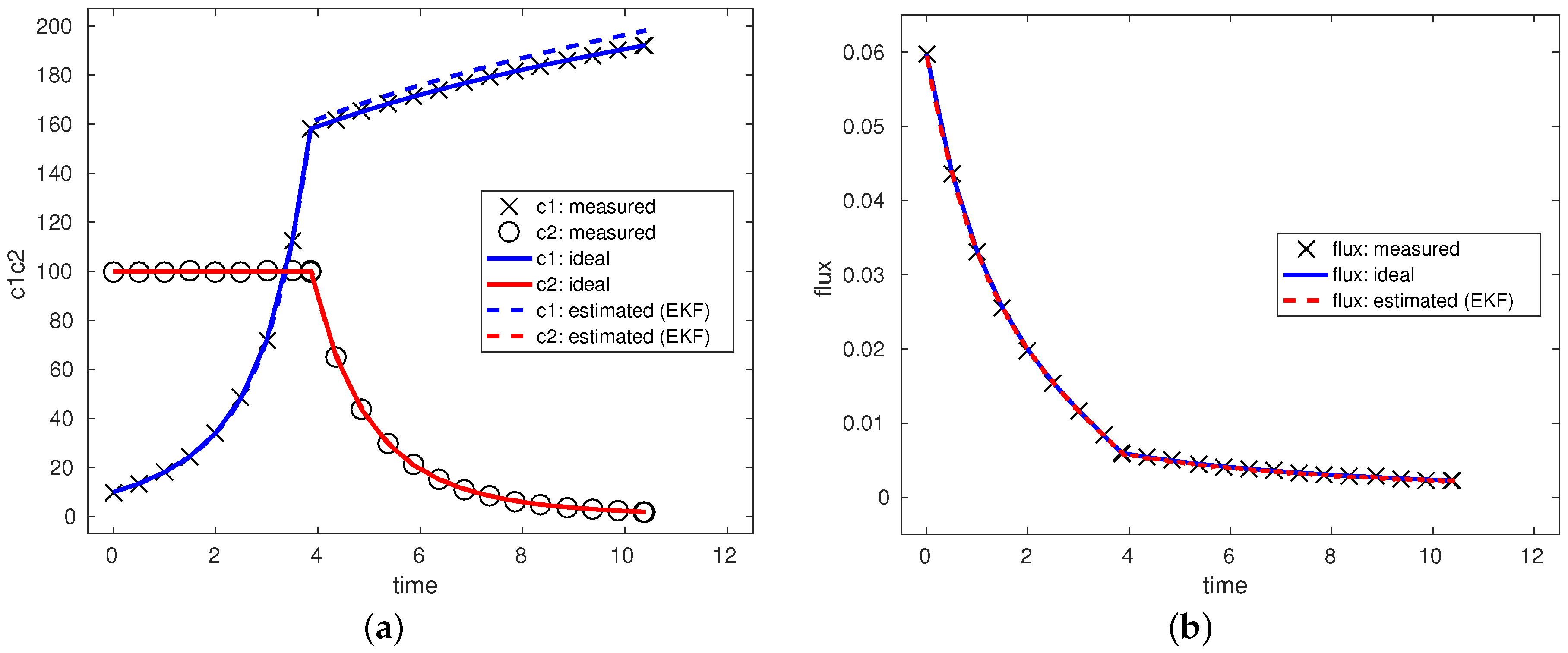
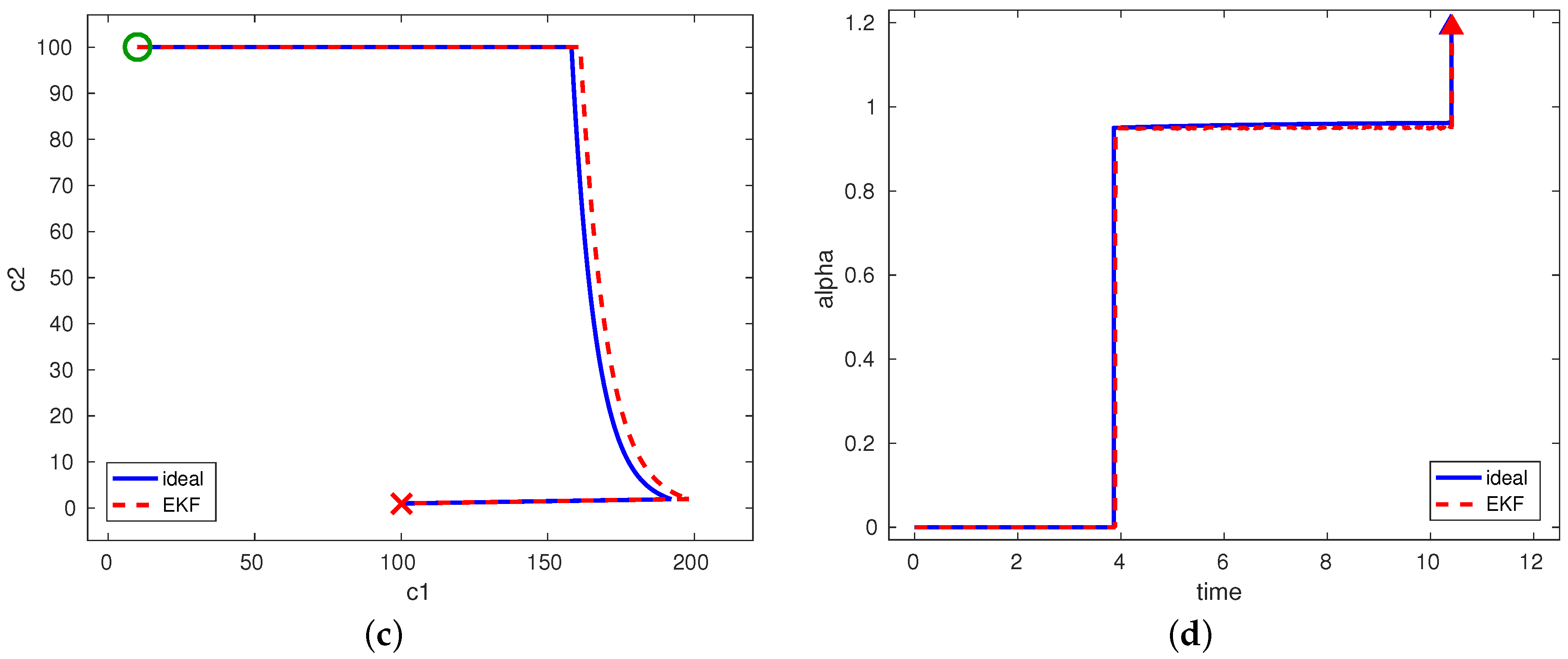
Figure 4 shows the concentration, flux and control trajectories for the ideal and estimated cases together with the considered measurements of concentrations and flux. The figures show only one of the estimation method (EKF) for
as the worst case scenario since in all other cases, the trajectories are closer to the ideal ones. In
Figure 4a, we show the considered measured outputs (denoted by the circle and cross) and the ideal and estimated concentration trajectories. However, due to the small sampling time, we only display some of the measured points. The considered measured flux with ideal and estimated parameters is shown in
Figure 4b. Moreover, in
Figure 4c,d, the optimal concentration state diagram and the optimal control profile are shown. In all figures, the solid lines represent the optimal scenario with a perfect knowledge of parameters. Further, we can observe that the estimated and ideal trajectories in the first step when the control is constant (
) are identical. This behavior was expected since the control in the first step does not depend on the unknown fouling parameters. The difference in the second interval is negligible. This was due to the convergence of the parameters during the first step. For this reason, the singular control in the second step is calculated with almost the true value of the parameters. The measured concentration of the macro-solute (blue dashed line in
Figure 4a) shows the increasing difference to the ideal one at the singular step. However, this has only a minor impact on the overall optimal operation. Based on the results, we can conclude that by using the estimated parameters obtained by all estimation techniques, the overall operation is very close to optimal one with only minor differences in the processing and switching times. Moreover, it should be also mentioned that even if satisfactory convergence was obtained with the EKF method, different Kalman filter methods, like the unscented Kalman filter [
40], could be also employed for the parameter estimation.
Next, we study the case where the initial concentrations are , while the same final concentrations have to be met as in the previous cases. The optimal control strategy starts with pure dilution in the first step and in the last step, which follows after an operation on a singular arc. We use the same estimators as before, with the same tuning matrices.
In
Figure 5, we show the results of the estimation of the unknown fouling parameters using the WLS method and the corresponding concentration state diagram and control profile of the on-line control strategy. As stated above (
Section 4), the entry to the singular arc (
50) can be determined without the knowledge of fouling parameters as
. On the singular arc, the estimation of the unknown fouling parameters commences. We can observe in
Figure 5a,b that the unknown fouling parameters were estimated accurately in the first three hours of operation where the overall time-optimal operation was approximately 37 hours. The suboptimality of the on-line control strategy w.r.t. the ideal one is
. The oscillations in the first minutes of the operation were mainly caused by a small set of measured outputs. A similar behavior was observed in the previous case. Once the amount of measured outputs is increased, we can observe a quick convergence of the estimated parameters towards the true values. The comparison of ideal and estimated concentrations and control trajectories is shown in
Figure 5c,d. As we can observe, the differences in the concentrations and control trajectories for ideal and estimated cases are negligible. This is due to the quick convergence of the estimated fouling parameters. We also performed simulations with the rest of the estimation methods.
In the case of the recursive methods (EKF and RLS), by using the same covariance matrices (
51) to (
54) as in the previous case, the estimated parameters diverged in the first hour of the batch and were not able to converge to the true values of the parameters. The same behavior was also observed in the case of the WLSMH method, since the covariance matrix
was updated based on the EKF method. The reasons for the divergence of the WLSMH, RLS and EKF methods was mainly caused due to the high sensitivity of the choice of the covariance matrices and the strong non-linearities of the process model. Other reasons for the possible divergence issues as discussed in
Section 4.3 are the insufficient amount of measured outputs, since the estimation starts at the singular surface, and insignificant sensitivity between the measured outputs and the estimated parameters on the singular surface. This was caused by almost constant flux on the singular surface.
Overall, we can conclude that even if in the first step, pure dilution mode has to be applied and the estimation of unknown fouling parameters is only performed during the singular control, the differences between the ideal and estimated trajectories are negligible. The results indicate that the estimated parameters converged reasonably close to the true values of the parameters in the first hours of operation. For this reason, the overall operation is very close to the optimal one with only negligible differences in the case when the WLS method is applied. However, in the rest of the estimation methods, strong divergence of the estimated parameters was observed.