Development of Chemical Process Design and Control for Sustainability
Abstract
:1. Introduction
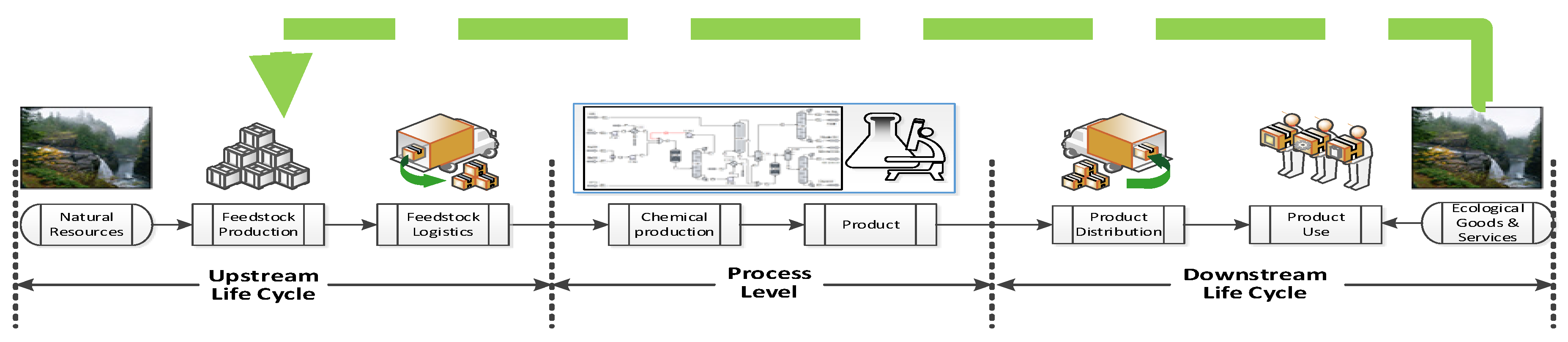
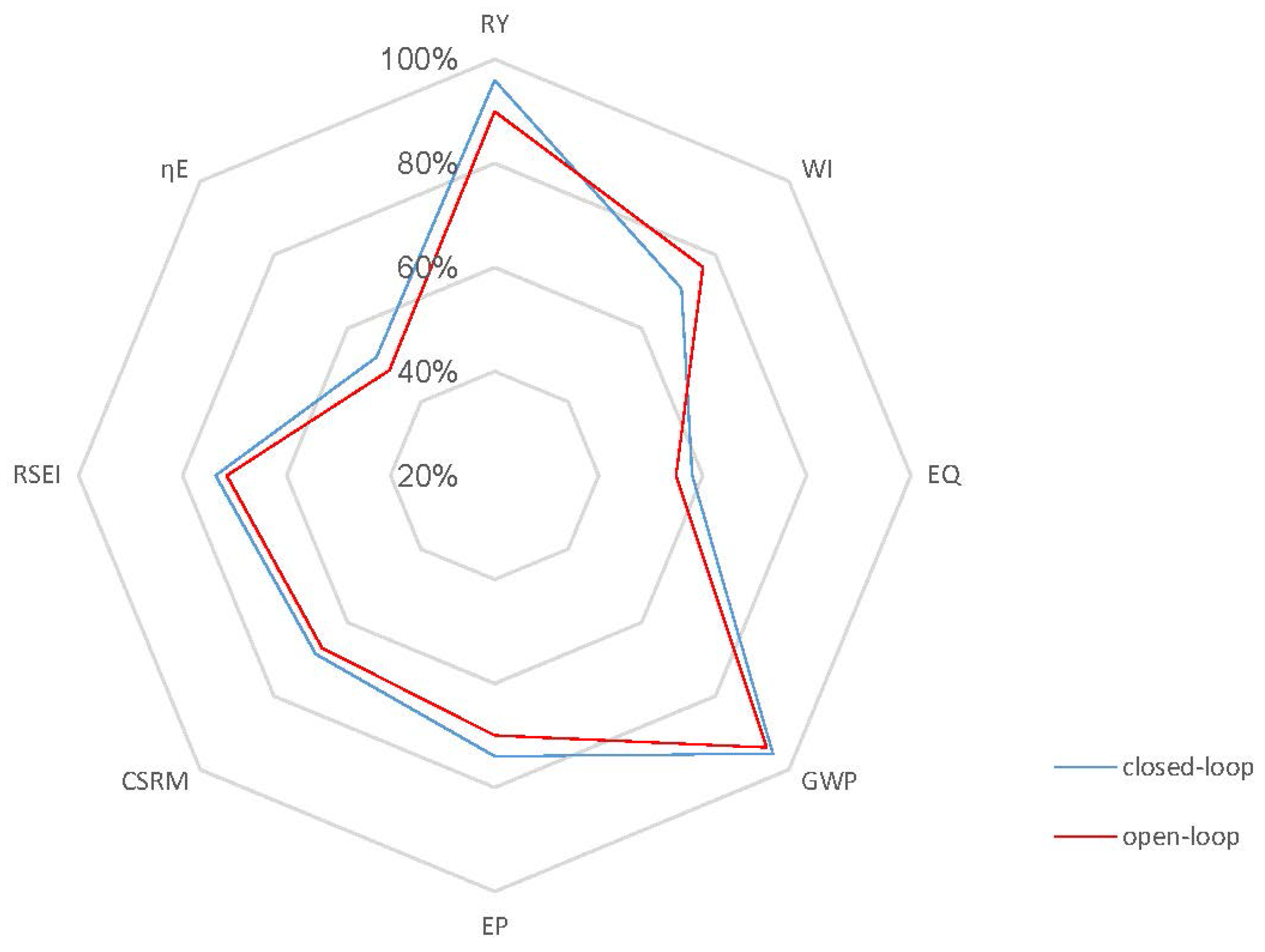
2. Process Sustainability Assessment and Design
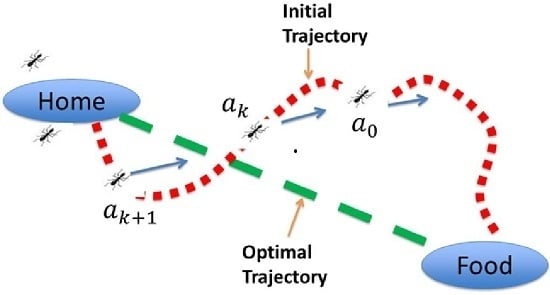
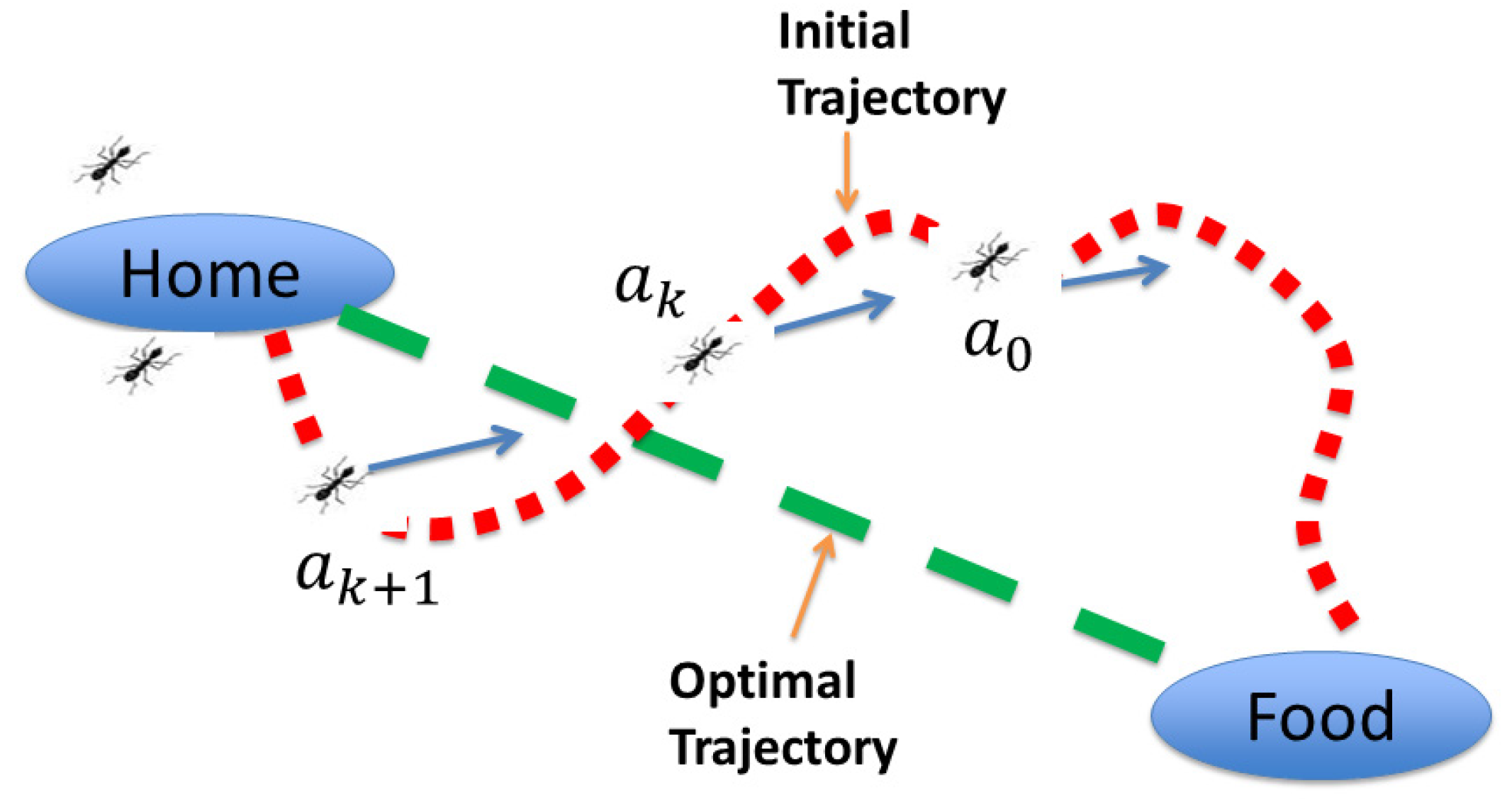
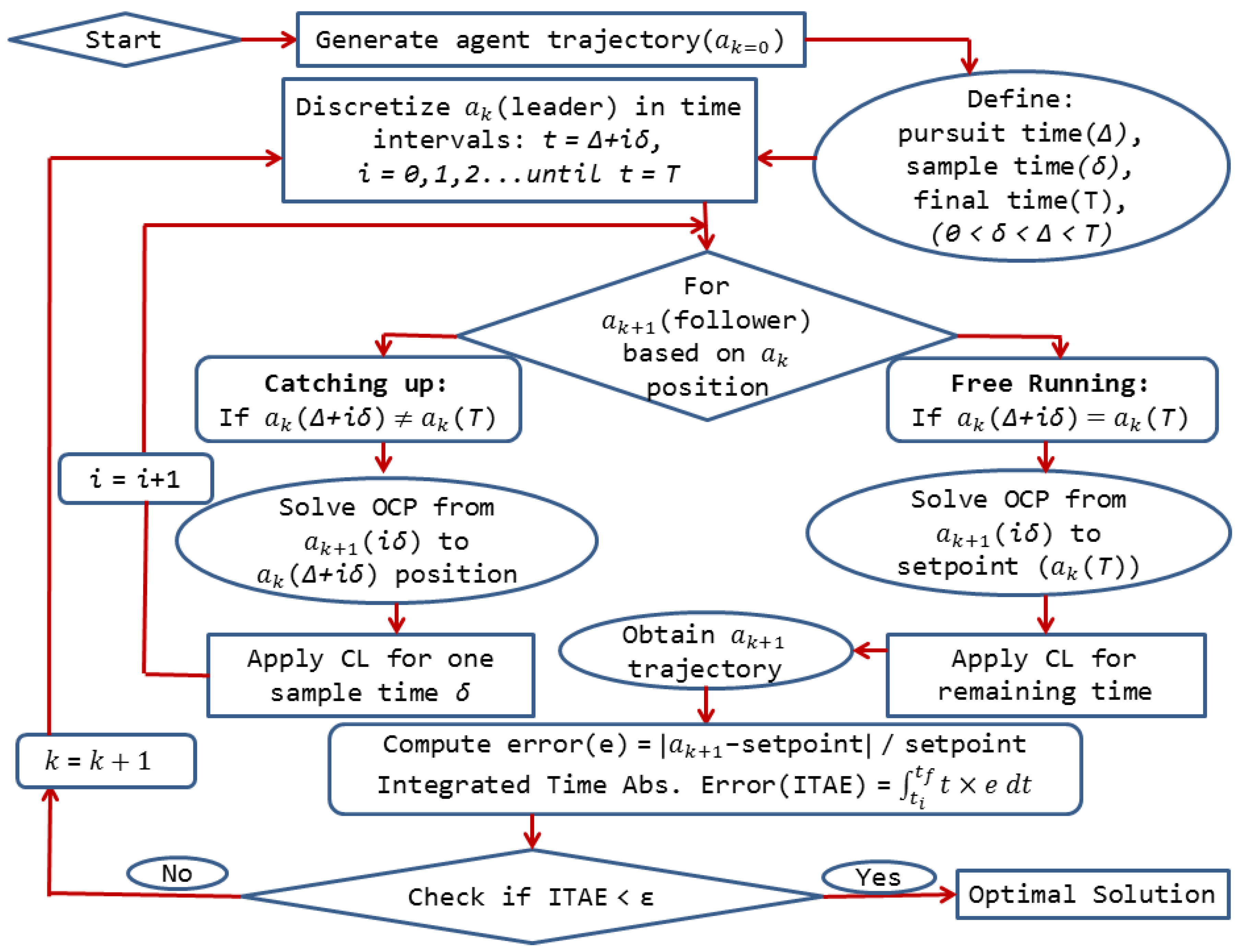
3. Novel Advanced Control Approach
4. New Approach for Process Modeling and Advanced Control for Sustainability
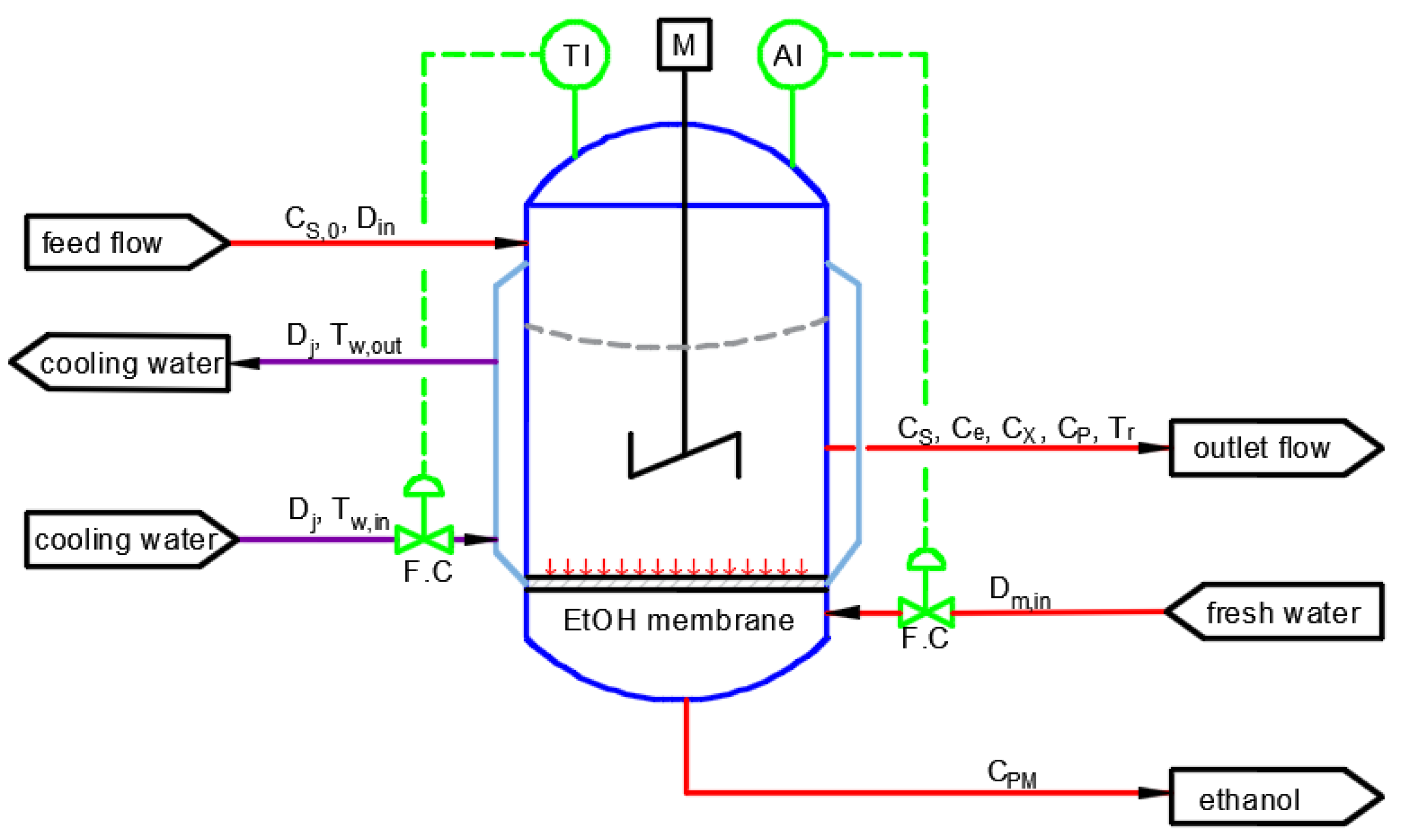
4.1. Bioethanol Manufacturing Process Model
4.2. Case Study: Fermentation for Bioethanol Production System
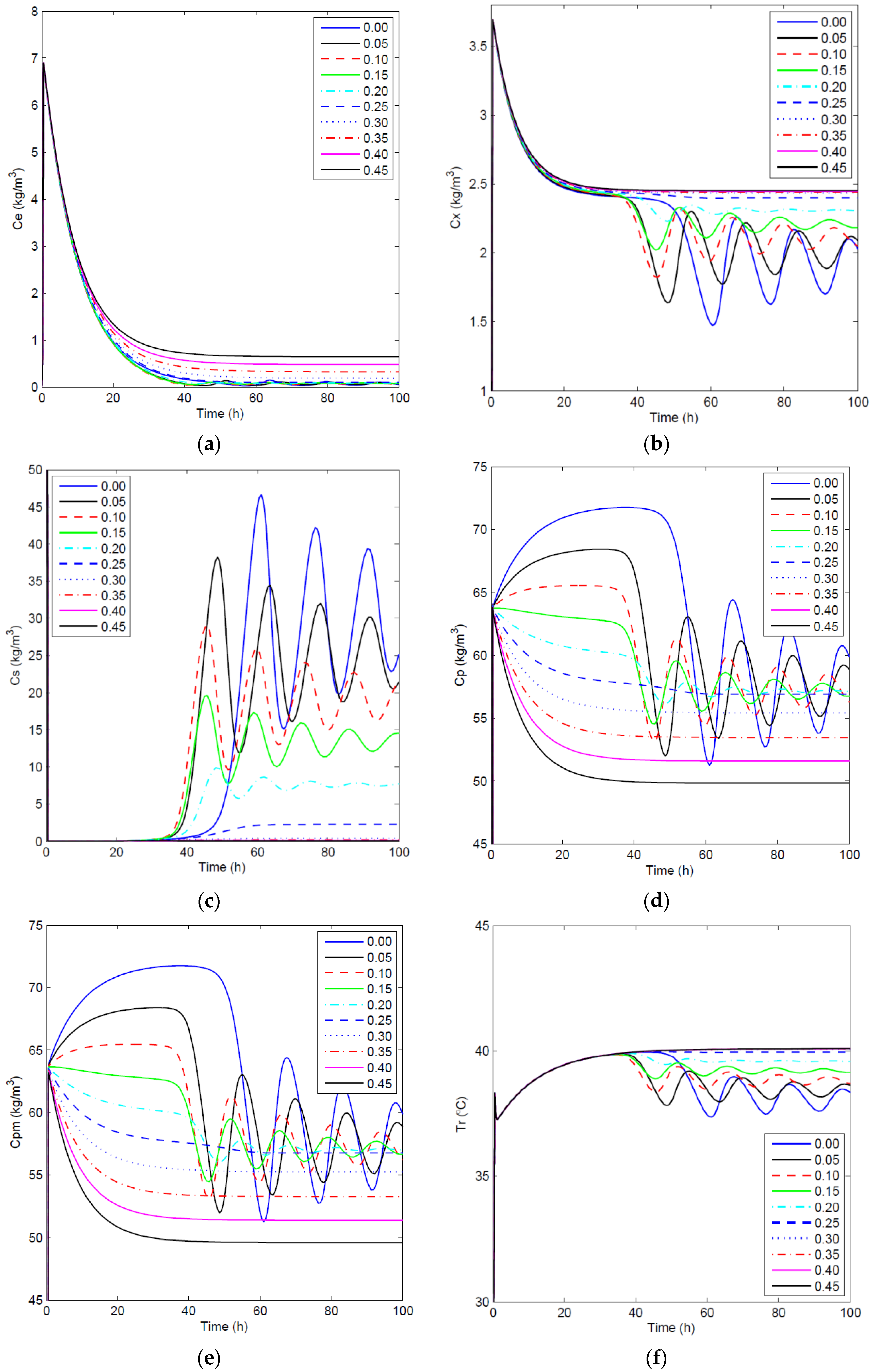
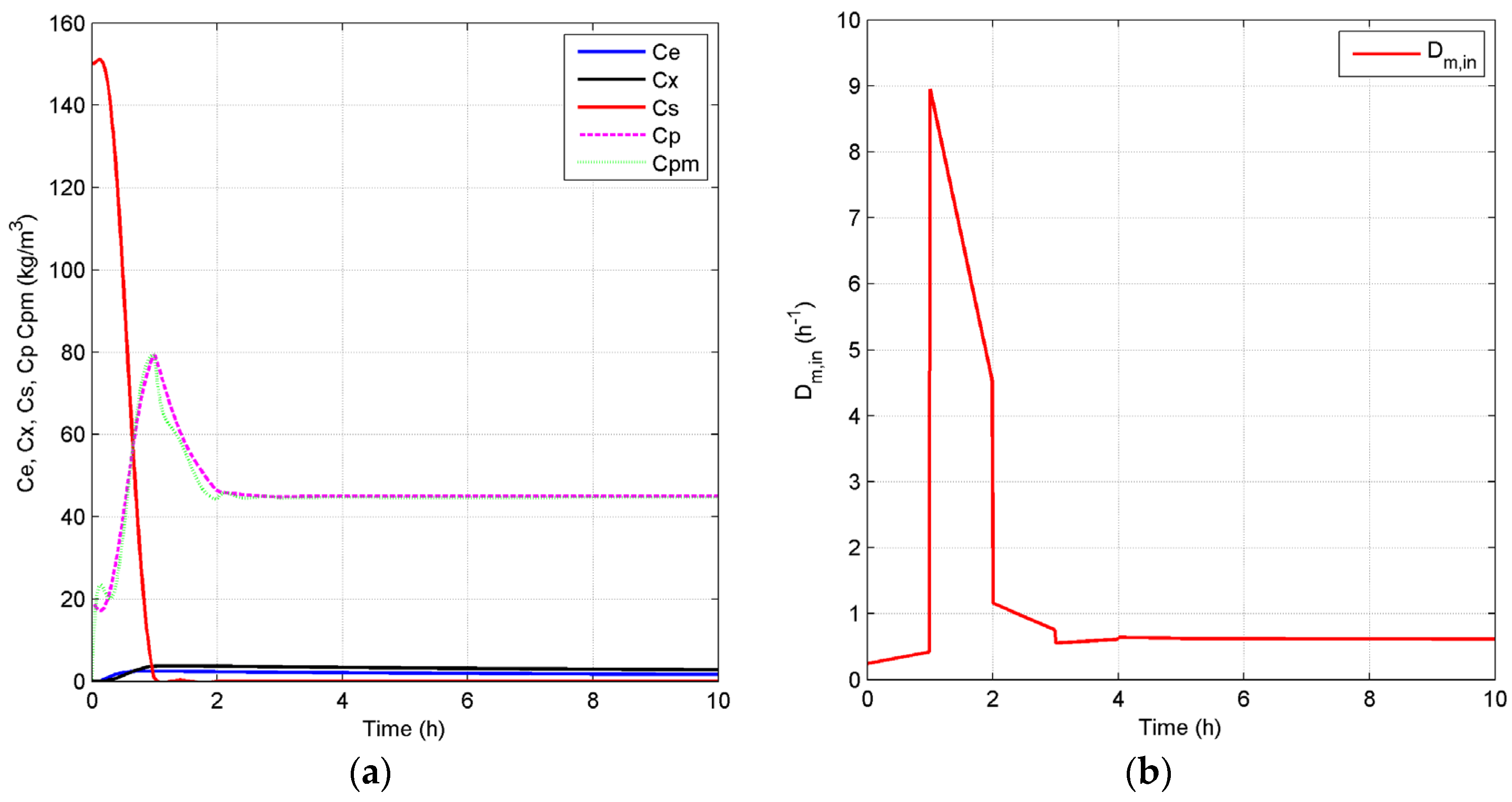
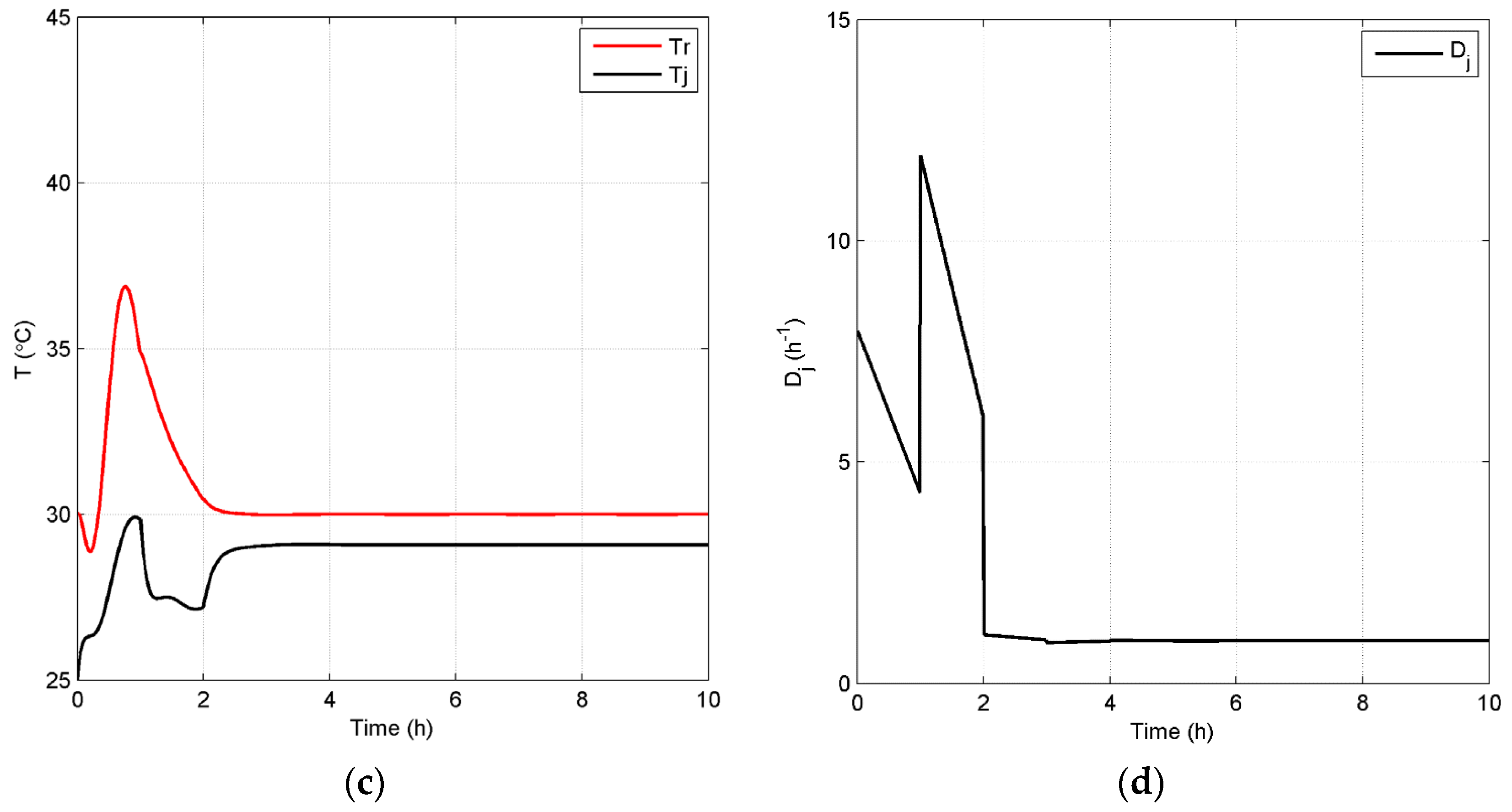
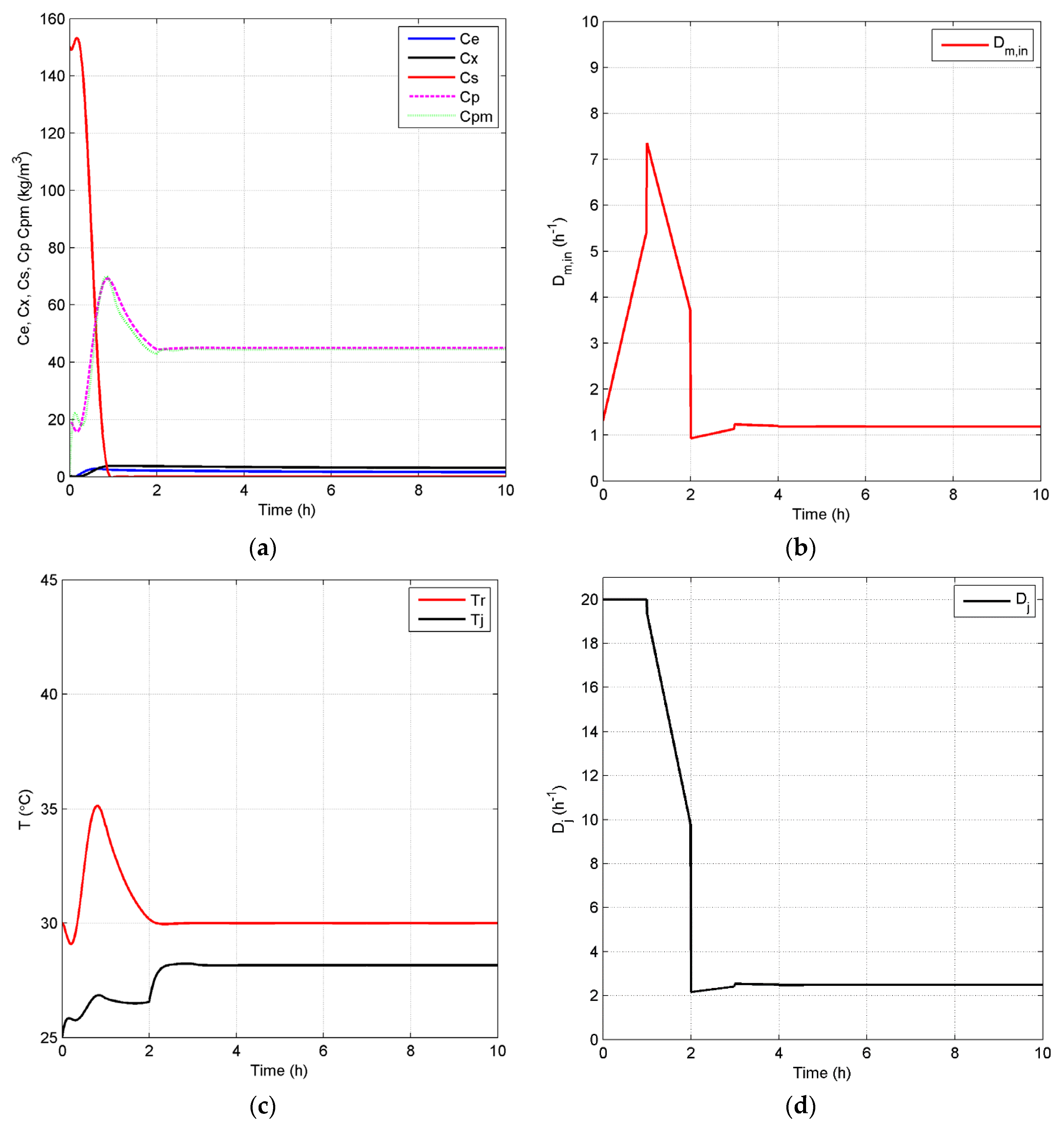
4.2.1. Open-Loop Dynamics of Fermentation Process
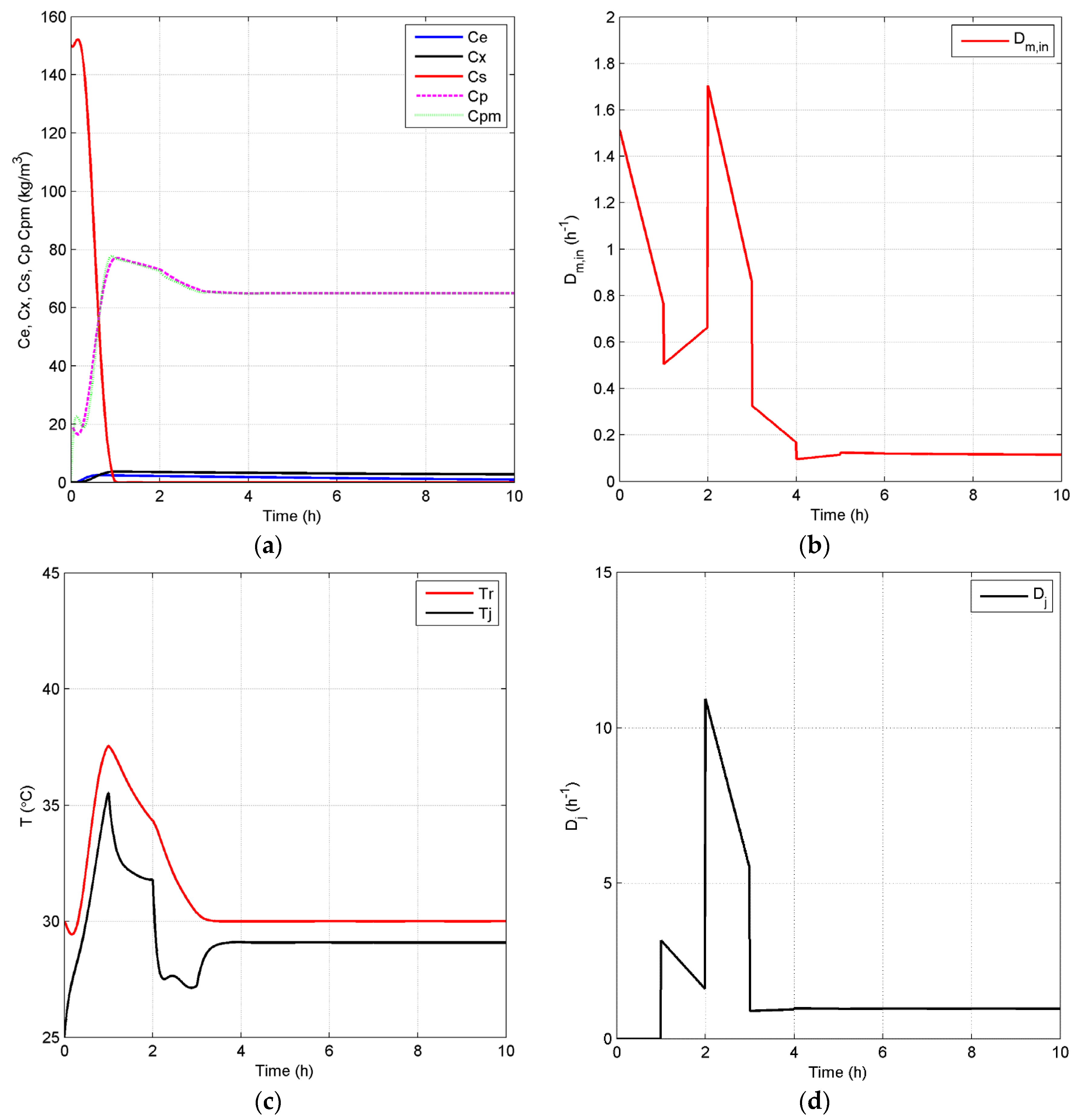
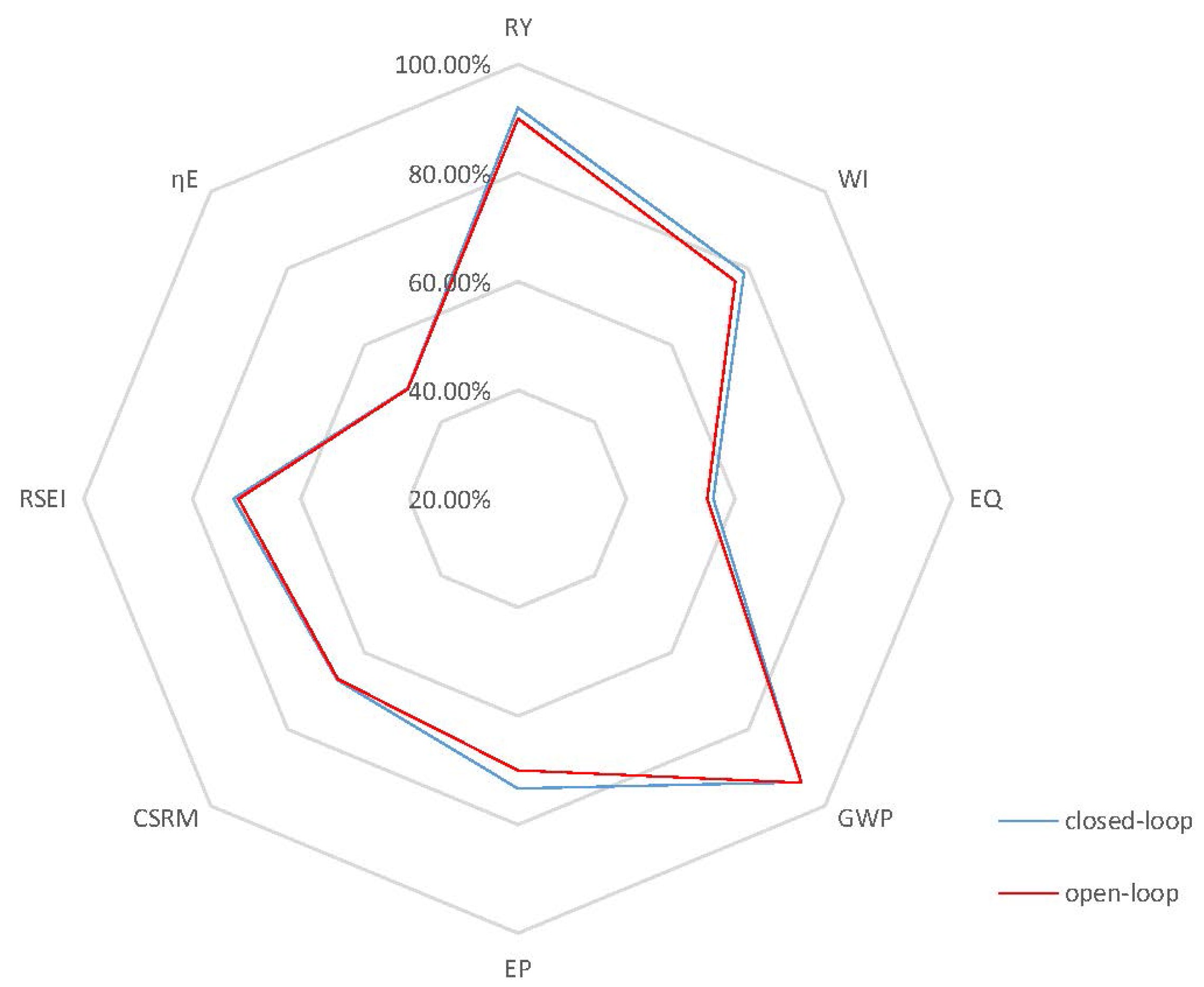
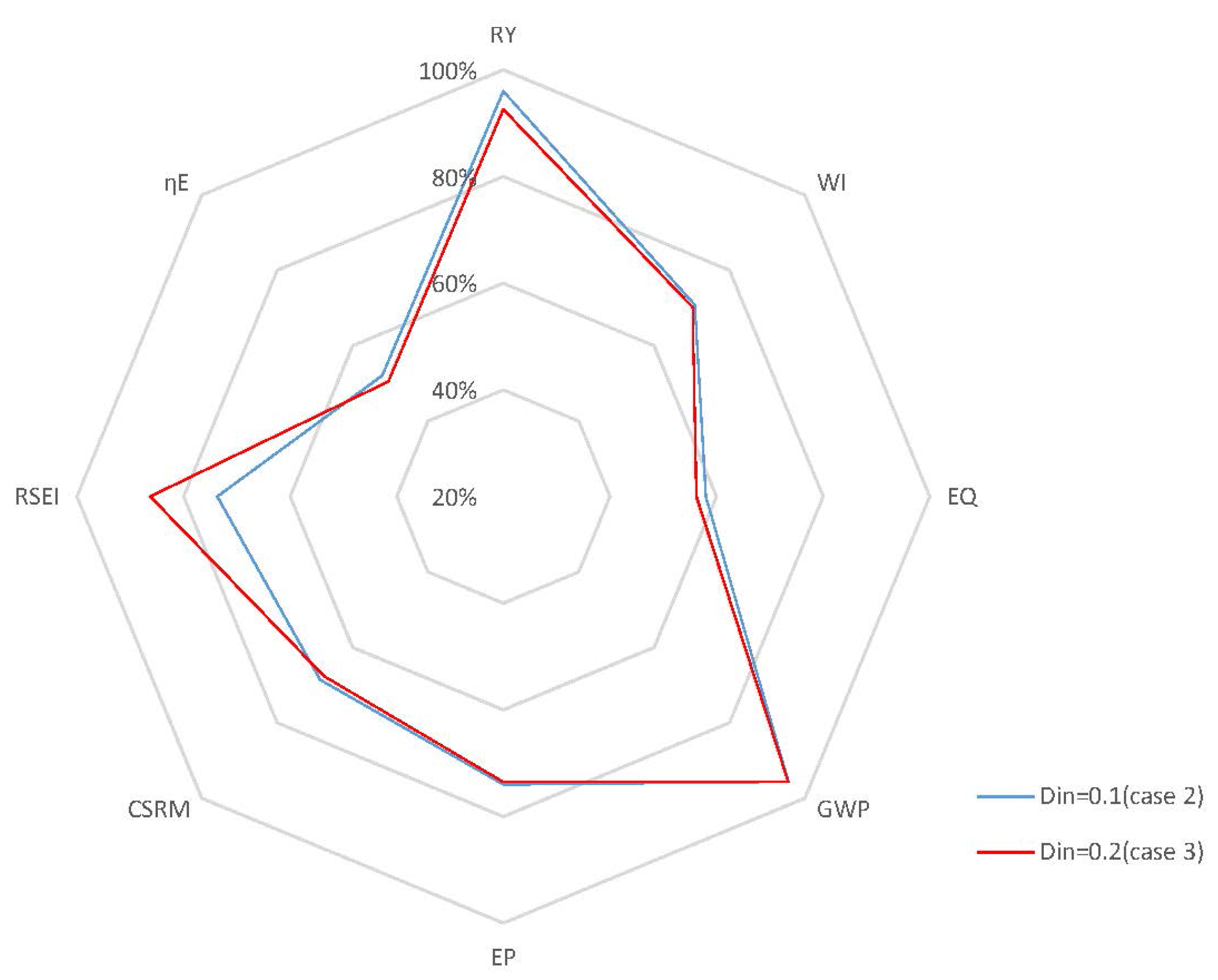
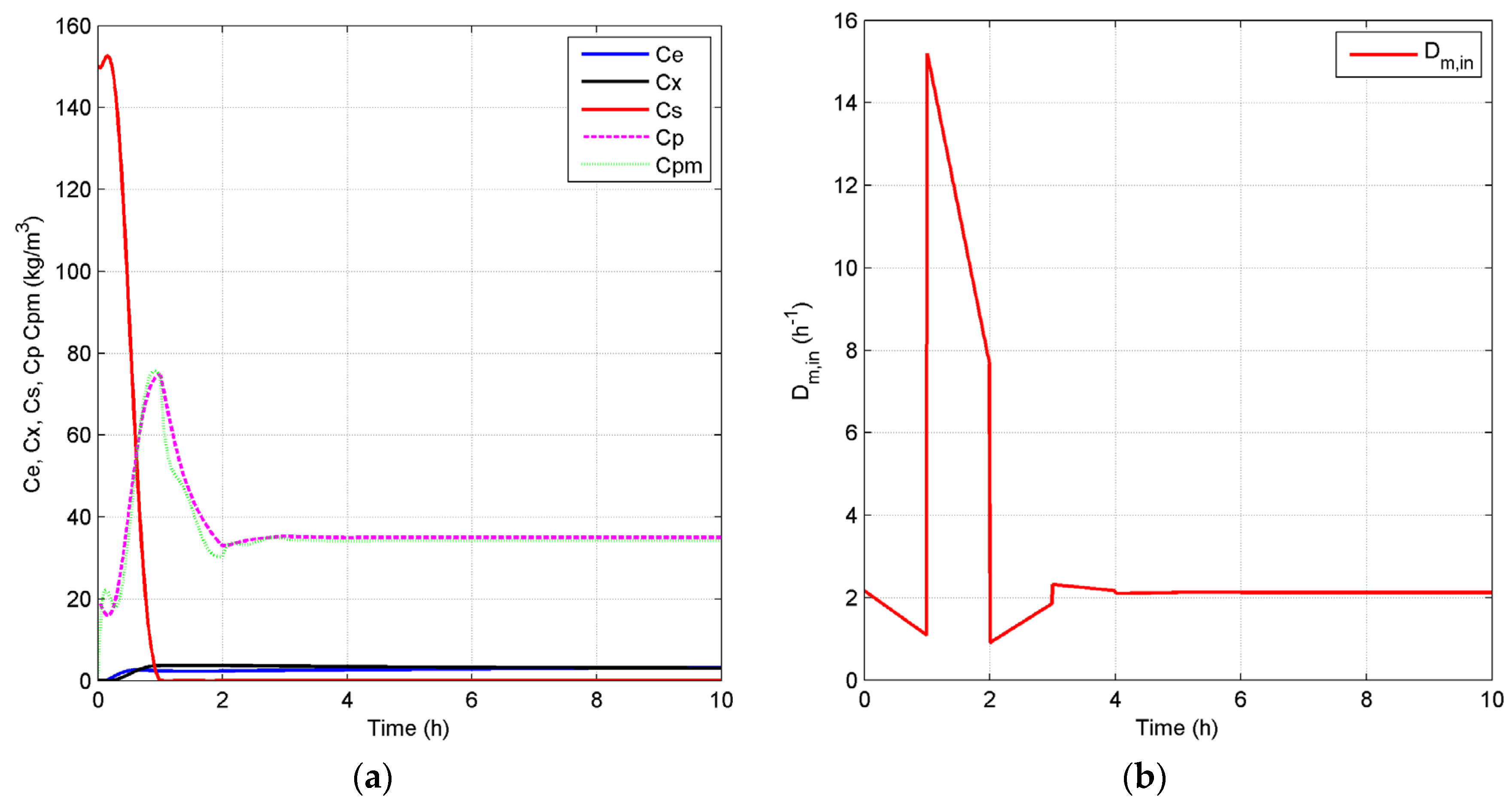
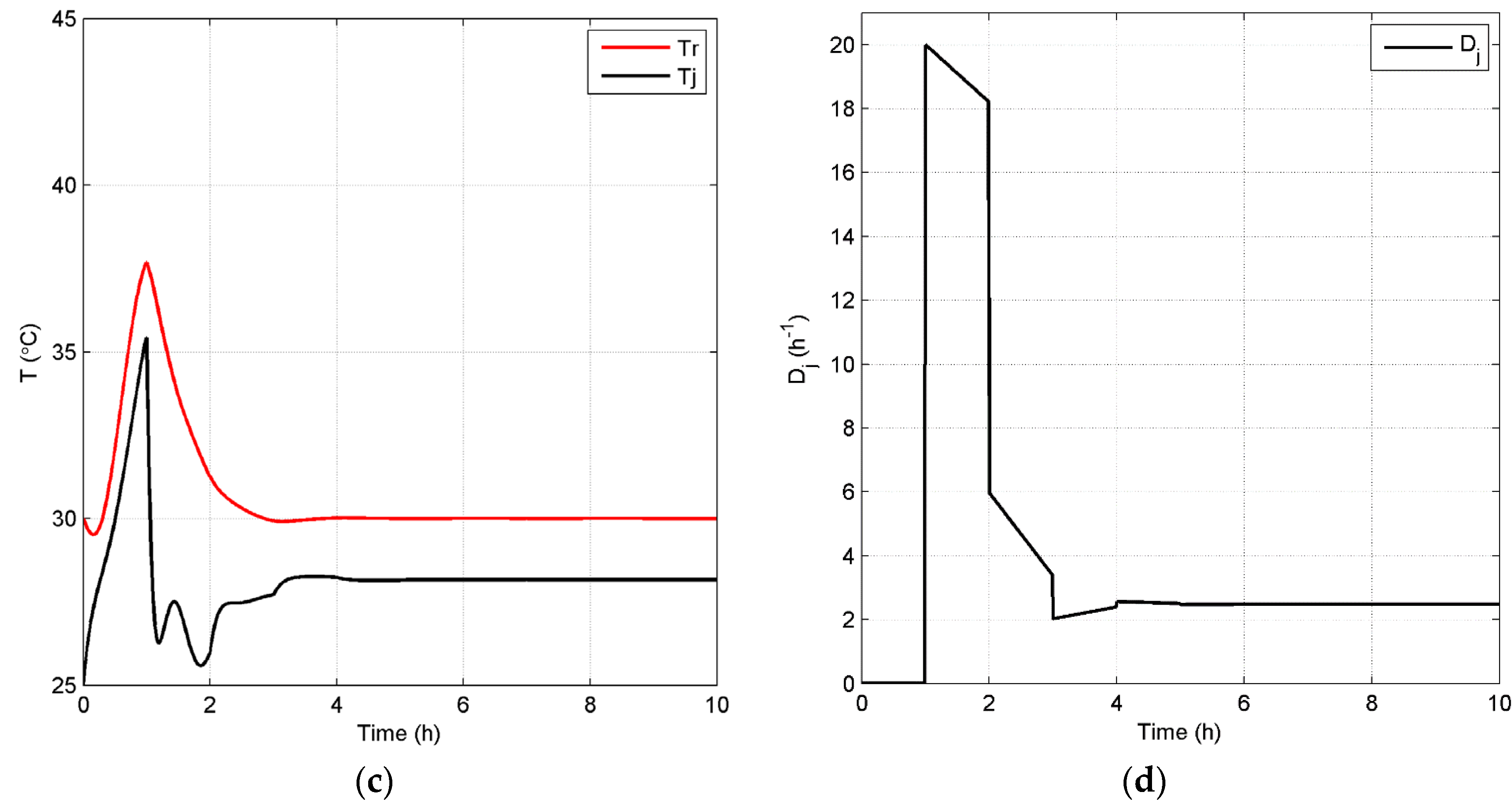
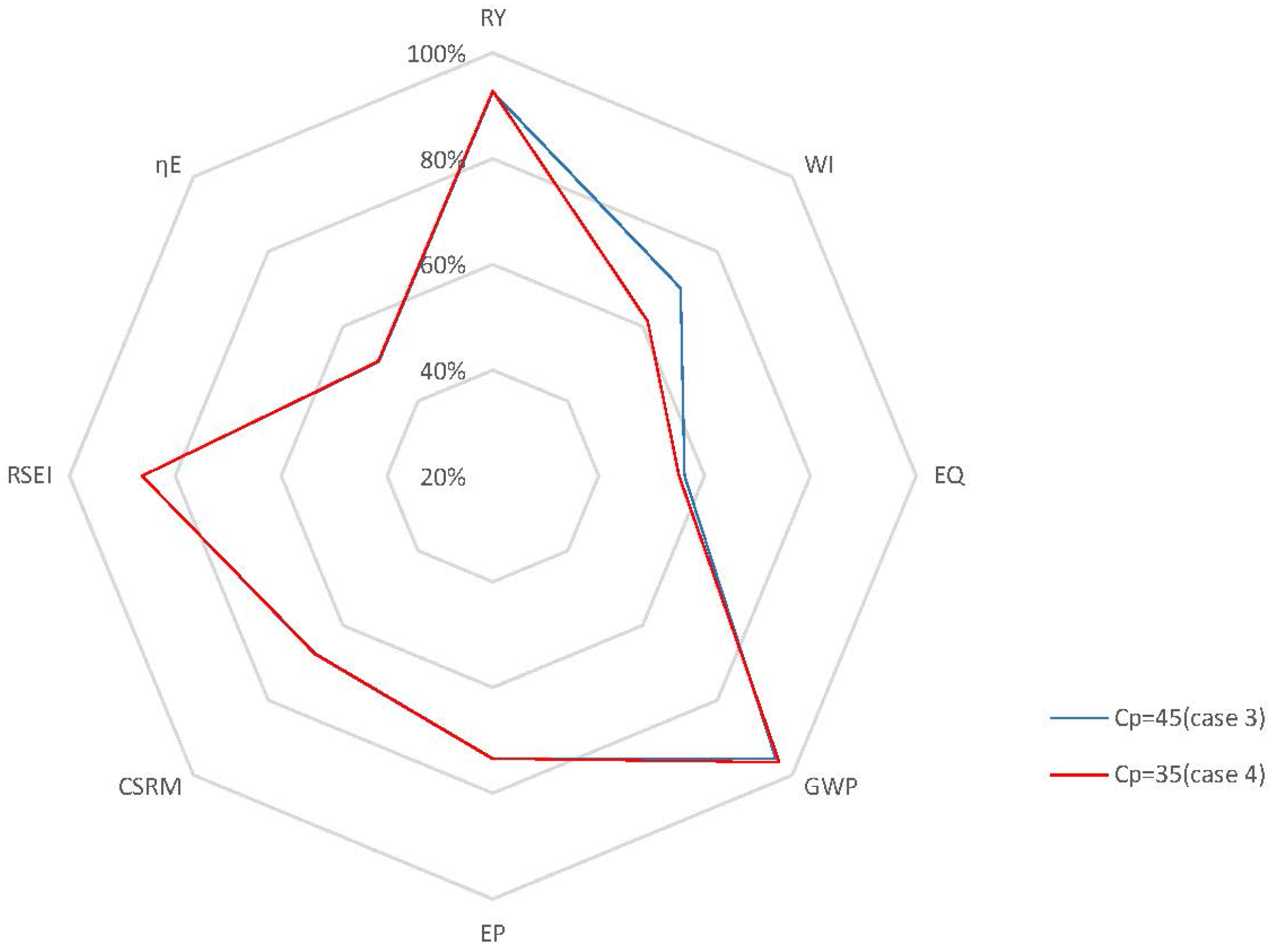
4.2.2. Closed-Loop Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Variables | Definition/Units |
| A1/A2 | Exponential factors in the Arrhenius equation |
| AM | Area of membrane (m2) |
| AI | Analysis indicator |
| AT | Heat transfer area (m2) |
| Ci | Concentration of component i (kg/m3) |
| cp,r | Heat capacity of the reactants (kJ/kg/K) |
| cp,w | Heat capacity of cooling water (kJ/kg/K) |
| Din | Inlet fermentor dilution rate (h−1) |
| Dj | Cooling water flow rate (h−1) |
| Dout | Outlet fermentor dilution rate (h−1) |
| Dm,in | Inlet membrane dilution rate (h−1) |
| Dm,out | Outlet membrane dilution rate (h−1) |
| Ea1/Ea2 | Active energy (kJ/mol) |
| KS | Monod constant (kg/m3) |
| KT | Heat transfer coefficient (kJ/h/m2/K) |
| k1 | Empirical constant (h−1) |
| k2 | Empirical constant (m3/kg·h) |
| k3 | Empirical constant (m6/kg2·h) |
| ms | Maintenance factor based on substrate (kg/kg·h) |
| mp | Maintenance factor based on product (kg/kg·h) |
| M | Mixer |
| MW | Molecular weight (g/mole) |
| PM | Membrane permeability (m/h) |
| P | Correction factor |
| ri | Production rate of component i (kg/m3) |
| R | Gas constant |
| TI | Temperature indicator |
| Tj | Temperature of cooling water (K) |
| Tw,in | Inlet temperature of cooling water (K) |
| Tr | Temperature of the reactants (K) |
| VF | Fermentor volume (m3) |
| VM | Membrane volume (m3) |
| Vj | Cooling jacket volume (m3) |
| Ysx | Yield factor based on substrate (kg/kg) |
| Ypx | Yield factor based on product (kg/kg) |
| Greek Symbols | |
| Reactants density (kg/m3) | |
| Cooling water density (kg/m3) | |
| Specific growth rate (h−1) | |
| Maximum specific growth rate (h−1) | |
| Reaction heat of fermentation (kJ/kg) | |
| Subscripts | |
| e | Key component inside the fermentor |
| e,0 | Inlet key component to the fermentor |
| P | Product (ethanol) inside the fermentor |
| P,0 | Inlet product to the fermentor |
| PM | Product (ethanol) inside the membrane |
| PM,0 | Inlet product to membrane |
| S | Substrate inside the fermentor |
| S,0 | Inlet substrate to the fermentor |
| X | Biomass inside the fermentor |
| X,0 | Inlet biomass to the fermentor |
Appendix A
| Category | Indicator | Formula | Unit | Sustainability Value | |
|---|---|---|---|---|---|
| Best Case (100%) | Worst Case (0%) | ||||
| Efficiency | Reaction Yield (RY) | kg/kg | 1.0 | 0 | |
| Water Intensity (WI) | m3/$ | 0 | 0.1 | ||
| Environmental | Environmental Quotient (EQ) | m3/kg | 0 | 2.5 | |
| Global Warming Potential (GWP) | kg/kg | 0 | Any waste released has a potency factor at least equal to 1 | ||
| Economic | Economic Potential (EP) | $/(kg product) | 1.5 | 0 | |
| Specific Raw Material Cost (CSRM) | $/kg | 0 | 0.5 | ||
| Energy | Specific Energy Intensity (RSEI) | kJ/kg | 0 | 100 | |
| Resource Energy Efficiency (ηE) | kJ/kJ | 0 | 1 | ||
References
- U.S. Department of Energy. Office of Energy, Efficiency & Renewable Energy. Available online: http://energy.gov/eere/office-energy-efficiency-renewable-energy (accessed on 4 December 2015).
- Bakshi, B.R. Methods and Tools for Sustainable Process Design. Curr. Opin. Chem. Eng. 2014, 6, 69–74. [Google Scholar] [CrossRef]
- Ruiz-Mercado, G.J.; Gonzalez, M.A.; Smith, R.L. Expanding Greenscope Beyond the Gate: A Green Chemistry and Life Cycle Perspective. Clean Technol. Environ. Policy 2014, 16, 703–717. [Google Scholar] [CrossRef]
- El-Halwagi, M.M. Pollution Prevention through Process Integration: Systematic Design Tools; Academic Press: San Diego, CA, USA, 1997. [Google Scholar]
- Stankiewicz, A.I.; Moulijn, J.A. Process Intensification: Transforming Chemical Engineering. Chem. Eng. Prog. 2000, 96, 22–34. [Google Scholar]
- Li, C.; Zhang, X.; Zhang, S.; Suzuki, K. Environmentally Conscious Design of Chemical Processes and Products: Multi-Optimization Method. Chem. Eng. Res. Des. 2009, 87, 233–243. [Google Scholar] [CrossRef]
- Baños, R.; Manzano-Agugliaro, F.; Montoya, F.; Gil, C.; Alcayde, A.; Gómez, J. Optimization Methods Applied to Renewable and Sustainable Energy: A Review. Renew. Sustain. Energy Rev. 2011, 15, 1753–1766. [Google Scholar] [CrossRef]
- Wang, B.; Gebreslassie, B.H.; You, F. Sustainable Design and Synthesis of Hydrocarbon Biorefinery Via Gasification Pathway: Integrated Life Cycle Assessment and Technoeconomic Analysis with Multiobjective Superstructure Optimization. Comput. Chem. Eng. 2013, 52, 55–76. [Google Scholar] [CrossRef]
- Gong, J.; You, F. Global Optimization for Sustainable Design and Synthesis of Algae Processing Network for CO2 Mitigation and Biofuel Production Using Life Cycle Optimization. AIChE J. 2014, 60, 3195–3210. [Google Scholar] [CrossRef]
- Rossi, F.; Manenti, F.; Mujtaba, I.M.; Bozzano, G. A Novel Real-Time Methodology for the Simultaneous Dynamic Optimization and Optimal Control of Batch Processes. Comput. Aided Chem. Eng. 2014, 33, 745–750. [Google Scholar]
- Rossi, F.; Manenti, F.; Pirola, C.; Mujtaba, I. A Robust Sustainable Optimization & Control Strategy (Rsocs) for (Fed-) Batch Processes Towards the Low-Cost Reduction of Utilities Consumption. J. Clean. Prod. 2016, 111, 181–192. [Google Scholar]
- Stefanis, S.K.; Pistikopoulos, E.N. Methodology for Environmental Risk Assessment of Industrial Nonroutine Releases. Ind. Eng. Chem. Res. 1997, 36, 3694–3707. [Google Scholar] [CrossRef]
- Chen, H.; Shonnard, D.R. Systematic Framework for Environmentally Conscious Chemical Process Design: Early and Detailed Design Stages. Ind. Eng. Chem. Res. 2004, 43, 535–552. [Google Scholar] [CrossRef]
- Othman, M.R.; Repke, J.U.; Wozny, G.; Huang, Y.L. A Modular Approach to Sustainability Assessment and Decision Support in Chemical Process Design. Ind. Eng. Chem. Res. 2010, 49, 7870–7881. [Google Scholar] [CrossRef]
- Nordin, M.Z.; Jais, M.D.; Hamid, M.K.A. Sustainable Integrated Process Design and Control for a Distillation Column System. Appl. Mech. Mater. 2014, 625, 470–473. [Google Scholar] [CrossRef]
- Zakaria, S.A.; Zakaria, M.J.; Hamid, M.K.A. Sustainable Integrated Process Design and Control for a Continuous-Stirred Tank Reactor System. Appl. Mech. Mater. 2014, 625, 466–469. [Google Scholar] [CrossRef]
- Ojasvi; Kaistha, N. Continuous Monoisopropyl Amine Manufacturing: Sustainable Process Design and Plantwide Control. Ind. Eng. Chem. Res. 2015, 54, 3398–3411. [Google Scholar] [CrossRef]
- Letcher, T.; Scott, J.; Patterson, D.A. Chemical Processes for a Sustainable Future; Royal Society of Chemistry: Cambridge, UK, 2014. [Google Scholar]
- Zhu, Q.; Lujia, F.; Mayyas, A.; Omar, M.A.; Al-Hammadi, Y.; Al Saleh, S. Production Energy Optimization Using Low Dynamic Programming, a Decision Support Tool for Sustainable Manufacturing. J. Clean. Prod. 2015, 105, 178–183. [Google Scholar] [CrossRef]
- Siirola, J.J.; Edgar, T.F. Process Energy Systems: Control, Economic, and Sustainability Objectives. Comput. Chem. Eng. 2012, 47, 134–144. [Google Scholar] [CrossRef]
- Ruiz-Mercado, G.J.; Smith, R.L.; Gonzalez, M.A. Greenscope.Xlsm Tool. Version 1.1; U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2013. [Google Scholar]
- Anastas, P.T.; Warner, J.C. Green Chemistry: Theory and Practice; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Anastas, P.T.; Zimmerman, J. Design through the 12 Principles of Green Engineering. IEEE Eng. Manag. Rev. 2007, 3. [Google Scholar] [CrossRef]
- Ruiz-Mercado, G.J.; Gonzalez, M.A.; Smith, R.L. Sustainability Indicators for Chemical Processes: III. Biodiesel Case Study. Ind. Eng. Chem. Res. 2013, 52, 6747–6760. [Google Scholar] [CrossRef]
- Ruiz-Mercado, G.J.; Smith, R.L.; Gonzalez, M.A. Sustainability Indicators for Chemical Processes: I. Taxonomy. Ind. Eng. Chem. Res. 2012, 51, 2309–2328. [Google Scholar] [CrossRef]
- Ruiz-Mercado, G.J.; Smith, R.L.; Gonzalez, M.A. Sustainability Indicators for Chemical Processes: II. Data Needs. Ind. Eng. Chem. Res. 2012, 51, 2329–2353. [Google Scholar] [CrossRef]
- Lima, F.V.; Li, S.; Mirlekar, G.V.; Sridhar, L.N.; Ruiz-Mercado, G.J. Modeling and Advanced Control for Sustainable Process Systems. In Sustainability in the Design, Synthesis and Analysis of Chemical Engineering Processes; Ruiz-Mercado, G.J., Cabezas, H., Eds.; Elsevier: Cambridge, MA, USA, 2016. [Google Scholar]
- Smith, R.L.; Ruiz-Mercado, G.J.; Gonzalez, M.A. Using Greenscope Indicators for Sustainable Computer-Aided Process Evaluation and Design. Comput. Chem. Eng. 2015, 81, 272–277. [Google Scholar] [CrossRef]
- Bruckstein, A.M. Why the Ant Trails Look So Straight and Nice. Math. Intell. 1993, 15, 59–62. [Google Scholar] [CrossRef]
- Humphrey, A.E. Fermentation Process Modeling: An Overview. Ann. N.Y. Acad. Sci. 1979, 326, 17–33. [Google Scholar] [CrossRef]
- Ghommidh, C.; Vaija, J.; Bolarinwa, S.; Navarro, J. Oscillatory Behaviour Ofzymomonas in Continuous Cultures: A Simple Stochastic Model. Biotechnol. Lett. 1989, 11, 659–664. [Google Scholar] [CrossRef]
- Jarzębski, A.B. Modelling of Oscillatory Behaviour in Continuous Ethanol Fermentation. Biotechnol. Lett. 1992, 14, 137–142. [Google Scholar] [CrossRef]
- Daugulis, A.J.; McLellan, P.J.; Li, J. Experimental Investigation and Modeling of Oscillatory Behavior in the Continuous Culture of Zymomonas Mobilis. Biotechnol. Bioeng. 1997, 56, 99–105. [Google Scholar] [CrossRef]
- Jöbses, I.M.L.; Egberts, G.T.C.; Luyben, K.C.A.M.; Roels, J.A. Fermentation Kinetics of Zymomonas Mobilis at High Ethanol Concentrations: Oscillations in Continuous Cultures. Biotechnol. Bioeng. 1986, 28, 868–877. [Google Scholar] [CrossRef] [PubMed]
- Jöbses, I.M.L.; Roels, J.A. The Inhibition of the Maximum Specific Growth and Fermentation Rate of Zymomonas Mobilis by Ethanol. Biotechnol. Bioeng. 1986, 28, 554–563. [Google Scholar] [CrossRef] [PubMed]
- Pirt, S. The Maintenance Energy of Bacteria in Growing Cultures. Proc. R. Soc. Lond. B: Biol. Sci. 1965, 163, 224–231. [Google Scholar] [CrossRef]
- Huang, S.Y.; Chen, J.C. Analysis of the Kinetics of Ethanol Fermentation with Zymomonas-Mobilis Considering Temperature Effect. Enzyme Microb. Technol. 1988, 10, 431–439. [Google Scholar] [CrossRef]
- Mahecha-Botero, A.; Garhyan, P.; Elnashaie, S.S.E.H. Non-Linear Characteristics of a Membrane Fermentor for Ethanol Production and Their Implications. Nonlinear Anal. Real Word Appl. 2006, 7, 432–457. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, N.; Qiu, T.; Zhao, J.; He, X.; Chen, B. Analysis of Hopf Points for a Zymomonas Mobilis Continuous Fermentation Process Producing Ethanol. Ind. Eng. Chem. Res. 2013, 52, 1645–1655. [Google Scholar] [CrossRef]
- Georges, B.; Dochain, D. On-Line Estimation and Adaptive Control of Bioreactors; Elsevier: New York, NY, USA, 1990. [Google Scholar]
| A1 = 0.6225 | KS = 0.5 kg/m3 |
| A2 = 0.000646 | KT = 360 kJ/(m2∙K∙h) |
| AT = 0.06 m2 | ms = 2.16 kg/(kg∙h) |
| AM = 0.24 m2 | mP = 1.1 kg/(kg∙h) |
| Ce,0 = 0 kg/m3 | P=4.54 |
| Cx,0 = 0 kg/m3 | PM = 0.1283 m/h |
| CS,0 = 150.3 kg/m3 | VF = 0.003 m3 |
| CP,0 = 0 kg/m3 | VM =0.0003 m3 |
| CPM,0 = 0 kg/m3 | Vj = 0.00006 m3 |
| cp,r = 4.18 kJ/(kg∙K) | Ysx = 0.0244498 kg/kg |
| cp,w = 4.18 kJ/(kg∙K) | YPx = 0.0526315 kg/kg |
| Ea1 = 55 kJ/mol | Tin = 30 °C |
| Ea2 = 220 kJ/mol | Tw,in = 25 °C |
| k1 = 16.0 h−1 | ∆H = 220 kJ/mol |
| k2 = 0.497 m3/(kg∙h) | ρr = 1080 kg/m3 |
| k3 = 0.00383 m6/(kg2∙h) | ρw = 1000 kg/m3 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Mirlekar, G.; Ruiz-Mercado, G.J.; Lima, F.V. Development of Chemical Process Design and Control for Sustainability. Processes 2016, 4, 23. https://doi.org/10.3390/pr4030023
Li S, Mirlekar G, Ruiz-Mercado GJ, Lima FV. Development of Chemical Process Design and Control for Sustainability. Processes. 2016; 4(3):23. https://doi.org/10.3390/pr4030023
Chicago/Turabian StyleLi, Shuyun, Gaurav Mirlekar, Gerardo J. Ruiz-Mercado, and Fernando V. Lima. 2016. "Development of Chemical Process Design and Control for Sustainability" Processes 4, no. 3: 23. https://doi.org/10.3390/pr4030023
APA StyleLi, S., Mirlekar, G., Ruiz-Mercado, G. J., & Lima, F. V. (2016). Development of Chemical Process Design and Control for Sustainability. Processes, 4(3), 23. https://doi.org/10.3390/pr4030023