A Multiwell Disc Appliance Used to Deliver Quantifiable Accelerations and Shear Stresses at Sonic Frequencies
Abstract
:1. Introduction
2. Experimental Section
2.1. Maximizing Vibration Regimens




2.2. Using SPH to Model Shear Stresses




2.3. Recoil Material Evaluation



2.4. Shear Stress Modeling





 .
.
3. Results and Discussion
3.1. Viscoelastic Properties of Recoil Materials
| Double-sided foam tape | Dimethyl silicon | Removable mounting squares | Hot melt pressure sensitive adhesive | |
|---|---|---|---|---|
| Elastic modulus | ||||
| Freq range of data used in extrapolation (Hz) | 0.1–100 | 10–100 | 0.1–100 | 0.1–100 |
| Line fit function | y = aln(x) + b | y = aebx | y = axb | y = ax + b |
| a (Pa) | 34,669 | 279,045 | 30,709 | 6877 |
| b (Pa) | 225,278 | 0.0016 | 0.078 | 0.1689 |
| R2 | 0.9961 | 0.7644 | 0.9818 | 0.9952 |
| Viscous modulus | ||||
| Freq range of data used in extrapolation (Hz) | 0.1–100 | 32–100 | 0.1–100 | 0.1–100 |
| Line fit function | y = aln(x) + b | y = ax + b | y = axb | y = ax + b |
| a (Pa) | 4079.9 | −11.813 | 4187.9 | 112.83 |
| b (Pa) | 54098 | 41086 | 0.1237 | 1899.6 |
| R2 | 0.7611 | 0.0105 | 0.9607 | 0.9631 |

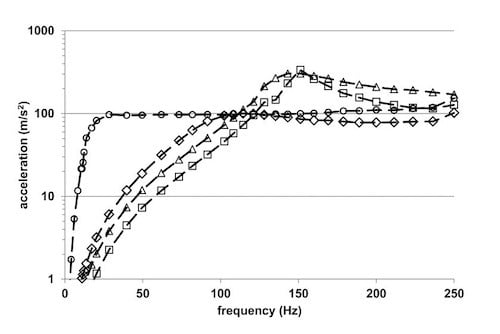
3.2. TRB-Multiwell Disc Accelerations

3.3. Stokes Second Equation Comparisons
| Acceleration (m/s2) | 0.4 | 1 | 2 | 5 | 10 | 15 | 20 | 40 | 60 | 80 | 100 | 200 | 300 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequency (Hz) | Approximate Elastic Modulus of Recoil Materials (kPa) | ||||||||||||
| 2 | 30 | ||||||||||||
| 4 | 30 | ||||||||||||
| 6 | 30 | ||||||||||||
| 8 | 10–300 | 10–35 | 30 | ||||||||||
| 10 | 10–300 | 40 | |||||||||||
| 20 | 11–300 | 40 | |||||||||||
| 50 | 10–400 | 10–40 | 40 | ||||||||||
| 80 | 10–400 | 10–50 | 50 | ||||||||||
| 100 | 20–400 | 20–50 | |||||||||||
| 130 | 20–400 | 400 | |||||||||||
| 150 | 20–400 | 400 | |||||||||||
| 180 | 20–400 | 400 | |||||||||||
| 200 | 20–400 | 50–400 | 400 | ||||||||||
| 220 | 20–400 | 50–400 | 400 | ||||||||||
| 250 | 20–400 | 50–400 | |||||||||||
| Acceleration (m/s2) | 0.4 | 1 | 2 | 5 | 10 | 15 | 20 | 40 | 60 | 80 | 100 | 200 | 300 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequency (Hz) | Approximate Viscous Modulus of Recoil Materials (kPa) | ||||||||||||
| 2 | 4 | ||||||||||||
| 4 | 5 | ||||||||||||
| 6 | 5 | ||||||||||||
| 8 | 3−70 | 3−5 | 5 | ||||||||||
| 10 | 4−60 | 5 | |||||||||||
| 20 | 5−60 | 6 | |||||||||||
| 50 | 7−70 | 7−8 | 7 | ||||||||||
| 80 | 8−70 | 8−10 | 8 | ||||||||||
| 100 | 8−70 | 8−10 | |||||||||||
| 130 | 8−70 | 70 | |||||||||||
| 150 | 8−70 | 40−70 | |||||||||||
| 180 | 8−70 | 40−70 | |||||||||||
| 200 | 8−80 | 80 | |||||||||||
| 220 | 8−80 | 80 | |||||||||||
| 250 | 8−80 | 80 | |||||||||||
| Frequency and amplitude conditions | 2D SPH | 3D SPH | Stokes 2nd problem |
|---|---|---|---|
| Shear stress (Pa) | |||
| 126 Hz; 0.46 mm | 0.3 | 0.5 | 1.6 |
| 126 Hz; 0.069 mm | 0.05 | 0.06 | 0.5 |
| 220 Hz; 0.063 mm | 0.07 | 0.1 | 0.2 |
| 220 Hz; 0.0094 mm | 0.01 | 0.03 | 0.08 |
3.4. Simulation of Shear Stress


4. Conclusions
Acknowledgments
Conflicts of Interest
Appendix
1. Supplemental Experimental Section: Fibroblast Adhesion
1.1. Cell Culture and Adhesion Assay
1.2. Vibration Regimens
1.3. Adhesion Ratio Calculation
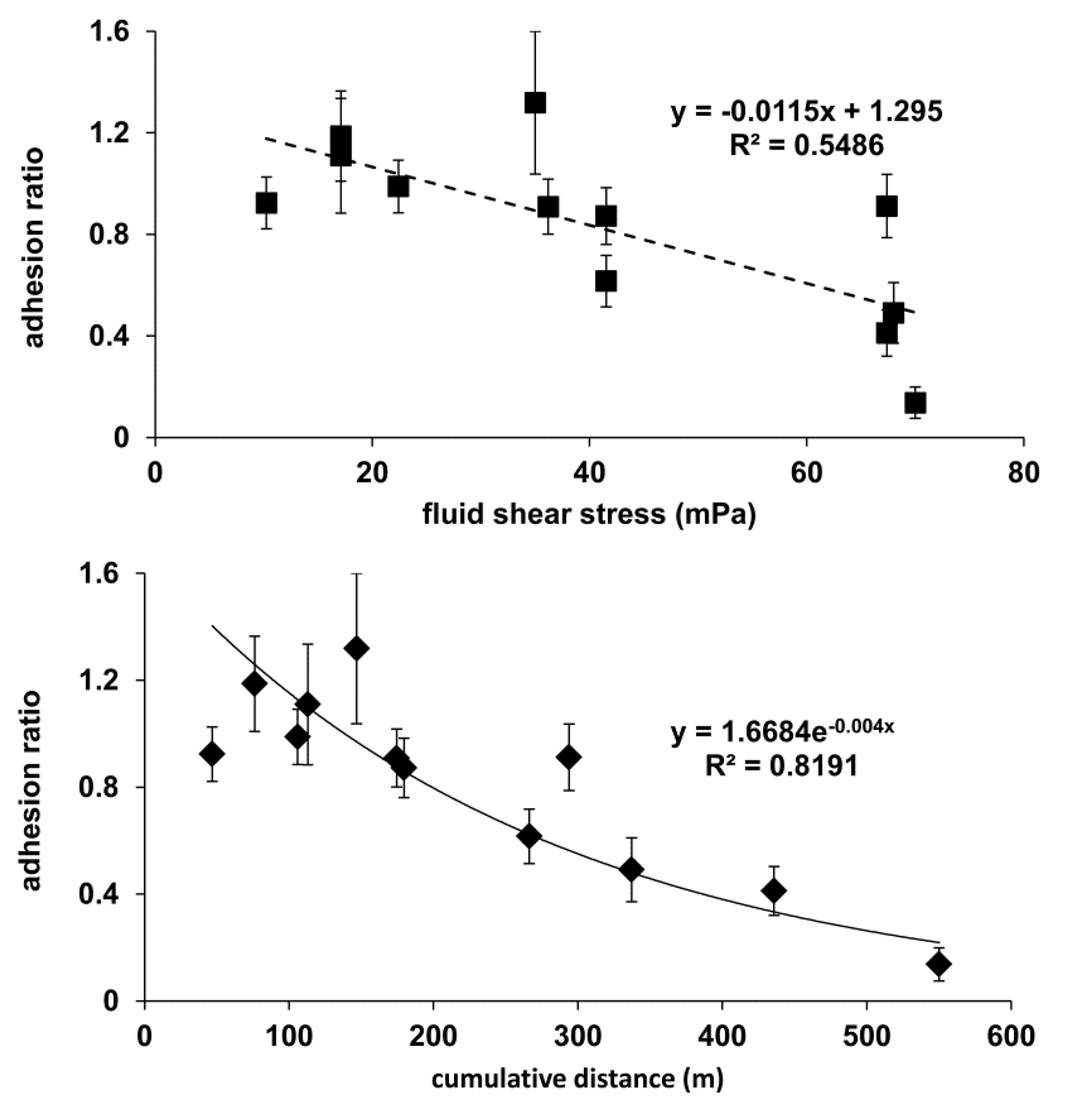
2. Supplementary Results
2.1. Adhesion Sensitivity to Vibration
References
- Titze, I.R. Mechanical stress in phonation. J. Voice 1994, 8, 99–105. [Google Scholar] [CrossRef]
- Tao, C.; Jiang, J.J. Mechanical stress during phonation in a self-oscillating finite-element vocal fold model. J. Biomech. 2007, 40, 2191–2198. [Google Scholar] [CrossRef]
- Solomon, N.P. Vocal fatigue and its relation to vocal hyperfunction. Int. J. Speech-Lang. Pathol. 2008, 10, 254–266. [Google Scholar] [CrossRef]
- Thibeault, S.L. Advances in our understanding of the Reinke space. Curr. Opin. Otolaryngol. Head Neck Surg. 2005, 13, 148–151. [Google Scholar]
- Hunter, E.J.; Tanner, K.; Smith, M.E. Gender differences affecting vocal health of women in vocally demanding careers. Logop. Phoniatr. Vocol. 2011, 36, 128–136. [Google Scholar] [CrossRef]
- Roy, N.; Merrill, R.M.; Thibeault, S.; Gray, S.D.; Smith, E.M. Voice disorders in teachers and the general population: effects on work performance, attendance, and future career choices. J. Speech Lang. Hear. Res. 2004, 47, 542–551. [Google Scholar] [CrossRef]
- Gaston, J.; Quinchia Rios, B.; Bartlett, R.; Berchtold, C.; Thibeault, S.L. The response of vocal fold fibroblasts and mesenchymal stromal cells to vibration. PLoS One 2012, 7, e30965. [Google Scholar]
- Titze, I.R.; Hitchcock, R.W.; Broadhead, K.; Webb, K.; Li, W.; Gray, S.D.; Tresco, P.A. Design and validation of a bioreactor for engineering vocal fold tissues under combined tensile and vibrational stresses. J. Biomech. 2004, 37, 1521–1529. [Google Scholar] [CrossRef]
- Webb, K.; Li, W.; Hitchcock, R.W.; Smeal, R.M.; Gray, S.D.; Tresco, P.A. Comparison of human fibroblast ECM-related gene expression on elastic three-dimensional substrates relative to two-dimensional films of the same material. Biomaterials 2003, 24, 4681–4690. [Google Scholar]
- Wolchok, J.C.; Brokopp, C.; Underwood, C.J.; Tresco, P.A. The effect of bioreactor induced vibrational stimulation on extracellular matrix production from human derived fibroblasts. Biomaterials 2009, 30, 327–335. [Google Scholar] [CrossRef]
- Titze, I.R.; Klemuk, S.A.; Gray, S. Methodology for rheological testing of engineered biomaterials at low audio frequencies. J. Acoust. Soc. Am. 2004, 115, 392–401. [Google Scholar] [CrossRef]
- Klemuk, S.A.; Jaiswal, S.; Titze, I.R. Cell viability viscoelastic measurement in a rheometer used to stress and engineer tissues at low sonic frequencies. J. Acoust. Soc. Am. 2008, 124, 2330–2339. [Google Scholar] [CrossRef]
- Titze, I.R.; Klemuk, S.A.; Lu, X. Adhesion of a monolayer of fibroblast cells to fibronectin under sonic vibrations in a bioreactor. Ann. Otol. Rhinol. Laryngol. 2012, 121, 364–374. [Google Scholar]
- Lucy, L. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Gingold, R.; Monaghan, J. Smoothed particle hydrodynamics-theory and application to non-spherical stars. Mon. Notices R. Astron. Soc. 1977, 181, 375–389. [Google Scholar]
- Monaghan, J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703. [Google Scholar] [CrossRef]
- Liu, M.; Liu, G. Smoothed particle hydrodynamics (SPH): An overview and recent developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Khan, M.; Iftikhar, F.; Anjum, A. Some unsteady flows of a jeffrey fluid between two side walls over a plane wall. Z. Fur Naturforschung Sect. A 2011, 66, 745–752. [Google Scholar]
- Horacek, J.; Laukkanen, A.M.; Sidlof, P.; Murphy, P.; Svec, J.G. Comparison of acceleration and impact stress as possible loading factors in phonation: A computer modeling study. Folia Phoniatr. Et Logop. 2009, 61, 137–145. [Google Scholar] [CrossRef]
- Titze, I.R.; Svec, J.G.; Popolo, P.S. Vocal dose measures: Quantifying accumulated vibration exposure in vocal fold tissues. J. Speech Lang. Hear. Res. 2003, 46, 919–932. [Google Scholar] [CrossRef]
- Van Dyke, W.S.; Sun, X.; Richard, A.B.; Nauman, E.A.; Akkus, O. Novel mechanical bioreactor for concomitant fluid shear stress and substrate strain. J. Biomech. 2012, 45, 1323–1327. [Google Scholar] [CrossRef]
- Wolchok, J.C.; Tresco, P.A. The isolation of cell derived extracellular matrix constructs using sacrificial open-cell foams. Biomaterials 2010, 31, 9595–9603. [Google Scholar] [CrossRef]
- Bacabac, R.G.; Smit, T.H.; van Loon, J.J.W.A.; Boulabi, B.Z.; Helder, M.; Klein-Nulend, J. Bone cell responses to high-frequency vibration stress: Does the nucleus oscillate within the cytoplasm? FASEB J. 2006, 20, 858–864. [Google Scholar] [CrossRef]
- Titze, I.R.; Broadhead, K.; Tresco, P.A.; Gray, S. Strain distribution in an elastic substrate vibrated in a bioreactor for vocal fold tissue engineering. J. Biomech. 2005, 38, 2406–2414. [Google Scholar] [CrossRef]
- Kutty, J.K.; Webb, K. Vibration stimulates vocal mucosa-like matrix expression by hydrogel-encapsulated fibroblasts. J. Tissue Eng. Regen. Med. 2010, 4, 62–72. [Google Scholar]
- Jiang, J.J.; Titze, I.R. Measurement of vocal fold intraglottal pressure and impact stress. J. Voice 1994, 8, 132–144. [Google Scholar] [CrossRef]
- Gunter, H.E. A mechanical model of vocal-fold collision with high spatial and temporal resolution. J. Acoust. Soc. Am. 2003, 113, 994–1000. [Google Scholar] [CrossRef]
- Chen, L.-J.; Mongeau, L. Verification of two minimally invasive methods for the estimation of the contact pressure in human vocal folds during phonation. J. Acoust. Soc. Am. 2011, 130, 1618–1627. [Google Scholar] [CrossRef]
- Gupton, S.L.; Waterman-Storer, C.M. Spatiotemporal feedback between actomyosin and focal-adhesion systems optimizes rapid cell migration. Cell 2006, 125, 1361–1374. [Google Scholar] [CrossRef]
- Lim, X.; Tateya, L.; Tateya, T.; Munoz-Del-Rio, A.; Bless, D.M. Immediate inflammatory response and scar formation in wounded vocal folds. Ann. Otol. Rhinol. Laryngol. 2006, 115, 921–929. [Google Scholar]
- Ling, C.; Raasch, J.L.; Welham, N.V. E-Cadherin and transglutaminase-1 epithelial barrier restoration precedes type IV collagen basement membrane reconstruction following vocal fold mucosal injury. Cells Tissues Organs 2011, 193, 158–169. [Google Scholar] [CrossRef]
- Welham, N.V.; Lim, X.; Tateya, I.; Bless, D.M. Inflammatory factor profiles one hour following vocal fold injury. Ann. Otol. Rhinol. Laryngol. 2008, 117, 145–152. [Google Scholar]
- Zaidel-Bar, R.; Cohen, M.; Addadi, L.; Geiger, B. Hierarchical assembly of cell-matrix adhesion complexes. Biochem. Soc. Trans. 2004, 32, 416–420. [Google Scholar] [CrossRef]
- Burridge, K.; Chrzanowska-Wodnicka, M. Focal adhesions, contractility, and signaling. Annu. Rev. Cell Dev. Biol. 1996, 12, 463–519. [Google Scholar] [CrossRef]
- Matthews, B.D.; Overby, D.R.; Mannix, R.; Ingber, D.E. Cellular adaptation to mechanical stress: Role of integrins, Rho, cytoskeletal tension and mechanosensitive ion channels. J. Cell Biol. 2006, 119, 508–518. [Google Scholar]
- Schwartz, M.A. Integrins and Extracellular Matrix in Mechanotransduction. Cold Spring Harb. Perspect. Biol. 2010, 2. [Google Scholar] [CrossRef]
- Jamney, P.A.; McCulloch, C.A. Cell mechanics: Integrating cell responses to mechanical stimuli. Annu. Rev. Biomed. Eng. 2007, 9, 1–34. [Google Scholar]
- Arbogast, K.B.; Margulies, S.S. Material characterization of the brainstem from oscillatory shear tests. J. Biomech. 1998, 31, 801–807. [Google Scholar] [CrossRef]
- Holt, B.; Tripathi, A.; Morgan, J. Viscoelastic response of human skin to low magnitude physiologically relevant shear. J. Biomech. 2008, 41, 2689–2695. [Google Scholar] [CrossRef]
- Chan, R.W. Measurements of vocal fold tissue viscoelasticity: Approaching the male phonatory frequency range. J. Acoust. Soc. Am. 2004, 115, 3161–3170. [Google Scholar] [CrossRef]
- McLeod, R.W.; Griffin, M.J. Effects of whole-body vibration waveform and display collimation on the performance of a complex manual control task. Aviat. Space Environ. Med. 1990, 61, 211–219. [Google Scholar]
- Dahlin, L.B.; Necking, L.E.; Lundstrom, R.; Lundborg, G. Vibration exposure and conditioning lesion effect in nerves: An experimental study in rats. J. Hand Surg. 1992, 17, 858–861. [Google Scholar] [CrossRef]
- Tyler, W.J. The mechanobiology of brain function. Nat. Rev. Neurosci. 2012, 13, 867–878. [Google Scholar] [CrossRef]
- LaPlaca, M.C.; Prado, G.R. Neural mechanobiology and neuronal vulnerability to traumatic loading. J. Biomech. 2010, 43, 71–78. [Google Scholar] [CrossRef]
- Liu, M.; Song, W.; Li, P.; Huang, Y.; Gong, X.; Zhou, G.; Jia, X.; Zheng, L.; Fan, Y. Galanin protects against nerve injury after shear stress in primary cultured rat cortical neurons. PLoS One 2013, 8, e63473. [Google Scholar]
- Chen, X.; Thibeault, S.L. Characteristics of age-related changes in cultured human vocal fold fibroblasts. Laryngoscope 2008, 118, 1700–1704. [Google Scholar] [CrossRef]
- Chen, X.; Thibeault, S.L. Novel isolation and biochemical characterization of immortalized fibroblasts for tissue engineering vocal fold lamina propria. Tissue Eng. C 2009, 15, 201–212. [Google Scholar] [CrossRef]
- Titze, I.R.; Hunter, E.; Svec, J.G. Voicing and silence periods in daily and weekly vocalizations of teachers. J. Acoust. Soc. Am. 2007, 121, 469–478. [Google Scholar] [CrossRef]
- Bevington, P.R.; Robinson, K.D. Data Reduction and Error Analysis for the Physical Sciences; Tubb, S.J., Morriss, J.M., Eds.; McGraw-Hill, Inc.: New York, NY, USA, 1992; pp. 1–328. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Klemuk, S.A.; Vigmostad, S.; Endapally, K.; Wagner, A.P.; Titze, I.R. A Multiwell Disc Appliance Used to Deliver Quantifiable Accelerations and Shear Stresses at Sonic Frequencies. Processes 2014, 2, 71-88. https://doi.org/10.3390/pr2010071
Klemuk SA, Vigmostad S, Endapally K, Wagner AP, Titze IR. A Multiwell Disc Appliance Used to Deliver Quantifiable Accelerations and Shear Stresses at Sonic Frequencies. Processes. 2014; 2(1):71-88. https://doi.org/10.3390/pr2010071
Chicago/Turabian StyleKlemuk, Sarah A., Sarah Vigmostad, Kalyan Endapally, Andrew P. Wagner, and Ingo R. Titze. 2014. "A Multiwell Disc Appliance Used to Deliver Quantifiable Accelerations and Shear Stresses at Sonic Frequencies" Processes 2, no. 1: 71-88. https://doi.org/10.3390/pr2010071
APA StyleKlemuk, S. A., Vigmostad, S., Endapally, K., Wagner, A. P., & Titze, I. R. (2014). A Multiwell Disc Appliance Used to Deliver Quantifiable Accelerations and Shear Stresses at Sonic Frequencies. Processes, 2(1), 71-88. https://doi.org/10.3390/pr2010071