Analysis of the Erosion Boundary of a Blast Furnace Hearth Driven by Thermal Stress Based on the Thermal–Fluid–Structural Model

Abstract

Irreversible erosion damage of the hearth lining determines the campaign life of a blast furnace (BF). Among the factors involved, structural thermal stress resulting from both internal and external temperature differences and external constraints is a key mechanism in the damage to the hearth lining. Based on a thermal–fluid–structural coupling model that accounts for molten iron flow and solidification, this study, building on thermal stress analysis of the hearth lining, proposes a method to determine the critical strength-based erosion boundary of the lining, using the compressive strength of carbon bricks as the criterion. It also investigates the influence of factors such as dead iron layer depth, tapping productivity, and molten iron temperature on the thermal stress-driven erosion boundary. The findings reveal that the depth of the dead iron layer determines the morphology of the hearth lining’s erosion. With increasing depth, the erosion pattern transitions from an elephant foot profile to a wide-face profile, while the radial erosion depth first increases and then decreases. Both increased tapping productivity and elevated molten iron temperature do not change the erosion shape but aggravate the erosion degree and induce axial displacement of the erosion zone. The research findings are of great significance for deepening the understanding of thermal stress damage in the hearth lining and provide an effective reference for long-term hearth design. Subsequent validation with a large amount of industrial data will further enhance the practical applicability of the proposed method.

1. Introduction

The hearth is the core component of a BF for storing molten iron, and its service life directly dictates the furnace’s campaign life [1,2,3]. During BF operation, the hearth lining is subjected to long-term exposure to the complex thermochemical environment of high-temperature molten slag and iron, with the resulting irreversible progressive erosion representing its primary failure mode [4,5]. When the erosion depth reaches the critical safety threshold, the hearth’s structural stability degrades sharply, and the risk of molten slag and iron leakage increases drastically. This forces the BF into unplanned shutdowns for maintenance, thereby severely jeopardizing the safe and stable operation of the BF system [6]. Therefore, the in-depth understanding of the mechanism of hearth erosion has become a key issue for breaking the technical bottleneck in BF long-life technology. However, due to the black box nature of BF and the complex physicochemical coupling mechanisms during the erosion process of the hearth lining [7,8,9], the development of hearth erosion is difficult to effectively predict through experimental methods [10,11]. Against this backdrop, numerical simulation, as an important supplementary research method, provides critical technical support for predicting erosion based on the BF hearth’s erosion mechanism [12]. Li et al. [13] established a mathematical model for molten iron flow at the BF hearth bottom and analyzed the influence of deadman floating behavior on molten iron flow and wall shear stress. Ni et al. [14] integrated the numerical analysis of iron flow and in-furnace heat transfer to investigate the hearth erosion of No. 1 BF of Wuhan Iron and Steel Corporation (WISCO). They simulated the distributions of wall shear stress and hearth temperature and analyzed the hearth sections with high erosion risk. Zhang et al. [15] established a tapping calculation model for the BF hearth considering the carbon mass transfer process and analyzed the effects of factors such as the state of the deadman, liquid iron production, inlet carbon concentration, and porosity of the coke region on the carbon brick erosion in the BF hearth. The above studies explicitly identify the causes and key drivers of hearth erosion, providing valuable references for the safe operation of BFs. However, these models generally assume a geometric–static framework. This assumption cannot capture the feedback among erosion morphology, flow field, and temperature field. Consequently, it is difficult to simulate the evolution and long-term trends of hearth erosion.

For the research on hearth erosion evolution and long-term trends, models based on the “inverse heat transfer problem” are widely adopted in engineering. Zhang et al. [16] developed a wear model for hearth erosion and iron skull formation. Based on thermocouple readings from the hearth lining, they solved a series of inverse heat-conduction problems for coaxial vertical slices. This approach enables rapid calculation of erosion lines and iron skull lines within the hearth. Helle et al. [17] constructed a lining wear model based on the inverse heat conduction problem, analyzing the evolution of lining morphology under different operating conditions, including stable operation and severe disturbances in the BF. The above studies have analyzed changes in hearth erosion under various production conditions, providing a reliable basis for optimizing BF operations. However, this method relies on real-time monitoring data of hearth production, exhibits a significant time lag, and thus is difficult to predict potential erosion risks in advance.

To integrate the advantages of the aforementioned methods and overcome their limitations, Liu et al. [18] established a CFD-based iterative model to simulate the progressive erosion of the hearth lining. This model couples fluid flow and heat transfer, with molten iron penetration identified as the primary erosion mechanism. It uses the 1150 °C isotherm as the erosion boundary and dynamically updates the flow and temperature fields. Through these couplings and updates, the model reveals the morphological evolution of the hearth lining under the combined action of molten iron, solidified iron layer, and residual refractory materials. Built on a clear physical mechanism, this model can effectively reflect the multi-field coupling process. Nevertheless, since its judgment relies on the isotherm criterion, the resulting erosion profile is relatively smooth, making it difficult to predict the non-uniform, concave erosion morphology that is prone to occur in the hearth corner region.

During the operation of a BF, a significant temperature difference exists between the interior and exterior of the hearth. Restricted by the mutual constraints of the BF structure, this temperature difference inevitably induces thermal stress in the refractory materials of the hearth lining [19,20]. In most existing thermal stress analyses of the hearth, the hot surface of the lining is usually treated as an isothermal boundary. This simplification ignores the actual temperature distribution resulting from molten iron flow, external cooling, and local erosion. Such a uniform temperature field will seriously affect the authenticity of the stress field in the hearth lining. Wang et al. [21] employed numerical simulation to model the flow of high-temperature molten iron in the hearth, simulating the molten iron flow field, temperature field, and corresponding thermal stress field distribution during the initial operation stage of the hearth under different BF refractory masonry conditions. The study investigated the effects of refractory masonry structures on heat transfer, thermal stress, and erosion resistance and analyzed lining erosion during the initial hearth operation stage, providing scientific and reasonable guidance for optimizing BF hearth design. Nevertheless, it did not consider the influence of hearth stress on the evolution of lining erosion morphology.

Studies [22,23] have confirmed that the erosion of BF linings is a complex, multi-factor coupled process. Among these factors, the synergistic effect of three key mechanisms constitutes the core cause of lining spalling failure: thermal stress-induced cracks, zinc and alkali metal corrosion, and carbon dissolution by molten iron. When the carbon brick structure is intact, zinc and alkali metal vapors can hardly penetrate its interior. Meanwhile, molten iron dissolution is confined to the brick surface. Consequently, the erosion rate remains slow. However, thermal stress-induced microcracks and macrocracks in carbon bricks provide channels for the penetration of zinc, alkali metal vapors, and molten iron. During penetration into the hearth lining, zinc and alkali metal vapors, together with molten iron, cool and condense, forming oxides. These oxides not only fill the pores of carbon bricks but also significantly exacerbate their internal embrittlement. Eventually, this leads to spalling failure of carbon bricks and significantly accelerates the hearth erosion process. Thus, microcracks and macrocracks induced by thermal stress are the primary prerequisite for spalling failure of hearth linings.

In previous studies, we established a thermal–fluid–structural sequential coupling model that considers molten iron flow and solidification [24]. This model can effectively analyze the effects of operating parameters and deadman state on the thermal stress of hearth linings with severe concave erosion. The study found that the hot surface of carbon bricks is mainly subjected to compressive stress, and crack initiation originates from compressive stress concentration. As a standard mandatory inspection index for carbon bricks, compressive strength has distinct advantages: it provides authoritative and reproducible data. Specifically, it serves as the core basis for material selection in BF design. Based on this understanding and the analysis of the hearth lining thermal stress, this paper proposes a search method for the lining’s critical strength-based erosion boundary. The compressive strength of carbon bricks is adopted as the criterion for this method. This approach systematically analyzes the thermal–stress–dominated erosion mechanism of the hearth lining. It also discusses the effects of key factors—including dead iron layer depth, tapping productivity, and molten iron temperature—on the critical stress erosion boundary. It thereby effectively predicts the erosion risk associated with the hearth structure and operational intensity. Compared with existing methods, the method proposed in this study significantly improves the prediction capability for areas prone to localized erosion, such as the hearth corner. The research results are of great significance for deepening the understanding of the stress–erosion mechanism of the hearth lining and provide an effective reference for long-term hearth design.

2. Materials and Methods

Based on thermal stress analysis and the material strength threshold, this paper proposes a method for determining the critical strength-based erosion boundary, consisting of two parts, thermal stress calculation and boundary search, as shown in Figure 1.

2.1. Thermal Stress Analysis Model of Hearth Lining

This study takes the hearth of the LG-5 BF (Liuzhou Iron and Steel Company, Liuzhou, China) as the research subject and develops a thermal–fluid–structural sequential coupling calculation model (Figure 2). Given that the temperature field exhibits a quasi-steady-state characteristic during BF operation, and hearth lining structural damage is mostly a sudden event rather than a gradual process, the adoption of the sequential coupling method for simulation analysis is reasonable and sufficient. This model’s calculation process comprises two main parts. First, in the thermal–flow coupling module, the quasi-steady temperature field of the lining is obtained through a steady-state solution of the flow and heat transfer of molten iron in the hearth [25]; subsequently, in the thermal stress analysis module, the aforementioned temperature field is applied to the structural model as a thermal load and the thermal stress distribution of the hearth lining. This model is based on the following key assumptions: neglecting radiative heat transfer within the hearth and plastic deformation of the lining materials.

2.1.1. Physical Model

The LG-5 BF has an effective volume of 1580 m³, and its hearth lining is composed of ultra-microporous carbon bricks (UMCBs), microporous carbon bricks (MCBs), and graphite bricks (GBs), with the masonry structure shown in Figure 3. The taphole of the hearth has an inner diameter of 60 mm and an inclination angle of 12°, and the mud block (MB) is simplified to a frustum with a height of 1000 mm. The deadman is modeled as a frustum-shaped porous region with a porosity of 0.3, and the surrounding area is a coke-free zone.

The computational model simplifies the hearth structure by neglecting the cooling stave structure and retaining only the ramming mass (RM) layer (80 mm thick) and the furnace shell (with an equivalent thickness of 71.28 mm), as shown in Figure 4. Material properties are listed in

Table 1. Physical properties of solid materials in the computational model [24].

Property	Density /kg·m−3	Specific Heat Capacity /J·kg−1·K−1	Thermal Conductivity /W·m−1·K−1	Young’s Modulus /GPa	Poisson’s Ratio	Thermal Expansion Coefficient /10−6·K−1
GB	1780	840	46.61 − 0.01342 T	7.9	0.15	2.16
MCB	1620	840	8.88 + 0.0044 T	7.9	0.15	2.84
UMCB	2150	840	13.58 + 0.005 T	7.9	0.15	3.38
Ramming mass	1650	876	12.5	15	0.1	3
Shell	7840	465	48	200	0.3	5.87

and

Table 2. Physical properties of molten iron [26].

Density /kg·m−3	Specific Heat Capacity /J·kg−1·K−1	Thermal Conductivity /W·m−1·K−1	Viscosity /kg·m−1·s−1	Latent Heat /J·kg−1	Solidification Temperature /K	Melting Temperature /K
6700	756	0.0158 T	0.007	103,343	1423	1573

, where the thermal conductivity is a temperature-dependent parameter, and T denotes temperature.

2.1.2. Mathematical Model

Molten iron flow in the BF hearth is a typical porous media flow problem [27,28,29]. Herein, molten iron is regarded as an incompressible fluid, and the solution to its flow process relies on the establishment of mass conservation and momentum conservation, whose equations are shown in Equations (1) and (2).

$$\nabla \cdot (\rho \overrightarrow{v})=0$$

(1)

$$\nabla \cdot (\rho \overrightarrow{v}\cdot \overrightarrow{v})=-\nabla p+\nabla \cdot {\mu }_{\mathrm{eff}}(\nabla \overrightarrow{v}+\nabla {\overrightarrow{v}}^{\mathrm{T}})+\rho \overrightarrow{g}+S_{\mathrm{DM}}$$

(2)

The macroscopic flow behavior of molten iron in the deadman of the BF hearth is described by adding a momentum source term to the fluid’s momentum equation [30]. This source term represents resistance of the porous medium to the fluid, consisting of a viscous loss term and an inertial loss term [31]; its specific form is as follows:

$$S_{\mathrm{DM}}={\displaystyle \frac{150\mu {(1-\phi )}^2}{{\phi }^3{d}_c^2}}\overrightarrow{v}+{\displaystyle \frac{1.75\rho (1-\phi )}{{\phi }^3{d}_c}}|\overrightarrow{v}|\overrightarrow{v}$$

(3)

Energy transfer during molten iron flow relies on the energy transport equation based on the local thermal equilibrium assumption, as shown in Equation (4). Under this assumption, the effective thermal conductivity in the energy equation is formed by the weighted combination of the thermal conductivities of molten iron and solid phases, weighted by porosity, and its expression is given in Equation (5).

$$\nabla \cdot \left[\rho \left(h+{\displaystyle \frac{{\overrightarrow{v}}^2}{2}}\right)\right]=\nabla \cdot \left({\lambda }_{\mathrm{eff}}\nabla T-\sum _i{h}_i{\overrightarrow{J}}_i+{\mu }_{\mathrm{eff}}(\nabla \overrightarrow{v}+\nabla {\overrightarrow{v}}^T)\cdot \overrightarrow{v}\right)+S$$

(4)

$${\lambda }_{\mathrm{eff}}=\phi {\lambda }_{\mathrm{s}}+(1-\phi ){\lambda }_{\mathrm{f}}$$

(5)

The formation of the solidified iron protective layer is simulated using the enthalpy–porosity method [32]. The mushy zone between the solidus and liquidus temperatures of molten iron is treated as a porous medium containing a solid–liquid mixture, with the liquid volume fraction determined by temperature. The enthalpy in the energy equation is treated uniformly to account for both the latent heat of phase change and sensible heat. Latent heat is a key parameter that determines the effect of solidification and can be expressed as a function of the liquid volume fraction, as shown in Equations (6) and (7).

$$\left\{\begin{array}{ccc}\varpi =0& \mathrm{if}& T<T_{\mathrm{s}}\\ \varpi =1& \mathrm{if}& T>T_{\mathrm{l}}\\ \varpi ={\displaystyle \frac{T-T_{\mathrm{s}}}{T_{\mathrm{l}}-T_{\mathrm{s}}}}& \mathrm{if}& T_{\mathrm{s}}<T<T_{\mathrm{l}}\end{array}\right.$$

(6)

$$h=h_s+\Delta h=h_s+\mathsf{𝜛}L$$

(7)

The Reynolds number of molten iron flow calculated based on the actual operating parameters of the BF hearth is much higher than the critical value, indicating that the molten iron in the hearth is in a fully developed turbulent flow state [33]. For this reason, this study adopts the k-ε turbulence model and mathematically describes the turbulent characteristics of molten iron by solving the transport equations for turbulent kinetic energy and turbulent dissipation rate (Equations (8) and (9)).

$$\nabla \cdot \left(\rho k\overrightarrow{v}\right)=\nabla \cdot \left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\right)\nabla k\right]+G_k-\rho \epsilon +S_k$$

(8)

$$\nabla \cdot \left(\rho \epsilon \overrightarrow{v}\right)=\nabla \cdot \left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_{\epsilon }}}\right)\nabla \epsilon \right]+\rho C_1{S}_k\epsilon -\rho C_2{\displaystyle \frac{{\epsilon }^2}{k+\sqrt{\nu \epsilon }}}+S_{\epsilon }$$

(9)

Since the hearth lining is a brittle material, its stress distribution is solved based on the thermoelastic constitutive equation [33] to simulate the material’s elastic behavior under thermo-mechanical coupling effects. According to thermoelasticity theory, the total strain can be decomposed into a linear superposition of mechanical and thermal strains. Among them, thermal strain manifests as volume expansion, inducing only normal strain, whose value is jointly contributed by linear expansion, Poisson effect, and thermal expansion. In contrast, the shear strain is described by the shear Hooke’s law. Within this theoretical framework, the thermal stress of the hearth lining is jointly established and solved using the mechanical equilibrium equation (Equation (10)), geometric compatibility equation (Equation (11)), and thermoelastic constitutive equation (Equation (12)).

$$\left\{\begin{array}{l}{\displaystyle \frac{\mathsf{\partial }{\sigma }_x}{\mathsf{\partial }x}}+{\displaystyle \frac{\mathsf{\partial }{\tau }_{y_x}}{\mathsf{\partial }y}}+{\displaystyle \frac{\mathsf{\partial }{\tau }_{zx}}{\mathsf{\partial }z}}=0\hfill \\ {\displaystyle \frac{\mathsf{\partial }{\sigma }_y}{\mathsf{\partial }y}}+{\displaystyle \frac{\mathsf{\partial }{\tau }_{xy}}{\mathsf{\partial }x}}+{\displaystyle \frac{\mathsf{\partial }{\tau }_{zy}}{\mathsf{\partial }z}}=0\hfill \\ {\displaystyle \frac{\mathsf{\partial }{\sigma }_z}{\mathsf{\partial }z}}+{\displaystyle \frac{\mathsf{\partial }{\tau }_{xz}}{\mathsf{\partial }x}}+{\displaystyle \frac{\mathsf{\partial }{\tau }_{yz}}{\mathsf{\partial }y}}=0\hfill \end{array}\right.$$

(10)

$$\left\{\begin{array}{l}{\epsilon }_x={\displaystyle \frac{\mathsf{\partial }u}{\mathsf{\partial }x}}, {\gamma }_{xy}={\displaystyle \frac{\mathsf{\partial }u}{\mathsf{\partial }y}}+{\displaystyle \frac{\mathsf{\partial }v}{\mathsf{\partial }x}}\hfill \\ {\epsilon }_y={\displaystyle \frac{\mathsf{\partial }v}{\mathsf{\partial }y}}, {\gamma }_{yz}={\displaystyle \frac{\mathsf{\partial }v}{\mathsf{\partial }z}}+{\displaystyle \frac{\mathsf{\partial }\omega }{\mathsf{\partial }y}}\hfill \\ {\epsilon }_z={\displaystyle \frac{\mathsf{\partial }\omega }{\mathsf{\partial }z}}, {\gamma }_{zx}={\displaystyle \frac{\mathsf{\partial }u}{\mathsf{\partial }z}}+{\displaystyle \frac{\mathsf{\partial }\omega }{\mathsf{\partial }x}}\hfill \end{array}\right.$$

(11)

$$\left\{\begin{array}{l}{\epsilon }_x={\displaystyle \frac{1}{E_T}}\left[{\sigma }_x-{\mu }_{\mathrm{p}}\left({\sigma }_y+{\sigma }_z\right)\right]+\alpha \left(T-T_0\right)\hfill \\ {\epsilon }_y={\displaystyle \frac{1}{E_T}}\left[{\sigma }_y-{\mu }_{\mathrm{p}}\left({\sigma }_x+{\sigma }_z\right)\right]+\alpha \left(T-T_0\right)\hfill \\ {\epsilon }_z={\displaystyle \frac{1}{E_T}}\left[{\sigma }_z-{\mu }_{\mathrm{p}}\left({\sigma }_x+{\sigma }_y\right)\right]+\alpha \left(T-T_0\right)\hfill \end{array}\right., \left\{\begin{array}{c}{\gamma }_{yz}={\displaystyle \frac{2(1+{\mu }_{\mathrm{p}})}{E_T}}{\tau }_{yz}\\ {\gamma }_{zx}={\displaystyle \frac{2(1+{\mu }_{\mathrm{p}})}{E_T}}{\tau }_{zx}\\ {\gamma }_{xy}={\displaystyle \frac{2(1+{\mu }_{\mathrm{p}})}{E_T}}{\tau }_{xy}\end{array}\right.$$

(12)

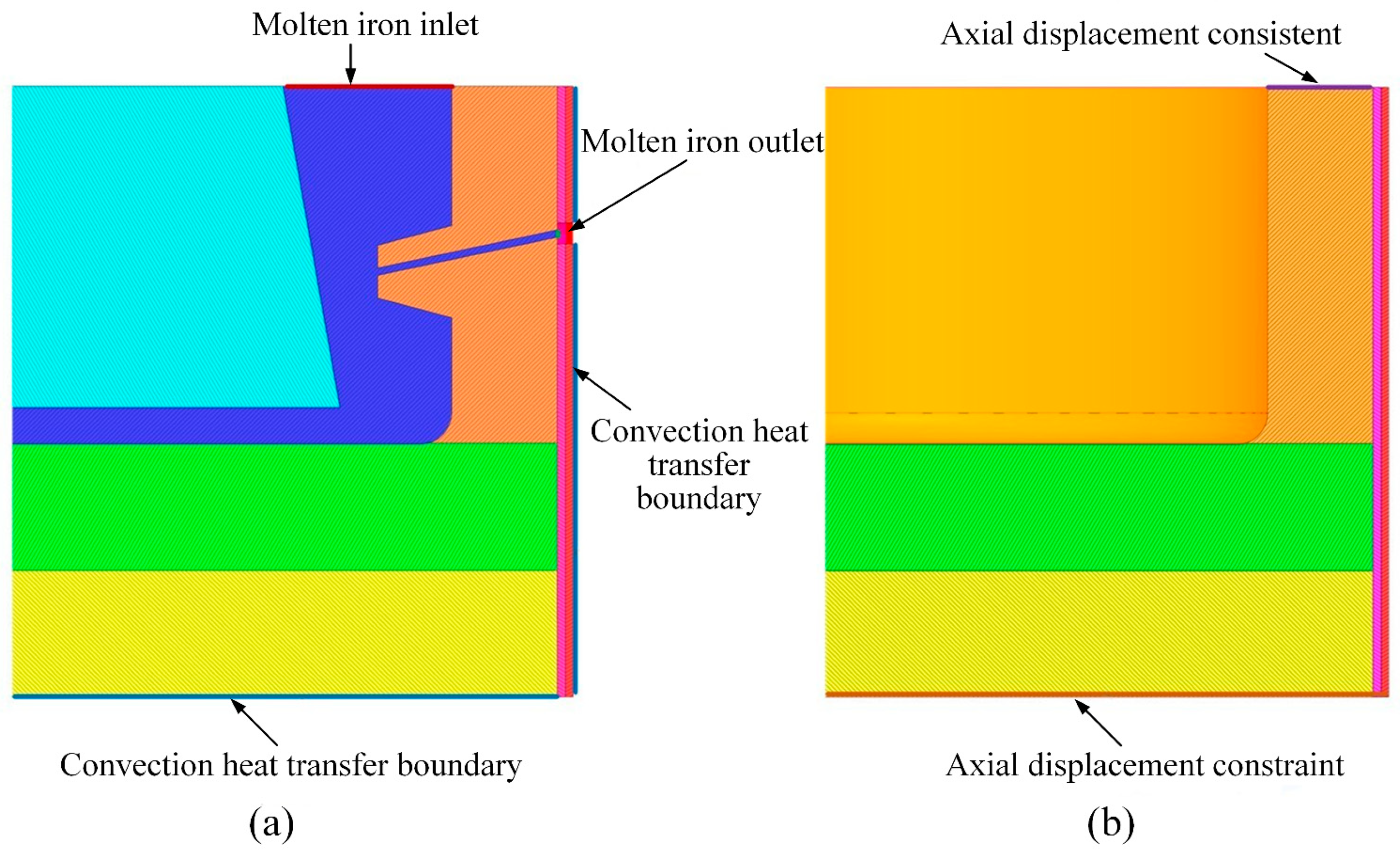
2.1.3. Boundary Conditions

The boundary conditions of the thermal–fluid–structural coupling model for the BF hearth lining consist of two parts: thermal–fluid coupling boundaries and stress analysis boundaries. The boundary conditions of the hearth’s thermal–fluid coupling model are classified into inlet–outlet conditions, heat transfer boundaries, and adiabatic boundaries, as illustrated in Figure 5a. The calculation of boundary conditions assumes average operating conditions. The molten iron inlet of the hearth is configured as a mass flow inlet, with an inlet molten iron temperature of 1773 K and a flow rate of 68.3 kg·s⁻¹. This flow rate value is calculated via Formulas (13) and (14) based on the BF’s effective utilization coefficient (set to 2.8 t·m⁻³·d⁻¹). The tapping hole is defined as a pressure outlet, with the pressure specified as standard atmospheric pressure.

$$M_i=r{V}_{\mathrm{eff}}$$

(13)

$$m_i={\displaystyle \frac{4000M_i}{3\times 24\times 60\times 60}}$$

(14)

The convective heat transfer coefficients for the convective heat transfer boundaries of the BF shell and hearth bottom are calculated by converting the convective heat transfer coefficient of the cooling water pipe wall surfaces, using the calculation methods for convective heat transfer coefficients of planar and cylindrical surfaces, with values of 500 W·m⁻²·K⁻¹ and 40 W·m⁻²·K⁻¹, respectively. Among them, the convective heat transfer coefficient of the cooling water pipe wall surfaces (with a cooling water flow velocity of 2.5 m·s⁻¹) at a cooling water temperature of 30 °C is obtained via empirical Formula (15), and the convective heat transfer coefficient of the cooling water pipe center plane is calculated using the wetted perimeter Formula (16). The calculation formulas for the convective heat transfer coefficients of planar and cylindrical surfaces are presented in Formulas (17) and (18), respectively.

$$h_w=208.8+47.5v_w$$

(15)

$$h_p={\displaystyle \frac{\pi d_p}{J_D}}{h}_w$$

(16)

$$h_f={\displaystyle \frac{1}{\frac{1}{h_p}+\frac{\Delta z}{{\lambda }_m}}}$$

(17)

$$h_{in}={\displaystyle \frac{r_{in}}{r_{out}}}\times {\displaystyle \frac{h_{out}{\lambda }_m}{{\lambda }_m+h_{out}{r}_{out}\ln (r_{out}/r_{in})}}$$

(18)

In the stress calculation model, the axial displacements of carbon bricks, packing material, and the bottom of the BF shell are constrained, and a uniform axial constraint is applied to the top of the carbon bricks [24], as illustrated in Figure 5b. In addition, the contacts between the carbon bricks, the packing layer, and the BF shell are accounted for, with the contact type set to frictionless.

2.1.4. Mesh Model

The hearth lining model is discretized using a tetrahedral/hexahedral hybrid mesh, as illustrated in Figure 6. The total number of meshes in this model is 5,505,237, among which the number of meshes in the solid region is 3,109,025, and that in the fluid region is 2,396,212. The target mesh sizes for local refinement are set as follows: 0.08 m for the fluid region, 0.01 m for the tapping hole region, and 0.06 m for the packing layer region. Five layers of inflation layer meshes are added at the interface between the molten iron and the carbon bricks, with a transition ratio of 0.272 and a growth rate of 1.05. The minimum orthogonal quality is 0.5. The mesh independence verification is presented in Figure 7. By comparing five mesh division schemes, all schemes converge, and the overall result variation rate is less than 1%, indicating that the mesh independence is valid.

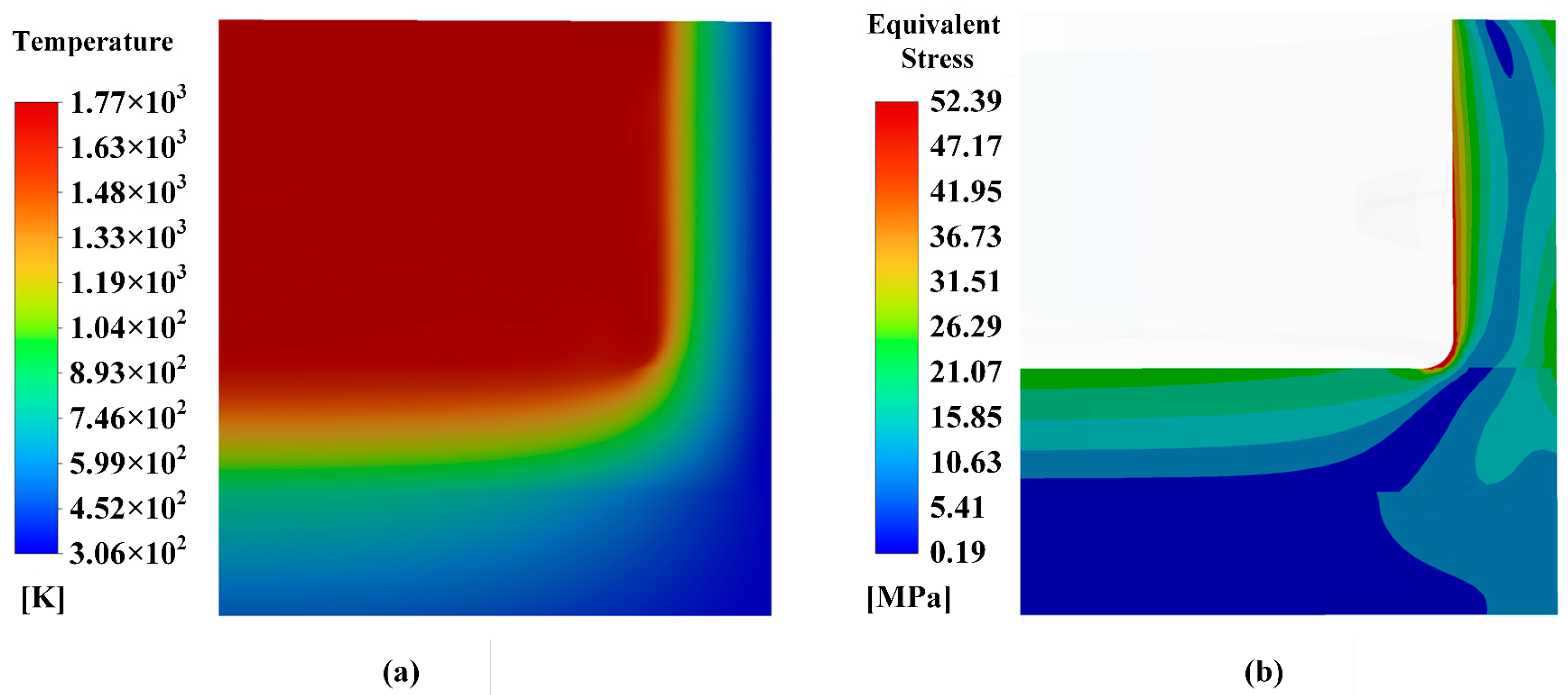
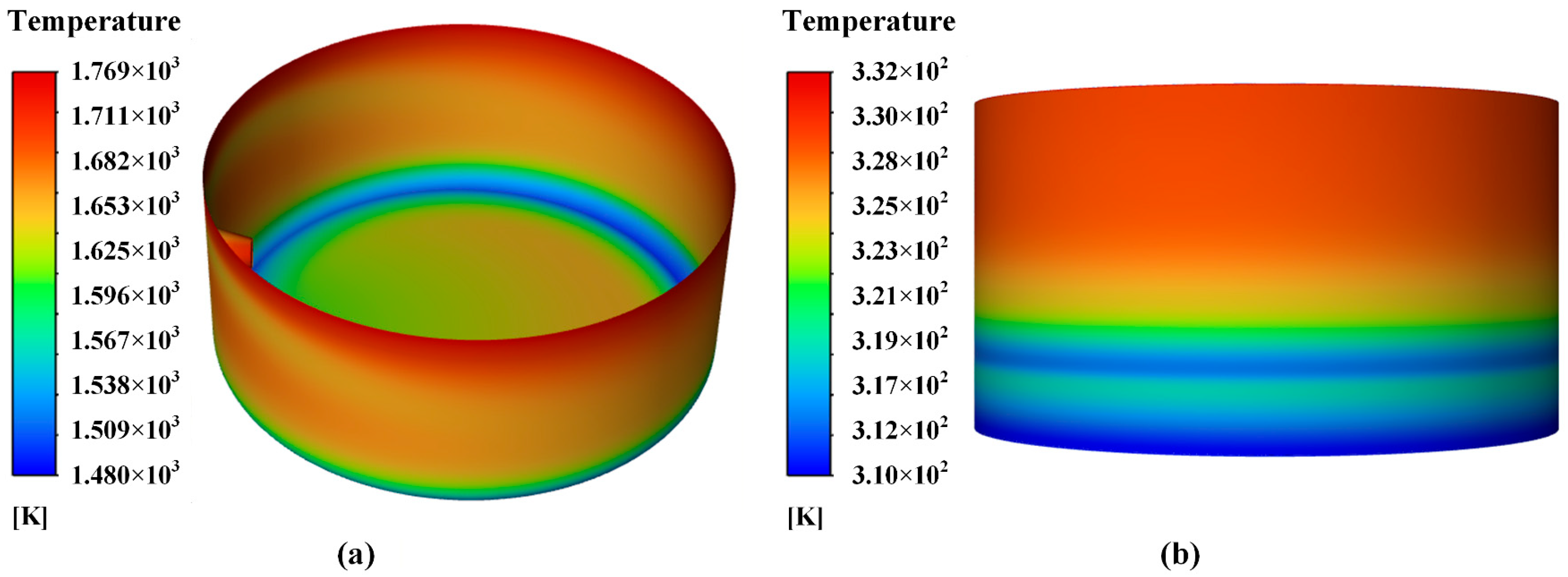
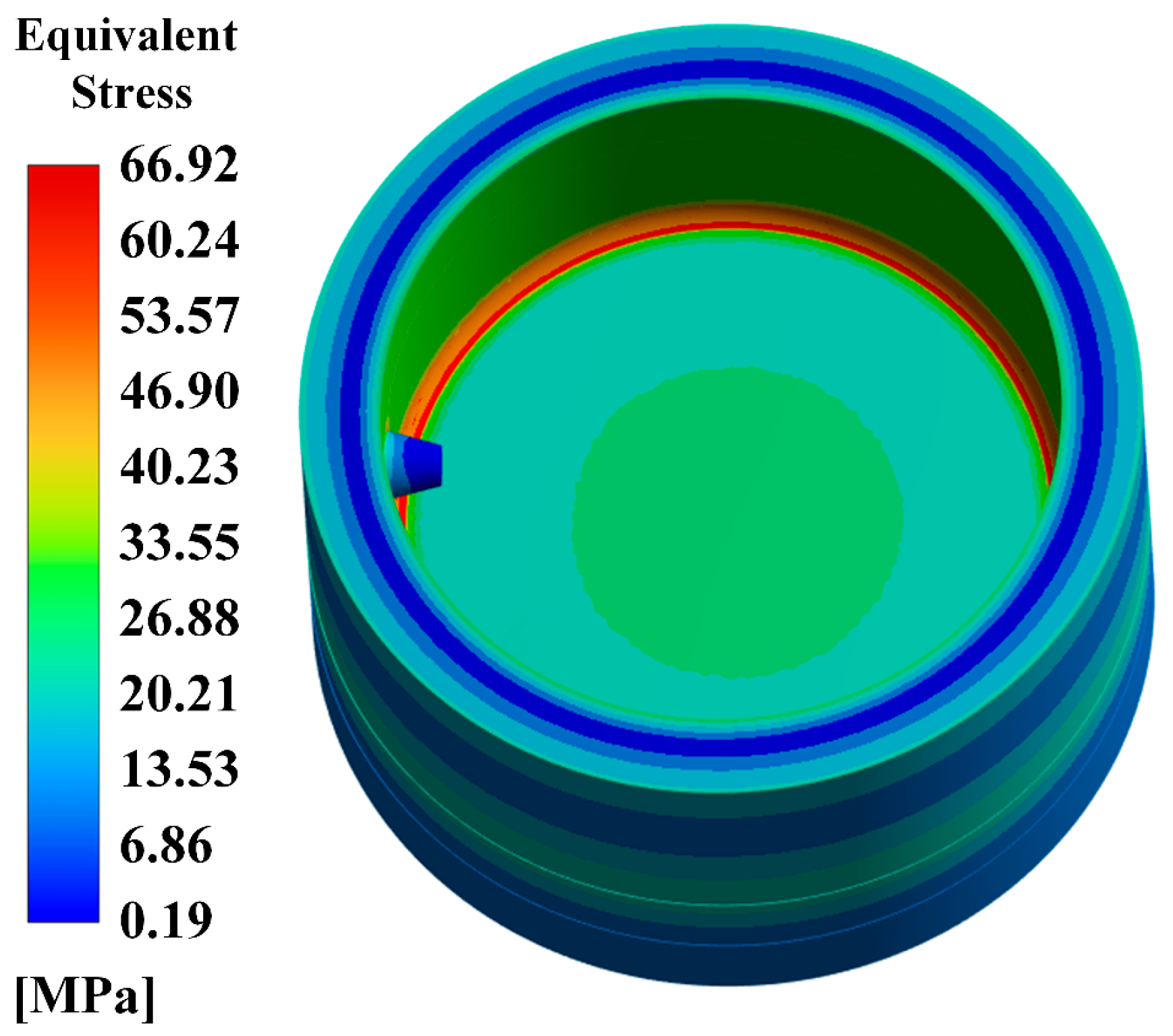
2.1.5. Results of Thermal–Fluid–Structural Coupling Model

The temperature and thermal stress distribution of the lining in the axial cross-section of the hearth taphole with a 15° angle are as shown in Figure 8. The temperature and thermal stress distributions of the hearth lining are relatively consistent, showing an overall trend of being higher inside and lower outside. The overall temperature ranges from 306 K to 1773 K, and the stress level ranges from 0.19 MPa to 52.39 MPa. Near the contact interface between molten iron and carbon bricks, due to the high temperature, thermal expansion deformation is significant, resulting in a high thermal stress level. The stress level in the hearth bottom area is generally lower than that in the hearth sidewall. In addition, affected by the masonry structure form, obvious stress concentration occurs in the hearth corner area, rendering this area a high-stress zone of the lining.

The temperature distribution at the key interfaces of the BF hearth is illustrated in Figure 9. The temperature at the contact surface between molten iron and the lining ranges from 1480 K to 1769 K, with higher temperatures in the inlet region and a gradual decrease along the furnace wall downward—this correlates with the residence time of molten iron in the hearth. The hearth corner exhibits the lowest temperature, ranging between the solidus (1423 K) and liquidus (1523 K) of molten iron, indicating that the molten iron here meets the solidification conditions but has not yet formed a stable solidified iron layer. This is primarily attributed to the high cooling intensity and abrupt geometric transition at this location. Additionally, a local high-temperature zone exists below the tapping hole, which is consistent with the existing simulation results. The temperature distribution of the furnace shell aligns with that of the furnace wall, ranging from 310 K to 332 K—below the safety warning threshold—and conforms to the temperature characteristics of a BF in the initial operation stage.

Figure 10 presents the thermal stress distribution of the hearth. The overall stress trend is consistent with the results of existing models [21]. Significant stress concentration is observed at the hearth corner, and the stress level increases circumferentially as it approaches the tapping hole. This distribution characteristic matches the actually observed erosion positions, further supporting the mechanism of thermal stress-driven erosion initiation.

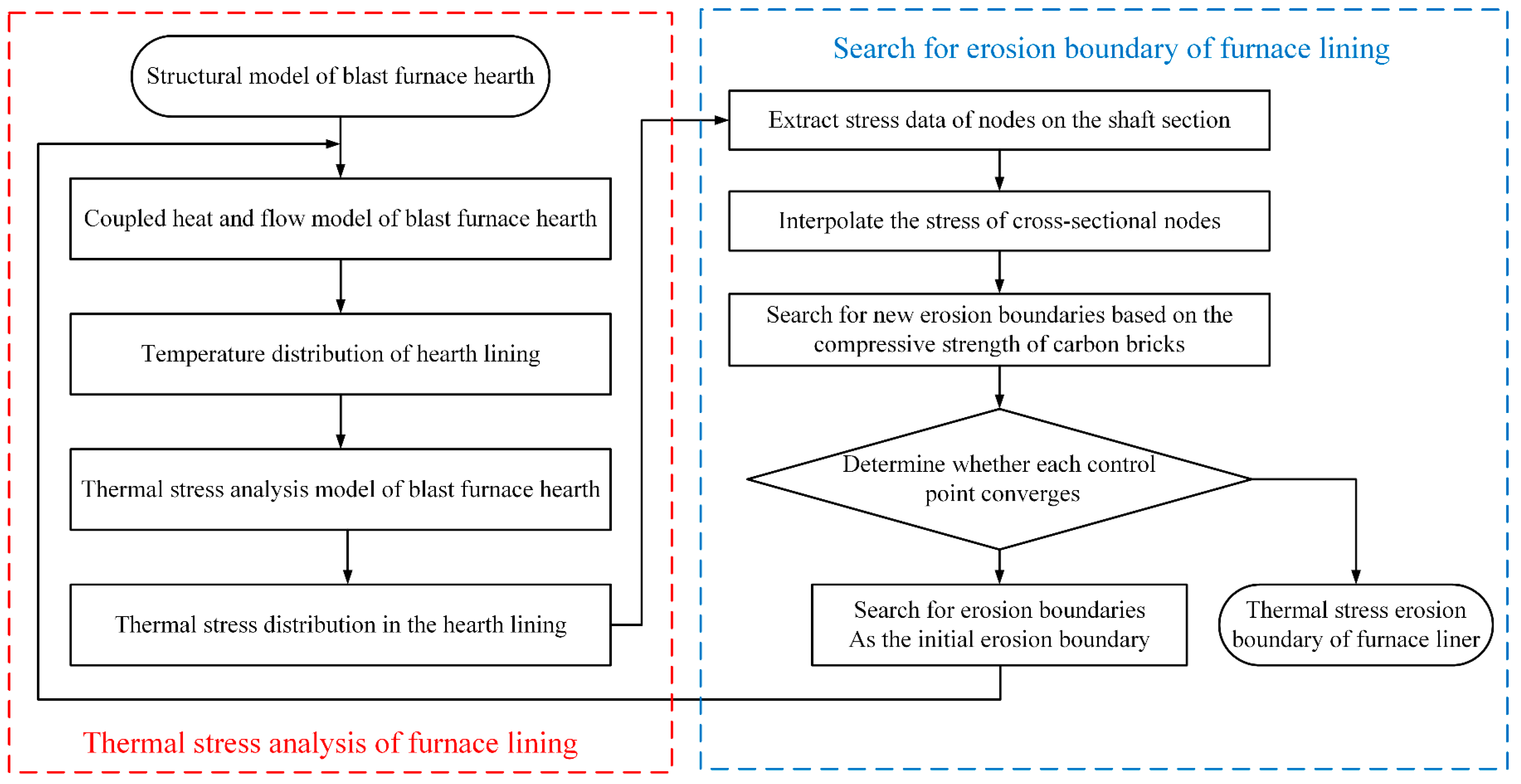
2.2. Search for Erosion Boundary Based on Lining Critical Strength

The search method for the hearth lining erosion boundary based on thermal stress analysis is illustrated in Figure 11. Taking the ultimate tensile strength of carbon bricks as the criterion, this method extracts valid control points by interpolating and verifying the thermal stress field of the axisymmetric section, then integrates and systematically sorts these points with existing boundary points, and finally iteratively generates the accurate erosion boundary that meets the strength criterion.

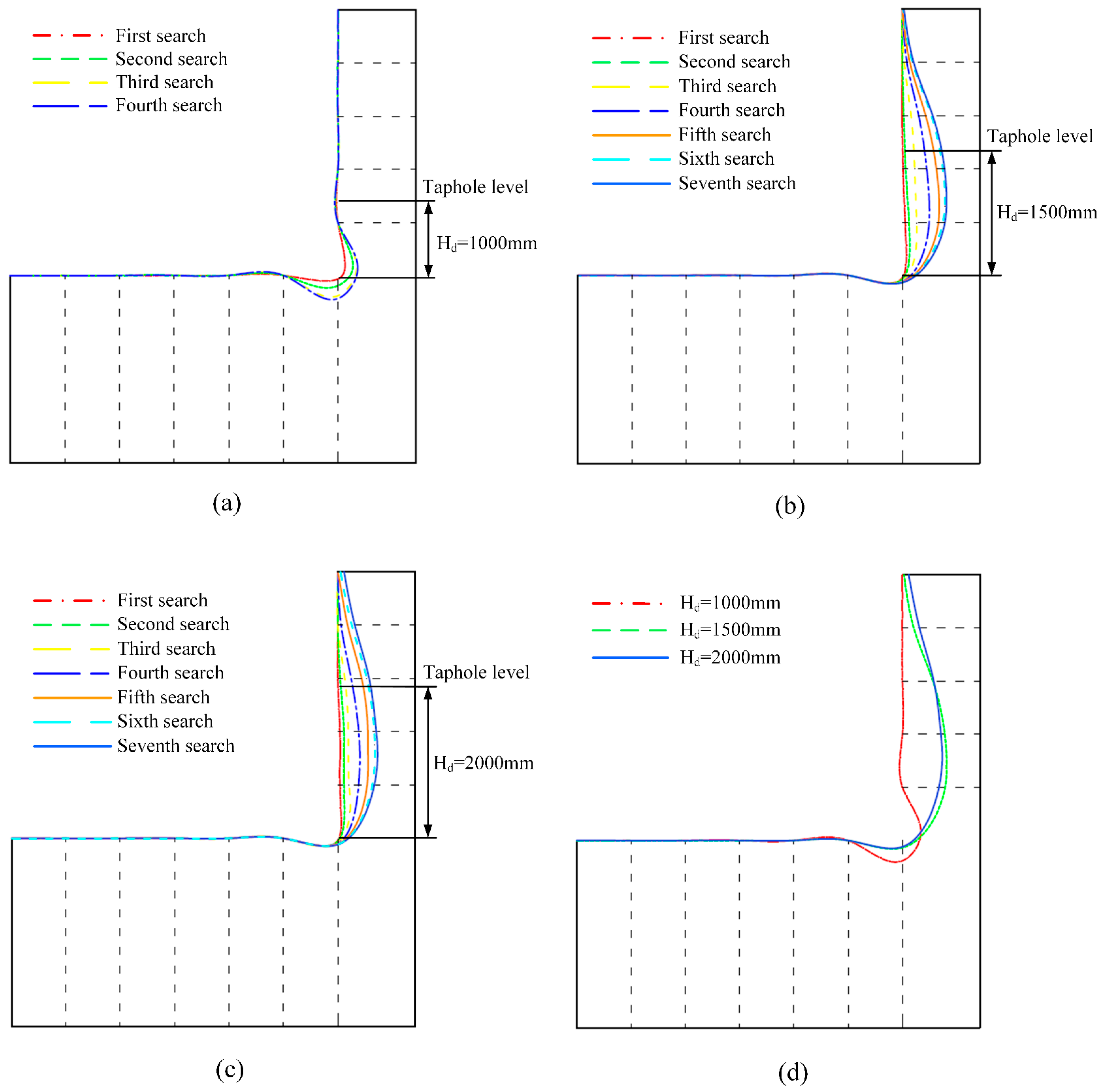
2.2.1. Search Method Description

Dense interpolation of thermal stress data at nodes along the hearth’s axial section improves the accuracy of isostress line searches in the lining [34]. Before interpolation, the effective calculation range must be limited according to the masonry structure to prevent distortion. Subsequently, a two-dimensional grid is established based on node coordinates, followed by dense linear interpolation. The distribution of isostress lines on the axial section of the lining is shown in Figure 12.

To achieve an accurate search of the erosion boundary, as illustrated in Figure 13, this study establishes seven evenly distributed regular control points (1–7) in the hearth bottom region for axially downward search and five evenly distributed regular control points (9–13) on the hearth sidewall for radially outward search [35]. Both the positions and search paths of the regular control points are fixed. Since the hearth sidewall is a weak zone of the hearth prone to local concave erosion, an additional non-fixed control point (No. 8) is added to capture the maximum axial erosion position in this zone.

Based on the compressive strengths of different carbon bricks (UMCB: 40 MPa; MCB: 30 MPa; GCB: 20 MPa), the control points on the corresponding isostress lines and the points with the maximum x-coordinate are extracted. After deduplication processing, the points with the smallest remaining lining thickness are retained. Subsequently, interpolation search is performed in the specified direction to replace old points with new ones, and the sorting is updated synchronously. Finally, the fitted erosion boundary and the distribution of control points are obtained and are shown in Figure 14.

2.2.2. Convergence Mechanism and Criterion

During the erosion of the BF hearth, the lining carbon bricks undergo spalling due to thermal stress and gradually thin, leading to a decrease in their overall thermal resistance and, in turn, a reduction in the hot-face temperature. When the hot-face temperature drops below the solidification point of molten iron, it solidifies to form a solidified iron layer. This study incorporates this solidification phase change behavior into the model. As illustrated in Figure 15, the solidified iron layer, with its relatively high thermal resistance, effectively inhibits heat transfer from the molten iron to the bulk carbon brick, thereby significantly reducing the temperature gradient inside the carbon bricks and consequently alleviating the thermal stress acting on the hearth lining. The reduction in thermal stress further stabilizes the erosion boundary, thereby yielding a definite critical stress.

In the upper-middle region of the hearth near the molten iron inlet, it is difficult to form a solidified iron layer due to the high temperature. If “carbon brick stress being lower than their compressive strength” is taken as the criterion for erosion cessation, the remaining thickness of the lining in this region would be significantly underestimated. Therefore, after ensuring the minimum number of iterations (3 times), the proposed search method employs the moving distance of the control points as the convergence criterion (set to 5%), as shown in Equation (19). When the movement of sidewall control points satisfies this condition, the search is stopped, thereby obtaining an erosion morphology more consistent with actual working conditions.

$${\displaystyle \frac{\Delta S_i}{L_i}}\times 100\%\le e_{\mathrm{s}}$$

(19)

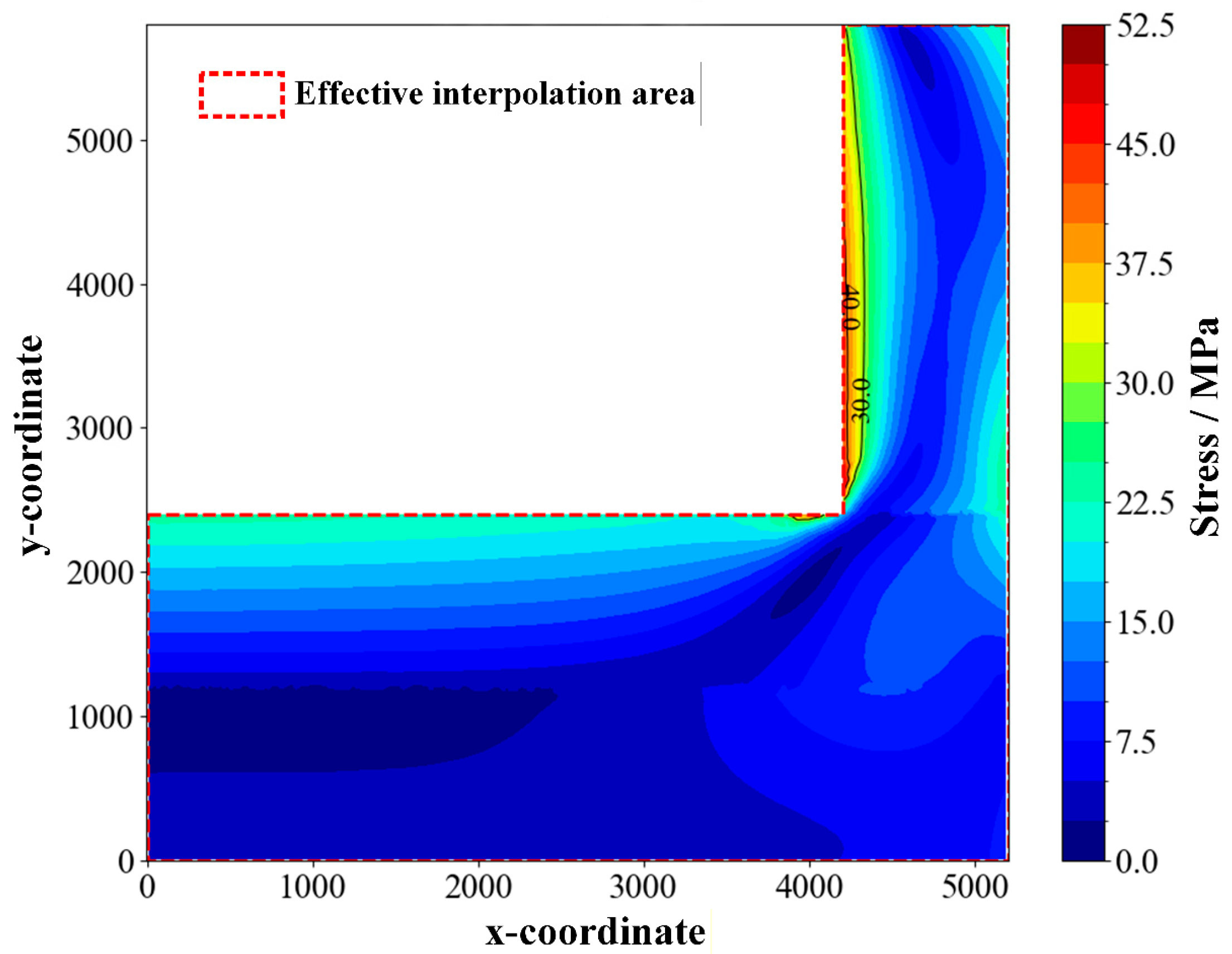
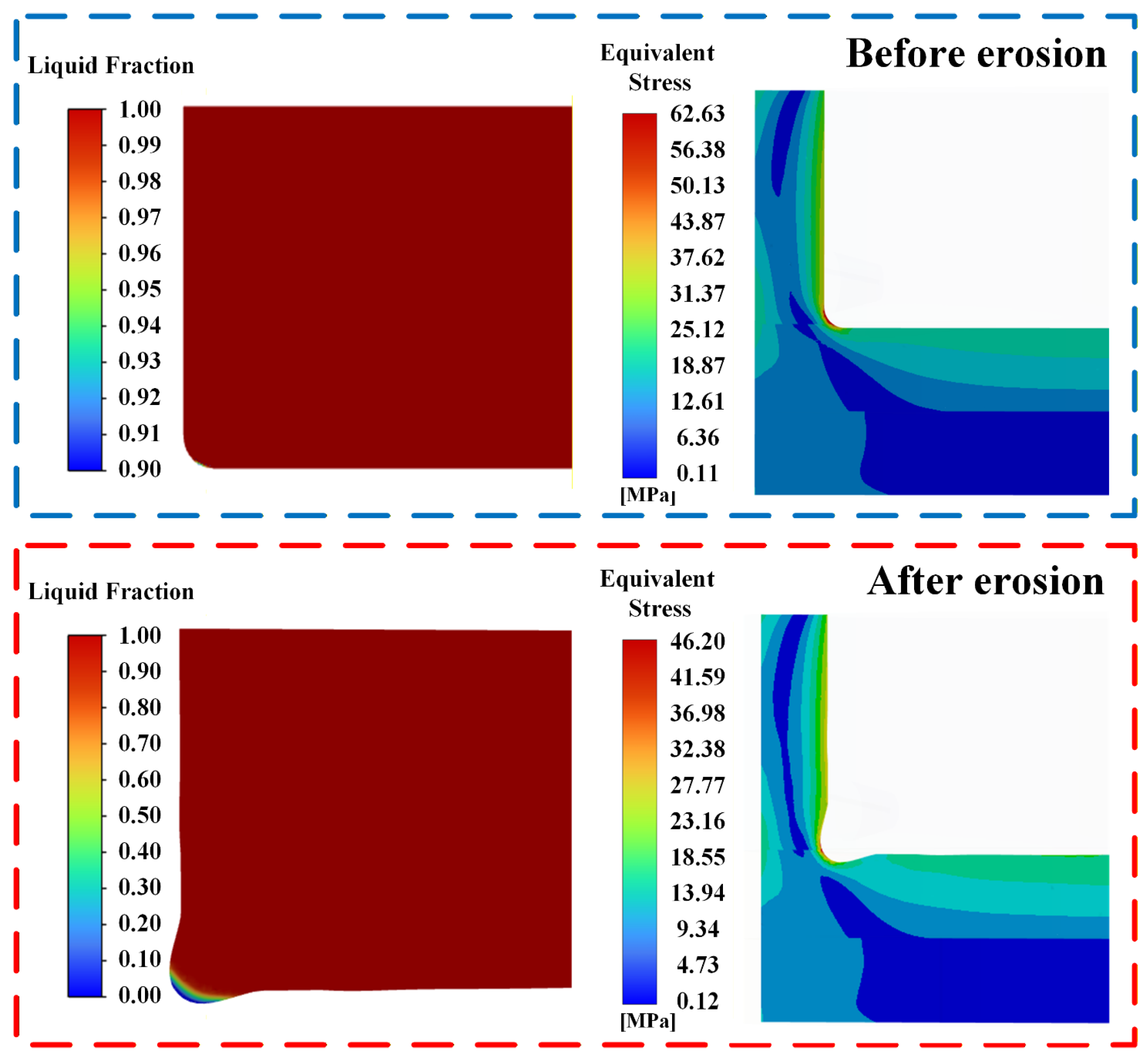
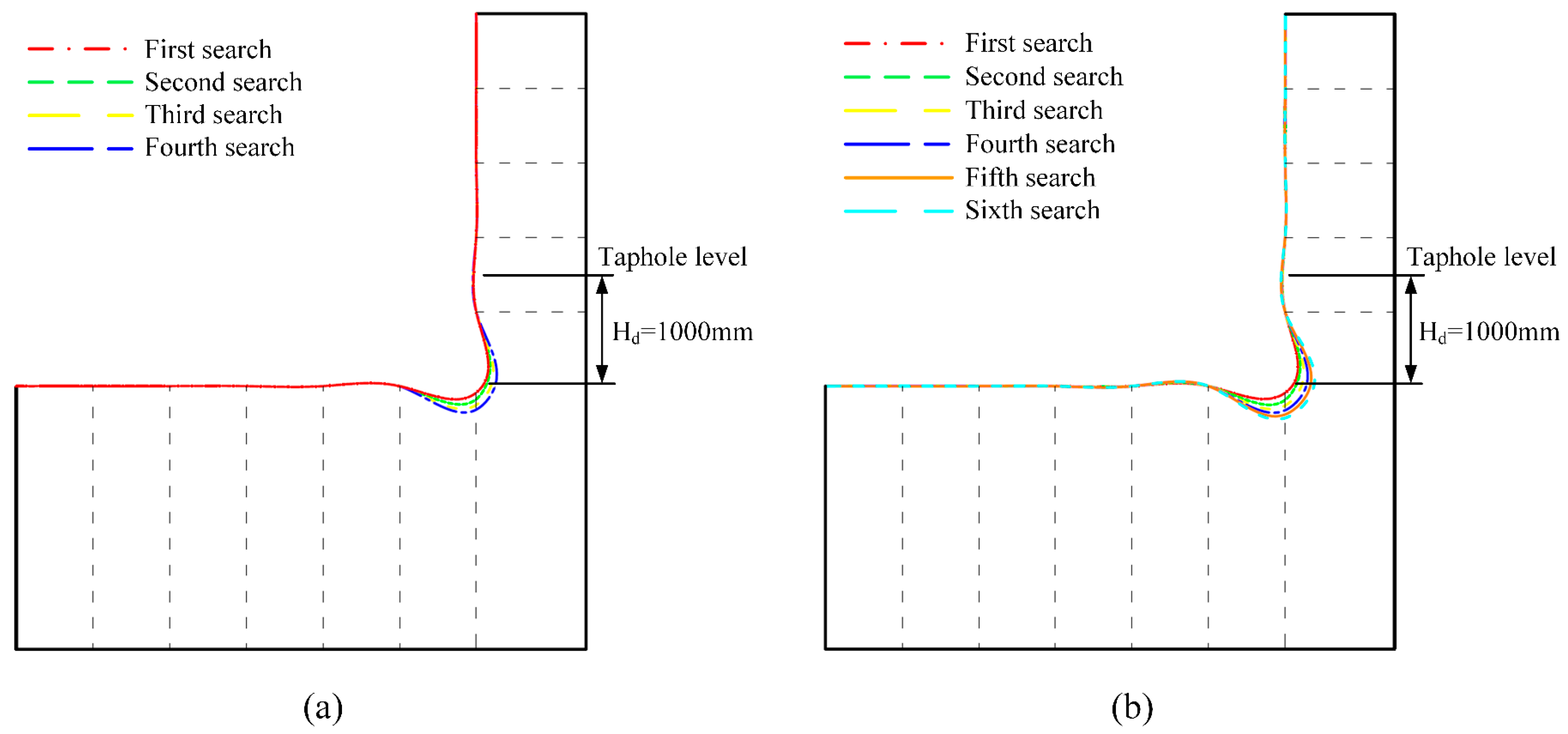
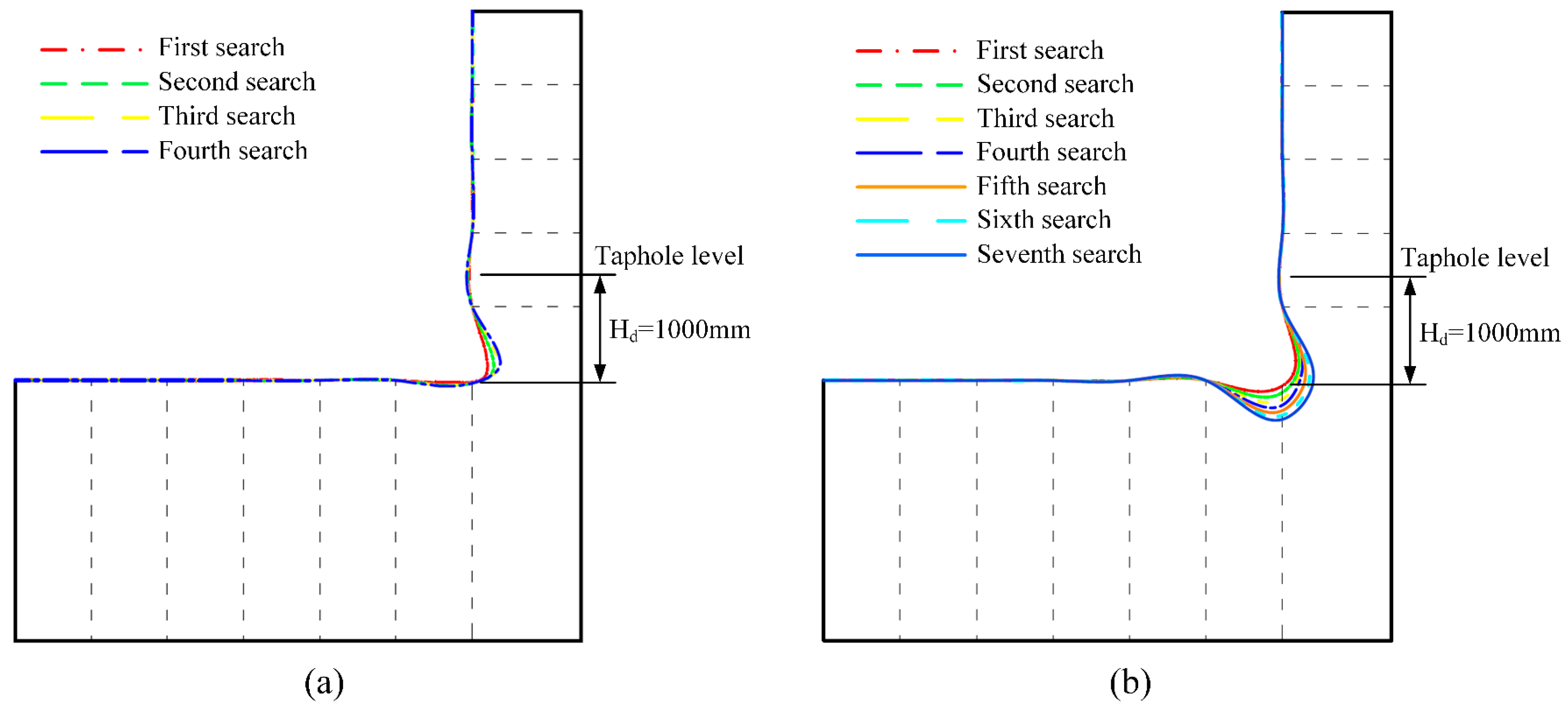
2.2.3. Validation of the Search Method

To verify the validity of the search results for the critical strength erosion boundary of the hearth lining, the on-site measured temperature data when the hearth lining first reaches a stable temperature state were selected, with the positions of each temperature monitoring point illustrated in Figure 3. These measured data were compared with the calculated temperatures at the same positions in the computational model corresponding to the 7th search result of the hearth lining erosion boundary under normal production conditions.

Table 3. Comparison of calculated and measured temperatures at monitoring points.

Temperature Monitoring Point	T1	T2	T3	T4	T5	T6	T7	T8	T9	T10
Measured/K	1136.8	645.9	784.2	576.4	639.3	713.4	759.8	768.5	723.7	716.8
Measured/K	1113.2	667.6	804.2	599.7	668.2	739.6	788.3	796.5	747.9	736.6
Error/%	2.08	3.35	2.55	4.04	4.53	3.67	3.75	3.64	3.34	2.76

presents the calculated and on-site measured temperatures of each monitoring point. It can be observed that the temperature errors at the monitoring points near the hearth corner (T4 and T5) are relatively large, with values of 4.04% and 4.53%, respectively, both of which are less than 5%. This meets the technical accuracy requirements of engineering practice, indicating that the calculated results for the lining’s critical strength erosion boundary are accurate and valid.

3. Results and Discussion

To systematically evaluate the impact of key operating parameters on the long-term stability of the BF hearth, this paper focuses on investigating the underlying mechanisms. Specifically, it explores how dead iron layer depth, tapping productivity, and molten iron temperature affect stress distribution and the evolution of the erosion boundary. A parametric study was conducted using the control variable method. This study quantitatively analyzes the influence of the aforementioned factors on the hearth thermal stress field and the critical strength line of carbon bricks. It thereby provides a theoretical basis for the long-term design of the BF hearth. Detailed results and analysis are as follows.

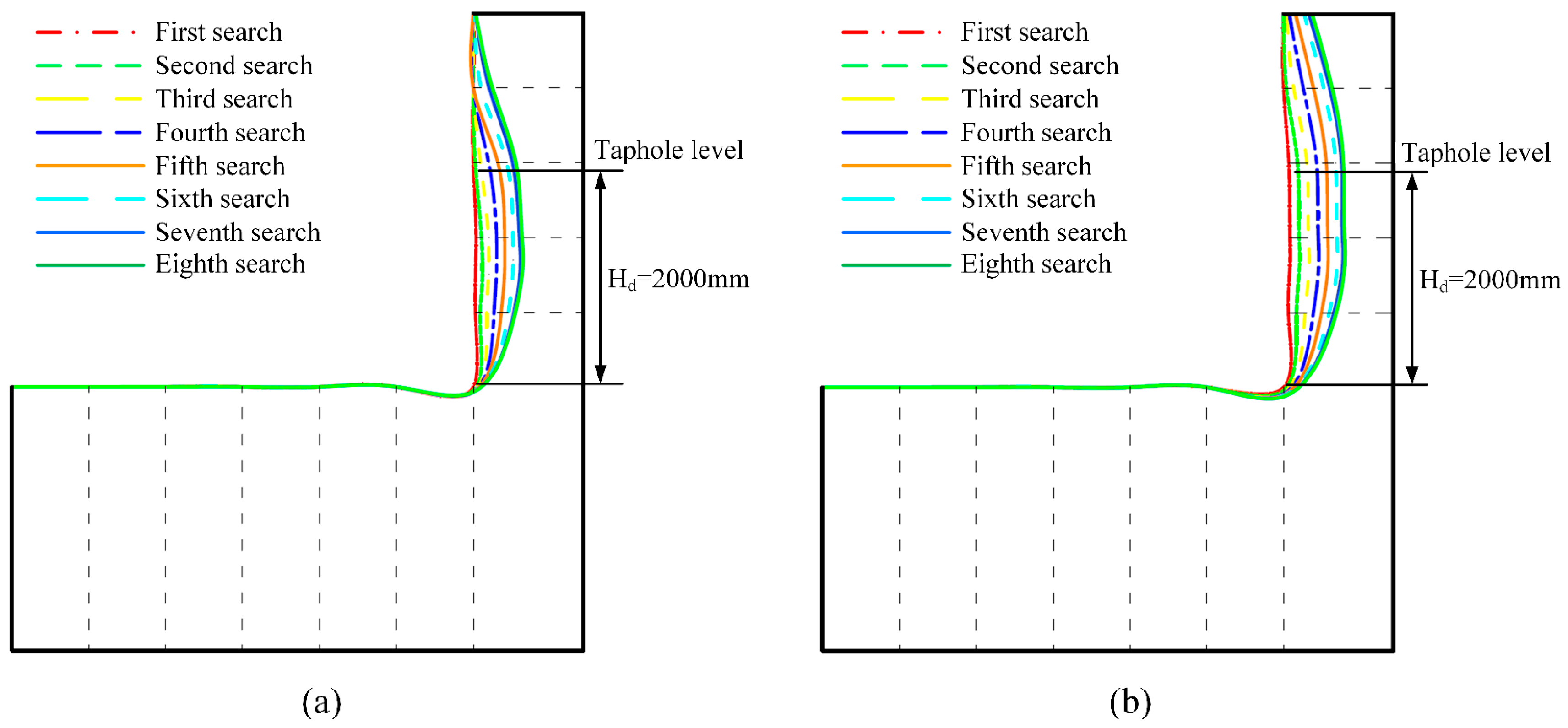
3.1. Dead Iron Layer Depth

The dead iron layer is a region below the taphole centerline that holds liquid slag and iron. Changes in its depth significantly alter the molten iron flow field in the hearth, thereby affecting the temperature and stress distributions in the lining and ultimately leading to changes in the stress–erosion boundary. Under fixed production conditions, numerical models were established with dead iron layer depths of 1000 mm, 1500 mm, and 2000 mm. By searching these models, the corresponding critical strength erosion boundaries of the lining were obtained, as shown in Figure 16a–c.

Figure 16a shows the erosion boundary search results under the condition with a dead iron layer depth of 1000 mm. The positions of Control Points 1–6 (hearth bottom area) and Control Points 9–13 (sidewall area) remain unchanged. This indicates that the thermal stress in the hearth bottom and the upper-middle part of the sidewall is lower than the compressive strength of the carbon bricks and that the erosion boundary remains stable. However, Control Point 7 in the hearth corner area moves toward the direction of erosion development, forming a downward-extending, elephant foot concave erosion. The maximum radial erosion point on the cross-section (Control Point 8) has a height of 2476.81 mm, and the maximum radial erosion depth within the cross-section is 251.28 mm.

When the dead iron layer depth increases to 1500 mm (Figure 16b), the erosion morphology of the hearth lining changes significantly. Among them, the carbon brick structure in the hearth bottom area remains stable, and the erosion boundary in the hearth corner area changes slightly, with Control Point 7 moving only 92.53 mm. Analysis suggests that stress concentration exists in the hearth corner area. However, the increase in dead iron layer depth effectively inhibits molten iron circulation and reduces the flow velocity in this region. It also promotes the formation of a protective, solidified iron layer. As a result, the temperature and stress level of carbon bricks are significantly reduced, inhibiting the development of erosion in the hearth corner. In contrast, the middle-lower part of the sidewall becomes the main area of erosion development; the movement of the erosion boundary at Control Points 9 and 10 is 548.53 mm and 545.94 mm, respectively, forming a typical wide-face erosion morphology. The maximum erosion depth corresponding to Control Point 8 is 571.73 mm, with an axial height of 3326.87 mm. When the dead iron layer depth is further increased to 2000 mm (Figure 16c), the erosion type remains wide-face. The variation range of Control Point 7 in the hearth corner area further decreases in the search calculation, with a moving distance of 80.53 mm. The erosion position shifts upward in the axial direction, and the maximum erosion depth decreases from 571.73 mm to 501.45 mm, while the axial height remains 3663.16 mm.

Figure 16d compares the critical strength erosion boundaries of the hearth lining under different dead iron layer depths. The results show that the dead iron layer depth significantly affects both the erosion type and the erosion depth. When the depth increases from 1000 mm to 1500 mm, the erosion morphology changes from a downward-extending elephant foot shape to a wide-face shape, and the maximum erosion depth increases. When the depth rises from 1500 mm to 2000 mm, the erosion morphology remains unchanged, but the erosion depth decreases slightly, and the erosion position shifts upward. This phenomenon can be explained as follows. An increase in the dead iron layer depth shifts the high-velocity molten iron region in the hearth away from the hearth corner. This avoids stress concentration in this region. Meanwhile, the high-thermal stress area shifts upward accordingly. As the dead iron layer depth increases, the intensity of molten iron circulation weakens. Additionally, the local heat concentration effect in the hearth wall area is alleviated. Ultimately, this leads to a significant reduction in erosion.

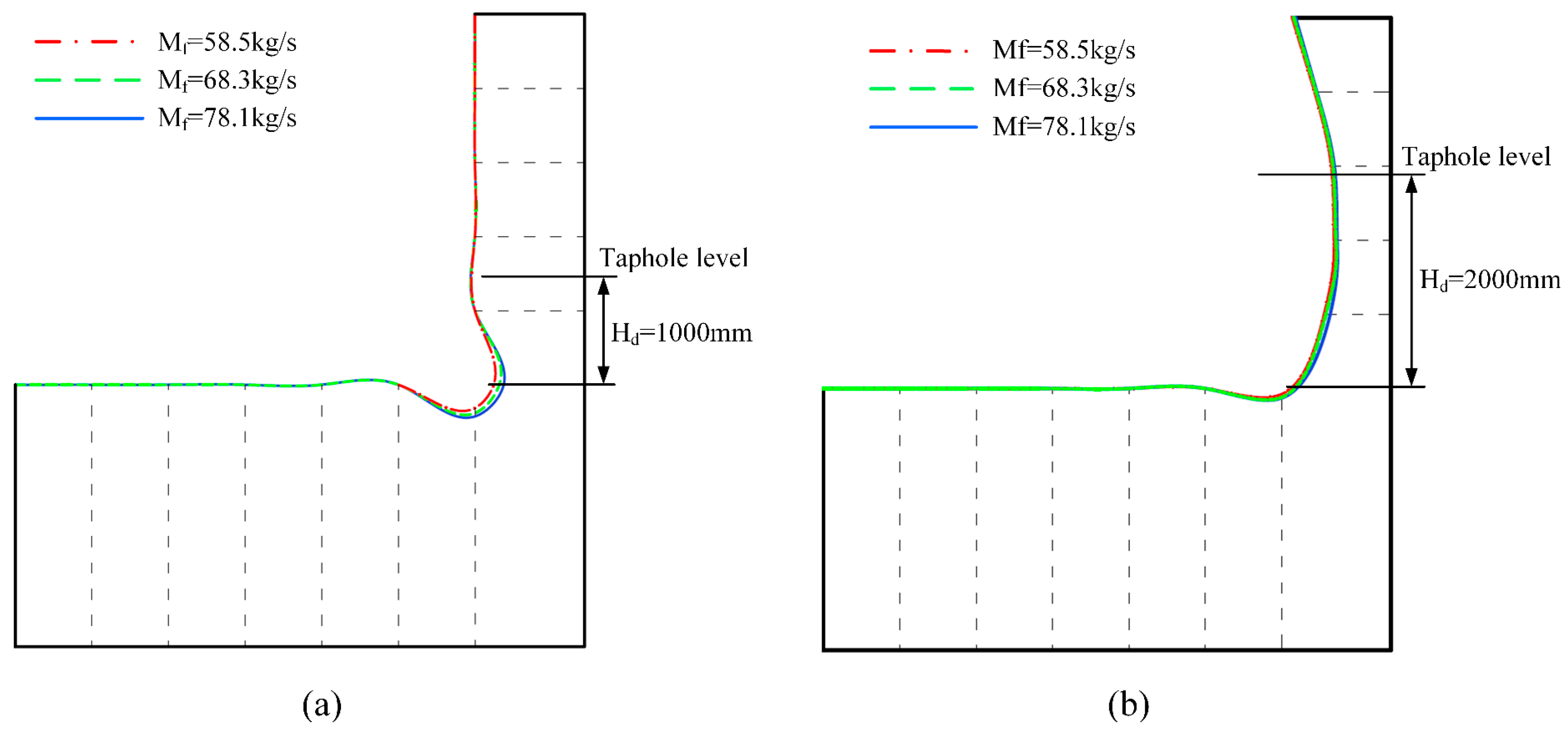
3.2. Tap Productivity

Tap productivity significantly affects the distribution of the lining’s thermal stress field by altering the molten iron flow velocity. Additionally, it is a key factor in determining the morphology and depth of the critical strength erosion boundary. To systematically investigate the influence, this study sets two comparative working conditions (58.5 kg·s⁻¹ and 78.1 kg·s⁻¹) based on normal production conditions (68.3 kg·s⁻¹). In combination with two dead iron layer depths (1000 mm and 2000 mm), the effect of tap productivity on the erosion boundary is analyzed under different hearth structures.

For the hearth with a dead iron layer depth of 1000 mm, the morphology of the erosion boundary does not change with the increase in tap productivity. The hearth bottom and the middle-upper part of the sidewall remain stable, with an elephant foot erosion forming in the hearth corner area. However, the degree of erosion is significantly intensified, as shown in Figure 17. At an inlet mass flow rate of 58.5 kg·s⁻¹, the critical strength erosion boundary of the hearth lining forms an elephant foot erosion in the hearth corner area, with a maximum radial erosion depth of 169.31 mm. When the mass flow rate increases from 58.5 kg·s⁻¹ to 78.1 kg·s⁻¹, the elephant foot erosion develops further. The maximum radial erosion depth increases to 260.71 mm (with a growth rate of approximately 54.0%), and the axial erosion depth of Control Point 7 increases from 214.52 mm to 290.67 mm.

Under working conditions with a dead iron layer depth of 2000 mm, as tap productivity increases, the erosion morphology consistently exhibits a wide-face erosion feature concentrated in the middle part of the sidewall, as shown in Figure 18. At an inlet mass flow rate of 58.5 kg·s⁻¹, the critical strength erosion boundary of the hearth lining shows distinct displacement characteristics. Control Point 7 in the hearth corner area has a relatively small displacement of only 54.18 mm. In contrast, erosion boundary Control Points 9, 10, and 11 have larger displacements: 389.47 mm, 480.8 mm, and 455.31 mm, respectively. The maximum radial erosion depth is 481.39 mm, and the axial height is 3714.92 mm. When tap productivity increases to 78.1 kg·s⁻¹, the erosion degree is significantly intensified. The displacement distances of erosion boundary Control Points 9, 10, and 11 increase to 443.05 mm, 501.2 mm, and 481.74 mm respectively; the displacement distance of the erosion boundary Control Point 7 in the hearth corner area increases to 86.69 mm; the depth of the severely eroded area increases to 511.50 mm (with a growth rate of approximately 6.3%); and the axial position decreases to 3611.41 mm. This indicates that the eroded area of the hearth with a deep, dead iron layer shifts downward overall under high tap productivity.

Figure 19 compares the effect of tap productivity on the hearth erosion boundary under two dead iron layer depths. As tap productivity increases from 58.5 kg·s⁻¹ to 78.1 kg·s⁻¹, the basic erosion morphology remains unchanged. Instead, it intensifies erosion and causes an overall downward shift. The reason is that the increase in tap productivity enhances the kinetic energy of molten iron flow and the efficiency of convective heat transfer. The accelerated molten iron velocity transfers heat from the high-temperature region to the lower hearth more rapidly, increasing the heat load in the middle and lower parts of the hearth. As a result, erosion is collectively intensified and shifted downward.

3.3. Molten Iron Temperature

Molten iron temperature significantly impacts both the temperature and stress distribution of the hearth lining. Additionally, it is a key factor in determining the morphology and depth of the critical strength erosion boundary. To investigate the effect of molten iron inlet temperature on the critical strength erosion boundary of hearths with different dead iron layer depths (1000 mm and 2000 mm), comparative calculation models were established. These models are based on the normal production model (1773 K), with the molten iron inlet temperature adjusted to 1723 K and 1823 K, respectively. The corresponding critical strength erosion boundaries of the lining were then searched. The molten iron inlet temperatures of the calculation models are set to 1723 K and 1823 K, respectively.

Figure 20 shows the search process of the hearth lining erosion boundary under two molten iron temperature conditions when the dead iron layer depth is 1000 mm. The results indicate that the erosion boundaries at the hearth bottom and the middle-upper part of the sidewall do not shift with changes in temperature, and the carbon bricks remain stable. In contrast, the erosion boundary in the hearth corner area continues to move inward, making this region the main site of erosion development. Eventually, an elephant foot erosion profile is formed. Specifically, at a molten iron temperature of 1723 K, after four searches, a small elephant foot erosion forms in the hearth corner and reaches a stable state, with a maximum radial erosion depth of 236.82 mm and a height of 2496.38 mm. When the temperature rises to 1823 K, the erosion degree intensifies significantly. The maximum radial erosion depth increases to 274.15 mm (with a growth rate of approximately 15.8%), the height decreases to 2360.90 mm, and the axial erosion depth at Control Point 7 surges from 26.95 mm to 358.41 mm, ultimately forming a larger and lower elephant foot erosion in the hearth corner area.

When the dead iron layer depth is 2000 mm, the search process of the hearth lining erosion boundary under two molten iron temperature working conditions is shown in Figure 21. The erosion type remains unchanged across different temperature conditions, consistently showing wide-face erosion. This erosion is mainly concentrated in the middle part of the sidewall. The hearth bottom area remains stable. The erosion boundary in the hearth corner area changes slightly. Erosion development is mainly focused on the middle area of the lining sidewall. At a molten iron inlet temperature of 1723 K, the erosion boundary control points show different displacement characteristics. Among them, Control Point 7 in the hearth corner area has a small variation range during the search process. Its displacement is only 45.65 mm. Meanwhile, the displacement distances of erosion boundary Control Points 9, 10, and 11 in the lining sidewall area are 382.75 mm, 443.81 mm, and 386.42 mm, respectively. After eight search iterations, the hearth lining forms a wide-face erosion in the middle of the sidewall and reaches a stable state. The maximum erosion depth is 451.62 mm, with a corresponding axial height of 3641.35 mm. As the molten iron temperature rises from 1723 K to 1823 K, the displacement distance of Control Point 7 in the hearth corner increases from 45.65 mm to 83.66 mm. The displacement distances of erosion boundary Control Points 9, 10, and 11 also increase to 480.35 mm, 555.77 mm, and 546.41 mm, respectively. After eight search iterations, the maximum radial erosion depth increases from 451.62 mm to 559.36 mm. This is a growth rate of 23.9%. The axial height of the severely eroded area also shifts upward, from 3641.35 mm to 3684.99 mm. This indicates that high temperatures not only deepen the erosion but also cause an overall upward shift in the eroded area.

Figure 22 compares the critical strength boundaries for the hearth lining at different molten iron inlet temperatures. Comprehensive analysis shows that the molten iron temperature significantly intensifies local hearth erosion. It affects the depth and distribution of the erosion boundary while not altering its basic erosion type. Specifically, in the BF hearth with a shallow dead iron layer (1000 mm), the lining critical strength boundaries at the three temperatures all exhibit elephant foot erosion. Additionally, increasing the molten iron inlet temperature causes the erosion to develop downward. For a deep dead iron layer (2000 mm), the lining critical strength boundaries at the three temperatures all exhibit wide-face erosion. The rise in molten iron temperature has a greater impact on erosion in the middle and upper regions of the hearth lining. This thereby leads to an overall upward shift in the wide-face erosion area.

4. Conclusions

This study established a multi-physical, field-coupled thermal stress calculation model for hearth lining, accounting for molten iron flow and the formation of a solidified iron layer. Based on the compressive strength of carbon bricks, a search method for the critical strength erosion boundary of the hearth lining was proposed. The effects of dead iron layer depth, tap productivity, and molten iron temperature on the erosion boundary were analyzed, providing a simulation reference and methodological support for predicting and assessing the safety of the BF hearth lining. The main conclusions are as follows:

• The dead iron layer depth is a key factor determining the erosion morphology. Its increase transforms the erosion from “elephant-foot-shaped” to “wide-face-shaped”, and the radial erosion depth first increases and then decreases. At depths of 1000 mm, 1500 mm, and 2000 mm, the maximum radial erosion depths are 251.28 mm, 571.73 mm, and 505.13 mm, respectively, with the most severe erosion moving upward as the depth increases.
• Increases in tapping productivity and molten iron temperature aggravate erosion without changing its basic type. When the productivity increases from 58.5 kg·s⁻¹ to 78.1 kg·s⁻¹, the radial erosion depth of the shallow dead iron layer increases by 54.0%, while that of the deep dead iron layer only increases by 6.3%. When the molten iron temperature rises from 1723 K to 1823 K, the radial erosion depths of the shallow and deep dead iron layer increase by approximately 15.8% and 23.9%, respectively.
• Under wide-face erosion, the axial position of the severely eroded zone is negatively correlated with tapping productivity and positively correlated with molten iron temperature.
• In the BF design, a reasonable and stable dead iron layer depth should be adopted to avoid severe concave erosion morphology. In operation, to ensure smooth furnace operation, the tapping productivity and molten iron temperature should be reasonably controlled to avoid long-term excessive values. Meanwhile, the growth of the solidified iron layer should be promoted to slow down the erosion process.

Although numerical simulation is an effective approach for analyzing the high-temperature stress behavior of carbon bricks, it is essentially a simplification of complex physical processes, leading to idealized deviations in its prediction results. Due to the scarcity of high-temperature experimental data, prohibitively high acquisition costs, and the strong parameter coupling that makes them difficult to measure independently, these factors will affect the reliability of the numerical simulation results. Therefore, the results of numerical simulations should be regarded as qualitative guidance on trends rather than absolute predictions. In future work, further efforts should be made to acquire precise high-temperature material parameters and compare them with extensive engineering measured data, thereby improving the reliability and effectiveness of the proposed model and search algorithms. In addition, the quasi-steady-state assumption adopted in this model is applicable to the analysis of the BF hearth under steady-state operation and can provide reliable support for revealing key physical laws. Meanwhile, the dynamic mechanisms of transient processes, such as blowing-on and blowing-off operations and severe fluctuations in furnace conditions, serve as key directions for subsequent research to further expand the model’s application scope.