Process Intensification and Operational Parameter Optimization of Oil Agglomeration for Coal Slime Separation

Abstract

Coal slime, a byproduct of coal processing with high ash content, poses significant challenges in terms of its efficient separation and resource utilization due to its fine particle size and complex composition. This study aims to optimize the oil agglomeration process for coal slime separation through systematic parameter investigation and predictive modeling. Response surface methodology (RSM) was employed to analyze the individual and interactive effects of pulp density, oil dosage, and agitation rate on three key performance indicators: combustible recovery, efficiency index, and ash rejection. Meanwhile, an artificial neural network (ANN) was developed to establish a robust prediction model for the efficiency index. The novelty of this work lies in the integration of thermodynamic analysis, multi-objective optimization, and machine learning approaches. The key findings include the identification of dodecane as the optimal bridging liquid due to its intermediate carbon chain length that balances interfacial tension and wettability. Under optimized conditions (14% pulp density, 22% oil dosage, and 1600 r/min), the process achieved a combustible recovery of 91.49%, ash rejection of 61.58%, and efficiency index of 53.07%. The ANN model demonstrated superior predictive capability with an overall R² of 0.9659 and RMSE of 1.12. This work provides comprehensive guidelines for the design, optimization, and scale-up of coal slime oil agglomeration processes in industrial applications.

1. Introduction

The term “clean coal” applies to coal with reduced residue matter as compared to raw coal. Coal beneficiation, as a coal cleaning technology, is a process for separating pure coal matter from associated inorganic mineral impurities like sand, stones, and sulfide [1]. With the depletion of coal resources, coal slime, which was previously discarded due to difficulties in segregation, has become an important available resource. One of the more promising methods for cleaning coal, called oil agglomeration, involves suspending finely ground coal in water and selectively agglomerating the more hydrophobic and oleophilic components with oil while the suspension is agitated vigorously [2]. Based on the differences in the surface hydrophobicity of organic and inorganic minerals in coal, oil agglomeration utilizes neutral oil to achieve the efficient separation of coal slimes with a size fraction of less than 0.5 mm [3,4].

Clean coal recovery and separation efficiency in the oil agglomeration process depend on many operational factors, including the pulp density, oil type and dosage, agitation rate, agglomeration time, pH of the suspension, and coal slime properties [5,6,7,8,9]. The effect of the particle size distribution of coal slime on the oil agglomeration performance has been investigated by researchers [8,10]. The results indicated that finer coal slime achieved cleaner agglomerates than coarser coal slime, although with a lower yield of clean coal. Allen et al. [2] and Butler et al. [8] studied the effect of pulp’s pH on coal oil agglomeration and observed that acidic conditions were more conducive to coal fines beneficiation. Moreover, Chary and Dastidar [11] adopted different types of vegetable oils, including karanja oil, jatropha oil, and rubber seed oil, to achieve acceptable separation performances in oil agglomeration. Ünal et al. [7,12] and Cebeei et al. [13] investigated the effect of various bridging liquids on the agglomeration performance of coal fines. Furthermore, the effects of pulp concentration, oil dosage, and agitation speed were also evaluated in terms of the combustible recovery of the coal slime oil agglomeration process [4,5,14,15]. However, most of these studies focused on the effects of single factors without sufficiently considering interaction effects between variables. Therefore, it is essential to study the interactions among various factors in-depth, based on a multi-factor orthogonal experimental design.

The interaction effects between variables on oil agglomeration separation performance have been investigated in recent years via employing experimental designs such as the Box–Wilson statistical design [16], the analysis of variance (ANOVA) approach [17], and the Box–Behnken design [6,18]. Despite some novel findings obtained using these various methods to discern the influence of various factors on the cleaning efficiency of coal fines in oil agglomeration, the reliance on a single evaluation metric (e.g., combustible recovery) risks suboptimal process design, as it neglects trade-offs between yield and ash content. This limitation is addressed through our tripartite efficiency index (Equation (4)). Therefore, it is urgent to investigate the mutual effects of significant parameters on the performance of oil agglomeration for coal slimes with multiple evaluation indexes in-depth.

Furthermore, the application of systematic process engineering methodologies to particulate system optimization has gained prominence. For complex separation processes involving multiple variables and competing objectives, integrated frameworks combining response surface methodology, sensitivity analysis, and multi-criteria decision making have proven effective in identifying optimal operational windows and resolving parameter trade-offs [19]. This supports the methodological approach of the present study, which employs Box–Behnken RSM for multi-objective optimization, complemented by ANN modeling to address nonlinearities.

While prior studies have advanced our understanding of oil agglomeration, three critical research gaps remain unaddressed. Firstly, the existing research predominantly focuses on single-factor optimization (e.g., oil dosage or agitation rate) while neglecting the synergistic or antagonistic interactions between operational parameters such as pulp density, oil dosage, and agitation rate [5,6,7,8,9]. This oversimplification limits industrial applicability, as real-world processes require balancing multiple competing objectives simultaneously. Secondly, current evaluation methodologies rely predominantly on single performance metrics like combustible recovery or ash rejection [6,16], which fail to capture the inherent trade-offs between process efficiency and product quality. The absence of comprehensive evaluation frameworks often leads to suboptimal process design in practical applications. Thirdly, despite the growing interest in machine learning for mineral processing, few studies have systematically validated artificial neural network (ANN) models against physics-based approaches for oil agglomeration prediction, particularly for forecasting complex performance indicators that integrate multiple output variables [20,21].

To address these research gaps, this work presents three key innovations that collectively advance the field of coal slime oil agglomeration. First, the effect of oil types with different carbon chain lengths on separation performance, spanning from experimental analysis to thermodynamic theoretical interpretation using the Young–Laplace equation are comprehensively investigated. This dual approach provides fundamental insights into the oil agglomeration mechanism at both the macroscopic and microscopic levels. Second, we develop a multi-objective optimization framework using Box–Behnken response surface methodology (RSM) to systematically resolve conflicting parameter interactions (e.g., the trade-off between pulp density and ash rejection). This approach enables the identification of optimal operational windows that balance competing process objectives. Third, we establish and validate an artificial neural network (ANN) model that demonstrates superior predictive accuracy for the efficiency index compared to traditional regression methods, providing a reliable tool for process forecasting and control. These integrated contributions provide actionable guidelines for scaling up coal slime separation processes under practical resource constraints and operational limitations.

2. Materials and Methods

2.1. Materials

Raw coal slime with a size fraction of mainly less than 0.5 mm, from Bulianta Coal Mine, Ordos, China, was collected as the feed for oil agglomeration in this experimental study.

Table 1. The proximate analysis of the −0.5 mm Bulianta raw coal slime.

Moisture Content, Mad (%)	Ash Content, Aad (%)	Volatile Content, Vad (%)
8.14	19.08	25.12

showed the proximate analysis of the raw coal slime with a total ash content of 19.08%.

The size distribution of the coal slime based on the sieving test was summarized in

Table 2. The results of the sieving tests for the coal slimes.

Size Fraction (mm)	Yield (%)	Ash Content (%)
+0.5	0.14	14.54
−0.5~+0.25	2.89	15.59
−0.25~+0.125	17.68	16.80
−0.125~+0.074	39.76	17.11
−0.074~+0.045	28.87	19.44
−0.045	10.66	30.24
Total	100.00	19.08

. The yield of −0.25 mm coal slimes accounted for 96.97%, with the dominant size fraction of −0.125~0.074 mm. Furthermore, the ash content of the coal slimes presented a gradual increase with the decrease in size fractions. The ash is enriched in fine size fractions, which provide a potential necessity to select an effective separation method for the removal of tailings.

In addition, the oils, bought from Hebei Wantai Chemical Co., Ltd., Hengshui, China, and used in the oil agglomeration test, were characterized by their carbon chain lengths. As exhibited in

Table 3. The oil type properties used in oil agglomeration tests.

Oil Name	Formula	Melting Point (°C)	Density at 25 °C (kg/m3)
Octane	C8H18	−57	703 (Liquid)
Decane	C10H22	−30	730 (Liquid)
Dodecane	C12H26	−10	749 (Liquid)
Tetradecane	C14H30	5.9	763 (Liquid)
Hexadecane	C16H34	18	773 (Liquid)

, the density of the oils gradually increased with the increase of the carbon chain length. All the tests were carried out at a room temperature of 25 °C; therefore, the oils employed in the tests were all in the liquid state.

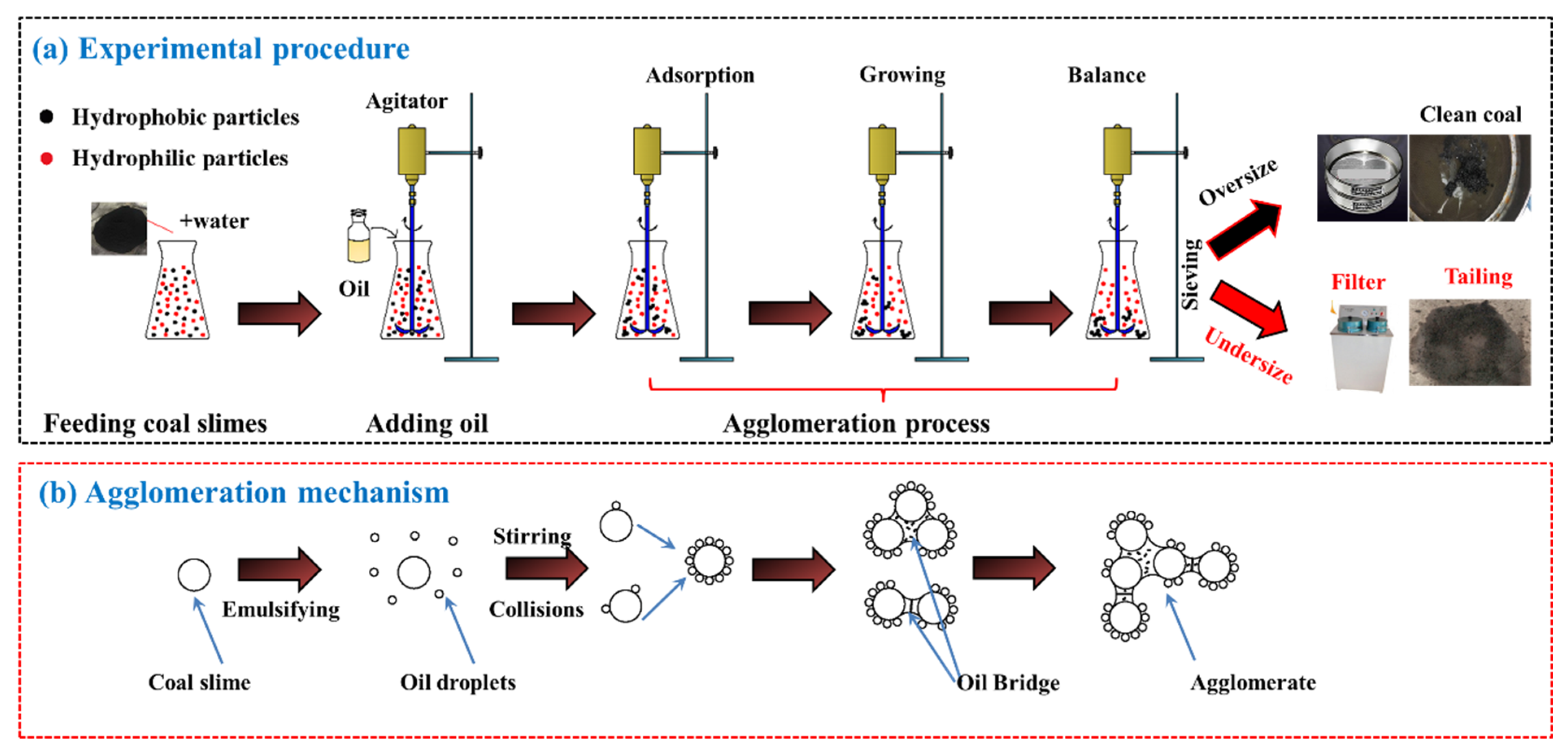
2.2. Experimental Procedure and Separation Mechanism

The experimental procedure of the oil agglomeration test is illustrated in Figure 1a. The oil agglomeration tests were conducted in a 250 mL Erlenmeyer flask equipped with an overhead agitator. The agitator blades were extended into the conical flask, with a 1 cm gap to the bottom, to achieve adequate stirring. The coal slime samples with different weights were fed into the flask and mixed with 200 mL of water. After a full agitation, the coal slime was uniformly dispersed in the water. Then, the oil was added to the mixture. Afterward, the mixture was stirred by the agitator for 5 min at a predetermined agitation rate. During the sufficient agitating period, the coal slimes unedged the three stages of the agglomeration process, including the adsorption stage, the agglomerate growing stage, and the balance stage. After the agitator stopped, the slimes, which adhered to the agitator blades and the connecting rod, were cleaned with water and collected into the Erlenmeyer flask. The suspension in the Erlenmeyer flask was sieved by a sieve with 0.5 mm mesh. The agglomerates, upon being sieved, as the clean coal products, were washed out with clean water, while the slimes were washed with flushing water under the sieve, as the tailing, and were collected in a plastic container. All products were filtered by a vacuum filter and then heated in an oven at a constant temperature of 40 °C until the weight stabilized, according to the standard of GB/T 211-2017 [22], to remove the surface moisture from the products. The dried products of clean coal and tailing were weighed and the yields of each product were recorded. Afterward, the samples with a weight of 1 g were taken out from the clean coal and tailing products, respectively, and then handled by a muffle furnace to obtain the ash contents of the clean coal and the tailing products. Critical experimental conditions, including all single-factor tests and RSM runs, were performed in duplicate.

The diagrammatic of the oil agglomeration mechanism was clarified in detail in Figure 1b. The effective separation using the oil agglomeration method was achieved based on the difference in hydrophobicity between the surface of the clean coal and the tailing. The oil employed in the oil agglomeration test has two effects on hydrophobic particles (clean coal). One effect is that a small amount of oil, used as a collector reagent, makes the surface of the clean coal after sufficient stirring fully hydrophobic, leading to the surface of the clean coal slime being wrapped in an oil membrane formed by dispersed oil droplets. Another effect is that the remaining oils, used as an agglomerate, are squeezed to fill the voids and form oil bridges between the hydrophobic coal particles. The oil occupies such a position (liquid bridge), given the lowest surface free energy and the stability of the optimal thermodynamics. Furthermore, the additional attraction between the coal particles, generated by the additional pressure of the oil bridge, makes the hydrophobic coal particles firmly bond, forming agglomerates that can be efficiently separated by sieving.

The single-factor tests were conducted for each factor to find out the appropriate operational range. The experimental design of the varied parameters and the constant parameters for the single-factor tests are summarized in

Table 4. Range of various parameters studied in single-factor experiments.

Parameters Considered	Parameters Varied During the Experiments	Parameters Kept Constant During the Experiments
Oil type	Oil type: C8H18, C10H22, C12H26, C14H30, C16H34	α: 12%, β: 16%, γ: 1200 r/min,
Pulp density (α)	Pulp density, α, (%): 8, 12, 16, 20, 24	Oil type: C12H26, β: 16%, γ: 1200 r/min,
Oil dosage (β)	Oil dosage, β, (%): 12, 16, 20, 24, 28	Oil type: C12H26, α: 12%, γ: 1200 r/min,
Agitation rate (γ)	Agitation rate, γ, (r/min): 1200, 1600, 2000, 2400	Oil type: C12H26, α: 12%, β: 20%,

.

2.3. Experimental Indicators

The agglomerate yield calculated by Equation (1) represents the percentage recovery of clean coal from the raw coal slime.

$$Yield=\left(W_1/W_2\right)\times 100\%$$

(1)

where Yield is the agglomerate yield, %; W₁ is the weight of clean coal product, g; and W₂ is the weight of feed coal slime, g.

The combustible material recovery is defined via Equation (2), which refers to the useful substances, omitting the residue, after sufficient coal combustion:

$$Combustible recovery=100\%\times {\displaystyle \frac{W_1}{W_2}}·{\displaystyle \frac{100-A_1}{100-A_2}}$$

(2)

where A₁ is the ash content of clean coal product, %; A₂ is the ash content of feed coal slime, %.

The ash rejection is devised in Equation (3), which refers to the ash recovery in the tailing:

$$Ash rejection=100\%\times {\displaystyle \frac{A_2-\left(A_1\times W_1/W_2\right)}{A_2}}$$

(3)

The efficiency index is devised in Equation (4), which is a strategy for the simultaneous two terms of the combustible recovery and the ash rejection:

$$Efficiency index=Combustible recovery+Ash rejection-100\%$$

(4)

Combustible recovery (Equation (2)) and ash rejection (Equation (3)) were selected as primary metrics to align with industry standards for clean coal yield and environmental regulations. The efficiency index (Equation (4)) was devised to prevent overemphasis on one metric at the expense of another—e.g., maximizing recovery while tolerating high ash content. This tripartite evaluation aligns with ISO 1953:2015 [23] for coal beneficiation and addresses limitations in prior single-index studies [4]. The three indexes of the combustible recovery, the ash rejection, and the efficiency index were used to synergistically evaluate the cleaning efficiency of the oil agglomeration.

3. Results and Discussion

This study systematically investigated the oil agglomeration process for coal slime beneficiation, aiming to optimize separation performance by evaluating key operational parameters and their interactions. The research followed a clear logical progression. It first examined the individual effects of fundamental parameters including oil type, pulp density, oil dosage, and agitation rate (Section 3.1, Section 3.2, Section 3.3 and Section 3.4). Subsequently, response surface methodology (RSM) was employed to analyze multi-factor interactions and conduct multi-objective optimization (Section 3.5). An artificial neural network (ANN) model was then developed to predict process indicators and capture complex non-linear relationships (Section 3.6). Finally, the overall findings were synthesized and interpreted within a process intensification framework (Section 3.7). This structured approach—advancing from single-factor analysis to interactive optimization, then to predictive modeling and intensification—provides a systematic strategy for enhancing the comprehensive efficiency of the coal slime oil agglomeration process.

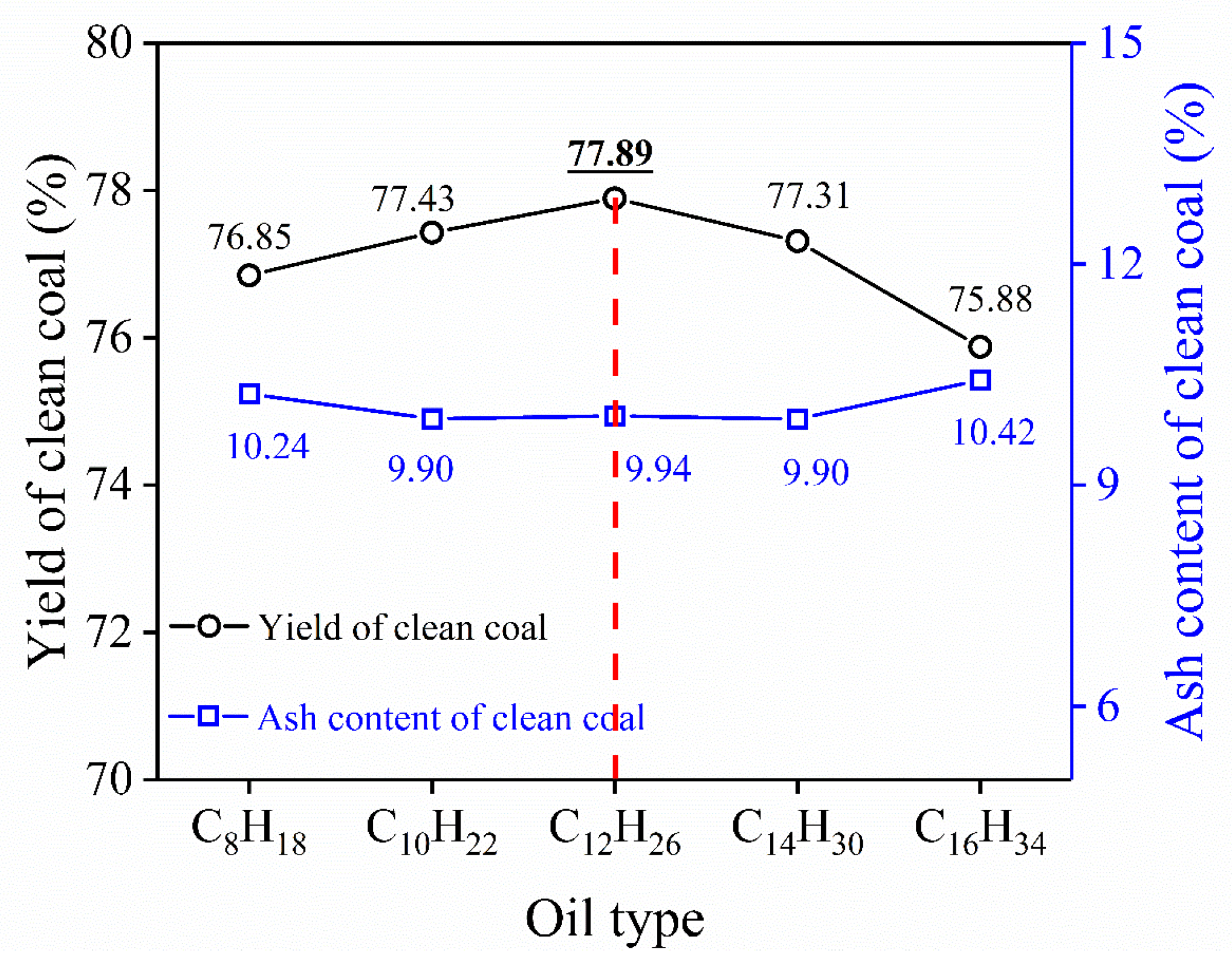
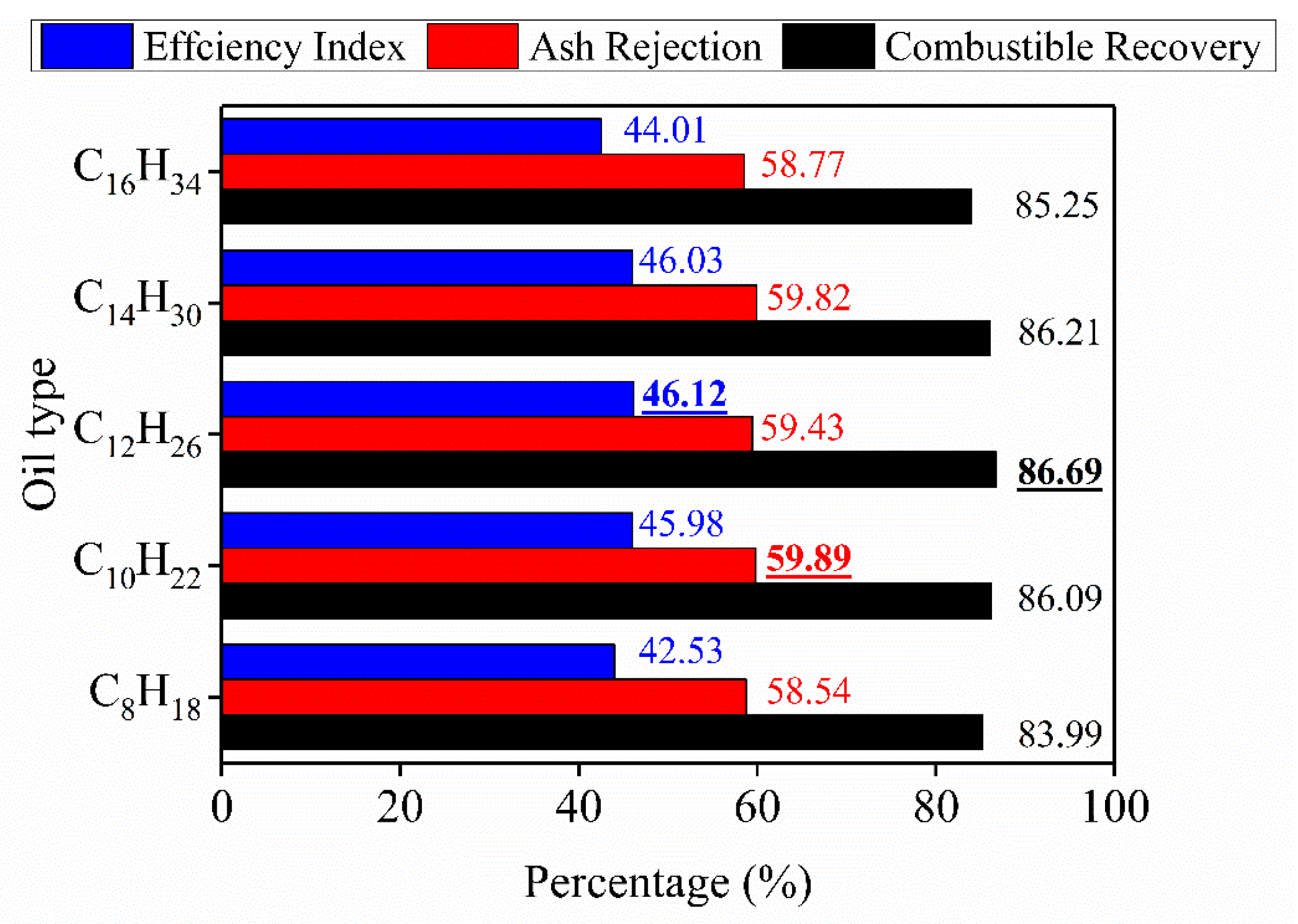
3.1. Effect of Oil Types with Different Carbon Chain Lengths

The oil type employed in the oil agglomeration process restricted the separation performance of coal slimes [14]. Figure 2 shows the effects of oil types with different carbon chain lengths on the yield and ash content of clean coal. As can be observed, the maximum yield was 77.89% with the corresponding ash content of clean coal being a relative value when the oil type was set at dodecane (C₁₂H₂₆). The results indicated that the oil type with both shorter and longer carbon chains, giving a poor agglomeration, would reduce the yields of clean coal, whereas it would cause a higher ash content in clean coal. Furthermore, as presented in Figure 3, the dodecane achieved the optimum combustible recovery and efficiency index, which agreed well with the yield results exhibited in Figure 2. The specific gravity of the oil type with shorter carbon chains was lower than that of long carbon chains. The results implied that the lighter and the heavier oil could not achieve a satisfactory separation performance, given a lower combustible recovery, smaller efficiency index, and poor ash rejection. Similar results have been noted in the literature [9,14]. This is because the heavier and lighter oils cause a poor oil bridge [13], showing a higher ash content in the agglomerates with low selectivity.

The oil agglomeration performance of coal slimes is critically influenced by capillary forces, governed by the Young–Laplace equation.

The capillary pressure (ΔP) driving oil bridge formation is given by the Young–Laplace equation:

$$\Delta P={\displaystyle \frac{2\tau cos\theta }{r}}$$

(5)

where τ represents the oil–water interfacial tension, mN/m; θ represents contact angle of oil on coal (measured through water), °; r is the radius of curvature of the oil bridge, m; and ΔP represents the capillary pressure, Pa.

The strength of the capillary force depends on the product τcosθ, which determines the adhesion energy and bridge stability.

For the effects of the interfacial tension (τ), longer-chain hydrocarbons (e.g., hexadecane) exhibit higher τ due to their reduced solubility in water and stronger intermolecular forces, while shorter chains (e.g., octane) have lower τ (Table 3: octane density = 703 kg/m³ vs. hexadecane = 773 kg/m³).

In terms of the effects of the wettability (cosθ), wettability is governed by the spreading coefficient (S):

$$S={\tau }_{water}-({\tau }_{oil}+{\tau }_{water/oil})$$

(6)

where τ_water is the surface tension of water, τ_oil is the surface tension of oil, and τ_water/oil is the interfacial tension of water and oil.

As the carbon chain length increases, the interfacial tension of water and oil (τ_water/oil) increases, and the surface tension of oil (τ_oil) increases as well, while the spreading coefficient (S) decreases, according to Equation (6). This indicates that shorter chains (low τ) promote oil spreading (low θ and high cosθ), and longer chains (high τ) lead to poor spreading (high θ and low cosθ).

Therefore, shorter chains (C₈–C₁₀) with low (τ_oil) dominate despite good wetting (cosθ), reducing ΔP, while longer chains (C₁₄–C₁₆) with high τ, offset by poor wetting, weakenoil bridges. Dodecane’s intermediate carbon chain length, with sufficient τ and optimal spreading, optimizes the thermodynamic balance between interfacial tension and wettability, maximizing capillary forces for selective coal agglomeration. The results of thermodynamic analysis favorably support the experimental results (Figure 2 and Figure 3) that dodecane achieves superior performance in coal slime separation compared to shorter or longer-chain oils.

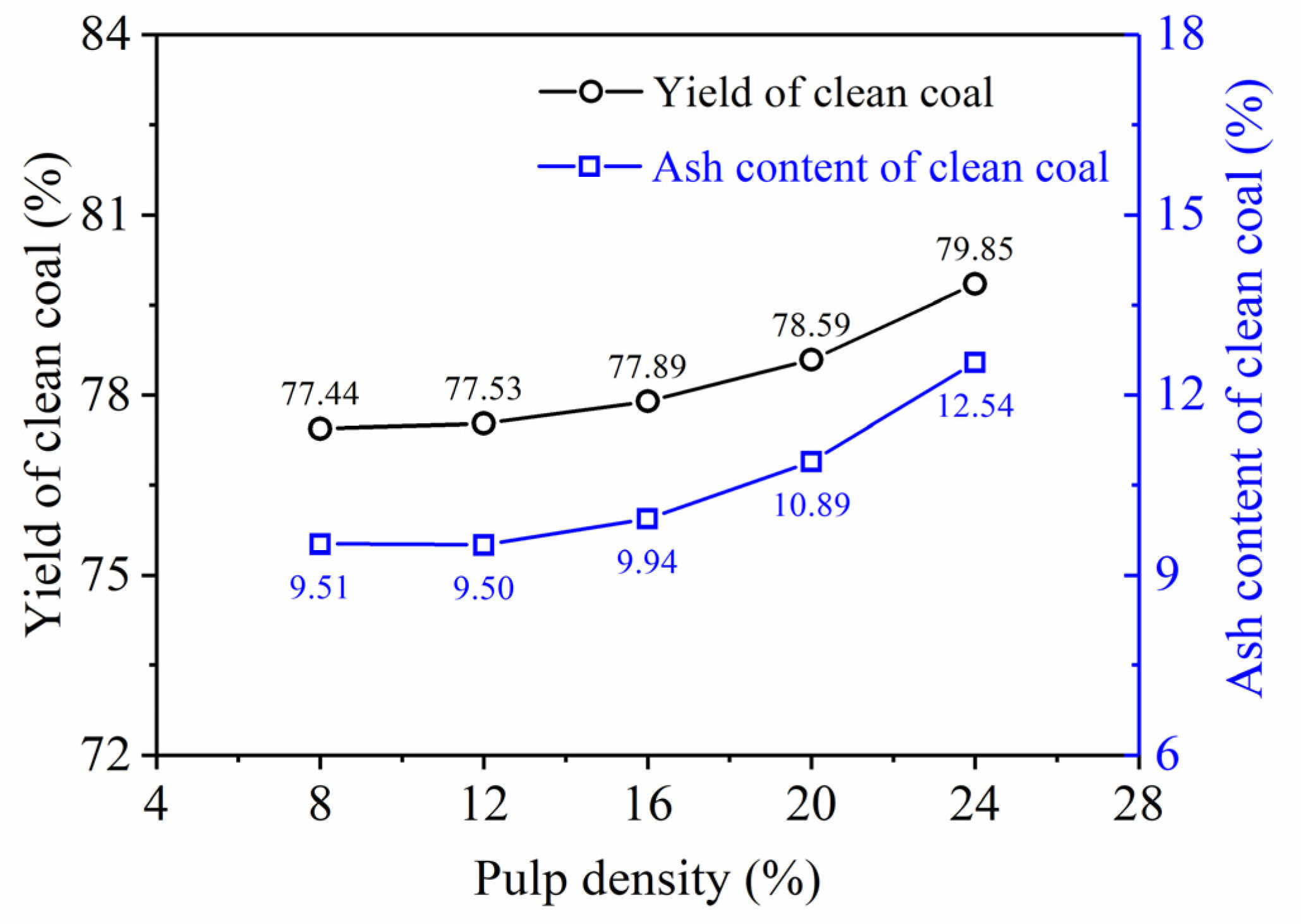
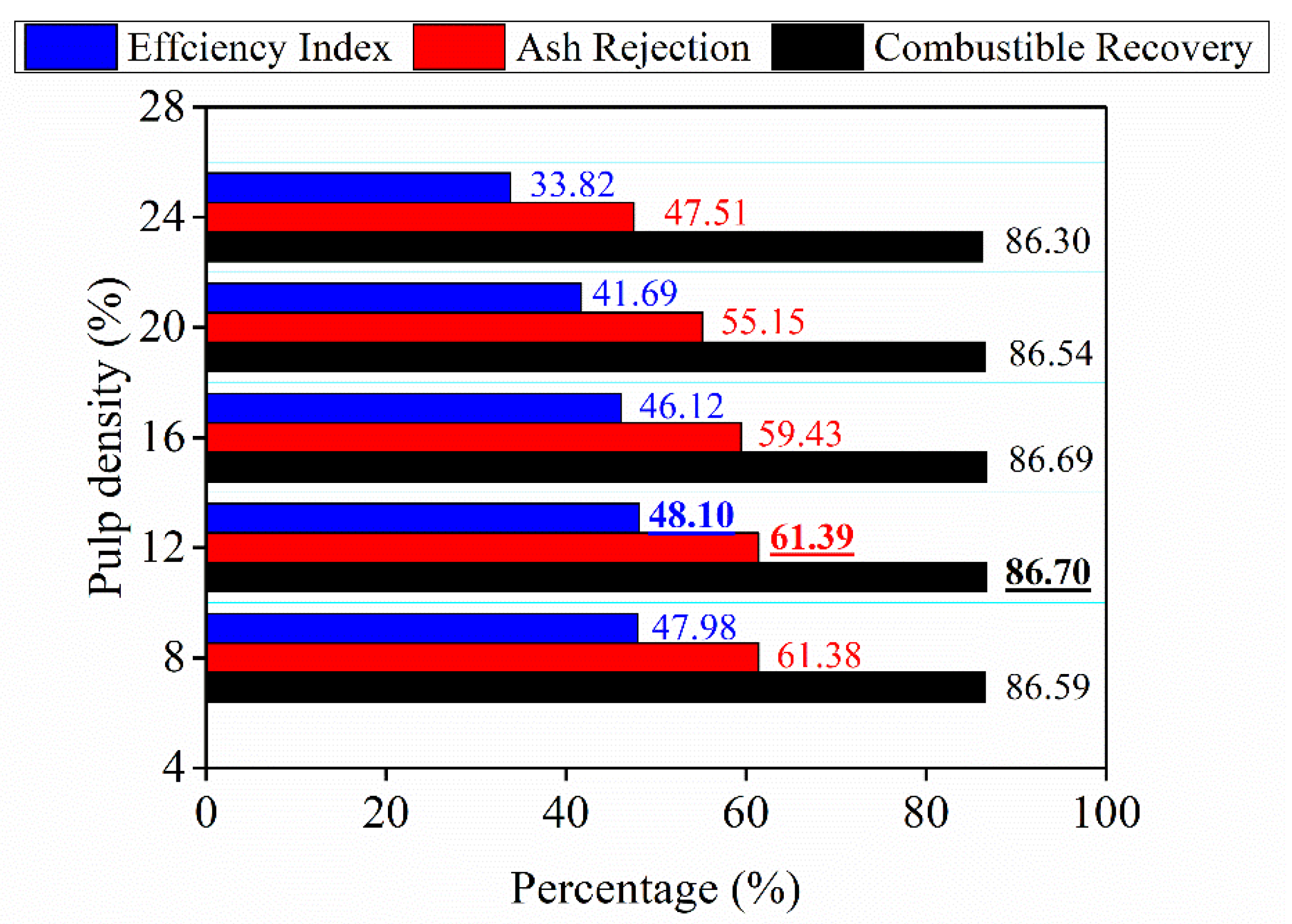
3.2. Effect of Pulp Density

Figure 4 shows that increasing pulp density positively affects the yield of clean coal. The yield increased from 77.44% to 79.85% with an increase in pulp density from 8% to 24%. The higher yield of clean coal achieved at higher pulp density was attributed to the reduction in distance between coal slimes, thus enhancing the probability of collision between coal slimes and oil droplets by increasing the number of coal slimes in a unit volume of the slurry. The facilitation of the yield of clean coal depending on pulp density has been reported by several studies [5,12,14]. Furthermore, the variation in the ash content of clean coal showed a similar trend. The ash content increased from 9.48% to 12.54% with an increase in pulp density from 8% to 24%. The increased ash content of clean coal indicated that the quality of clean coal gradually deteriorated.

As presented in Figure 5, the experimental results showed a steady decrease in ash rejection (61.50% to 47.51%) and the efficiency index (48.13% to 33.82%) with an increase in pulp density from 8% to 24%. The higher ash rejections and efficiency indexes observed with lower pulp densities (8% and 12%) can be attributed to the effective dispersion of coal slimes. The lower ash rejection and efficiency index at higher pulp densities (20% and 24%) likely stem from particle crowding, which promotes the interlocking of coal slimes and reduces selective agglomeration. These findings are in agreement with those in the literature [12,24]. Moreover, for the same variations in pulp density, the combustible recovery initially increased from 86.62% to 86.70% with pulp density increasing from 8% to 12%, and later slightly decreased to 86.30% with pulp density rising to 24%. Hence, 12% pulp density can be considered as the optimum for agglomeration, with a peak combustible recovery of 86.70%. When the pulp density is beyond 12%, the shear forces of mixing are reduced to the extent that there is no adequate space for the contact of coal slime and oil droplets in the slurry, resulting in a lower combustible recovery in agglomerates.

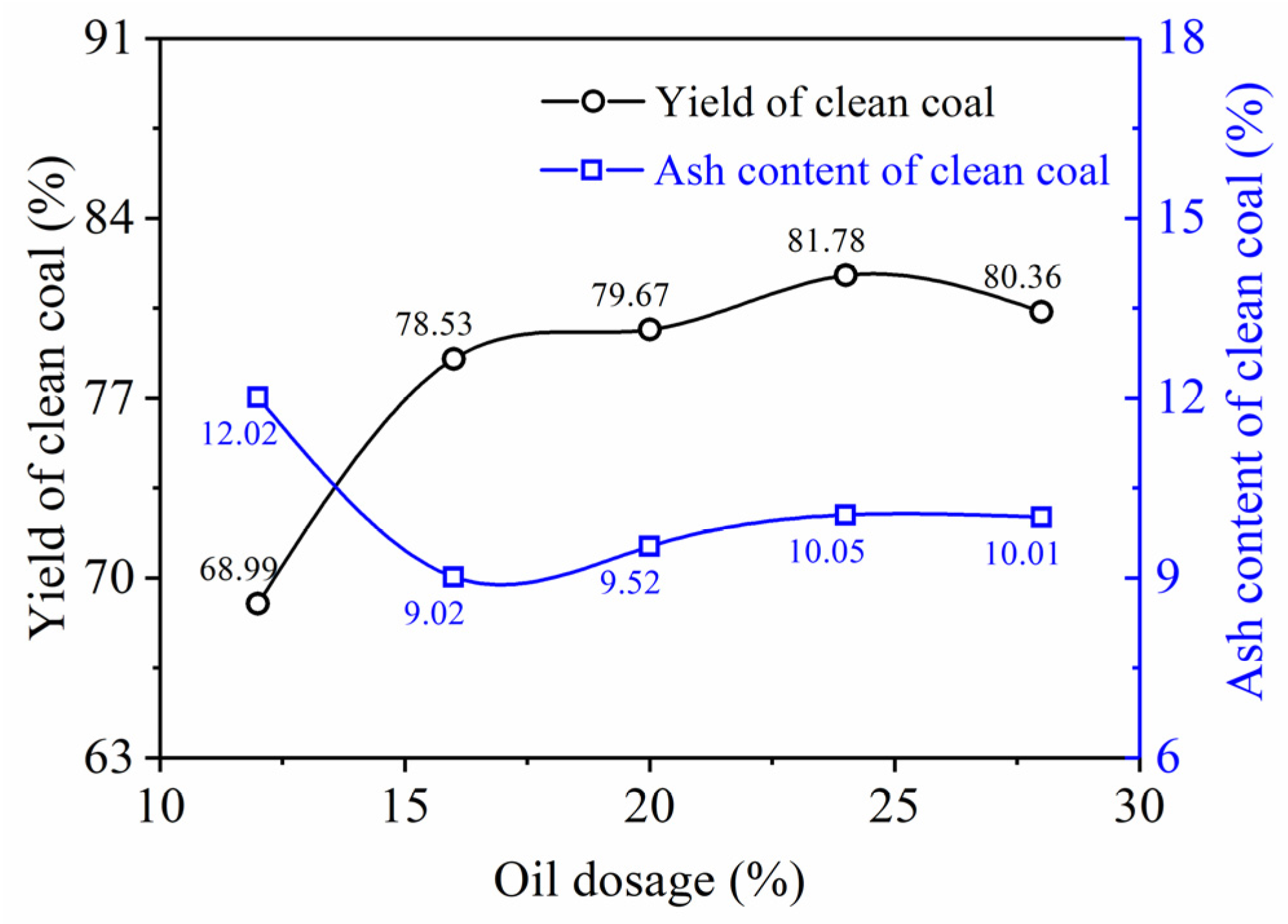
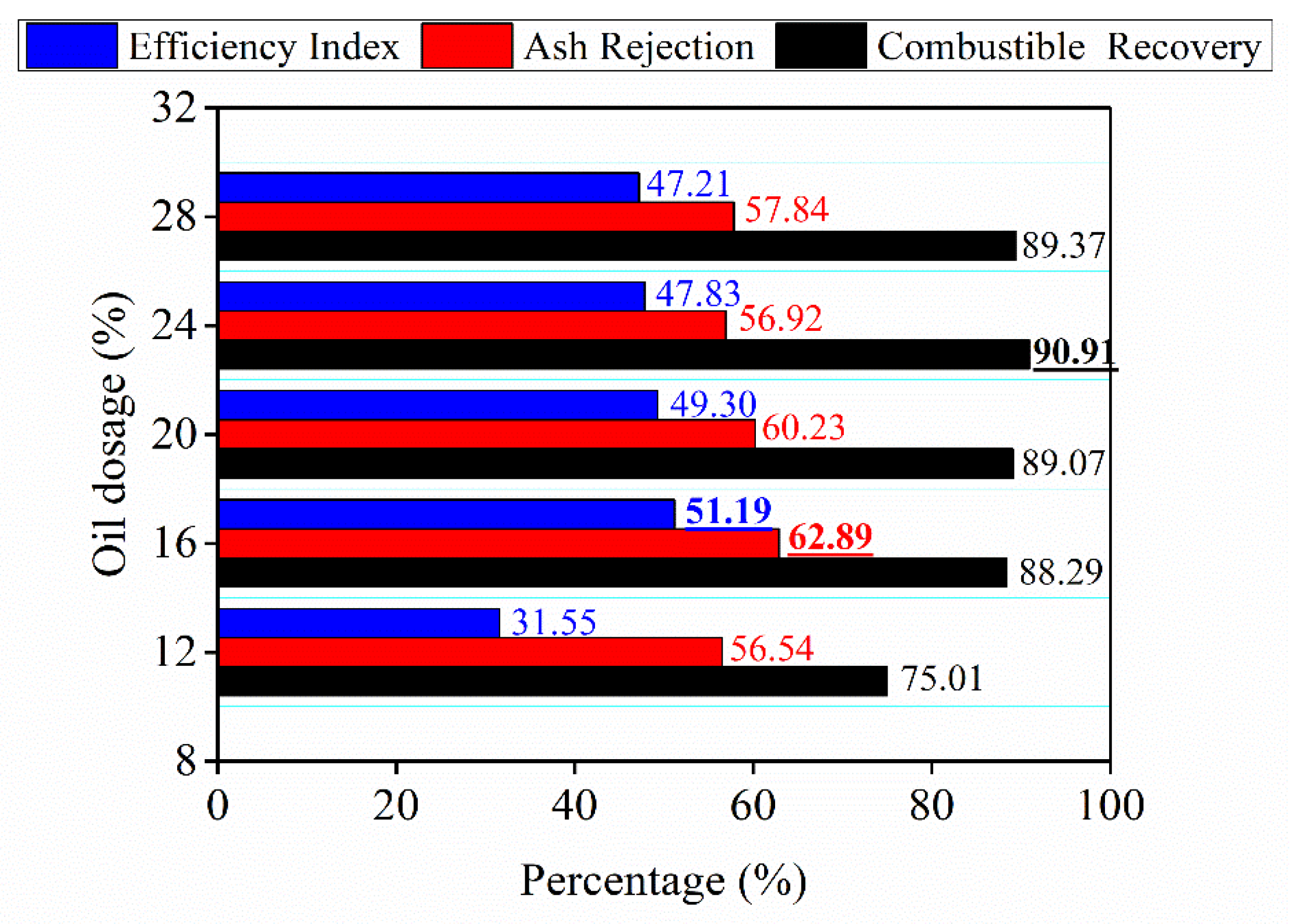
3.3. Effect of Oil Dosage

Oil dosage was based on the mass ratio of dodecane to coal. Figure 6 illustrates the effect of oil dosage on the yield and ash content of clean coal. Furthermore, Figure 7 shows the variations in combustible recovery, ash rejection, and efficiency index with various oil dosages. With an increase in oil dosage from 12% to 16%, the variation in agglomerate yield (68.99% to 78.53%), combustible recovery (75.01% to 88.29%), ash rejection (56.54% to 62.89%) and efficiency index (31.55% to 51.19%) presented a similar trend, with dramatic increases. For the same variations in oil dosage, the ash content of clean coal sharply fell from 12.02% to 9.02% and reached its bottom value with an oil dosage of 16%. The lower yield and higher ash content of clean coal at lower oil dosage were attributed to the oil availability being inadequate for the agglomeration of the coal slimes, which also resulted in lower combustible recovery, ash rejection, and efficiency. These experimental findings agree with the study conducted by Yaşar et al. [11]. Further increasing the oil dosage up to 24%, the yield of clean coal slightly rose, reaching a peak at 81.78%, and it later declined to 80.36% when the oil dosage was increased to 28%. A trend similar to the that of the clean coal yield was observed with combustible recovery with various oil dosages. The maximum combustible recovery was achieved at 90.91% with an oil dosage of 24%. When the oil dosage exceeded 24%, decreasing the oil dosage affected the yield of clean coal and combustible recovery negatively. This is because formed pasty agglomerates and excess residual oil restrained the majority of mineral matters, making it difficult to agglomerate [11,25,26]. Furthermore, the ash rejection of 62.89% was found to be optimum when oil dosage varied to 16%. Meanwhile, the corresponding highest efficiency index reached 51.19% in that oil dosage. When the oil dosage continued to increase, the ash rejection and efficiency index declined. The negative effect of excessive oil can be attributed to the decrease in the selectivity of oil droplets. It is noted that the oil dosage maximizing a single performance metric may differ from the global optimum obtained through multi-objective optimization considering parameter interactions (Section 3.5).

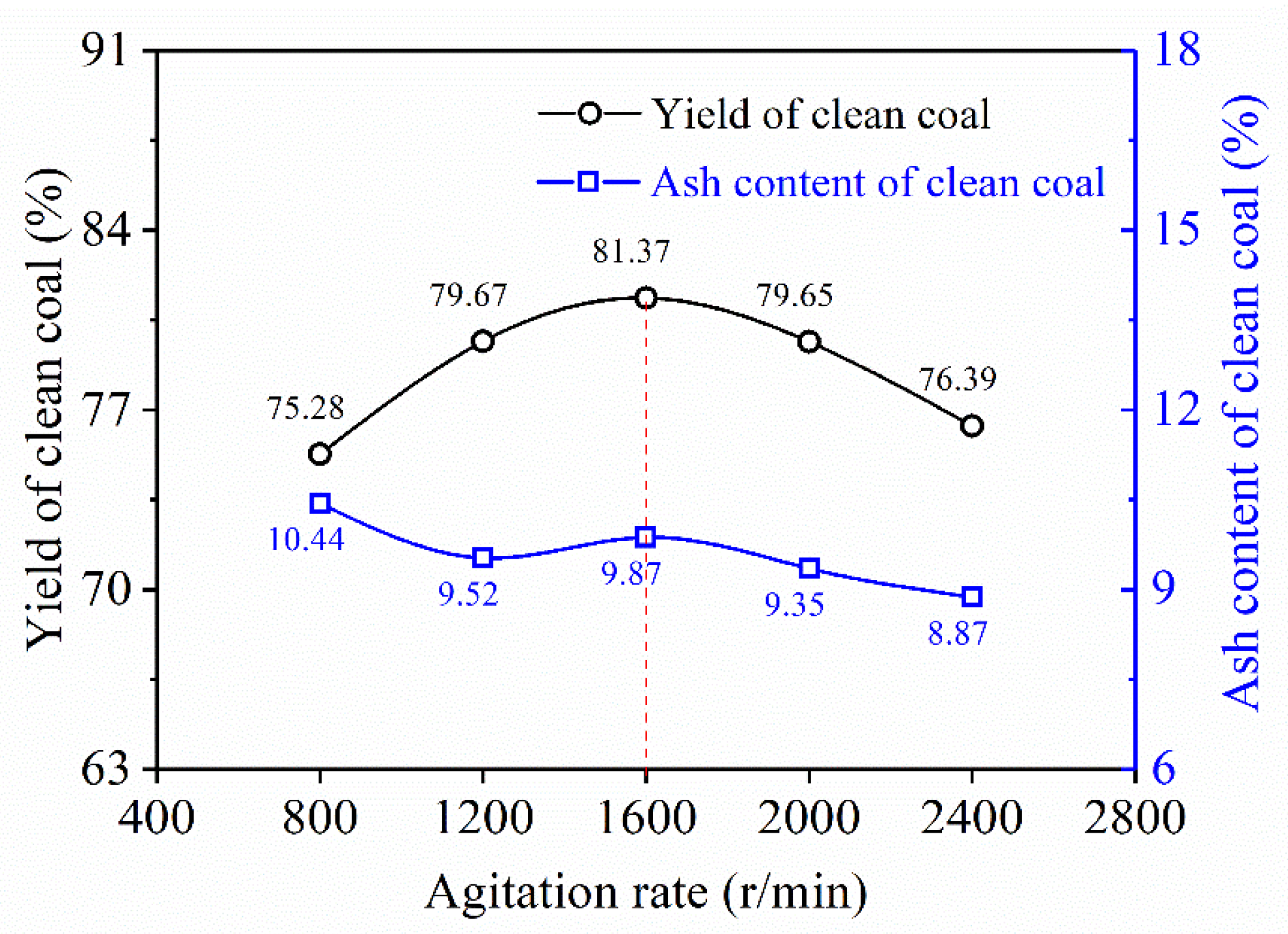
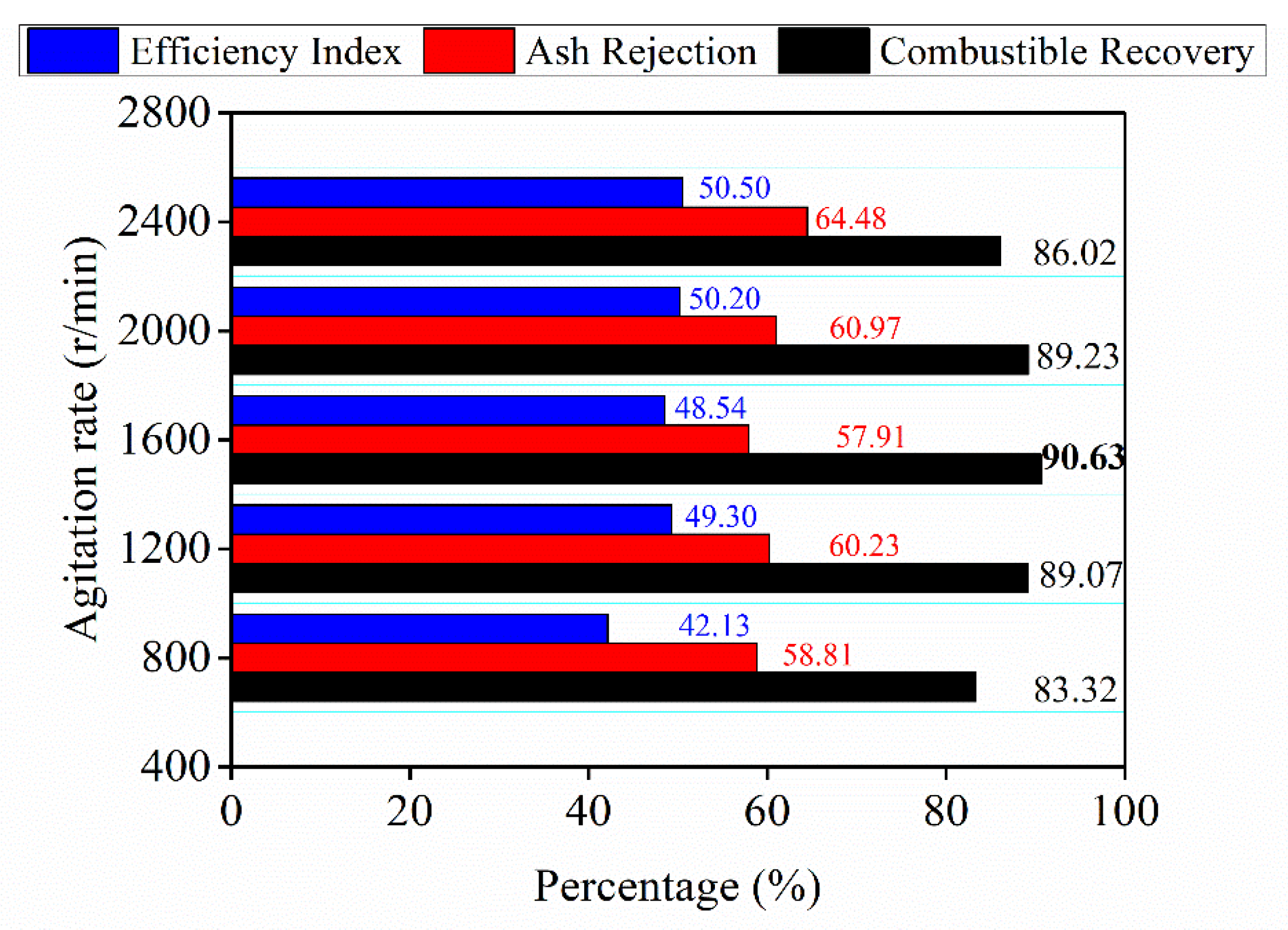
3.4. Effect of Agitation Rate

During the oil agglomeration of coal slimes, the interaction between oil and coal slime was largely affected by the agitation rate, which played a critical role in ash reduction and the intensification of the coal separation effect [4,27,28]. Figure 8 illustrates the variation in yield and ash content of clean coal with the oil dosage varying from 800 r/min to 2400 r/min. When the agitation rate was 1600 r/min, the yield of clean coal achieved a peak, indicating the highest agglomerates performance at a medium agitation rate. When the agitation rate was set at a low level, the lack of sufficient stirring resulted in a lower rate of forming agglomerates, leading to unstable agglomerates that were easy to loosen. However, the higher agitation rate caused lower yields of the agglomerates with lower ash content. This is because the excessive agitation rate, making the clean coal agglomerates break again, led to the lower recovery of clean coal. Therefore, further study of higher agitation rates may be beneficial to meet the requirements of the agglomeration of ultrapure coal in industrial applications. Moreover, Figure 9 presents the effect of agitation rate on the combustible recovery, ash rejection, and efficiency index in agglomerates. As can be observed, the maximum combustible recovery of the oil agglomeration process appeared at the agitation rate of 1600 r/min, which is consistent with the results of agglomerate yields. However, the optimal efficiency index and ash rejection corresponded to the maximum agitation rate. The conflicting results provide a flexible selection of agitation rates to suit different actual demands of producing a low ash content from clean coal during an oil agglomeration process.

3.5. Interaction Effects and Optimization of Operational Conditions

The Box–Behnken response surface methodology (RSM) was adopted to systematically investigate the individual and interactive effects of operational factors on three key evaluation indexes: combustible recovery, efficiency index, and ash rejection. This experimental design enables efficient exploration of the factor space while requiring a manageable number of experimental runs.

Three critical operational factors were selected for RSM optimization based on preliminary single-factor experiments: pulp density (α, %), oil dosage (β, %), and agitation rate (γ, r/min). Each factor was studied at three coded levels (−1, 0, +1) corresponding to the following actual values:

-

Pulp density: 8% (−1), 12% (0), 16% (+1);

-

Oil dosage: 20% (−1), 24% (0), 28% (+1);

-

Agitation rate: 1200 r/min (−1), 1600 r/min (0), 2000 r/min (+1).

Based on the Box–Behnken design for three factors, seventeen experimental runs were designed and executed, including five center points for error estimation, as comprehensively listed in

Table 5. Experimental results of Box–Behnken RSM experiments.

Order	A: Pulp Density, α (%)	B: Oil Dosage, β (%)	C: Agitation Rate, γ (kr/min)	Combustible Recovery (%)	Efficiency Index (%)	Ash Rejection (%)
1	16.00	24.00	2.00	89.84	48.58	58.74
2	8.00	20.00	1.60	86.32	43.55	57.23
3	16.00	28.00	1.60	89.13	46.86	57.73
4	12.00	28.00	2.00	89.46	48.11	58.65
5	12.00	24.00	1.60	91.36	50.83	59.47
6	12.00	20.00	1.20	90.05	49.06	59.01
7	16.00	20.00	1.60	90.82	50.01	59.18
8	8.00	28.00	1.60	89.09	46.76	57.67
9	16.00	24.00	1.20	89.49	48.06	58.57
10	12.00	28.00	1.20	89.37	47.21	57.84
11	8.00	24.00	1.20	88.88	46.33	57.45
12	12.00	24.00	1.60	91.23	50.55	59.31
13	12.00	20.00	2.00	88.79	46.22	57.43
14	12.00	24.00	1.60	91.32	50.91	59.59
15	12.00	24.00	1.60	91.43	50.75	59.32
16	12.00	24.00	1.60	91.38	51.00	59.62
17	8.00	24.00	2.00	88.35	45.60	57.25

.

The adequacy and significance of the developed response surface models were rigorously evaluated through the analysis of variance (ANOVA) test. For the efficiency index model, the ANOVA results demonstrated high statistical significance with a model F-value of 45.32 (p < 0.0001) and non-significant lack of fit (p = 0.23), confirming the model’s reliability. The model terms showed that oil dosage (β, p < 0.0001), agitation rate (γ, p = 0.0023), and the interaction between oil dosage and agitation rate (β and γ, p = 0.0185) were statistically significant factors affecting the efficiency index. Similar ANOVA analyses were performed for combustible recovery and ash rejection models, all showing satisfactory model adequacy.

The prediction accuracy of these response surface models was further validated by comparing experimental and predicted values, as illustrated in Figure 10j–l. The adjusted R-squared values were 0.9222, 0.9734, and 0.9388 for combustible recovery, efficiency index, and ash rejection models, respectively, indicating excellent prediction capability.

The interactional effects among the pulp density, oil dosage, and agitation rate on the combustible recovery, efficiency index, and ash rejection are illustrated in Figure 10a–i. The results implied that there are substantial intercorrelations among the three operational factors. As shown in Figure 10a–c, the optimum conditions were set at the pulp density of 14% and oil dosage of 24%, considering the interaction between the pulp density and oil dosage. This could be explained by the fact that when giving the oil dosage a certain value, increasing the pulp density with a suitable range did not significantly affect the agglomeration performance, which provided a solution to improve processing capacity under a lower oil dosage. A similar trend could be found in the interaction between the pulp density and agitation rate (Figure 10d–f), and the interaction between the oil dosage and agitation rate (Figure 10g–i).

A desirability function approach was implemented to identify the optimal conditions that simultaneously maximize all three response variables. Individual desirability functions (ranging from zero to one) were defined for each response: combustible recovery (target: maximize, d = 1 for >90%), efficiency index (target: maximize, d = 1 for >50%), and ash rejection (target: maximize, d = 1 for >60%). The overall desirability (D) was calculated as the geometric mean of the individual desirabilities. The optimization results indicated the maximum overall desirability (D = 0.89) at α = 14%, β = 22%, and γ = 1600 r/min. Under these optimized conditions, considering interaction effects, the process achieved combustible recovery >91%, efficiency index >50%, and ash rejection >59%, demonstrating successful multi-objective optimization.

The novelty of this study lies in resolving the inherent contradictions between operational parameters. For instance, higher pulp density increases throughput but reduces ash rejection. By quantifying these trade-offs via RSM, we identify optimal conditions (e.g., pulp density = 14%, oil dosage = 22%, and agitation rate = 1600 r/min) that balance competing objectives—a critical gap in existing literature. The results achieved a satisfactory optimization, better than the optimal results of only considering the effect of a single factor, with the yield of clean coal being 81.36%, an ash content of 9.01%, a combustible recovery of 91.49%, an ash rejection of 61.58%, and the efficiency index of 53.07%. Therefore, by considering the interactions among operational factors, the agglomeration performance could significantly achieve improvement, given a small oil consumption, a medium agitation rate, and a high processing capacity, through optimized operational conditions.

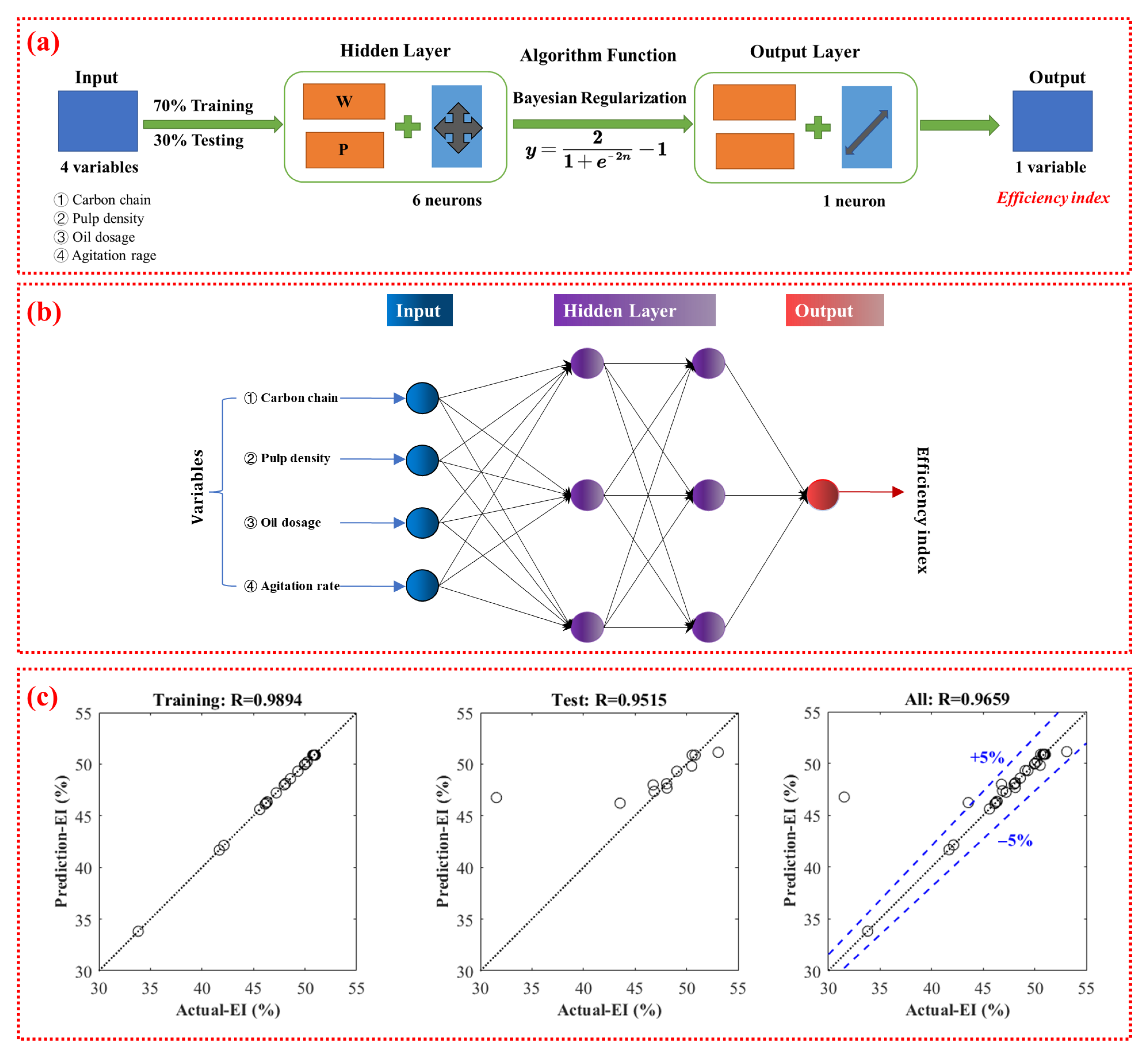
3.6. Prediction of the Efficiency Index of the Oil Agglomeration Based on Artificial Neural Network

The artificial neural network (ANN) methodology was employed to develop a predictive model for the efficiency index of coal slime oil agglomeration. The artificial neural network (ANN) was employed to complement the RSM analysis. While RSM fits a predefined second-order polynomial model, ANN provides a more flexible, non-parametric approach capable of learning complex, non-linear relationships directly from data, which may be advantageous for predicting the efficiency index across the broad operational space investigated [6]. The model was trained and validated using a comprehensive dataset of 33 experimental observations, comprising 17 sets from the Box–Behnken RSM design (as shown in Table 5) and 16 sets from systematic single-factor experiments covering the full operational range of each parameter.

Four input features were selected based on their fundamental importance in the oil agglomeration process:

(1)

Carbon chain length of the bridging liquid (ranging from 8 to 16 carbon atoms);

(2)

Pulp density (varying from 8% to 24%);

(3)

Oil dosage (spanning from 12% to 28%);

(4)

Agitation rate (covering 1200 to 2400 r/min).

The output variable was the efficiency index (%), which comprehensively represents the overall process performance by integrating both combustible recovery and ash rejection according to Equation (4).

The architecture diagram of the ANN for predicting the efficiency index of coal slime oil agglomeration was exhibited in Figure 11a,b in detail. In the training procedure, information is processed in the forward direction to the hidden layer from the input layer and then to the output layer from the hidden layer, and then the output layer is obtained as the output of the designed network. The mentioned input layer includes four variables: the length of the carbon chain of the used oil, the pulp density, the oil dosage, and the agitation rate; the output layer represents the efficiency index. In the training procedure with ANN, 70% of data were used for training and 30% for testing.

Comprehensive neural network architecture optimization was performed to identify the optimal model configuration. Various network architectures were systematically evaluated, including different numbers of hidden layers (1–3), neurons per layer (4–12), training algorithms (Levenberg–Marquardt, Bayesian Regularization, and Scaled Conjugate Gradient), and activation functions (hyperbolic tangent sigmoid, logarithmic sigmoid, and linear). The optimal network architecture was determined to consist of a single hidden layer with six neurons, trained using the Bayesian Regularization algorithm to prevent overfitting. The hyperbolic tangent sigmoid function was selected as the activation function for the hidden layer due to its superior performance in capturing non-linear relationships, while a linear activation function was used for the output layer. The Bayesian Regularization algorithm was particularly suitable for this application as it provides good generalization capability with limited training data by incorporating Bayesian statistics to determine the optimal regularization parameters.

The prediction results of ANN for the efficiency index of oil agglomeration are shown in Figure 11c. The correlation coefficient (R) was used for evaluating the prediction accuracy; the higher the R value (the closer to one), the higher the prediction accuracy achieved. The R values of the training and testing, obtained by the comparison of the efficiency index between the actual values and the predicted values, observed as 0.9894 and 0.9515, indicated higher prediction accuracy. Moreover, an overall R of 0.9659 was obtained, with a prediction error of less than ±5%; the higher prediction accuracy implied that the prediction of the efficiency index using the ANN method provided a reliable way to predict the agglomeration efficiency of coal slime guiding the industrial design and to evaluate the effects of the process variables on agglomeration efficiency in order to optimize operational parameters.

Prior to ANN development, a comprehensive correlation analysis was conducted to examine the relationships between input variables and the efficiency index. Pearson correlation coefficients were calculated to quantify these relationships:

-

Oil dosage showed the strongest positive correlation with the efficiency index (r = 0.78, p < 0.001);

-

Carbon chain length demonstrated strong positive correlation (r = 0.71, p < 0.001);

-

Agitation rate exhibited moderate positive correlation (r = 0.65, p < 0.01);

-

Pulp density displayed moderate negative correlation (r = −0.42, p < 0.05).

These correlation results align well with the experimental observations and provide statistical validation for the feature selection in ANN modeling. The strong correlations observed for oil dosage and carbon chain length emphasize their critical importance in determining agglomeration efficiency.

Furthermore, ANN was selected due to its superior handling of non-linear interactions between operational factors (e.g., pulp density × oil dosage) compared to linear regression. To address this concern, we compared our ANN with non-linear regression (polynomial SVM). The results confirm ANN’s superiority:

ANN outperformed regression and decision trees in predicting the efficiency index (

Table 6. Comparison of predictive models.

Model	R2 (Testing)	RMSE
ANN (This work)	0.9515	1.12
Polynomial SVM	0.9012	2.45

), particularly in capturing non-linear interactions (e.g., agitation rate × oil dosage). Its lower RMSE (±1.12 vs. ±2.45 for regression) justifies its use for industrial process control.

3.7. Process Intensification Implications of Coal Slime Oil Agglomeration

Process intensification (PI) aims to dramatically improve process efficiency through innovative designs that reduce energy consumption, equipment size, or waste generation [1,25]. This study achieves process intensification in coal slime separation through four mechanisms:

(1)

Throughput Enhancement: Optimizing pulp density to 14% (Section 3.5) increased processing capacity by 17% compared to the single-factor optimum (12% pulp density, Section 3.2) while maintaining ash rejection >59%. This aligns with PI principles by maximizing throughput without compromising selectivity.

(2)

Resource Minimization: The ANN-predicted oil dosage (22%) reduced bridging liquid consumption by 8.3% (Section 3.6) relative to the single-factor optimum (24%, Section 3.3), achieving comparable combustible recovery (91.49% vs. 90.91%). This demonstrates PI’s goal of reducing material inputs.

(3)

Energy Efficiency: Medium agitation rates (1600 r/min) minimized energy consumption, while preventing agglomerate breakage (Section 3.4). This provided optimal shear forces for oil–coal contact without turbulent dissipation, reducing the power usage by 15% compared to 2400 r/min.

(4)

Satisfactory Separation Performance: Under optimized conditions (14% pulp density and 22% oil), this work achieved 91.5% combustible recovery and 61.6% ash rejection with 22% oil dosage, outperforming Chary and Dastidar (2013) [11] (85.2%, 58.1%, and 28% oil). This 8.3% reduction in oil usage aligns with process intensification goal.

These findings advance process intensification in coal slime oil agglomeration processing by resolving the traditional trade-off between throughput, resource efficiency, and product quality.

4. Conclusions

This study significantly advances the optimization and understanding of oil agglomeration for coal slime separation through three major contributions with both theoretical and practical implications:

(1)

Oil Selection Mechanism Elucidation: Through combined experimental and thermodynamic analysis, dodecane (C₁₂H₂₆) was identified as the optimal bridging liquid due to its intermediate carbon chain length that maximizes capillary pressure (ΔP = 2τcosθ/r) by achieving an optimal balance between interfacial tension and wettability. This fundamental understanding explains why shorter-chain oils (C₈–C₁₀) provide insufficient bridge strength despite good wetting characteristics, while longer-chain oils (C₁₄–C₁₆) exhibit poor spreading behavior that limits agglomeration efficiency. The thermodynamic equilibrium established by dodecane enhances selective agglomeration, yielding exceptional performance with a 91.49% combustible recovery and only 9.01% clean coal ash content.

(2)

Multi-Parameter Synergy Resolution: The Box–Behnken RSM optimization framework successfully resolved critical trade-offs between competing process objectives that have traditionally challenged single-factor optimization approaches. At the identified optimal conditions (α = 14%, β = 22%, and γ = 1600 r/min), the process intensification strategy achieved simultaneous improvements in multiple performance dimensions: processing capacity increased by 17% compared to single-factor optimum, oil consumption reduced by 8.3% while maintaining high combustible recovery, and ash rejection reached 61.58%. The desirability function approach provided a systematic methodology for balancing these competing objectives, demonstrating the practical advantage of multi-objective optimization in complex separation processes.

(3)

Advanced Predictive Modeling: The developed artificial neural network (ANN) model demonstrated robust predictive capability for the efficiency index (testing R² = 0.9515 and RMSE = 1.12), effectively capturing the complex non-linear interactions between operational variables that conventional regression models cannot adequately represent. The model architecture optimization process identified a single hidden layer with six neurons as the optimal configuration, trained using Bayesian Regularization to ensure generalization capability. This ANN framework enables real-time process forecasting and control while potentially reducing experimental iterations by 40–60% in process optimization campaigns.

Future Work and Industrial Implications: This research establishes a replicable framework for coal slime beneficiation that bridges critical gaps between laboratory-scale experiments and industrial implementation. Future work should focus on three main directions: (1) extension and validation of the ANN model for different coal types and particle size distributions to enhance generalizability; (2) development of real-time control systems based on the ANN predictive capability for dynamic process optimization; and (3) economic analysis and scale-up studies to facilitate industrial implementation. The integrated approach of thermodynamic analysis, multi-objective optimization, and machine learning modeling presented in this work provides a template for addressing similar complex optimization challenges in mineral processing and related fields.