Internal Flow and Pressure Pulsation Characteristics of a High-Head Francis Turbine Under Wide Load Conditions
Abstract
1. Introduction
2. Calculation Model
2.1. Basic Parameters of the Model Turbine
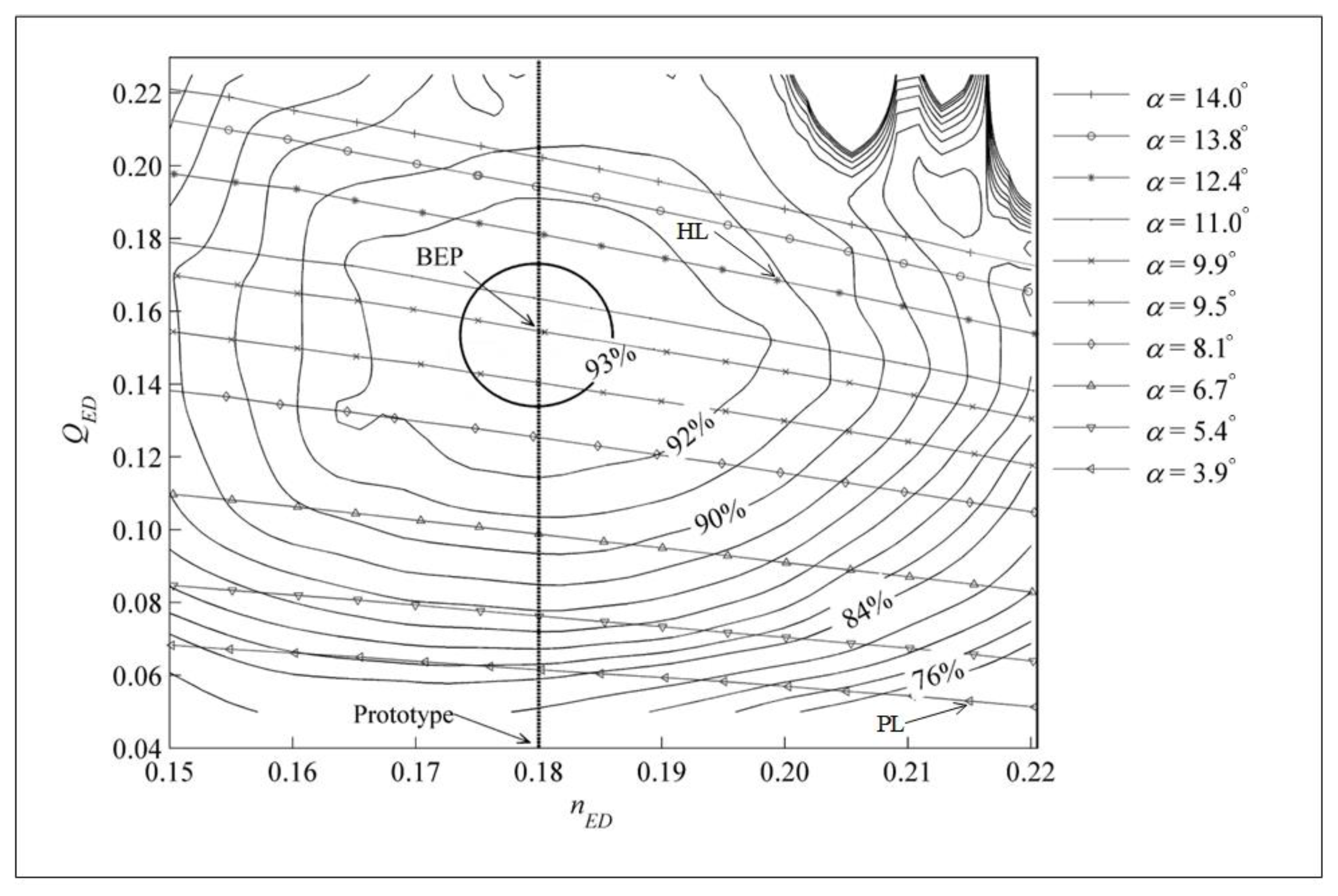
2.2. Detail Characteristics Curve of the Model Turbine
- (1)
- PL working condition, that is, the small flow and low load working condition, nED = 0.215 and QED = 0.07;
- (2)
- BEP condition, that is, the optimal condition, with nED = 0.18 and QED = 0.2;
- (3)
- HL operation, that is, the high-flow and high-load operation, has nED = 0.195 and QED = 0.19.
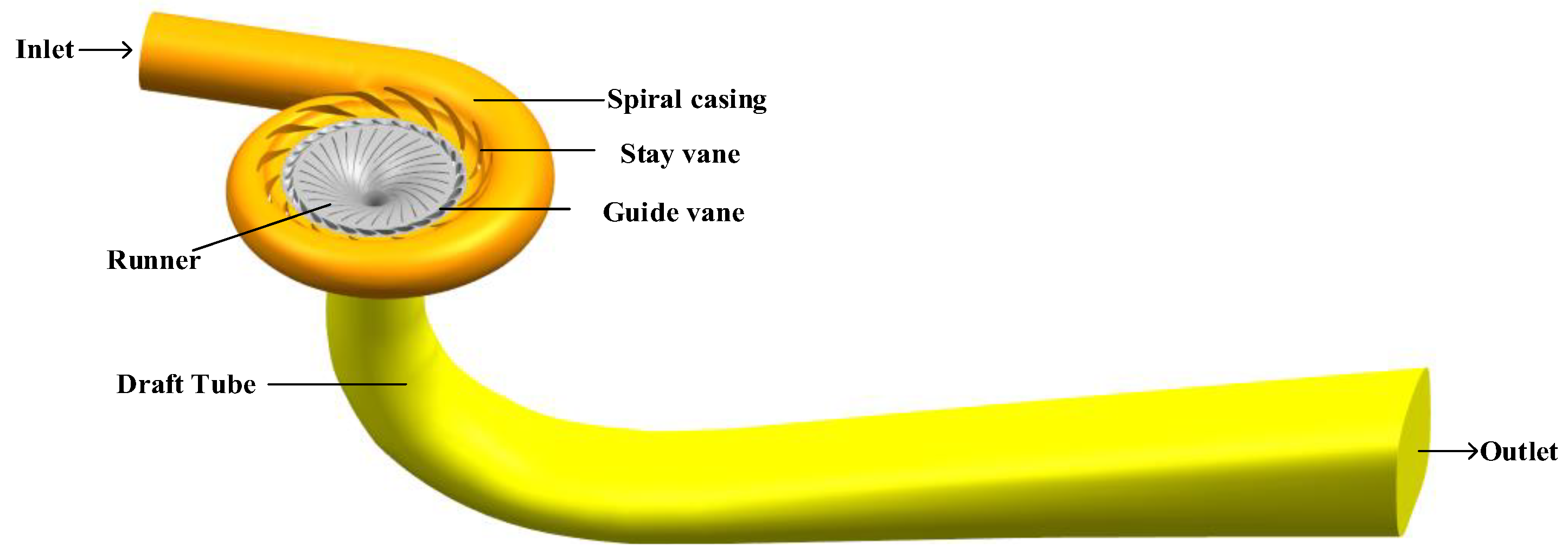
2.3. Establishment of a Three-Dimensional Geometric Model
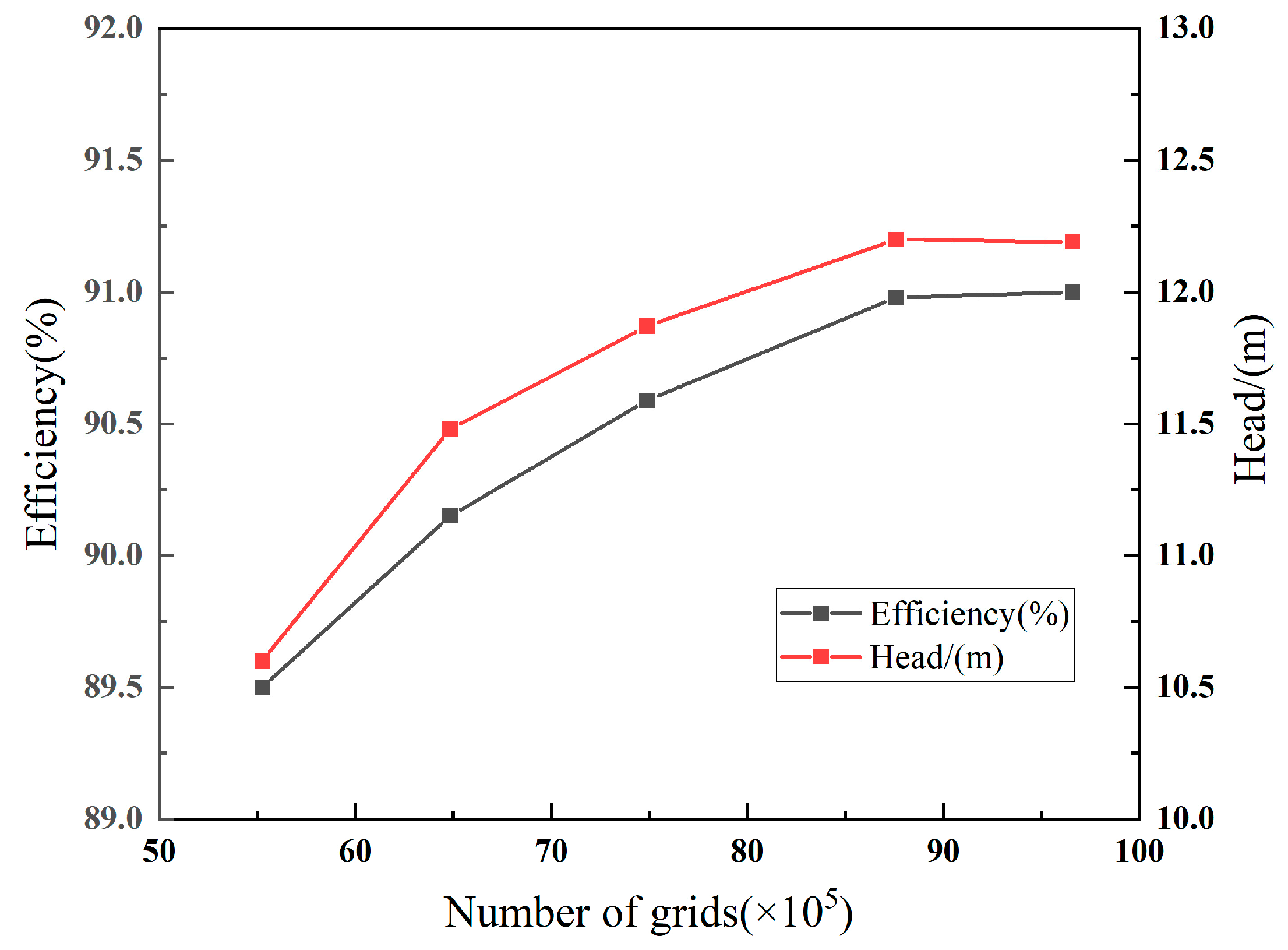
2.4. Grid Division and Independence Verification
3. Numerical Computation Method
3.1. Turbulence Flow Simulation Model
3.2. Pressure Pulsation Equation
3.3. Boundary Condition Setting
4. Calculations and Analysis of Results
4.1. Verification in the Accuracy of Numerical Calculation Results
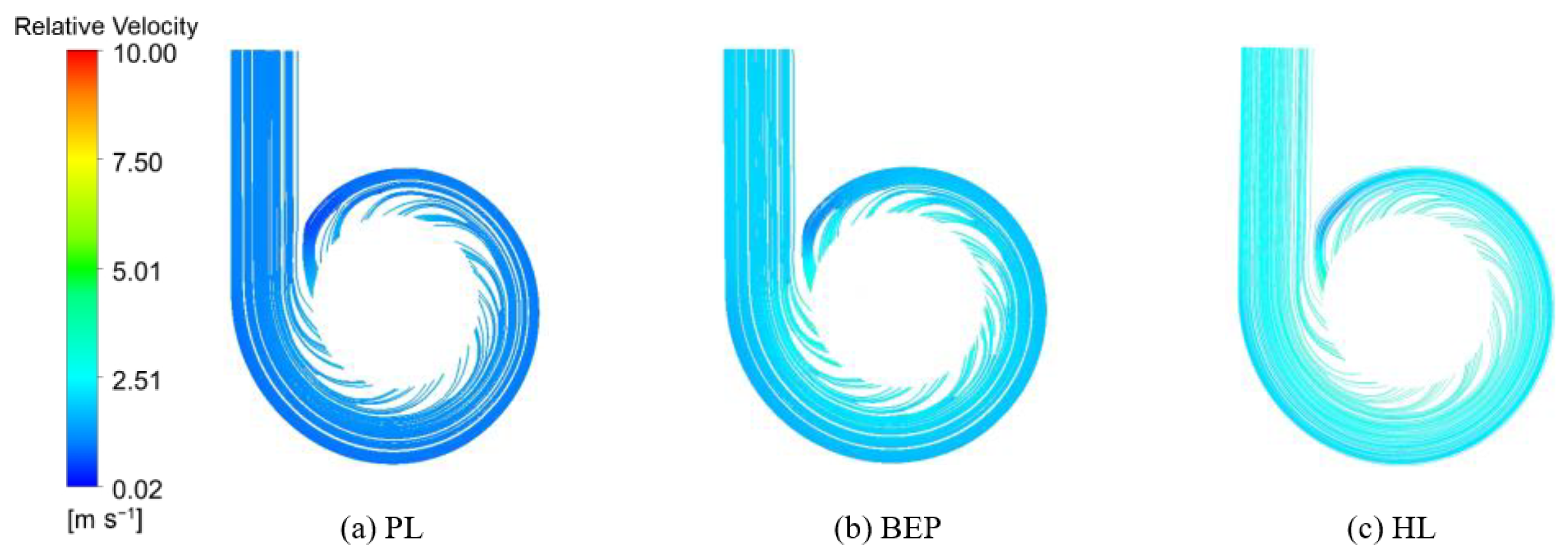
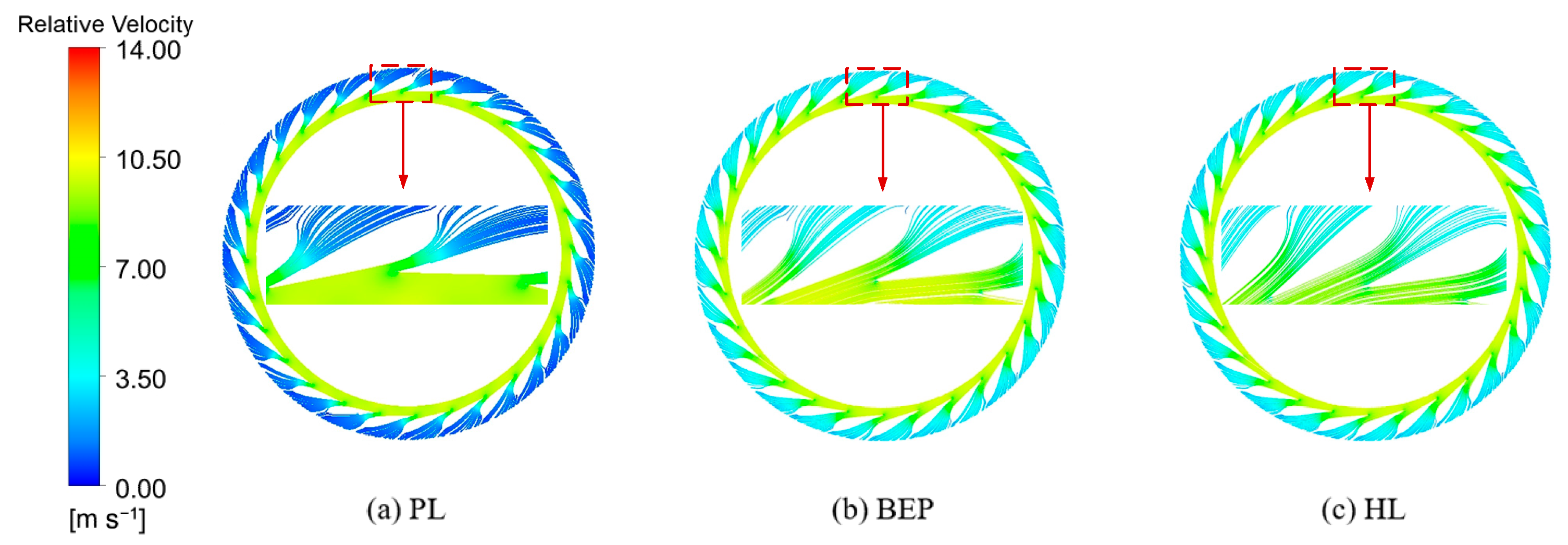
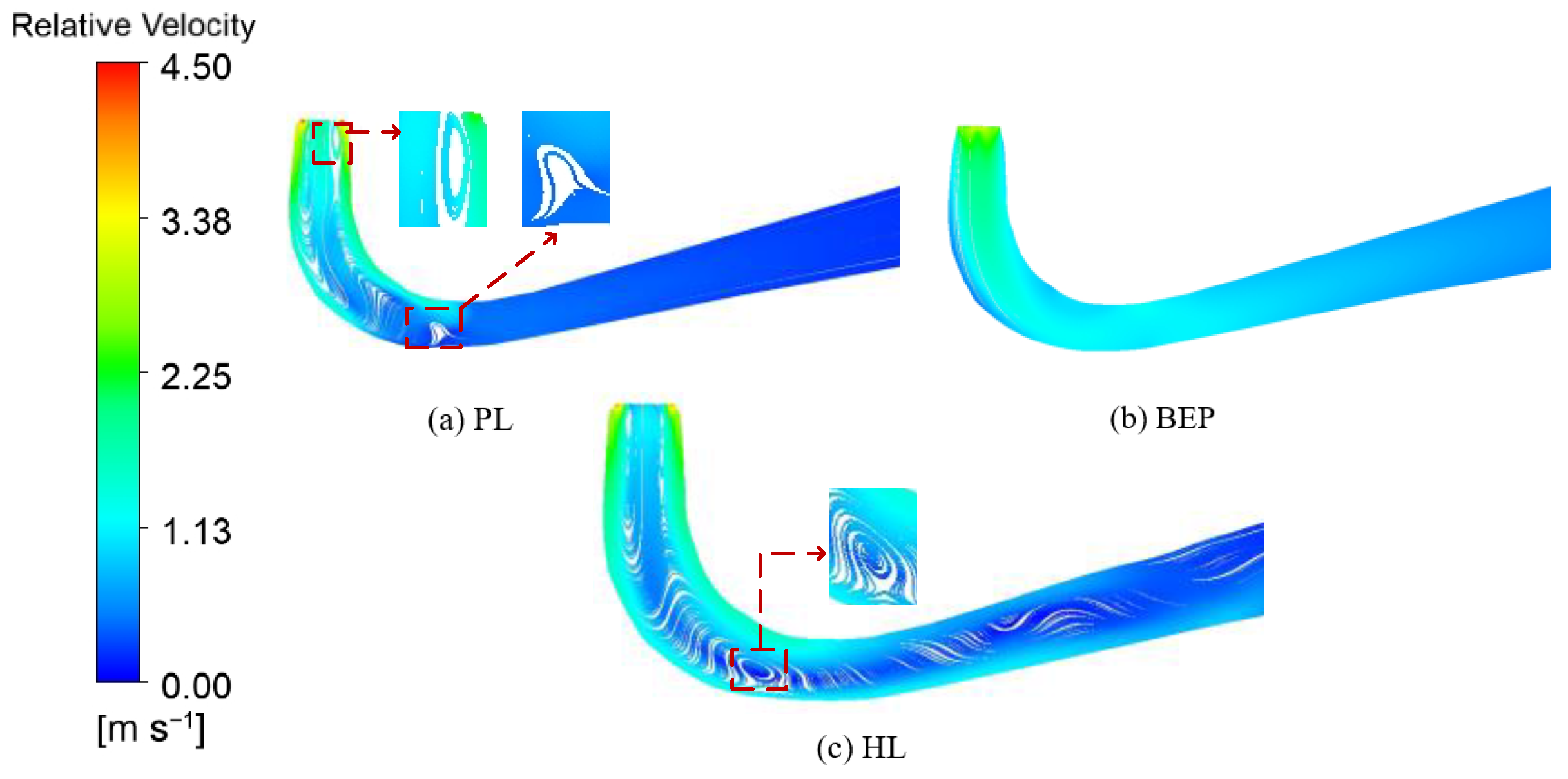
4.2. Speed Characteristics
- (1)
- Water-conveying component
- (2)
- Runner
- (3)
- Draft tube
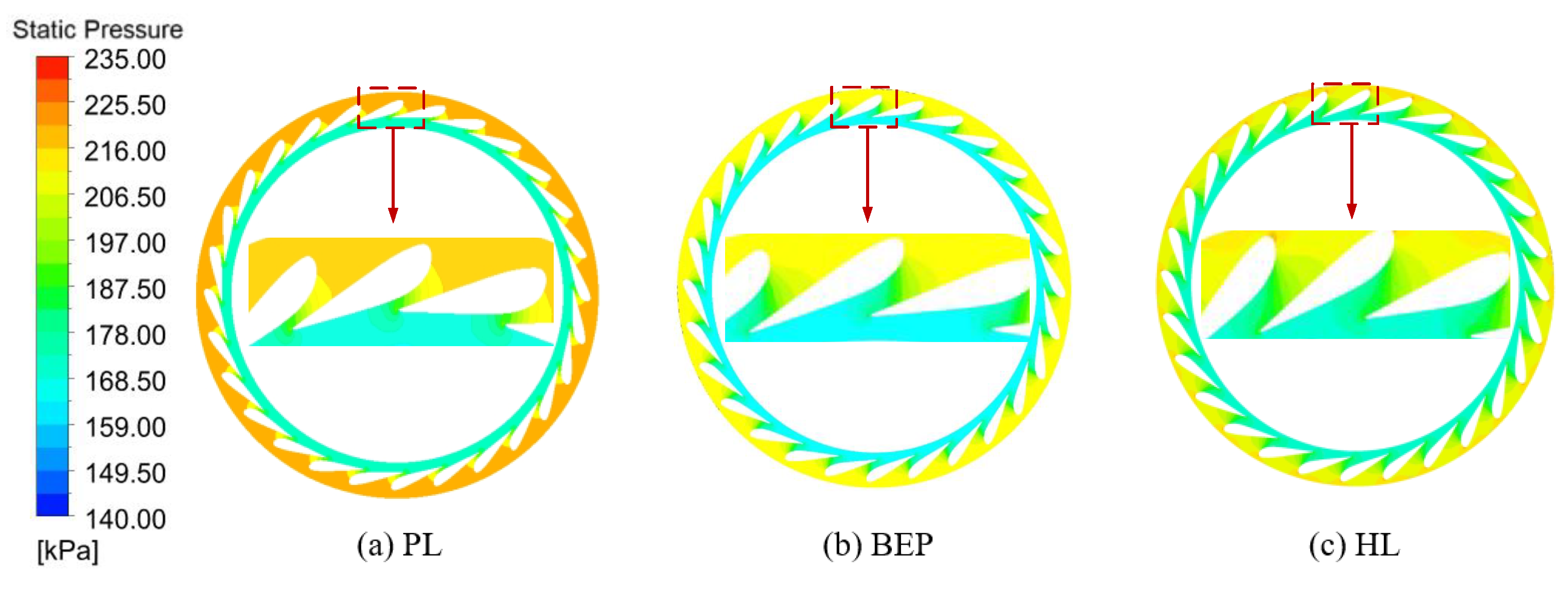
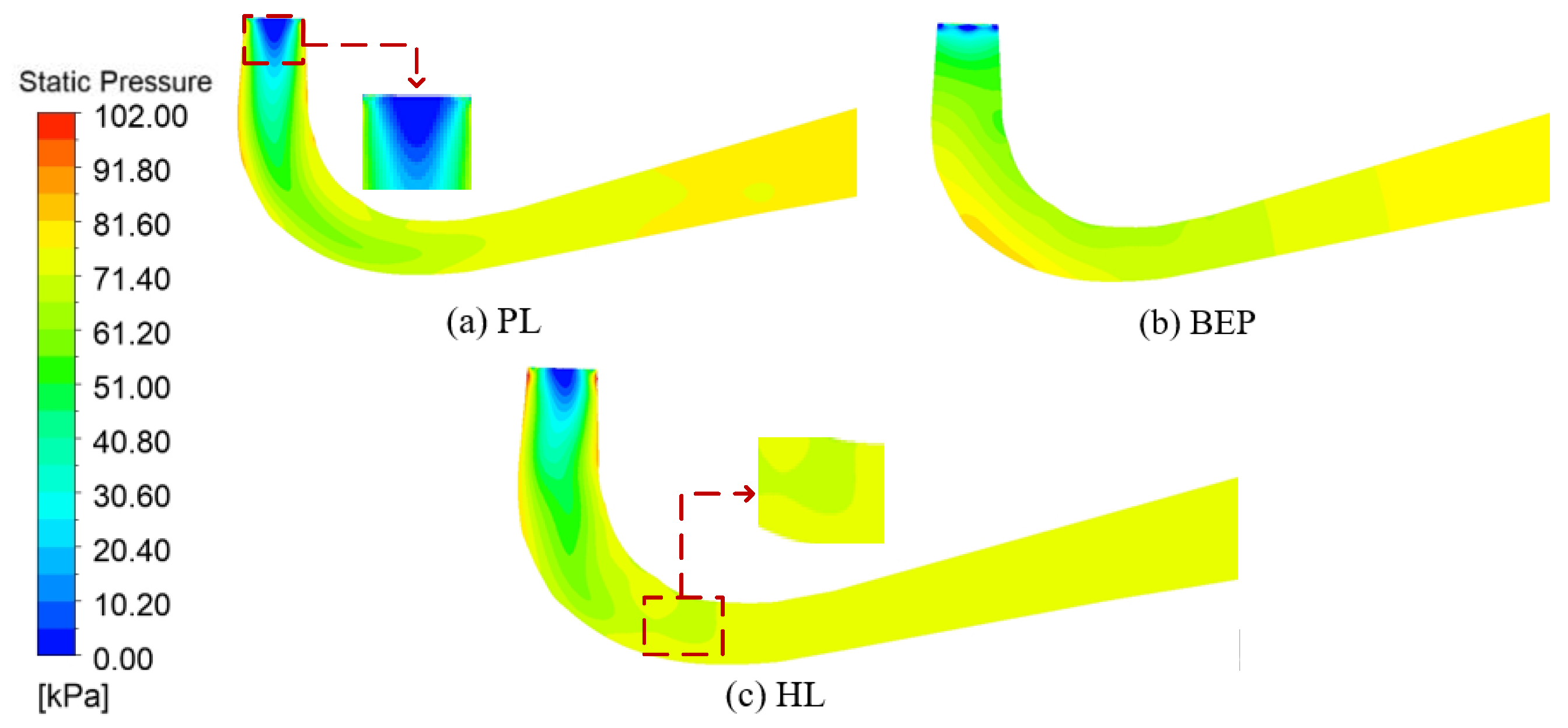
4.3. Pressure Characteristics
- (1)
- Water-conveying component
- (2)
- Runner
- (3)
- Draft tube
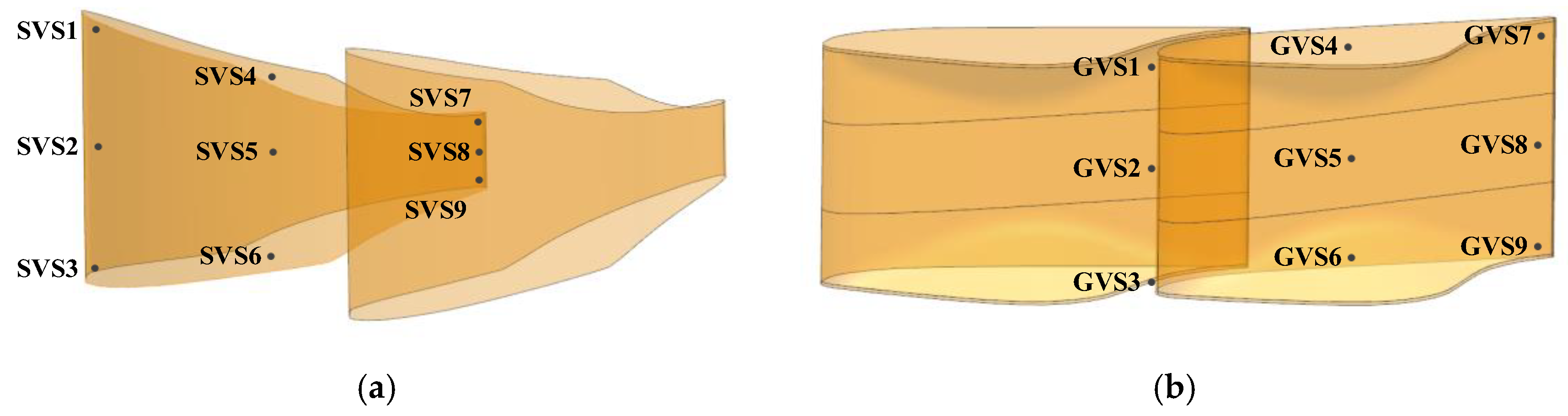
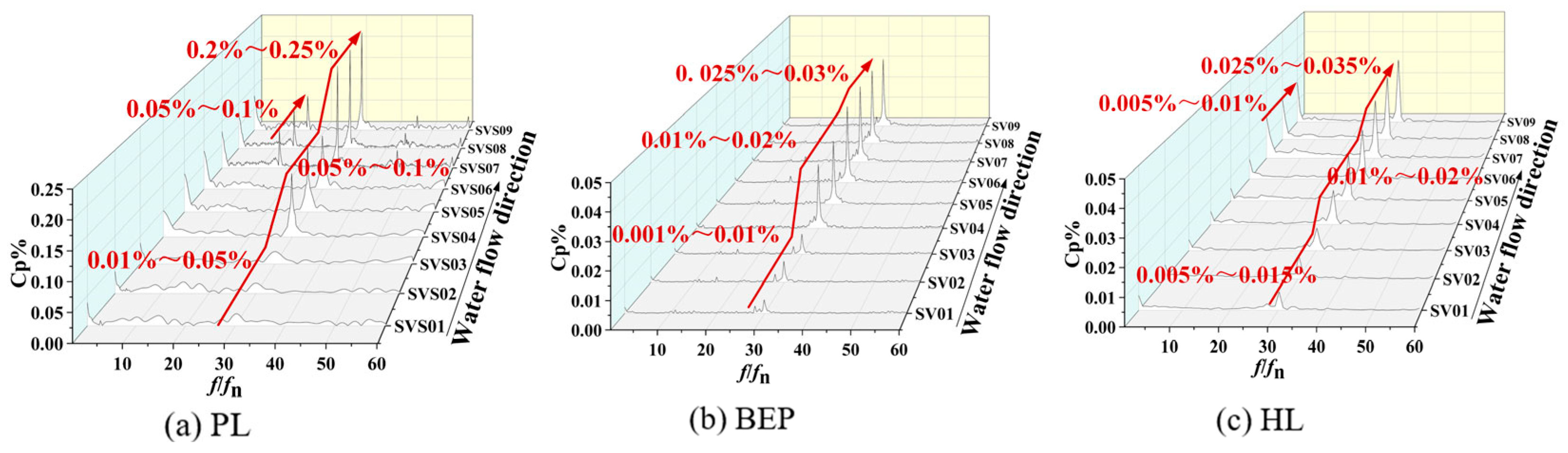
4.4. Pressure Pulsation Characteristics
- (1)
- Stay vane
- (2)
- Active guide vane
- (3)
- Runner
- (4)
- Draft tube
5. Conclusions
- (1)
- Under all working conditions, the streamline distributions in the spiral casing and stay vane are uniform and symmetrical, with no evidence of flow separation or vortex formation. There is a progressive rise in flow velocity between the spiral casing inlet and the fixed guide vane outlet. Inside the runner, the water flow’s kinetic energy is efficiently transformed into rotational mechanical energy. However, in the areas of the runner and the draft tube, vortex bands are generated at some operating points, resulting in an increase in energy loss. The above research data provides a reference for the in-depth future study of the internal flow and vortex belts in water turbines. Furthermore, these data also serve as a valuable resource for improving the units’ stability, efficiency, and reliability.
- (2)
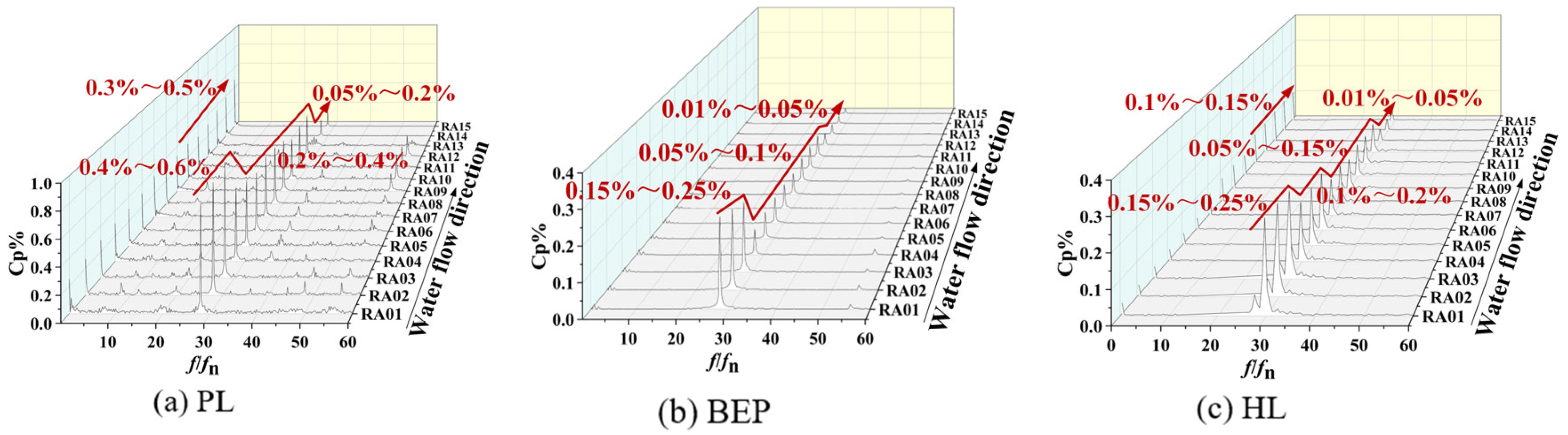
- Due to the dynamic and static interference induced by the rotation of the runner, the dominant pressure pulsation frequency within the water guide mechanism is 30fn. The maximum amplitude of this frequency occurs near the bladeless region. The peak amplitudes of the main frequency under the PL, BEP, and HL operating conditions are 0.25%, 0.03%, and 0.035%, respectively. In the runner, the main frequency of 28fn originates from the influence of the guide vane, with the highest amplitude appearing in the inlet region. As the water progresses downstream, the amplitude of this frequency gradually decreases. The runner’s movement causes pressure pulsation. This pulsation is transmitted to components like the draft tube, guide vane, and spiral casing, which leads to unit vibration. However, this phenomenon cannot be eliminated. Therefore, it is necessary to control it within a safe range through design optimization and operation management.
- (3)
- According to the pressure pulsation data obtained in this paper, the pressure pulsation of the mixed-flow turbine is mainly caused by the dynamic and static interference of the rotor rotation and the vortex band in the draft tube. To effectively control pressure pulsation, the following two technical measures are mainly adopted: one is to suppress the formation process of vortex nuclei, and the other is to restrict the further development of vortex belts. To improve the pressure pulsation inside the turbine, several solutions are available. These are supplementing air to the draft tube, setting up a pressure stabilizing device, or installing a high-frequency pressure sensor. Furthermore, the air replenishment system or load adjustment should be triggered during the initial stage of the turbine belt’s operation. Avoid extended operation in load ranges where vortex belts are likely to occur. Alternatively, prevent vortex belt formation by adjusting parameters like guide vane opening and rotational speed. Both measures are necessary to ensure stable operation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jhankal, N.K.; Kumar, A. Experimental investigations of pressure fluctuations in low-head francis turbine model. Proc. Inst. Mech. Eng. Part A J. Power Energy 2024, 238, 1321–1337. [Google Scholar] [CrossRef]
- Li, J.; Liu, Q.; Wang, W.; Song, X.; Wang, Z.; Zhu, D.; Tao, R. Pressure pulsation test of Wanjiazhai Francis turbine at different loads. J. Phys. Conf. Ser. 2024, 2707, 012059. [Google Scholar] [CrossRef]
- Jamali, R.; Sohani, A.; Hemmatpour, K.; Behrang, M.; Ghobeity, A. Experimental study of pressure pulsation in a large-scale hydropower plant with Francis turbine units and a common penstock. Energy Convers. Manag. X 2022, 16, 100308. [Google Scholar] [CrossRef]
- Favrel, A.; Nicolle, J.; Morissette, J.F.; Giroux, A.M. On the correlation between runner blade dynamic stresses and pressure fluctuations in a prototype Francis turbine. IOP Conf. Ser. Earth Environ. Sci. 2022, 1079, 012115. [Google Scholar] [CrossRef]
- Iliev, I.; Trivedi, C.; Agnalt, E.; Dahlhaug, O.G. Variable-speed operation and pressure pulsations in a Francis turbine and a pump-turbine. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 072034. [Google Scholar] [CrossRef]
- Wang, D.; Li, Z.; Zhao, Q.; Li, D.; Deng, W.; Ji, L.; Peng, S. Pressure pulsation analysis of runner and draft tube of pump turbine under different working conditions. IOP Conf. Ser. Earth Environ. Sci. 2022, 1037, 012036. [Google Scholar] [CrossRef]
- Pang, J.; Yao, B.; Liu, X.; Li, J.; Xiao, M.; Jiang, D.; Tang, W.; Zhou, L.; Lai, Z. Influence of guide vane opening on channel vortex and pressure pulsation in Francis turbine runners. Phys. Fluids 2024, 36, 043325. [Google Scholar] [CrossRef]
- Guo, B.; Yu, R.; Ye, Y.; Li, X.; Xiao, Y. Experimental analysis of the pressure fluctuations for a prototype pump-turbine at different operating conditions. J. Phys. Conf. Ser. 2024, 2752, 012039. [Google Scholar] [CrossRef]
- Yang, J.; Liu, X.; Pang, J.; Song, H.; Peng, Y.; Xu, L. Numerical study on the Pressure Pulsation Characteristics of the Turbine in Yangjiawan Hydropower Station in the Multi-energy Complementary Power Generation System. Hydropower Pumped Storage 2021, 7, 59–63. [Google Scholar]
- Song, H.; Pang, J.; Wang, H. The influence of guide vane opening on the pressure pulsation characteristics of mixed-flow turbines. Gansu Water Resour. Hydropower Technol. 2021, 57, 44–48. [Google Scholar] [CrossRef]
- Zheng, X.B.; Sun, S.H.; Wang, Z.R.; Ren, P.; Qin, Z.L.; Yu, Y.; Zhou, H. Study on partial load vortex and pressure pulsation characteristics of Francis turbine. J. Phys. Conf. Ser. 2024, 2752, 012018. [Google Scholar] [CrossRef]
- Gohil, P.P.; Saini, R.P. Investigation into cavitation damage potentiality using pressure pulsation phenomena in a low head Francis turbine for small hydropower schemes. Ocean Eng. 2022, 263, 112230. [Google Scholar] [CrossRef]
- Sannes, D.B.; Iliev, I.; Agnalt, E.; Dahlhaug, O.G. Pressure pulsation in a high head Francis turbine operating at variable speed. J. Phys. Conf. Ser. 2018, 1042, 012005. [Google Scholar] [CrossRef]
- Sonin, V.; Ustimenko, A.; Kuibin, P.; Litvinov, I.; Shtork, S. Study of the velocity distribution influence upon the pressure pulsations in draft tube model of hydro-turbine. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 082020. [Google Scholar] [CrossRef]
- Shi, F.; Yang, J.; Wang, X. Analysis on characteristic of pressure fluctuation in hydraulic turbine with guide vane. Int. J. Fluid Mach. Syst. 2016, 9, 237–244. [Google Scholar] [CrossRef]
- Chen, T.J.; Wu, X.J.; Liu, J.T.; Wu, Y.L. Prediction of pressure fluctuation of a hydraulic turbine at no-load condition. IOP Conf. Ser. Mater. Sci. Eng. 2015, 72, 042049. [Google Scholar] [CrossRef]
- Minakov, A.V.; Platonov, D.V.; Dekterev, A.A.; Sentyabov, A.V.; Zakharov, A.V. The analysis of unsteady flow structure and low frequency pressure pulsations in the high-head Francis turbines. Int. J. Heat Fluid Flow 2015, 53, 183–194. [Google Scholar] [CrossRef]
- Pang, J.; Liu, X.; Song, H.; Deng, H.; Yang, H.; Peng, Y.; Yang, J. Research on the Working Condition stability of the mixed-flow Turbine Based on the Water-light-storage complementary Combined power generation System in the Ultra-low output Zone. Hydropower Pumped Storage 2021, 7, 39–46. [Google Scholar]
- Ye, C.; Yuan, L.; Tan, J.; Gong, L.; Liu, R.; Deng, X. Research on Pressure Pulsation in the Vortex Zone of Medium and Low Head Mixed-Flow Turbines. Yangtze River 2025, 56, 158–166+182. [Google Scholar] [CrossRef]
- Li, S.; Pang, J.; Dan, C.; Xiang, W.; Yi, X.; Liu, X. Influence of Load Variation on the Flow Field and Stability of the Francis Turbine. J. Mar. Sci. Eng. 2025, 13, 316. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J.; Dahlhaug, O.G. Experimental and numerical studies of a high-head Francis turbine: A review of the Francis-99 test case. Energies 2016, 9, 74. [Google Scholar] [CrossRef]

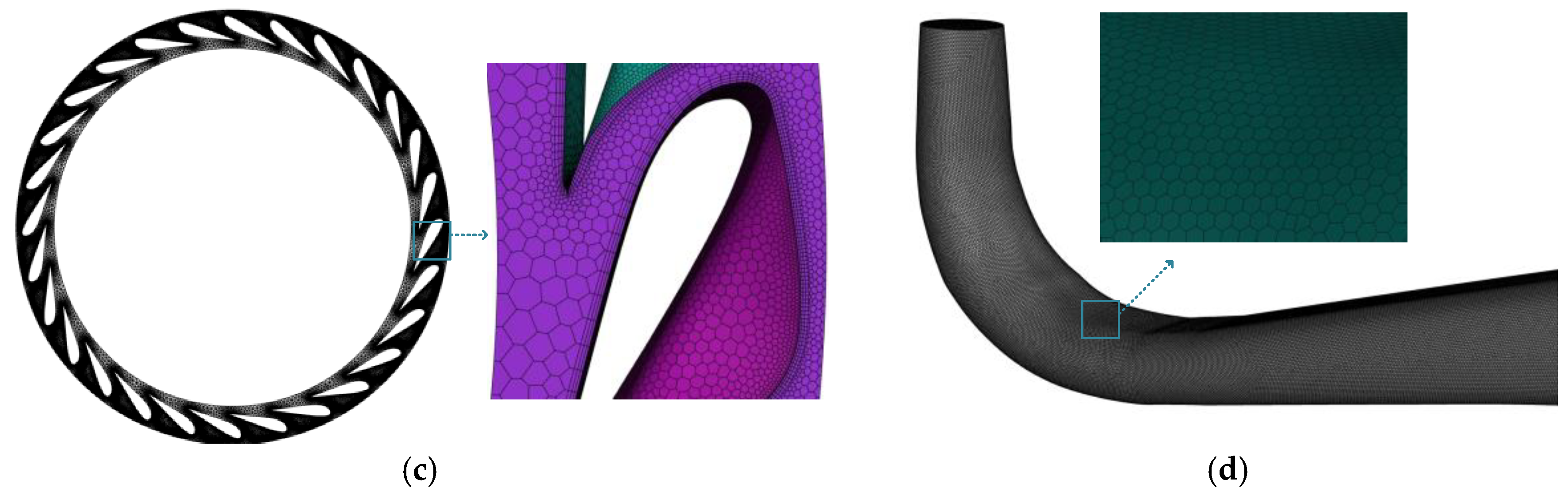



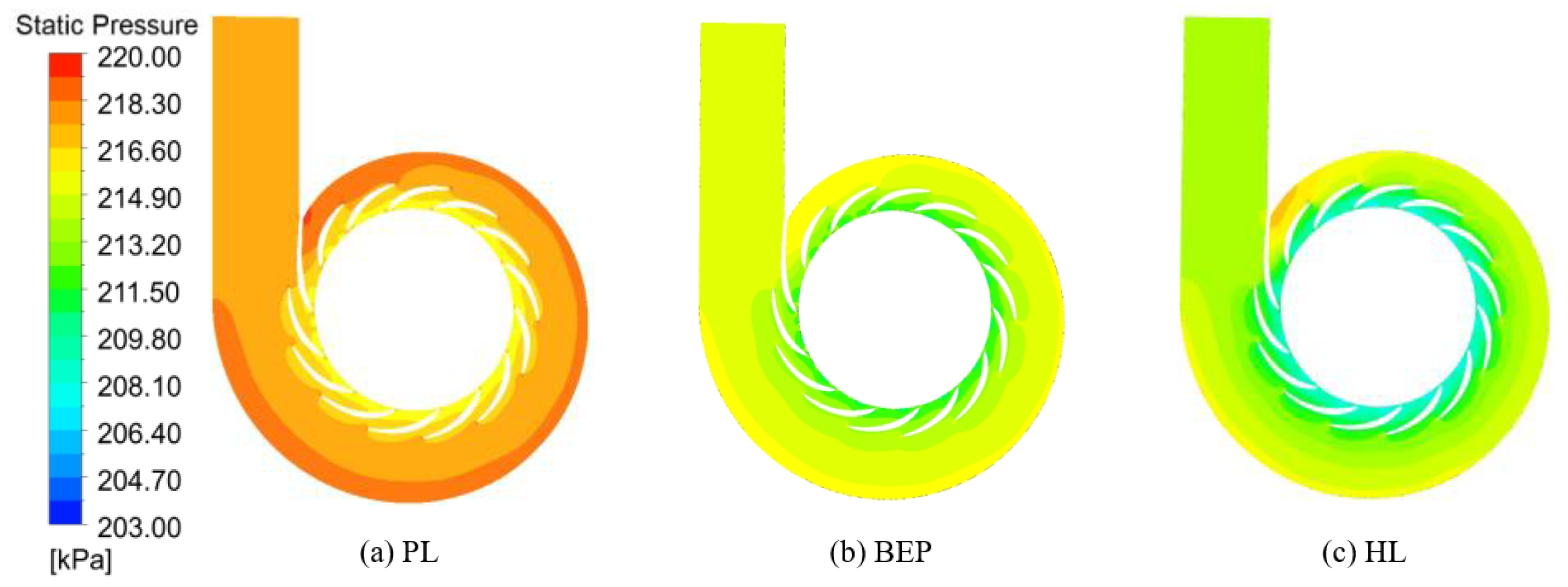



| Parameter | Value |
|---|---|
| Runner diameter (m) | 0.349 |
| Guide vane count | 28 |
| Stay vane count | 14 |
| Short blades count | 15 |
| Long blades count | 15 |
| Parameter | Number of Grids |
|---|---|
| Spiral casing and stay vane | 2,346,342 |
| Guide vane | 2,033,191 |
| Runner | 2,627,719 |
| Draft tube | 1,751,812 |
| Parameter | Working Condition 1 (PL) | Working Condition 2 (BEP) | Working Condition 3 (HL) |
|---|---|---|---|
| Hydrostatic head (m) | 12.29 | 11.91 | 11.24 |
| Flow rate (m3/s) | 0.071 | 0.203 | 0.221 |
| Guide blade angle (°) | 3.91 | 9.84 | 12.44 |
| Inlet velocity boundary (m/s) | 0.814 | 2.328 | 2.534 |
| Pressure outlet (kPa) | 99.54 | 101.56 | 95.98 |
| Runner speed (rpm) | 406.2 | 335.4 | 369.6 |
| Parameter | Experiment Hydraulic Efficiencies (%) | Numerical Simulation Hydraulic Efficiencies | Pressure Inlet (kPa) |
|---|---|---|---|
| PL | 71.69 | 76.22 | 4.53 |
| BEP | 92.61 | 92.63 | 0.02 |
| HL | 90.66 | 94.2 | 3.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, Y.; Lai, Z.; Liu, X.; Deng, X.; Pang, J. Internal Flow and Pressure Pulsation Characteristics of a High-Head Francis Turbine Under Wide Load Conditions. Processes 2025, 13, 2939. https://doi.org/10.3390/pr13092939
Xiong Y, Lai Z, Liu X, Deng X, Pang J. Internal Flow and Pressure Pulsation Characteristics of a High-Head Francis Turbine Under Wide Load Conditions. Processes. 2025; 13(9):2939. https://doi.org/10.3390/pr13092939
Chicago/Turabian StyleXiong, Yufan, Zhenming Lai, Xiaobing Liu, Xin Deng, and Jiayang Pang. 2025. "Internal Flow and Pressure Pulsation Characteristics of a High-Head Francis Turbine Under Wide Load Conditions" Processes 13, no. 9: 2939. https://doi.org/10.3390/pr13092939
APA StyleXiong, Y., Lai, Z., Liu, X., Deng, X., & Pang, J. (2025). Internal Flow and Pressure Pulsation Characteristics of a High-Head Francis Turbine Under Wide Load Conditions. Processes, 13(9), 2939. https://doi.org/10.3390/pr13092939





