CFD-Based Analysis of Sound Wave Attenuation in Stratified Gas–Liquid Pipelines for Leak Detection Applications
Abstract
1. Introduction
2. Theoretical Analysis
2.1. CFD Method
2.2. Multiphase Flow VOF Model
- The control volume is devoid of the qth phase fluid (βq = 0);
- The control volume is entirely occupied by the qth phase fluid (βq = 1);
- The control volume contains a fraction of the qth phase fluid (0 < βq < 1), indicating the presence of an interface between the qth phase and other fluid phases.
2.3. Equation of State for Gases
2.4. Numerical Calculation Methods
- The compressible gas phase is modeled based on the prevailing pressure conditions within the tube.
- At low pressure, the ideal gas equation of state (EOS) is used to describe the gas behavior.
- At high pressure, the gas deviates from ideality and no longer adheres to the ideal gas EOS. Instead, it is characterized using the Peng–Robinson equation of state (PR-EOS), which accounts for the real gas effects, including intermolecular forces and molecular volume corrections.
3. Simulation Analysis
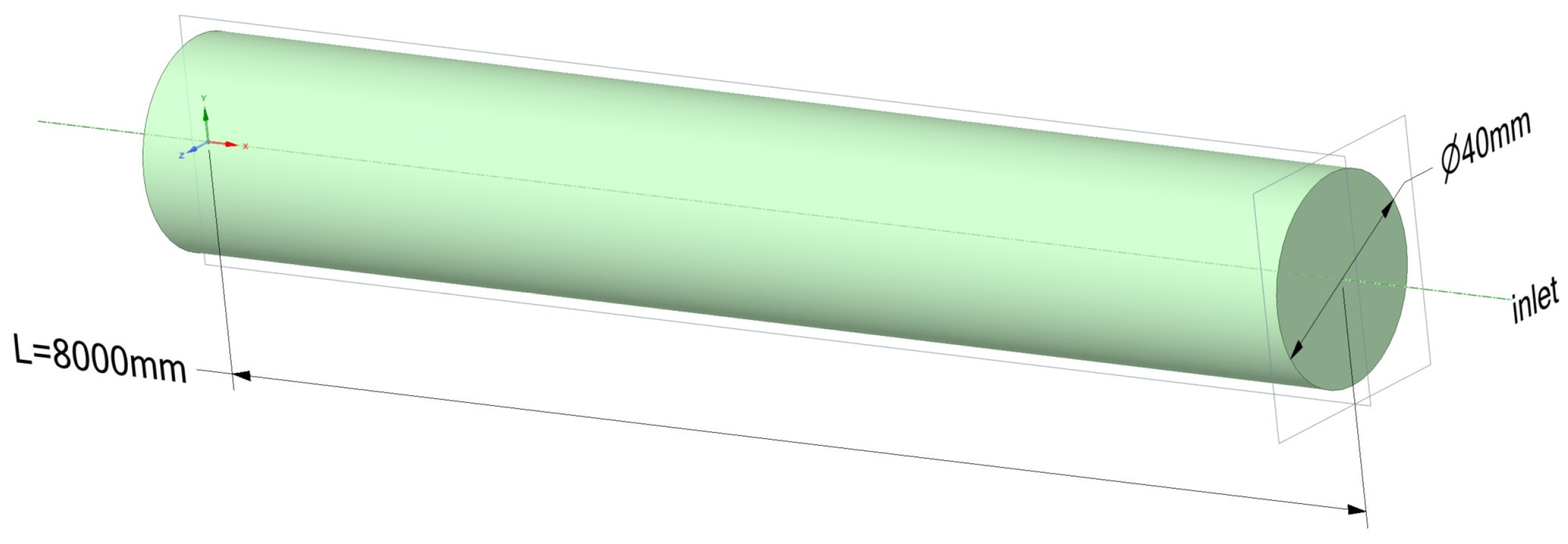
3.1. Establishment of the Simulation Model

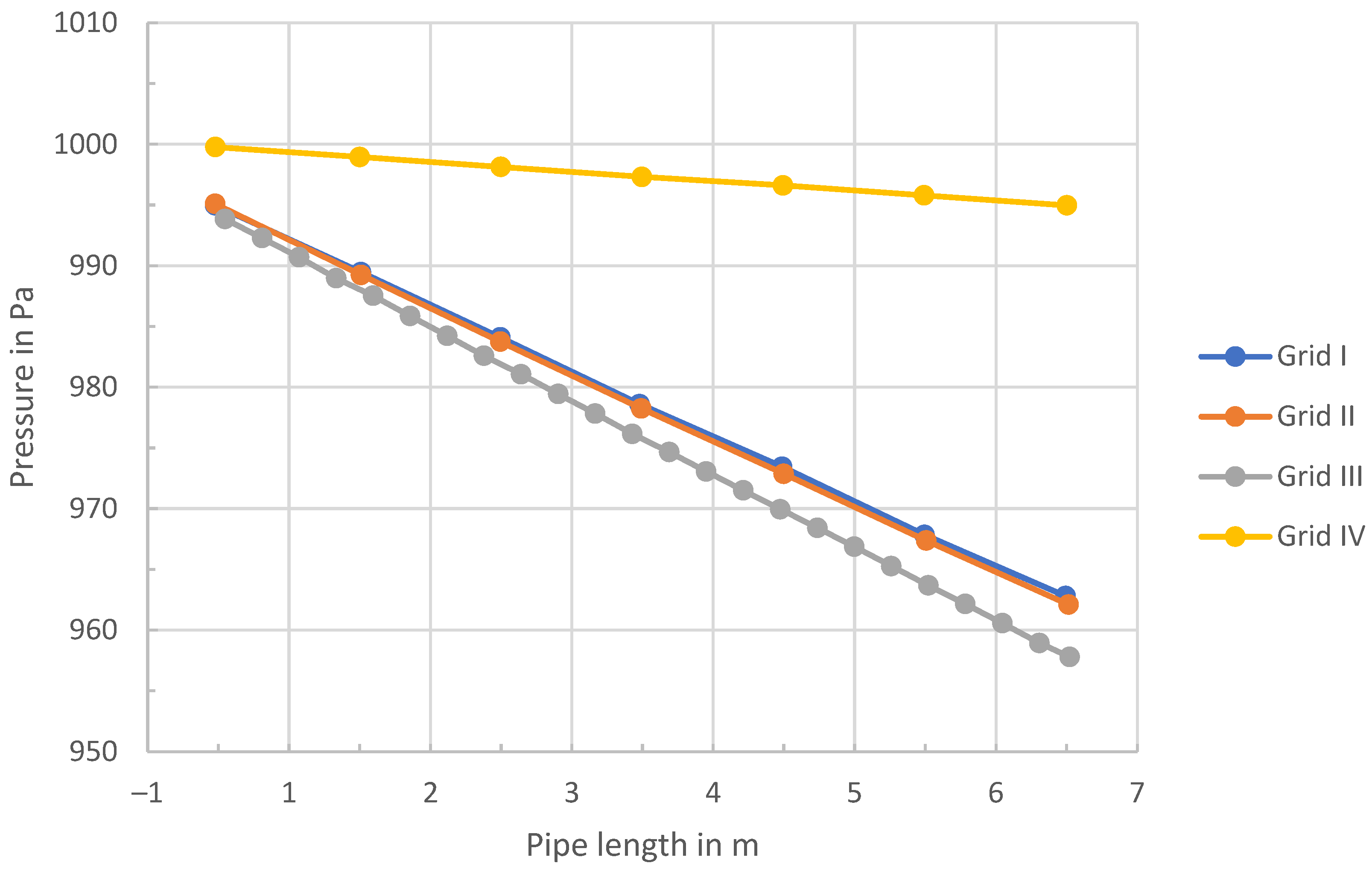
3.2. Mesh Independence Validation
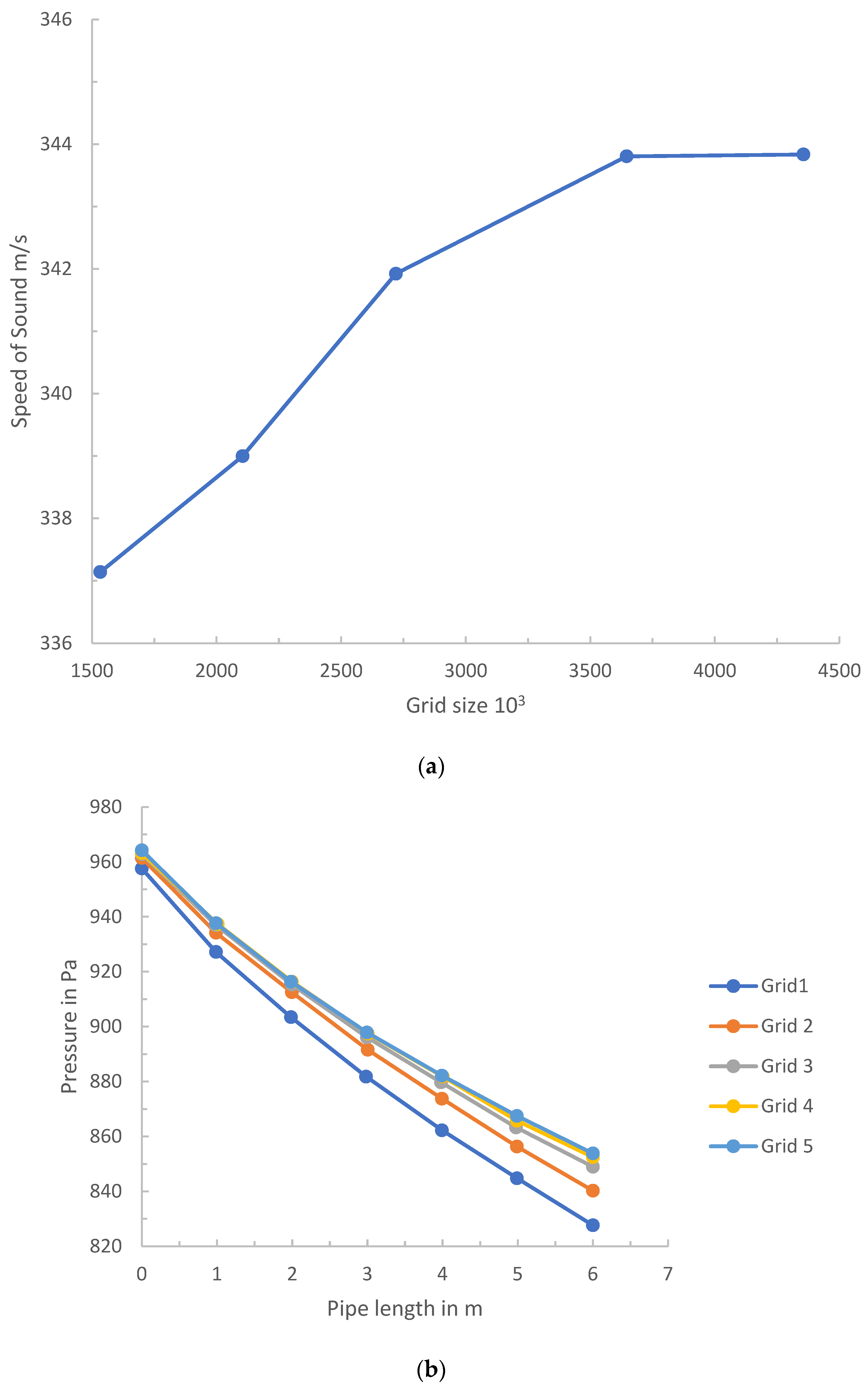
3.3. Wavelength and Cell Size Comparison
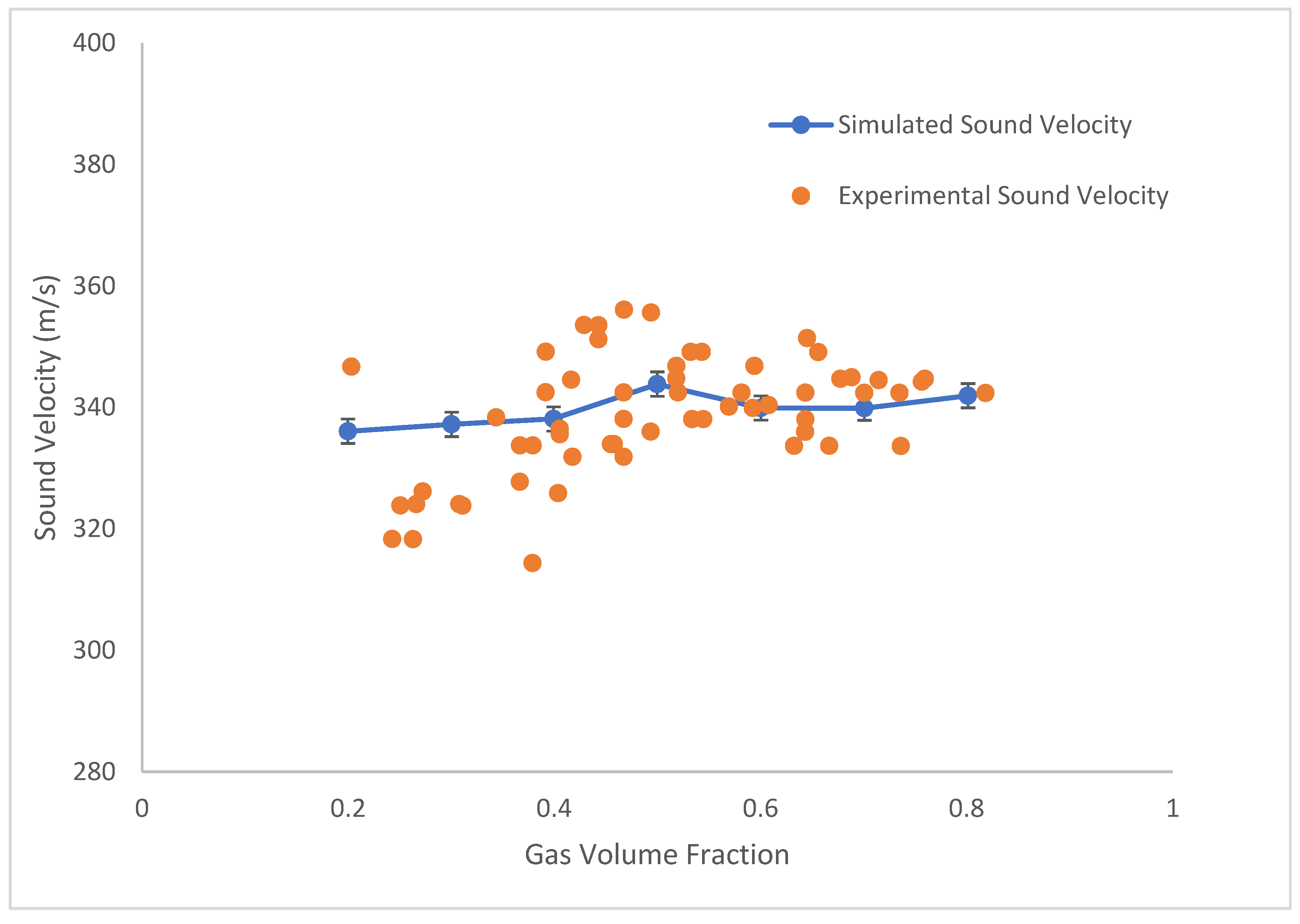
4. Model Reliability Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Silberman, E. Sound Velocity and Attenuation in Bubbly Mixtures Measured in Standing Wave Tubes. J. Acoust. Soc. Am. 1957, 29, 925–933. [Google Scholar] [CrossRef]
- Commander, K.W.; Prosperetti, A. Linear Pressure Waves in Bubbly Liquids: Comparison between Theory and Experiments. J. Acoust. Soc. Am. 1988, 85, 732–746. [Google Scholar] [CrossRef]
- Brennen, C.E. Fundamentals of Multiphase Flow; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Costigan, G.; Whalley, P.B. Measurements of the Speed of Sound in Air-Water Flows. Chem. Eng. J. 1997, 66, 131–135. [Google Scholar] [CrossRef]
- Fu, K.; Deng, X.; Jiang, L.; Wang, P. Direct Numerical Study of Speed of Sound in Dispersed Air-Water Two-Phase Flow. Wave Motion 2020, 98, 102616. [Google Scholar] [CrossRef]
- Fuster, D.; Montel, F. Mass Transfer Effects on Linear Wave Propagation in Diluted Bubbly Liquids. J. Fluid Mech. 2015, 779, 598–621. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, Z.; Du, X. Wave Propagation in Liquids with Oscillating Vapor-Gas Bubbles. Appl. Therm. Eng. 2018, 133, 483–492. [Google Scholar] [CrossRef]
- Li, X.; Xue, Y.; Li, Y.; Feng, Q. Computational Fluid Dynamic Simulation of Leakage Acoustic Waves Propagation Model for Gas Pipelines. Energies 2023, 16, 615. [Google Scholar] [CrossRef]
- Gao, Y.; Sui, F.; Muggleton, J.M.; Yang, J. Simplified Dispersion Relationships for Fluid-Dominated Axisymmetric Wave Motion in Buried Fluid-Filled Pipes. J. Sound Vib. 2016, 375, 386–402. [Google Scholar] [CrossRef]
- Hu, Z.; Tariq, S.; Zayed, T. A Comprehensive Review of Acoustic Based Leak Localization Method in Pressurized Pipelines. Mech. Syst. Signal Process. 2021, 161, 107994. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS FLUENT Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2013; pp. 90311–90312. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A Continuum Method for Modeling Surface Tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Peng, D.-Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fund. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Li, C.; Zhuang, Y.; Cheng, Y.; Li, Y. Study on Pressure Wave Propagation through Cryogenic Condensing Two-Phase Flow in Liquid Rocket Propellant Feedline. Cryogenics 2020, 112, 103193. [Google Scholar] [CrossRef]
- Xue, Y.; Yue, L.; Xiao, K.; Li, Y.; Liu, C. Investigation on Propagation Mechanism of Leakage Acoustic Waves in Gas-Liquid Stratified Flow. Ocean Eng. 2022, 266, 112962. [Google Scholar] [CrossRef]


| Parameter | Working Values |
|---|---|
| Cross-sectional gas content | 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0 |
| Pressure in tube (MPa) | 0.6, 2, 4, 6, 12 |
| Sound wave frequency (Hz) | 50, 75, 100, 125, 150, 175, 200 |
| Sound wave amplitude (kPa) | 1, 5, 10, 15, 20 |
| Grid | Number of Meshes (106) | Simulated Value of Sound Velocity (m·s−1) | Theoretical Value of Sound Velocity (m·s−1) | Analog Value of Attenuation Coefficient (m−1) | Theoretical Value of Attenuation Coefficient (m−1) |
|---|---|---|---|---|---|
| I | 1.407 | 346.21 | 346.9 | 0.005552 | 0.005353 |
| II | 1.138 | 346.23 | 346.9 | 0.005582 | 0.005353 |
| III | 0.876 | 346.39 | 346.9 | 0.006245 | 0.005353 |
| IV | 0.823 | 346.65 | 346.9 | 0.000822 | 0.005353 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kironde, B.J.; Kasali, J.J.; Li, Y. CFD-Based Analysis of Sound Wave Attenuation in Stratified Gas–Liquid Pipelines for Leak Detection Applications. Processes 2025, 13, 2661. https://doi.org/10.3390/pr13082661
Kironde BJ, Kasali JJ, Li Y. CFD-Based Analysis of Sound Wave Attenuation in Stratified Gas–Liquid Pipelines for Leak Detection Applications. Processes. 2025; 13(8):2661. https://doi.org/10.3390/pr13082661
Chicago/Turabian StyleKironde, Birungi Joseph, Johnson Joachim Kasali, and Yuxing Li. 2025. "CFD-Based Analysis of Sound Wave Attenuation in Stratified Gas–Liquid Pipelines for Leak Detection Applications" Processes 13, no. 8: 2661. https://doi.org/10.3390/pr13082661
APA StyleKironde, B. J., Kasali, J. J., & Li, Y. (2025). CFD-Based Analysis of Sound Wave Attenuation in Stratified Gas–Liquid Pipelines for Leak Detection Applications. Processes, 13(8), 2661. https://doi.org/10.3390/pr13082661






