Abstract
Downhole kick is one of the most severe safety hazards in deep and ultra-deep well drilling operations. Traditional monitoring methods, which rely on surface flow rate and fluid level changes, are limited by their delayed response and insufficient sensitivity, making them inadequate for early warning. This study proposes a real-time monitoring technique for gas content in drilling fluid based on the attenuation principle of Ba-133 γ-rays. By integrating laboratory static/dynamic experiments and Geant4-11.2 Monte Carlo simulations, the influence mechanism of gas–liquid two-phase media on γ-ray transmission characteristics is systematically elucidated. Firstly, through a comparative analysis of radioactive source parameters such as Am-241 and Cs-137, Ba-133 (main peak at 356 keV, half-life of 10.6 years) is identified as the optimal downhole nuclear measurement source based on a comparative analysis of penetration capability, detection efficiency, and regulatory compliance. Compared to alternative sources, Ba-133 provides an optimal energy range for detecting drilling fluid density variations, while also meeting exemption activity limits (1 × 106 Bq) for field deployment. Subsequently, an experimental setup with drilling fluids of varying densities (1.2–1.8 g/cm3) is constructed to quantify the inverse square attenuation relationship between source-to-detector distance and counting rate, and to acquire counting data over the full gas content range (0–100%). The Monte Carlo simulation results exhibit a mean relative error of 5.01% compared to the experimental data, validating the physical correctness of the model. On this basis, a nonlinear inversion model coupling a first-order density term with a cubic gas content term is proposed, achieving a mean absolute percentage error of 2.3% across the full range and R2 = 0.999. Geant4-based simulation validation demonstrates that this technique can achieve a measurement accuracy of ±2.5% for gas content within the range of 0–100% (at a 95% confidence interval). The anticipated field accuracy of ±5% is estimated by accounting for additional uncertainties due to temperature effects, vibration, and mud composition variations under downhole conditions, significantly outperforming current surface monitoring methods. This enables the high-frequency, high-precision early detection of kick events during the shut-in period. The present study provides both theoretical and technical support for the engineering application of nuclear measurement techniques in well control safety.
1. Introduction
During oil and gas drilling operations, downhole kick—referring to the abnormal influx of formation fluids into the wellbore—remains one of the most critical safety hazards encountered [1,2]. Statistics indicate that approximately 60% of well control incidents worldwide are attributed to the failure to promptly detect downhole kick events [3,4]. When the formation pressure exceeds the hydrostatic pressure of the wellbore fluid, formation fluids enter the wellbore, leading to an increase in the gas content and a decrease in the density of the drilling fluid [5,6]. This, in turn, creates a vicious cycle that may ultimately result in catastrophic accidents such as blowouts, fires, or even explosions, causing casualties, equipment damage, and environmental pollution [7,8]. For example, the Macondo well blowout disaster in the Gulf of Mexico in 2010 prompted the industry to place greater emphasis on downhole parameter monitoring for early kick detection [9]. A statistical analysis of historical data from 149 wells in an oilfield in the Middle East revealed a total of 117 kick events, with at least 60% directly attributable to human factors. Moreover, approximately 2.56% of kicks ultimately escalated into blowouts [10]. These findings underscore the critical importance of early kick detection during drilling operations to prevent catastrophic incidents such as blowouts. The timely identification of kick warning signs and prompt intervention can significantly reduce the risk of blowout occurrences.
Traditional kick detection primarily relies on changes in surface parameters, such as mud tank level, inflow and outflow mud flow rates, and wellhead and standpipe pressures. Although these approaches can, to some extent, reflect downhole conditions, they are essentially indirect methods, resulting in delayed responses and a limited sensitivity [5,6,11]. Compared with various downhole monitoring technologies, surface-based methods exhibit significant limitations in terms of measurement accuracy, response speed, and environmental adaptability. For instance, electrical resistivity methods, while highly sensitive to water content changes, are limited by high-temperature electronic component performance and mud conductivity interference. Acoustic/ultrasonic methods, though providing a fast response through continuous Doppler frequency monitoring, suffer from mud noise and wellbore reflection interference at great depths. Nuclear magnetic resonance (NMR) techniques, despite a high accuracy in static fluid analysis, require long magnetization–relaxation cycles and are sensitive to magnetic interference from drilling tools, making them less suitable for real-time monitoring [12]. Traditional density logging, while mature and accurate for formation evaluation, requires close contact with the wellbore wall and is affected by mud density variations. In the case of early-stage, low-volume influxes, changes in mud tank level and flow rate at the surface are often subtle and easily overlooked [11,12]. Additionally, external interferences—such as rig vibrations and variations in mud properties—may further compromise monitoring accuracy, leading to missed or false alarms. In complex operational scenarios such as deep and ultra-deep wells, conventional monitoring methods struggle to promptly and accurately capture kick signals, and their technical limitations are becoming increasingly evident [11,12]. In deepwater drilling operations, where riser volumes are large, surface-based mud volume monitoring may be delayed by several minutes or longer, while downhole gamma sensors can detect density decreases when gas is still downhole, providing valuable reaction time for well control.
To address these challenges, novel nuclear-based monitoring technologies have begun to attract attention [13,14,15]. Among them, gamma-ray nuclear measurement technology offers a promising solution for real-time downhole monitoring due to its strong penetration capability and sensitivity to density changes [16,17,18]. Recent advances in nuclear measurement technology have demonstrated success in various industrial applications, particularly in multiphase flow measurements. Gamma-ray attenuation techniques have been successfully implemented in surface-based industrial systems with commercial multiphase flowmeters utilizing gamma sources for density measurements in oil and gas production facilities [19,20]. However, the specific application of gamma-ray technology for real-time downhole drilling fluid monitoring during active drilling operations remains limited in the literature. As high-energy electromagnetic waves, they exhibit excellent penetration and stability and are widely used in fluid property monitoring applications. During transmission, their intensity decays exponentially with an increasing propagation distance. This attenuation is mainly influenced by the physical and chemical properties of the medium, including density, atomic number, and thickness [17,18,19]. For a given thickness, gamma-ray attenuation follows the exponential decay equation as follows:
where I0 is the incident gamma-ray intensity, I is the transmitted intensity after passing through the material, μ is the linear attenuation coefficient—which depends on the material’s composition, density, and the energy of the gamma ray and characterizes the material’s absorption ability—and x is the thickness of the material. Note that while I and I0 represent the intrinsic gamma-ray intensity before and after attenuation in the medium, C and C0 correspond to the measured count rates recorded by the detector under real drilling conditions. Gamma rays can penetrate downhole drilling fluids and undergo attenuation in gas–liquid two-phase media, with the degree of attenuation closely related to the density and composition of the medium [18,19,20]. When gas is entrained in the drilling fluid, the overall density decreases, resulting in changes in the attenuation characteristics of gamma rays [20]. Based on this principle, it is feasible to directly detect variations in drilling fluid gas content downhole, with the added advantage that this method is relatively insensitive to downhole high temperature, high pressure, and complex wellbore geometries, thus enabling real-time, continuous monitoring. In practical applications, only the baseline count rate C0 without gas influx and the real-time count rate C during gas influx need to be measured. Combined with pre-calibrated medium attenuation coefficients, the gas volume fraction in drilling fluid can be calculated in real time, providing direct means for downhole gas influx monitoring with significant early warning implications. Compared with conventional surface-based monitoring, gamma-ray nuclear techniques offer a higher sensitivity and penetration, facilitating earlier and more accurate identification of downhole kick events. Overall, gamma-ray attenuation monitoring, with its high penetration and direct sensitivity to density changes, is becoming a key physical parameter for early kick detection in complex wellbores and provides a solid experimental and methodological foundation for multi-physics well control algorithms [17,18,19,20]. Experimental simulations have shown that when mud gas content increases by only 1–2%, downhole gamma count rates can detect significant changes, while mud tank levels show no obvious fluctuations during the same period.
However, despite the promising advantages of gamma-ray multiphase flow detection technology, existing techniques still face several challenges that warrant further research breakthroughs. These include (1) radiation source safety and alternatives—traditional gamma density tools using radioactive isotope sources present radiation safety and transportation management issues [21,22,23]; (2) the quantitative interpretation of three-phase flow–current gamma-ray methods is relatively mature for gas–liquid two-phase flow parameters, but still faces challenges in oil–water–gas three-phase mixture component interpretation [24,25,26]; (3) flow regime and non-uniformity effects—existing models mostly assume uniform gas–liquid mixing, lacking correction for different flow regimes [27]; (4) detector performance under extreme downhole conditions—gamma detectors require the validation of their performance stability under high-temperature and high-vibration environments [21,22]; and (5) data transmission and processing—real-time kick monitoring requires immediate feedback on abnormal signals, but MWD transmission bandwidth limitations necessitate downhole preprocessing or threshold alarm algorithms [7,8].
Recent advances have demonstrated the integration of Monte Carlo simulation with experimental validation as a frontier approach in gamma-ray multiphase flow measurement research [28,29,30]. Scholars have constructed digital models of downhole flow channels using universal MC codes (such as MCNP and GEANT4) to simulate gamma-ray attenuation processes under different gas contents and flow regimes, obtaining detector count rate response data under various operating conditions. This simulation–experiment coupling method has become a frontier trend in gamma nuclear logging technology development, with some research further using simulation-generated sample data to train machine learning models (such as artificial neural networks) for the intelligent inversion of complex multiphase conditions [24,25,26,27].
To verify the feasibility of gamma-ray nuclear technology for kick monitoring, this study adopts a combined approach integrating field experiments and GEANT4-based Monte Carlo simulations. On the one hand, laboratory measurements are conducted to investigate gamma-ray transmission through drilling fluids; on the other, a downhole gamma-ray detection model is constructed using GEANT4 [28,29,30], with both experimental and simulated media set to drilling fluid with a density of 1.2 g/cm3, to simulate the propagation and attenuation of gamma rays in gas-bearing drilling fluids under different conditions. This comprehensive validation framework integrating laboratory experiments with Monte Carlo simulations enables understanding gamma-ray behavior in complex drilling fluid media across a broader range of operating conditions than traditional calibration methods. The contributions of this study are threefold, as follows: (1) the specific adaptation and optimization of Ba-133 gamma-ray detection for drilling fluid gas content measurement under dynamic conditions, addressing the need for compact, high-temperature resistant instrumentation; (2) the development of a comprehensive validation framework integrating laboratory experiments with Monte Carlo simulations to understand gamma-ray behavior in complex drilling fluid media across various operating conditions; and (3) the establishment of a robust nonlinear inversion model that couples density effects with gas content variations to achieve an improved accuracy across the full measurement range (0–100% gas content), particularly in high-gas-content intervals where traditional linear models show significant limitations.
2. Monitoring Mathematical Model and Theoretical Model Development
In practical applications, many media are not single-phase, but consist of two-phase or multiphase fluids such as gas–liquid mixtures. Regarding the attenuation characteristics of gamma rays, the composition and phase content of gas–liquid two-phase media have a significant influence on their transmission properties [31,32,33]. As drilling fluid is a typical gas–liquid two-phase fluid, the attenuation of gamma rays is closely related to the gas content, with the attenuation coefficient varying as the gas fraction changes [34]. For gas–liquid two-phase media, the equivalent attenuation coefficient of the two-phase fluid can be calculated using the volume-fraction-weighted average method, as follows:
where μeff is the effective attenuation coefficient of the gas–liquid mixture, μ is the attenuation coefficient of the liquid phase (drilling fluid), μg is the attenuation coefficient of the gas phase (gas in the drilling fluid), and αg is the volumetric fraction of the gas phase (gas content). This mathematical model indicates that as the gas content αg increases, the effective attenuation coefficient μeff of the mixed medium decreases, resulting in reduced gamma-ray attenuation and, thus, increased transmission. But the volume-fraction-weighted model described in Equation (2) is based on the assumption of a uniform bubble distribution within the drilling fluid, which represents a substantial simplification of actual downhole conditions. In practice, factors such as bubble coalescence, non-uniform flow patterns, and gravitational segregation frequently result in heterogeneous phase distributions, especially at higher gas contents (>30%), where gas bubbles may aggregate, form slug flow, or stratify according to density differences. To mitigate these limitations, the model is principally validated under dispersed bubble flow regimes, which are characteristic of initial gas influx conditions. For flow regimes such as slug or stratified flow, further correction factors may be necessary. Future advancements should focus on integrating flow pattern recognition algorithms and multi-point measurement geometries to more accurately account for complex multiphase flow behaviors and further improve model reliability under varying field conditions.
Currently, the application of gamma-ray technology in fluid monitoring mainly includes transmission methods, scattering methods, and density logging. The transmission method analyzes changes in gamma-ray intensity after passing through a fluid, offering a simple structure suitable for real-time monitoring in pipelines or containers. The scattering method measures the intensity of gamma rays scattered by the fluid, which is suitable for single-sided measurement. Density logging utilizes the gamma–gamma interaction principle to measure formation density and is widely used in oilfield exploration. In the past five years, research has mainly focused on the development of density logging techniques, while there have been relatively few studies on nuclear measurement for kick monitoring, especially for the detection of gas content in drilling fluids. Based on the exponential attenuation equation and the concept of equivalent attenuation coefficients, this study derives a mathematical model for gas content measurement, as follows:
(1) In downhole drilling environments, the theoretical attenuation coefficient model above can be transformed into a relationship between the counting rate and gas content, as follows:
(2) Taking the natural logarithm of both sides yields the following:
(3) Rearranging the equation to solve for αg gives the final formula for calculating gas content, as follows:
where αg is the gas content of the drilling fluid; C and C0 are the gamma-ray counting rates under gassy and gas-free conditions, respectively; μ and μg are the linear attenuation coefficients of the drilling fluid and gas, respectively; and x is the gamma-ray path length through the medium. This formula demonstrates that provided that the attenuation coefficients and the path length are known, the ratio of the measured counting rates can be used to calculate the gas content in the drilling fluid. The mathematical model provides a theoretical basis for the real-time monitoring of gas content in drilling fluids, and with gamma-ray transmission measurement technology, enables the effective quantitative analysis and monitoring of downhole gas content. This is of significant practical importance for optimizing drilling processes, providing early warnings of gas influx, and ensuring well control safety.
Figure 1 illustrates the monitoring structure for downhole flow channels, which utilizes the principle of gamma-ray attenuation to monitor the gas–liquid two-phase state of drilling fluids. The system is primarily composed of a cylindrical detector, which contains a photon source that emits gamma rays. These rays penetrate the flow channel and are subsequently received by the detector; by analyzing the attenuation of gamma-ray intensity, the composition of the fluid can be determined. The internal fluid within the flow channel comprises both a gas phase and a marked liquid phase, while the channel wall is constructed from metallic materials. The left side of the diagram represents the radioactive source, which emits gamma rays. The system leverages the differential attenuation of gamma rays as they traverse media of varying densities, and, together with the average attenuation coefficient model for gas–liquid mixtures, enables the precise determination of gas content in drilling fluids.
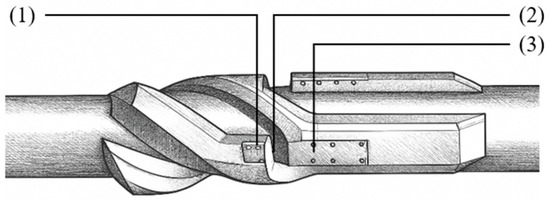
Figure 1.
Downhole flow channel monitoring structure. (1) Radioactive source, (2) flow channel, and (3) detector.
3. Gamma-Ray Transmission Experiments
In this section, on-site experiments are conducted based on the theoretically inferred ideal structural model. In Section 3.1, a static equivalent model for the real-time detection of gas content in drilling fluid is designed using an optimized radioactive source and two sets of laboratory static test protocols are established, with more than 20 tests performed in total. In Section 3.2, in order to further investigate the effects of different gas contents and source-to-detector distances on the measurement results, dynamic tests for varying gas content are carried out.
3.1. Laboratory Static Testing
In gamma-ray-based downhole gas content measurement systems, the selection of the radioactive source is a key factor in system design.
As shown in Figure 2, the radioactive source storage used in this study was provided by China National Nuclear Corporation. A comparative analysis was performed for several commonly used sources, including Am-241, Co-57, Ba-133, Cs-137, and Co-60, taking into account factors such as isotope energy levels, half-life, activity, and market availability to ensure an optimal balance among measurement sensitivity, stability, and economic considerations. Table 1 presents the main parameters of each source.

Figure 2.
Radioactive source storage.

Table 1.
Comparison of common radioactive source parameters.
Based on a systematic comparative analysis, Ba-133 was identified as the optimal radioactive source for the system due to its advantageous parameters. As a gamma-ray isotope, Ba-133 offers an excellent penetration and stability; its physical half-life of 3862 days (approximately 10.6 years) far exceeds the minimum two-year safety period required by the system. The primary gamma emission energies (80 keV, 303 keV, and 356 keV) are especially suitable for detecting gas content in drilling fluid. Moreover, it meets the national exemption limit of 1 × 106 Bq. Additionally, as a commonly used isotope, Ba-133 demonstrates a superior supply chain stability and cost-effectiveness.
As shown in Figure 3, we developed a miniaturized signal processing circuit suitable for high-temperature environments. The circuit underwent six rounds of iterative optimization. To ensure system reliability under downhole conditions, we conducted a three-hour, high-temperature test on both the miniaturized signal processing circuit and the detector. The temperature resistance performance of key components is summarized in the accompanying Table 2.


Figure 3.
Miniaturized signal processing circuit and high temperature test.

Table 2.
Temperature resistance performance table of main components.
As illustrated in Figure 4, a static experimental model was designed using the selected Ba-133 source, and a series of tests were conducted. The experimental setup consisted of the following three main components: the radioactive source (labeled 1), the flow channel (labeled 2), and the detector (labeled 3). The source was mounted on a fixed support, the flow channel was made of acrylic and could be filled with different media (air, water, or drilling fluid), and the detector was positioned opposite the flow channel to receive gamma rays transmitted through the medium.

Figure 4.
Static test setup: (1) radioactive source, (2) flow channel, and (3) detector.
To comprehensively evaluate the system performance, the following two static test protocols were established (Table 3): Experiment I (source distance variation) and Experiment II (medium variation) [35]. These tests aimed to systematically assess the effects of source-to-detector distance and medium type on the detection results.

Table 3.
Laboratory static test protocols.
As shown in Figure 5, Experiment I first demonstrates the quantitative effect of the source-to-detector distance on the measurement results. With pure water as the medium and the detector closely attached to the acrylic plate, the number of particles received by the detector decreases from 5834.8 to 2058.35 as the distance increases from 5 mm to 40 mm, displaying a clear attenuation trend. Detailed analysis reveals that the relationship between distance and particle count approximately follows the inverse-square law and can be expressed as , where N is the particle count, d is the distance, K is a proportionality constant, and n is the attenuation index (about 1.8, close to the theoretical value of 2). The high degree of fit (R2 = 0.998) validates this relationship and provides a quantitative basis for optimizing source-to-detector distance. Sensitivity calculations for different distance intervals reveal that sensitivity decreases significantly with an increasing distance: 286.3 particles/mm (5–10 mm interval), 85 particles/mm (20–25 mm), and only 45 particles/mm (35–40 mm). This finding has important implications for system design, indicating that smaller distances should be selected when a high sensitivity is required. Experiment II, conducted at a fixed source distance of 20 mm, examines the effects of different media (air, pure water, and 1.2 g/cm3 drilling fluid) on the measurement results. The particle counts received by the detector decrease significantly with an increasing medium density: 3355.75 (air), 3211.45 (water), and 3009.84 (drilling fluid). This trend clearly demonstrates that the attenuation of gamma rays increases with medium density, verifying the feasibility of using gamma-ray attenuation principles to measure the gas content in drilling fluids.
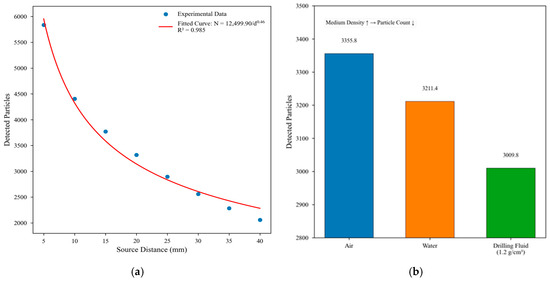
Figure 5.
Static test data. (a) Source distance vs. detected particles and (b) medium type vs. detected particles.
In addition, based on static experimental setups, we conducted detection limit tests for gas content using source-to-detector distances of 25 mm, 35 mm, and 50 mm, as well as scintillation crystal diameters of 25 mm and 10 mm. The results indicated that a shorter source-to-detector distance corresponded to a lower detection limit for gas content (2.5% for 25 mm, 5.0% for 35 mm, and 7.0% for 50 mm). Furthermore, increasing the crystal size led to a higher detection limit.
Through systematic static testing, this study validated the feasibility and effectiveness of a Ba-133-gamma-source-based system for downhole drilling fluid gas content monitoring. The system demonstrated good discrimination among different-density media (air, water, and drilling fluid), with the particle count decreasing as the medium density increased, consistent with theoretical predictions. A clear mathematical relationship between distance and particle count, conforming to radiation attenuation theory, can be used for system calibration. Sensitivity decreased with an increasing distance, indicating the need to select appropriate distances based on the specific requirements in practical applications. Furthermore, the geometric configuration of the system significantly affected the measurement results and should be considered in design.
These experimental results lay a solid foundation for subsequent dynamic testing and practical downhole applications, and also provide an important basis for establishing a quantitative relationship model between drilling fluid gas content and gamma-ray counting rate.
3.2. Dynamic Testing of Gas Content
To further investigate the quantitative relationship between drilling fluid gas content and gamma-ray counting rate, a series of dynamic tests were designed and conducted in this section. As shown in Figure 6, a compact performance testing apparatus was developed, which integrated five types of gas outlet nozzles, adjustable source-to-detector distances (10–50 mm), and the precise control of gas flow rates from 0.1 to 5 L/min. The radioactive source unit (1) employed the selected Ba-133 isotope source; the flow channel system (2) enabled direct observation of the internal fluid state; the detector system (3) received gamma-ray signals transmitted through the channel; and the gas exhaust system (4) was capable of simulating different bubble size distributions. The compact design facilitated laboratory operation, the transparent material allowed for visualizing bubble distributions, and the modular structure supported the independent adjustment of multiple parameters. High-precision gas flow control ensured the stability and reproducibility of experimental conditions.

Figure 6.
Compact detector performance testing apparatus: (1) radioactive source, (2) flow channel, (3) detector, and (4) gas outlet.
The experimental procedure strictly followed standardized protocols. First, the baseline counting rate (background value) was recorded under stable system operation without gas injection. Subsequently, the gas flow was gradually increased to 0.2 L/min, 0.5 L/min, and 1 L/min, and finally reduced again to 0.2 L/min for verification measurements. For each gas flow condition, the system was maintained in stable operation for at least 20 min, and the Ba-133 gamma-ray counting rate was continuously recorded. High-speed camera imaging was used to capture the bubble distribution characteristics at different flow rates, providing additional data for subsequent analysis. As shown in Figure 7, the experimental results clearly revealed a positive correlation between gas content and gamma-ray counting rate. During the baseline phase, the counting rate was stable at approximately 800–900 cps, primarily contributed by the environmental background and electronic noise. When the gas flow increased from the baseline to 0.2 L/min, the counting rate rose significantly to approximately 1100–1300 cps—an increase of about 40%. Further increases to 0.5 L/min and 1 L/min led to counting rates of approximately 1700–1900 cps and 2300–2500 cps, respectively, exhibiting an obvious stepwise upward trend. This phenomenon is attributed to the enhanced gamma-ray scattering effect caused by the introduction of bubbles, with more scattered photons being detected and, thus, increasing the total counting rate.
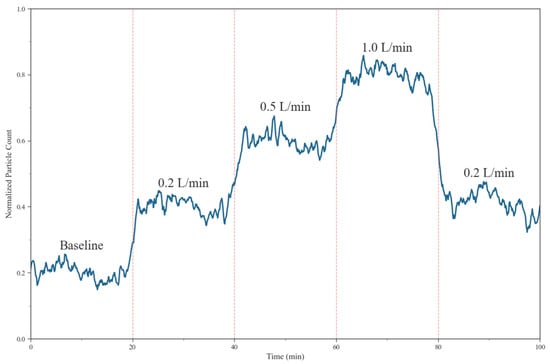
Figure 7.
Response of counting rate to gas content.
Analysis of the average counting rates at the four measurement points (baseline, 0.2 L/min, 0.5 L/min, and 1 L/min) showed a strong linear relationship between counting rate increments and the gas flow rate, with a correlation coefficient R2 exceeding 0.95. This indicated an excellent linear response within the tested range. Notably, when the gas flow was reduced from 1 L/min back to 0.2 L/min, the counting rate decreased correspondingly to about 1100–1300 cps, essentially identical to the previous measurement at the same flow rate. The relative deviation between the two measurements was less than 3%, fully demonstrating the reproducibility and stability of the measurement system and providing a reliable technical foundation for practical applications.
Although the raw time-series plots are not available for direct display, statistical analysis was performed over the full measurement period at each flow rate. The measured counting rates exhibited a mean value of 800–900 cps, with a calculated standard deviation of less than 27.4 cps and a relative deviation below 3.24%, indicating a high stability and low statistical variance throughout the experiments. This provides further evidence for the robustness and reliability of the measurement system.
Further analysis showed that the amplitude of counting rate fluctuations was positively correlated with gas flow rate, reflecting the increased randomness of bubble size and distribution at higher flows, which caused more pronounced instantaneous changes in the gamma-ray transmission path. This characteristic imposes greater requirements on signal processing and smoothing algorithm design in practical applications, necessitating the optimization of data processing methods for different gas content ranges.
Based on the dynamic test results, this study confirms that the gamma-ray attenuation-based drilling fluid gas content monitoring system can effectively detect dynamic changes in gas content within the fluid. The system exhibits a clear positive response to increasing gas content, with the counting rate increasing accordingly, which is consistent with theoretical predictions. Within the tested range (0–1 L/min), the system demonstrates an outstanding linear response and high measurement repeatability, providing a solid foundation for application in real downhole environments. The successful dynamic tests validate the system’s real-time monitoring capability for changes in drilling fluid gas content. Together with the static tests in Section 3.1, these results comprehensively verify the feasibility of this technical approach and lay a solid foundation for the subsequent development of gamma-ray-based early kick detection technology in downhole applications.
4. Development of a Monte Carlo Model for Gamma-Ray Gas Detection While Drilling
In this section, a simulation framework is developed for the drilling fluid gas content measurement system based on field experiments, utilizing the Geant4.11.2 toolkit [36]. The corresponding Monte Carlo physical model is constructed and validated. In Section 4.1, the Monte Carlo model is developed using field experimental data and geometric structures, and its validity is verified. Section 4.2 analyzes the composition of drilling fluids, investigates the influence of different media on gamma-ray transmission, and, through the simulation and analysis of gamma-ray transmission characteristics in drilling fluids under various source-to-detector distances, quantifies the impact of medium variations on measurement accuracy. Section 4.3 systematically examines the effects of gas content and density on gamma-ray transmission in drilling fluids and further analyzes the combined effects of density and gas content, establishing a gamma-ray attenuation model under multivariate conditions. In Section 4.4, based on the preceding analyses, a gamma-ray transmission correction formula considering multiple factors is derived, resulting in a mathematical model suitable for field measurement conditions.
4.1. Construction and Validation of the Monte Carlo Model
In this study, the Livermore low-energy physics model is employed to accurately simulate gamma-ray interactions within the energy range from 10 eV to 2 MeV. The simulation incorporates the principal microscopic interaction mechanisms, including the photoelectric effect—which predominates at lower energies (<100 keV) and is particularly significant for the 80 keV emission line of Ba-133—as well as Compton scattering, which is the dominant process at the primary peak energy (356 keV) of Ba-133. Rayleigh scattering, responsible for small-angle photon deflection through coherent processes, and secondary processes such as fluorescence and Auger electron emission following K-shell photoelectric absorption are also included. The simulation domain is defined as a 500 mm cubic volume, effectively eliminating boundary artifacts and ensuring complete photon tracking. The aforementioned physical models provide the basis for the subsequent construction of a measurement model for drilling fluid gas content, as illustrated in Figure 8. Drawing on both field experimental data and the actual geometric structure, the Monte Carlo model employs a point source of Ba-133 with primary emission energies of 356 keV (62%) and 81 keV (34%), emitting photons isotropically in all directions. As shown in Table 4, the simulated flow channel’s outer shell is made of polymethyl methacrylate (PMMA) and the geometric structure strictly follows the dimensions of the experimental apparatus, with overall dimensions of 250 mm × 29.6 mm × 250 mm. The detector is located on the left side of the channel, with its sensitive detection surface tightly attached to the PMMA shell’s circular end face, measuring 25 mm × 60 mm [37]. The position of the radioactive source is adjustable and situated outside the right outer wall of the flow channel.
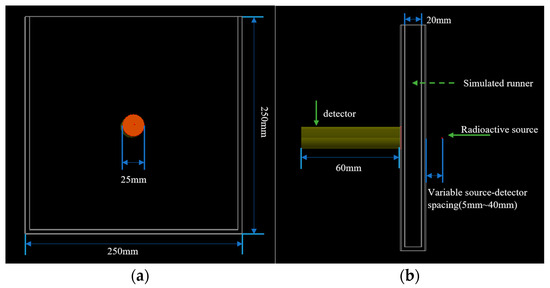
Figure 8.
Monte Carlo physical model. (a) Top view of the Monte Carlo simulation model showing the circular detector surface (25 mm in diameter) and outer dimensions of the flow channel. (b) Side view of the physical model illustrating the radioactive source position, variable source-to-detector distance (5–40 mm), and the detector placement relative to the PMMA channel wall.

Table 4.
Geometrical dimensions of experiment and simulation.
As shown in Table 4, to validate the accuracy of the simulation model, water was used as the filling medium and the emission direction of the source was set to isotropic (360°) emission. The system was tested at different source-to-channel distances (ranging from 5 mm to 20 mm in 5 mm increments). Since Monte Carlo simulations converge at a photon count of 1010 [38,39], 2 × 108 photon particles were emitted for each source distance setting to ensure a sufficient statistical accuracy. The number of particles detected by the sensitive surface of the detector was recorded.
As illustrated in Figure 9 and Table 5, both the experimental and simulated data closely follow an exponential attenuation pattern. The difference in attenuation constants between the two is only 1.02%, indicating that the Monte Carlo model accurately captures the attenuation behavior of photons in the medium [40]. The lower RMSE value for the simulated data (0.0012) shows a closer fit to the ideal exponential decay model, while the higher RMSE value for the experimental data (186.85) reflects natural variations and noise in actual measurements. Across the entire 5–20 mm distance range, both the experimental and simulated data exhibit consistent exponential decay trends, with the mean error between the simulated and experimental data being around 10% and the average relative error being 5.01%, well within a reasonable error range. This effectively validates the physical correctness of the simulation model, indicating that it can reliably predict photon counts at unmeasured distances and serve as a robust baseline model for subsequent drilling fluid gas content analysis.
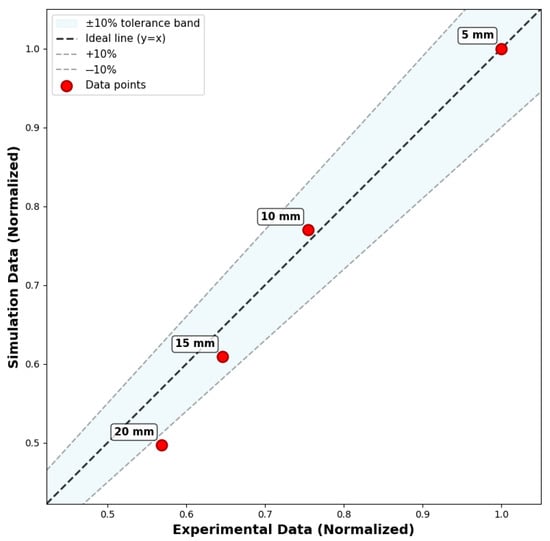
Figure 9.
Normalized comparison of experimental and simulated data.

Table 5.
Comparison of experimental and simulation data parameters.
4.2. Analysis and Comparison of Gamma-Ray Transmission Through Drilling Fluid at Different Source-to-Detector Distances
To ensure the accuracy and reliability of the simulation data, a detailed compositional analysis of the drilling fluid used in the experiments was performed. Both organic and inorganic components of the drilling fluid were comprehensively characterized using elemental analysis (EA) and inductively coupled plasma optical emission spectrometry (ICP-OES). The equipment used included the Elementar vario MICRO cube high-precision organic elemental analyzer (Elementar, Langenselbold, Germany) and the Agilent 730 ICP-OES spectrometer (Agilent Technologies Inc., Santa Clara, CA, USA). Through this analysis, the proportion of each element in the drilling fluid was precisely determined, covering both major and trace elements.
As shown in Table 6, the EA analysis results indicate that the nitrogen content in the drilling fluid samples was extremely low (0.09% for Sample 1 and 0.00% for Sample 2), and the carbon content was around 2.2% (2.31% for Sample 1 and 2.23% for Sample 2). The hydrogen content was relatively high, at 8.669% and 9.253%, respectively, while the sulfur contents were 1.199% and 1.040%. Oxygen was the most abundant element, reaching 61.649% and 60.906%. These results suggest that the drilling fluid was predominantly water-based, with a relatively low organic content.

Table 6.
EA analysis results of drilling fluid.
As illustrated in Figure 10, comprehensive ICP-OES analysis revealed the detailed composition of inorganic elements in the drilling fluid. The most abundant elements detected were silicon (Si, 8.1860 mg/L) and aluminum (Al, 7.3790 mg/L), followed by calcium (Ca, 4.2350 mg/L), iron (Fe, 3.9670 mg/L), and phosphorus (P, 3.2680 mg/L). Additional elements detected at relatively high concentrations included potassium (K, 1.8410 mg/L), strontium (Sr, 1.7010 mg/L), barium (Ba, 1.6700 mg/L), chromium (Cr, 1.9670 mg/L), magnesium (Mg, 1.1510 mg/L), and tin (Sn, 1.1660 mg/L). The presence of these elements reflects typical drilling fluid additives such as weighting agents (e.g., barite), clay components (e.g., bentonite), and various other additives. It is noteworthy that several trace elements, including rare earths (Er, Eu, Tm, Tb, etc.) and precious metals (Au, Pd, Pt, etc.), were also detected, generally at levels below 0.01 mg/L. While these trace elements have a limited influence on gamma-ray attenuation, their cumulative effect should still be considered in the development of high-precision gas content detection models.
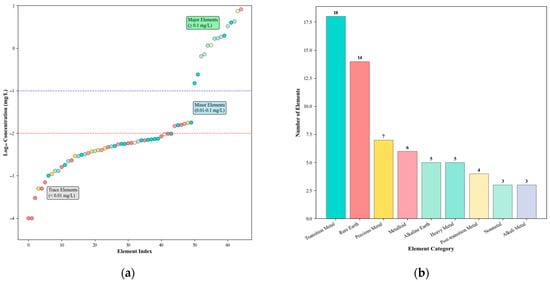
Figure 10.
ICP-OES elemental analysis results of drilling fluid. (a) Element concentration distribution in drilling fluid\n(ICP-OES Full Scan Analysis) and (b) element distribution by category.
Based on the elemental analysis results, a Monte Carlo physical model was constructed to accurately reflect the actual composition of the drilling fluid. In this process, only elements with relatively high concentrations (greater than 0.1 mg/L, as determined by ICP-OES) were explicitly included in the Geant4 simulation, while trace elements below this threshold—such as rare earths—were neglected due to their negligible influence on gamma-ray attenuation. Using this compositionally informed model, a comparative analysis of the gamma-ray transmission characteristics in pure water and drilling fluid at different source-to-detector distances was performed.
The experimental data in Figure 11 show that as the source-to-detector distance increases from 5 mm to 40 mm, both the detection efficiency and energy deposition of gamma rays in drilling fluid and pure water exhibit typical exponential attenuation, in accordance with the Beer–Lambert law. Quantitative analysis reveals significant differences in attenuation characteristics between the drilling fluid and pure water. Under identical source-to-detector distances, the detection performance for drilling fluid is systematically lower than that for pure water. For example, at a source-to-detector distance of 20 mm, the detection efficiency for pure water is 5.52 × 10−2 and the total energy deposition is 5795.39 MeV; for drilling fluid, these values decrease to 3.00 × 10−2 and 3801.65 MeV, representing reductions of 45.70% and 34.40%, respectively. Across the entire measurement range, the ratios of detection efficiencies and energy depositions for drilling fluid to water remain consistent, averaging approximately 1.84 and 1.52, respectively. This consistency reflects the fundamental differences in atomic composition and density between the two media. Drilling fluid contains significant amounts of high-atomic-number (Z) elements (e.g., Si: Z = 14, Al: Z = 13, Fe: Z = 26, Ba: Z = 56), whereas pure water is mainly composed of light elements (H: Z = 1, O: Z = 8). Due to the photoelectric effect cross-section scaling as Z4 and the linear dependence of Compton scattering on electron density, high-Z elements markedly enhance gamma-ray absorption.
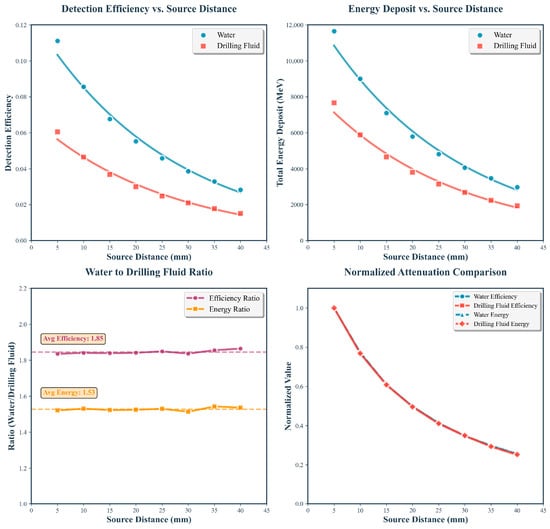
Figure 11.
Comparative analysis of gamma-ray attenuation characteristics in water and drilling fluid.
The relationship between the source-to-detector distance and detection efficiency exhibits clear exponential decay, with the following fitted equations for the experimental data:
where N is the number of particles detected, N0 is the reference particle count at the initial position, and x is the source-to-detector distance (mm). The difference in attenuation coefficients (0.0283 vs. 0.0415) quantitatively characterizes the distinct gamma-ray attenuation capacities of the two media. Exponential fitting shows that the linear attenuation coefficient for drilling fluid is approximately 1.47 times that of pure water, a ratio consistent with the effective atomic number and electron density differences between the two media. This difference is attributable not only to the atomic number disparities, but also to the higher mass density of the drilling fluid, both of which contribute to stronger gamma-ray attenuation. These results provide key parameters for the design of downhole gas content monitoring systems, particularly in optimizing the source-to-detector distance.
4.3. Analysis and Comparison of Gamma-Ray Transmission in Drilling Fluids at Different Gas (Methane) Contents and Densities
To systematically investigate the influence of gas content and density on gamma-ray transmission characteristics, this study examined three types of drilling fluids with different base densities (1.2 g/cm3, 1.5 g/cm3, and 1.8 g/cm3) at a fixed source-to-detector distance of 20 mm. The gamma-ray transmission properties were analyzed as the gas (methane) content was varied from 0% to 100% in 5% increments (it should be noted that the Geant4 simulations represent idealized scenarios and are, therefore, not limited by the practical upper or lower detection thresholds).
As shown in Figure 12, the relationship between gas content and detection efficiency was established for drilling fluids with different base densities. The data reveal that detection efficiency exhibited an approximately exponential growth trend with an increasing gas content. For drilling fluid with a density of 1.2 g/cm3, as the gas content increased from 0% to 100%, the detection efficiency rose from 0.000838% to 0.0103705%, representing a 12.37-fold increase. For drilling fluids with densities of 1.5 g/cm3 and 1.8 g/cm3, the detection efficiency increased by 17.27 times and 23.56 times, respectively.
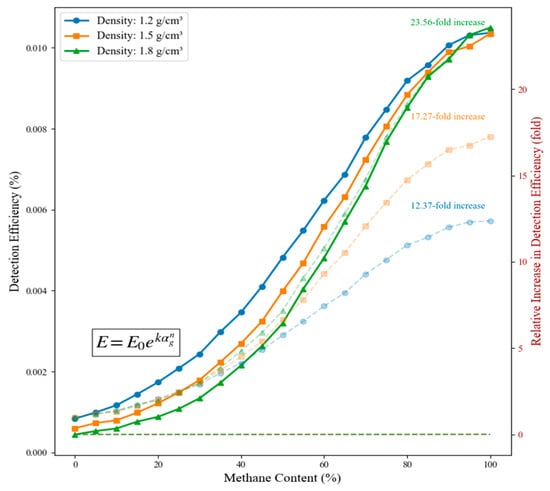
Figure 12.
Relationship curves between gas content and detection efficiency for drilling fluids of different densities.
It is noteworthy that in the low gas content range (0–30%), the growth rate of detection efficiency is relatively modest, while in the medium to high gas content range (30–70%), the growth rate becomes significantly higher. Once the gas content exceeds 70%, the growth rate levels off again. This nonlinear pattern is associated with the distribution state of gas within the liquid phase and phase transition processes. Further analysis shows that the relationship between detection efficiency E and gas content αg can be accurately fitted by the following modified exponential function: , where E0 is the baseline detection efficiency for the pure liquid phase, k is the decay coefficient correction factor, and n is the nonlinearity exponent (typically between 1.2 and 1.5). The fitting results for the three densities indicate that the model yields coefficients of determination (R2) exceeding 0.998, demonstrating an excellent accuracy. Comparative analysis at the same gas content for the three densities confirms that base fluid density has a significant effect on gamma-ray transmission characteristics.
Figure 13 quantitatively presents the detection efficiency as a function of methane content for drilling fluids with different densities, as well as the relative ratios between them. The left panel directly illustrates the nonlinear growth law between detection efficiency and methane content, with all three curves displaying typical exponential growth but differing in rate and amplitude. Quantitative analysis shows that over the entire methane content range (0–100%), the 1.2 g/cm3 drilling fluid consistently exhibits the highest detection efficiency, reaching 0.0104% at maximum—about 1.2% higher than the 1.8 g/cm3 fluid. The efficiency ratio analysis (right panel) further reveals the relative changes in detection performance among different densities. Most notably, the 1.2:1.8 density ratio decreases significantly from 1.88 at a low gas content to 0.99 at a high gas content, indicating that the detection advantage of low-density fluids at a low gas content is gradually lost as the methane concentration increases. In contrast, the 1.5:1.8 and 1.2:1.5 ratios fluctuate modestly around 1.3 and 1.4, respectively, suggesting a relatively stable performance for medium-density fluids. Particularly noteworthy is that when the methane content exceeds 80%, all density ratios converge toward 1.0. This convergence indicates that, under high-gas-content conditions, the influence of base fluid density on detection efficiency is greatly diminished, and gas content becomes the dominant factor.
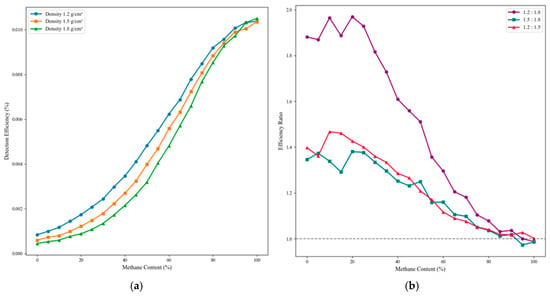
Figure 13.
Comparison of detection efficiencies across the full gas content range for drilling fluids with different densities. (a) Detection efficiency vs. gas content and (b) efficiency ratios between densities.
Figure 14 presents the three-dimensional relationship between drilling fluid density, methane content, and detection efficiency, along with a projection on the base plane. The 3D surface clearly shows that detection efficiency increases nonlinearly with methane content, with pronounced differences depending on the fluid density. The contour map on the base plane further reveals the variation in detection efficiency in the two-dimensional parameter space, where yellow-green regions indicate a high efficiency and purple regions indicate a low efficiency.
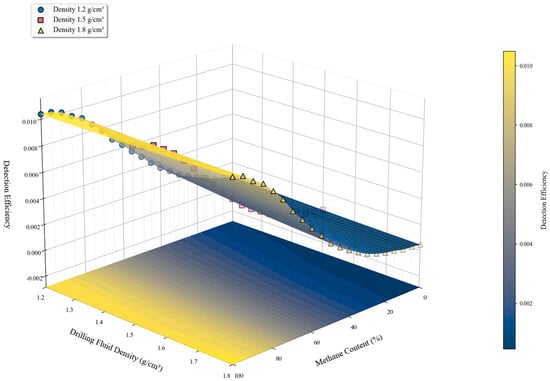
Figure 14.
Three-dimensional distribution of density, gas content, and detection efficiency.
Across the full range of gas content, the growth in detection efficiency can be divided into three regimes. In the low-gas-content region (0–30%), the efficiency increases moderately—for example, from 0.000838% to approximately 0.002% for a fluid density of 1.2 g/cm3—primarily due to a reduction in the linear attenuation coefficient as high-density liquid is gradually replaced by low-density gas, a process governed by the dominance of Compton scattering at the 356 keV emission of Ba-133. In the transition region (30–70%), the increase in efficiency accelerates markedly by a factor of 3–5 depending on the fluid density, reflecting not only enhanced photon transmission through the gas-dominated phase, but also the onset of complex multiphase flow effects and multiple scattering, which introduce significant nonlinearity and deviate from simple attenuation models. At a high gas content (70–100%), the efficiency growth rate stabilizes and the differences between different fluid densities converge, indicating that gas content becomes the primary determinant of detection efficiency; this supports the use of a volumetric averaging approach for high gas fractions. Notably, the difference in detection efficiency between fluids of varying densities is most pronounced in the 0–30% gas content range, precisely where early gas invasion detection is critical; for instance, the detection efficiency of a 1.2 g/cm3 fluid can be nearly twice that of a 1.8 g/cm3 fluid at low gas contents, offering superior early warning for less dense drilling fluids. However, the practical application of these findings may be limited by factors such as statistical noise at low gas contents, flow regime dependence (as the homogeneous mixing assumption may not strictly apply in the field), and the need to balance counting statistics with the temporal resolution required for real-time monitoring. These findings elucidate the nonlinear relationship between gas content and gamma-ray detection efficiency, highlighting both the sensitivity of the technique to early gas invasion and the critical physical mechanisms that govern signal variation across different flow regimes.
4.4. Inversion Model for Drilling Fluid Gas Content Based on Gamma-Ray Transmission Characteristics
Based on Monte Carlo simulations and experimental validation, a comprehensive mathematical inversion model for drilling fluid gas content was established, enabling the precise calculation of gas content from gamma-ray transmission characteristics [29].
According to the Beer–Lambert law and the equivalent attenuation coefficient theory, for drilling fluids of a known base density, gas content can be calculated using Equation (5). A comparison of experimental data with model predictions shows that the model achieves a high accuracy for gas contents in the 0–60% range, with a mean relative error less than 5%. However, when the gas content exceeds 60%, the error of the simple linear model increases progressively, likely due to non-uniform gas–liquid distribution at high gas fractions. To enhance the applicability of the model for drilling fluids of varying densities, we adopted a regression approach combining a first-order density term and a cubic polynomial in gas content for the logarithmic attenuation derived from the Beer–Lambert law, thereby constructing a new inversion model valid across the entire gas content range.
- (1)
- The normalized logarithmic transmittance is defined as follows:where C and C0 are the measured counting rates for gas-bearing and gas-free drilling fluid, respectively.
- (2)
- For gas–liquid mixtures with a non-uniform distribution, the effective attenuation coefficient becomes spatially dependent, as follows:Here, μeff(x,y,z) denotes the effective linear attenuation coefficient at spatial position (x,y,z), characterizing the overall gamma-ray attenuation capacity at that location. The term μliquid refers to the linear attenuation coefficient of the liquid phase (i.e., the drilling fluid), while μgas represents the corresponding value for the gas phase (i.e., gas bubbles). The parameter αg(x,y,z) denotes the local volume fraction of gas at position (x,y,z).
- (3)
- When integrated over the measurement volume, this leads to a nonlinear relationship between the measured transmission and gas content. The Taylor expansion of the logarithmic transmission around the pure liquid state yields the following:The linear term (a1⋅αg) primarily reflects the main attenuation effect associated with a uniform and dilute gas distribution. The quadratic term (a2⋅αg2) accounts for secondary scattering effects and bubble interactions, while the cubic term (a3⋅αg3) represents higher-order phenomena, including multiple scattering events and transitions in the flow regime.
- (4)
- This density dependence of the coefficients, as expressed by the form (a1ρ + a0), originates from the fundamental relationship between material density and the attenuation cross-section, namely μ = σρ(NA/A), where σ is the interaction cross-section, ρ is the density, NA is Avogadro’s constant, and A is the atomic mass. Consequently, for materials with different base densities, the attenuation coefficient scales linearly with density. Building on this theoretical basis, the regression results demonstrate that y and f follow a cubic relationship, and the coefficients of each order are observed to depend approximately linearly on the drilling fluid density ρ.
The fitted regression coefficients for the nonlinear inversion model are summarized in Table 7:

Table 7.
Regression coefficients for the nonlinear inversion model.
- (5)
- The final inversion model applicable across the full range is as follows:
Figure 15 shows the validation results for the improved nonlinear model. The scatter distribution of measured versus predicted values visually reflects the overall model performance. All prediction points for drilling fluids with different densities are tightly clustered near the 1:1 ideal prediction line, indicating excellent agreement.
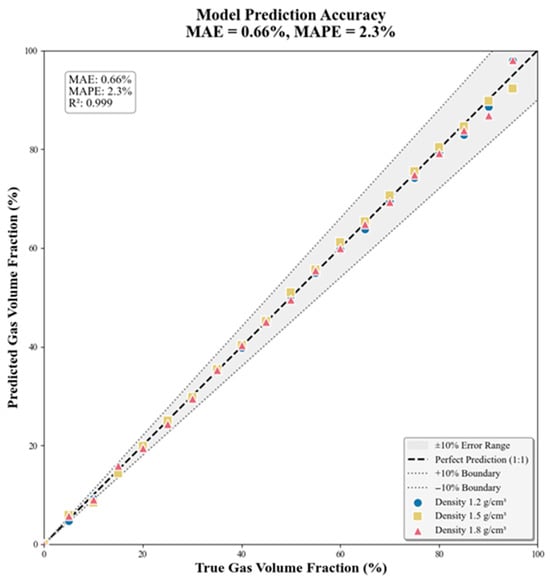
Figure 15.
Model accuracy verification.
To comprehensively evaluate the predictive performance, the cubic polynomial model developed in this work is compared with several alternative model forms, including pure exponential and logarithmic models. For the pure exponential model, the obtained R2 is 0.892 and the MAPE is 8.7%, indicating substantial deviation from the ideal prediction, especially at higher gas contents. The logarithmic model achieves an improved performance with R2 = 0.934 and MAPE = 5.2%, yet still fails to provide an adequate accuracy across the full range of gas content. In contrast, the cubic polynomial model demonstrates the highest predictive accuracy, with R2 = 0.999 and MAPE = 2.3%, thus reducing prediction errors by more than half compared to the logarithmic model and by over 70% compared to the pure exponential model. This detailed comparison highlights the superiority of the cubic polynomial approach in capturing the complex, nonlinear relationship between gamma-ray transmission and gas content in multiphase drilling fluids.
Further analysis of prediction accuracy in different gas content intervals shows that, in the engineering-relevant medium-to-high-gas-content region (30–100%), the improved model exhibits an outstanding predictive stability. Especially in the high-gas-content region (>60%), the prediction error is controlled within 1.5%, reducing the error by more than 75% compared to linear interpolation methods. This fully demonstrates the effectiveness of the nonlinear coupling correction mechanism. The model maintains a consistent predictive accuracy across different fluid densities, with no significant systematic error distribution, indicating a good universality of the established density–gas content coupled model.
These results provide a robust theoretical foundation for the real-time monitoring of gas content in different drilling fluid systems during field applications and further confirm the applicability and accuracy of gamma-ray-transmission-based gas content detection technology under complex drilling conditions.
For practical application, to ensure system accuracy, we recommend a two-point calibration method: first, obtain the baseline counting rate C0 using gas-free drilling fluid; then, acquire a second calibration point using a standard sample with a known gas content (preferably in the 30–50% range), which is used to determine the actual system parameter ρ. Considering the complexity of the downhole environment, it is recommended to perform system calibration before each drilling operation and conduct periodic verification during drilling to eliminate the potential effects of temperature, pressure, and other environmental factors.
With the above model and calibration procedure, the system enables the real-time monitoring of drilling fluid gas content during drilling operations, providing reliable technical support for early kick detection. Under laboratory conditions, the model achieved a measurement accuracy of ±2.5%; for field applications, a measurement accuracy of ±5% is expected when accounting for environmental influences, fully meeting the technical requirements for downhole kick monitoring.
5. Discussion and Limitations
To provide a comprehensive perspective on downhole multiphase flow monitoring, it is essential to compare the gamma-ray technique with other mainstream measurement methods. Each technique is characterized by distinct operating principles, measurement capabilities, and application scenarios. Table 8 summarizes the key performance differences between the gamma-ray method and widely used alternatives—including resistivity, acoustic/ultrasonic, nuclear magnetic resonance, and conventional density logging—across several critical metrics.

Table 8.
Comparison of mainstream multiphase flow measurement technologies.
Over the past decade, field and laboratory evaluations have confirmed that gamma-ray absorption meters can maintain volumetric fraction errors within ±3% at pressures up to 200 bar and temperatures up to 180 °C [11,41,42], whereas resistivity and density tools tend to drift once the gas volume fraction exceeds 40% [42,45]. This superior robustness is primarily attributed to the high-energy photon penetration of gamma-ray methods, which remains largely unaffected by conductive mud filtrate—a factor that routinely undermines resistivity measurements in saline or complex fluid environments [43,45]. Ultrasonic systems, while effective at rapid flow-regime identification through speed-of-sound contrasts, are increasingly constrained by acoustic attenuation as depth and temperature rise, limiting their operational envelope [43,44]. Nuclear magnetic resonance logging delivers unparalleled fluid discrimination, but depends on bulky Halbach magnets and slow pulse sequences, rendering acquisition impractical for high-rate drilling operations [46]. Conventional neutron-gamma density logs are indispensable for static porosity evaluation; however, gas expansion and borehole rugosity can introduce errors of 10–15 porosity units, restricting their value for dynamic multiphase quantification [46]. Spectroscopic implementations such as the Vx Spectra have extended gamma-ray measurements to gas volume fractions above 95% by leveraging full-energy spectrum analysis, thereby eliminating the need for external PVT sampling [13,47,48]. Market surveys consistently rank gamma-based systems among the few multiphase flow meters (MPFMs) that combine sub-percent long-term drift with a compact wellhead footprint [46]. Comprehensive reviews further note that, despite rising interest in non-nuclear meters, radiation-based technologies remain the metrological benchmark for harsh subsea and HPHT environments [46]. Emerging dual-energy gamma-ray tomography also suggests that combining densitometry with cross-sectional imaging may significantly enhance flow pattern recognition and phase discrimination [47].
Despite these strengths, the present study has several limitations. First, the present validation was conducted under controlled laboratory conditions, whereas actual field applications will involve greater complexity, including variable mud compositions, dynamic temperature and pressure fluctuations, mechanical vibrations, positional uncertainties, and potential electromagnetic interference from drilling equipment. Second, the current model assumes a uniform bubble distribution, which may not adequately represent flow heterogeneity under all drilling scenarios. Future work should incorporate flow pattern recognition (e.g., slug and stratified flows), adaptive algorithms, and multi-point measurement strategies to enhance robustness. Third, the scope of this study is limited to gas–liquid two-phase systems; extension to oil–water–gas three-phase flow will require dual-energy gamma measurements, integration with complementary sensing modalities (such as resistivity or acoustic tools), and more advanced inversion algorithms. Furthermore, long-term stability under continuous field operation must be validated, including source decay correction, detector reliability, and calibration protocols. Finally, practical deployment requires careful attention paid to radioactive source handling, regulatory compliance, and personnel safety, which may vary across operational environments. Addressing these limitations will be essential for advancing the technology toward reliable and comprehensive field implementation.
6. Conclusions and Perspectives
In summary, this study systematically investigated the use of Ba-133 gamma-ray attenuation for gas content measurement in drilling fluids, integrating Geant4 Monte Carlo simulations with laboratory experiments. The optimized detection system demonstrated a stable performance under dynamic and high-temperature laboratory conditions, with a mean relative error of 5.01% between the simulation and experimental results across a range of source-to-detector distances (5–40 mm). The developed nonlinear inversion model, which accounts for density effects and gas content variations, achieved an improved accuracy throughout the full measurement range (0–100% gas content), particularly in high-gas-content intervals where conventional linear models were inadequate.
Compared to traditional methods, the integrated experimental and simulation framework established in this work enables a more comprehensive understanding of the gamma-ray behavior in complex fluid media under controlled conditions. These findings provide a solid theoretical and methodological basis for further research on advanced gamma-ray measurement techniques in multiphase flow systems and support future extension to more complex three-phase systems or field-scale validation.
Future Perspectives:
This technology holds great promise for further application and expansion in the following areas:
- Multiphase flow monitoring: By optimizing detector configurations and algorithms, the system can be extended to monitor the component proportions of oil–gas–water three-phase fluids, providing a novel approach for reservoir dynamic monitoring.
- Real-time evaluation of downhole fluid properties: In combination with technologies such as nuclear magnetic resonance, the comprehensive real-time monitoring of downhole fluid parameters, including density and viscosity, can be achieved.
- Intelligent drilling decision support: Integrating gas content data obtained from this technique into drilling control systems will provide essential data support for automated drilling and intelligent well control.
- Evaluation of unconventional hydrocarbon reservoirs: The method is applicable for gas content evaluation in unconventional reservoirs such as tight gas and shale gas, offering a new tool for dynamic reservoir analysis.
Future research will focus on addressing the following key scientific challenges: (1) the interaction mechanisms between gamma rays and gas–liquid two-phase flows under high-temperature and high-pressure conditions; (2) the effects of multi-physical field coupling on measurement accuracy in complex downhole environments; and (3) the development of integrated downhole multi-parameter inversion algorithms based on big data and machine learning. Through these in-depth studies, the applicability and accuracy of the technology will be further enhanced, providing more reliable technical support for the safe and efficient development of oil and gas resources.
Author Contributions
Conceptualization, X.W. (Xingming Wang); methodology, X.W. (Xingming Wang); software, X.W. (Xiangyu Wang); validation, X.W. (Xiangyu Wang); formal analysis, X.W. (Xiangyu Wang); investigation, Z.X.; resources, X.H.; Data curation, Q.W.; writing—original draft, X.W. (Xiangyu Wang); writing—review & editing, Y.Y. and L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China (Grants No. 52327803, Grants No. 52204006), the Tianfu Yongxing Laboratory Organized Research Project Funding (Grants No. 2023KJGG13) and the China Postdoctoral Science Foundation (Grants No. 2022M723399).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to confidentiality.
Conflicts of Interest
Author Xiong Han was employed by the CNPC Chuanqing Drilling Engineering Company Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Yin, Q.; Yang, J.; Tyagi, M.; Zhou, X.; Hou, X.; Wang, H. Machine learning for deepwater drilling: Gas-kick-alarm classification using pilot-scale rig data with combined surface-riser-downhole monitoring. SPE J. 2021, 26, 1773–1799. [Google Scholar] [CrossRef]
- Osarogiagbon, A.; Muojeke, S.; Venkatesan, R.; Khan, F.; Gillard, P. A new methodology for kick detection during petroleum drilling using long short-term memory recurrent neural network. Process Saf. Environ. Prot. 2020, 142, 126–137. [Google Scholar] [CrossRef]
- Bhandari, J.; Abbassi, R.; Garaniya, V.; Khan, F. Risk analysis of deepwater drilling operations using Bayesian network. J. Loss Prev. Process Ind. 2015, 38, 11–23. [Google Scholar] [CrossRef]
- Tarr, B.A.; Ladendorf, D.W.; Sanchez, D.; Milner, G.M. Next-generation kick detection during connections: Influx detection at pumps stop (IDAPS) software. SPE Drill. Complet. 2016, 31, 250–260. [Google Scholar] [CrossRef]
- Raza, M.A.; Salehi, S.; Ghazal, S.; Ybarra, V.T.; Naqvi, S.A.M.; Cokely, E.T.; Teodoriu, C. Situational awareness measurement in a simulation-based training framework for offshore well control operations. J. Loss Prev. Process Ind. 2019, 62, 103921. [Google Scholar] [CrossRef]
- Khakzad, N.; Khan, F.; Amyotte, P. Quantitative risk analysis of offshore drilling operations: A Bayesian approach. Saf. Sci. 2013, 57, 108–117. [Google Scholar] [CrossRef]
- Hu, C.; Yu, L.; Wang, D.; He, H.; Li, Y. Gas–liquid two-phase flow measurement by using electrical tomography sensors and Venturi. Flow Meas. Instrum. 2025, 102, 102763. [Google Scholar] [CrossRef]
- Meribout, M.; Azzi, A.; Ghendour, N.; Kharoua, N.; Khezzar, L.; AlHosani, E. Multiphase Flow Meters Targeting Oil & Gas Industries. Measurement 2020, 165, 108111. [Google Scholar] [CrossRef]
- Mahmoud, A.; Gajbhiye, R.; Elkatatny, S. Advances in drilling fluid technology: Recent innovations, performance enhancements, and future trends in high-performance and eco-friendly formulations. J. Pet. Sci. Eng. 2024, 234, 211181. [Google Scholar] [CrossRef]
- Cao, F.; Dang, R.; Dang, B.; Zheng, H.; Ji, A.; Chen, Z.; Zhao, J.; Sun, Z. Flow regimes identification of air water counter current flow in vertical annulus using differential pressure signals and machine learning. Sci. Rep. 2024, 14, 12572. [Google Scholar] [CrossRef]
- Mayet, A.M.; Gorelkina, E.I.; Parayangat, M.; Guerrero, J.W.G.; Raja, M.R.; Muqeet, M.A.; Mohammed, S.A. Enhancing accuracy in X-ray radiation-based multiphase flow meters: Integration of grey wolf optimization and MLP neural networks. Flow Meas. Instrum. 2024, 100, 102734. [Google Scholar] [CrossRef]
- Jeshvaghani, P.A.; Khorsandi, M.; Panahi, R. Flow regime identification and gas volume fraction prediction in two-phase flows using a simple gamma-ray gauge combined with parallel artificial neural networks. Flow Meas. Instrum. 2022, 95, 102151. [Google Scholar] [CrossRef]
- Dam, R.S.F.; Salgado, W.L.; Conti, C.C.; Schirru, R.; Salgado, C.M. Volume fraction detection in multiphase systems using neutron activation analysis and artificial neural network. Appl. Radiat. Isot. 2024, 214, 111504. [Google Scholar] [CrossRef]
- Roshani, M.; Sattari, M.A.; Ali, P.J.M.; Roshani, G.H.; Nazemi, B.; Corniani, E.; Nazemi, E. Application of GMDH neural network technique to improve measuring precision of a simplified photon attenuation based two-phase flowmeter. Flow Meas. Instrum. 2020, 75, 101804. [Google Scholar] [CrossRef]
- Roshani, G.H.; Nazemi, E.; Feghhi, S.A.H.; Setayeshi, S. Flow regime identification and void fraction prediction in two-phase flows based on gamma ray attenuation. Measurement 2015, 62, 25–32. [Google Scholar] [CrossRef]
- Zych, M.; Petryka, L.; Kępiński, J.; Hanus, R.; Bujak, T.; Puskarczyk, E. Radiometric methods in the measurement of particle-laden flows. Powder Technol. 2017, 318, 491–500. [Google Scholar] [CrossRef]
- Varignier, G.; Fondement, V.; Carasco, C.; Collot, J.; Pérot, B.; Marchais, T.; Chuilon, P.; Caroli, E.; Doan, M.-L. Comparison between GEANT4 and MCNP for well logging applications. EPJ Web Conf. 2023, 288, 01002. [Google Scholar] [CrossRef]
- Jin, Z.; Kilby, S.; Avachat, A.; Kanies, B.; Woolstenhulme, N.; Lee, H.K. Accelerated radiation transport modeling techniques for pencil beam computed tomography using gamma rays. Nucl. Instrum. Methods Phys. Res. Sect. A 2022, 1039, 167165. [Google Scholar] [CrossRef]
- Ge, Y.; Liang, J.; Zhang, Q.; Tang, W.; Munoz-Garcia, A. A comparison study of GEANT4 and MCNP6 on neutron-induced gamma simulation. Appl. Radiat. Isot. 2022, 190, 110514. [Google Scholar] [CrossRef] [PubMed]
- Huurman, J.; Mondal, K.; Martinez, O. An Overview of Emerging Nuclear Sensor Technologies: Challenges, Advancements and Applications. Appl. Sci. 2025, 15, 2338. [Google Scholar] [CrossRef]
- Arteaga-Arteaga, H.B.; Mora-Rubio, A.; Florez, F.; Murcia-Orjuela, N.; Diaz-Ortega, C.E.; Orozco-Arias, S.; delaPava, M.; Bravo-Ortíz, M.A.; Robinson, M.; Guillen-Rondon, P.; et al. Machine learning applications to predict two-phase flow patterns. PeerJ Comput. Sci. 2021, 7, e798. [Google Scholar] [CrossRef]
- Manami, M.; Seddighi, S.; Örlü, R. Deep learning models for improved accuracy of a multiphase flowmeter. Measurement 2023, 206, 112254. [Google Scholar] [CrossRef]
- Du, S.; Huang, C.; Ma, X.; Fan, H. A Review of Data-Driven Intelligent Monitoring for Geological Drilling Processes. Processes 2024, 12, 2478. [Google Scholar] [CrossRef]
- Khoshouei, M.; Bagherpour, R.; Yari, M. A smart look at monitoring while drilling (MWD) and optimizing using acoustic emission technique (AET). Sci. Rep. 2024, 14, 19766. [Google Scholar] [CrossRef] [PubMed]
- Lu, F.; Shen, X.; Wu, C. Research on Highly Reliable Self-Powered Vibration Sensors for Geological Drilling. Processes 2024, 12, 2310. [Google Scholar] [CrossRef]
- Liu, N.; Zhang, D.; Gao, H.; Hu, Y.; Duan, L. Real-time measurement of drilling fluid rheological properties: A review. Sensors 2021, 21, 3592. [Google Scholar] [CrossRef]
- Villafañe, L.; Aliseda, A.; Ceccio, S.; Di Marco, P.; Machicoane, N.; Heindel, T.J. 50 Years of International Journal of Multiphase Flow: Experimental Methods for Dispersed Multiphase Flows. Int. J. Multiph. Flow 2025, 189, 105239. [Google Scholar] [CrossRef]
- Michail, C.; Liaparinos, P.; Kalyvas, N.; Kandarakis, I.; Fountos, G.; Valais, I. Radiation Detectors and Sensors in Medical Imaging. Sensors 2024, 24, 6251. [Google Scholar] [CrossRef]
- Cortés-Giraldo, M.A.; Cucinotta, F.A.; Guatelli, S.; Vlachoudis, V. Editorial: Challenges for Radiation Transport Modelling: Monte Carlo and Beyond. Front. Phys. 2022, 10, 884140. [Google Scholar] [CrossRef]
- Alakbari, F.S.; Ayoub, M.A.; Awad, M.A.; Mohyaldinn, M.E.; Ganat, T.A. A robust pressure drop prediction model in vertical multiphase flow: A machine learning approach. Sci. Rep. 2025, 15, 13420. [Google Scholar] [CrossRef]
- Alamoudi, M.; Sattari, M.A.; Balubaid, M.A.; Eftekhari-Zadeh, E.; Nazemi, E.; Taylan, O.; Kalmoun, E. Application of gamma attenuation technique and artificial intelligence to detect scale thickness in pipelines in which two-phase flows with different flow regimes and void fractions exist. Symmetry 2021, 13, 1198. [Google Scholar] [CrossRef]
- Silva, V.; Dantas, C.; Melo, S.B.; Lima, F.; Oliveira, P.; Filho, T.A.R.; Lins, J.A.G.; Vieira, E.B.; Andrade, B.G.; Viana, M.S. Determination of fluid dynamic parameters through imports of CFD images validated in experiments for the MCNPX code. Braz. J. Radiat. Sci. 2021, 8, 18. [Google Scholar] [CrossRef]
- Umar, M.; Saidu, A.; Aliyu, J.; Shehu, A.I. Investigation of attenuation properties of liquid materials by gamma ab-sorption-scattering method. Int. J. Res. Innov. Appl. Sci. 2022, 7, 76–81. [Google Scholar] [CrossRef]
- Knoll, G.F. Radiation Detection and Measurement; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- Choi, J.J.; Park, B.; Ha, C.; Kim, K.W.; Kim, S.-W.; Kim, Y.; Ko, Y.; Lee, H.; Lee, S.; Olsen, S. Improving the light collection using a new NaI(tl) crystal encapsulation. Nucl. Instrum. Methods Phys. Res. Sect. A-Accel. Spectrometers Detect. Assoc. Equip. 2020, 981, 164556. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent de-velopments in GEANT4. Nucl. Instrum. Methods Phys. Res. Sect. A-Accel. Spectrometers Detect. Assoc. Equip. 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Agostinelliae, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A Simulation Toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A 2003, 506(3), 250–303. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, J.; Zhang, Q.; Wang, X. Development and verification of Geant4-based parallel computing monte carlo simulations for nuclear logging applications. Ann. Nucl. Energy 2022, 172, 109079. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q. A characterization study on perovskite X-ray detector performance based on a digital radiography system. Nucl. Sci. Technol. 2023, 34, 69. [Google Scholar] [CrossRef]
- Jin, H.; Jespersen, D.; Mehrotra, P.; Biswas, R.; Huang, L.; Chapman, B. High performance computing using MPI and OpenMP on multi-core parallel systems. Parallel Comput. 2011, 37, 562–575. [Google Scholar] [CrossRef]
- Zhu, J.H.; Munjal, R.; Sivaram, A.; Paul, S.R.; Tian, J.; Jolivet, G. Flow Regime Detection Using Gamma-Ray-Based Multiphase Flowmeter: A Machine Learning Approach. Int. J. Comput. Methods Exp. Meas. 2022, 10, 26–37. [Google Scholar] [CrossRef]
- Ramakrishnan, V.; Arsalan, M. A Pressure-Based Multiphase Flowmeter: Proof of Concept. Sensors 2023, 23, 7267. [Google Scholar] [CrossRef] [PubMed]
- Ünalmis, Ö.H. A Methodology for In-Well Multiphase Flow Measurement with Strategically Positioned Local and/or Distributed Acoustic Sensors. Sensors 2023, 23, 5969. [Google Scholar] [CrossRef]
- Figueiredo, M.M.F.; Goncalves, J.L.; Nakashima, A.M.V.; Fileti, A.M.F.; Carvalho, R.D.M. The use of an ultrasonic technique and neural networks for identification of the flow pattern and measurement of the gas volume fraction in multiphase flows. Exp. Therm. Fluid Sci. 2016, 70, 29–50. [Google Scholar] [CrossRef]
- Arief, H.A.; Wiktorski, T.; Thomas, P.J. A Survey on Distributed Fibre Optic Sensor Data Modelling Techniques and Machine Learning Algorithms for Multiphase Fluid Flow Estimation. Sensors 2021, 21, 2801. [Google Scholar] [CrossRef]
- Hansen, L.S.; Pedersen, S.; Durdevic, P. Multi-Phase Flow Metering in Offshore Oil and Gas Transportation Pipelines: Trends and Perspectives. Sensors 2019, 19, 2184. [Google Scholar] [CrossRef]
- Stavland, S.H.; Tjugum, S.-A.; Hallanger, A.; Sætre, C.; Maad, R.; Hjertaker, B.T. Characterization of multiphase flow through Venturi nozzle using gamma-ray tomography. Flow Meas. Instrum. 2024, 98, 102632. [Google Scholar] [CrossRef]
- Mathew, J.; Kshirsagar, R.; Abidin, D.Z.; Parimala, P.S.; Kolekar, M.H.; Kolhe, M.L. A comparison of machine learning methods to classify radioactive elements using prompt-gamma-ray neutron activation data. Sci. Rep. 2023, 13, 9948. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).