Modeling Prediction of Physical Properties in Sustainable Biodiesel–Diesel–Alcohol Blends via Experimental Methods and Machine Learning

Abstract

This study investigated the production of biodiesel from canola oil, the formulation of sustainable ternary fuel blends with diesel and alcohol (ethanol or propanol), and the experimental and machine learning-based modeling of their physical properties, including density and viscosity over a temperature range of 10 °C to 40 °C. Biodiesel was synthesized via alkali-catalyzed transesterification (6:1 methanol-to-oil molar ratio, 0.5 wt % NaOH of oil) and blended with diesel and alcohols (ethanol and propanol) in varying volume ratios. The experimental results revealed that blend density decreased from 0.8622 g/cm³ at 10 °C to 0.8522 g/cm³ at 40 °C for a blend containing ethanol. Similarly, the viscosity showed a significant reduction with temperature, e.g., the blend exhibited a viscosity decline from 8.5 mPa·s at 10 °C to 7.2 mPa·s at 40 °C. Increasing the alcohol or diesel content further reduced density and viscosity due to the lower intrinsic properties of these components. The machine learning models, Gaussian process regression (GPR), support vector regression (SVR), artificial neural networks (ANN), and decision tree regression (DTR), were applied to predict the properties of these blends. GPR demonstrated the best predictive performance for both density and viscosity. These findings confirm the strong potential of GPR for the accurate and reliable prediction of fuel blend properties, supporting the formulation of alternative fuels optimized for diesel engine performance. These aspects contribute new insights into modelling strategies for sustainable fuel formulations.

1. Introduction

1.1. Sustainable Diesel Alternatives

The rising global energy demand, coupled with the depletion of fossil fuel reserves, has significantly increased interest in renewable energy sources across the world [1,2]. This growing demand for alternative fuels is particularly critical in sectors heavily reliant on diesel engines, such as transportation and agriculture. For centuries, many nations have largely depended on fossil fuels, namely, petroleum, natural gas, and coal, to secure their energy supply [3,4,5,6]. However, these resources are finite and their extensive use represents a major source of environmental degradation. It is estimated that fossil fuel consumption accounts for nearly 63% of total global greenhouse gas emissions and approximately 85% of CO₂ emissions released into the atmosphere [7,8,9,10]. Moreover, about half of global fossil fuel consumption is used to meet the energy requirements of the agricultural and transportation sectors [11,12]. Among these, transportation remains one of the most energy-intensive sectors, with most of its energy demand especially for heavy trucks, urban buses, and locomotives being met by petroleum-based diesel. In 2018, diesel fuel consumption within the European Union (EU) was reported to be around 2.72 times higher than that of gasoline, while in Türkiye this ratio stood at approximately 10.67 [13,14]. This reflects the significant role of diesel fuel in developing economies. However, in recent years, shifts in energy policy, heightened environmental concerns, and a growing trend toward alternative fuel use have contributed to notable changes in these consumption patterns. According to 2023 data, the diesel-to-gasoline consumption ratio in the EU rose to approximately 3.12, with diesel consumption reaching 218.8 million tons of oil equivalent (Mtoe) and gasoline consumption remaining at 70.3 Mtoe. This modest increase compared to 2018 highlights the continued prevalence of diesel-powered vehicles in heavy transport and industrial applications [15,16]. In Türkiye, diesel consumption averaged 63.45 thousand m³ per day in 2023, while gasoline consumption was recorded at 11.04 thousand m³ per day, corresponding to a decline in the diesel-to-gasoline consumption ratio to approximately 5.75 [17]. Stricter emission standards, evolving environmental regulations, and supportive policies for electric vehicles have been among the key drivers of this transformation. Diesel engines continue to play a vital role in various applications due to their high reliability, combustion efficiency, and power output, particularly in agriculture, heavy transport, and industrial sectors. Nevertheless, the significant levels of pollution and emissions associated with diesel fuels have made the development of advanced technologies aimed at reducing emissions and improving fuel efficiency a priority in internal combustion engine research. In recent years, efforts to mitigate environmental pollution and preserve petroleum resources have increasingly focused on alternative fuels for transportation. A prominent trend is the blending of biofuels with conventional fossil fuels or their use as direct replacements. Today, diesel is often marketed as a blend containing biodiesel, and other biofuels such as bio alcohols are being explored as promising alternatives to conventional diesel fuels [18].

Biodiesel is recognized as a processed fuel equivalent to conventional diesel, derived from various biological resources. Chemically, biodiesel is classified as a mixture of long-chain mono alkyl esters of fatty acids. According to ASTM D6751 standards, biodiesel, referred to as B100, is composed of long-chain mono alkyl esters of fatty acids sourced from vegetable oils or animal fats [19]. Its physicochemical properties closely resemble those of petroleum diesel, making biodiesel a promising alternative fuel.

Transesterification is the most widely adopted method for biodiesel production. This process involves the reaction of fats or fatty acids with alcohol, yielding esters and glycerol as products. The reaction can proceed either with or without a catalyst. In the absence of a catalyst, higher temperatures and pressures are required, and the yield tends to be lower. The use of a catalyst enhances both the reaction rate and yield. During transesterification, free fatty acids react with alcohol to produce fatty acid methyl esters (FAME) and glycerol [20]. As the reaction is reversible, excess alcohol shifts the equilibrium towards FAME formation. Both primary and secondary alcohols containing carbon chains ranging from C1 to C8 can be used, and the choice of catalyst is influenced by factors such as conversion efficiency, separation ease, and potential corrosion [21]. The conversion of triglycerides to methyl or ethyl esters through transesterification reduces the molecular weight of the product to roughly one-third of that of the original triglycerides. This process also decreases viscosity by nearly eightfold and slightly enhances volatility. Biodiesel exhibits viscosity characteristics comparable to those of petroleum diesel and contains about 10–11% oxygen by weight, which promotes more complete combustion than hydrocarbon-based diesel fuels. The cetane number of biodiesels is typically around 50. Biodiesel has a volumetric heating value approximately 12% lower than that of petroleum diesel but benefits from a higher cetane number and flash point. It is regarded as a clean fuel, as it contains no sulfur or aromatic compounds. The inherent oxygen content facilitates more complete combustion, and blending biodiesel with petroleum diesel improves ignition quality due to its higher cetane number [22,23].

Biodiesel is widely considered an environmentally friendly fuel because of its biodegradability, low toxicity, and renewable nature. The selection of raw materials plays a crucial role in determining both production costs and fuel quality. It is well documented that 70–80% of biodiesel production costs are attributable to feedstock expenses [22]. Among potential feedstocks, canola oil is regarded as ideal for biodiesel production due to its high oil content (40–45%), low saturated fatty acid composition, and favorable viscosity [24,25]. The application of refined canola oil in biodiesel production provides notable advantages, primarily due to its low free fatty acid (FFA) content. This characteristic minimizes the occurrence of undesirable side reactions, such as saponification, during the transesterification process. As a result, product quality is enhanced, and subsequent purification steps, including washing, are simplified. Alkali-catalyzed transesterification is typically preferred for converting refined canola oil into biodiesel, with catalyst concentrations of 0.5–1% wt. of NaOH and methanol-to-oil molar ratios between 6:1 and 9:1 commonly yielding high conversion efficiencies [26,27]. The use of refined oil not only enables the production of high-purity biodiesel with lower alcohol and catalyst requirements but also contributes to reduced production costs and environmental impacts. Consequently, refined canola oil represents an environmentally and economically advantageous feedstock for producing high-quality biodiesel and holds significant potential in the development of sustainable diesel engine fuels.

1.2. Canola Oil Biodiesel

Research on biodiesel derived from refined canola oil is well-represented in the literature, largely due to its high conversion rates and favorable physical properties. For example, it is reported that canola-based biodiesel offers a high cetane number (61.5) and low sulfur content, making it a promising environmentally friendly alternative for diesel engines [28]. Similarly, Chen et al. (2023) demonstrated that biodiesel produced from refined canola oil meets key standards for viscosity and density specified by ASTM D6751 and EN 14214 [24,29,30]. Although most studies in Türkiye have focused on waste vegetable oils, experimental research involving refined canola oil has shown that this feedstock achieves high conversion rates and results in more stable biodiesel blends [31]. Canola oil-based biodiesel is regarded as a promising alternative fuel, offering significant advantages over other biodiesel sources. Canola oil typically contains 40–45% oil, comparable to sunflower oil and significantly higher than that of soybeans, which contain approximately 18–20% oil [32]. Its fatty acid composition includes approximately 60% oleic acid, 21.2% linoleic acid, 9.6% linolenic acid, 4.2% palmitic acid, and smaller amounts of other fatty acids [33]. The density of canola biodiesel are reported between 880 and 890 kg/m³ [25,34], while its oxygen content is approximately 10.8 wt% [35]. The dynamic viscosity at 40 °C is estimated to fall within the range of 3.7–4.3 mPa·s. The cetane number of COB is 61.5, which is around 10.2% higher than that of conventional diesel [36], and its calorific value is reported at 39.49 MJ/kg [34]. Additional fuel properties of canola oil-based biodiesel are summarized in

Table 1. Properties of canola oil-based biodiesel [34].

Property	Pure Diesel	BD100 (Biodiesel)
Density (kg/m3 at 15 °C)	836.8	880
Viscosity (mPa·s at 40 °C)	2.27	3.78
Calorific value (MJ/kg)	43.96	39.49
Cetane number	55.8	61.5
Flash point (°C)	55	182
Pour point (°C)	−21	−8
Oxidation stability (h/110 °C)	25	15
Ester content (%)	-	98.9
Oxygen content (%)	0	10.8

.

1.3. Ternary Fuel Blends

While biodiesel is often regarded as one of the most promising choices among biofuels, its direct use as a fuel in diesel engines presents several challenges. As a result, the application of ternary fuel blends in diesel engines comprising diesel, biodiesel, and alcohol has emerged as a potential strategy to mitigate the disadvantages associated with biodiesel and alcohol. Extensive research has been conducted to examine the effects of ternary blends on diesel engine combustion characteristics, performance metrics, and pollutant emissions, including smoke, nitrogen oxides (NOx), carbon monoxide (CO), and hydrocarbons (HC). A review of the literature reveals that the density of such blends generally falls within the range of 830–870 kg/m³, depending on the type of biodiesel utilized. Similarly, the viscosity of these blends typically ranges from 2 to 4 mm²/s [37,38,39,40,41]. Density is a key fuel property that directly influences engine performance, as characteristics such as cetane number and heating value are closely linked to fuel density. The density of a fuel affects atomization efficiency and combustion behavior. Despite its importance, relatively few studies have focused on modeling the density and viscosity characteristics of ternary fuel blends. For instance, Bietresato et al. (2021) investigated the measurement and modeling of the viscosity of diesel–biodiesel–bioethanol blends as a function of blend composition and temperature, reporting that the model’s coefficient of determination (R²) improved substantially at elevated temperatures [42]. Mestila (2019) noted that the viscosity and density of ternary blends containing canola oil-based biodiesel–bioethanol improved fuel atomization and combustion characteristics in diesel engines, while contributing to a reduction in particulate emissions [43].

1.4. Machine Learning Techniques in Ternary Blends

Machine learning (ML) is an artificial intelligence approach that enables systems to learn patterns from historical data and make predictions. In biodiesel blends, physical properties such as density and viscosity are critical for engine performance and fuel injection systems and require accurate modelling of these properties [44,45]. ML enables fast, low-cost, and accurate predictions of these properties under varying blend conditions. This provides advantages for fuel design, quality control, and engine compatibility. Gülüm et al. created seven different blends by adding 2–20% isopropyl alcohol (IPA) to the B20 blend formed by blending canola biodiesel with diesel at a ratio of 20% and measured the density and viscosity values of these blends. Although machine learning was not used in the study, linear regression models for density and four-term exponential regression models for viscosity were developed and the obtained models showed high agreement (R² ≈ 1). This study is particularly important in terms of visualizing the effect of increasing alcohol content on physical properties [46]. Lapuerta et al. comparatively investigated the effect of alcohol types on the biodiesel–diesel–alcohol system and modelled the viscosity properties of blends containing ethanol and n-butanol with Grunberg–Nissan-type empirical correlations. It was found that ethanol-containing blends may be outside the viscosity limits, whereas more suitable blends can be obtained with n-butanol [47]. Razzaq et al. evaluated density and viscosity data with classical modelling methods on 30 different blends formed by mixing five different biodiesels with diesel and ethanol. The developed models achieved high accuracy levels and MAPE values were reported as 0.05% (density) and 1.4–3.5% (viscosity) [6]. Belmadani et al. performed density and viscosity predictions with an artificial neural network (ANN) over a large data set. The model, which was trained with a total of 1025 data points, was tested with 238 new data and obtained highly successful results with R² = 0.998 in density predictions and R² = 0.965 in viscosity predictions. This model makes it possible to predict new mixtures with high accuracy without experimentation [48]. Modelling approaches used in the studies vary in terms of data coverage, accuracy and applicability. While classic regression models provide simple and applicable solutions for specific systems, machine learning methods provide higher generalization capacity and accuracy, especially in systems with multiple components and variables.

The present study focuses on the production of biodiesel from canola oil, the formulation of ternary blends combining the produced biodiesel with diesel and alcohol, and the experimental analysis of the physical properties, namely, the density and viscosity, of these blends. Biodiesel was synthesized through transesterification reactions under constant reaction conditions. The resulting biodiesel was blended with diesel and alcohol in different proportions, and the density and viscosity of the blends were measured across a range of temperatures. Finally, machine learning techniques, including decision trees, gaussian process regression, support vector machines, and artificial neural networks, were employed to model and evaluate the experimental data. Unlike classical regression methods or holdout validation techniques, this study adopts a two-stage approach within a machine learning framework. Initially, the dataset is partitioned into 85% training and 15% testing subsets using holdout validation. Subsequently, cross-validation combined with hyperparameter optimization is employed to enhance the reliability and generalizability of the predictive outcomes. These aspects contribute new insights into modelling strategies for sustainable fuel formulations.

2. Material and Methods

The canola oil used in this study was sourced from a local commercial supplier. The commercial-grade diesel fuel was obtained from a local gas station. Ethanol and propanol (purity ≥ 99.8%) were used as the alcohol components in the ternary fuel blends, ensuring accurate blend composition. Methanol used in the transesterification reactions was of analytical grade to maintain reagent quality and reaction reliability. Sodium hydroxide (NaOH), used as the catalyst, was supplied in pellet form with analytical purity. Sodium sulfate (Na₂SO₄) was utilized as a drying agent. Distilled water was used for washing the biodiesel and for pycnometer calibration.

The instruments and equipment used included a three-neck reactor (1 L) for biodiesel synthesis, a separatory funnel for separation of glycerin, biodiesel and wash water, a pycnometer for density measurements, an R/S Plus rheometer with a concentric cylinder (CC25) geometry for viscosity analysis, and a cooperative fuel research (CFR) engine for cetane number determination. A high-performance liquid chromatography (HPLC) instrument (Agilent 1200 series) was employed to verify biodiesel conversion efficiency.

2.1. Canola Oil-Based Biodiesel Synthesis

Biodiesel synthesis was carried out via transesterification reactions under the following process sequence and experimental conditions.

Initially, canola oil was preheated at 100 °C for 1 h in a heater to eliminate moisture and volatile compounds. Then, the transesterification reaction was conducted using 0.5% by weight NaOH catalyst, using a methanol-to-canola oil molar ratio of 6:1 at 65 °C in 1.5 h with 100% conversion. Upon completion, the biodiesel was separated from the glycerin phase using a separatory funnel. The biodiesel was subsequently washed six times with distilled water to remove residual glycerin. Finally, the remaining water was removed by drying the biodiesel with sodium sulfate (Na₂SO₄), and the product was filtered to obtain the purified biodiesel. Following the production of the biodiesel, the conversion efficiency (100%) was determined using an HPLC instrument (Agilent 1200 series) consisting of a gradient pump, an UV detector (at 205 nm) and an Agilent column (Eclipse XDB-C18, 5 µm) at 40 °C, using methanol as the mobile phase at a flow rate of 1 cm³/min [25,27].

2.2. Preparation of Blends (v/v)

Diesel–biodiesel–alcohol ternary blends were prepared in various volume percentages, totaling 25 mL, except for the cetane number analysis, which required a total volume of 250 mL and used ethanol and propanol as the alcohol types. The sample compositions (biodiesel, diesel, and alcohol) of the ternary blends prepared in this study are presented in

Table 2. Preparation composition of ternary blends.

Sample Code	Diesel (D) (v/v)	Biodiesel (B) (v/v)	Alcohol (A) (v/v)
30D65B5A	30	65	5
35D60B5A	35	60	5
40D55B5A	40	55	5
45D50B5A	45	50	5
50D45B5A	50	45	5
55D40B5A	55	40	5
60D35B5A	60	35	5
65D30B5A	65	30	5
70D25B5A	70	25	5
75D20B5A	75	20	5
80D15B5A	80	15	5
85D10B5A	85	10	5
90D5B5A	90	5	5
30D60B10A	30	60	10
35D55B10A	35	55	10
40D50B10A	40	50	10
45D45B10A	45	45	10
50D40B10A	50	40	10
55D35B10A	55	35	10
60D30B10A	60	30	10
65D25B10A	65	25	10
70D20B10A	70	20	10
75D15B10A	75	15	10
80D10B10A	80	10	10
85D5B10A	85	5	10

. In the study, measurements of all blends were made immediately after preparation.

2.3. Density Measurement of Blends

The density of the blends was determined using a pycnometer. Initially, the density of pure water was measured at various temperatures for calibration purposes. The measurements were performed at temperatures ranging from 10 °C to 40 °C, in increments of 5 °C. Following this calibration, enough of each blend was introduced into the pycnometer, and the density measurements were carried out under the same temperature conditions (10 °C to 40 °C, at 5 °C intervals). The mass of the blends was recorded at each temperature, and the density of the blends was calculated using the following equation:

$${\rho }_s={\displaystyle \frac{M_s-M_p}{M_w-M_p}}$$

(1)

where ρ_s is the density of the blend (g/cm³), M_s is the mass of the pycnometer filled with the blend (g), M_w is the mass of the pycnometer filled with pure water (g) and M_p is the mass of the empty pycnometer (g).

2.4. Viscosity Measurement of Blends

Viscosity measurements of the blends were conducted using an R/S plus rheometer. After switching on both the rheometer and the connected computer, the Rheo 3000 software was launched to control the measurement process. The connection between the rheometer and the computer was established through the software interface by activating the remote function on the rheometer. A concentric cylinder geometry and the CC25-coded sample chamber were mounted on the device, and the chamber was filled with the sample (25 mL) at the specified temperature to be analyzed. The measurement parameters, including the shear rate range (200–1250, 1/s), analysis duration (300 s.) and number of data (50) were defined within the software. The shear rate (1/s) and shear stress (Pa) data were recorded during the analysis. Viscosity values (Pa·s) of the blends were measured from the slope of the fitted curve drawn between the shear rate (1/s) and shear stress (Pa) data. The viscosity measurement graph of a blend (at 25 °C with ethanol) is shown in Figure 1 as an example.

2.5. Cetane Number Analysis of Blends

The determination of cetane numbers for the fuel blends was carried out at the Scientific and Technological Research Council of Türkiye (TUBITAK), Marmara Research Center (MAM) following the ASTM D613 standard [49]. The measurements were performed using a cooperative fuel research (CFR) engine, which was calibrated with reference fuels of known cetane numbers before testing commenced. Each fuel blend was introduced into the fuel system of the CFR engine and evaluated accordingly. During the tests, key parameters including compression ratio, injection timing, and compressed air temperature were adjusted and maintained in accordance with the specified standards. The cetane number for each blend was calculated based on the ignition delay, measured in crank angle degrees, and determined through linear interpolation by comparison with the reference fuels. Multiple measurements were conducted for each blend, and the average cetane number was recorded and reported.

2.6. Machine Learning Modeling

In machine learning applications, three primary evaluation strategies are commonly utilized, with k-fold cross-validation and the hold-out method being the most prevalent. The hold-out approach divides the dataset into three subsets: the training set, the validation set, and the test (hold-out) set. The model is trained on the training set, with tuning based on the validation set performance, and ultimately assessed on the test set to determine its generalization capability [50,51]. This method offers a straightforward yet effective mechanism for initial model benchmarking, although its reliance on a single data partition can introduce variance in performance estimates. Conversely, k-fold cross-validation (KCV) partitions the dataset randomly into k equally sized folds. The model is trained on k-1 folds and validated on the remaining fold. This process is repeated k times, ensuring that each data point serves for both training and validation across different iterations [52,53]. KCV reduces variance associated with random splits and provides a robust estimation of model performance. Recent studies emphasize its value in enhancing model reliability, particularly in complex datasets [54]. The unbiased prediction error estimate derived from KCV is one of the reasons for its wide adoption in machine learning workflows [55].

2.6.1. Regression Analysis

Regression analysis is a core supervised learning technique in predictive modeling. It estimates unknown outputs by learning patterns from labeled samples, utilizing weight computations and optimization algorithms. Regression models are extensively applied in domains ranging from financial forecasting to healthcare analytics [56]. Advances in hybrid regression models combining machine learning with statistical methods have further broadened their applicability [57].

2.6.2. Decision Trees, Regression Trees, and Random Forest

Decision trees structure data through recursive binary splits, where each internal node represents a selected feature maximizing separation power at that stage. The tree grows until subsets become homogeneous or meet stopping criteria designed to balance complexity and predictive accuracy. In regression trees, candidate splits are determined by calculating sums of squared errors across all potential splits, selecting the one that minimizes this error. Splitting continues recursively until optimal partitioning is achieved [58]. Random forests aggregate multiple decision trees, enhancing stability and generalization by reducing overfitting typically associated with individual trees [59].

2.6.3. Support Vector Machine (SVM)

Support vector machines (SVM) extend beyond classification to support regression, clustering, anomaly detection, and ranking tasks. The key strength of SVM lies in learning non-linear decision boundaries through kernel-induced feature spaces. The associated optimization problem remains convex, ensuring a unique global solution that is sparse and computationally efficient [53,60]. The choice of kernel function is critical and often determined empirically based on domain-specific knowledge.

2.6.4. Artificial Neural Network (ANN)

Artificial neural networks consist of layered nodes (neurons), where each neuron applies weights to incoming signals and passes the result through an activation function. This structure enables ANNs to model complex, non-linear mappings between inputs and outputs. Modern architectures, including deep neural networks, convolutional and recurrent networks, have demonstrated exceptional performance across vision, language, and time-series applications [61,62].

2.6.5. Gaussian Process Regression (GPR)

Gaussian process regression (GPR) provides a non-parametric Bayesian approach to regression, defining a distribution over possible functions consistent with observed data. At any set of input points, the function outputs follow a joint Gaussian distribution, enabling uncertainty quantification in predictions. The output is modeled as the following equation:

$$y=f\left(x\right)+\mathsf{ϵ}$$

(2)

where f(x) represents the latent function, ϵ is the observation noise. GPR is particularly valuable in small sample settings where uncertainty estimation is critical [51].

2.6.6. Opportunities and Limitations in the Application of Machine Learning

Machine learning is a valuable tool for predicting the physical properties of sustainable biodiesel–diesel–alcohol blends. In this study, SVR, ANN, DTR, and GPR were applied. These methods can model complex and nonlinear relationships in experimental data. They offer good prediction accuracy and flexibility across various data types. GPR also provides uncertainty estimates, which is useful for assessing prediction confidence for calculating physical properties. However, ANN and DTR can over-fit, especially with small datasets. SVR uses kernel to capture nonlinear relationships. But both SVR and GPR require careful tuning of hyper-parameters, which can be time-consuming. Models like ANN and GPR often act as black boxes, making them less interpretable. Despite these limitations, machine learning offers significant benefits for studying sustainable fuel blends.

3. Results and Discussion

3.1. Density Measurement Results of Blends

The obtained density values of the ternary blends using ethanol and propanol are presented in

Table 3. Density (g/cm³) data of ternary blends with ethanol.

Sample Code	10 °C	15 °C	20 °C	25 °C	30 °C	35 °C	40 °C
30D65B5A	0.8622	0.8623	0.8624	0.8606	0.8574	0.8546	0.8522
35D60B5A	0.8598	0.8599	0.8599	0.8575	0.8548	0.8521	0.8498
40D55B5A	0.8594	0.8602	0.8606	0.8580	0.8563	0.8534	0.8503
45D50B5A	0.8561	0.8570	0.8575	0.8567	0.8541	0.8515	0.8500
50D45B5A	0.8530	0.8532	0.8534	0.8515	0.8486	0.8458	0.8433
55D40B5A	0.8501	0.8502	0.8503	0.8481	0.8456	0.8428	0.8404
60D35B5A	0.8479	0.8481	0.8484	0.8464	0.8437	0.8409	0.8383
65D30B5A	0.8449	0.8450	0.8451	0.8433	0.8406	0.8379	0.8358
70D25B5A	0.8469	0.8470	0.8472	0.8462	0.8442	0.8427	0.8412
75D20B5A	0.8410	0.8412	0.8413	0.8394	0.8369	0.8341	0.8319
80D15B5A	0.8388	0.8391	0.8394	0.8375	0.8351	0.8322	0.8298
85D10B5A	0.8375	0.8375	0.8376	0.8353	0.8321	0.8291	0.8273
90D5B5A	0.8351	0.8351	0.8352	0.8324	0.8298	0.8269	0.8249
30D60B10A	0.8587	0.8593	0.8591	0.8576	0.8554	0.8524	0.8504
35D55B10A	0.8570	0.8576	0.8588	0.8559	0.8538	0.8510	0.8491
40D50B10A	0.8532	0.8533	0.8519	0.8488	0.8458	0.8422	0.8430
45D45B10A	0.8512	0.8513	0.8514	0.8481	0.8454	0.8422	0.8402
50D40B10A	0.8497	0.8498	0.8500	0.8469	0.8442	0.8413	0.8392
55D35B10A	0.8463	0.8463	0.8464	0.8434	0.8407	0.8376	0.8356
60D30B10A	0.8442	0.8443	0.8445	0.8418	0.8388	0.8357	0.8340
65D25B10A	0.8419	0.8419	0.8420	0.8393	0.8363	0.8333	0.8314
70D20B10A	0.8409	0.8410	0.8414	0.8390	0.8371	0.8354	0.8338
75D15B10A	0.8391	0.8396	0.8400	0.8379	0.8354	0.8314	0.8311
80D10B10A	0.8347	0.8346	0.8328	0.8296	0.8264	0.8224	0.8228
85D5B10A	0.8326	0.8332	0.8338	0.8325	0.8304	0.8270	0.8259

and

Table 4. Density (g/cm³) data of ternary blends with propanol.

Sample Code	10 °C	15 °C	20 °C	25 °C	30 °C	35 °C	40 °C
30D65B5A	0.8621	0.8622	0.8623	0.8602	0.8574	0.8549	0.8526
35D60B5A	0.8603	0.8603	0.8604	0.8583	0.8557	0.8531	0.8510
40D55B5A	0.8591	0.8597	0.8603	0.8597	0.8574	0.8548	0.8525
45D50B5A	0.8558	0.8564	0.8572	0.8569	0.8549	0.8525	0.8505
50D45B5A	0.8526	0.8527	0.8515	0.8486	0.8460	0.8429	0.8427
55D40B5A	0.8502	0.8503	0.8504	0.8490	0.8463	0.8435	0.8414
60D35B5A	0.8482	0.8484	0.8486	0.8474	0.8448	0.8419	0.8398
65D30B5A	0.8456	0.8456	0.8457	0.8444	0.8417	0.8390	0.8368
70D25B5A	0.8435	0.8436	0.8439	0.8426	0.8398	0.8372	0.8351
75D20B5A	0.8412	0.8412	0.8414	0.8399	0.8372	0.8346	0.8325
80D15B5A	0.8388	0.8389	0.8392	0.8383	0.8356	0.8330	0.8298
85D10B5A	0.8363	0.8364	0.8365	0.8359	0.8332	0.8299	0.8281
90D5B5A	0.8336	0.8337	0.8338	0.8332	0.8307	0.8277	0.8258
30D60B10A	0.8591	0.8597	0.8596	0.8600	0.8579	0.8543	0.8527
35D55B10A	0.8558	0.8563	0.8568	0.8571	0.8551	0.8517	0.8505
40D50B10A	0.8545	0.8546	0.8536	0.8526	0.8497	0.8466	0.8445
45D45B10A	0.8498	0.8498	0.8499	0.8494	0.8470	0.8436	0.8419
50D40B10A	0.8479	0.8481	0.8482	0.8479	0.8454	0.8419	0.8400
55D35B10A	0.8455	0.8455	0.8464	0.8434	0.8407	0.8376	0.8356
60D30B10A	0.8442	0.8443	0.8445	0.8418	0.8388	0.8357	0.8340
65D25B10A	0.8407	0.8408	0.8409	0.8400	0.8377	0.8347	0.8334
70D20B10A	0.8391	0.8392	0.8394	0.8390	0.8364	0.8334	0.8314
75D15B10A	0.8370	0.8375	0.8375	0.8351	0.8327	0.8289	0.8272
80D10B10A	0.8365	0.8365	0.8365	0.8329	0.8290	0.8256	0.8263
85D5B10A	0.8330	0.8332	0.8333	0.8310	0.8287	0.8252	0.8233

in units of g/cm³.

In all samples, the density values exhibited a consistent decline as temperature increased. This outcome is anticipated, as elevated temperatures cause the fuel mixture to expand, leading to a reduction in mass per unit volume. For instance, in the case of the 30D65B5A blend (an ethanol-containing mixture), the density decreased from 0.8622 g/cm³ at 10 °C to 0.8522 g/cm³ at 40 °C. Additionally, increasing the alcohol content in the blend (e.g., from 5% to 10%) resulted in a clear reduction in density at all tested temperatures. This trend can be explained by the lower intrinsic density of alcohols compared to diesel and biodiesel. Similarly, blends with a higher diesel content (such as the transition from 30D65B5A to 90D5B5A) showed a tendency toward lower density values, since diesel possesses a lower density than biodiesel. At a constant temperature and alcohol concentration, an increase in the biodiesel proportion contributed to higher density values. For example, at 25 °C, a blend containing 30% diesel and 65% biodiesel (30D65B5A) had a higher density compared to a blend containing 90% diesel and 5% biodiesel (90D5B5A) at the same temperature. When comparing blends containing ethanol and propanol, it was found that the type of alcohol had a negligible effect on the density of the mixtures.

3.2. Viscosity Measurement Results of Blends

The obtained viscosity values of the ternary blends using ethanol and propanol are presented in

Table 5. Viscosity (cP) data of ternary blends with ethanol and propanol.

	Ethanol			Propanol
Sample Code	10 °C	25 °C	40 °C	10 °C	25 °C	40 °C
30D65B5A	8.5	8.6	7.2	7.4	8.6	6.2
35D60B5A	8.1	8.3	7.5	7.1	8.3	6.1
40D55B5A	7.8	8.0	6.8	7.3	7.7	6.1
45D50B5A	7.3	7.8	7.1	7.1	7.3	5.7
50D45B5A	7.4	6.7	6.7	6.9	7.3	5.7
55D40B5A	7.3	7.5	6.6	6.8	7.1	5.9
60D35B5A	7.1	7.6	6.5	6.3	7.2	5.9
65D30B5A	7.1	7.2	6.3	6.6	6.8	5.9
70D25B5A	7.0	6.9	6.2	6.5	6.5	5.3
75D20B5A	6.9	6.8	6.1	6.4	6.2	5.3
80D15B5A	6.7	7.0	5.6	6.4	6.2	5.3
85D10B5A	6.7	6.7	5.6	6.3	6.3	5.0
90D5B5A	6.6	6.6	5.9	6.2	6.0	5.1
30D60B10A	7.1	7.2	6.0	7.0	6.7	5.7
35D55B10A	6.4	7.0	6.2	6.7	6.6	5.7
40D50B10A	6.1	6.8	5.8	6.6	6.4	5.4
45D45B10A	6.9	6.7	5.7	6.6	6.2	5.3
50D40B10A	6.7	6.6	5.5	6.5	6.2	5.6
55D35B10A	6.4	6.5	5.9	6.4	6.2	5.2
60D30B10A	6.4	6.4	5.5	6.3	6.2	5.4
65D25B10A	6.5	6.4	5.5	6.5	6.0	5.2
70D20B10A	6.3	6.3	5.3	6.4	6.0	5.2
75D15B10A	6.2	6.3	5.2	6.1	5.7	5.1
80D10B10A	6.3	6.0	5.2	6.2	5.9	5.2
85D5B10A	5.7	5.9	4.9	6.2	5.8	5.0

in units of cP.

In all tested blends, viscosity showed a clear decreasing trend with increasing temperature. This phenomenon can be explained by the reduction in intermolecular forces and the enhanced molecular mobility as the temperature rises. For instance, the viscosity of the 30D65B5A blend containing ethanol decreased from 8.5 mPa·s at 10 °C to 7.2 mPa·s at 40 °C. Similarly, for the 30D65B5A blend containing propanol, the viscosity declined from 7.4 mPa·s to 6.2 mPa·s over the same temperature range. Blends with a higher biodiesel content exhibited higher viscosity at a constant temperature and alcohol concentration. This is attributed to the long-chain methyl ester structure of biodiesel, which contributes to greater internal friction. For example, at 25 °C, the 30D65B5A blend with 65% biodiesel demonstrated higher viscosity compared to blends with lower biodiesel proportions. In contrast, increasing the diesel and alcohol content resulted in lower viscosity, which is consistent with the lower viscosity values of diesel and alcohol compared to biodiesel. Both ethanol and propanol were effective in reducing the viscosity of the blends. However, in certain cases, the blends containing propanol showed slightly lower viscosity than their ethanol-containing counterparts. This difference may be due to the molecular chain length of propanol and its interactions within the diesel–biodiesel matrix.

3.3. Cetane Number Analysis Results of Blends

The experimental findings indicate a clear relationship between the biodiesel content in the ternary fuel blends and their cetane number values. As the proportion of biodiesel in the blends decreased, a corresponding reduction in cetane number was observed. This trend is consistent across the various fuel formulations tested. Of all the samples, the highest cetane number recorded was 54.5, while the lowest was measured at 52.1. These results highlight the positive contribution of biodiesel to enhancing the ignition quality of the blends, given biodiesel’s inherently higher cetane rating compared to the diesel and alcohol components. Moreover, the cetane number results confirm that blends with higher diesel and alcohol contents tend to exhibit reduced cetane numbers, further demonstrating the role of biodiesel in supporting favorable combustion characteristics. Overall, the study underscores the significance of optimizing biodiesel content within ternary fuel mixtures to achieve the desired ignition performance in diesel engines.

3.4. Validation of Experimental Behavior and Fuel Blend Characteristics

The experimental findings exhibited a high degree of consistency with trends reported in the literature, offering valuable insights for the formulation of alternative fuel blends and their potential application in engine systems. As the temperature increased, the density of all blends consistently decreased, a trend that aligns with previous studies highlighting the inverse relationship between temperature and density in biodiesel–diesel mixtures [33]. Increasing the alcohol content (ethanol/propanol) led to a reduction in blend density, which corresponds to the lower intrinsic densities of alcohols and is consistent with earlier reports [63]. While a higher diesel ratio decreased the density, an increase in biodiesel proportion resulted in higher density values. This observation supports the established understanding that diesel has a lower density compared to biodiesel, which possesses a higher density due to its methyl ester structure [33]. The type of alcohol (ethanol or propanol) did not cause a significant difference in density at low concentrations (5–10% by volume), in agreement with findings from [63,64]. Furthermore, the results are consistent with the literature emphasizing that fuel density influences spray characteristics and combustion performance, aspects that must be considered in engine design [65]. The study also suggests that increasing the biodiesel content may enhance density and potentially improve spray quality [66].

In terms of viscosity, all blends showed a significant reduction as temperature increased. This finding aligns with established knowledge that the fluidity of liquids improves at higher temperatures, leading to lower viscosity values [67]. The increase in alcohol content reduced the blend viscosity, a result attributed to the low viscosity of alcohols and their dilution effect, as supported by previous studies [63,64]. A higher diesel ratio contributed to lower viscosity, while increasing the biodiesel proportion led to higher viscosity values, in line with reports that diesel has a lower viscosity; and biodiesel, owing to its methyl ester content, exhibits higher viscosity [33]. Regarding alcohol type, in certain cases, blends containing propanol exhibited slightly lower viscosities than those with ethanol at lower temperatures, a difference that could be linked to variations in molecular structure and blend behavior, consistent with observations highlighted in the literature [63].

3.5. Machine Learning Studies of Blends

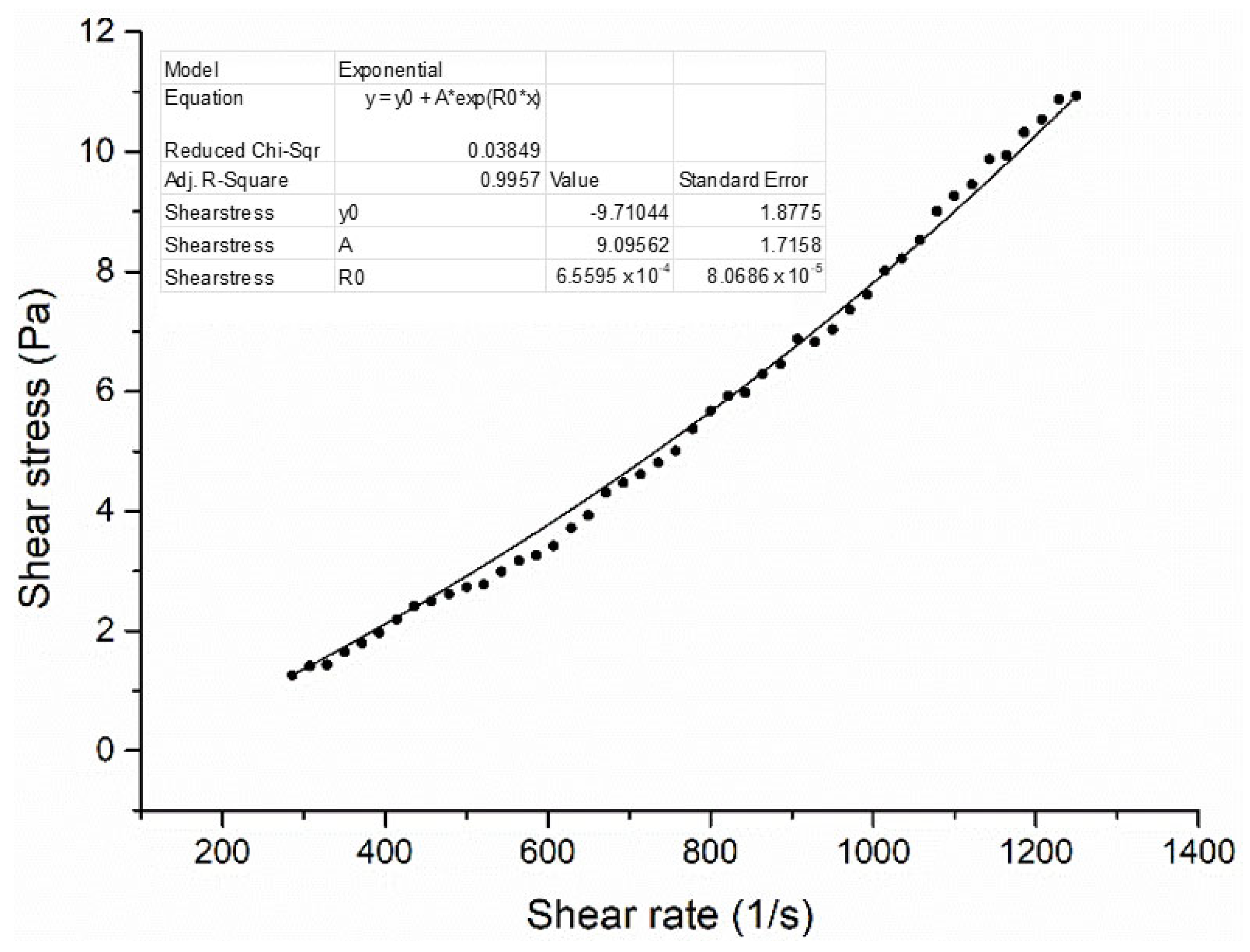
The density and viscosity data obtained from the experimental study were analyzed using machine learning techniques in Regression Learner, a toolbox of MATLAB R2024a. In this process, the dataset is partitioned into 85% training and 15% testing subsets using holdout validation. Subsequently, cross-validation combined with hyperparameter optimization is employed to enhance the reliability and generalizability of the predictive outcomes. Various statistical indicators and graphical outputs were generated during the regression analysis, enabling a comprehensive evaluation of model performance and predictive capability.

3.5.1. Machine Learning Modeling for Viscosity

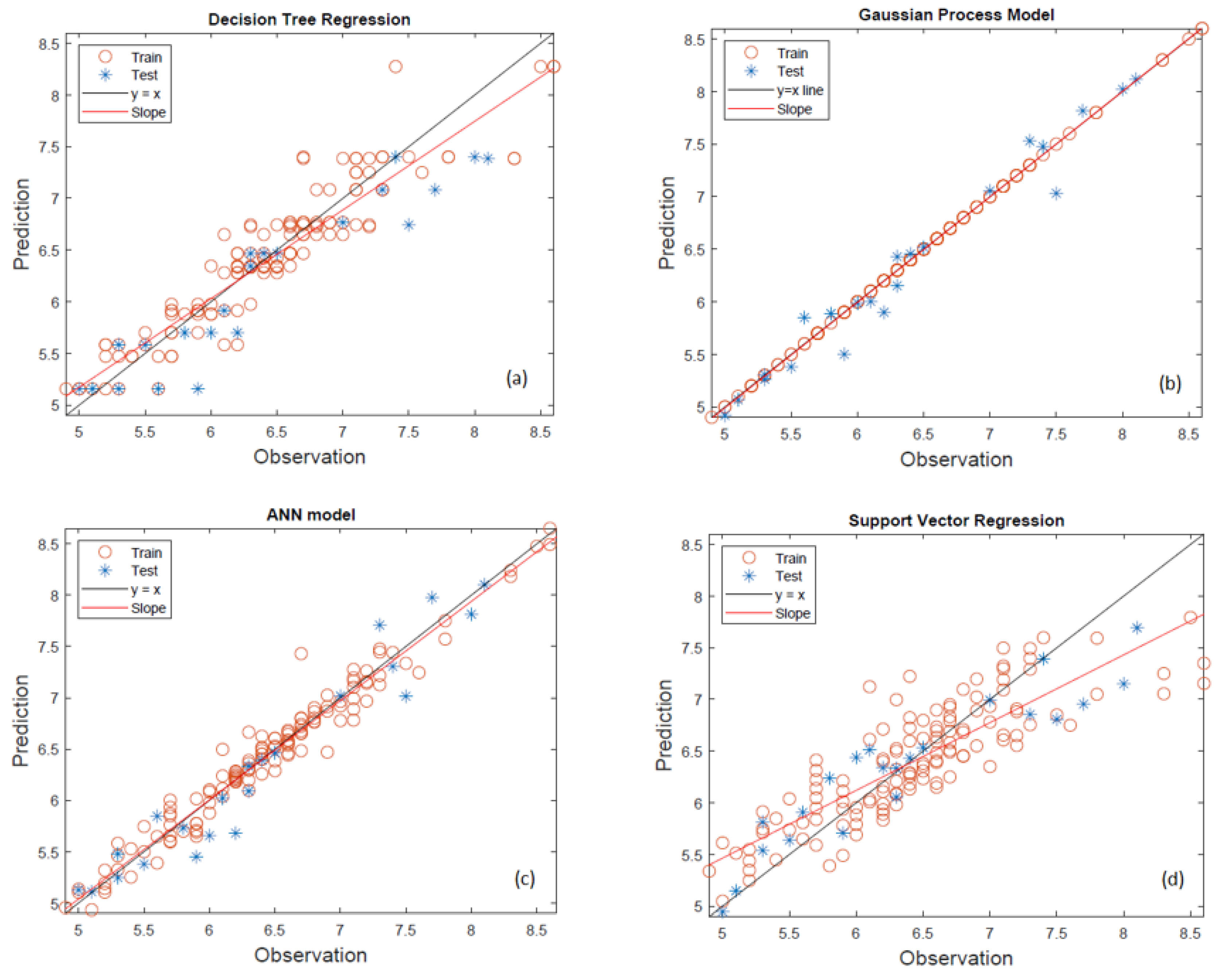
In the machine learning study conducted for viscosity, the viscosity values of 50 fuel blends measured at three different temperatures were modeled. The performances of the decision tree regression (DTR), Gaussian process regression (GPR), artificial neural network (ANN) and support vector regression (SVR) models for predicting the viscosity of the studied blends were evaluated through a comparison of predicted and observed values, as illustrated in Figure 2 for the machine learning models.

In the DTR model given in Figure 2a, the model demonstrates relatively poor generalization capacity, especially in the mid-to-high viscosity range. Although the training data show a clustering along the diagonal, the test data are scattered and deviate noticeably from the ideal line. This inconsistency is particularly pronounced for viscosities above 7.0 cP, where the model tends to underestimate the values. The slope of the regression line differs significantly from the unity line, indicating a lack of predictive robustness. The performance suggests that DTR may be prone to over-fitting, capturing local variations within the training set but failing to extrapolate effectively to unseen cases.

The Gaussian process regression (GPR) model given in Figure 2b displays the most accurate and consistent predictions across the full viscosity range (5.0–8.5 cP). Both training and testing data points align very closely with the y = x line, and the slope of the regression line is nearly identical to the ideal. This reflects strong agreement between predicted and observed values and highlights the model’s ability to handle both linear and non-linear relationships effectively. The GPR model’s probabilistic framework and ability to provide smooth, continuous predictions make it particularly well-suited for modeling the relatively narrow yet nonlinear viscosity interval in this study. As shown in Figure 2c, the ANN model also performs well, capturing the general trend of the viscosity data across both training and testing sets. The predictions are reasonably close to the ideal line, though slight deviations are observed, especially in the lower and upper ends of the viscosity range. While the model tends to slightly underestimate some high-viscosity values, the regression slope remains close to unity, suggesting overall reliability. These results indicate that the ANN model effectively learns the underlying patterns in the dataset, although its performance could potentially be further improved with additional optimization or regularization. The support vector regression model given in Figure 2d exhibits the weakest performance across the studied viscosity interval. The predicted values, particularly for the testing dataset, are widely dispersed and fail to align with the observed values. The regression line deviates substantially from the y = x line, indicating a consistent bias in the model’s predictions. SVR struggles particularly in capturing the non-linear variation in the mid-to-high viscosity range (6.5–8.5 cP), which may be due to limitations in kernel selection or insufficient tuning of the model parameters. Four machine learning models (DTR, GPR, SVR, and ANN) were evaluated for their ability to predict viscosity based on the available dataset. The performance metrics, including coefficient of determination (R²), adjusted R² (adjR²), root mean square error (RMSE), normalized RMSE (NRMSE), and average absolute error (AAE), are summarized in

Table 6. Performance metrics of the machine learning models applied for viscosity prediction.

	R2	adjR2	RMSE	NRMSE	AAE
DTR	0.8297	0.7764	0.38307	0.05646	0.04444
GPR	0.9636	0.9522	0.17709	0.02745	0.01968
SVR	0.8294	0.7761	0.38337	0.05617	0.04434
ANN	0.9315	0.9101	0.24286	0.03767	0.02819

.

The GPR model consistently outperforms all others, achieving the highest R² value (0.9636), lowest RMSE (0.17709), and lowest AAE (0.01968), confirming its ability to pro-duce highly accurate and reliable predictions across the full viscosity range. The ANN model also performs well, with an R² of 0.9315 and a relatively low RMSE (0.24286), demonstrating that it is capable of capturing non-linear relationships in the data while maintaining good generalization.

By contrast, the DTR and SVR models yield almost identical performance metrics (R² ≈ 0.83, RMSE ≈ 0.38, AAE ≈ 0.044), suggesting limited capability in accurately modeling viscosity behavior. Both models tend to show larger deviations from actual values, particularly in the mid-to-high viscosity region (6.5–8.5 cP), which is critical in fuel performance applications. The relatively high normalized RMSE values (≈0.056) further indicate that both DTR and SVR may be sensitive to outliers or insufficiently tuned to the dataset’s complexity.

When combining both statistical metrics and visual insights, Gaussian process regression (GPR) emerges as the most effective model for predicting viscosity in the range of 5.0–8.5 cP. Its superior accuracy, low error margins, and strong generalization across unseen data make it highly suitable for modeling complex physicochemical properties. The artificial neural network (ANN) model also shows strong performance and may be considered a practical alternative when computational efficiency or data scaling flexibility is desired.

In contrast, decision tree regression and support vector regression, while producing moderately acceptable results, fall short in predictive precision and should be used with caution or after further optimization. These findings emphasize the importance of selecting machine learning algorithms not only based on training accuracy but also on their ability to generalize across critical operational ranges; a key requirement in material property prediction and process modeling.

In summary, the findings of this study highlight the importance of choosing machine learning algorithms that are appropriate for the structure of the dataset and the complexity of the target variable. In applications where precise viscosity prediction is required, for example, for fuel formulation and engineering design, the Gaussian process regression model demonstrated the most consistent and effective performance.

3.5.2. Machine Learning Modeling for Density

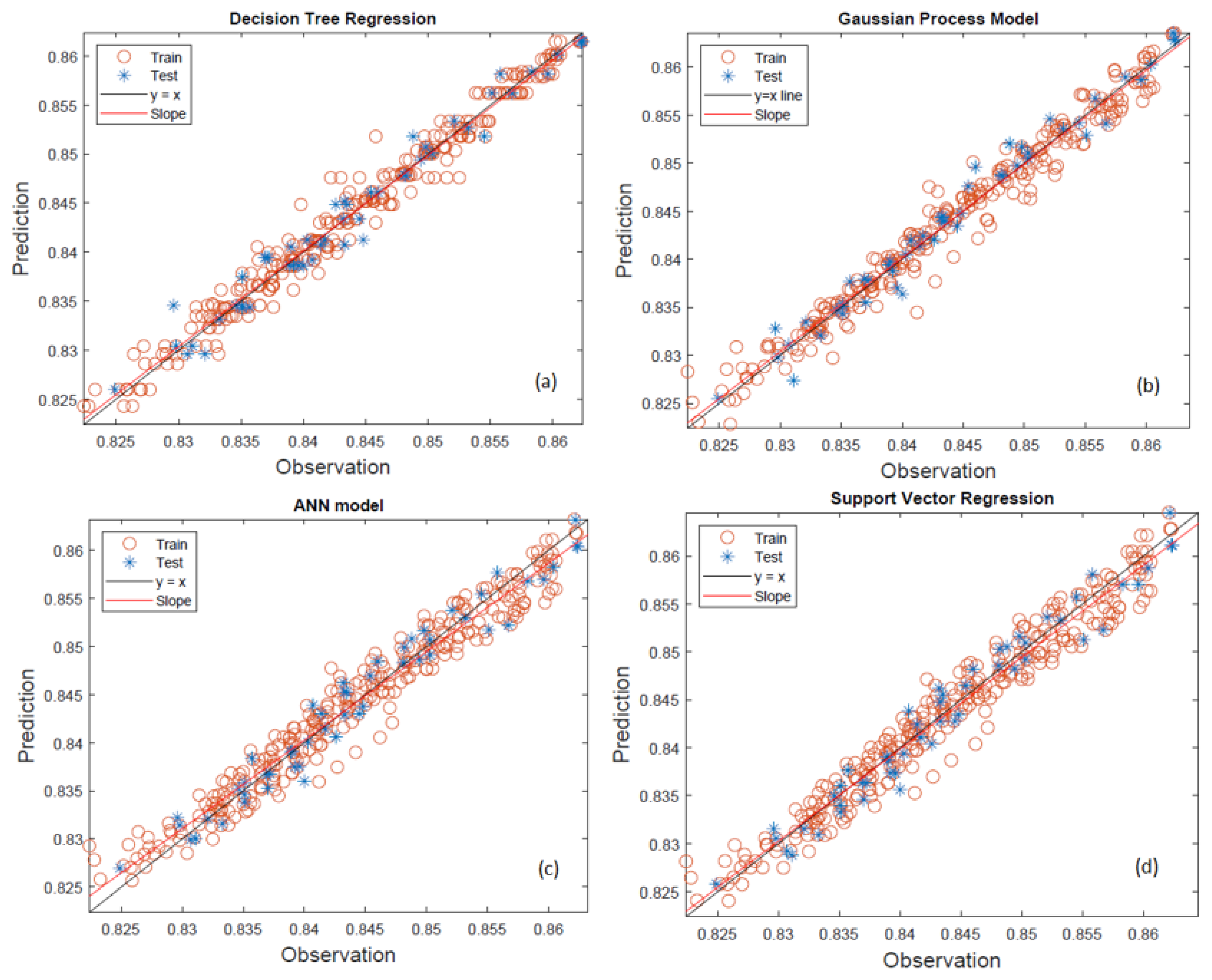
In the machine learning study conducted for viscosity, the viscosity values of 50 fuel blends measured at seven different temperatures (10 °C to 40 °C) were modeled. The same machine learning models (DTR, GPR, ANN, SVR) were applied to predict the density values of the studied blends, as illustrated in Figure 3 for the machine learning models.

The decision tree regression model shows a moderate predictive performance, with noticeable scatter around the ideal line of equality (y = x), especially among the training data in Figure 3a. The red circles (training) tend to deviate more than the blue stars (test), suggesting that the model may be overfitting specific patterns in the training set rather than learning the underlying relationship. While many data points lie close to the reference line, a systematic underestimation and overestimation can be seen at both lower (<0.835 g/cm³) and upper (>0.855 g/cm³) ends of the density spectrum. The fitted slope line deviates slightly from the ideal 45° line, indicating that the regression is not capturing the trend perfectly across the entire range. Additionally, there is a lack of homogeneity of variance, as the variance of the residuals seems to change across the density values, lower density predictions are more accurate, while higher densities show increasing deviation. This non-uniform spread may stem from the model’s inability to capture complex nonlinear relationships due to its inherently piecewise-constant structure. In the context of fuel property modeling, where small deviations can impact formulation decisions, this limitation reduces DTR’s reliability. DTR is interpretable and easy to implement, but in this study, it displays insufficient generalization capability, potentially due to the narrow range and high precision required for density predictions. Its performance suggests it may be better suited as a benchmarking or supplementary model rather than a primary predictor in such regression tasks. Gaussian process regression demonstrates the most accurate and reliable performance of the four models shown in Figure 3b. Both training and test data points show a tight clustering along the y = x line, with very few deviations. The blue test stars closely follow the distribution of the training points, which indicates excellent model generalization and robustness to unseen data. The slope line overlaps almost perfectly with the identity line, reflecting near-ideal regression behavior with negligible bias. The spread of data points is also homogeneous across the entire observed range (0.8250–0.8600 g/cm³), meaning that the model performs consistently regardless of the density value. This uniformity is particularly important in precision-sensitive applications like fuel blending, where a 0.001 g/cm³ deviation could lead to real-world performance issues. GPR’s Bayesian non-parametric nature allows it to model complex, nonlinear dependencies while providing predictive uncertainty, which makes it highly advantageous in experimental modeling. GPR provides superior predictive accuracy, minimal residual error, and consistent behavior across all data segments. It is the most suitable model for high-resolution regression problems like predicting the density of ternary fuel blends in this study. The artificial neural network model also shows strong predictive capability, closely rivaling GPR in visual alignment between predictions and actual observations in Figure 3c. The training data and test data exhibit minimal spread and follow the y = x reference line closely. However, compared to GPR, a slightly higher dispersion is observed, especially at the boundaries of the density range (near 0.8250 and 0.8600 g/cm³). This suggests that while the model learns general trends well, it may struggle slightly in edge cases or regions with sparse data representation. ANN is known for its ability to model complex nonlinear relationships, and this is reflected in its close-fitting slope line. However, the variability in prediction accuracy across the density range indicates that additional hyperparameter tuning (e.g., learning rate, hidden layers) or data preprocessing might further enhance performance. There is also a possibility that the training dataset, though narrow in density range, has a non-uniform sample distribution, which could affect ANN’s interpolation ability. The ANN model performs robustly with high correlation to observed data, but small improvements are needed for edge case precision. It is a strong candidate for primary modeling, especially when paired with careful optimization and regularization techniques. Support vector regression presents a reasonably good fit to the data but with noticeably more scatter compared to the GPR and ANN models in Figure 3d. The training points show alignment with the y = x line but with wider variance, particularly in the mid-to-upper range of the density spectrum (e.g., 0.845–0.855 g/cm³). The test data follow the general trend but include several outliers, indicating that the model may be sensitive to the kernel choice or hyperparameter settings like the regularization parameter (C) and epsilon (ε) tube. Although the slope line lies close to the ideal 45° reference, the asymmetrical spread suggests that the model exhibits bias in certain subregions, possibly due to an underfitting effect in localized areas. This may be due to the margin-based learning mechanism in SVR, which prioritizes fitting within a defined tolerance rather than minimizing absolute errors. SVR captures the overall relationship but with less precision and greater variability, especially under limited or unevenly distributed datasets. Its performance in this study indicates that parameter optimization is essential for SVR to be competitive with ANN and GPR in density prediction tasks. Four machine learning models (DTR, GPR, SVR, and ANN) were applied to predict density within the studied formulation intervals (0.825–0.86 g/cm³). The key performance metrics, including the coefficient of determination (R²), adjusted R² (adjR²), root mean square error (RMSE), normalized RMSE (NRMSE), and average absolute error (AAE), are summarized in

Table 7. Performance metrics of machine learning models applied for density prediction.

	R2	adjR2	RMSE	NRMSE	AAE
DTR	0.9718	0.9688	0.00158	0.00189	0.00144
GPR	0.9743	0.9716	0.00151	0.00180	0.00132
SVR	0.9609	0.9567	0.00187	0.00221	0.00189
ANN	0.9628	0.9588	0.00182	0.00216	0.00179

.

In examining the plots, all models display a strong linear correlation between predicted and observed density values, with predictions clustering around the ideal y = x reference line. However, this apparent uniformity masks subtle deviations in alignment and distribution that become more evident when contrasted with the numerical metrics in Table 7. For instance, the model showing the most visually coherent clustering and minimal scatter, particularly in the central region of the density range, is the one that also scores the highest across all metrics: Gaussian process regression (GPR), with an R² of 0.9743, RMSE of 0.00151, and AAE of 0.00132. These values reflect not only a high degree of fit but also an exceptionally low prediction error, which is visually supported by the minimal deviation of both training and test data from the ideal prediction line.

Yet, the 0.0025 difference in R² between GPR and the second-best model decision tree regression (DTR), which achieved an R² of 0.9718, RMSE of 0.00158, and AAE of 0.00144, is not trivial within such a constrained density range. While DTR’s metrics suggest near-identical predictive performance, the scatter plot tells a slightly different story: data points, particularly in the test set, show visibly more variance and drift from the ideal line, especially at the upper and lower ends of the density spectrum. This inconsistency suggests that although DTR can approximate global trends effectively, its segmented, hierarchical structure may limit its local smoothness, resulting in slight overfitting to the training data patterns and reduced generalization outside high-density clusters.

Similarly, artificial neural networks (ANN) and support vector regression (SVR) yield slightly lower performance metrics (R² values of 0.9628 and 0.9609, respectively), which correspond closely to what is observed in the parity plots: both models produce predictions aligned with the target trend but exhibit more pronounced dispersion around the y = x line, especially under conditions where data density is low. While their RMSE and AAE values (ANN: 0.00182 and 0.00179; SVR: 0.00187 and 0.00189) remain within an acceptable range for practical modeling, the greater spread of residuals in both models hints at less precise calibration to the subtle nonlinearity of the dataset. In summary, the integration of graphical and statistical evaluations confirms that GPR stands out as the most robust and precise modeling approach for density prediction in this study, while the overall model performances emphasize the critical role of both algorithm selection and data structure in high-resolution regression tasks.

Table 8. Ternary blends preparation and modelling studies.

Ternary Blends	Parameters	Model Type	Data Size	Model Accuracy	Ref.
Canola biodiesel + diesel (20% BD) + isopropanol (2–20%)	Density (15 °C), Viscosity (40 °C)	Linear and exponential regression	~8 samples	R2 ≈ 1, error not specified	[46]
Biodiesel + diesel + ethanol or n-Butanol (0–40%)	Viscosity (40 °C, various alcohol ratios)	Grunberg–Nissan correlation	Dozens	No numerical error; good model agreement	[47]
Five biodiesel types (inc. mustard biodiesel) + diesel (45–92%) + ethanol (3–15%)	Density (15 °C), viscosity (40 °C)	Parametric regression (Kay, Grunberg–Nissan, etc.)	~30 blends × 2 temps ≈ 60 samples	MAPE: density 0.05%; viscosity 1.4–3.5%	[6]
Various biodiesels (inc. Canola biodiesel) + diesel + ethanol/methanol (34 systems)	Density and viscosity (–10 °C to 200 °C)	Artificial neural network (ANN)	1025 training, 238 test samples	R2 (test): density 0.998; Viscosity 0.965	[48]
Canola biodiesel) + diesel + ethanol/propanol	Density and viscosity (10 °C to 40 °C)	DTR, GPR, ANN, SVR	50 blends × 2 = 100 samples	R2 (test): density 0.974; viscosity 0.963 for GPR	This study

presents a comparative overview of existing research focused on ternary bio-diesel blends and their modeling approaches. When analyzed in relation to the presented literature, the current study demonstrates several distinguishing strengths in both methodological scope and predictive performance. First, while prior works have often focused on limited blend compositions such as single biodiesel–diesel–alcohol ratios or specific temperature points, this study investigates a broader matrix of 50 ternary blends, encompassing varied biodiesel concentrations and alcohol types (ethanol and propanol) across a temperature range of 10 °C to 40 °C. This provides a richer dataset and allows for more generalizable conclusions regarding fluid properties under operationally relevant conditions. Second, in contrast to earlier studies where the sample size ranged from 8 to approximately 60, the present study incorporates 100 samples (2 × 50 measurements for density and viscosity), thus enhancing the statistical robustness of the machine learning models employed. Furthermore, regarding modeling accuracy, the current study achieves R² values of 0.974 for density and 0.963 for viscosity using GPR, outperforming or matching the performance metrics reported in other studies. For example, the study using artificial neural networks with over 1000 samples reported high accuracy (R² = 0.998), but it does not simultaneously model both density and viscosity within a ternary fuel system context, nor does it explore blend-level variations as comprehensively. On the other hand, the present work adopts a multi-model comparative approach (DTR, GPR, SVR, ANN), offering insights into the relative performance and generalization ability of different algorithms, in contrast to most previous works that utilized only a single model type, limiting comparative interpretability. Finally, the comprehensive blend coverage, balanced dataset size, dual-property modeling (density and viscosity), and superior predictive performance position this study as a significant contribution to the field of biodiesel blend optimization and machine learning-based property estimation.

4. Conclusions

This study comprehensively evaluated the predictive performance of four machine learning models (DTR, GPR, SVR and ANN) for the estimation of viscosity and density in complex formulation systems. The results clearly demonstrated that model choice has a substantial impact on predictive accuracy, depending on the property being modeled.

A key insight from this work is that GPR offers not only the highest accuracy but also robustness across different target properties, confirming its potential as a preferred approach in the prediction of material properties in engineering and formulation sciences. The conclusions drawn here suggest several directions for future work. First, expanding the dataset to cover a broader formulation space and wider property ranges could further validate model generalizability. Second, ensemble techniques (e.g., random forest, gradient boosting, or stacked models combining GPR and SVR) could be explored to enhance predictive performance while balancing accuracy, interpretability, and computational cost. Finally, incorporating uncertainty quantification (as naturally enabled by GPR) could provide valuable insights for risk-aware decision-making in formulation and process design. In addition, these findings pave the way for the development of cleaner, more efficient alternative fuels, supporting global efforts toward sustainable energy solutions. Future research directions include the use of spectrophotometric analyses for the detailed characterization of fuel properties, as well as experimental investigations into the engine performance of fuel blends. The findings of the present study provide a foundation for these prospective areas of investigation.