Modeling and Optimization of Natural Gas Non-Catalytic Partial Oxidation with Hierarchical-Integrated Mechanism
Abstract
1. Introduction
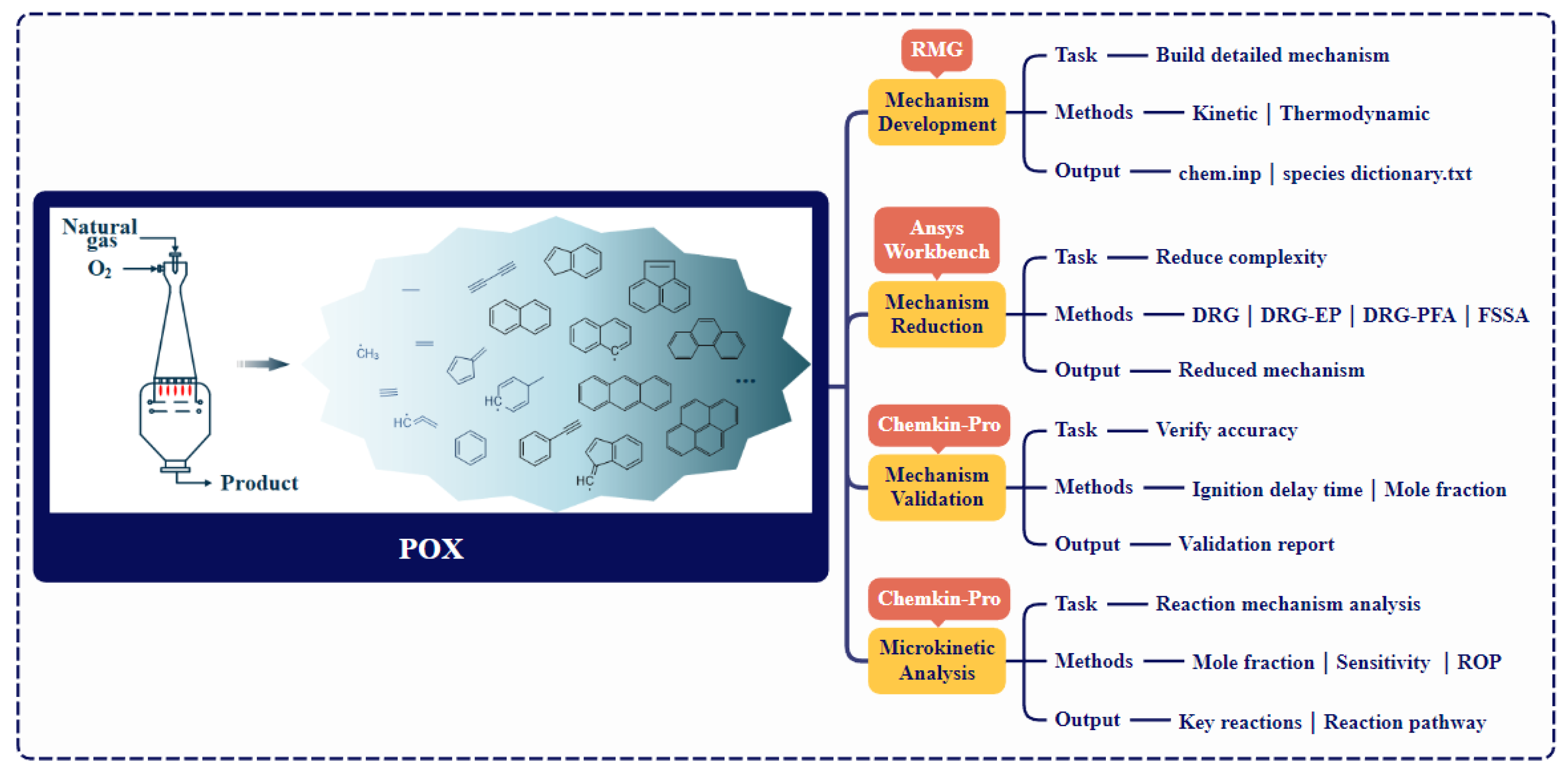
2. Computational Details
2.1. Reactor System and Process Parameters
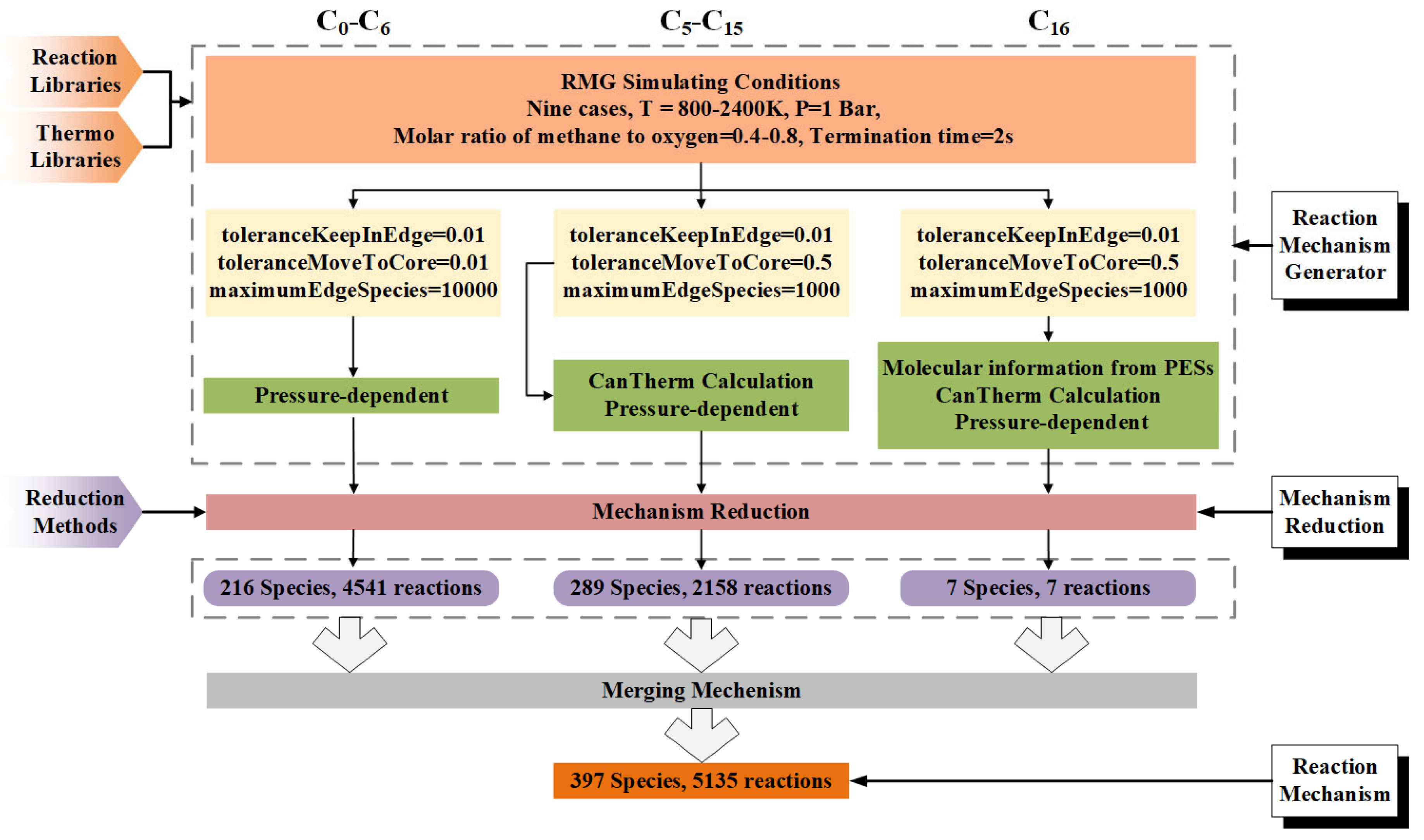
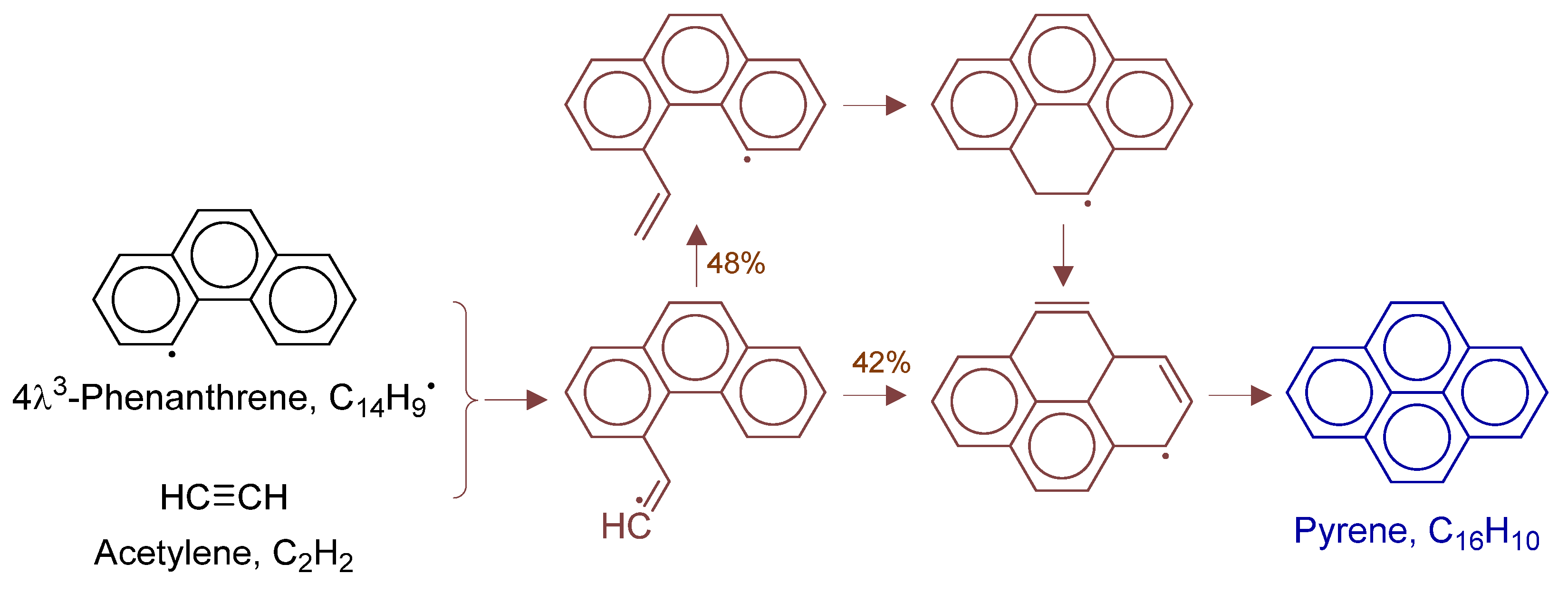
2.2. Development of HI-Mechanism
2.2.1. Kinetic Parameter Database Development
2.2.2. Thermodynamic Parameter Database Development
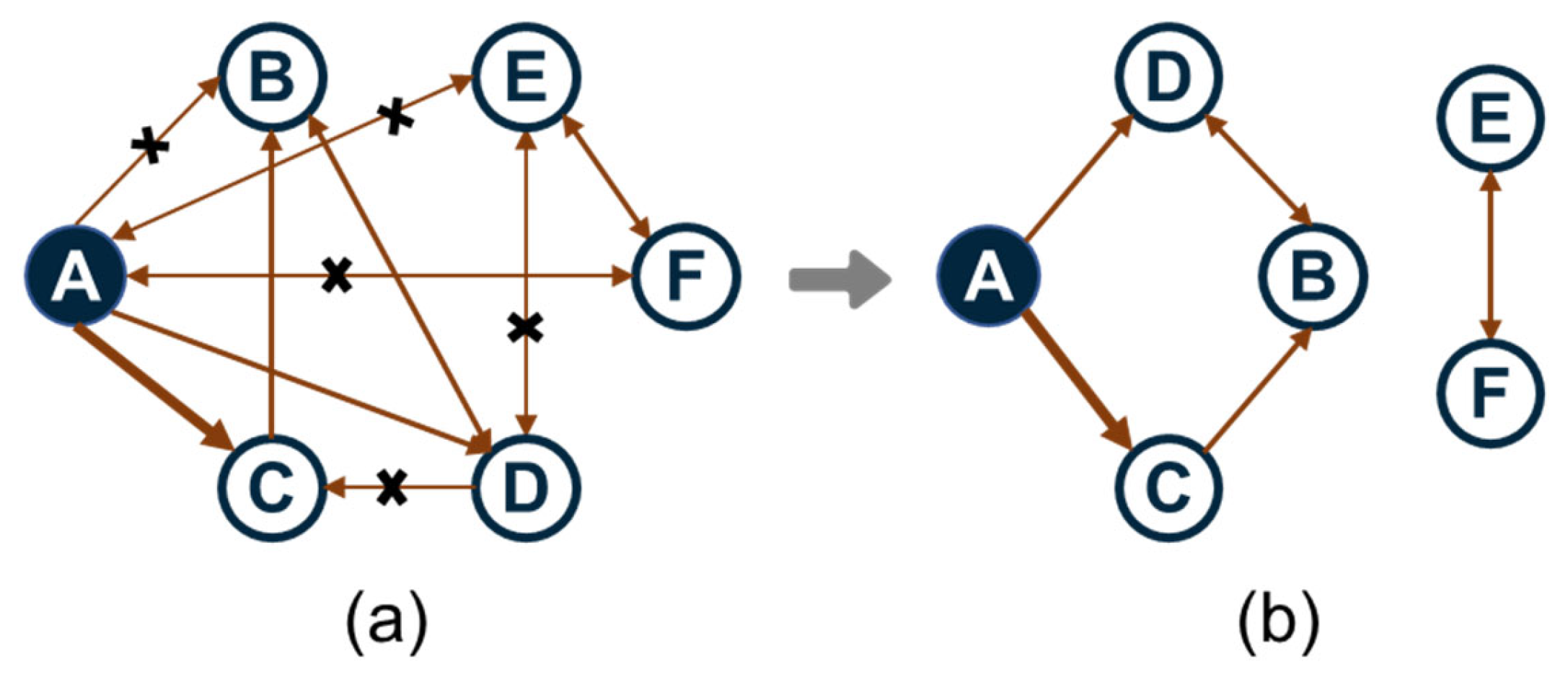
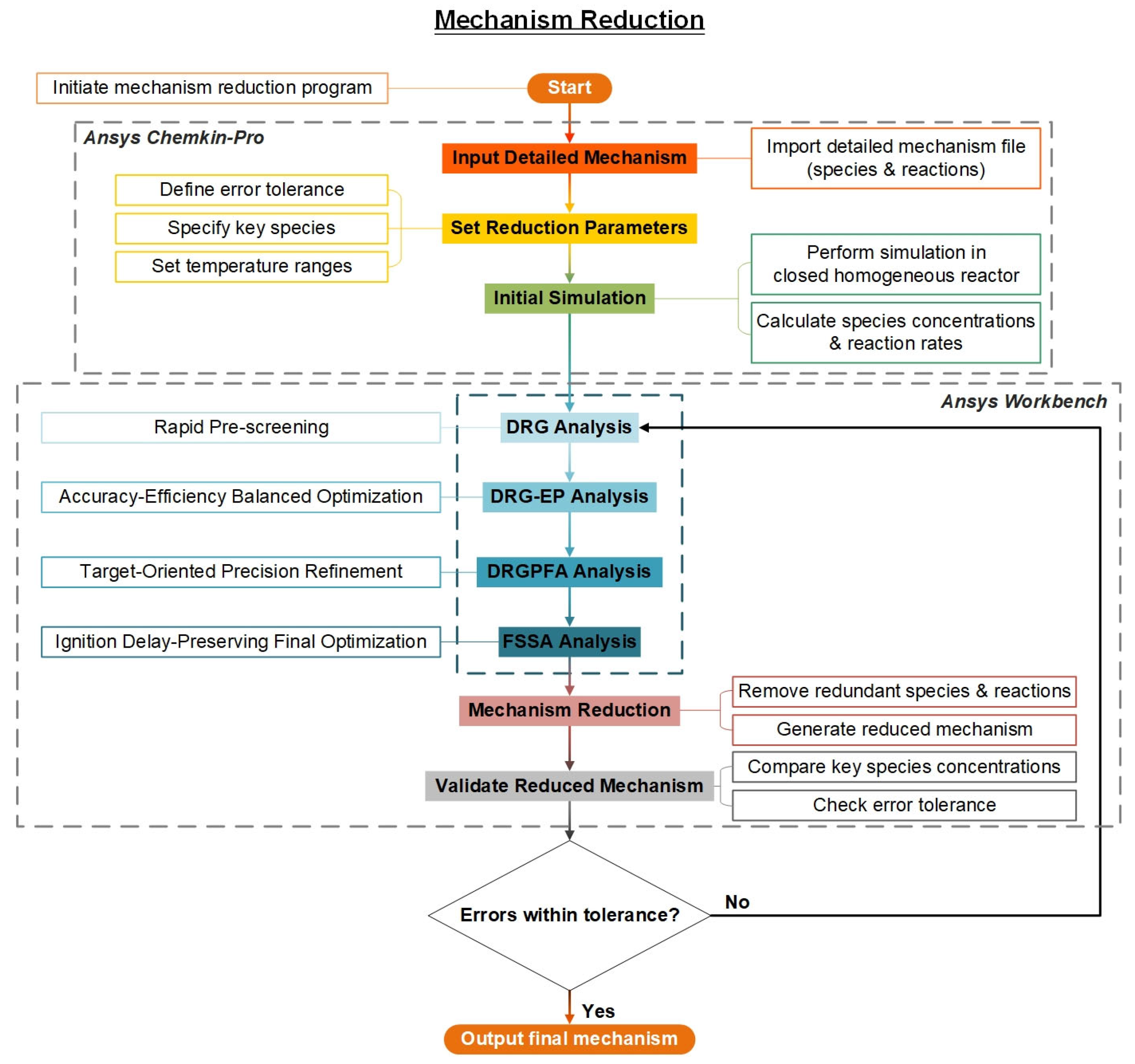
2.3. Target-Oriented Mechanism Reduction
3. Mechanism Validation and Microkinetic Analysis Methods
3.1. Ignition Delay Time
3.2. Key Component Concentrations
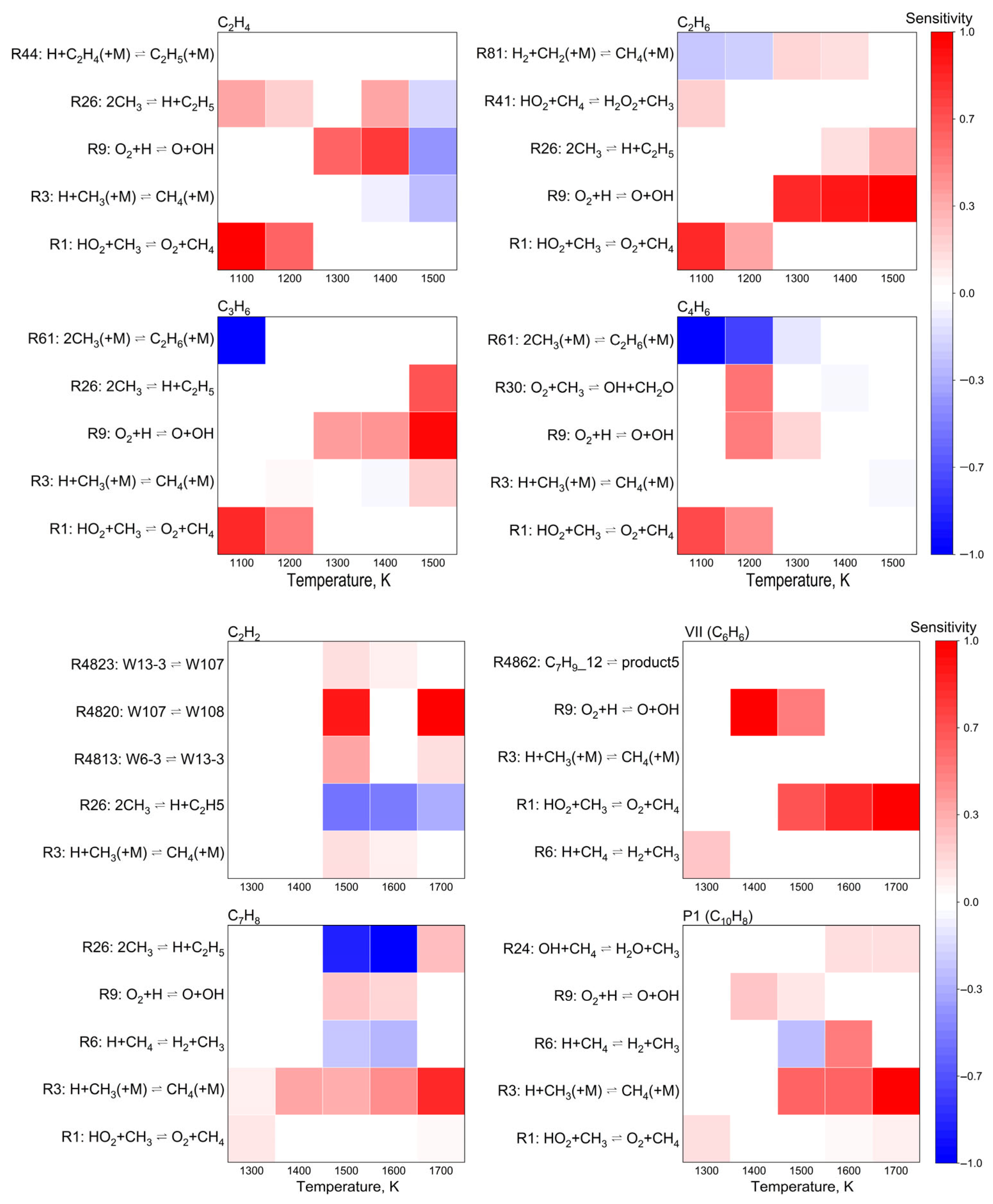
3.3. Sensitivity Analysis
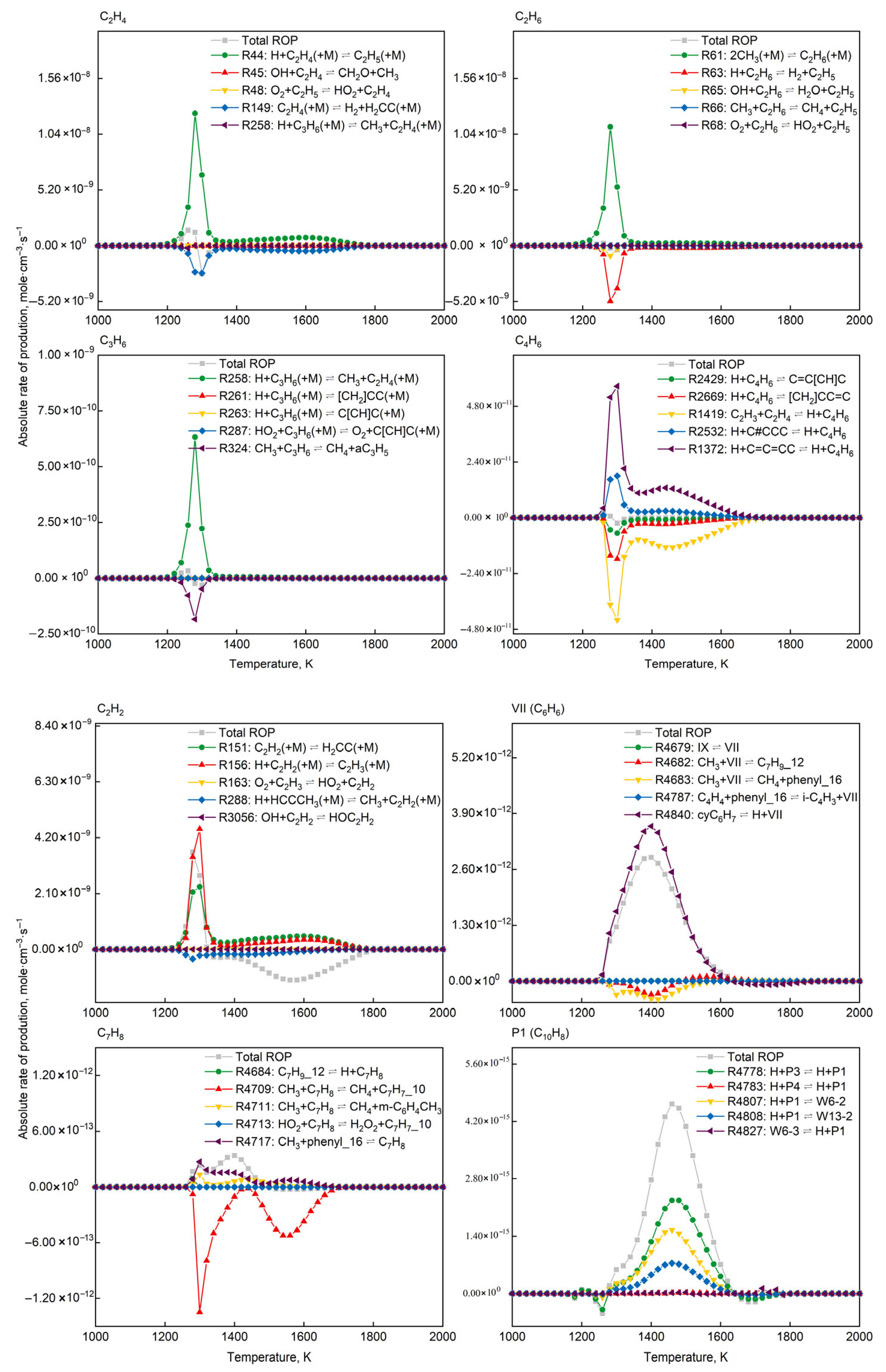
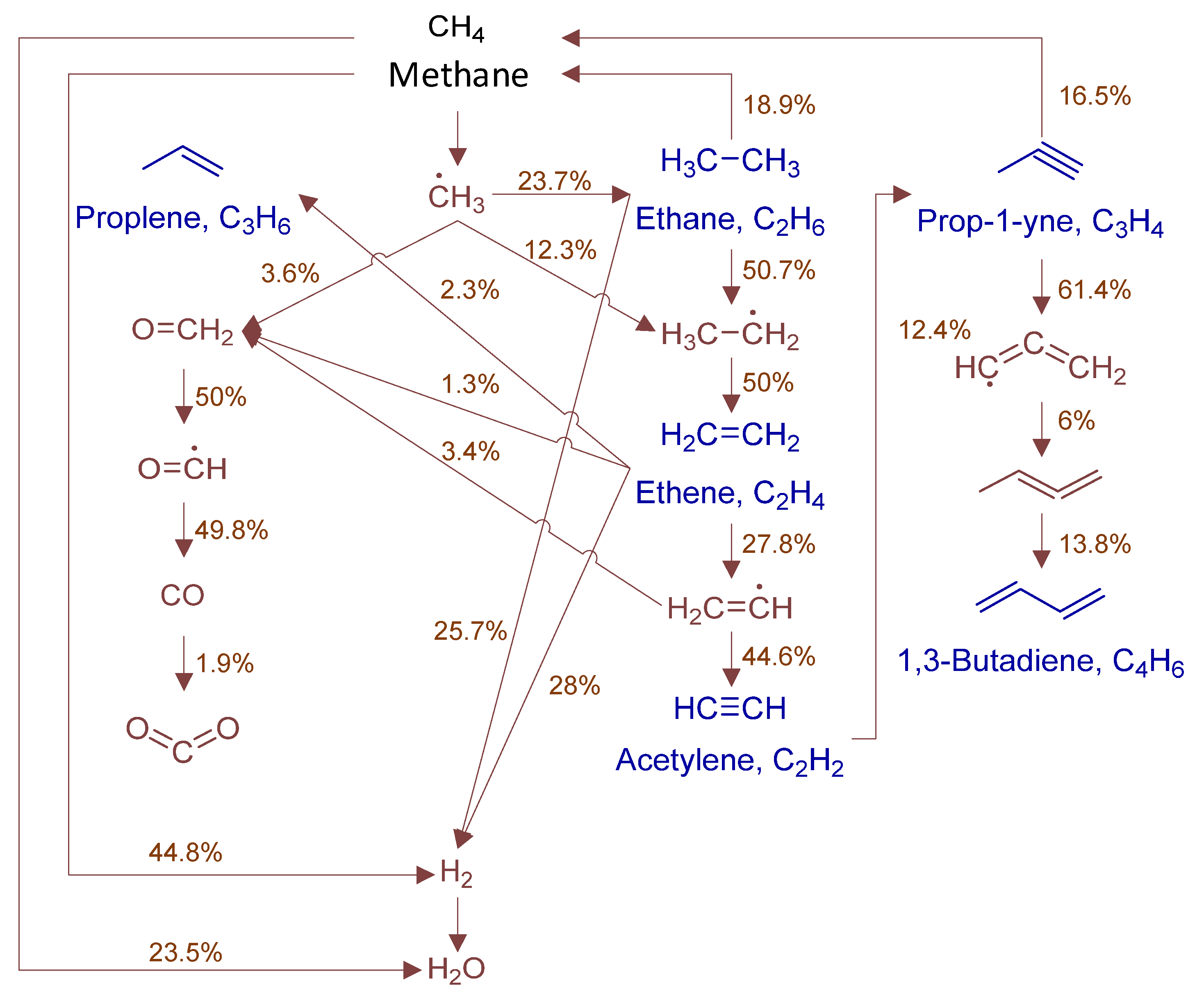
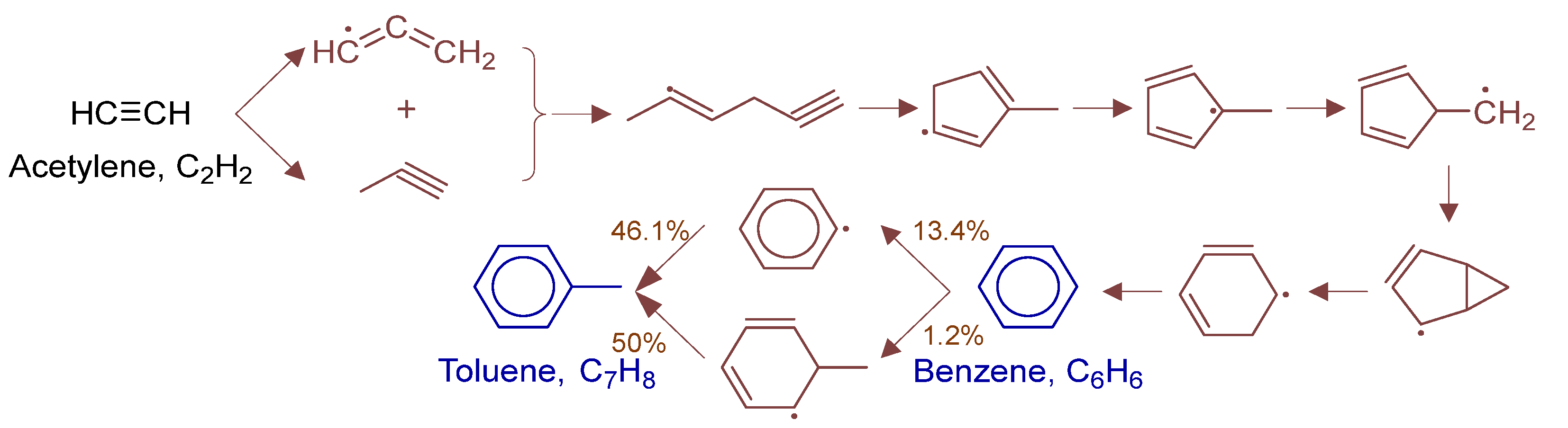
3.4. Rate-of-Production and Reaction Pathway Analysis
4. Results and Discussion
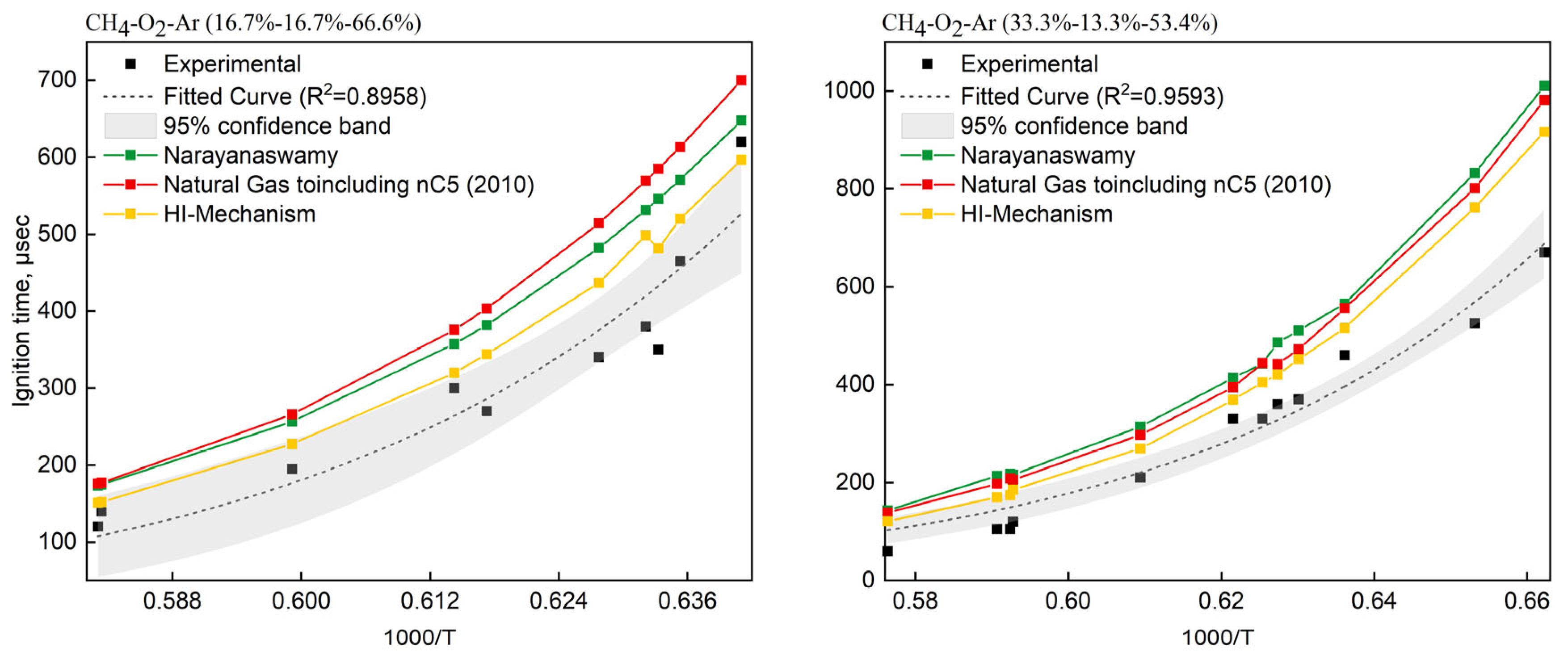
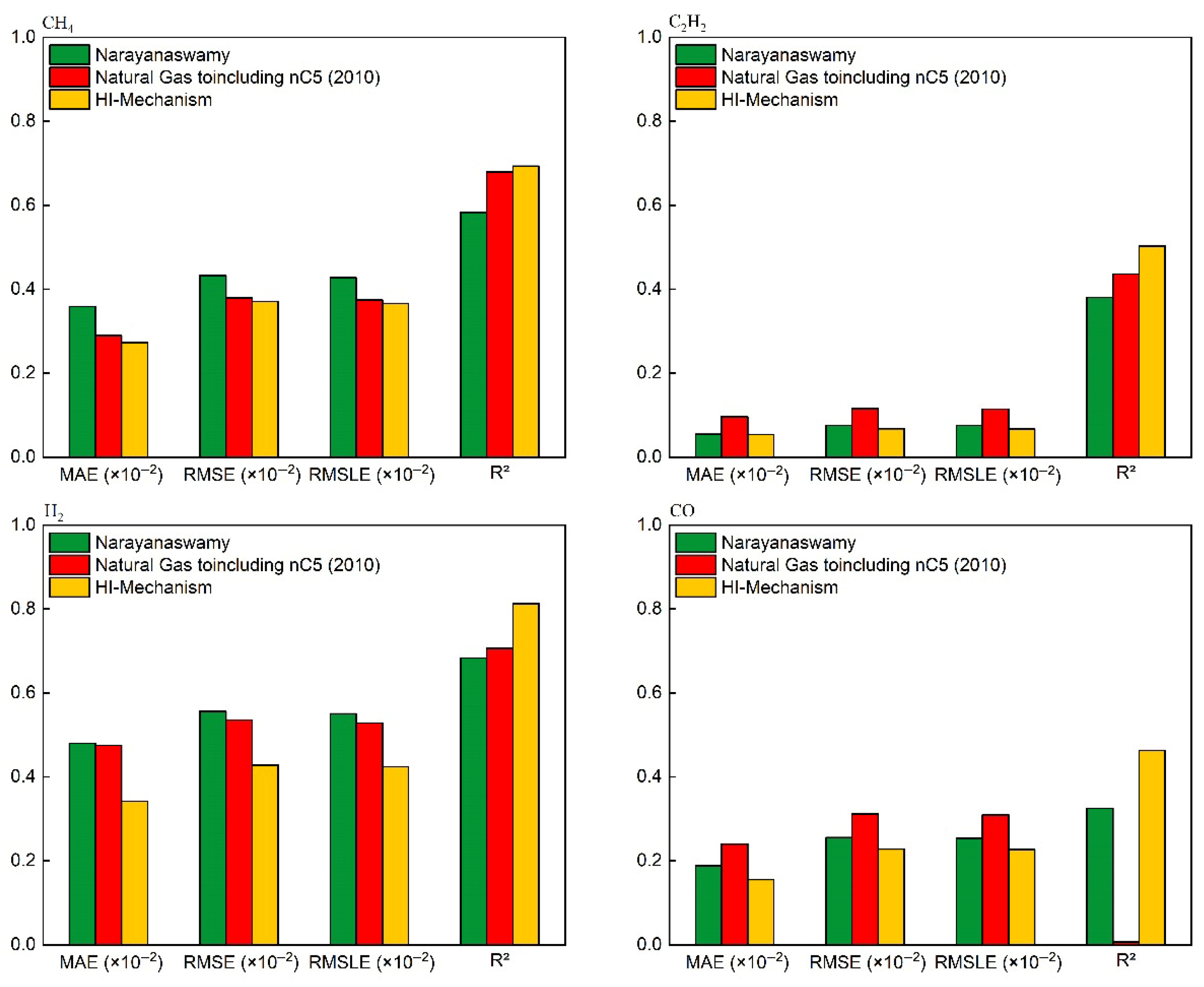
4.1. Mechanism Validation
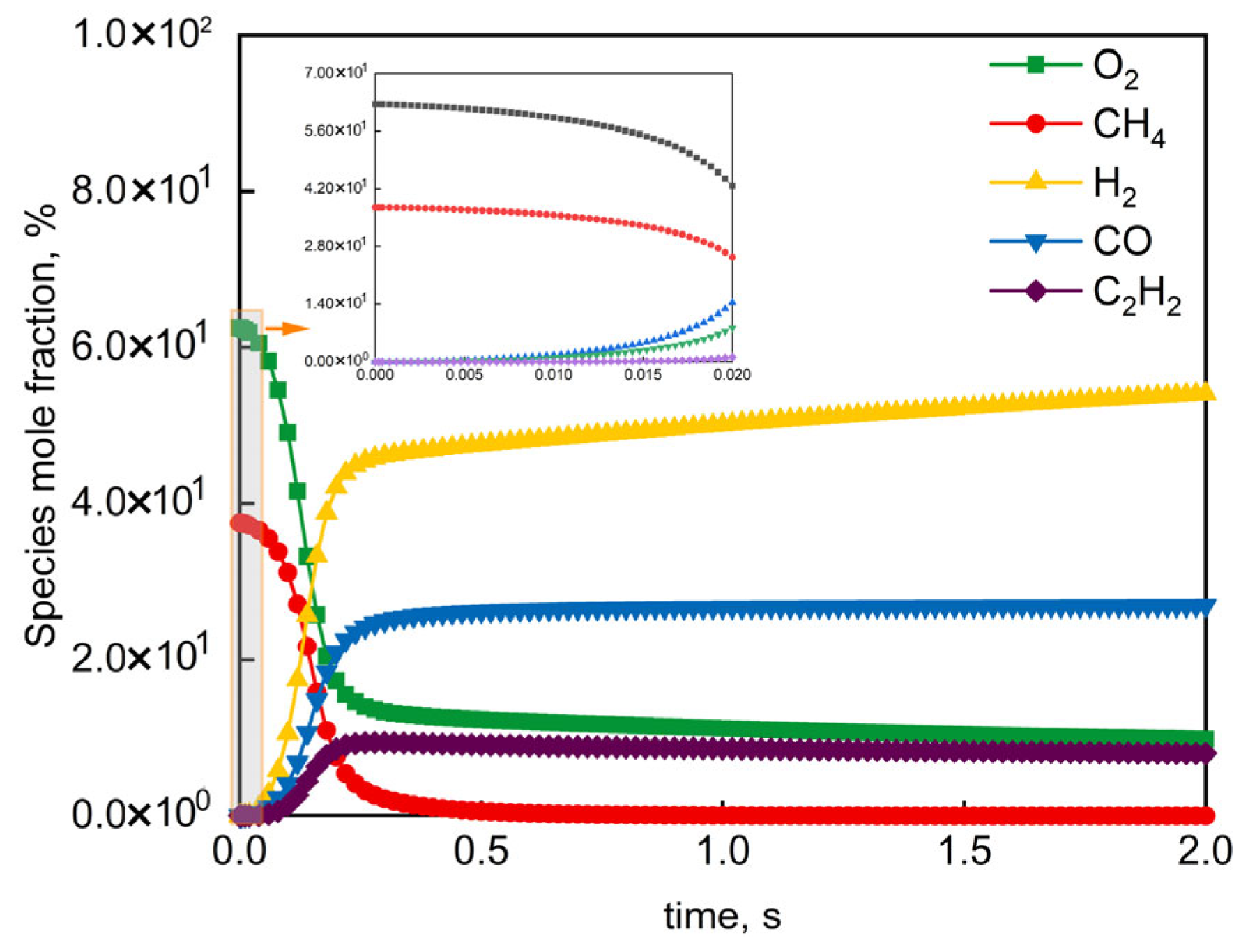
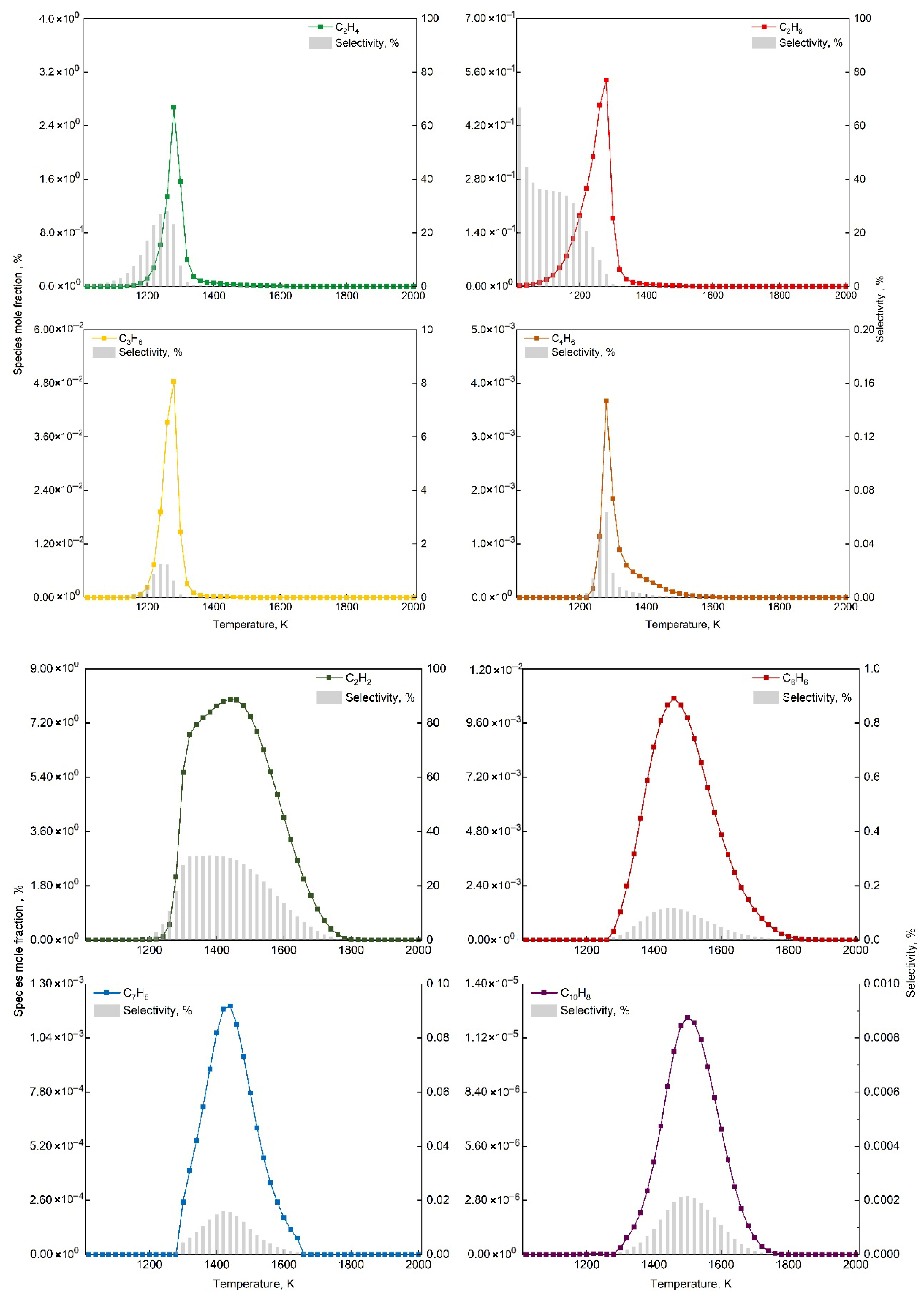
4.2. Microkinetic Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| POX | non-catalytic partial oxidation |
| PAHs | polycyclic aromatic hydrocarbons |
| HI-Mechanism | Hierarchical-Integrated Mechanism |
| RMG | Reaction Mechanism Generator |
| DRG | directed relation graph |
| DRG-EP | DRG with error propagation |
| DRG-PFA | path flux analysis |
| FSSA | full species sensitivity analysis |
| RCMs | rapid compression machines |
References
- Adler, T.B.; Knizia, G.; Werner, H.J. A simple and efficient CCSD(T)-F12 approximation. J. Chem. Phys. 2007, 127, 22. [Google Scholar] [CrossRef] [PubMed]
- Raimi, D.; Campbell, E.; Newell, R.G.; Prest, B.; Villanueva, S.; Wingenroth, J. Global Energy Outlook 2022: Turning Points and Tension in the Energy Transition; Resources for the Future: Washington, DC, USA, 2022; Available online: https://www.rff.org/publications/reports/global-energy-outlook-2022/ (accessed on 10 June 2025).
- Rizvi, S.K.A.; Naqvi, B.; Boubaker, S.; Mirza, N. The power play of natural gas and crude oil in the move towards the financialization of the energy market. Energy Econ. 2022, 112, 106131. [Google Scholar] [CrossRef]
- Makaryan, I.A.A.; Salgansky, E.A.A.; Arutyunov, V.S.S.; Sedov, I.V.V. Non-Catalytic Partial Oxidation of Hydrocarbon Gases to Syngas and Hydrogen: A Systematic Review. Energies 2023, 16, 2916. [Google Scholar] [CrossRef]
- Cohen, K.; Blanchard, J., Jr.; Rodriguez, P.; Kelly, K.; Dorman, J.A.; Dooley, K.M. Non-Catalytic Direct Partial Oxidation of Methane to Methanol in a Wall-Coated Microreactor. Chem. Eng. J. 2024, 482, 149049. [Google Scholar] [CrossRef]
- Norinaga, K.; Yatabe, H.; Matsuoka, M.; Hayashi, J.-i. Application of an Existing Detailed Chemical Kinetic Model to a Practical System of Hot Coke Oven Gas Reforming by Noncatalytic Partial Oxidation. Ind. Eng. Chem. Res. 2010, 49, 10565–10571. [Google Scholar] [CrossRef]
- Martinez-Gomez, J.; Napoles-Rivera, F.; Ponce-Ortega, J.M.; El-Halwagi, M.M. Optimization of the production of syngas from shale gas with economic and safety considerations. Appl. Therm. Eng. 2017, 110, 678–685. [Google Scholar] [CrossRef]
- Nourbakhsh, H.; Shahrouzi, J.R.; Zamaniyan, A.; Ebrahimi, H.; Nasr, M.R.J. A thermodynamic analysis of biogas partial oxidation to synthesis gas with emphasis on soot formation. Int. J. Hydrogen Energy 2018, 43, 15703–15719. [Google Scholar] [CrossRef]
- Osswald, P.; Zinsmeister, J.; Kathrotia, T.; Alves-Fortunato, M.; Burger, V.; van der Westhuizen, R.; Viljoen, C.; Lehto, K.; Sallinen, R.; Sandberg, K.; et al. Combustion kinetics of alternative jet fuels, Part-I: Experimental flow reactor study. Fuel 2021, 302, 120735. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, B. Visualization of ignition modes in methane-based mixture induced by shock wave focusing. Combust. Flame 2023, 247, 112491. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, J.; Su, S.; Qing, M.; Wang, L.; Cui, X.; Mostafa, M.E.; Zhang, C.; Hu, S.; Wang, Y.; et al. Formation and reduction of NO from the oxidation of NH3/CH4 with high concentration of H2O. Fuel 2019, 247, 19–25. [Google Scholar] [CrossRef]
- Garten, B.; Hunger, F.; Messig, D.; Stelzner, B.; Trimis, D.; Hasse, C. Detailed radiation modeling of a partial-oxidation flame. Int. J. Therm. Sci. 2015, 87, 68–84. [Google Scholar] [CrossRef]
- Koehler, M.; Osswald, P.; Xu, H.; Kathrotia, T.; Hasse, C.; Riedel, U. Speciation data for fuel-rich methane oxy-combustion and reforming under prototypical partial oxidation conditions. Chem. Eng. Sci. 2016, 139, 249–260. [Google Scholar] [CrossRef]
- Di, Q.; Dai, L.; Wang, Y.; Zanobetti, A.; Choirat, C.; Schwartz, J.D.; Dominici, F. Association of Short-term Exposure to Air Pollution With Mortality in Older Adults. Jama-J. Am. Med. Assoc. 2017, 318, 2446–2456. [Google Scholar] [CrossRef] [PubMed]
- Shindell, D.; Kuylenstierna, J.C.I.; Vignati, E.; van Dingenen, R.; Amann, M.; Klimont, Z.; Anenberg, S.C.; Muller, N.; Janssens-Maenhout, G.; Raes, F.; et al. Simultaneously Mitigating Near-Term Climate Change and Improving Human Health and Food Security. Science 2012, 335, 183–189. [Google Scholar] [CrossRef] [PubMed]
- Smith, G.P. The GRI-Mech 3.0 Mechanism. Available online: http://combustion.berkeley.edu/gri-mech (accessed on 10 June 2025).
- Donato, N.; Aul, C.; Petersen, E.; Zinner, C.; Curran, H.; Bourque, G. Ignition and Oxidation of 50/50 Butane Isomer Blends. J. Eng. Gas. Turbines Power-Trans. ASME 2010, 132, 9. [Google Scholar] [CrossRef]
- Healy, D.; Kalitan, D.M.; Aul, C.J.; Petersen, E.L.; Bourque, G.; Curran, H.J. Oxidation of C1-C5 Alkane Quinternary Natural Gas Mixtures at High Pressures. Energy Fuels 2010, 24, 1521–1528. [Google Scholar] [CrossRef]
- Healy, D.; Donato, N.S.; Aul, C.J.; Petersen, E.L.; Zinner, C.M.; Bourque, G.; Curran, H.J. Isobutane ignition delay time measurements at high pressure and detailed chemical kinetic simulations. Combust. Flame 2010, 157, 1540–1551. [Google Scholar] [CrossRef]
- Smith, G.P.; Tao, Y.; Wang, H. Available online: https://web.stanford.edu/group/haiwanglab/FFCM1 (accessed on 10 June 2025).
- Wang, Q.D. Skeletal Mechanism Generation for High-Temperature Combustion of H2/CO/C1-C4 Hydrocarbons. Energy Fuels 2013, 27, 4021–4030. [Google Scholar] [CrossRef]
- Blanquart, G.; Pepiot-Desjardins, P.; Pitsch, H. Chemical mechanism for high temperature combustion of engine relevant fuels with emphasis on soot precursors. Combust. Flame 2009, 156, 588–607. [Google Scholar] [CrossRef]
- Skjoth-Rasmussen, M.S.; Glarborg, P.; Ostberg, M.; Johannessen, J.T.; Livbjerg, H.; Jensen, A.D.; Christensen, T.S. Formation of polycyclic aromatic hydrocarbons and soot in fuel-rich oxidation of methane in a laminar flow reactor. Combust. Flame 2004, 136, 91–128. [Google Scholar] [CrossRef]
- Narayanaswamy, K.; Blanquart, G.; Pitsch, H. A consistent chemical mechanism for oxidation of substituted aromatic species. Combust. Flame 2010, 157, 1879–1898. [Google Scholar] [CrossRef]
- Slavinskaya, N.A.; Frank, P. A modelling study of aromatic soot precursors formation in laminar methane and ethene flames. Combust. Flame 2009, 156, 1705–1722. [Google Scholar] [CrossRef]
- Savchenko, V.I.; Zimin, Y.S.; Busillo, E.; Nikitin, A.V.; Sedov, I.V.; Arutyunov, V.S. Equilibrium Composition of Products Formed by Non-catalytic Conversion of Hydrocarbons. Pet. Chem. 2022, 62, 515–525. [Google Scholar] [CrossRef]
- Voloshchuk, Y.; Richter, A. Reduced order modeling and large-scale validation for non-catalytic partial oxidation of natural gas. Chem. Eng. Sci. 2022, 255, 117620. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Y.; Chen, T.; Yu, X.; Wang, J.; Wang, T. Simulations of methane partial oxidation by CFD coupled with detailed chemistry at industrial operating conditions. Chem. Eng. Sci. 2016, 142, 126–136. [Google Scholar] [CrossRef]
- Gao, C.W.; Allen, J.W.; Green, W.H.; West, R.H. Reaction Mechanism Generator: Automatic construction of chemical kinetic mechanisms. Comput. Phys. Commun. 2016, 203, 212–225. [Google Scholar] [CrossRef]
- Burke, M.P.; Chaos, M.; Ju, Y.G.; Dryer, F.L.; Klippenstein, S.J. Comprehensive H2/O2 kinetic model for high-pressure combustion. Int. J. Chem. Kinet. 2012, 44, 444–474. [Google Scholar] [CrossRef]
- Senosiain, J.P.; Klippenstein, S.J.; Miller, J.A. The reaction of acetylene with hydroxyl radicals. J. Phys. Chem. A 2005, 109, 6045. [Google Scholar] [CrossRef]
- Miller, J.A.; Klippenstein, S.J. The recombination of propargyl radicals and other reactions on a C6H6 potential. J. Phys. Chem. A 2003, 107, 7783–7799. [Google Scholar] [CrossRef]
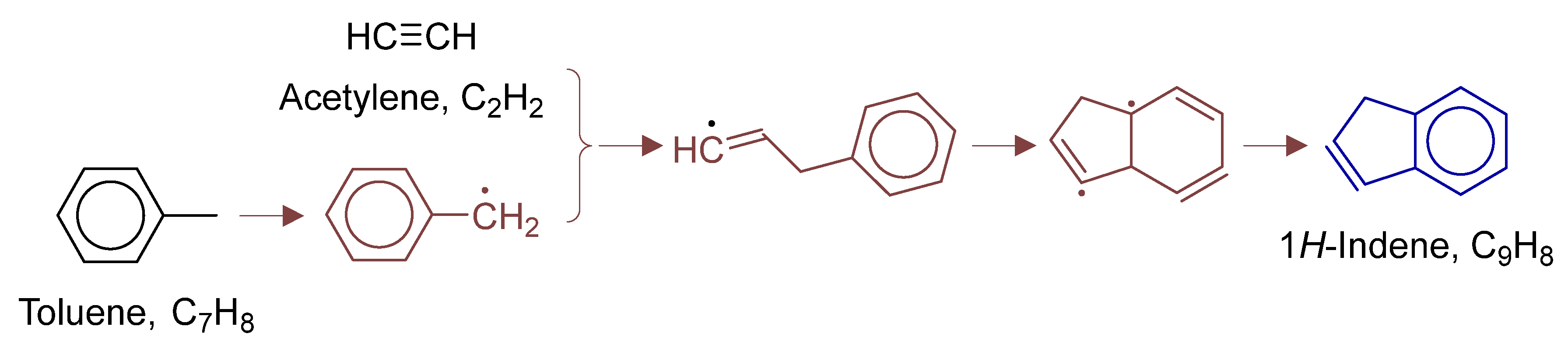
- Kislov, V.V.; Mebel, A.M. Ab initio G3-type/statistical theory study of the formation of indene in combustion flames. I. Pathways involving benzene and phenyl radical. J. Phys. Chem. A 2007, 111, 3922–3931. [Google Scholar] [CrossRef]
- Mebel, A.M.; Georgievskii, Y.; Jasper, A.W.; Klippenstein, S.J. Pressure-dependent rate constants for PAH growth: Formation of indene and its conversion to naphthalene. Faraday Discuss. 2016, 195, 637–670. [Google Scholar] [CrossRef]
- Mebel, A.M.; Landera, A.; Kaiser, R.I. Formation Mechanisms of Naphthalene and Indene: From the Interstellar Medium to Combustion Flames. J. Phys. Chem. A 2017, 121, 901–926. [Google Scholar] [CrossRef]
- Vervust, A.J.; Djokic, M.R.; Merchant, S.S.; Carstensen, H.H.; Long, A.E.; Marin, G.B.; Green, W.H.; Van Geem, K.M. Detailed Experimental and Kinetic Modeling Study of Cyclopentadiene Pyrolysis in the Presence of Ethene. Energy Fuels 2018, 32, 3920–3934. [Google Scholar] [CrossRef]
- Long, A.E.; Merchant, S.S.; Vandeputte, A.G.; Carstensen, H.H.; Vervust, A.J.; Marin, G.B.; Van Geem, K.M.; Green, W.H. Pressure dependent kinetic analysis of pathways to naphthalene from cyclopentadienyl recombination. Combust. Flame 2018, 187, 247–256. [Google Scholar] [CrossRef]
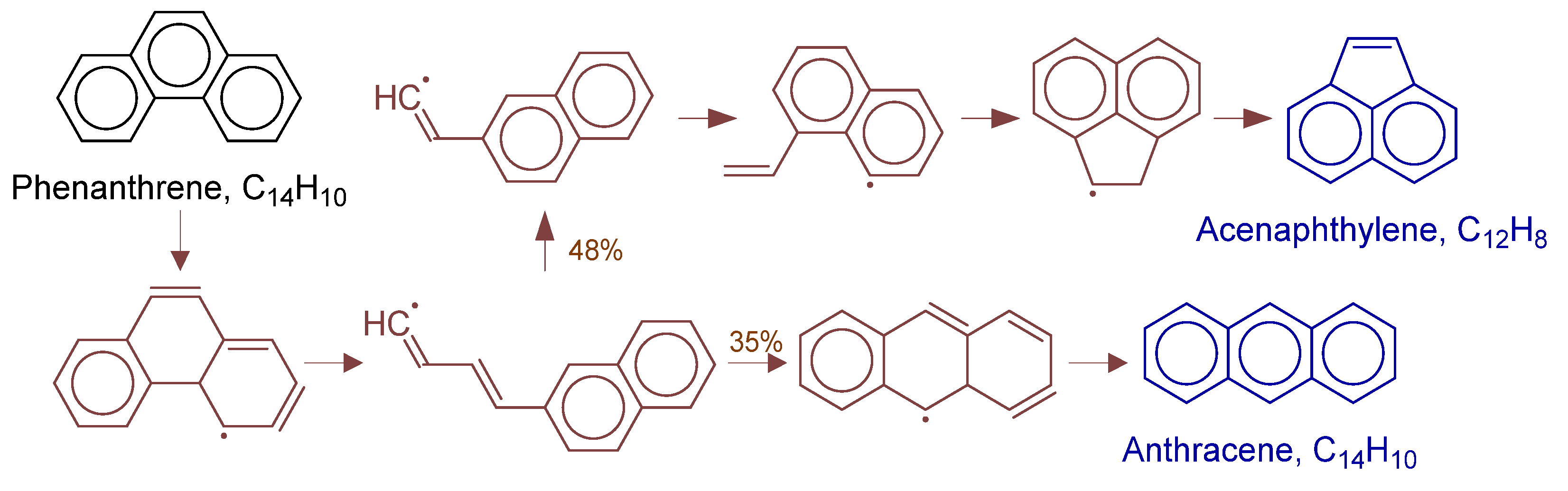
- Kislov, V.V.; Sadovnikov, A.I.; Mebel, A.M. Formation Mechanism of Polycyclic Aromatic Hydrocarbons beyond the Second Aromatic Ring. J. Phys. Chem. A 2013, 117, 4794–4816. [Google Scholar] [CrossRef] [PubMed]
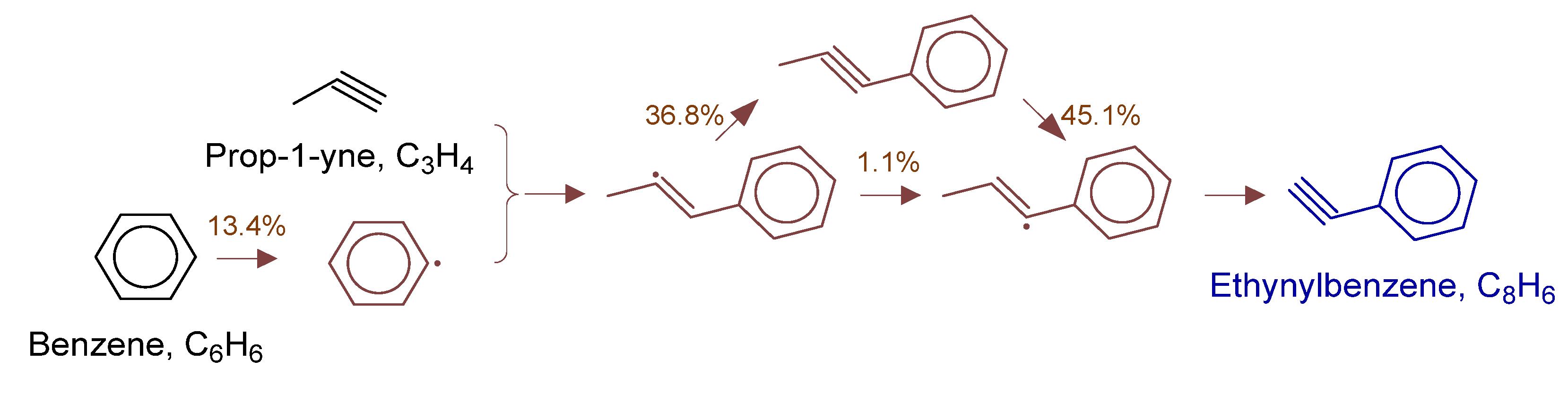
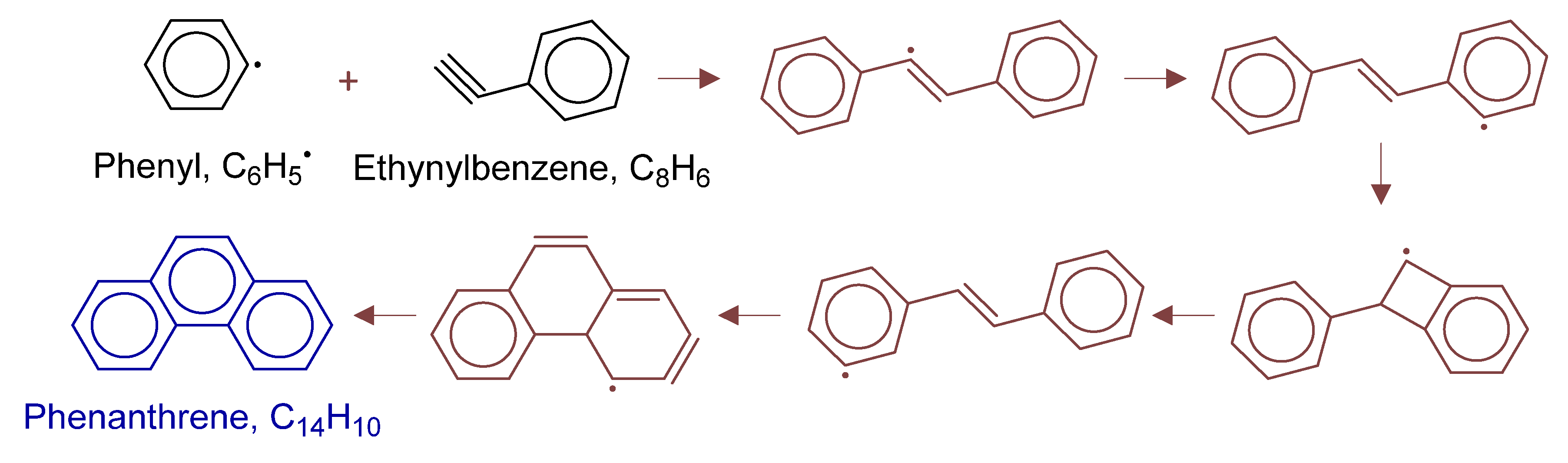
- Aguilera-Iparraguirre, J.; Klopper, W. Density functional theory study of the formation of naphthalene and phenanthrene from reactions of phenyl with vinyl- and phenylacetylene. J. Chem. Theory Comput. 2007, 3, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Frenklach, M.; Singh, R.I.; Mebel, A.M. On the low-temperature limit of HACA. Proc. Combust. Inst. 2019, 37, 969–976. [Google Scholar] [CrossRef]
- Richter, H.; Howard, J.B. Formation of polycyclic aromatic hydrocarbons and their growth to soot—A review of chemical reaction pathways. Prog. Energy Combust. Sci. 2000, 26, 565–608. [Google Scholar] [CrossRef]
- Zhao, L.; Kaiser, R.I.; Xu, B.; Ablikim, U.; Ahmed, M.; Joshi, D.; Veber, G.; Fischer, F.R.; Mebel, A.M. Pyrene synthesis in circumstellar envelopes and its role in the formation of 2D nanostructures. Nat. Astron. 2018, 2, 413–419. [Google Scholar] [CrossRef]
- Ribeiro, J.M.; Mebel, A.M. Reaction mechanism and product branching ratios of the CH + C3H4 reactions: A theoretical study. Phys. Chem. Chem. Phys. 2017, 19, 14543–14554. [Google Scholar] [CrossRef]
- Hahn, D.K.; Klippenstein, S.J.; Miller, J.A. A theoretical analysis of the reaction between propargyl and molecular oxygen. Faraday Discuss. 2001, 119, 79–100. [Google Scholar] [CrossRef] [PubMed]
- Harding, L.B.; Klippenstein, S.J.; Georgievskii, Y. On the combination reactions of hydrogen atoms with resonance-stabilized hydrocarbon radicals. J. Phys. Chem. A 2007, 111, 3789–3801. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Yang, B.; Zhang, F. Initiation mechanism of 1,3-butadiene combustion and its effect on soot precursors. Combust. Flame 2017, 184, 167–175. [Google Scholar] [CrossRef]
- Kislov, V.V.; Singh, R.I.; Edwards, D.E.; Mebel, A.M.; Frenklach, M. Rate coefficients and product branching ratios for the oxidation of phenyl and naphthyl radicals: A theoretical RRKM-ME study. Proc. Combust. Inst. 2015, 35, 1861–1869. [Google Scholar] [CrossRef]
- Narendrapurapu, B.S.; Simmonett, A.C.; Schaefer, H.F.; Miller, J.A.; Klippenstein, S.J. Combustion Chemistry: Important Features of the C3H5 Potential Energy Surface, Including Allyl Radical, Propargyl+H2, Allene+H, and Eight Transition States. J. Phys. Chem. A 2011, 115, 14209–14214. [Google Scholar] [CrossRef]
- Klippenstein, S.J.; Miller, J.A. The addition of hydrogen atoms to diacetylene and the heats of formation of i-C4H3 and n-C4H3. J. Phys. Chem. A 2005, 109, 4285–4295. [Google Scholar] [CrossRef]
- Petersson, G.A.; Malick, D.K.; Wilson, W.G.; Ochterski, J.W.; Montgomery, J.A.; Frisch, M.J. Calibration and comparison of the Gaussian-2, complete basis set, and density functional methods for computational thermochemistry. J. Chem. Phys. 1998, 109, 10570–10579. [Google Scholar] [CrossRef]
- Knizia, G.; Adler, T.B.; Werner, H.J. Simplified CCSD(T)-F12 methods: Theory and benchmarks. J. Chem. Phys. 2009, 130, 20. [Google Scholar] [CrossRef]
- Pfeiffer, F.; Rauhut, G.; Feller, D.; Peterson, K.A. Anharmonic zero point vibrational energies: Tipping the scales in accurate thermochemistry calculations? J. Chem. Phys. 2013, 138, 10. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y.L.; Ning, H.B.; Shi, J.C.; Wang, H.Y.; Luo, S.N. Chemical kinetics of H-abstractions from dimethyl amine by H, CH3, OH, and HO2 radicals with multi-structural torsional anharmonicity. Phys. Chem. Chem. Phys. 2019, 21, 12685–12696. [Google Scholar] [CrossRef]
- Lu, T.F.; Law, C.K. On the applicability of directed relation graphs to the reduction of reaction mechanisms. Combust. Flame 2006, 146, 472–483. [Google Scholar] [CrossRef]
- Wu, Y.C.; Liu, Y.F.; Lu, T.F. A linearized error propagation method for skeletal mechanism reduction. Combust. Flame 2020, 211, 303–311. [Google Scholar] [CrossRef]
- Liu, Z.T.; Yang, L.P.; Song, E.Z.; Wang, J.Q.; Zare, A.; Bodisco, T.A.; Brown, R.J. Development of a reduced multi-component combustion mechanism for a diesel/natural gas dual fuel engine by cross-reaction analysis. Fuel 2021, 293, 19. [Google Scholar] [CrossRef]
- Pepiot-Desjardins, P.; Pitsch, H. An efficient error-propagation-based reduction method for large chemical kinetic mechanisms. Combust. Flame 2008, 154, 67–81. [Google Scholar] [CrossRef]
- Stagni, A.; Frassoldati, A.; Cuoci, A.; Faravelli, T.; Ranzi, E. Skeletal mechanism reduction through species-targeted sensitivity analysis. Combust. Flame 2016, 163, 382–393. [Google Scholar] [CrossRef]
- Li, H.Y.; Zhang, H.W.; Chen, Z. Effects of endothermic chain-branching reaction on spherical flame initiation and propagation. Combust. Theory Model. 2019, 23, 496–514. [Google Scholar] [CrossRef]
- Petersen, E.L.; Hall, J.M.; Smith, S.D.; de Vries, J.; Amadio, A.R.; Crofton, M.W. Ignition of lean methane-based fuel blends at gas turbine pressures. J. Eng. Gas. Turbines Power-Trans. ASME 2007, 129, 937–944. [Google Scholar] [CrossRef]
- Rickard, M.J.A.; Hall, J.M.; Petersen, E.L. Effect of silane addition on acetylene ignition behind reflected shock waves. Proc. Combust. Inst. 2005, 30, 1915–1923. [Google Scholar] [CrossRef]
- Seery, D.J.; Bowman, C.T. An experimental and analytical study of methane oxidation behind shock waves. Combust. Flame 1970, 14, 37–47. [Google Scholar] [CrossRef]
- Healy, D.; Donato, N.S.; Aul, C.J.; Petersen, E.L.; Zinner, C.M.; Bourque, G.; Curran, H.J. n-Butane: Ignition delay measurements at high pressure and detailed chemical kinetic simulations. Combust. Flame 2010, 157, 1526–1539. [Google Scholar] [CrossRef]
- Healy, D.; Kopp, M.M.; Polley, N.L.; Petersen, E.L.; Bourque, G.; Curran, H.J. Methane/n-Butane Ignition Delay Measurements at High Pressure and Detailed Chemical Kinetic Simulations. Energy Fuels 2010, 24, 1617–1627. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, C.; Xie, B.; Wu, X. Revisiting the chemical kinetics of CH3 + O2 and its impact on methane ignition. Combust. Flame 2019, 200, 125–134. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, X.; Wei, L.; Zhang, J.; Tang, C.; Huang, Z. Experimental and modeling study on auto-ignition characteristics of methane/hydrogen blends under engine relevant pressure. Int. J. Hydrogen Energy 2012, 37, 19168–19176. [Google Scholar] [CrossRef]
- Konnov, A.A.; Zhu, J.N.; Bromly, J.H.; Zhang, D.K. Noncatalytic partial oxidation of methane into syngas over a wide temperature range. Combust. Sci. Technol. 2004, 176, 1093–1116. [Google Scholar] [CrossRef]
- Pässler, P.; Hefner, W.; Buckl, K.; Meinass, H.; Meiswinkel, A.; Wernicke, H.J.; Ebersberg, G.; Müller, R.; Bässler, J.; Behringer, H. Acetylene; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2000. [Google Scholar]
- Jasper, A.W.; Miller, J.A. Collisional Energy Transfer in Unimolecular Reactions: Direct Classical Trajectories for CH4 ⇆ CH3 + H in Helium. J. Phys. Chem. A 2009, 113, 5612–5619. [Google Scholar] [CrossRef]
- Barnes, R.W.; Pratt, G.L.; Wood, S.W. Pressure dependence of methane dissociation. J. Chem. Soc.-Faraday Trans. Ii 1989, 85, 229–238. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, W.; Ye, H.; Liu, W.; Wang, Q.; Dong, H. Modeling and Optimization of Natural Gas Non-Catalytic Partial Oxidation with Hierarchical-Integrated Mechanism. Processes 2025, 13, 2287. https://doi.org/10.3390/pr13072287
Yu W, Ye H, Liu W, Wang Q, Dong H. Modeling and Optimization of Natural Gas Non-Catalytic Partial Oxidation with Hierarchical-Integrated Mechanism. Processes. 2025; 13(7):2287. https://doi.org/10.3390/pr13072287
Chicago/Turabian StyleYu, Wanqiu, Haotian Ye, Wei Liu, Qiyao Wang, and Hongguang Dong. 2025. "Modeling and Optimization of Natural Gas Non-Catalytic Partial Oxidation with Hierarchical-Integrated Mechanism" Processes 13, no. 7: 2287. https://doi.org/10.3390/pr13072287
APA StyleYu, W., Ye, H., Liu, W., Wang, Q., & Dong, H. (2025). Modeling and Optimization of Natural Gas Non-Catalytic Partial Oxidation with Hierarchical-Integrated Mechanism. Processes, 13(7), 2287. https://doi.org/10.3390/pr13072287





