Simulation of Pb(II) and Ni(II) Adsorption in a Packed Column: Effects of Bed Height, Flow Rate, and Initial Concentration on Performance Metrics
Abstract
1. Introduction
2. Materials and Methods
2.1. Physical Properties, Parameters, and Mathematical Models Required for Aspen Adsorption
2.2. Mathematical Fundamentals
2.3. Parametric Evaluation
3. Results and Discussion
3.1. Data Obtained from Simulations of the Oil Palm-Packed Column for Removing Pb (II) and Ni (II)
3.2. Effect of the Change in the Initial Concentration of Pb(II) and Ni(II)
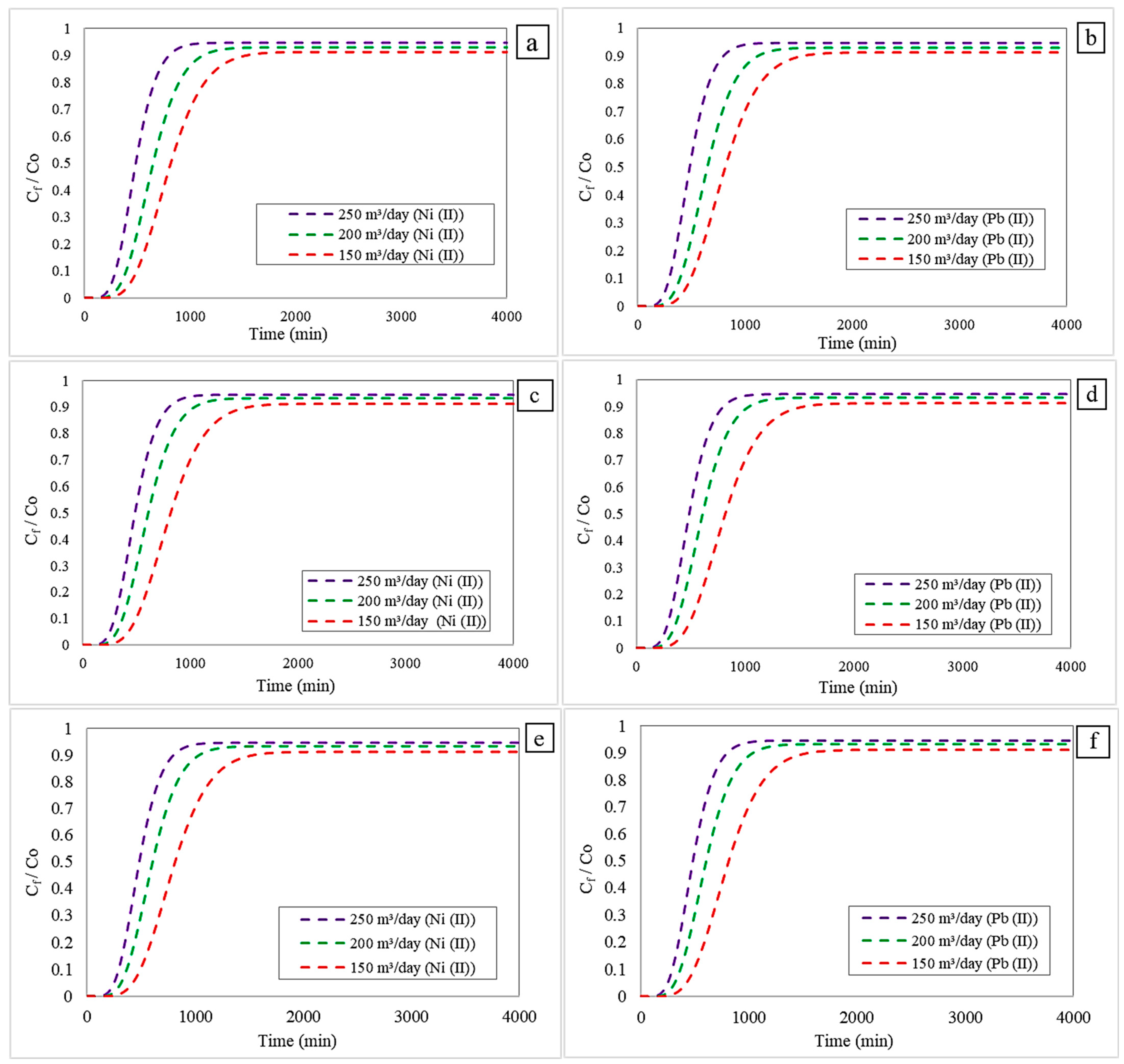
3.3. Effect of Changing the Inlet Flow Rate
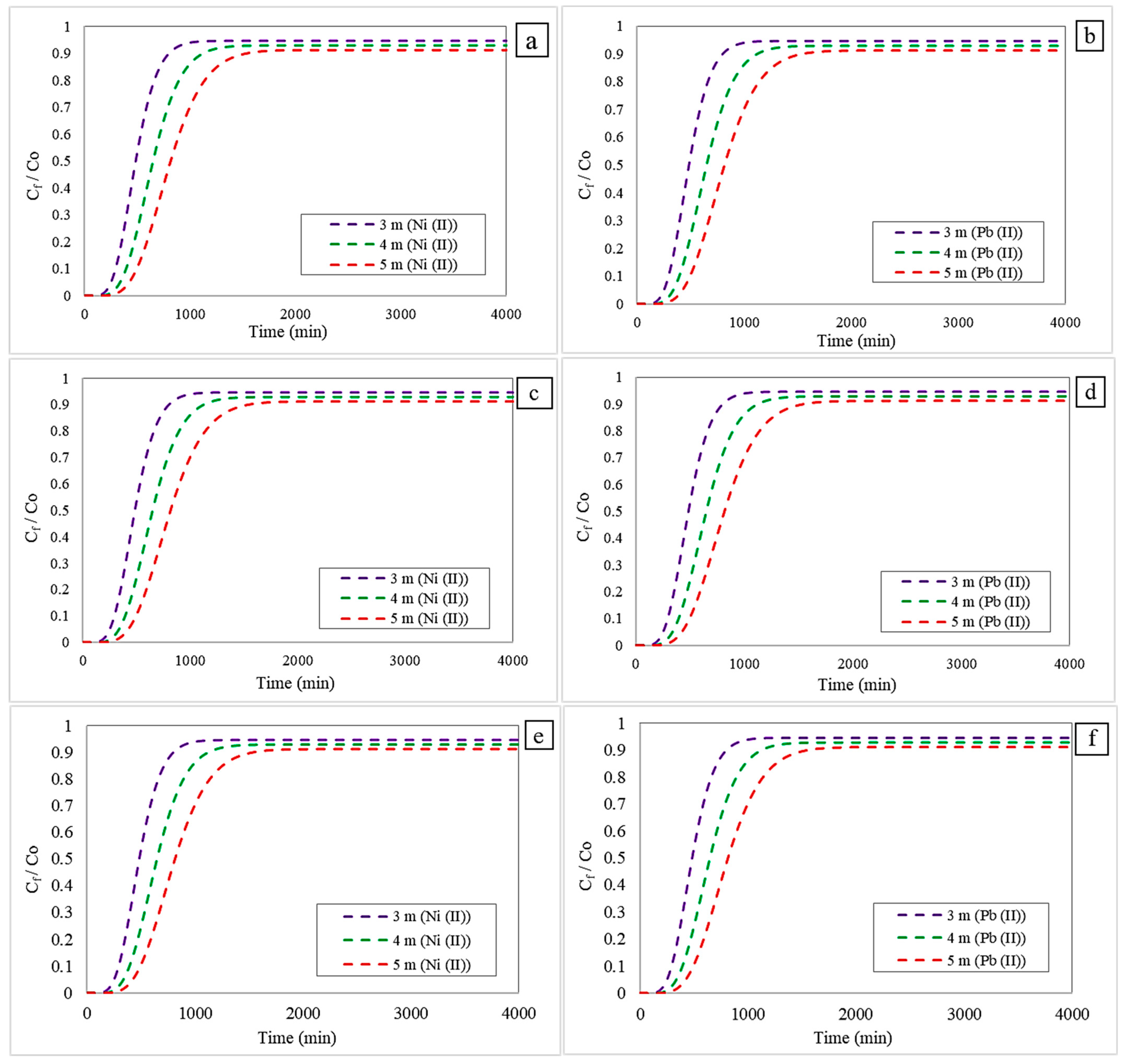
3.4. Effect of Column Height Change
3.5. Comparison with Other Results Found in the Literature
3.6. Model Limitations and Assumptions
3.6.1. Dependence of Constants of Isothermal Models
- The specific characteristics of the selected biomass, the pollutant being removed and its chemical properties, the experimental conditions established in each particular study, and the chemical interactions between the adsorbent material and the contaminant.
- This dependence on specific factors may limit the direct applicability of these values to the system studied in this work, potentially affecting the accuracy of the simulation results.
3.6.2. Restricted Operating Conditions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meza, C.D.R.L.; Kou, M.D.R.S.; Mancilla, H.D.B.; Arroyo, T.K.C. Biosorption of lead (II) in aqueous solution with biomass of prickly pear cladodes (Opuntia ficus indica). Rev. Colomb. Quim. 2020, 49, 36–46. [Google Scholar] [CrossRef]
- Oladoye, P.O. Natural, low-cost adsorbents for toxic Pb(II) ion sequestration from (waste)water: A state-of-the-art review. Chemosphere 2022, 287, 132130. [Google Scholar] [CrossRef]
- Sharma, R.; Jasrotia, T.; Sharma, S.; Sharma, M.; Kumar, R.; Vats, R.; Kumar, R.; Umar, A.; Akhtar, M.S. Sustainable removal of Ni(II) from waste water by freshly isolated fungal strains. Chemosphere 2021, 282, 130871. [Google Scholar] [CrossRef] [PubMed]
- Nasir, Z.; Sabir, A.; Salman, H.M.; Ashraf, M.U.; Khalid, M.B.; Khalid, Z.; Tahir, A.; Arshad, F.; Ejaz, H.G.; Ashraf, S.; et al. Fingerprinting of heavy metal and microbial contamination uncovers the unprecedented scale of water pollution and its implication on human health around transboundary Hudiara drain in South Asia. Environ. Technol. Innov. 2023, 30, 103040. [Google Scholar] [CrossRef]
- World Health Organization. Guías Para la Calidad del Agua de Consumo Humano: Cuarta Edición que Incorpora la Primera Adenda, 4th ed.; WHO: Ginebra, Geneva, 2011. Available online: http://apps.who.int/ (accessed on 22 January 2025).
- Wang, J.; Guo, X. Adsorption kinetics and isotherm models of heavy metals by various adsorbents: An overview. Crit. Rev. Environ. Sci. Technol. 2023, 53, 1837–1865. [Google Scholar] [CrossRef]
- Raji, Z.; Karim, A.; Karam, A.; Khalloufi, S. Adsorption of Heavy Metals: Mechanisms, Kinetics, and Applications of Various Adsorbents in Wastewater Remediation—A Review. Waste 2023, 1, 775–805. [Google Scholar] [CrossRef]
- Agarwal, A.; Upadhyay, U.; Sreedhar, I.; Anitha, K. Simulation studies of Cu(II) removal from aqueous solution using olive stone. Clean. Mater. 2022, 5, 100128. [Google Scholar] [CrossRef]
- Benyahia, F.; O’NEill, K.E. Enhanced voidage correlations for packed beds of various particle shapes and sizes. Part. Sci. Technol. 2005, 23, 169–177. [Google Scholar] [CrossRef]
- Dixon, A.G. Correlations for wall and particle shape effects on fixed bed bulk voidage. Can. J. Chem. Eng. 1988, 66, 705–708. [Google Scholar] [CrossRef]
- Ezeoha, S.L.; Akubuo, C.O.; Ani, A.O. Proposed Average Values of Some Engineering Properties of Palm Kernels. Niger. J. Technol. 2012, 31, 167–173. [Google Scholar]
- Omar, M.; Kadir, A.; Azizi, M.; Yunus, C. Determination of Overall Mass Transfer Coefficient of Palm Kernel Extracted Using Supercritical Carbon Dioxide. 2008. Available online: https://www.researchgate.net/publication/279363082 (accessed on 20 January 2025).
- Adornado, A.P.; Soriano, A.N.; Orfiana, O.N.; Pangon, M.B.J.; Nieva, A.D. Simulated Biosorption of Cd(II) and Cu(II) in Single and Binary Metal Systems by Water Hyacinth (Eichhornia crassipes) using Aspen Adsorption. ASEAN J. Chem. Eng. 2017, 16, 21–43. [Google Scholar] [CrossRef]
- Durán, I.; Rubiera, F.; Pevida, C. Modeling a biogas upgrading PSA unit with a sustainable activated carbon derived from pine sawdust. Sensitivity analysis on the adsorption of CO2 and CH4 mixtures. Chem. Eng. J. 2022, 428, 132564. [Google Scholar] [CrossRef]
- Fouad, M.R. Physical characteristics and Freundlich model of adsorption and desorption isotherm for fipronil in six types of Egyptian soil. Curr. Chem. Lett. 2023, 12, 207–216. [Google Scholar] [CrossRef]
- Amrutha; Jeppu, G.; Girish, C.R.; Prabhu, B.; Mayer, K. Multi-component Adsorption Isotherms: Review and Modeling Studies. Environ. Process. 2023, 10, 1–52. [Google Scholar] [CrossRef]
- Jeppu, G.P.; Clement, T.P. A modified Langmuir-Freundlich isotherm model for simulating pH-dependent adsorption effects. J. Contam. Hydrol. 2012, 129, 46–53. [Google Scholar] [CrossRef]
- Ahmad, T.; Manzar, M.S.; Khan, S.; Al-Sharafi, M.A.; Georgin, J.; Franco, D.S.; Ullah, N. Enhanced adsorption of bisphenol-A from water through the application of isocyanurate based hyper crosslinked resin. J. Mol. Liq. 2024, 395, 123861. [Google Scholar] [CrossRef]
- Tovar, C.T.; Paternina, E.R.; Mercado, J.G.; Bohorquez, J.M. Evaluación de la biosorción con bagazo de palma africana para la eliminación de Pb (II) en solución. Prospectiva 2015, 13, 59–67. [Google Scholar] [CrossRef][Green Version]
- Palet, C.; Bastos-Arrieta, J.; Villabona-Ortíz, A.; Tejada-Tovar, C.; Darío González-Delgado, Á. Elimination of Chromium (VI) and Nickel (II) Ions in a Packed Column Using Oil Palm Bagasse and Yam Peels. Water 2022, 14, 1240. [Google Scholar] [CrossRef]
- Dadebo, D.; Atukunda, A.; Ibrahim, M.G.; Nasr, M. Integrating chemical coagulation with fixed-bed column adsorption using rice husk-derived biochar for shipboard bilgewater treatment: Scale-up design and cost estimation. Chem. Eng. J. Adv. 2023, 16, 100520. [Google Scholar] [CrossRef]
- de Araujo, C.M.B.; Ghislandi, M.G.; Rios, A.G.; da Costa, G.R.B.; Nascimento, B.F.D.; Ferreira, A.F.P.; Sobrinho, M.A.d.M.; Rodrigues, A.E. Wastewater treatment using recyclable agar-graphene oxide biocomposite hydrogel in batch and fixed-bed adsorption column: Bench experiments and modeling for the selective removal of organics. Colloids Surfaces A Physicochem. Eng. Asp. 2022, 639, 128357. [Google Scholar] [CrossRef]
- Li, T.; Ji, X.; Wang, D.; Zhang, Q.; Zhang, M.; Zhang, H.; Yu, G.; Deng, S. Industrial-scale highly efficient nickel recovery from electroplating wastewater using resin adsorption followed by aeration mixing acid regeneration. J. Water Process. Eng. 2024, 58, 104801. [Google Scholar] [CrossRef]
- Kumar, V.; Dwivedi, S.; Oh, S. A critical review on lead removal from industrial wastewater: Recent advances and future outlook. J. Water Process. Eng. 2022, 45, 102518. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, X.; Liu, S.; Gao, Y.; Tao, L.; Yang, Q.; Hao, H.; Lei, D.; Liu, J. Constructing physical and chemical synergistic effect of graphene aerogels regenerated from spent graphite anode of lithium ion batteries achieves high efficient adsorption of lead in wastewater. Appl. Surf. Sci. 2023, 633, 157623. [Google Scholar] [CrossRef]
- Ronda, A.; Martín-Lara, M.A.; Osegueda, O.; Castillo, V.; Blázquez, G. Scale-up of a packed bed column for wastewater treatment. Water Sci. Technol. 2018, 77, 1386–1396. [Google Scholar] [CrossRef]
- Upadhyay, U.; Gupta, S.; Agarwal, A.; Sreedhar, I.; Anitha, K.L. Adsorptive removal of Cd2+ ions using dolochar at an industrial-scale process optimization by response surface methodology. Environ. Sci. Pollut. Res. 2023, 30, 8403–8415. [Google Scholar] [CrossRef]

| Tab | Considerations |
|---|---|
| General | Upwind Differencing Scheme 1 (UDS1) discretisation method with a number of nodes of 10 |
| Material/momentum balance | Convection is in the liquid phase Velocity is constant No pressure drop is present |
| Kinetic model | Linear Driving Force Kinetic Model (LDF) |
| Isothermal model | Langmuir isothermal model Freundlich isothermal model Langmuir-Freundlich isothermal model |
| Energy balance | Isothermal process |
| Model | Concentration (mg/L) | Bed Height (m) | Flow Rate (m3/day) | R.T (min) | S.T (min) |
|---|---|---|---|---|---|
| Freundlich–LDF | 2000 | 3 | 250 | 161 | 1165 |
| 200 | 218 | 1549 | |||
| 150 | 275 | 1927 | |||
| 4 | 250 | 204 | 1455 | ||
| 200 | 275 | 1927 | |||
| 150 | 347 | 2412 | |||
| 5 | 250 | 275 | 1928 | ||
| 200 | 370 | 2568 | |||
| 150 | 467 | 3193 | |||
| 3500 | 3 | 250 | 161 | 1168 | |
| 200 | 218 | 1545 | |||
| 150 | 275 | 1930 | |||
| 4 | 250 | 204 | 1451 | ||
| 200 | 275 | 1930 | |||
| 150 | 348 | 2400 | |||
| 5 | 250 | 275 | 1930 | ||
| 200 | 371 | 2556 | |||
| 150 | 467 | 3195 | |||
| 5000 | 3 | 250 | 161 | 1170 | |
| 200 | 218 | 1547 | |||
| 150 | 275 | 1931 | |||
| 4 | 250 | 204 | 1453 | ||
| 200 | 275 | 1931 | |||
| 150 | 347 | 2401 | |||
| 5 | 250 | 275 | 1931 | ||
| 200 | 371 | 2557 | |||
| 150 | 468 | 3180 | |||
| Langmuir–LDF | 2000 | 3 | 250 | 161 | 1167 |
| 200 | 218 | 1565 | |||
| 150 | 275 | 1945 | |||
| 4 | 250 | 204 | 1470 | ||
| 200 | 275 | 1945 | |||
| 150 | 347 | 2424 | |||
| 5 | 250 | 275 | 1946 | ||
| 200 | 371 | 2577 | |||
| 150 | 467 | 3205 | |||
| 3500 | 3 | 250 | 161 | 1172 | |
| 200 | 218 | 1549 | |||
| 150 | 275 | 1945 | |||
| 4 | 250 | 204 | 1456 | ||
| 200 | 275 | 1945 | |||
| 150 | 347 | 2423 | |||
| 5 | 250 | 275 | 1945 | ||
| 200 | 371 | 2577 | |||
| 150 | 467 | 3210 | |||
| 5000 | 3 | 250 | 161 | 1178 | |
| 200 | 218 | 1561 | |||
| 150 | 275 | 1956 | |||
| 4 | 250 | 203 | 1466 | ||
| 200 | 275 | 1955 | |||
| 150 | 347 | 2429 | |||
| 5 | 250 | 275 | 1951 | ||
| 200 | 371 | 2596 | |||
| 150 | 468 | 3230 | |||
| Langmuir-Freundlich–LDF | 2000 | 3 | 250 | 161 | 1172 |
| 200 | 218 | 1564 | |||
| 150 | 275 | 1947 | |||
| 4 | 250 | 204 | 1469 | ||
| 200 | 275 | 1947 | |||
| 150 | 347 | 2412 | |||
| 5 | 250 | 275 | 1939 | ||
| 200 | 371 | 2567 | |||
| 150 | 467 | 3193 | |||
| 3500 | 3 | 250 | 161 | 1176 | |
| 200 | 218 | 1561 | |||
| 150 | 275 | 1950 | |||
| 4 | 250 | 204 | 1461 | ||
| 200 | 275 | 1950 | |||
| 150 | 347 | 2429 | |||
| 5 | 250 | 275 | 1947 | ||
| 200 | 371 | 2567 | |||
| 150 | 467 | 3194 | |||
| 5000 | 3 | 250 | 161 | 1177 | |
| 200 | 218 | 1558 | |||
| 150 | 275 | 1951 | |||
| 4 | 250 | 204 | 1464 | ||
| 200 | 275 | 1948 | |||
| 150 | 347 | 2425 | |||
| 5 | 250 | 275 | 1952 | ||
| 200 | 371 | 2567 | |||
| 150 | 468 | 3193 |
| Model | Concentration (mg/L) | Bed Height (m) | Flow Rate (m3/día) | R.T (min) | S.T (min) |
|---|---|---|---|---|---|
| Freundlich–LDF | 2000 | 3 | 250 | 161 | 1165 |
| 200 | 218 | 1549 | |||
| 150 | 275 | 1927 | |||
| 4 | 250 | 204 | 1455 | ||
| 200 | 275 | 1927 | |||
| 150 | 347 | 2412 | |||
| 5 | 250 | 275 | 1928 | ||
| 200 | 370 | 2568 | |||
| 150 | 467 | 3193 | |||
| 3500 | 3 | 250 | 161 | 1168 | |
| 200 | 218 | 1545 | |||
| 150 | 275 | 1930 | |||
| 4 | 250 | 204 | 1451 | ||
| 200 | 275 | 1930 | |||
| 150 | 348 | 2400 | |||
| 5 | 250 | 275 | 1930 | ||
| 200 | 371 | 2556 | |||
| 150 | 467 | 3195 | |||
| 5000 | 3 | 250 | 161 | 1170 | |
| 200 | 218 | 1547 | |||
| 150 | 275 | 1931 | |||
| 4 | 250 | 204 | 1453 | ||
| 200 | 275 | 1931 | |||
| 150 | 347 | 2401 | |||
| 5 | 250 | 275 | 1931 | ||
| 200 | 371 | 2557 | |||
| 150 | 468 | 3180 | |||
| Langmuir–LDF | 2000 | 3 | 250 | 161 | 1165 |
| 200 | 218 | 1549 | |||
| 150 | 275 | 1927 | |||
| 4 | 250 | 204 | 1455 | ||
| 200 | 275 | 1927 | |||
| 150 | 347 | 2412 | |||
| 5 | 250 | 275 | 1928 | ||
| 200 | 370 | 2568 | |||
| 150 | 467 | 3193 | |||
| 3500 | 3 | 250 | 161 | 1168 | |
| 200 | 218 | 1545 | |||
| 150 | 275 | 1930 | |||
| 4 | 250 | 204 | 1451 | ||
| 200 | 275 | 1930 | |||
| 150 | 348 | 2400 | |||
| 5 | 250 | 275 | 1930 | ||
| 200 | 371 | 2556 | |||
| 150 | 467 | 3195 | |||
| 5000 | 3 | 250 | 161 | 1170 | |
| 200 | 218 | 1547 | |||
| 150 | 275 | 1931 | |||
| 4 | 250 | 204 | 1453 | ||
| 200 | 275 | 1931 | |||
| 150 | 347 | 2401 | |||
| 5 | 250 | 275 | 1931 | ||
| 200 | 371 | 2557 | |||
| 150 | 468 | 3180 | |||
| Langmuir-Freundlich–LDF | 2000 | 3 | 250 | 161 | 1172 |
| 200 | 218 | 1564 | |||
| 150 | 275 | 1947 | |||
| 4 | 250 | 204 | 1469 | ||
| 200 | 275 | 1947 | |||
| 150 | 347 | 2457 | |||
| 5 | 250 | 275 | 1954 | ||
| 200 | 371 | 2618 | |||
| 150 | 467 | 3266 | |||
| 3500 | 3 | 250 | 161 | 1176 | |
| 200 | 218 | 1561 | |||
| 150 | 275 | 1950 | |||
| 4 | 250 | 204 | 1461 | ||
| 200 | 275 | 1950 | |||
| 150 | 347 | 2429 | |||
| 5 | 250 | 275 | 1947 | ||
| 200 | 371 | 2604 | |||
| 150 | 467 | 3267 | |||
| 5000 | 3 | 250 | 161 | 1177 | |
| 200 | 218 | 1558 | |||
| 150 | 275 | 1951 | |||
| 4 | 250 | 204 | 1464 | ||
| 200 | 275 | 1948 | |||
| 150 | 347 | 2425 | |||
| 5 | 250 | 275 | 1952 | ||
| 200 | 371 | 2606 | |||
| 150 | 468 | 3251 |
| Parameter | Pb(II) | Cd(II) | Cu(II) | Pb(II)/Ni(II) |
|---|---|---|---|---|
| Adsorbent | Olive tree pruning | Dolochar | Olive stone | Oil palm |
| Initial concentration (mg/L) | 100 | 55 | 583 | 5000 |
| Inlet flow rate (m3/day) | 128.04 | 75 | 43.2 | 250 |
| Bed height (m) | 2.26 | 0.65 | 1 | 3 |
| Rupture time (min) | 201.6 | 666 | 9828 | 161/161 |
| Saturation time (min) | 503 | - | 1178/1177 | |
| Source | [26] | [27] | [8] | This study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tejada-Tovar, C.; Villabona-Ortíz, Á.; Gonzalez-Delgado, Á.; Ortega-Toro, R.; Ortega-Puente, S. Simulation of Pb(II) and Ni(II) Adsorption in a Packed Column: Effects of Bed Height, Flow Rate, and Initial Concentration on Performance Metrics. Processes 2025, 13, 2141. https://doi.org/10.3390/pr13072141
Tejada-Tovar C, Villabona-Ortíz Á, Gonzalez-Delgado Á, Ortega-Toro R, Ortega-Puente S. Simulation of Pb(II) and Ni(II) Adsorption in a Packed Column: Effects of Bed Height, Flow Rate, and Initial Concentration on Performance Metrics. Processes. 2025; 13(7):2141. https://doi.org/10.3390/pr13072141
Chicago/Turabian StyleTejada-Tovar, Candelaria, Ángel Villabona-Ortíz, Ángel Gonzalez-Delgado, Rodrigo Ortega-Toro, and Sebastián Ortega-Puente. 2025. "Simulation of Pb(II) and Ni(II) Adsorption in a Packed Column: Effects of Bed Height, Flow Rate, and Initial Concentration on Performance Metrics" Processes 13, no. 7: 2141. https://doi.org/10.3390/pr13072141
APA StyleTejada-Tovar, C., Villabona-Ortíz, Á., Gonzalez-Delgado, Á., Ortega-Toro, R., & Ortega-Puente, S. (2025). Simulation of Pb(II) and Ni(II) Adsorption in a Packed Column: Effects of Bed Height, Flow Rate, and Initial Concentration on Performance Metrics. Processes, 13(7), 2141. https://doi.org/10.3390/pr13072141











