Investigation on Corrosion-Induced Wall-Thinning Mechanisms in High-Pressure Steam Pipelines Based on Gas–Liquid Two-Phase Flow Characteristics
Abstract
1. Introduction
2. Methodology
2.1. Experimental Detection
2.1.1. Introduction to In-Service Pipe Bends
2.1.2. Measurement of Pipe Bend Wall Thickness
2.1.3. Sample Preparation and Microstructural Analysis Overview
2.2. Introduction to CFD Numerical Simulation
2.2.1. Mathematical Model
2.2.2. Model Construction and Setup
- Inlet: Pressure inlet with a static pressure of 3.89 MPa.
- Outlet: Pressure outlet with a gauge pressure of 0 Pa.
- Wall: No-slip condition applied to all pipe walls; roughness constants (0.1, 0.5, 1.0)
- defined at the bend region.
- Discrete phase: Bubble injection from the inlet with predefined mass flow rates at gas volume fractions of 10%, 40%, and 70%.
- Turbulence model: Standard RNG k–ε model with enhanced wall treatment.
3. Results and Discussion
3.1. Experimental Results
3.1.1. Wall Thickness Measurement
3.1.2. Analysis of Corrosion Cross-Sections and Surfaces
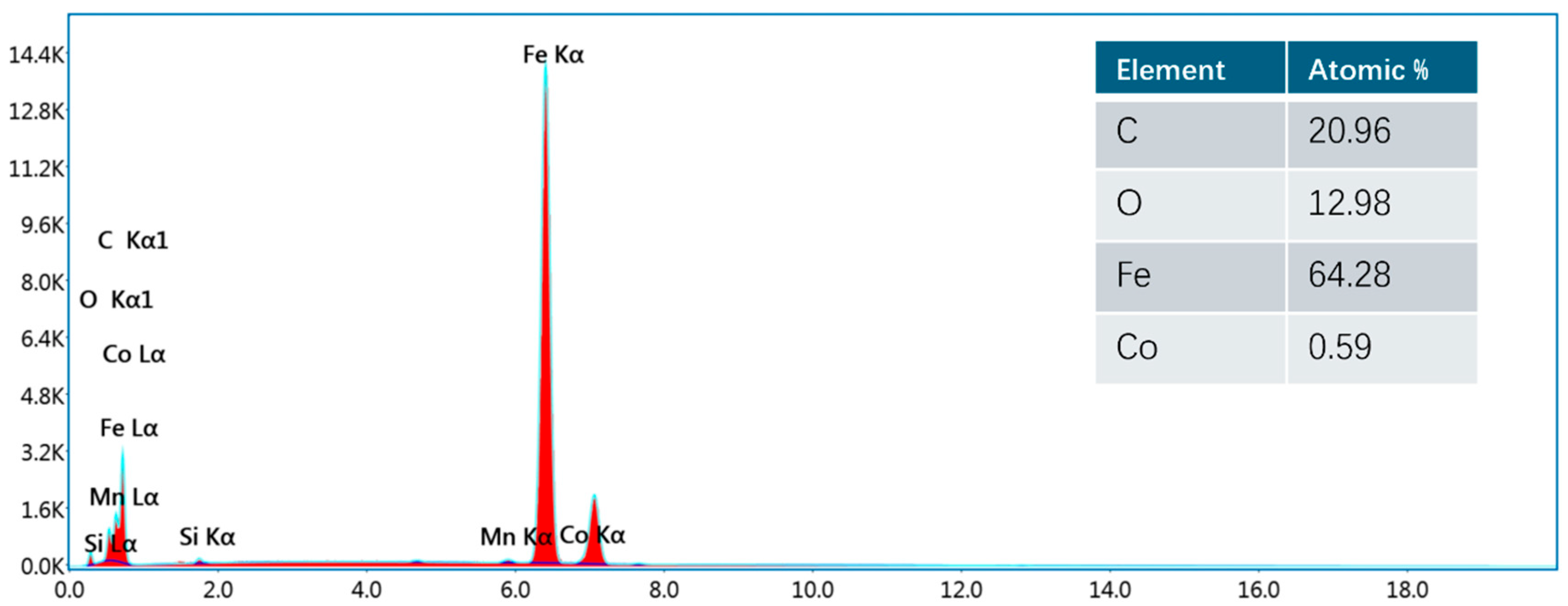
3.1.3. Energy Spectrum Analysis
3.2. Experimental Results
3.2.1. Wall Thickness Measurement
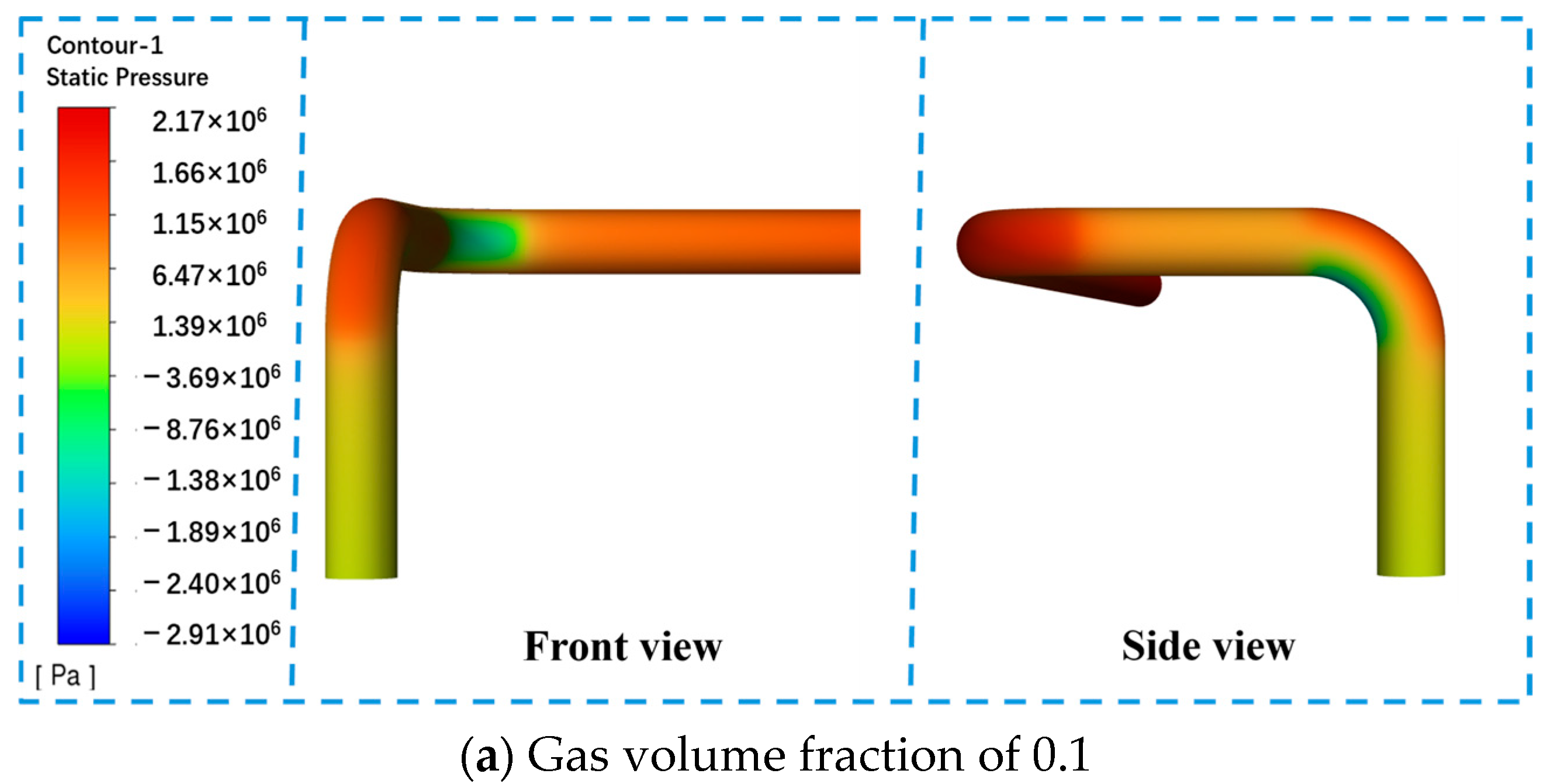
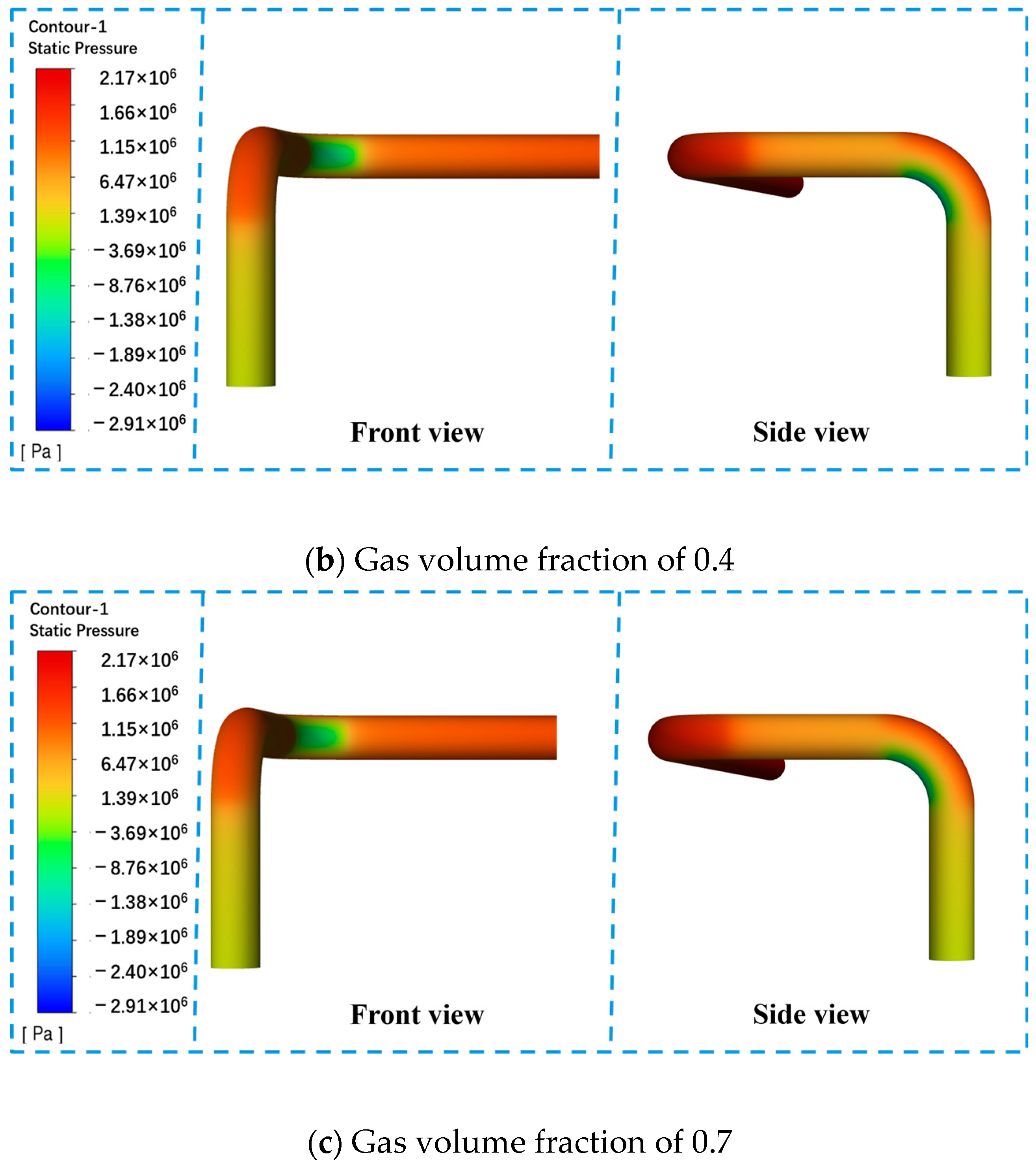
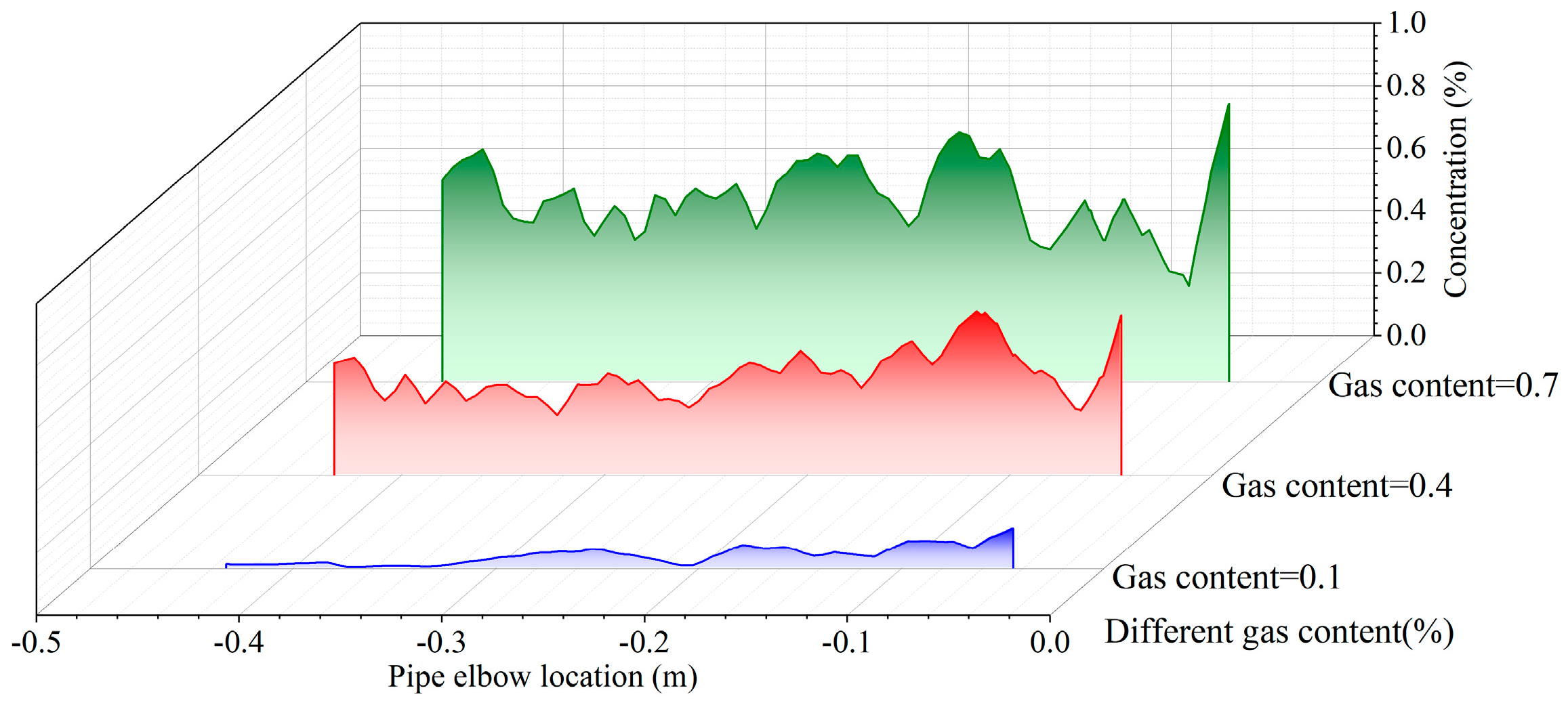
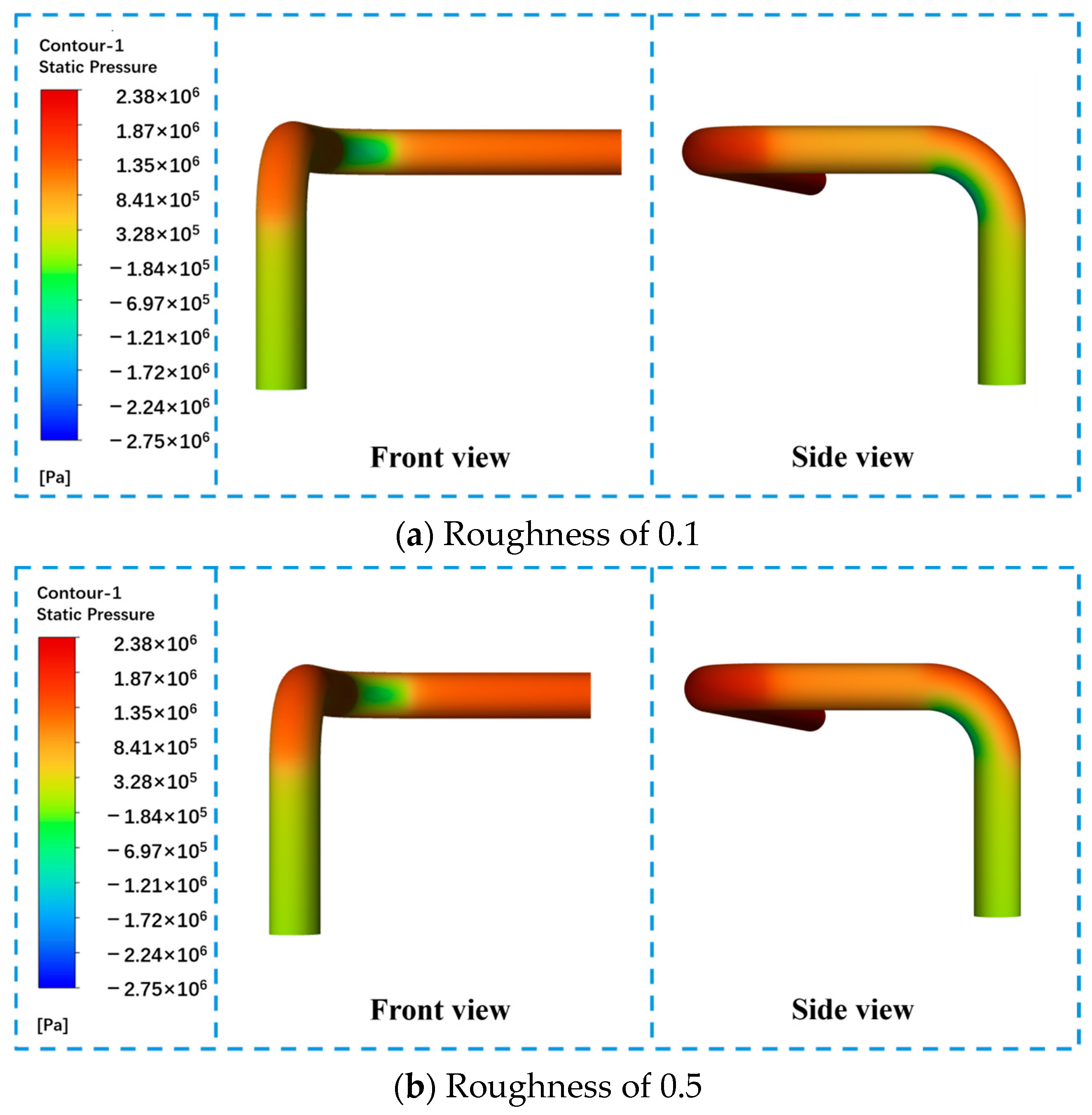
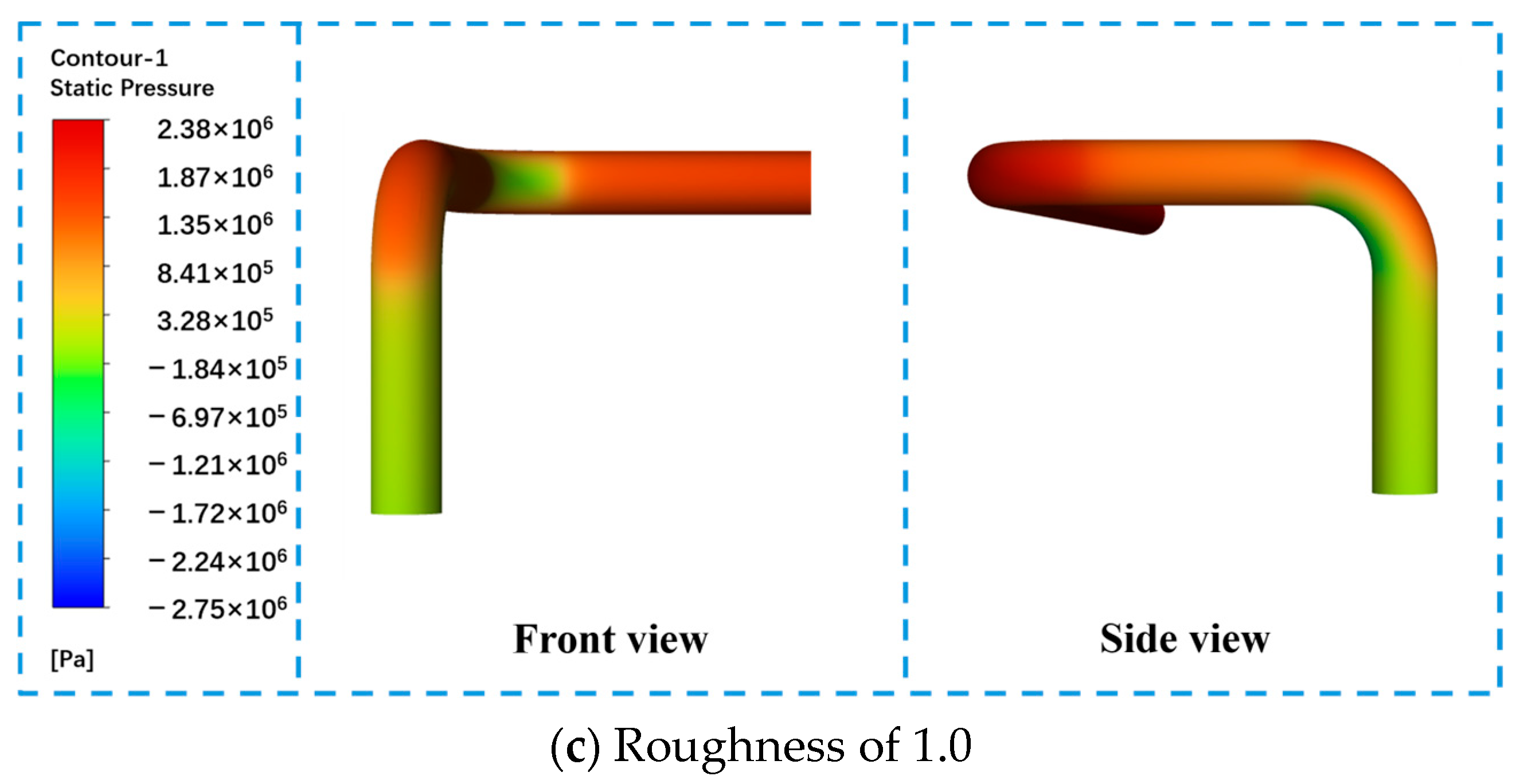
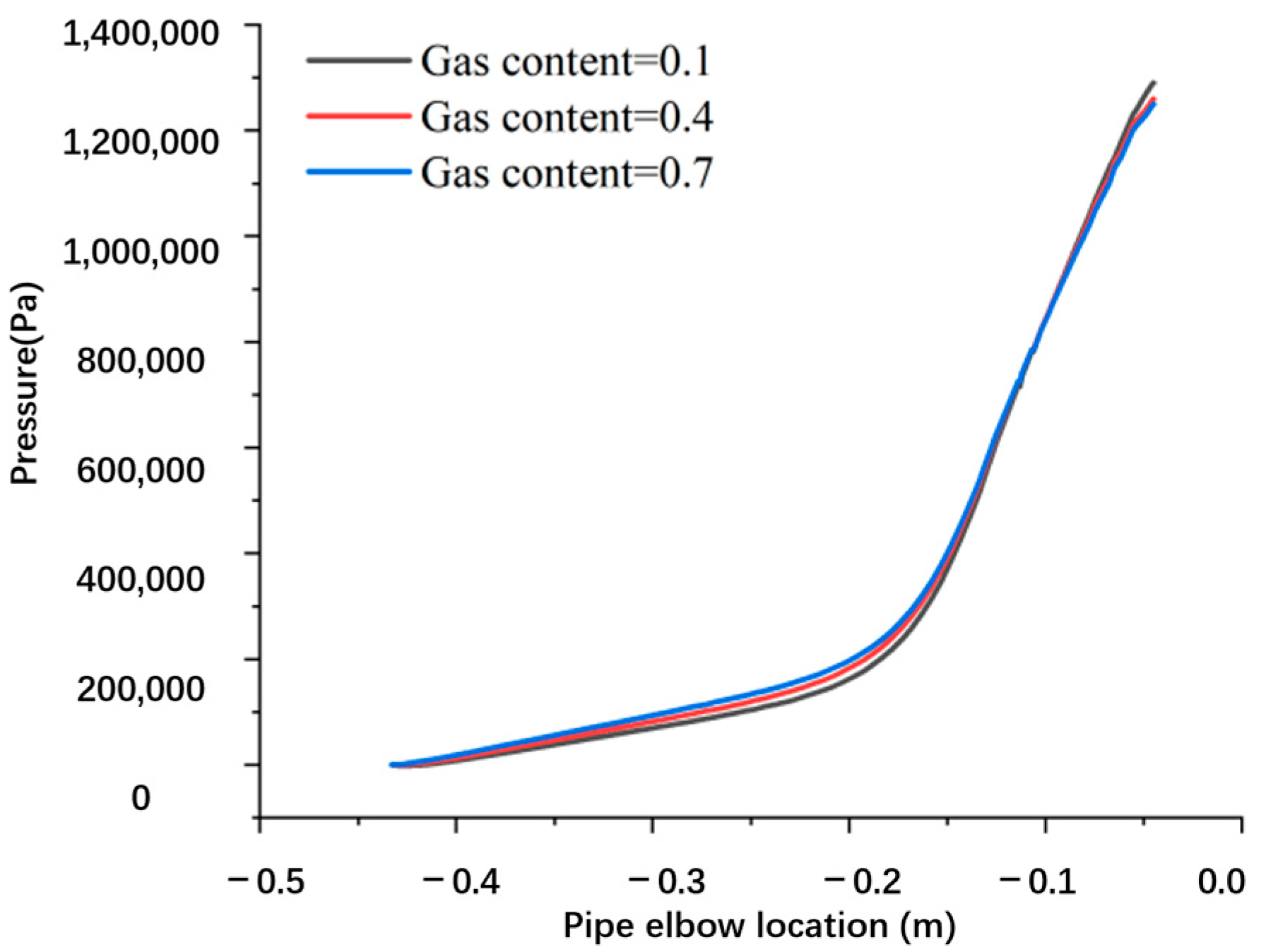
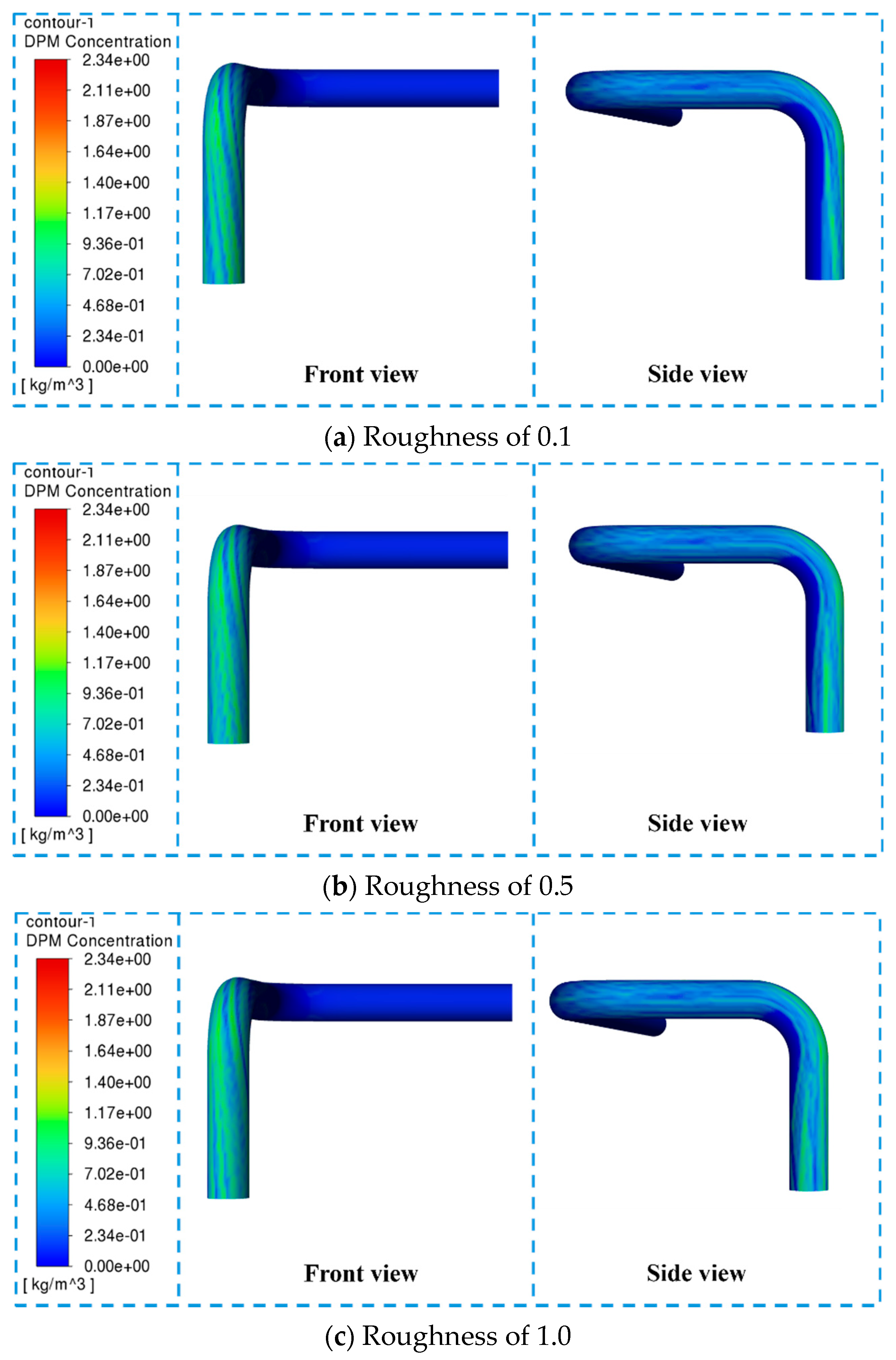
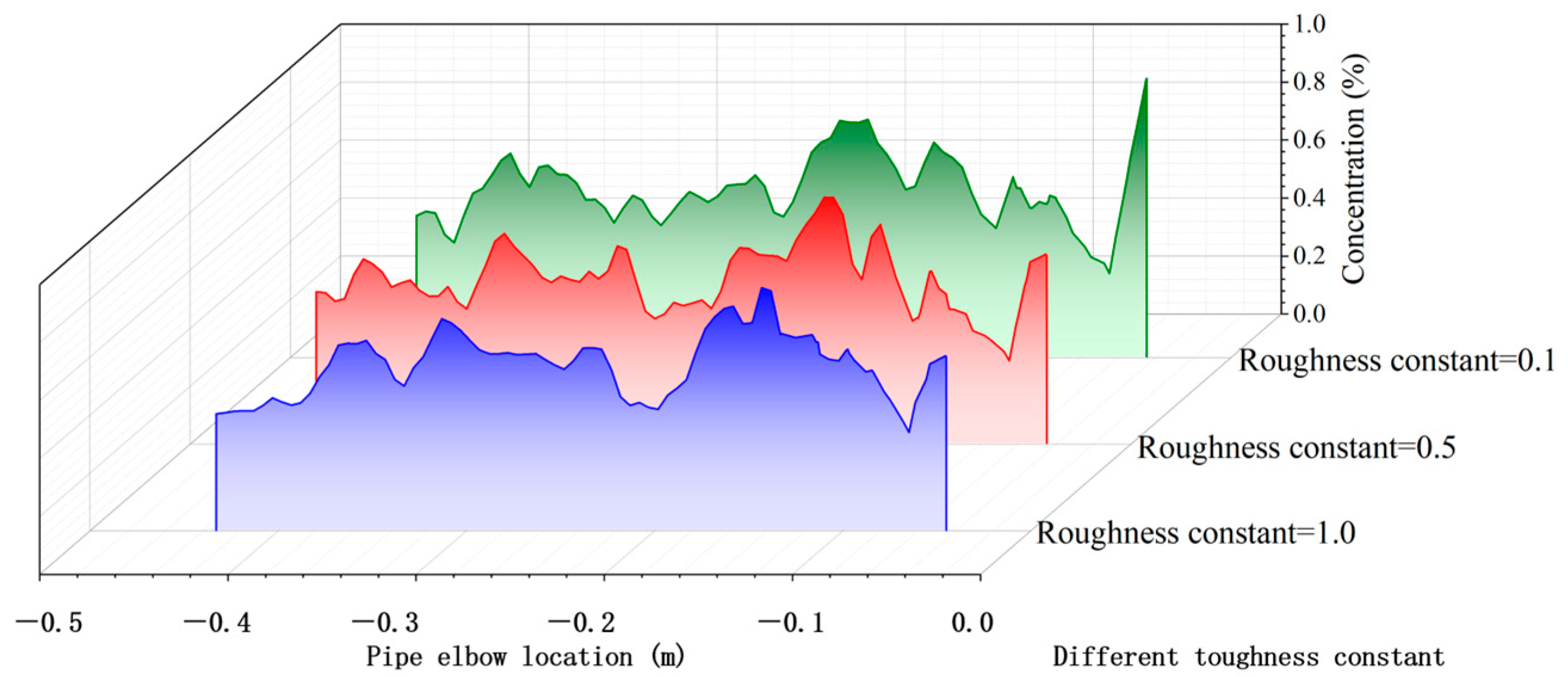
3.2.2. Effects of Pipe Bend Inner Surface Roughness on Pressure Distribution and DPM in Gas–Liquid Two-Phase Flow
4. Conclusions
- (1)
- An increased void fraction significantly enhances turbulence intensity and centrifugal force effects, leading to localized pressure peaks and higher DPM (Discrete Phase Model) particle concentrations at the pipe bend, which accelerates erosion and cyclic corrosion product detachment.
- (2)
- Greater surface roughness disrupts flow attachment and reattachment behavior, amplifies flow instability, and shifts the location of DPM deposition upstream. This results in increased wall pressure, non-uniform distribution, and intensified local corrosion, as confirmed by SEM imaging.
- (3)
- The interaction of high void fraction and roughness exhibits a strong synergistic effect, where extreme pressure and DPM values are reached. This coupling amplifies erosion–corrosion mechanisms and raises the risk of rapid wall thinning, especially at critical flow regions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Description | Unit | Reference |
| ρ | Fluid density | kg/m3 | [21] |
| t | Time | s | [21] |
| ux, uy, uz | Fluid velocity components in x, y, and z directions | m/s | [21] |
| x, y, z | Spatial coordinates in x, y, and z directions | m | [21] |
| τij | Second-order stress tensor | Pa | [22] |
| Fi | Body force per unit volume in x/y/z direction | N/m3 | [22] |
| E | Total energy of fluid element | J/kg | [23] |
| JE | Molecular heat flux | W/m2 | [23] |
| J_m | Diffusion flux of component m | mol/(m2·s) | [23] |
| h_m | Enthalpy of component m | J/kg | [23] |
| μ | Dynamic viscosity | Pa·s | [23] |
| μt | Turbulent viscosity | Pa·s | [23] |
| YM | Compressibility-induced dissipation correction | — | [23] |
| Prt | Turbulent Prandtl number | — | [23] |
| k | Turbulent kinetic energy | m2/s2 | [23] |
| ε | Dissipation rate of turbulent kinetic energy | m2/s3 | [23] |
| σk, σε | Prandtl numbers for k and ε | — | [23] |
| C1ε, C2ε, Cμ | Empirical constants in turbulence model | — | [23] |
| V | Gas volume | m3 | [24] |
| N | Molar amount of gas | mol | [24] |
| Z | Gas compressibility factor | — | [24] |
| Ym | Mass fraction of component m | — | [25] |
References
- Berrichon, J.D.; Louahlia-Gualous, H.; Bandelier, P.; Bariteau, N. Experimental and theoretical investigations on condensation heat transfer at very low pressure to improve power plant efficiency. Energy Convers. Manag. 2014, 87, 539–551. [Google Scholar] [CrossRef]
- Zhang, C.; Gallichan, R.; Leung, D.P.; Budgett, D.M.; McCormick, D. A high-precision and low-power capacitive pressure sensor interface IC with wireless power and data transfer for a pressure sensor implant. IEEE Sens. J. 2023, 23, 7105–7114. [Google Scholar] [CrossRef]
- Rusin, A.; Tomala, M.; Łukowicz, H.; Nowak, G.; Kosman, W. On-line control of stresses in the power unit pressure elements taking account of variable heat transfer conditions. Energies 2021, 14, 4708. [Google Scholar] [CrossRef]
- Brodov, Y.M.; Aronson, K.E.; Ryabchikov, A.Y.; Nirenshtein, M.A.; Murmanskii, I.B.; Zhelonkin, N.V. State of the art and trends in the design and operation of high- and low-pressure heaters for steam turbines at thermal and nuclear power plants in Russia and abroad: Part 2. Heater design and operation peculiarities. Therm. Eng. 2020, 67, 790–799. [Google Scholar] [CrossRef]
- Qu, M.; Yan, X.; Wang, H.; Hei, Y.; Liu, H.; Li, Z. Energy, exergy, economic and environmental analysis of photovoltaic/thermal integrated water source heat pump water heater. Renew. Energy 2022, 194, 1084–1097. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Z.-D.; Li, K.; Li, H.-X.; Zhao, J.-F. Influence of heater thermal capacity on bubble dynamics and heat transfer in nucleate pool boiling. Appl. Therm. Eng. 2015, 88, 118–126. [Google Scholar] [CrossRef]
- Zahedi, R.; Babaee Rad, A. Numerical and experimental simulation of gas-liquid two-phase flow in 90-degree elbow. Alexandria Eng. J. 2022, 61, 2536–2540. [Google Scholar] [CrossRef]
- Zhang, G.; Cai, W.; Tong, B.; Sun, Y.; Hu, E. Interfacial wave of the gas-liquid two-phase flow in unsaturated reservoir pores. Colloids Surf. A Physicochem. Eng. Asp. 2023, 670, 131597. [Google Scholar] [CrossRef]
- Dong, F.; Zhang, S.; Shi, X.; Wu, H.; Tan, C. Flow regimes identification-based multidomain features for gas-liquid two-phase flow in horizontal pipe. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Shao, C.; Bao, N.; Wang, S.; Zhou, J. Study on the prediction method and the flow characteristics of gas-liquid two-phase flow patterns in the suction chamber. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 2700–2718. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L.; Zhang, R.; Chen, X.; Zhao, Y.; Yuan, S. Numerical simulation of gas-liquid two-phase flow in the micro-fracture networks in fractured reservoirs. J. Nat. Gas Sci. Eng. 2021, 94, 104101. [Google Scholar] [CrossRef]
- Wei, N.; Xu, C.; Meng, Y.; Li, G.; Ma, X.; Liu, A. Numerical simulation of gas-liquid two-phase flow in wellbore based on drift flux model. Appl. Math. Comput. 2018, 338, 175–191. [Google Scholar] [CrossRef]
- Guo, W.; Wang, L.; Liu, C. Prediction of gas-liquid two-phase flow rates through a vertical pipe based on thermal diffusion. Ind. Eng. Chem. Res. 2021, 60, 2686–2697. [Google Scholar] [CrossRef]
- Xie, C.; Li, X.; Liu, Y.; Zeng, F.; Luo, C. Experimental analysis and model evaluation of gas-liquid two-phase flow through choke in a vertical tube. J. Petrol. Sci. Eng. 2022, 209, 109902. [Google Scholar] [CrossRef]
- Sha, W.; Leng, G.; Xu, R.S.; Li, S. Numerical simulation of inlet void fraction affecting oil-gas two-phase flow characteristics in 90° elbows. J. Appl. Fluid Mech. 2024, 17, 1524–1535. [Google Scholar]
- Chen, D.; Lin, Z. Numerical investigation of gas-liquid two-phase flow in a swirl meter. MAPAN 2021, 36, 521–532. [Google Scholar] [CrossRef]
- Ma, Y.; Yan, G.; Scheuermann, A. Discrete bubble flow in granular porous media via multiphase computational fluid dynamic simulation. Front. Earth Sci. 2022, 10, 947625. [Google Scholar] [CrossRef]
- Govindaraj, P.; Arun, C.S. Investigating ovality and wall-thinning behaviors in free-form bending of thin pipe bends with varying guider length and roller die diameter. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 605. [Google Scholar] [CrossRef]
- Li, W.; Liu, W.; Liu, H.; Ma, Z.; Hu, G.; Song, J.; Wang, T.; Zhang, Y.; Zhang, H. Effect of different powers on microstructure evolution and corrosion behavior of 5SiC-Ni60 coatings by directed energy deposition. Opt. Laser Technol. 2025, 180, 111456. [Google Scholar] [CrossRef]
- Dyck, O.; Almutlaq, J.; Lingerfelt, D.; Swett, J.L.; Oxley, M.P.; Huang, B.; Lupini, A.R.; Englund, D.; Jesse, S. Direct imaging of electron density with a scanning transmission electron microscope. Nat. Commun. 2023, 14, 7550. [Google Scholar] [CrossRef]
- Li, X.; Tian, R.; He, L.; Lv, Y.; Zhou, S.; Li, Y. A novel numerical approach for assessing the gas-liquid flow characteristics in pipelines utilizing a two-fluid model. Appl. Math. Model. 2024, 131, 233–252. [Google Scholar] [CrossRef]
- Marrocos, P.H.; Fernandes, I.S.; Pituco, M.M.; Lopes, J.C.B.; Dias, M.M.; Santos, R.J.; Vilar, V.J.P. CFD and lower order mechanistic models for gas-liquid flow in NETmix: Pressure drop and gas hold-up. Chem. Eng. Sci. 2024, 284, 119478. [Google Scholar] [CrossRef]
- Hao, L.; Zhai, X.W.; Wang, K. Study on the diffusion characteristics of small hole leakage of high-sulfur natural gas in gathering and transmission pipelines. Int. Commun. Heat Mass Transf. 2025, 164, 108942. [Google Scholar] [CrossRef]
- Zhang, P.; Ma, L.; Sun, J.; Chen, R.; Pei, G.; Chen, X.; Fan, J. Numerical investigation of air flow field evolution and leakage patterns in large-scale goaf areas. Phys. Fluids 2025, 37, 027151. [Google Scholar] [CrossRef]
- Niño, L.; Gelves, R.; Ali, H.; Solsvik, J.; Jakobsen, H. Applicability of a modified breakage and coalescence model based on the complete turbulence spectrum concept for CFD simulation of gas-liquid mass transfer in a stirred tank reactor. Chem. Eng. Sci. 2020, 211, 115272. [Google Scholar] [CrossRef]
- Shirzadi, M.; Mirzaei, P.A.; Naghashzadegan, M. Improvement of k-epsilon turbulence model for CFD simulation of atmospheric boundary layer around a high-rise building using stochastic optimization and Monte Carlo sampling technique. J. Wind Eng. Ind. Aerodyn. 2017, 171, 366–379. [Google Scholar] [CrossRef]
- Anand, S.; Chambe, J.E.; Bouvet, C.; Rivallant, S. Stacking sequence optimization of composite tubes submitted to crushing using the discrete ply model (DPM). Mech. Adv. Mater. Struct. 2024, 31, 820–833. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, S.; Yue, P.; Kulik, A.S.; Li, G. Surface pressure calculation method of multi-field coupling mechanism under the action of flow field. Symmetry 2023, 15, 1064. [Google Scholar] [CrossRef]
- Chen, H.; Sun, Z.; Li, Y.; Su, H. Simulation of flow and heat transfer in high-temperature and high-pressure reservoir based on multi-physical field coupling model at pore scale. Can. J. Chem. Eng. 2025, 103, 914–926. [Google Scholar] [CrossRef]
- Hu, R.; Fang, F.; Salinas, P.; Pain, C.C.; Sto. Domingo, N.D.; Mark, O. Numerical simulation of floods from multiple sources using an adaptive anisotropic unstructured mesh method. Adv. Water Resour. 2019, 123, 173–188. [Google Scholar] [CrossRef]
- Ma, X.; Gu, Z.; Ni, D.; Li, C.; Zhang, W.; Zhang, F.; Tian, M. Experimental study on gas-liquid two-phase flow upstream and downstream of U-bends. Processes 2024, 12, 277. [Google Scholar] [CrossRef]







| Element | C | Si | Mn | Cr | Ni | Cu |
|---|---|---|---|---|---|---|
| Content (wt%) | 0.17~0.23 | 0.35~0.63 | 0.35~0.63 | ≤0.25 | ≤0.30 | ≤0.25 |
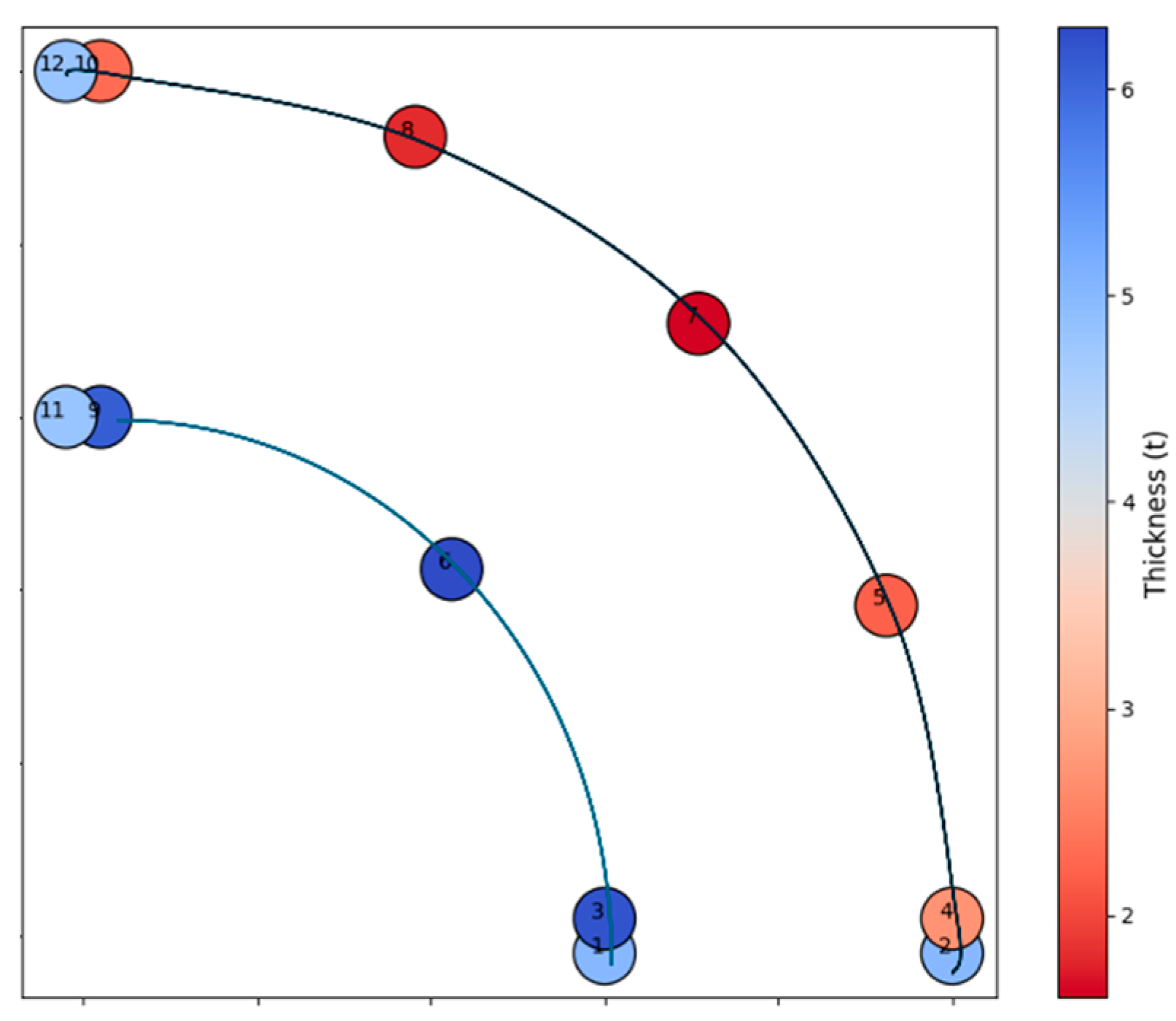
| Test point | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Thickness (mm) | 5.0 | 5.0 | 6.2 | 2.7 | 2.2 | 6.3 | 1.6 | 1.8 | 6.1 | 2.3 | 4.8 | 4.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; He, W.; Zhang, P.; Wang, H.; Wei, Z. Investigation on Corrosion-Induced Wall-Thinning Mechanisms in High-Pressure Steam Pipelines Based on Gas–Liquid Two-Phase Flow Characteristics. Processes 2025, 13, 2096. https://doi.org/10.3390/pr13072096
Li G, He W, Zhang P, Wang H, Wei Z. Investigation on Corrosion-Induced Wall-Thinning Mechanisms in High-Pressure Steam Pipelines Based on Gas–Liquid Two-Phase Flow Characteristics. Processes. 2025; 13(7):2096. https://doi.org/10.3390/pr13072096
Chicago/Turabian StyleLi, Guangyin, Wei He, Pengyu Zhang, Hu Wang, and Zhengxin Wei. 2025. "Investigation on Corrosion-Induced Wall-Thinning Mechanisms in High-Pressure Steam Pipelines Based on Gas–Liquid Two-Phase Flow Characteristics" Processes 13, no. 7: 2096. https://doi.org/10.3390/pr13072096
APA StyleLi, G., He, W., Zhang, P., Wang, H., & Wei, Z. (2025). Investigation on Corrosion-Induced Wall-Thinning Mechanisms in High-Pressure Steam Pipelines Based on Gas–Liquid Two-Phase Flow Characteristics. Processes, 13(7), 2096. https://doi.org/10.3390/pr13072096






