An Enhanced Control of Grid-Connected Solid-Oxide Fuel Cell System Using Beluga Whale-Optimized Fractional-Order PID Control
Abstract
1. Introduction
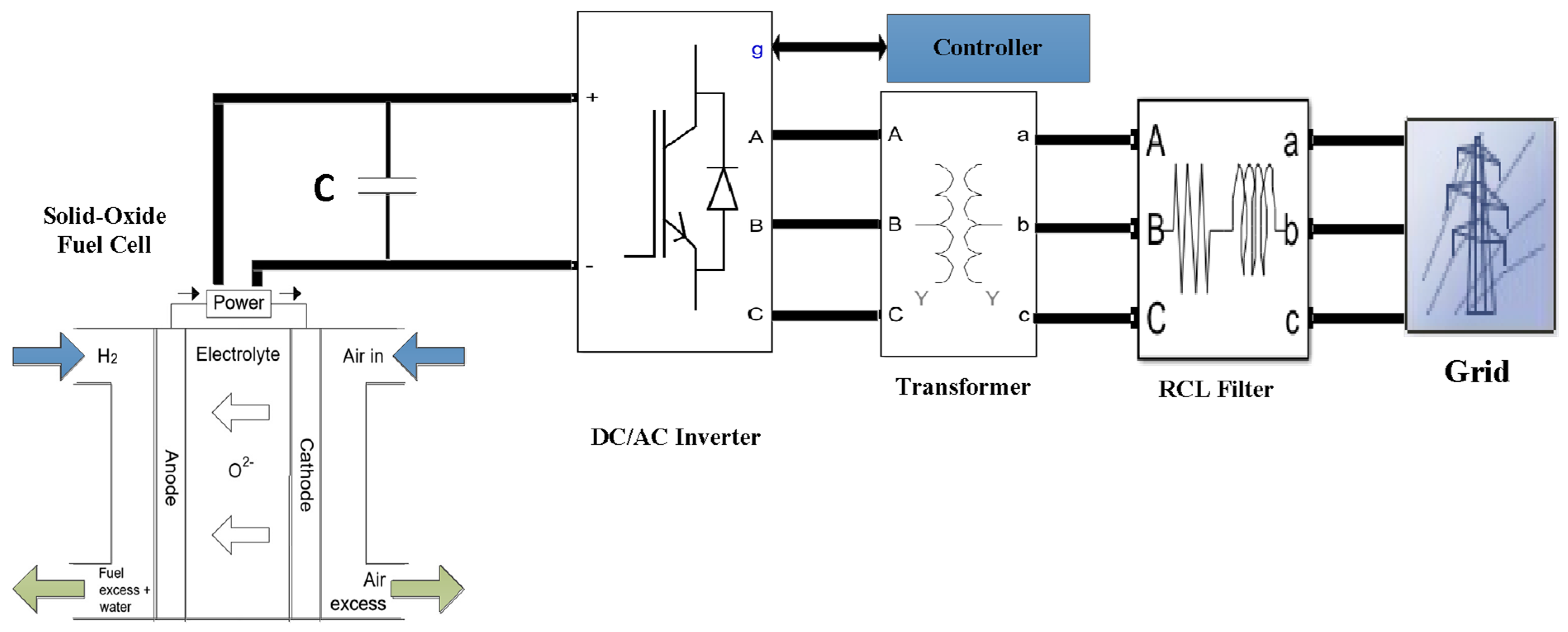
2. The System Description of Solid-Oxide Fuel Cell with Grid Connection
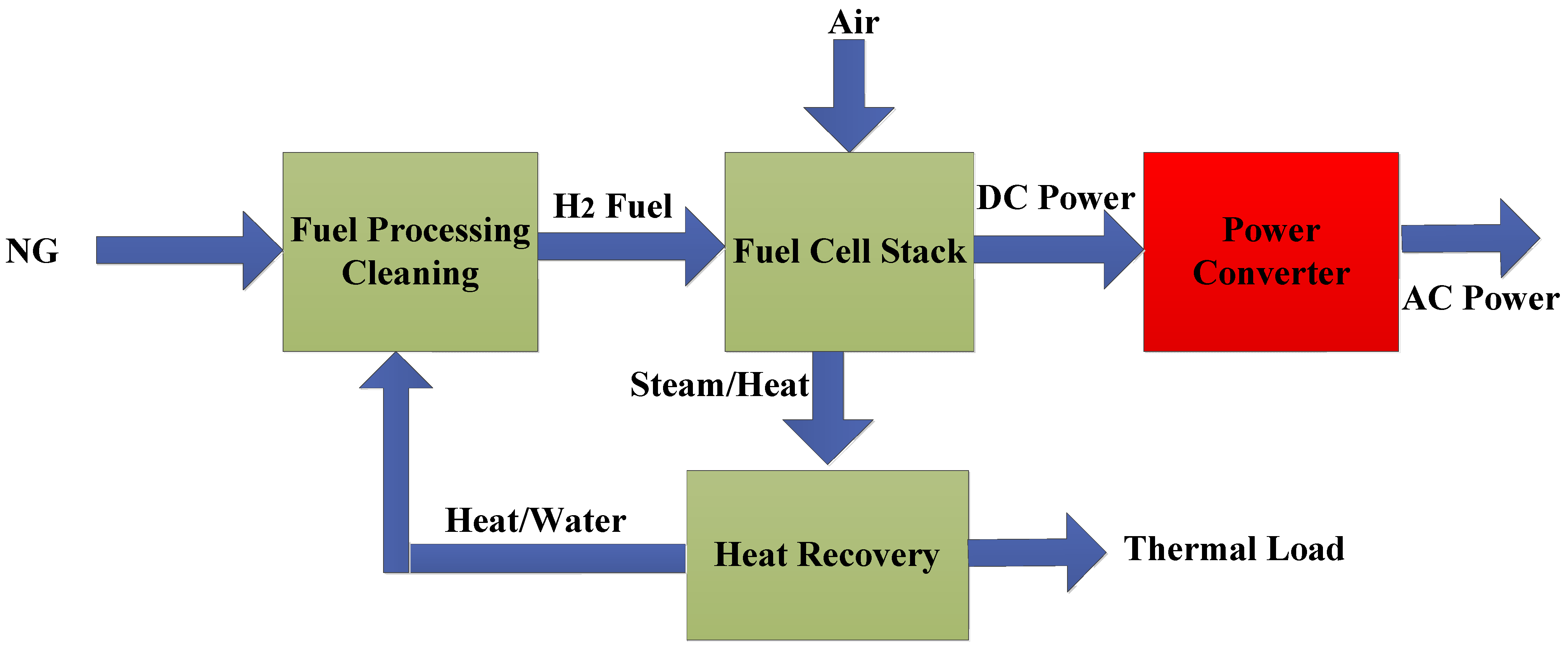
2.1. Solid-Oxide Fuel Cell
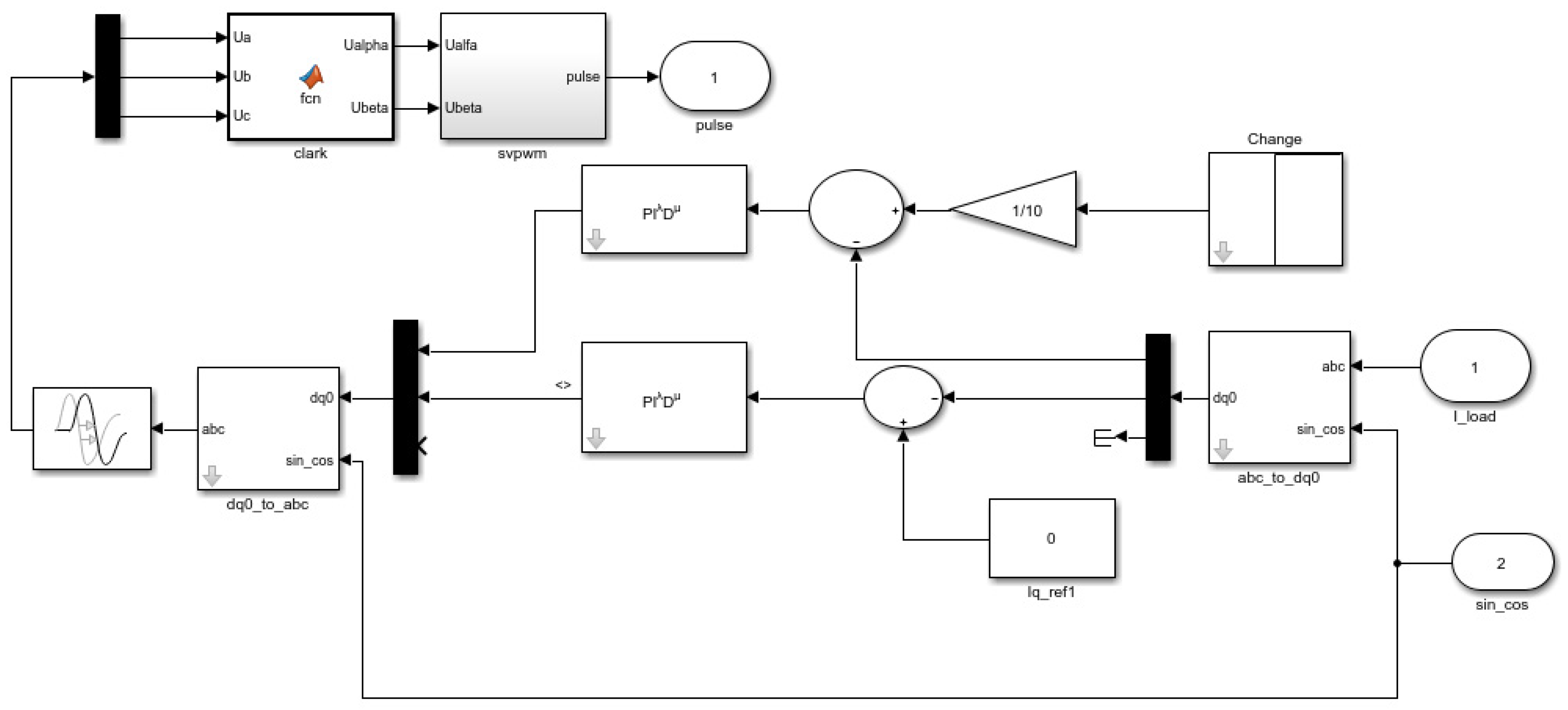
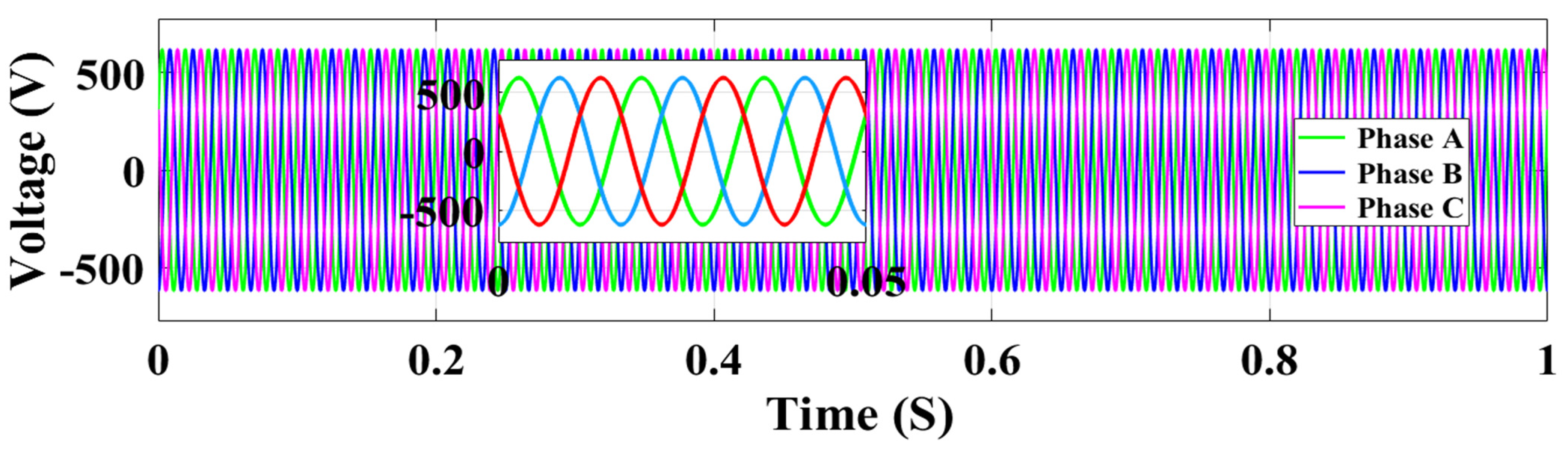
2.2. Control in Inverter
Fractional-Order PID
- The Riemann–Liouville (R-L) description:
- 2.
- The description of Grunwald–Letnikov (G-L) is shown in Equation (8):
- 3.
- The Caputo definition is given by:
3. Optimization Techniques
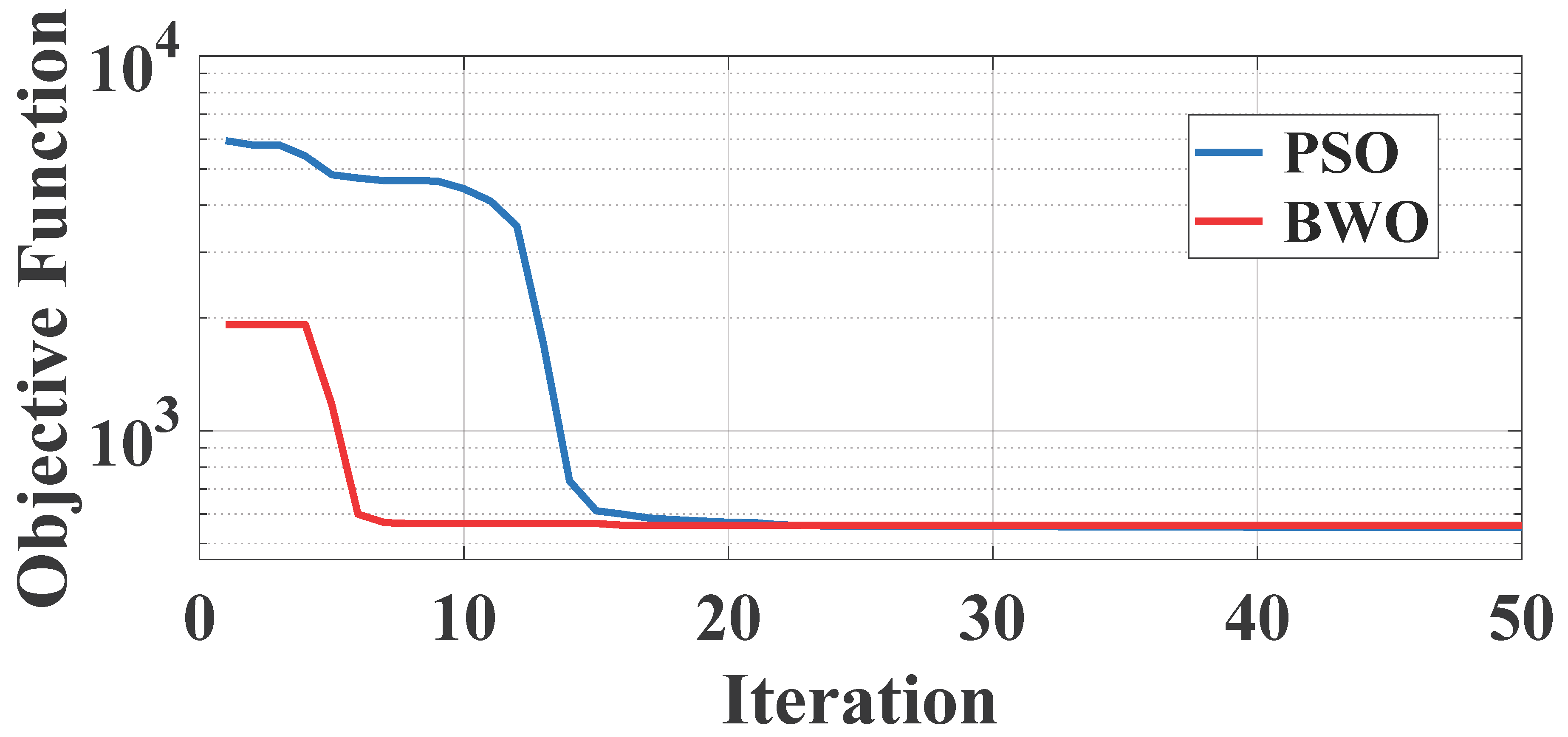
3.1. Beluga Whale Optimization
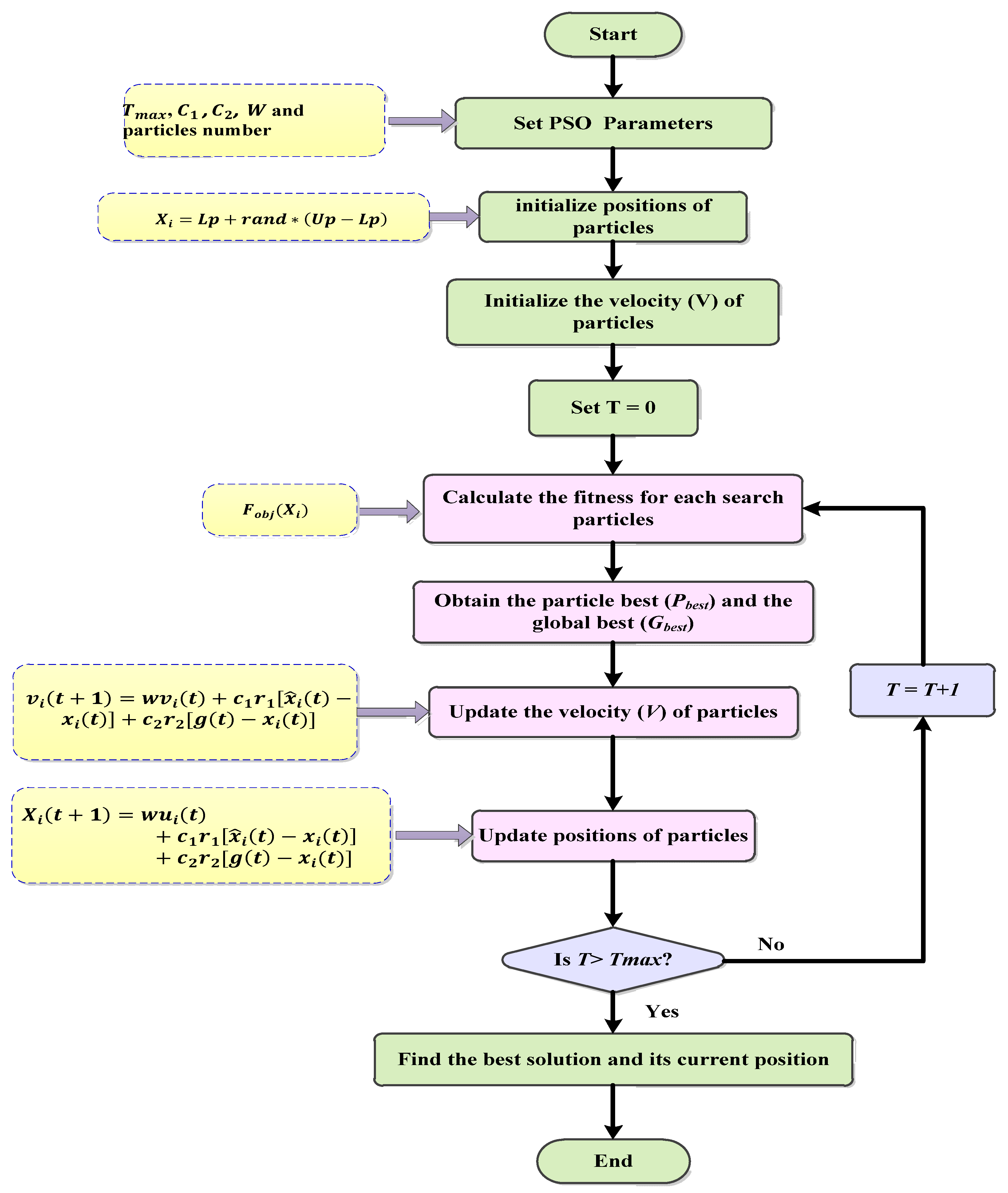
3.2. Particle Swarm Optimization
4. Simulation Results and Discussion
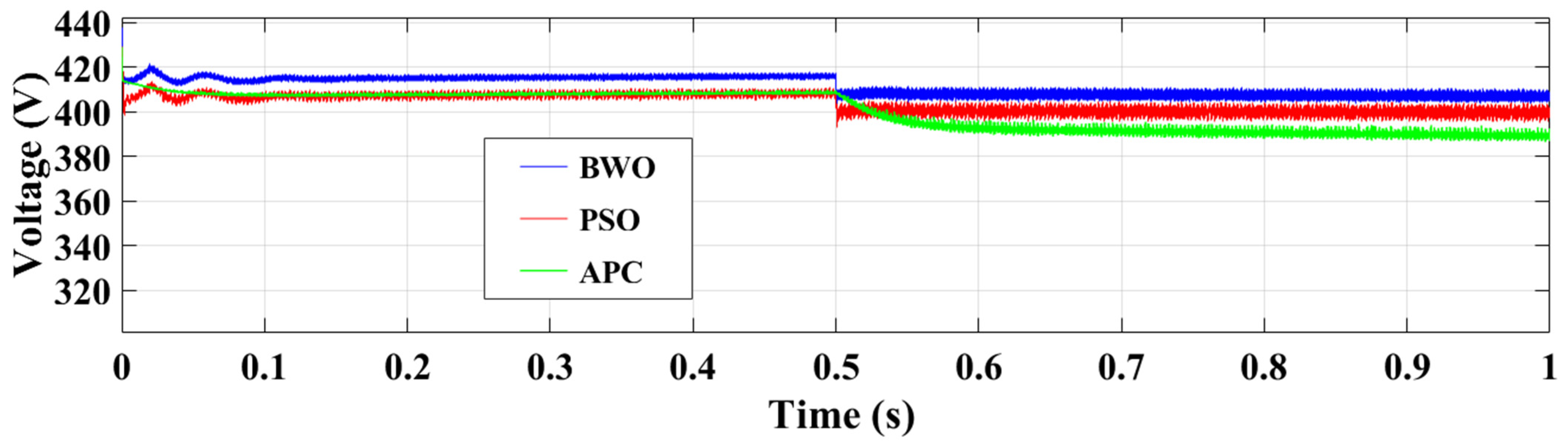
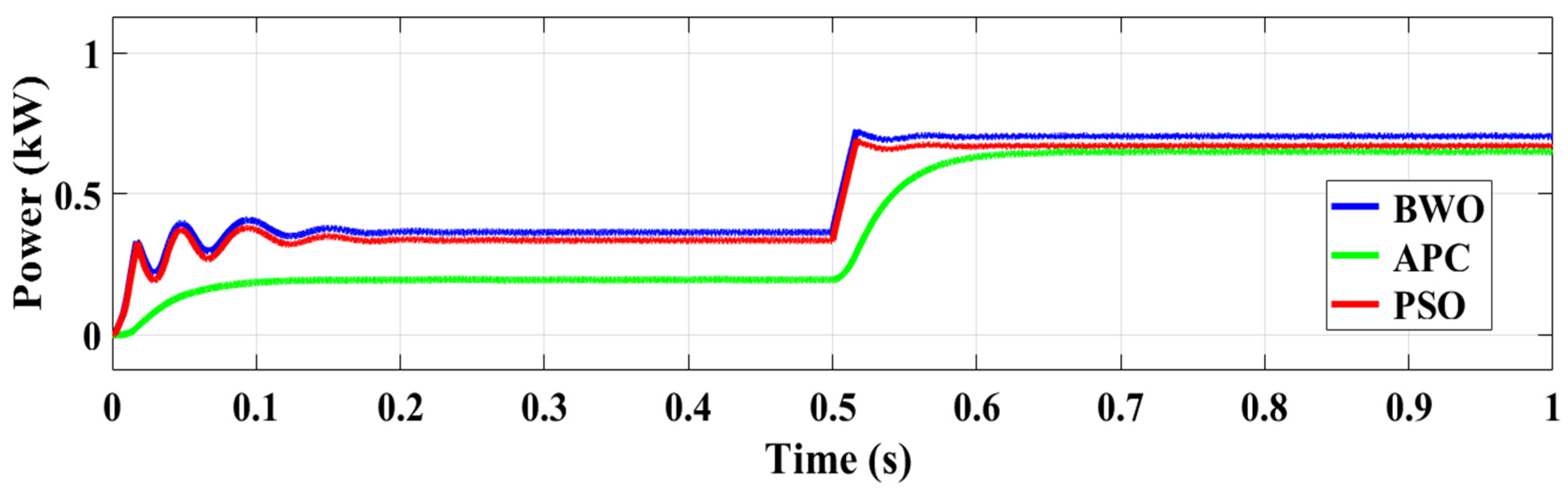
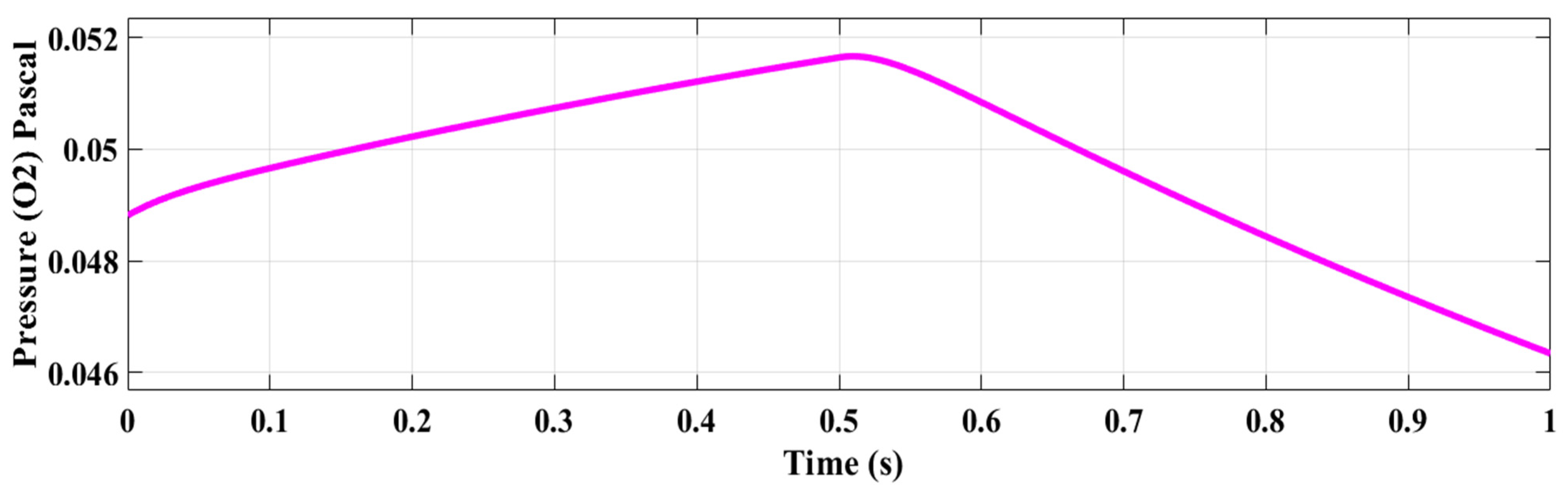
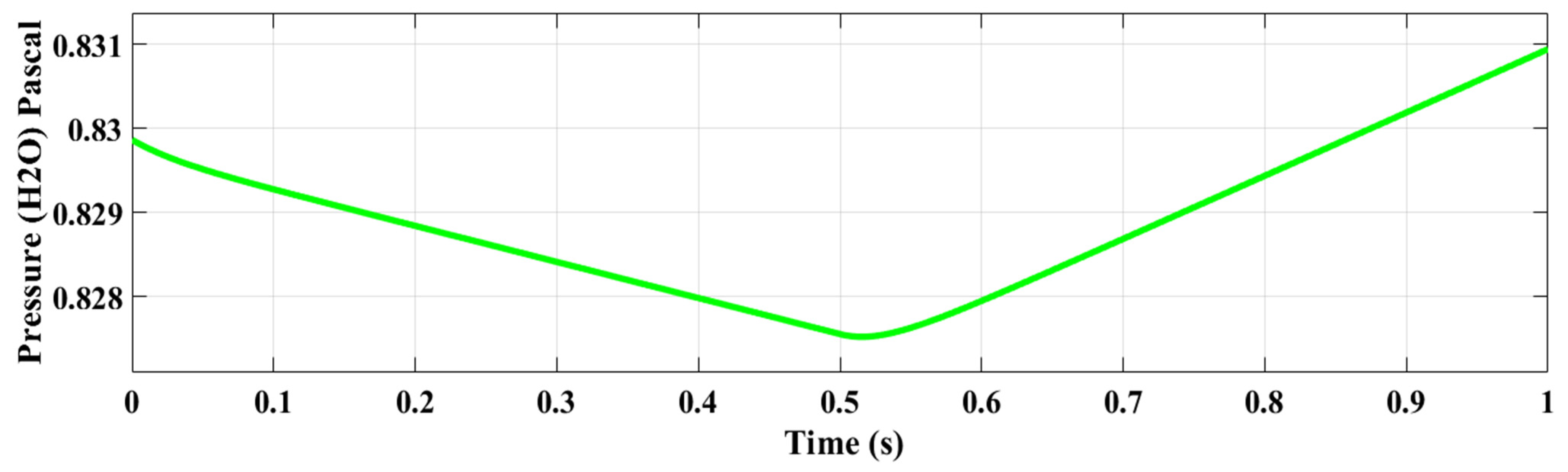
4.1. Scenario 1: Simulation Under a Steady Reference Current Controller
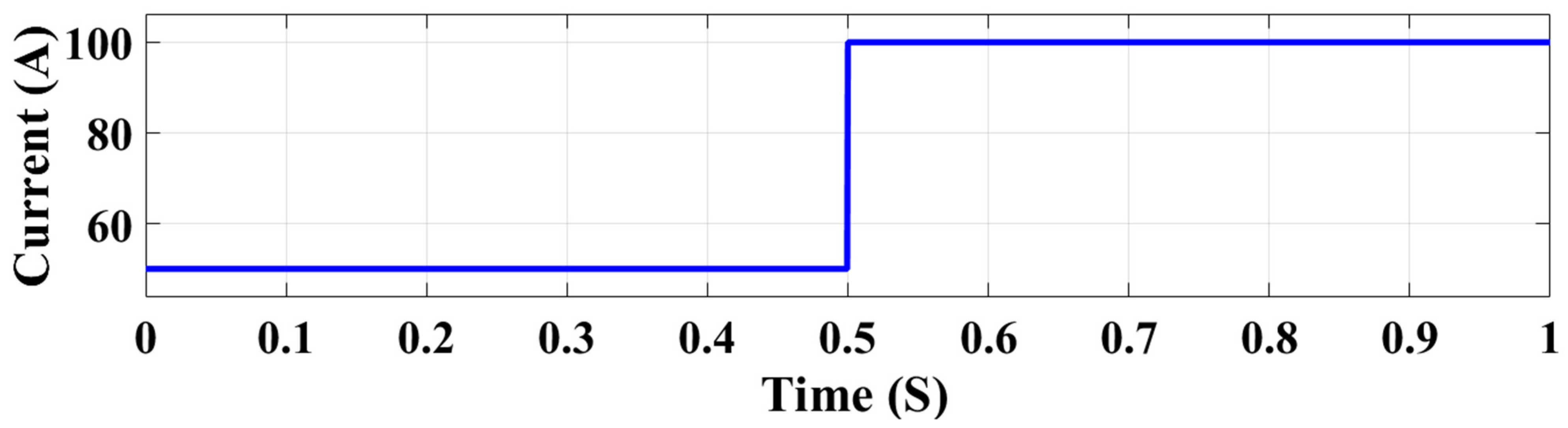
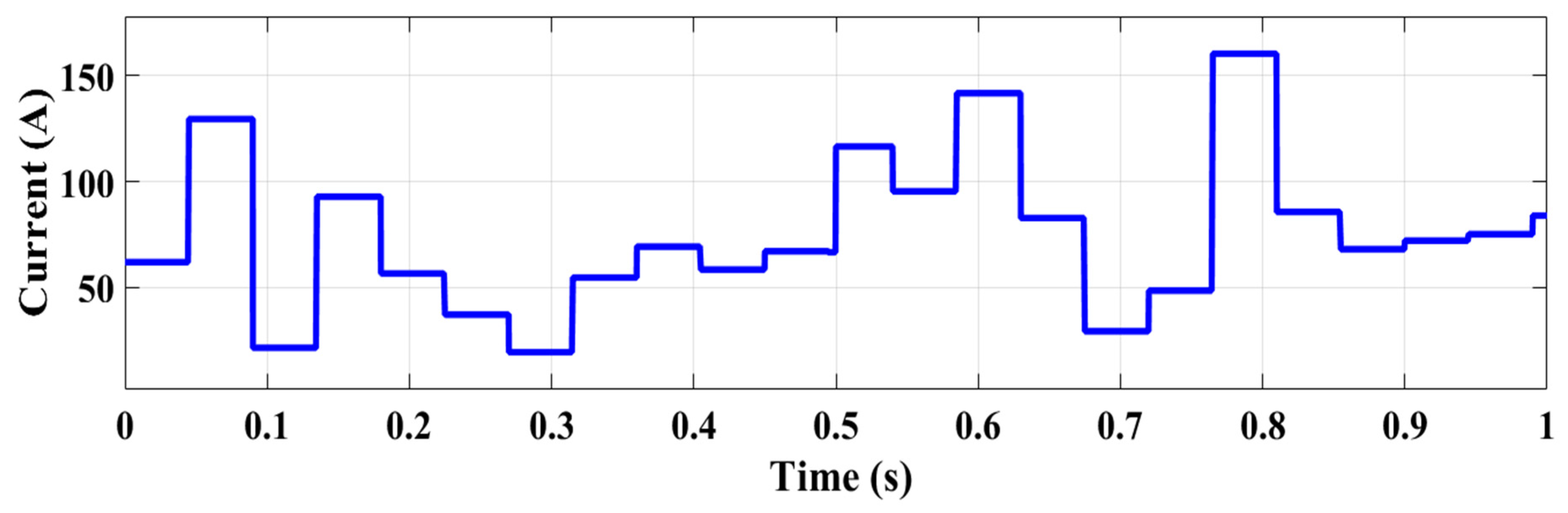
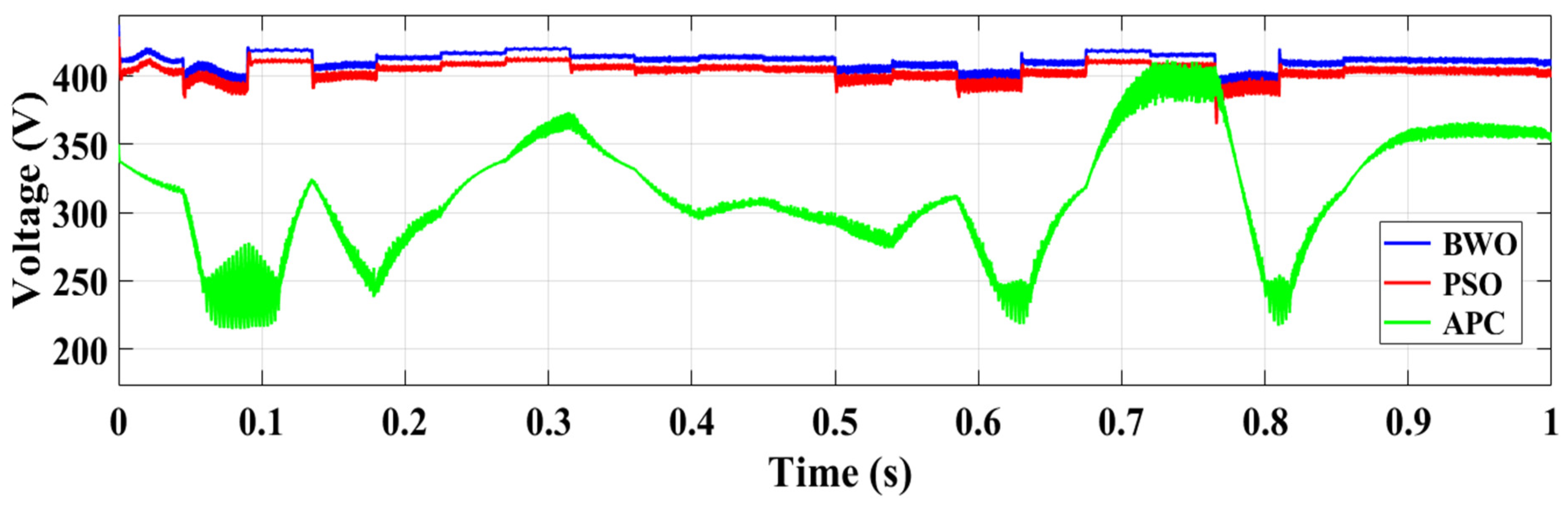
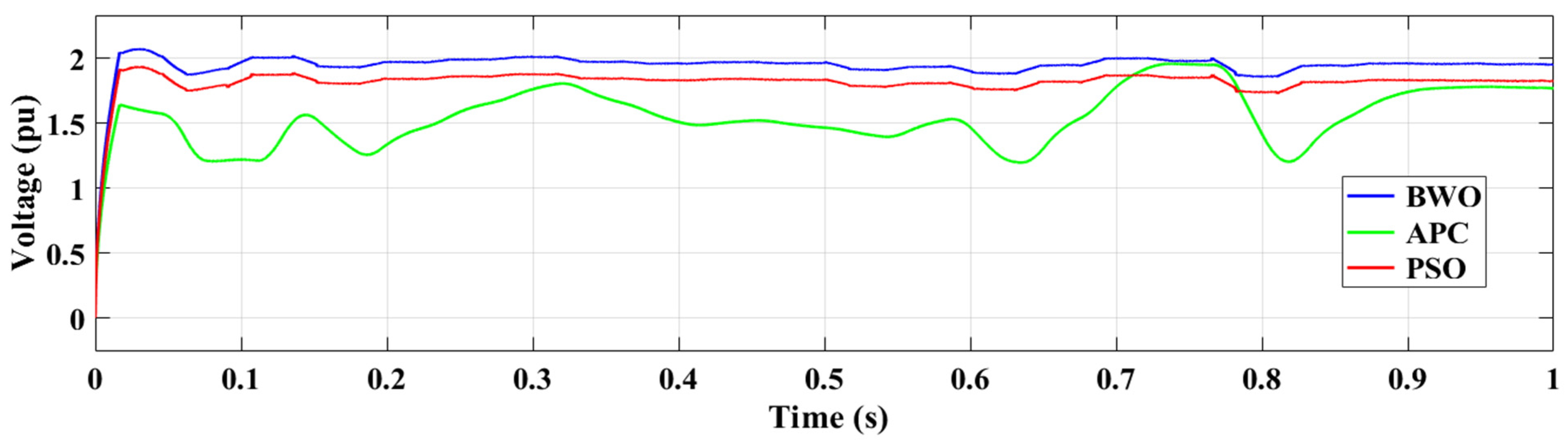
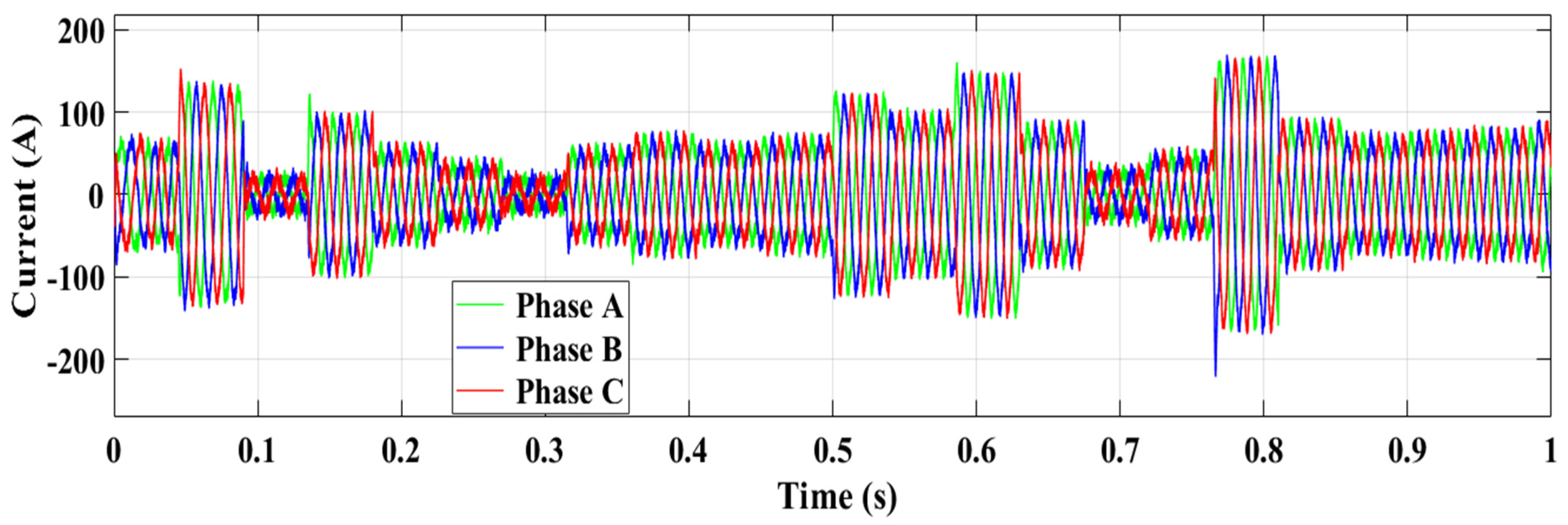
4.2. Scenario 2: Simulation Under a Random Current Controller Changes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols and Abbreviations | |||
| i | particle index | r3, r4 | denote the number of randoms |
| w | inertial coefficient | u and v | refer to random values obtained from the normal distribution |
| c1, c2 | hastening constants | Β | a constant equal to 1.5 |
| r1, r2 | random values | , and | Represent random numbers |
| (t) | particle’s velocity | Represents a random value in the range [0–1]. | |
| (t) | position particle’s | represents a randomly selected BW’s location | |
| (t) | particle in best solution | a fractional-order integration | |
| g(t) | swarm in best solution | a fractional-order derivation | |
| Acronyms | |||
| PSO | Particle Swarm Optimization | ||
| FCs | Fuel Cell | ||
| FOPID | Fractional-Order Proportion–Integral–Derivative | ||
| SOFC | Solid-Oxide Fuel Cell | ||
| APC | Active Power Controller | ||
| BWO | Beluga Whale Optimization | ||
| RCC | Reference Current Control | ||
References
- Giddey, S.; Badwal, S.P.S.; Kulkarni, A.; Munnings, C. A comprehensive review of direct carbon fuel cell technology. Prog. Energy Combust. Sci. 2012, 38, 360–399. [Google Scholar] [CrossRef]
- Badwal, S.P.S.; Giddey, S.; Munnings, C.; Kulkarni, A. Review of progress in high temperature solid oxide fuel cells. J. Aust. Ceram. Soc. 2015, 50, 23–37. [Google Scholar]
- Han, Y.; Li, H.; Shen, P.; Coelho, E.A.A.; Guerrero, J.M. Review of active and reactive power sharing strategies in hierarchical controlled microgrids. IEEE Trans. Power Electron. 2016, 32, 2427–2451. [Google Scholar] [CrossRef]
- Xia, Y.; Shimomura, M.; Paserba, J. Active power control for preventing voltage instability using an adjustable speed machine. In 2001 Power Engineering Society Summer Meeting. IEEE Conf. Proc. 2001, 2, 866–871. [Google Scholar]
- Ranganayakulu, R.; Babu, G.U.B.; Rao, A.S.; Patle, D.S. A comparative study of fractional order PIλ/PIλDµ tuning rules for stable first order plus time delay processes. Resour.-Effic. Technol. 2016, 2, S136–S152. [Google Scholar] [CrossRef]
- Nataraj, D.; Subramanian, M. Design and optimal tuning of fractional order PID controller for paper machine headbox using jellyfish search optimizer algorithm. Sci. Rep. 2025, 15, 1631. [Google Scholar] [CrossRef]
- Saleh, B.; Yousef, A.M.; Ebeed, M.; Abo-Elyousr, F.K.; Elnozahy, A.; Mohamed, M.; Abdelwahab, S.A.M. Design of PID controller with grid-connected hybrid renewable energy system using optimization algorithms. J. Electr. Eng. Technol. 2021, 16, 3219–3233. [Google Scholar] [CrossRef]
- Masadeh, R.; Alsharman, N.; Sharieh, A.; Mahafzah, B.A.; Abdulrahman, A. Task scheduling on cloud computing based on sea lion optimization algorithm. Int. J. Web Inf. Syst. 2021, 17, 99–116. [Google Scholar] [CrossRef]
- Ranganayakulu, R.; Uday Bhaskar Babu, G.; Seshagiri Rao, A. Fractional filter IMC-PID controller design for second order plus time delay processes. Cogent Eng. 2017, 4, 1366888. [Google Scholar] [CrossRef]
- Zamani, M.; Karimi-Ghartemani, M.; Sadati, N.; Parniani, M. Design of a fractional order PID controller for an AVR using particle swarm optimization. Control Eng. Pract. 2009, 17, 1380–1387. [Google Scholar] [CrossRef]
- Padula, F.; Visioli, A. On the fragility of fractional-order PID controllers for FOPDT processes. ISA Trans. 2016, 60, 228–243. [Google Scholar] [CrossRef]
- Padula, F.; Visioli, A. Tuning rules for optimal PID and fractional-order PID controllers. J. Process Control 2011, 21, 69–81. [Google Scholar] [CrossRef]
- Wang, W.; Su, C.; Wu, Y.; Ran, R.; Shao, Z. Progress in solid oxide fuel cells with nickel-based anodes operating on methane and related fuels. Chem. Rev. 2013, 113, 8104–8151. [Google Scholar] [CrossRef]
- Haddad, A.; Ramadan, M.; Khaled, M.; Ramadan, H.; Becherif, M. Study of hybrid energy system coupling fuel cell, solar thermal system and photovoltaic cell. Int. J. Hydrogen Energy 2020, 45, 13564–13574. [Google Scholar] [CrossRef]
- Wachsman, E.D.; Lee, K.T. Lowering the temperature of solid oxide fuel cells. Science 2011, 334, 935–939. [Google Scholar] [CrossRef] [PubMed]
- Madaci, B.; Chenni, R.; Kurt, E.; Hemsas, K.E. Design and control of a stand-alone hybrid power system. Int. J. Hydrogen Energy 2016, 41, 12485–12496. [Google Scholar] [CrossRef]
- Cao, J.Y.; Liang, J.; Cao, B.G. Optimization of fractional order PID controllers based on genetic algorithms. In Proceedings of the 2005 International Conference on Machine Learning and Cybernetics IEEE, Guangzhou, China, 18–21 August 2005; Volume 9, pp. 5686–5689. [Google Scholar]
- Verma, S.K.; Yadav, S.; Nagar, S.K. Optimization of fractional order PID controller using grey wolf optimizer. J. Control Autom. Electr. Syst. 2017, 28, 314–322. [Google Scholar] [CrossRef]
- Zhao, D.; Li, F.; Ma, R.; Zhao, G.; Huangfu, Y. An unknown input nonlinear observer based fractional order PID control of fuel cell air supply system. IEEE Trans. Ind. Appl. 2020, 56, 5523–5532. [Google Scholar] [CrossRef]
- Fathy, A.; Rezk, H.; Alanazi, T.M. Recent approach of forensic-based investigation algorithm for optimizing fractional order PID-based MPPT with proton exchange membrane fuel cell. IEEE Access 2021, 9, 18974–18992. [Google Scholar] [CrossRef]
- Silaa, M.Y.; Barambones, O.; Derbeli, M.; Napole, C.; Bencherif, A. Fractional order PID design for a proton exchange membrane fuel cell system using an extended grey wolf optimizer. Processes 2022, 10, 450. [Google Scholar] [CrossRef]
- Da Silva, F.S.; de Souza, T.M. Novel materials for solid oxide fuel cell technologies: A literature review. Int. J. Hydrogen Energy 2017, 42, 26020–26036. [Google Scholar] [CrossRef]
- Wang, J.; Lam, K.Y.; Saccoccio, M.; Gao, Y.; Chen, D.; Ciucci, F. Ca and In co-doped BaFeO3−δ as a cobalt-free cathode material for intermediate-temperature solid oxide fuel cells. J. Power Sources 2016, 324, 224–232. [Google Scholar] [CrossRef]
- Jung, G.B.; Chang, C.T.; Yeh, C.C.; Nguyen, X.V.; Chan, S.H.; Lin, C.Y.; Yu, J.W.; Lee, W.T.; Chang, S.W.; Kao, I.C. Study of reversible solid oxide fuel cell with different oxygen electrode materials. Int. J. Hydrogen Energy 2016, 41, 21802–21811. [Google Scholar] [CrossRef]
- Wang, S.F.; Hsu, Y.F.; Chang, J.H.; Cheng, S.; Lu, H.C. Characteristics of Cu and Mo-doped Ca3Co4O9−δ cathode materials for use in solid oxide fuel cells. Ceram. Int. 2016, 42, 11239–11247. [Google Scholar] [CrossRef]
- Shaikh, S.P.; Muchtar, A.; Somalu, M.R. A review on the selection of anode materials for solid-oxide fuel cells. Renew. Sustain. Energy Rev. 2015, 51, 1–8. [Google Scholar] [CrossRef]
- Boldrin, P.; Brandon, N.P. Progress and outlook for solid oxide fuel cells for transportation applications. Nat. Catal. 2019, 2, 571–577. [Google Scholar] [CrossRef]
- Elnozahy, A.; Yousef, A.M.; Abo-Elyousr, F.K.; Mohamed, M.; Abdelwahab, S.A.M. Performance improvement of hybrid renewable energy sources connected to the grid using artificial neural network and sliding mode control. J. Power Electron. 2021, 21, 1166–1179. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PI/sup/spl lambda//D/sup/spl mu//-controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl.-Based Syst. 2022, 251, 109215. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A comprehensive survey on particle swarm optimization algorithm and its applications. Math. Probl. Eng. 2015, 1, 931256. [Google Scholar] [CrossRef]
- Ahmadi, S.; Abdi, S.; Kakavand, M. Maximum power point tracking of a proton exchange membrane fuel cell system using PSO-PID controller. Int. J. Hydrogen Energy 2017, 42, 20430–20443. [Google Scholar] [CrossRef]
- Said, M.; El-Rifaie, A.M.; Tolba, M.A.; Houssein, E.H.; Deb, S. An Efficient Chameleon Swarm Algorithm for Economic Load Dispatch Problem. Mathematics 2021, 9, 2770. [Google Scholar] [CrossRef]
- Haklı, H.; Uğuz, H. A novel particle swarm optimization algorithm with Levy flight. Appl. Soft Comput. 2014, 23, 333–345. [Google Scholar] [CrossRef]
- Abualigah, L.; Sheikhan, A.; Ikotun, A.M.; Zitar, R.A.; Alsoud, A.R.; Al-Shourbaji, I.; Hussien, A.G.; Jia, H. Particle swarm optimization algorithm: Review and applications. In Metaheuristic Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2024; pp. 1–14. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Tolba, M.A.; El-Magd, A.G.A.; Zaky, M.M.; El-Rifaie, A.M. Fuel cell parameters estimation via marine predators and political optimizers. IEEE Access 2020, 8, 166998–167018. [Google Scholar] [CrossRef]
- Alnami, H.; El-Rifaie, A.M.; Moustafa, G.; Hakmi, S.H.; Shaheen, A.M.; Tolba, M.A. Optimal allocation of TCSC devices in transmission power systems by a novel adaptive dwarf mongoose optimization. IEEE Access 2023, 12, 6063–6087. [Google Scholar] [CrossRef]
- Mohamed, M.; El-Rifaie, A.M.; Boulkaibet, I.; Elnozahy, A. Optimal Economic and Environmental Aspects in Different Types of Loads via Modified Capuchin Algorithm for Standalone Hybrid Renewable Generation Systems. Processes 2024, 12, 2902. [Google Scholar] [CrossRef]














| Parameter | Value | Unit |
|---|---|---|
| Absolute temperature of SOFC | 1273 | K |
| Original current of SOFC | 100 | A |
| Faraday’s constant of gas | 96.487 × 106 | C/kmol |
| Common continuous of gas | 8314 | J/ kmol K |
| Perfect ordinary voltage | 1.18 | V |
| Cells in series | 450 | |
| Fuel maximum use of SOFC | 0.9 | |
| Fuel minimal use of SOFC | 0.8 | |
| Optimum fuel use of SOFC | 0.85 | |
| In case of molar constant, hydrogen value | 8.43 × 10−4 | (kmol/ (s atm) |
| In case of molar constant, water value | 2.81 × 10−4 | (kmol/(s atm) |
| In case of molar constant, oxygen value | 2.52 × 10−4 | (kmol/(s atm) |
| Time response in hydrogen of SOFC | 26.1 | s |
| Time response in water of SOFC | 78.3 | s |
| Time at oxygen flow of SOFC | 2.91 | s |
| Ohmic loss of SOFC | 3.2813 × 10−0.04 | Ohm |
| The response time in an electrical | 0.8 | s |
| fuel processor response time | 5 | s |
| hydrogen and oxygen ratio/value | 1.145 | |
| Snubber resistance Rs of inverter | 1 × 105 | (Ohm) |
| Power Electronic device of inverter | IGBT/Diodes | |
| Ron of Inverter | 1 × 10−3 | (Ohm) |
| Number of bridge arms of inverter | 3 | |
| p-H2 of SOFC | 0.05 | |
| p-H2O of SOFC | 0.829 | |
| p-O2 of SOFC | 0.0495 |
| Parameter | Value |
|---|---|
| Kp of FOPID controller in d-access at PSO | 0.0988 |
| Ki of FOPID controller in d-access at PSO | 67.1347 |
| Kd of FOPID controller in d-access at PSO | 0.0853 |
| Lambda of FOPID controller in d-access at PSO | 0.8962 |
| Mu of FOPID controller in d-access at PSO | 0.1839 |
| Kp of FOPID controller in q-access at PSO | 0.0995 |
| Ki of FOPID controller in q-access at PSO | 348.38 |
| Kd of FOPID controller in q-access at PSO | 0.0720 |
| Lambda of FOPID controller in q-access at PSO | 0.9900 |
| Mu of FOPID controller in q-access at PSO | 0.0462 |
| Kp of FOPID controller in d-access at BWO | 0.09715 |
| Ki of FOPID controller in d-access at BWO | 52 |
| Kd of FOPID controller in d-access at BWO | 0.09715 |
| Lambda of FOPID controller in d-access at BWO | 0.9618 |
| Mu of FOPID controller in d-access at BWO | 1.0000 × 10−3 |
| Kp of FOPID controller in q-access at BWO | 0.097154566550583 |
| Ki of FOPID controller in q-access at BWO | 132.6 |
| Kd of FOPID controller in q-access at BWO | 0.0971 |
| Lambda of FOPID controller in q-access at BWO | 0.9618 |
| Mu of FOPID controller in q-access at BWO | 0.1097 |
| Numerator of APC (1/S) | 3000 |
| No | Parameter | Lower | Upper |
|---|---|---|---|
| 1 | Kp of FOPID controller in d-access | 0.001 | 0.1 |
| 2 | Ki of FOPID controller in d-access | 52 | 600 |
| 3 | Kd of FOPID controller in d-access | 0.001 | 0.1 |
| 4 | Lambda of FOPID controller in d-access | 0.001 | 0.99 |
| 5 | Mu of FOPID controller in d-access | 0.001 | 0.99 |
| 6 | Kp of FOPID controller in q-access | 0.001 | 0.1 |
| 7 | Ki of FOPID controller in q-access | 54 | 600 |
| 8 | Kd of FOPID controller in q-access | 0.001 | 0.1 |
| 9 | Lambda of FOPID controller in q-access | 0.001 | 0.99 |
| 10 | Mu of FOPID controller in q-access | 0.001 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, M.; Boulkaibet, I.; Ebeed, M.; El-Rifaie, A.M. An Enhanced Control of Grid-Connected Solid-Oxide Fuel Cell System Using Beluga Whale-Optimized Fractional-Order PID Control. Processes 2025, 13, 2044. https://doi.org/10.3390/pr13072044
Mohamed M, Boulkaibet I, Ebeed M, El-Rifaie AM. An Enhanced Control of Grid-Connected Solid-Oxide Fuel Cell System Using Beluga Whale-Optimized Fractional-Order PID Control. Processes. 2025; 13(7):2044. https://doi.org/10.3390/pr13072044
Chicago/Turabian StyleMohamed, Moayed, Ilyes Boulkaibet, Mohamed Ebeed, and Ali M. El-Rifaie. 2025. "An Enhanced Control of Grid-Connected Solid-Oxide Fuel Cell System Using Beluga Whale-Optimized Fractional-Order PID Control" Processes 13, no. 7: 2044. https://doi.org/10.3390/pr13072044
APA StyleMohamed, M., Boulkaibet, I., Ebeed, M., & El-Rifaie, A. M. (2025). An Enhanced Control of Grid-Connected Solid-Oxide Fuel Cell System Using Beluga Whale-Optimized Fractional-Order PID Control. Processes, 13(7), 2044. https://doi.org/10.3390/pr13072044







