Analysis on the Influence of the Active Power Recovery Rate on the Transient Stability Margin of a New Power System
Abstract
1. Introduction
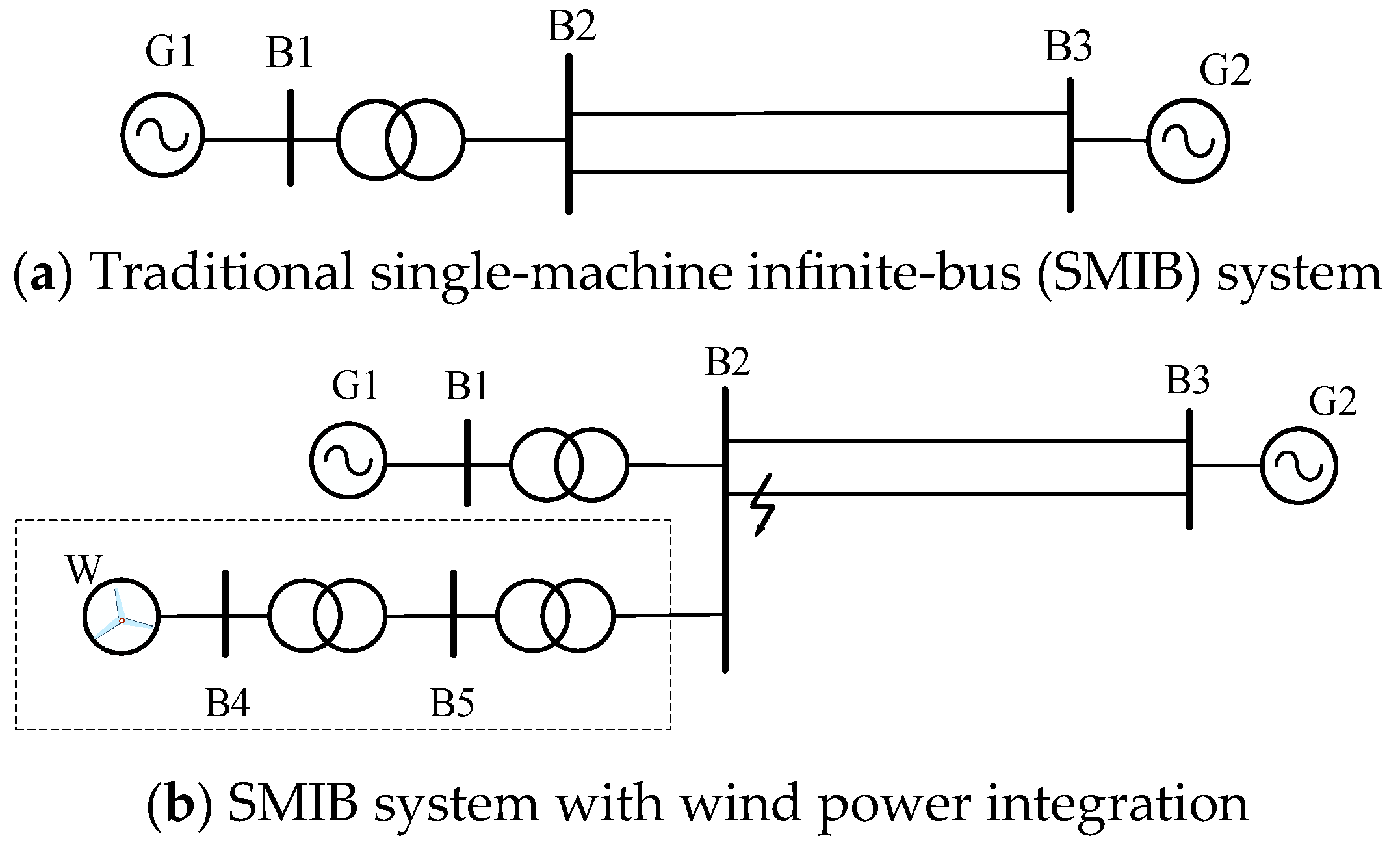
2. Materials and Methods
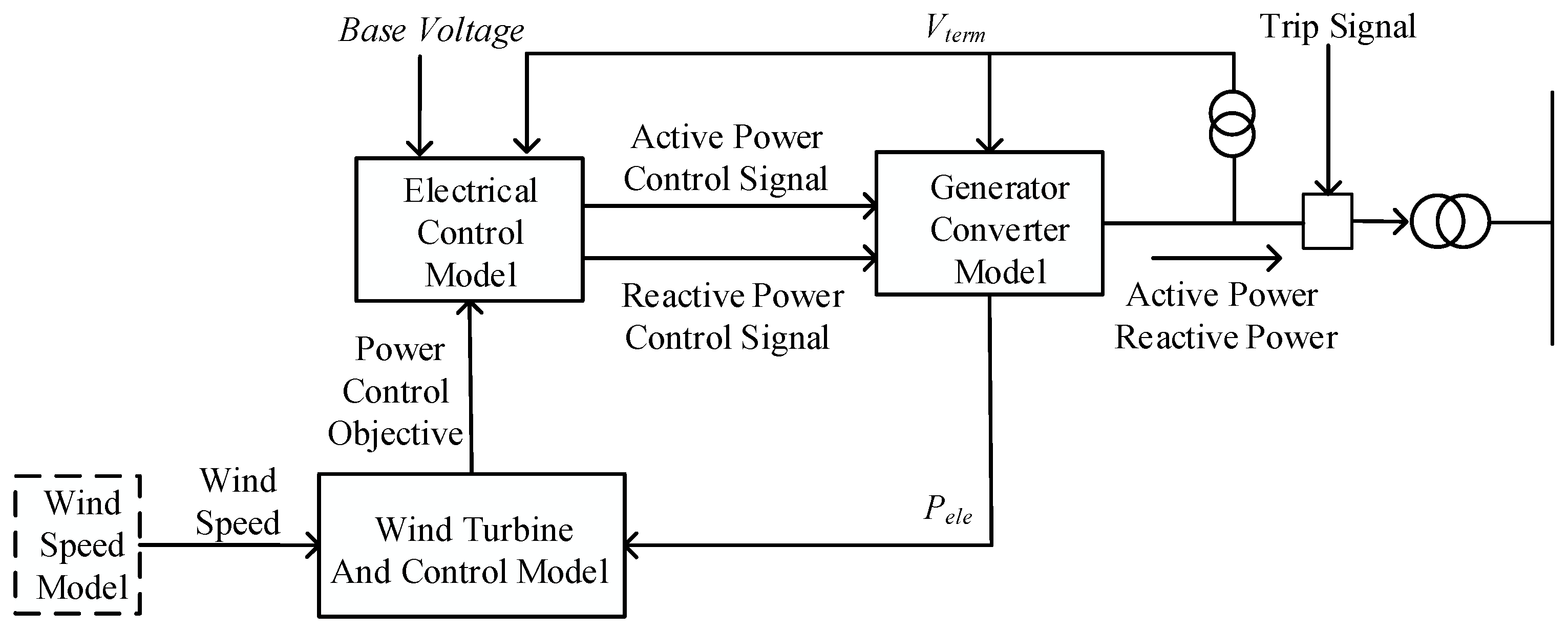
2.1. Model of Doubly Fed Induction Generator (DFIG)
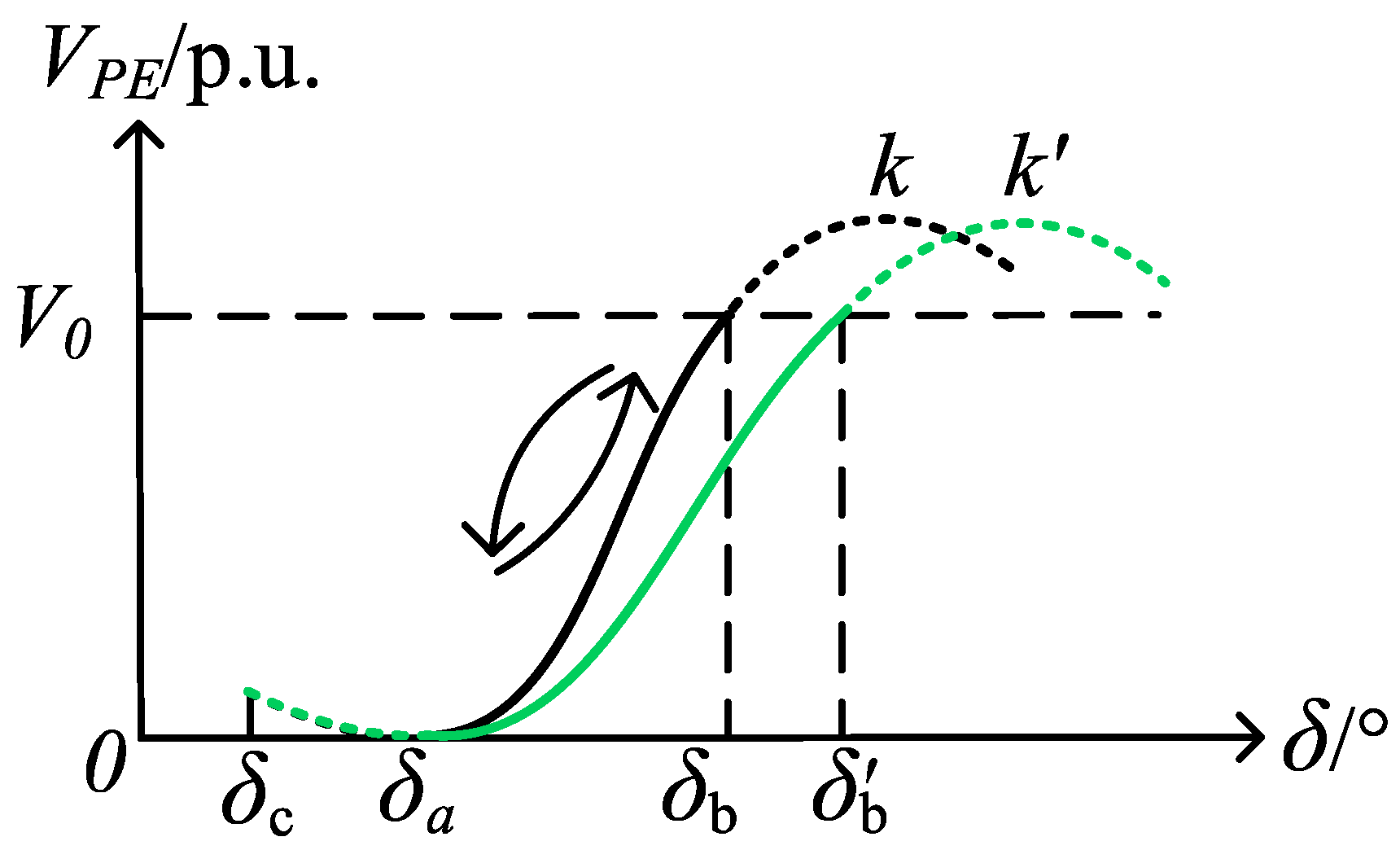
2.2. Stability Margin Index of Trajectory Analysis Method
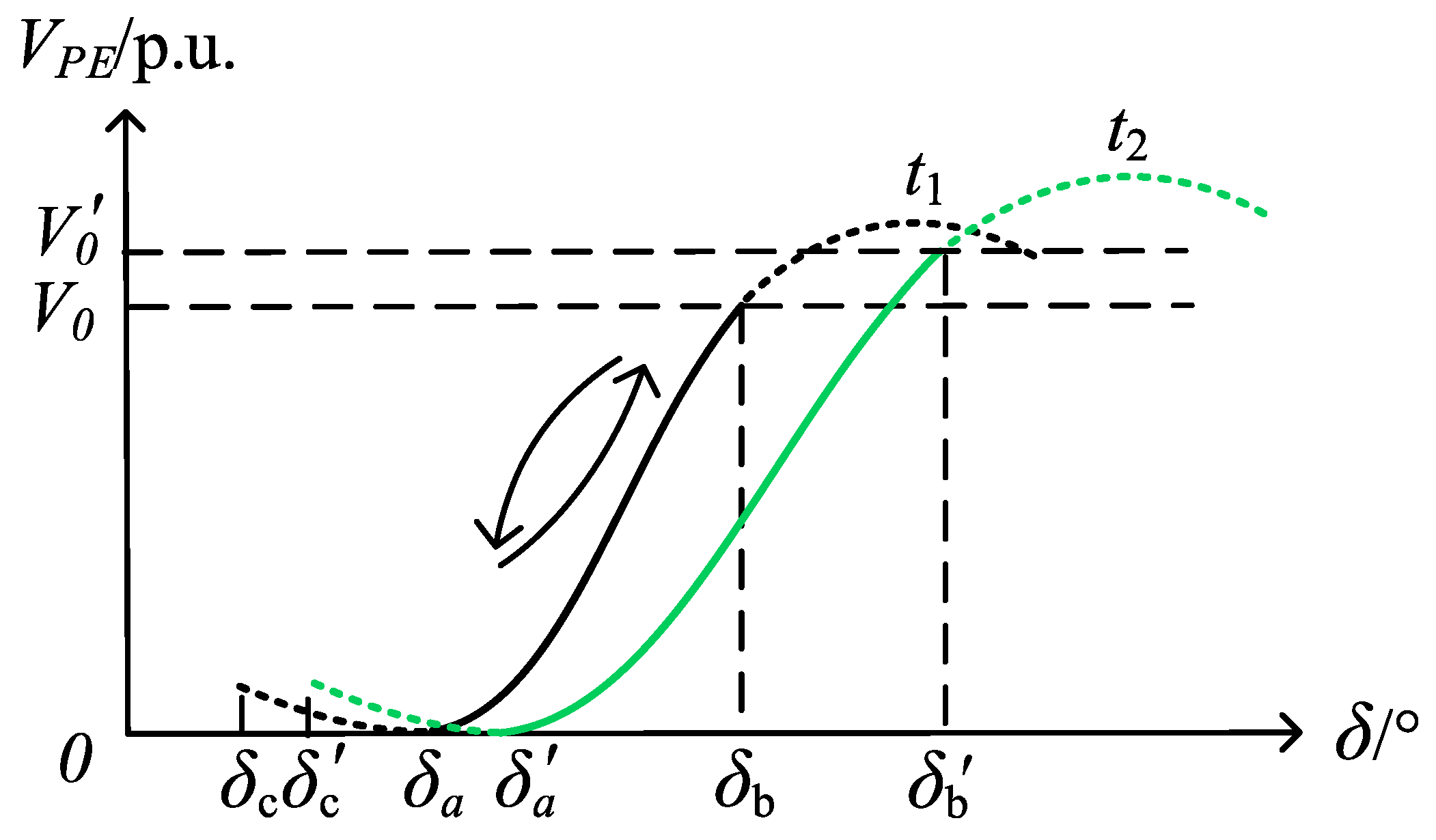
2.3. Construction of Sensitivity Model
3. Results
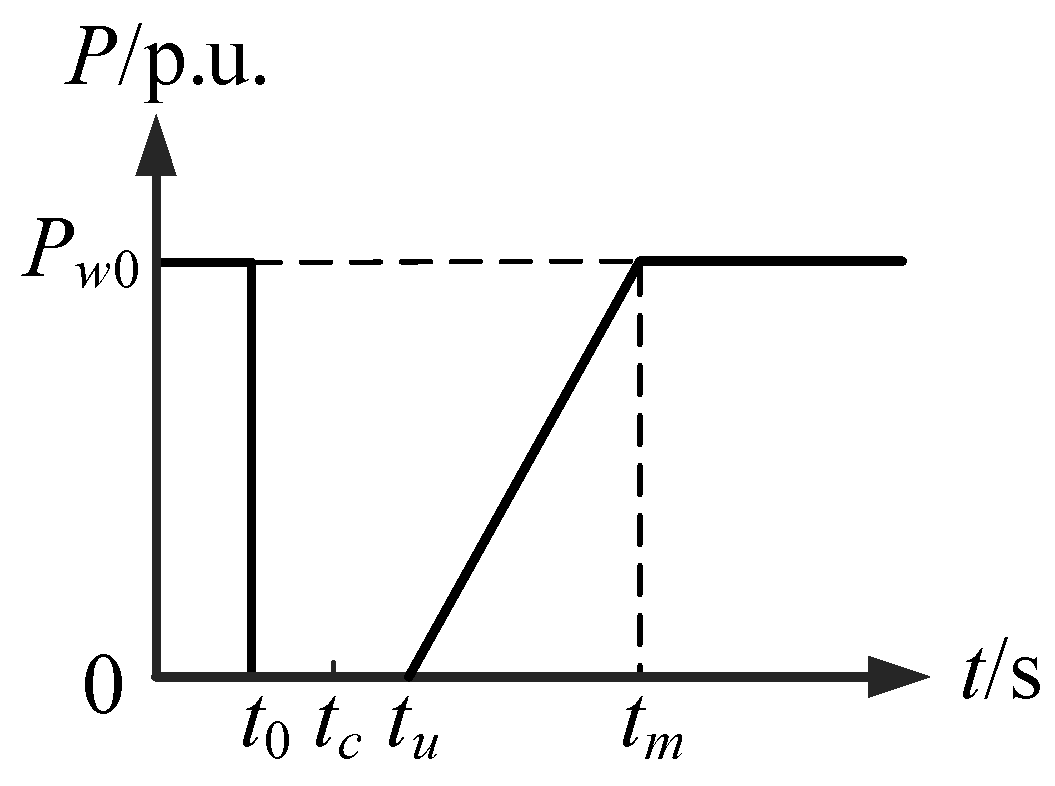
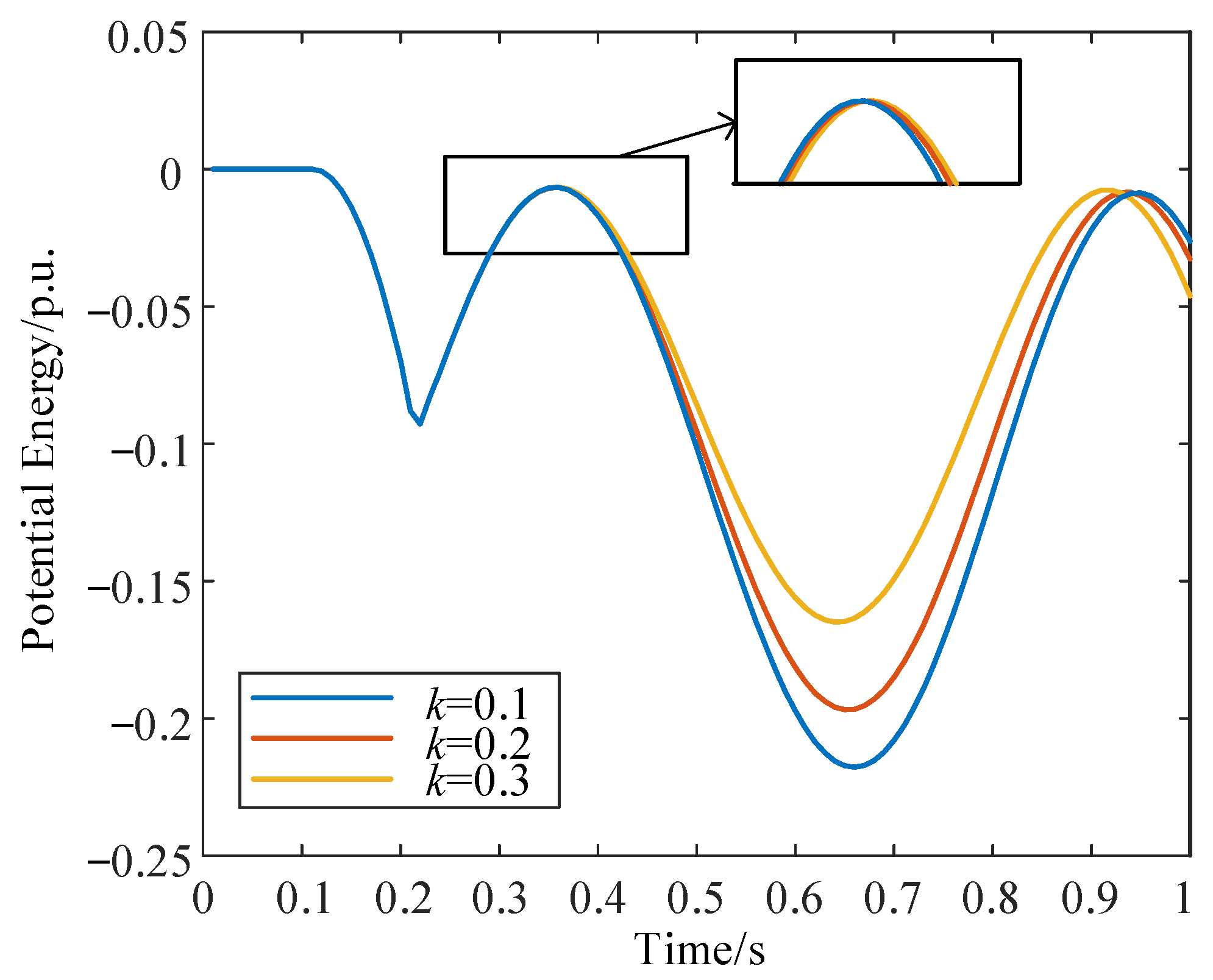
3.1. Analysis of the Influence of the Active Recovery Rate of Wind Turbine on System Stability
- (1)
- Accelerating power of synchronous machine
- (2)
- The speed of the synchronous machine
- (3)
- The change in potential energy and power angle of the synchronous machine
- (4)
- The time when the potential energy of the synchronous machine reaches its peak for the first time
- (5)
- Stability index of synchronous machine
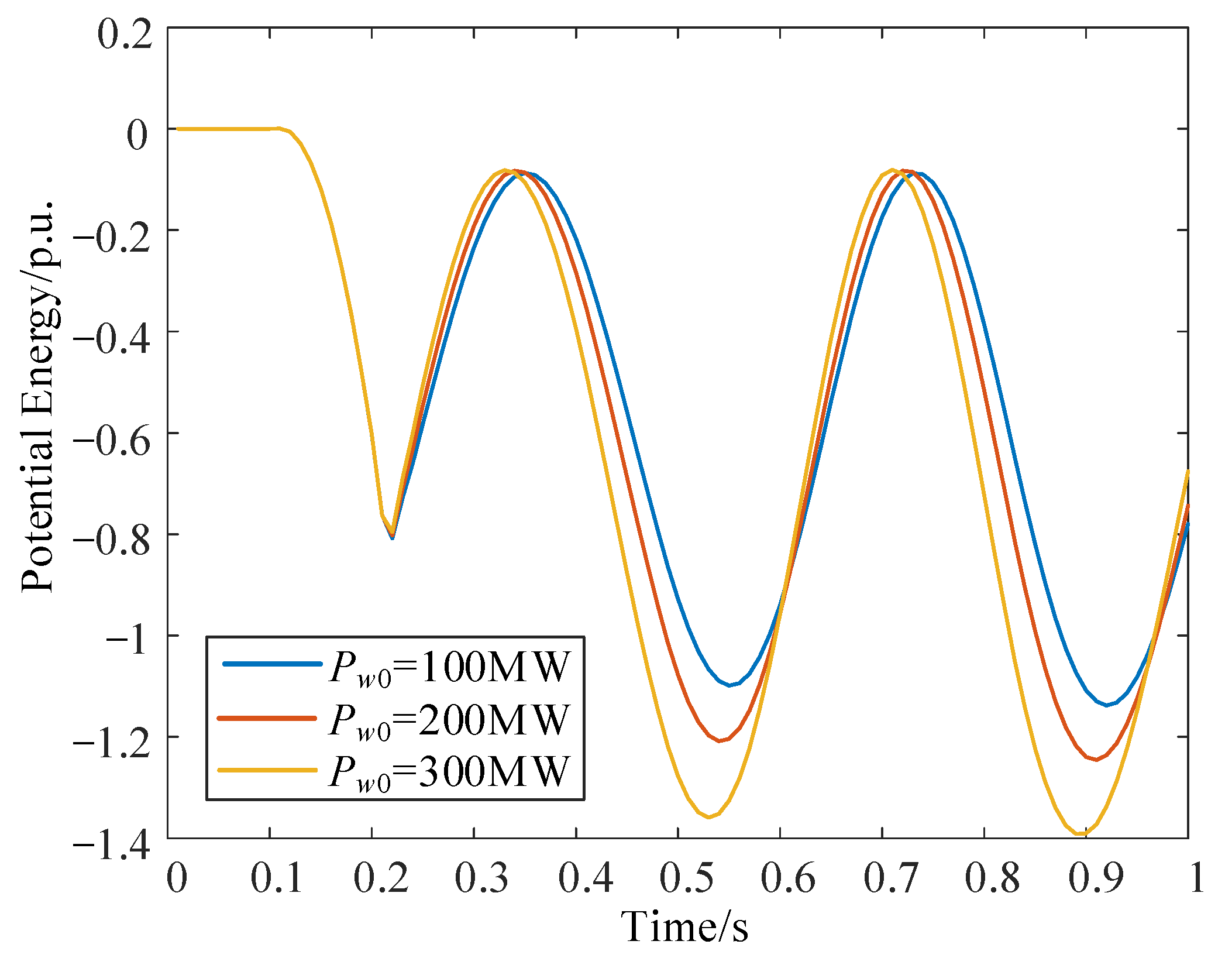
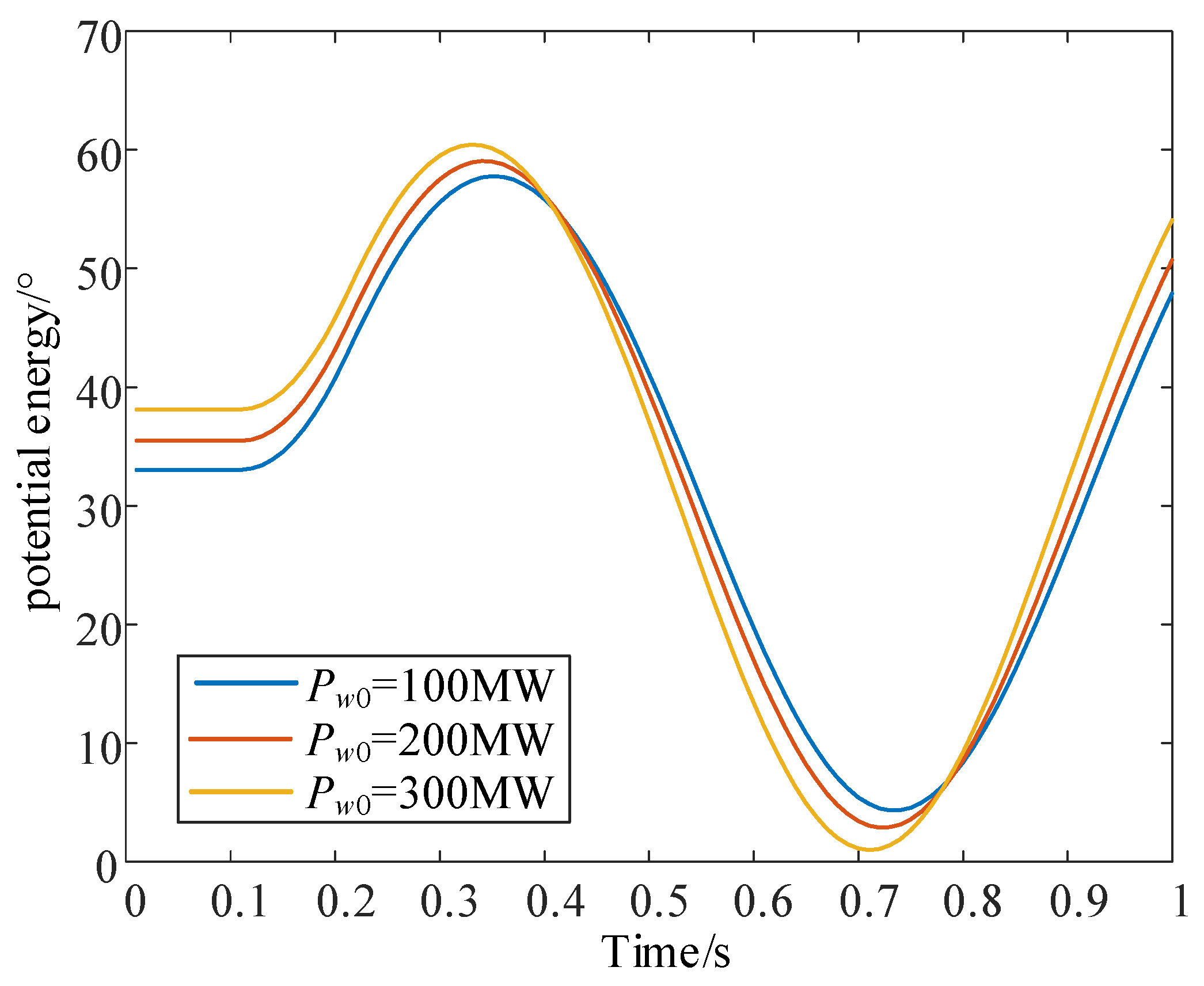
3.2. Analysis of the Influence of the Initial Active Power of the Wind Turbine on the Stability of the System
- (1)
- The acceleration power of the synchronous machine
- (2)
- The change in potential energy
- (3)
- The time when the potential energy of the synchronous machine reaches its peak for the first time tb
- (4)
- The stability index S of the synchronous machine
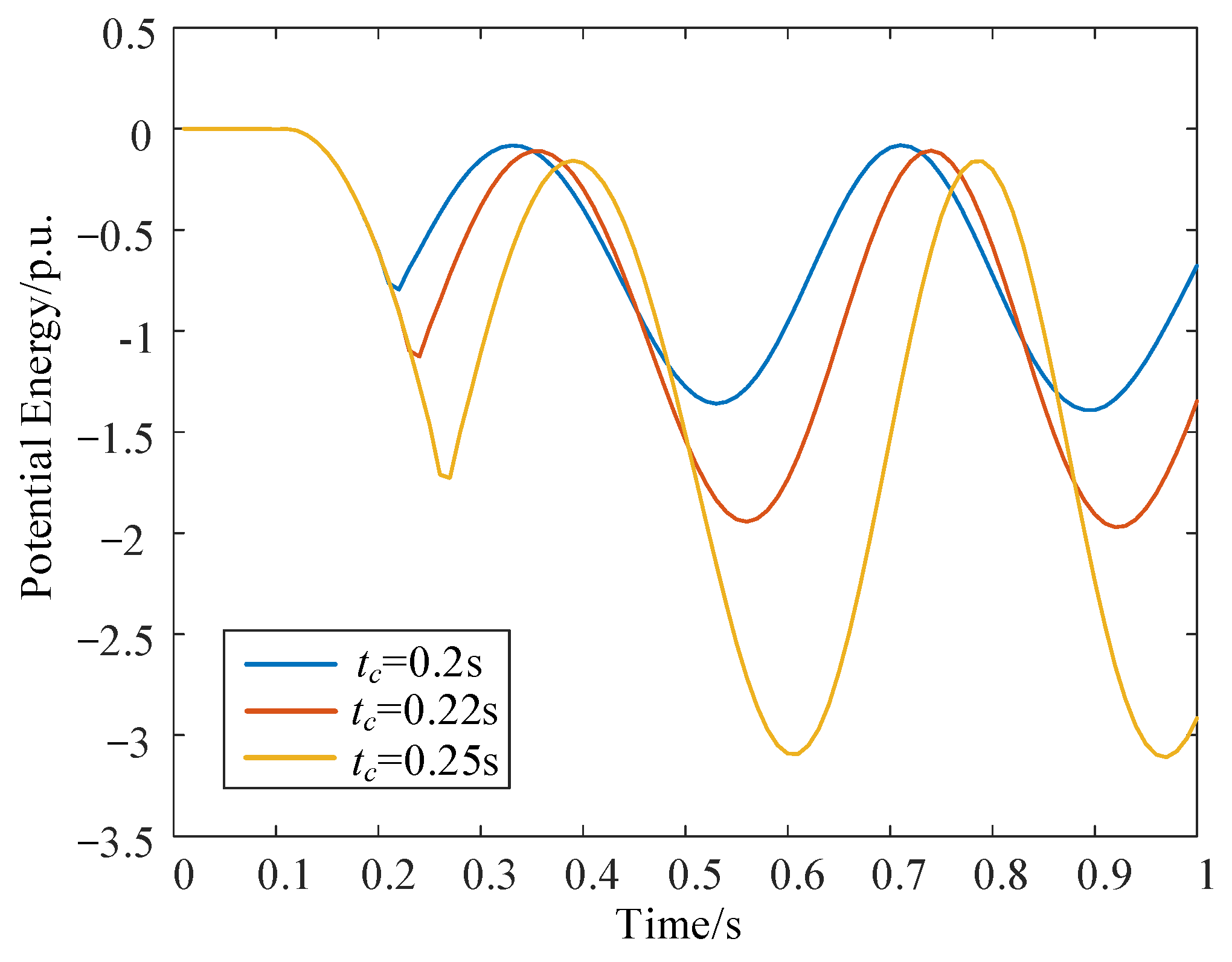
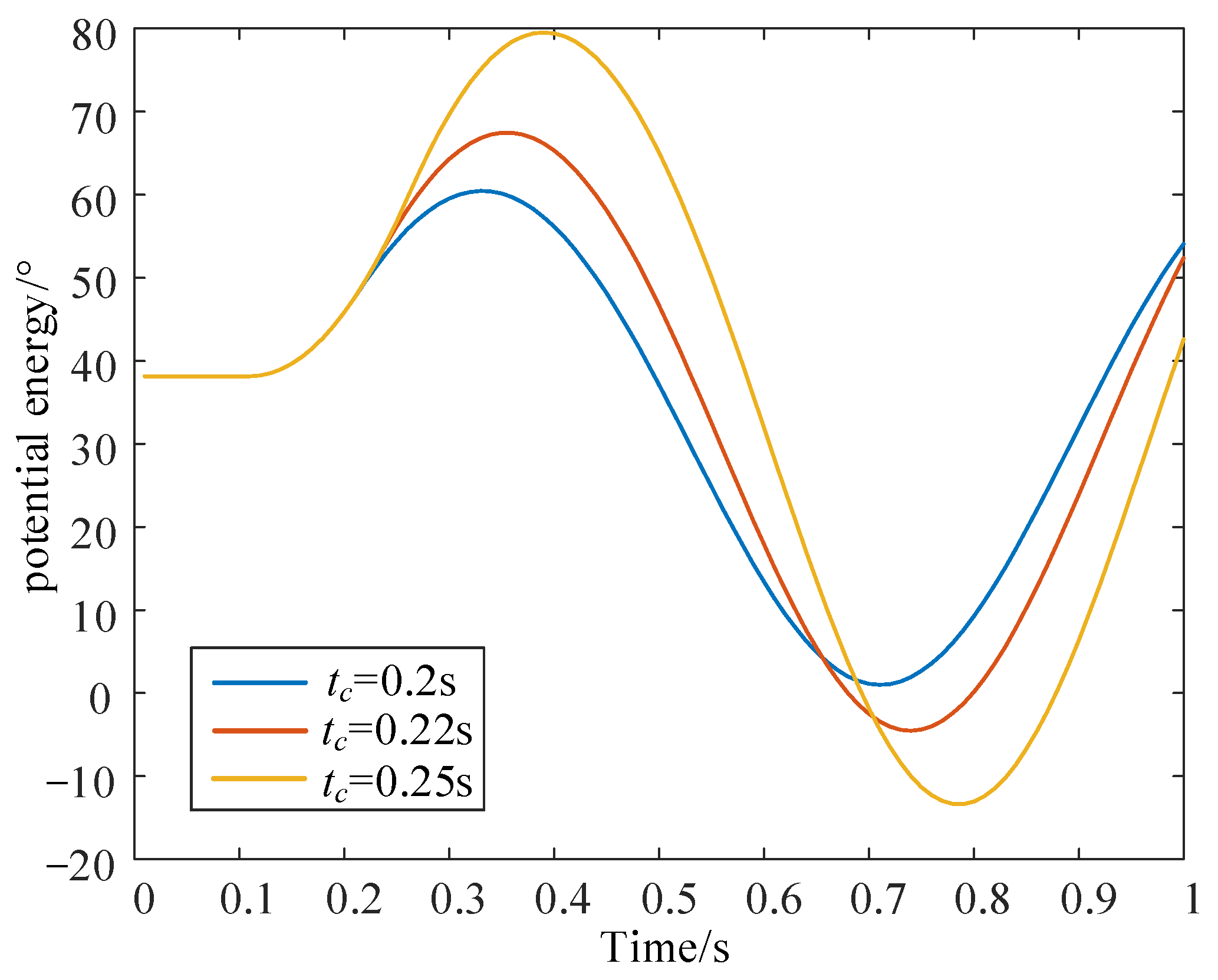
3.3. Analysis of the Impact of Fault Duration on System Stability
- (1)
- The acceleration power of the synchronous machine
- (2)
- The change in potential energy
- (3)
- The time when the potential energy of the synchronous machine reaches its peak for the first time tb
- (4)
- The stability index S of the synchronous machine
4. Discussion
4.1. Single-Machine System Simulation Analysis
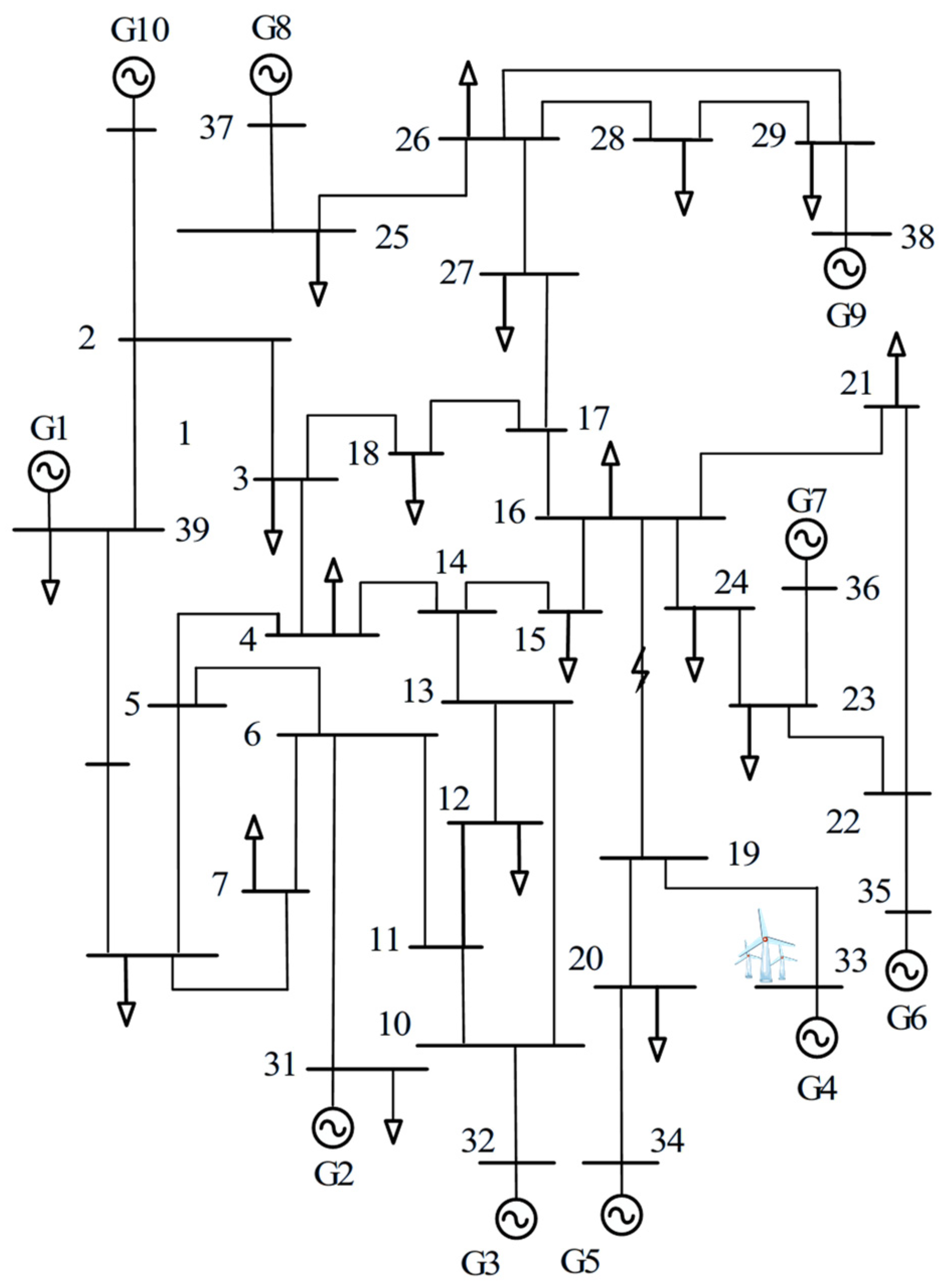
4.2. Multi-Machine System Simulation Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
Appendix A.2
References
- Xie, X.R.; He, J.B.; Mao, H.Y.; Li, H.Z. New Issues and Classification of Stability in “Double-High” Power Systems. Proc. CSEE 2021, 41, 461–475. [Google Scholar]
- Yang, P.; Liu, F.; Jiang, Q.R.; Mao, H.Y. Large-Disturbance Stability of “Double-High” Power Systems: Challenges and Prospects. J. Tsinghua Univ. (Sci. Technol.) 2021, 61, 403–414. [Google Scholar]
- Lima, L.T.G.; Bezerra, L.H.; Tomei, C.; Martins, N. New Methods for Fast Small-Signal Stability Assessment of Large Scale Power Systems. IEEE Trans. Power Syst. 1995, 10, 1979–1985. [Google Scholar] [CrossRef]
- Yu, C.; James, G.; Xue, Y.; Xue, F. Impacts of Large Scale Wind Power on Power System Transient Stability. In Proceedings of the 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Weihai, China, 6–9 July 2011. [Google Scholar]
- Liu, M.S.; Sun, Z.Y.; Liu, G.S.; Li, M.P.; Qiu, X.Y. Study on the Influence of Large-Scale Wind Power Integration on Transient Stability of Power System. In Proceedings of the 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection, Xi’an, China, 21–24 October 2019. [Google Scholar]
- Liu, F.Y.; Zeng, P.; Li, Z. Transient Stability Analysis of Full-Scale Wind Farm Internal Units Under Grid Faults. Power Syst. Prot. Control 2022, 50, 43–54. [Google Scholar]
- Vittal, E.; O’Malley, M.; Keane, A. Rotor Angle Stability With High Penetrations of Wind Generation. IEEE Trans. Power Syst. 2012, 27, 353–362. [Google Scholar] [CrossRef]
- Zheng, Y.J.; Xue, A.C.; Wang, Q.; Bi, T.S.; Zheng, T.Y.; Sun, Y. The Impact of LVRT on the Transient Stability of Power System With Large Scale Wind Power. In Proceedings of the 2013 IEEE PES Asia-Pacific Power and Energy Engineering Conference, Hong Kong, China, 8–11 December 2013; pp. 1–5. [Google Scholar]
- Meegahapola, L.; Flynn, D. Impact on Transient and Frequency Stability for a Power System at Very High Wind Penetration. In Proceedings of the IEEE Power & Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010. [Google Scholar]
- Kundur, P. Power System Stability and Control, 1st ed.; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Mu, P.T.; Zhao, D.M.; Wang, J.C. Mechanism Analysis of Large-Scale Wind Power Integration Impacts on Power System Angle Stability. Proc. CSEE 2017, 37, 1325–1334. [Google Scholar]
- Yu, Q.; Sun, H.D.; Tang, Y.; Zhao, B.; Gu, Z.Y. Impact of DFIG-Based Wind Turbines on Power System Angle Stability. Power Syst. Technol. 2013, 37, 3399–3405. [Google Scholar]
- Sheng, S.Q.; Yu, K.; Zhang, W.C.; Zhao, F.; Wang, M.; Zhao, W. Impact of Large-Scale Wind Power Integration on Angle Stability of Sending-End Systems. Power Syst. Prot. Control 2022, 50, 82–90. [Google Scholar]
- Tang, L.; Shen, C.; Zhang, X.M. Impact of Large-Scale Concentrated Wind Power Integration on Transient Angle Stability of Power Systems (I): Theoretical Basis. Proc. CSEE 2015, 35, 3832–3842. [Google Scholar]
- Tang, L.; Shen, C.; Zhang, X.M. Impact of Large-Scale Concentrated Wind Power Integration on Transient Angle Stability of Power Systems (II): Influencing Factors Analysis. Proc. CSEE 2015, 35, 4043–4051. [Google Scholar]
- Liu, C.; Zhang, H.X.; Zhu, X.F.; Zhang, Y.J.; Xu, H.T.; Zhang, Y.P. Transient Stability Assessment of Power Systems Based on Stochastic Network Energy. J. Northeast Electr. Power Univ. 2022, 42, 90–99. [Google Scholar]
- Jiang, H.L.; Zhou, Z.Q.; Cai, J.C. Analysis Method for Impact of Wind Power Penetration Level on Transient Angle Stability of Power Systems. Electr. Power Autom. Equip. 2020, 40, 53–67. [Google Scholar]
- Ji, T.P.; Zhao, W.; Li, Y.D.; Lin, Y.F.; Wang, T. Transient Synchronization Stability Analysis of DFIG-Based Wind Farms With Virtual Inertia Control Using Energy Function Method. Power Syst. Prot. Control 2022, 50, 38–48. [Google Scholar]
- Wang, Q.; Xue, A.C.; Zheng, Y.J.; Bi, T.S. Impact of Centralized DFIG-Based Wind Power Integration on Transient Angle Stability. Power Syst. Technol. 2016, 40, 875–881. [Google Scholar]
- Dong, Z.; Zhou, M.; Li, G.Y.; Li, M.J. Mechanism of Wind Turbine Active Power Control on Second-Swing Transient Stability of Power Systems. Proc. CSEE 2017, 37, 4680–4690+4893. [Google Scholar]
- Dong, Z. Mechanism and Control Strategies of Active Power Recovery Control in DFIG-Based Wind Farms on Power System Transient Stability. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2019. [Google Scholar]
- Tian, X.S.; Wang, W.S.; Chi, Y.N.; Li, G.Y.; Tang, H.Y.; Li, Y. Fault Behavior of DFIG-Based Wind Turbines and Its Impact on Power System Transient Stability. Autom. Electr. Power Syst. 2015, 39, 16–21. [Google Scholar]
- Zhang, F.; Chen, W.H.; Li, K.J.; Guo, X.L.; Xue, A.C. Impact of Active Power Recovery Control in DFIG-Based Wind Farms on First-Swing Stability of Wind-Thermal Bundled Systems and Improved Control Strategy. Power Syst. Prot. Control 2025, 53, 136–150. [Google Scholar]
- Yu, Z.; Shen, C.; Zhang, X.M. Influence of Power Recovery Rate After Fault Ride-Through on Transient Stability of DFIG-Integrated Systems. Proc. CSEE 2018, 38, 3781–3791+4019. [Google Scholar]
- Mu, G.; Wang, Z.H.; Han, Y.D.; Huang, M. Quantitative Analysis of Transient Stability: Trajectory Analysis Method. Proc. CSEE 1993, 13, 25–32. [Google Scholar]
- Zhang, M.L.; Xu, J.Y.; Li, J.J. Research on Transient Stability of Sending-End Systems With High Wind Power Penetration. Power Syst. Technol. 2013, 37, 740–745. [Google Scholar]
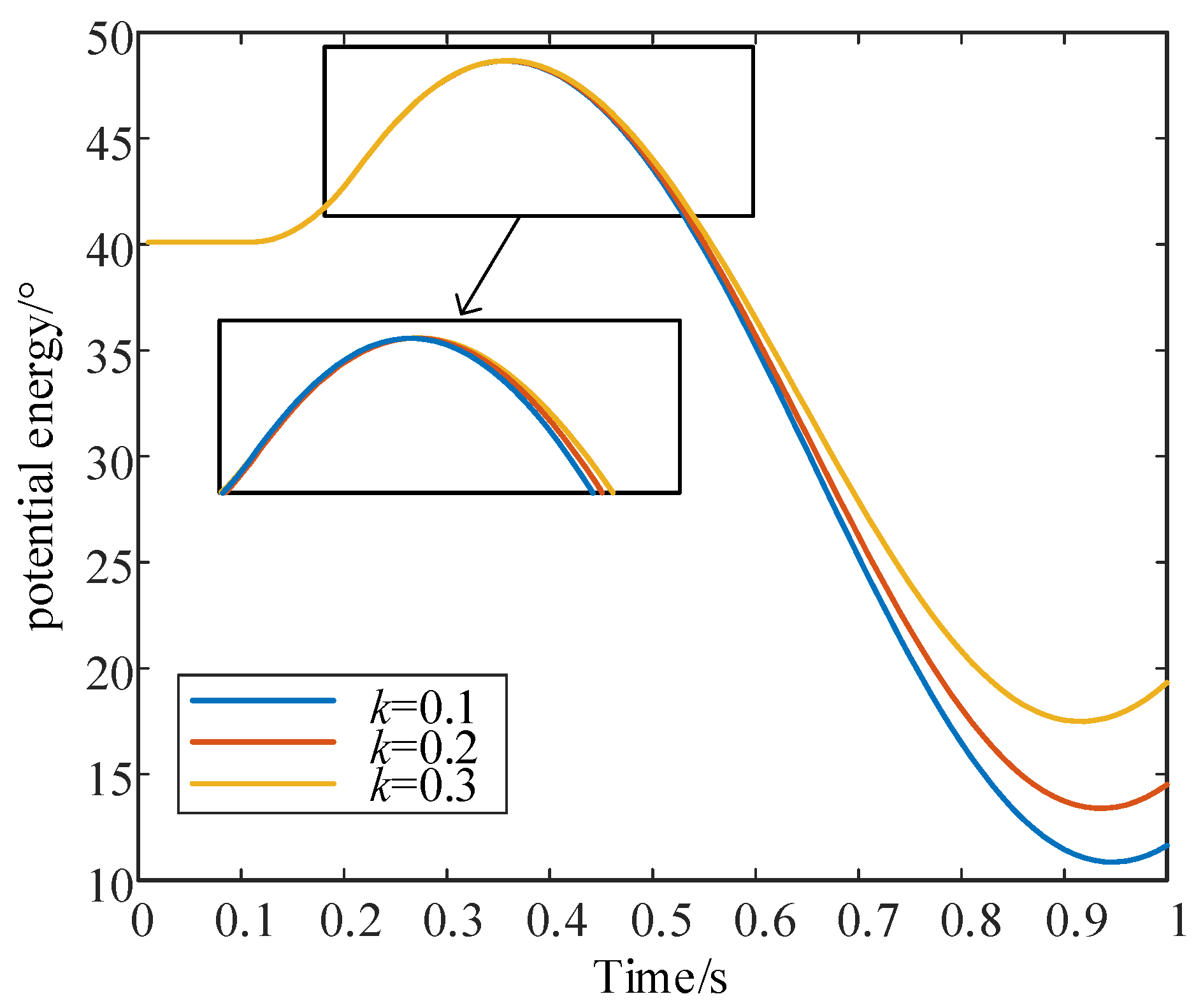
| Rate of Recovery from Injury (p.u./s) | Sensitivity ∂S/∂k (s−1) | Stable Index S | Power Angle (°) | Accelerating Power (p.u) | Time tb (s) |
|---|---|---|---|---|---|
| 0.1 | 5.8093 | −3.8861 | 59.0581 | −4.1838 | 0.33 |
| 0.2 | 5.8004 | −2.7781 | 59.0601 | −4.1769 | 0.34 |
| 0.3 | 5.7810 | −1.8941 | 59.0640 | −4.1631 | 0.35 |
| Initial Wind Turbine Power/MW | Sensitivity ∂S/∂k (s−1) | Stable Index S | Power Angle (°) | Accelerating Power (p.u) | Time tb (s) |
|---|---|---|---|---|---|
| 100 | 5.5258 | −6.9259 | 57.7846 | −3.9828 | 0.33 |
| 200 | 5.8004 | −2.7781 | 59.0601 | −4.1769 | 0.34 |
| 300 | 6.2260 | −0.7062 | 60.4478 | −4.4443 | 0.35 |
| Fault Duration (p.u./s) | Sensitivity ∂S/∂k (s−1) | Stable Index S | Power Angle (°) | Accelerating Power (p.u) | Time tb (s) |
|---|---|---|---|---|---|
| 0.1 | 5.8004 | −2.7781 | 59.0601 | −4.1769 | 0.34 |
| 0.12 | 5.0123 | −2.8638 | 67.4442 | −5.0925 | 0.35 |
| 0.15 | 3.7519 | −3.2999 | 79.5363 | −5.8965 | 0.39 |
| Rate of Recovery from Injury (p.u./s) | Sensitivity ∂S/∂k (s−1) | Stable Index S | Power Angle (°) | Accelerating Power (p.u) | Time tb (s) |
|---|---|---|---|---|---|
| 0.2 | 5.9668 | −26.1593 | 51.1421 | −3.2967 | 0.3800 |
| 0.3 | 4.5567 | −10.6870 | 51.1531 | −3.2896 | 0.3800 |
| 0.5 | 3.8488 | −5.4864 | 51.2418 | −3.2322 | 0.3900 |
| Rate of Recovery from Injury (p.u./s) | Sensitivity ∂S/∂k (s−1) | Stable Index S | |||||
|---|---|---|---|---|---|---|---|
| G4 | G5 | G8 | G4 | G5 | G8 | G4 | |
| 0.2 | −26.1593 | −29.6819 | −56.6577 | 5.9668 | 6.0554 | 18.4255 | −26.1593 |
| 0.3 | −10.6870 | −13.2363 | −25.2185 | 4.5567 | 5.0320 | 15.3420 | −10.6870 |
| 0.5 | −5.4864 | −7.7542 | −14.7289 | 3.8488 | 4.9912 | 14.1969 | −5.4864 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Y.; Zhou, Y. Analysis on the Influence of the Active Power Recovery Rate on the Transient Stability Margin of a New Power System. Processes 2025, 13, 2020. https://doi.org/10.3390/pr13072020
Gu Y, Zhou Y. Analysis on the Influence of the Active Power Recovery Rate on the Transient Stability Margin of a New Power System. Processes. 2025; 13(7):2020. https://doi.org/10.3390/pr13072020
Chicago/Turabian StyleGu, Yanxin, and Yibo Zhou. 2025. "Analysis on the Influence of the Active Power Recovery Rate on the Transient Stability Margin of a New Power System" Processes 13, no. 7: 2020. https://doi.org/10.3390/pr13072020
APA StyleGu, Y., & Zhou, Y. (2025). Analysis on the Influence of the Active Power Recovery Rate on the Transient Stability Margin of a New Power System. Processes, 13(7), 2020. https://doi.org/10.3390/pr13072020




