A Discrete Improved Gray Wolf Optimization Algorithm for Dynamic Distributed Flexible Job Shop Scheduling Considering Random Job Arrivals and Machine Breakdowns
Abstract
1. Introduction
2. Literature Review
2.1. Distributed Flexible Job Shop Scheduling
2.2. Dynamic Flexible Scheduling
2.3. GWO for Production Scheduling
3. Formulation of the DDFJSP
3.1. Description of the DDFJSP
- (1)
- At any time, each machine can only process one operation;
- (2)
- A job can be processed by only one machine at a time;
- (3)
- All jobs cannot be processed across factories;
- (4)
- The processing of operations on the machines should not be interrupted except when machine breakdown occurs;
- (5)
- Transportation time among machines is negligible, and the machine setup time is included in the processing time.
3.2. Mathematical Model of MODDFJSP
4. Predictive–Reactive Scheduling Method
4.1. Framework of the Predictive–Reactive Scheduling Method
4.2. Hybrid Periodic- and Event-Driven Rescheduling Strategy
4.3. Construction of a Static Scheduling Window
- If one machine malfunctions, it will be removed from the set of eligible machines. Conversely, if a machine is repaired, it will be added to the set of capable machines.
- With respect to the first operation of the job, if there are no machines in any of the factories that can process it, then it is considered unavailable; otherwise, even if the operation cannot be processed in the current factory, the job to which it belongs will be transferred to another factory.
- Regarding the non-first operation of the job, factory transfer cannot be considered. At this point, if there are no machines available to process it, then it is considered unavailable, and all of its subsequent operations within the same job cannot be processed either.
- When the faulty machine corresponding to the unavailable operation is repaired, the operation becomes a processable operation.
- If an operation cannot be processed due to the previous operation within the same job being a non-machinable operation, then, when it is released for processing, the operation is also made available.
- If an operation is being processed on a faulty machine at the rescheduling point, then the work should be stopped until the machine has been repaired.
5. Solving the Static Scheduling Window Based on DIGWO
5.1. Basic Concepts of Multi-Objective Optimization
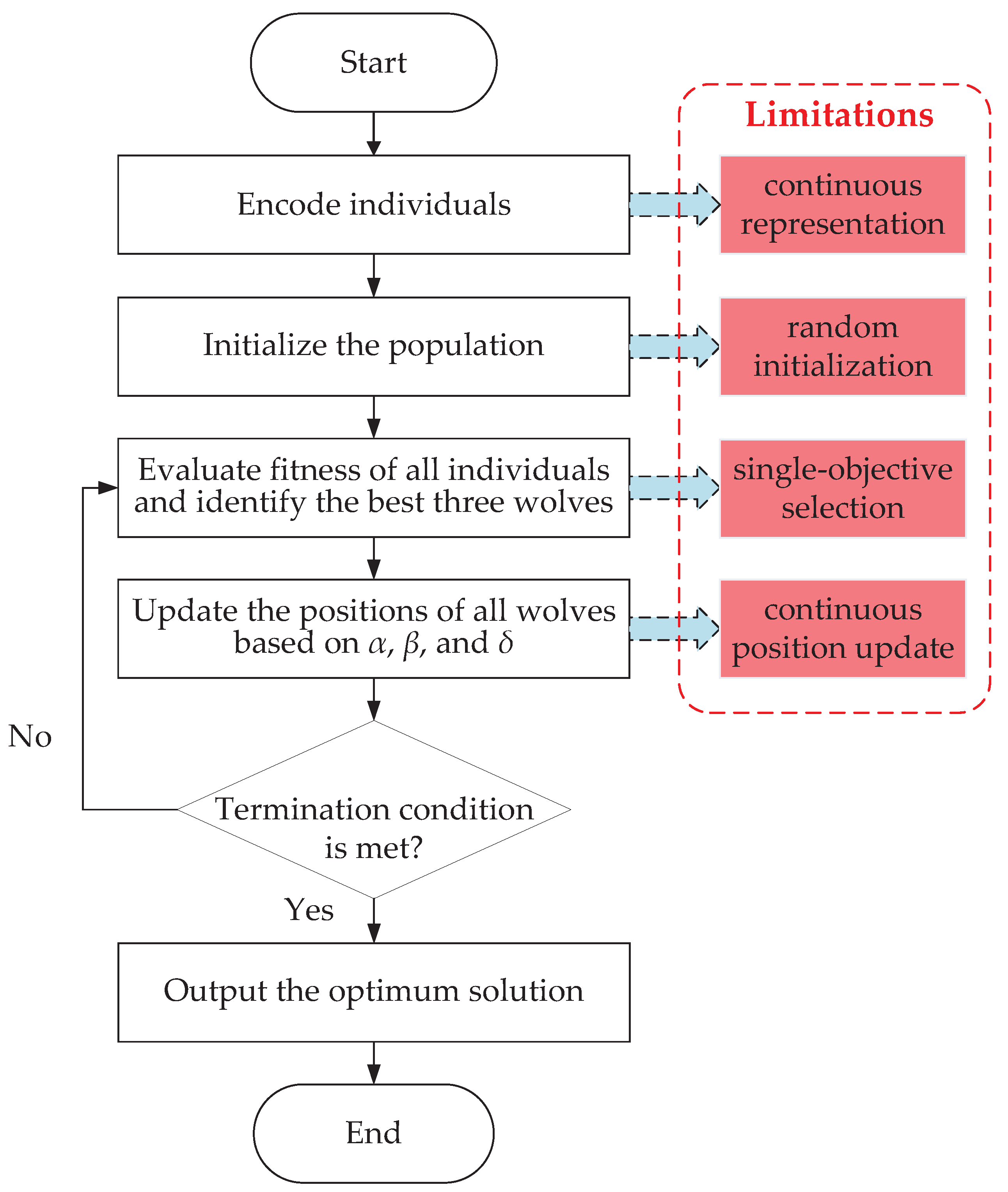
5.2. Original GWO and Its Limitations in Solving DFJSSP
5.3. Framework of the Proposed DIGWO
| Algorithm 1 Pseudocode of DIGWO. |
|
5.4. The Improvements Introduced in DIGWO
5.4.1. Discrete Encoding Scheme and Corresponding Decoding Method
5.4.2. Problem-Specific Population Initialization Strategy
5.4.3. Multi-Objective-Based Leader Wolf Pack Selection Mechanism
5.4.4. Discrete Search Operators for GWO
5.4.5. External Archive Update Strategy
6. Experiment and Analysis
6.1. Experimental Environments
6.2. Other Algorithms in Comparsion
6.2.1. MOEAs for Comparsion
6.2.2. Variation of DIGWO for Comparsion
6.3. Performance Metrics
6.4. Results and Discussion
6.4.1. Performance Comparison in the Whole Dynamic Scheduling Process
- (1)
- DIGWO significantly outperformed DIGWOrand at 46 out of the 94 rescheduling points for HV and IGD and at 35 rescheduling points out of 94 for the C metric; meanwhile, DIGWOrand significantly outperformed DIGWO at only one point for HV and at two points for IGD and C. This demonstrates the effectiveness of the proposed initialization method well.
- (2)
- DIGWO was the best among all the compared algorithms. It can be seen that, when compared with any other algorithms, DIGWO obtained better values for HV, IGD, and C at more rescheduling points. Meanwhile, DIGWO had the best average performance score.
- (3)
- SPEA2 demonstrated competitiveness to some extent and obtained the second best average performance score. Specially for HV, it can be seen that the number of rescheduling points where SPEA2 was significantly better than DIGWO was only one less than the number of rescheduling points where DIGWO was significantly better than SPEA2. However, for the IGD and C metrics, DIGWO had a significant advantage over SPEA2.
- (4)
- MOEA/D had the worst performance among all algorithms because it obtained the worst performance scores at almost all the rescheduling points. In conclusion, Pareto domination is more suitable than the decomposition technique for solving MODDFJSP.
6.4.2. Performance Comparisons to Existing Dynamic Scheduling Methods
6.4.3. Further Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FJSP | Flexible Job Shop Scheduling Problem |
| DFJSP | Distributed Flexible Job Shop Scheduling Problem |
| DDFJSP | Dynamic Distributed Flexible Job Shop Scheduling Problem |
| MODFJSP | Multi-objective Distributed Flexible Job Shop Scheduling Problem |
| MODDFJSP | Multi-objective Dynamic Distributed Flexible Job Shop Scheduling Problem |
| MOEA | Multi-objective Evolutionary Algorithm |
| GA | Genetic Algorithm |
| GWO | Gray Wolf Optimization Algorithm |
| DIGWO | Discrete Improved Gray Wolf Optimization |
| NSGA-II | Nondominated Sorting Genetic Algorithm II |
References
- Li, R.; Gong, W.; Wang, L.; Lu, C.; Zhuang, X. Surprisingly Popular-Based Adaptive Memetic Algorithm for Energy-Efficient Distributed Flexible Job Shop Scheduling. IEEE Trans. Cybern. 2023, 53, 8013–8023. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Li, Y.; Qian, B.; Hu, R.; Yang, J. A multidimensional probabilistic model based evolutionary algorithm for the energy-efficient distributed flexible job-shop scheduling problem. Eng. Appl. Artif. Intell. 2024, 135, 108841. [Google Scholar] [CrossRef]
- Wang, J.; Han, H.; Wang, L. A Feedback Learning-Based Memetic Algorithm for Energy-Aware Distributed Flexible Job-Shop Scheduling with Transportation Constraints. IEEE Trans. Evol. Comput. 2024, 1. [Google Scholar] [CrossRef]
- Zhang, Z.; Yin, Y.; Fu, Y. An ensemble of brain storm optimization and Q-learning methods for distributed flexible job shop scheduling problems with distribution operations. Int. J. Gen. Syst. 2024, 53, 863–897. [Google Scholar] [CrossRef]
- Li, R.; Gong, W.; Wang, L.; Lu, C.; Jiang, S. Two-stage knowledge-driven evolutionary algorithm for distributed green flexible job shop scheduling with type-2 fuzzy processing time. Swarm Evol. Comput. 2022, 74, 101139. [Google Scholar] [CrossRef]
- Liu, Y.; As’arry, A.; Hassan, M.K.; Hairuddin, A.A.; Mohamad, H. Review of the grey wolf optimization algorithm: Variants and applications. Neural Comput. Appl. 2024, 36, 2713–2735. [Google Scholar] [CrossRef]
- Li, X.; Xie, J.; Ma, Q.; Gao, L.; Li, P. Improved gray wolf optimizer for distributed flexible job shop scheduling problem. Sci. China Technol. Sci. 2022, 65, 2105–2115. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, X.; Cao, D.; Li, M. A shuffled cellular evolutionary grey wolf optimizer for flexible job shop scheduling problem with tree-structure job precedence constraints. Appl. Soft Comput. 2022, 125, 109235. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Ren, S.; Wang, C.; Wang, W. Evolutionary game based real-time scheduling for energy-efficient distributed and flexible job shop. J. Clean. Prod. 2021, 293, 126093. [Google Scholar] [CrossRef]
- Zhu, K.; Gong, G.; Peng, N.; Zhang, L.; Huang, D.; Luo, Q.; Li, X. Dynamic distributed flexible job-shop scheduling problem considering operation inspection. Expert Syst. Appl. 2023, 224, 119840. [Google Scholar] [CrossRef]
- Zhang, H.; Qin, C.; Xu, G.; Chen, Y.; Gao, Z. An energy-saving distributed flexible job shop scheduling with machine breakdowns. Appl. Soft Comput. 2024, 167, 112276. [Google Scholar] [CrossRef]
- Zhu, N.; Gong, G.; Lu, D.; Huang, D.; Peng, N.; Qi, H. An effective reformative memetic algorithm for distributed flexible job-shop scheduling problem with order cancellation. Expert Syst. Appl. 2024, 237, 121205. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm For Multiobjective Optimization. In Proceedings of the Evolutionary Methods for Design, Optimization and Control with Applications to Industrial Problems, EUROGEN’2001, Athens, Greece, 19–21 September 2001. [Google Scholar]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Chan, F.T.; Chung, S.; Chan, P. An adaptive genetic algorithm with dominated genes for distributed scheduling problems. Expert Syst. Appl. 2005, 29, 364–371. [Google Scholar] [CrossRef]
- De Giovanni, L.; Pezzella, F. An Improved Genetic Algorithm for the Distributed and Flexible Job-shop Scheduling problem. Eur. J. Oper. Res. 2010, 200, 395–408. [Google Scholar] [CrossRef]
- Ziaee, M. A heuristic algorithm for the distributed and flexible job-shop scheduling problem. J. Supercomput. 2014, 67, 69–83. [Google Scholar] [CrossRef]
- Xie, J.; Li, X.; Gao, L.; Gui, L. A hybrid genetic tabu search algorithm for distributed flexible job shop scheduling problems. J. Manuf. Syst. 2023, 71, 82–94. [Google Scholar] [CrossRef]
- Zhang, Z.; Fu, Y.; Gao, K.; Zhang, H.; Wang, L. A cooperative evolutionary algorithm with simulated annealing for integrated scheduling of distributed flexible job shops and distribution. Swarm Evol. Comput. 2024, 85, 101467. [Google Scholar] [CrossRef]
- Samhouri, M.; Qareish, S.Z. Hybrid fuzzy genetic algorithm for the integration of process planning and scheduling for distributed flexible job shop. Neural Comput. Appl. 2025, 37, 2775–2798. [Google Scholar] [CrossRef]
- Wang, C.; Wei, M.; Liu, Q.; Zhang, X.; Li, X. An improved adaptive hybrid algorithm for solving distributed flexible job shop scheduling problem. Swarm Evol. Comput. 2025, 94, 101873. [Google Scholar] [CrossRef]
- Du, Y.; Li, J.; Luo, C.; Meng, L. A hybrid estimation of distribution algorithm for distributed flexible job shop scheduling with crane transportations. Swarm Evol. Comput. 2021, 62, 100861. [Google Scholar] [CrossRef]
- Yu, F.; Lu, C.; Zhou, J.; Yin, L.; Wang, K. A knowledge-guided bi-population evolutionary algorithm for energy-efficient scheduling of distributed flexible job shop problem. Eng. Appl. Artif. Intell. 2024, 128, 107458. [Google Scholar] [CrossRef]
- Zhao, F.; Li, M.; Zhu, N.; Xu, T.; Jonrinaldi. Multi-objective fitness landscape-based estimation of distribution algorithm for distributed heterogeneous flexible job shop scheduling problem. Appl. Soft Comput. 2025, 171, 112780. [Google Scholar] [CrossRef]
- Yan, Q.; Wang, H.; Yang, S. A Learning-Assisted Bi-Population Evolutionary Algorithm for Distributed Flexible Job-Shop Scheduling with Maintenance Decisions. IEEE Trans. Evol. Comput. 2024, 1. [Google Scholar] [CrossRef]
- Deng, L.; Qiu, Y.; Di, Y.; Zhang, L. A knowledge-driven memetic algorithm for distributed green flexible job shop scheduling considering the endurance of machines. Appl. Soft Comput. 2025, 170, 112697. [Google Scholar] [CrossRef]
- Wu, X.; Liu, X.; Zhao, N. An improved differential evolution algorithm for solving a distributed assembly flexible job shop scheduling problem. Memetic Comput. 2019, 11, 335–355. [Google Scholar] [CrossRef]
- Du, B.; Han, S.; Guo, J.; Li, Y. A hybrid estimation of distribution algorithm for solving assembly flexible job shop scheduling in a distributed environment. Eng. Appl. Artif. Intell. 2024, 133, 108491. [Google Scholar] [CrossRef]
- Sang, Y.; Tan, J. Intelligent factory many-objective distributed flexible job shop collaborative scheduling method. Comput. Ind. Eng. 2022, 164, 107884. [Google Scholar] [CrossRef]
- Zadeh, M.S.; Katebi, Y.; Doniavi, A. A heuristic model for dynamic flexible job shop scheduling problem considering variable processing times. Int. J. Prod. Res. 2019, 57, 3020–3035. [Google Scholar] [CrossRef]
- Al-Hinai, N.; ElMekkawy, T. Robust and stable flexible job shop scheduling with random machine breakdowns using a hybrid genetic algorithm. Int. J. Prod. Econ. 2011, 132, 279–291. [Google Scholar] [CrossRef]
- Soofi, P.; Yazdani, M.; Amiri, M.; Adibi, M.A. Robust Fuzzy-Stochastic Programming Model and Meta-Heuristic Algorithms for Dual-Resource Constrained Flexible Job-Shop Scheduling Problem Under Machine Breakdown. IEEE Access 2021, 9, 155740–155762. [Google Scholar] [CrossRef]
- Duan, J.; Wang, J. Robust scheduling for flexible machining job shop subject to machine breakdowns and new job arrivals considering system reusability and task recurrence. Expert Syst. Appl. 2022, 203, 117489. [Google Scholar] [CrossRef]
- Shen, X.; Han, Y.; Fu, J. Robustness measures and robust scheduling for multi-objective stochastic flexible job shop scheduling problems. Soft Comput. 2017, 21, 6531–6554. [Google Scholar] [CrossRef]
- Luo, S.; Zhang, L.; Fan, Y. Dynamic multi-objective scheduling for flexible job shop by deep reinforcement learning. Comput. Ind. Eng. 2021, 159, 107489. [Google Scholar] [CrossRef]
- Wu, Z.; Fan, H.; Sun, Y.; Peng, M. Efficient Multi-Objective Optimization on Dynamic Flexible Job Shop Scheduling Using Deep Reinforcement Learning Approach. Processes 2023, 11, 2018. [Google Scholar] [CrossRef]
- Nguyen, S.; Mei, Y.; Zhang, M. Genetic programming for production scheduling: A survey with a unified framework. Complex Intell. Syst. 2017, 3, 41–66. [Google Scholar] [CrossRef]
- Ozturk, G.; Bahadir, O.; Teymourifar, A. Extracting priority rules for dynamic multi-objective flexible job shop scheduling problems using gene expression programming. Int. J. Prod. Res. 2019, 57, 3121–3137. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Liu, Y. Game theory based real-time multi-objective flexible job shop scheduling considering environmental impact. J. Clean. Prod. 2017, 167, 665–679. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.; Wen, L.; Zhang, G. An efficient memetic algorithm for dynamic flexible job shop scheduling with random job arrivals. Int. J. Softw. Sci. Comput. Intell. 2013, 5, 63–77. [Google Scholar] [CrossRef]
- Shen, X.N.; Yao, X. Mathematical modeling and multi-objective evolutionary algorithms applied to dynamic flexible job shop scheduling problems. Inf. Sci. 2015, 298, 198–224. [Google Scholar] [CrossRef]
- Xu, W.; Shao, L.; Yao, B.; Zhou, Z.; Pham, D.T. Perception data-driven optimization of manufacturing equipment service scheduling in sustainable manufacturing. J. Manuf. Syst. 2016, 41, 86–101. [Google Scholar] [CrossRef]
- Sreekara Reddy, M.; Ratnam, C.; Rajyalakshmi, G.; Manupati, V. An effective hybrid multi objective evolutionary algorithm for solving real time event in flexible job shop scheduling problem. Measurement 2018, 114, 78–90. [Google Scholar] [CrossRef]
- Komaki, G.; Kayvanfar, V. Grey Wolf Optimizer algorithm for the two-stage assembly flow shop scheduling problem with release time. J. Comput. Sci. 2015, 8, 109–120. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, C. Application of Grey Wolf Optimization for Solving Combinatorial Problems: Job Shop and Flexible Job Shop Scheduling Cases. IEEE Access 2018, 6, 26231–26240. [Google Scholar] [CrossRef]
- Zhang, W.; Zheng, Y.; Ahmad, R. An energy-efficient multi-objective scheduling for flexible job-shop-type remanufacturing system. J. Manuf. Syst. 2023, 66, 211–232. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, Y.; Zhang, Y.; Xu, G. Energy-Saving Distributed Flexible Job Shop Scheduling Optimization with Dual Resource Constraints Based on Integrated Q-Learning Multi-Objective Grey Wolf Optimizer. Comput. Model. Eng. Sci. 2024, 140, 1459–1483. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Tan, Y.; Jiao, Y.; Li, H.; Wang, X. MOEA/D + uniform design: A new version of MOEA/D for optimization problems with many objectives. Comput. Oper. Res. 2013, 40, 1648–1660. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Kong, X.; Yao, Y.; Yang, W.; Yang, Z.; Su, J. Solving the Flexible Job Shop Scheduling Problem Using a Discrete Improved Grey Wolf Optimization Algorithm. Machines 2022, 10, 1100. [Google Scholar] [CrossRef]
- Zhang, G.; Gao, L.; Shi, Y. An effective genetic algorithm for the flexible job-shop scheduling problem. Expert Syst. Appl. 2011, 38, 3563–3573. [Google Scholar] [CrossRef]
- Wang, X.; Gao, L.; Zhang, C.; Shao, X. A multi-objective genetic algorithm based on immune and entropy principle for flexible job-shop scheduling problem. Int. J. Adv. Manuf. Technol. 2010, 51, 757–767. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, G.; Xu, Y.; Liu, M. An enhanced Pareto-based artificial bee colony algorithm for the multi-objective flexible job-shop scheduling. Int. J. Adv. Manuf. Technol. 2012, 60, 1111–1123. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, L.; Li, X. A hybrid intelligent algorithm and rescheduling technique for job shop scheduling problems with disruptions. Int. J. Adv. Manuf. Technol. 2013, 65, 1141–1156. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Bosman, P.; Thierens, D. The balance between proximity and diversity in multiobjective evolutionary algorithms. IEEE Trans. Evol. Comput. 2003, 7, 174–188. [Google Scholar] [CrossRef]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of Multiobjective Evolutionary Algorithms: Empirical Results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef]
- Bader, J.; Zitzler, E. HypE: An Algorithm for Fast Hypervolume-Based Many-Objective Optimization. Evol. Comput. 2011, 19, 45–76. [Google Scholar] [CrossRef]
- Demšar, J. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Yuan, Y.; Xu, H.; Wang, B.; Yao, X. A New Dominance Relation-Based Evolutionary Algorithm for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2016, 20, 16–37. [Google Scholar] [CrossRef]











| the rescheduling point | the number of jobs which contain unprocessed and available operations at | ||
| i | the index of jobs, | f | the number of factories |
| l | the index of factories, | the lth factory | |
| the number of available machines in at | the kth available machine in | ||
| k | the index of available machines in | the ith job at | |
| the number of operations that are assigned on | the ath operation that is processed on | ||
| the processing time of | j | the index of operations belonging to | |
| the weight of | the completion time of | ||
| the index of the first unprocessed operation of | the number of unprocessed and available opertaions corresponding to | ||
| the due date of | the jth operation of , | ||
| the starting time of | the set of unprocessed and available operations which appear at both and | ||
| the set of jobs which contain unprocessed and available operations at both and | if is processed in , ; otherwise, | ||
| the set of available machines in which appear at both and | if is processed on , ; otherwise, | ||
| the time when arrives at the distributed workshop | the tightness factor which follows a normal distribution with a mean of 1.5 and variance of 0.5 | ||
| the average processing time of | if has already had an operation processed at , ; otherwise, | ||
| the average processing time of related to | the completion time of | ||
| the set of available machines in that can process at | the processing time of on | ||
| the initial release time of | the completion time of the last operation of which is completed before | ||
| the initial available time of | the completion time of the last operation processed on before | ||
| the completion time of | if is the ath operation processed on ; otherwise, |
| Job | Instance | ||||||
|---|---|---|---|---|---|---|---|
| * | |||||||
| 3 | 4 | 7 | 7 | 4 | |||
| − | 4 | 3 | 4 | 2 | − | ||
| 5 | − | 5 | 3 | − | 3 | ||
| 2 | 4 | 3 | 4 | 3 | − | ||
| 3 | − | 4 | − | 5 | 7 | ||
| − | 1 | 2 | 3 | 1 | 3 | ||
| 6 | 8 | − | 4 | 5 | 5 | ||
| 5 | − | 7 | 8 | 2 | 5 | ||
| 6 | 4 | 6 | 7 | 5 | 8 | ||
| 1 | 3 | − | 6 | − | 3 | ||
| 5 | 5 | 2 | 3 | 2 | 4 | ||
| 2 | − | 4 | 3 | 1 | 5 | ||
| Characteristics | Specifications |
|---|---|
| Distributed flexible job shop | |
| Number of factories | 2 |
| Number of machines in each factory, m | 8 |
| Shop utilization, u | 0.8 |
| Mean time between failures () | * |
| Mean time to repair () | |
| Time interval between failures () | Exponential distribution with mean of |
| Time to repair () | Exponential distribution with mean of |
| Jobs | |
| Number of operations in each job | |
| Number of candidate machines for each job | |
| Time between new job arrivals () | Exponential distribution with mean of |
| Processing time of each opeartion | Exponential distribution with mean of 2 |
| Parameter | DIGWO | NSGA-II | SPEA2 | MOEA/D |
|---|---|---|---|---|
| Population size, N | 100 | 100 | 100 | 100 |
| Crossover probability | – * | 0.8 | 0.8 | – |
| Mutation probability | 0.1 | 0.1 | 0.1 | 0.1 |
| Neighborhood size, T | – | – | – | 0.1N |
| External archive size | same as N | – | same as N | same as N |
| Number of runs | 20 | 20 | 20 | 20 |
| Maximum number of objective evaluations | 20,000 | 20,000 | 20,000 | 20,000 |
| NSGA-II | SPEA2 | MOEA/D | DIGWOrand | ||
|---|---|---|---|---|---|
| DIGWO vs. (HV) | B | 36 | 18 | 91 | 46 |
| W | 7 | 17 | 0 | 1 | |
| E | 51 | 59 | 3 | 47 | |
| DIGWO vs. (IGD) | B | 61 | 42 | 92 | 46 |
| W | 0 | 7 | 0 | 2 | |
| E | 33 | 45 | 2 | 46 | |
| DIGWO vs. (C) | B | 22 | 83 | 92 | 35 |
| W | 9 | 3 | 0 | 2 | |
| E | 63 | 8 | 2 | 57 |
| Algorithm | HV | IGD | |
|---|---|---|---|
| DIGWO | Mean | 1.079 | 0.069 |
| Std | 0.231 | 0.041 | |
| NSGA-II | Mean | 1.057(+) | 0.085(+) |
| Std | 0.246 | 0.052 | |
| SPEA2 | Mean | 1.078(=) | 0.074(+) |
| Std | 0.229 | 0.040 | |
| MOEA/D | Mean | 0.903(+) | 0.146(+) |
| Std | 0.247 | 0.068 | |
| DIGWOrand | Mean | 1.054(+) | 0.077(+) |
| Std | 0.235 | 0.044 |
| DIGWO(A) vs. NSGA-II(B) | DIGWO(A) vs. SPEA2(C) | DIGWO(A) vs. MOEA/D(D) | DIGWO(A) vs. DIGWOrand(E) | |||||
|---|---|---|---|---|---|---|---|---|
| C(A,B) | C(B,A) | C(A,C) | C(C,A) | C(A,D) | C(D,A) | C(A,E) | C(E,A) | |
| Mean | 0.196 | 0.162 | 0.350 | 0.104 | 0.592 | 0.143 | 0.269 | 0.158 |
| Std | 0.194 | 0.176 | 0.214 | 0.134 | 0.303 | 0.181 | 0.221 | 0.180 |
| Scheduling Methods | Makespan | Weighted Average Job Tardiness | Avg Factory Load |
|---|---|---|---|
| FAR1+MAR1+SPT | 570.78 | 84.53 | 901.00 |
| FAR1+MAR2+SPT | 1122.50 | 526.69 | 2018.63 |
| FAR1+MAR3+SPT | 1175.85 | 559.73 | 2049.72 |
| FAR2+MAR1+SPT | 577.57 | 88.41 | 886.10 |
| FAR2+MAR2+SPT | 1115.62 | 520.96 | 2033.60 |
| FAR2+MAR3+SPT | 1182.18 | 546.12 | 2042.13 |
| FAR1+MAR1+FIFO | 737.41 | 180.09 | 891.85 |
| FAR1+MAR2+FIFO | 1374.00 | 705.88 | 2042.89 |
| FAR1+MAR3+FIFO | 1491.61 | 784.76 | 2051.19 |
| FAR2+MAR1+FIFO | 737.41 | 177.12 | 888.20 |
| FAR2+MAR2+FIFO | 1391.53 | 716.15 | 2050.48 |
| FAR2+MAR3+FIFO | 1491.48 | 792.41 | 2055.87 |
| FAR1+MAR1+LIFO | 747.26 | 186.82 | 896.39 |
| FAR1+MAR2+LIFO | 1425.64 | 748.86 | 2038.31 |
| FAR1+MAR3+LIFO | 1485.88 | 794.63 | 2067.00 |
| FAR2+MAR1+LIFO | 750.44 | 178.68 | 889.75 |
| FAR2+MAR2+LIFO | 1402.42 | 740.66 | 2045.95 |
| FAR2+MAR3+LIFO | 1465.94 | 782.29 | 2048.33 |
| DIGWO | 440.05 | 34.72 | 1022.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Chen, J.; Xu, B.; Liu, S. A Discrete Improved Gray Wolf Optimization Algorithm for Dynamic Distributed Flexible Job Shop Scheduling Considering Random Job Arrivals and Machine Breakdowns. Processes 2025, 13, 1987. https://doi.org/10.3390/pr13071987
Wang C, Chen J, Xu B, Liu S. A Discrete Improved Gray Wolf Optimization Algorithm for Dynamic Distributed Flexible Job Shop Scheduling Considering Random Job Arrivals and Machine Breakdowns. Processes. 2025; 13(7):1987. https://doi.org/10.3390/pr13071987
Chicago/Turabian StyleWang, Chun, Jiapeng Chen, Binzi Xu, and Sheng Liu. 2025. "A Discrete Improved Gray Wolf Optimization Algorithm for Dynamic Distributed Flexible Job Shop Scheduling Considering Random Job Arrivals and Machine Breakdowns" Processes 13, no. 7: 1987. https://doi.org/10.3390/pr13071987
APA StyleWang, C., Chen, J., Xu, B., & Liu, S. (2025). A Discrete Improved Gray Wolf Optimization Algorithm for Dynamic Distributed Flexible Job Shop Scheduling Considering Random Job Arrivals and Machine Breakdowns. Processes, 13(7), 1987. https://doi.org/10.3390/pr13071987






