Importance Analyses on Phenomenological Parameters for the Aerosol Dynamics Models in I-COSTA for a Severe Nuclear Power Plant Accident
Abstract
1. Introduction
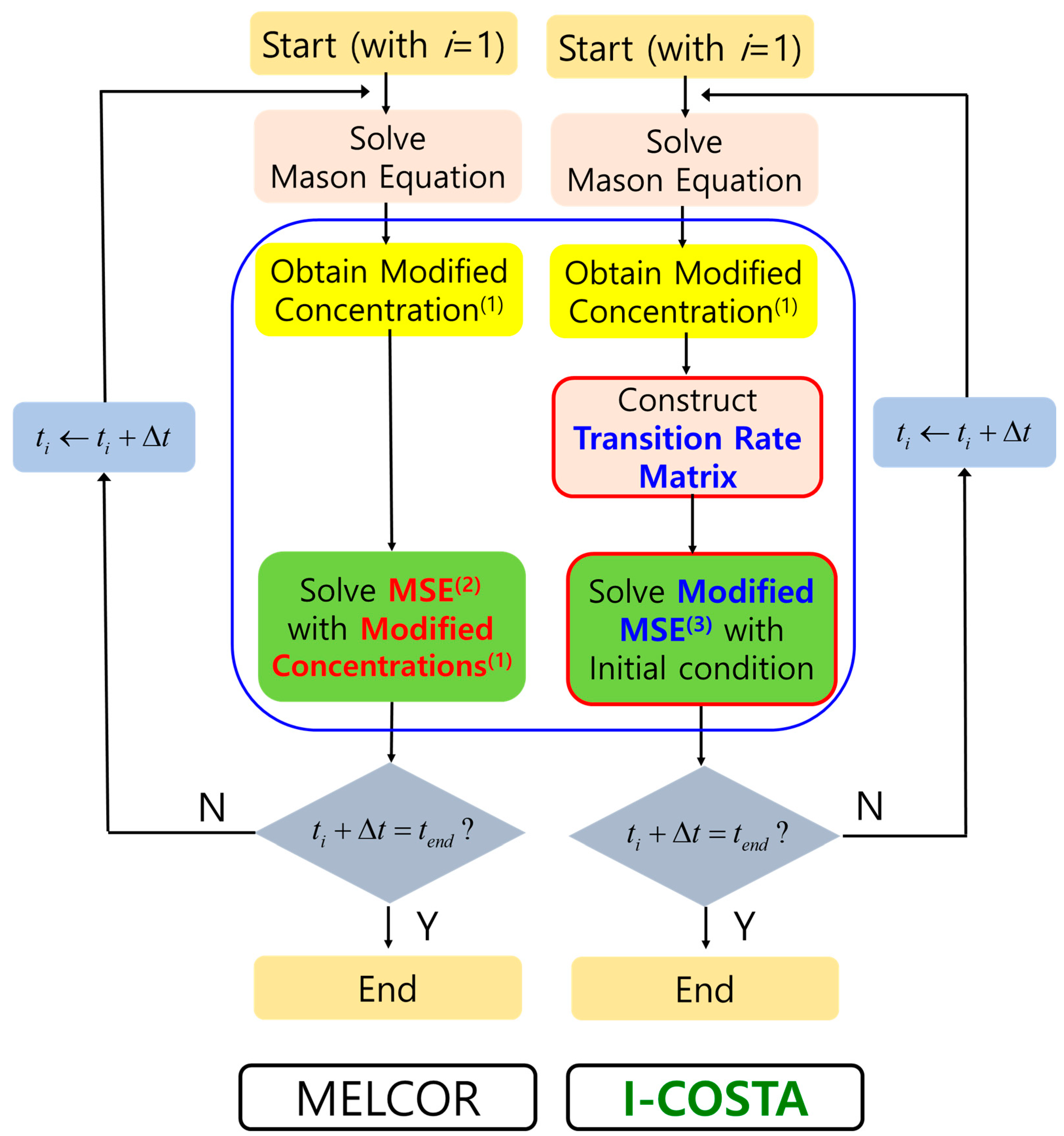
2. Summary of the Numerical Methods in the I-COSTA Code
2.1. Summary of Multicomponent Sectional Equations and Mason Equations for Hygroscopic Growth in I-COSTA
- : mass concentration of aerosol particles of component k in section l,
- : coagulation rate of the aerosol particles in sections lower than l forming an aerosol particle in section l,
- ncomp: number of components of the aerosol particles considered in the multicomponent sectional equations,
- : coagulation rate of the aerosol particles in section l and sections lower than l forming an aerosol particle larger than those in section l,
- : coagulation rate of the aerosol particles in section l and sections lower than l forming an aerosol particle remaining section l,
- : intra-sectional coagulation rate of the aerosol particles in section l forming an aerosol particle larger than those in section l,
- : coagulation rate of the aerosol particles in section l forming an aerosol particle larger than those in section l,
- : injection rates of the aerosol particles in section l,
- : removal rates of the aerosol particles in section l via deposition.
- ul, vl: mass of a single aerosol particle in section l,
- S: saturation ratio, in other words, relative humidity in the containment,
- Sr,k: effective saturation ratio at the surface of the aerosol particles expressed as
- ak: thermal conduction of the latent heat associated with condensation from particles to the atmosphere, expressed as
- bk: diffusion of water vapor from the atmosphere to the particle surface of component k expressed as
- : effective vapor diffusion coefficient for component k expressed as
- : effective thermal conductivity of atmosphere in the containment expressed asand the coefficients and nomenclatures used in Equations (14)–(18) are described in the nomenclature section.
2.2. Summary of Coupling Scheme of Multicomponent Sectional Equations and Mason Equations for Hygroscopic Growth in I-COSTA
- v: mass of a single particle,
- slopl,k: slope of the mass concentration function for component k in section l, defined as
- : mass concentration of aerosol particles of component k that remain in section l after hygroscopic growth for the time step of Δt,
- : mass concentration of aerosol particles of component k that grow in size to section l + 1 after hygroscopic growth for the time step of Δt,
- frl,k: fraction of the aerosol particles of component k in section l that remain in section l after hygroscopic growth, which is expressed as
- trl,k: fraction of the aerosol particles of component k in section l that grow up to section l + 1 after hygroscopic growth, which is expressed asThe relationship among the variables delineated in Equations (19)–(24) is shown in Figure 1.
- nbin: number of sections of the aerosol particles considered in the multicomponent sectional equations.
- : mass concentration of aerosol particles of component k that remain in section l after hygroscopic growth for the time step of Δt.
2.3. Comparison of the Coupling Scheme in I-COSTA and That in the Conventional Codes
2.4. Selected Parameters and Their Uncertainty Range for Importance Analysis
2.5. Summaries of the Framework for Importance Analysis
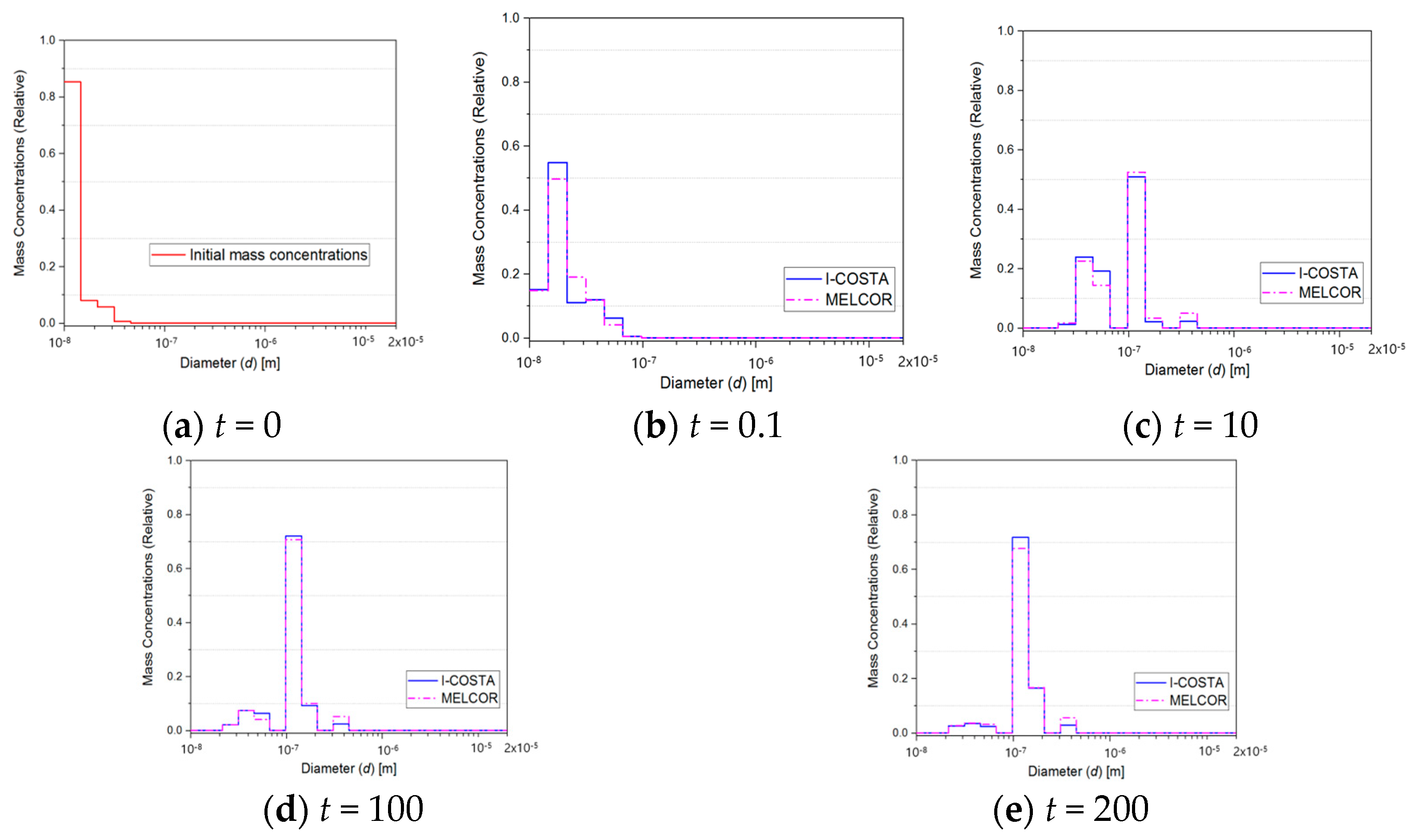
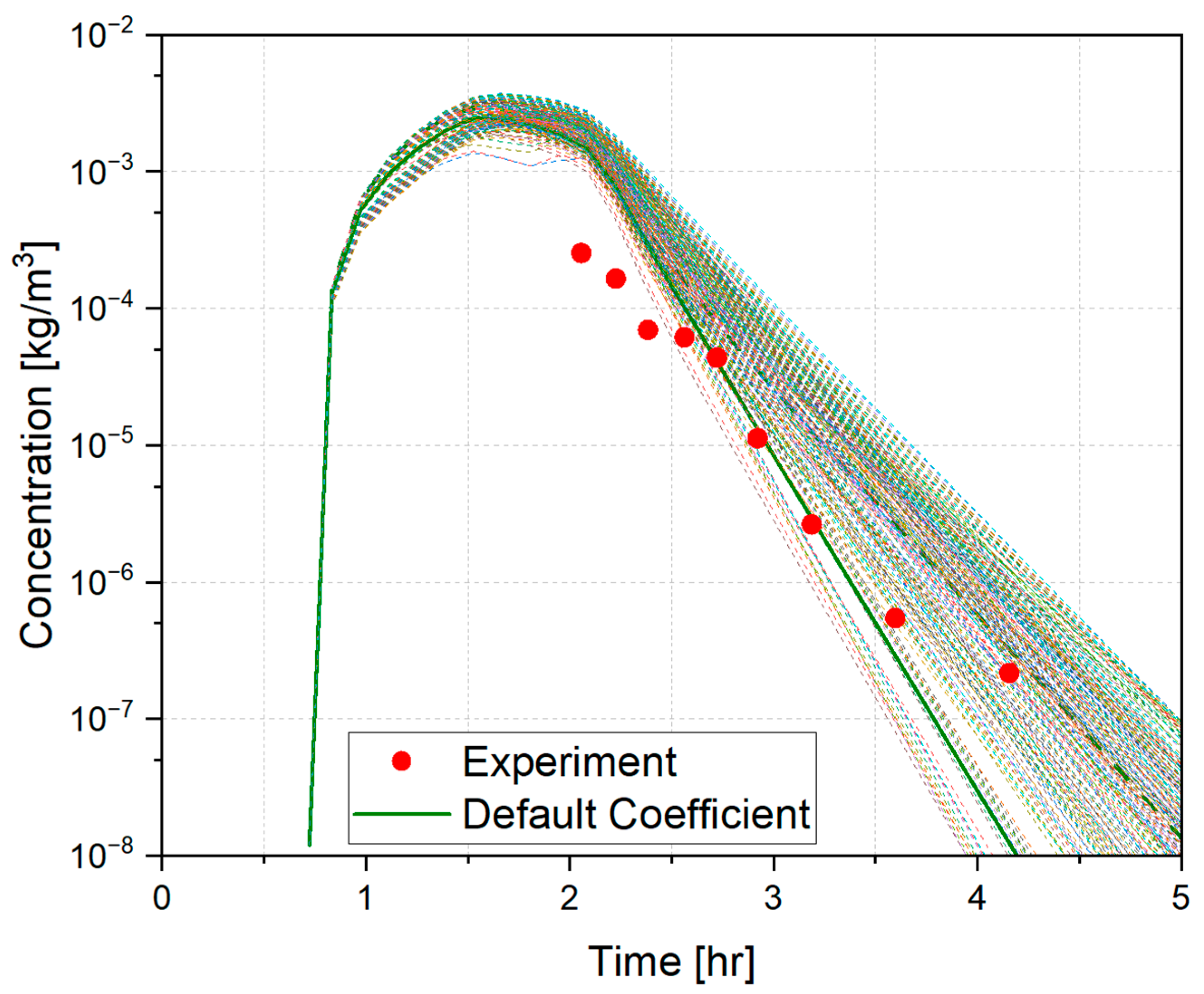
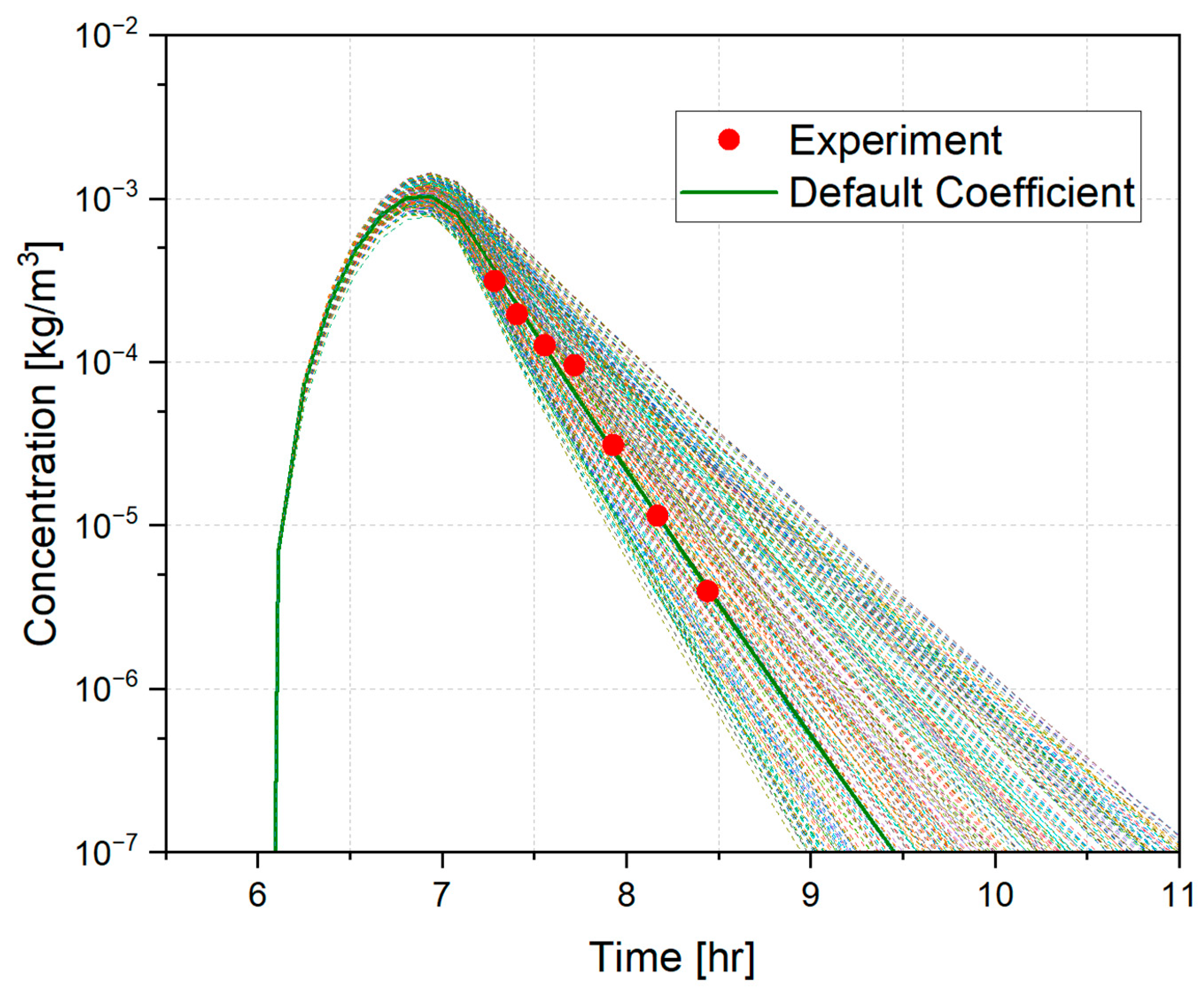
3. Numerical Results
3.1. Computation Conditions on the Importance Analysis
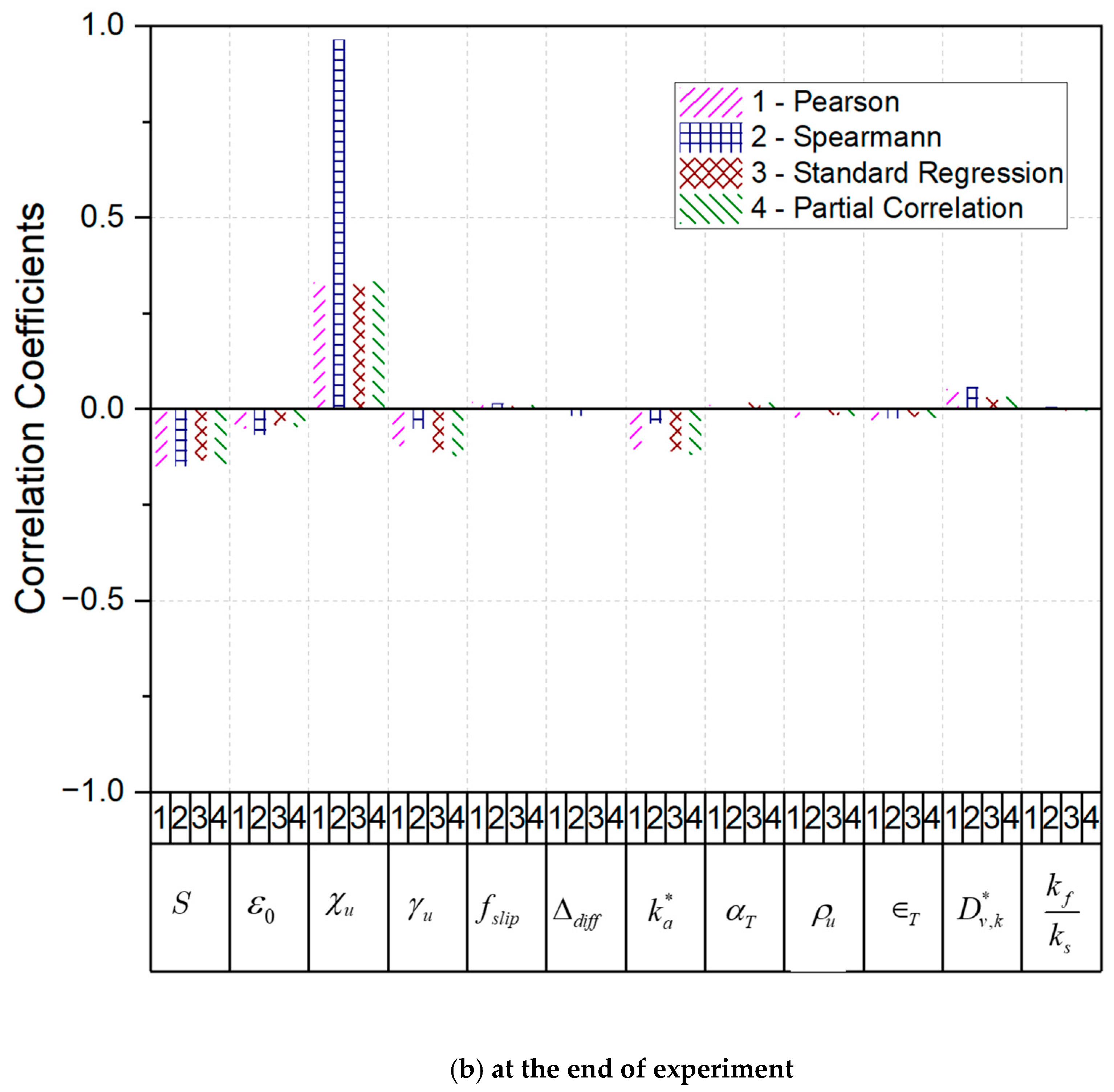
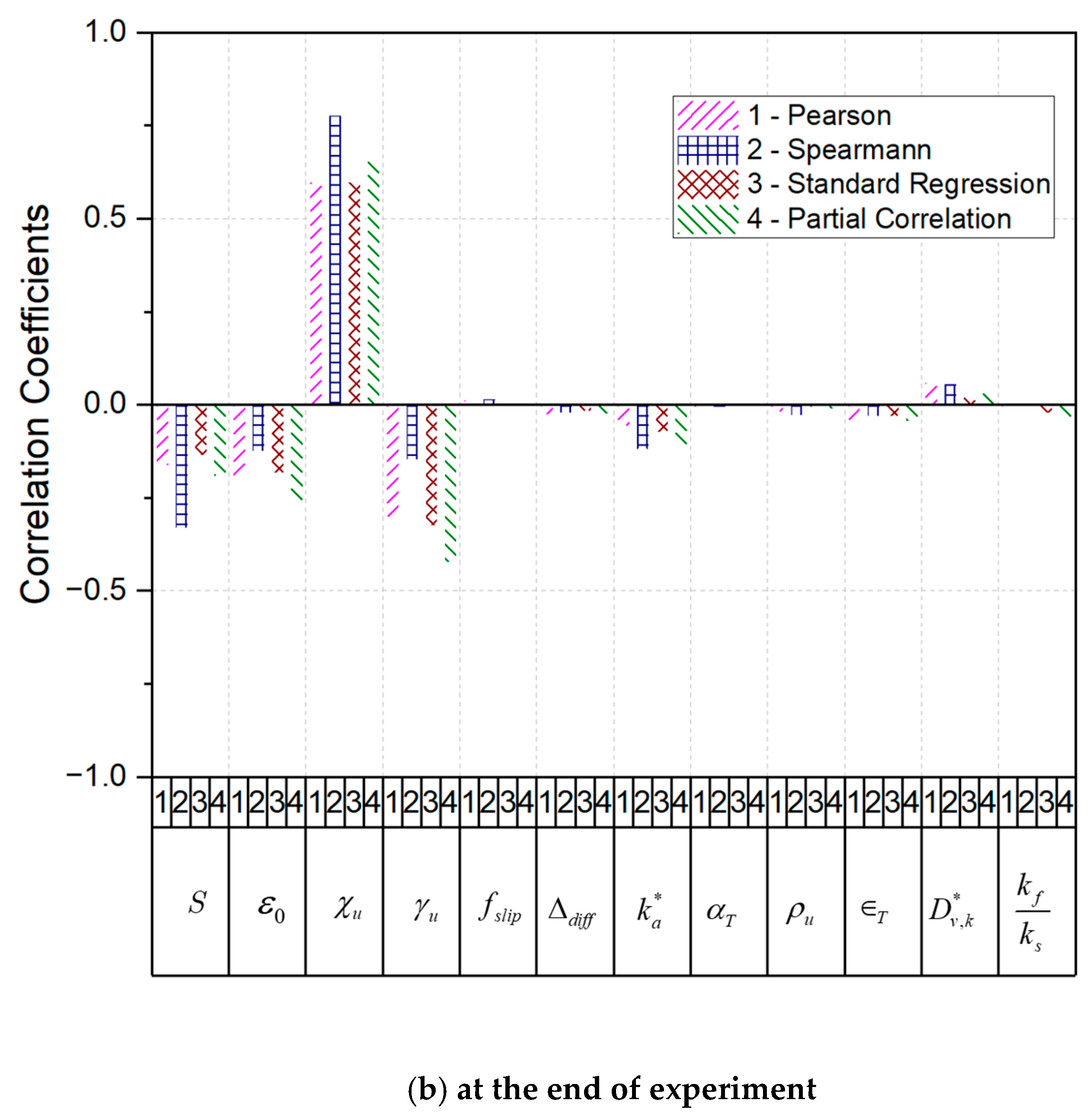
3.2. Importance Analyses on the Phenomenological Parameters for the Aerosol Dynamics
4. Summary and Conclusions
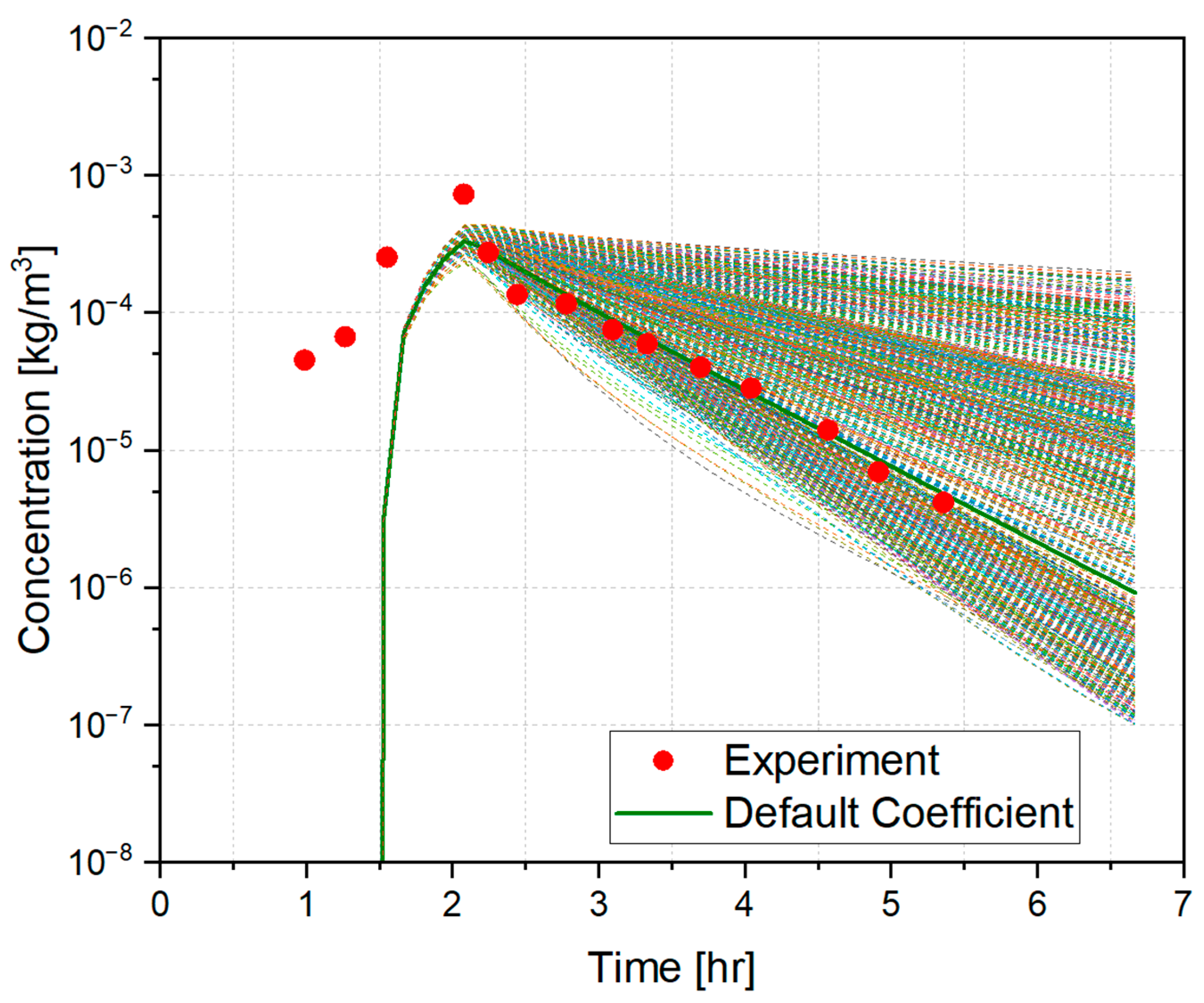
- The range of the phenomenological parameters taken from previous studies leads to 50% of the airborne concentration of the aerosol particles obtained from experimental values.
- The range of sensitivity of the maximum airborne aerosol concentrations is seven times the uncertainty range of the measurement during experiment, i.e., the uncertainty range of the measurement is known to be 7% of the concentrations [17].
- The larger range of sensitivity compared to the range of measurement appears to be caused by the uncertainty range of the phenomenological parameters. In order to make the accuracy of the aerosol dynamics model comparable to that of the experimental measurement, the uncertainty of the parameters should be reduced.
- From the correlation coefficients between the phenomenological parameters and the airborne concentrations, the dynamic shape factor and the saturation ratio were found to be important parameters with respect to the airborne concentrations of the aerosol particles.
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
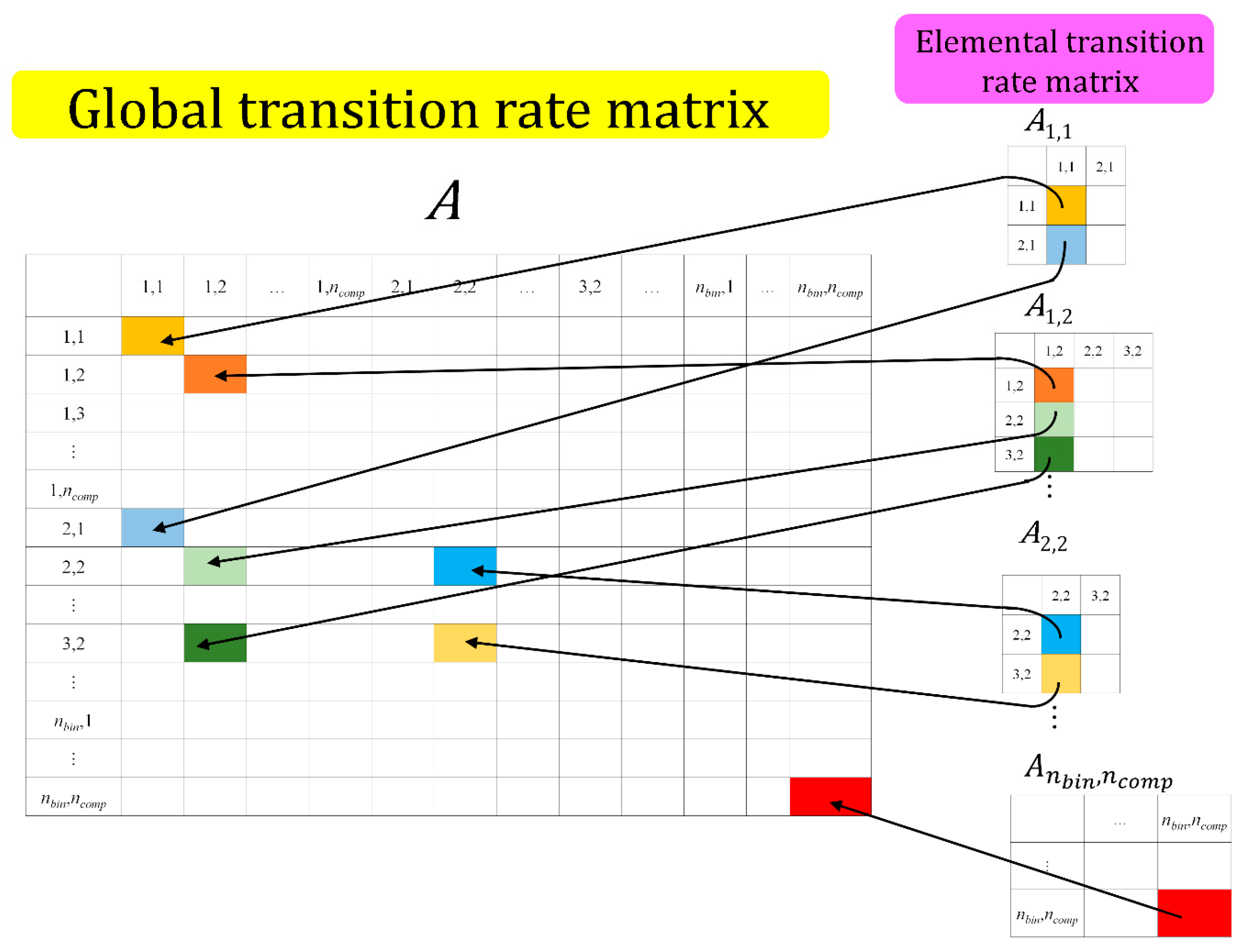
| A | Global transition rate matrix |
| Al,k | Elemental transition rate matrix for aerosol particles of component k in section l |
| ak | Thermal conduction of the latent heat associated with condensation from particles to the atmosphere |
| Ar,k | Activity of the aerosol particles |
| bk | Diffusion of water vapor from the atmosphere to the particle surface of component k |
| Vapor diffusion coefficient for component k | |
| Effective vapor diffusion coefficient for component k | |
| Slip correction factor | |
| Radius function of the aerosol particles for component k with respect to the mass of particles u | |
| frl,k | Fraction of the aerosol particles of component k in section l that remain in section l after hygroscopic growth |
| Thermal conductivity of atmosphere in the containment | |
| Effective thermal conductivity of atmosphere in the containment | |
| Mw | Molecular weight of the water |
| nbin | Number of sections of the aerosol particles considered in the multicomponent sectional equations |
| ncomp | Number of components of the aerosol particles considered in the multicomponent sectional equations |
| no, ni, | Number of Gaussian quadrature sets |
| Vector form of the multicomponent sectional equations of the aerosol particles | |
| Mass concentration of aerosol particles of component k in section l | |
| Mass concentration of aerosol particles of component k that remain section l after hygroscopic growth for the time step of Δt | |
| Mass concentration of aerosol particles of component k that grow up to section l + 1 after hygroscopic growth for the time step of Δt | |
| R | Gas constant |
| Removal rates of the aerosol particles in section l via deposition, | |
| S | Saturation ratio, in other words, relative humidity in the containment |
| Injection rates of the aerosol particles in section l | |
| Sr,k | Effective saturation ratio at the surface of the aerosol particles |
| slopl,k | Slope of the mass concentration function for component k in section l |
| T∞ | Temperature of the atmosphere in the containment |
| trl,k | Fraction of the aerosol particles of component k in section l that grow up to section l + 1 after hygroscopic growth |
| U(u,t) | Deposition via thermophoresis, |
| VT(u) | Deposition via gravitational settling |
| Diffu(u) | Deposition via diffusiophoresis, |
| Abscissas for Gaussian quadrature | |
| ul | Mass of a single aerosol particle in section l |
| v | Mass of a single particle |
| vl | Mass of a single aerosol particle in section l |
| Weights for Gaussian quadrature | |
| xl | Radius of a single aerosol particle in section l |
| αc | Condensation coefficient |
| αT | Thermal accommodation coefficient |
| (u,v) | Kernel for Brownian, gravitational, and turbulent shear coagulations for particles having masses of u and v |
| (u,v) | Brownian coagulation kernel, |
| (u,v) | Gravitational coagulation kernel |
| (u,v) | Turbulent inertial coagulation kernel |
| (u,v) | Turbulent shear coagulation kernel |
| Coagulation rate of the aerosol particles in sections lower than l forming an aerosol particle in section l | |
| Coagulation rate of the aerosol particles in section l and sections lower than l forming an aerosol particle larger than those in section l | |
| Intra-sectional coagulation rate of the aerosol particles in section l forming an aerosol particle larger than those in section l | |
| Coagulation rate of the aerosol particles in section l forming an aerosol particle larger than those in section l | |
| Diffusion boundary thickness | |
| Collision shape factor of an aerosol particle with mass u | |
| Sticking efficiency of the two aerosol particles | |
| Gas viscosity | |
| Mean free path of an aerosol particle, | |
| λl,k | Transition rate of aerosol particles of component k in section l |
| ρw | Density of the water |
| σ | Surface tension of water |
| Dynamic shape factor of an aerosol particle with mass u | |
| Turbulent energy dissipation rate |
Appendix A. Description on the Coefficients Used in Equations (1)–(29)
References
- Hart, M.; Herviou, K.; Wu, J.; Taehee, K.; Shapovalov, A.; Thomas, K.; Wallace, D. SMR Regulators’ Forum, Pilot Project Report: Report from Working Group on Emergency Planning Zone; International Atomic Energy Agency (IAEA): Wien, Austria, 2018; Available online: https://www.iaea.org/sites/default/files/18/01/smr-rf-report-appendix-iv-29012018.pdf (accessed on 31 May 2025).
- Haste, T.; Payot, F.; Bottomley, P.D.W. Transport and deposition in the Phébus FP circuit. Ann. Nucl. Energy 2013, 61, 102–121. [Google Scholar] [CrossRef]
- Mascari, F.; Bersano, A.; Massone, M.; Agnello, G.; Coindreau, O.; Beck, S.; Tiborcz, L.; Paci, S.; Angelucci, M.; Herranz, L.E.; et al. Main outcomes of the Phebus FPT1 uncertainty and sensitivity analysis in the EU-MUSA project. Ann. Nucl. Energy 2024, 196, 110205. [Google Scholar] [CrossRef]
- Yu, M. Main outputs from the OECD/NEA ARC-F Project. In Proceedings of the 20th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-20), Washington, DC, USA, 20–25 August 2023. [Google Scholar]
- Doi, T.; Masumoto, K.; Toyoda, A.; Tanaka, A.; Shibata, Y.; Hirose, K. Anthropogenic radionuclides in the atmosphere observed at Tsukuba: Characteristics of the radionuclides derived from Fukushima. J. Environ. Radioact. 2013, 122, 55–62. [Google Scholar] [CrossRef] [PubMed]
- Grégoire, A.C.; Le Fessant, E.; Cantrel, L. ESTER Program—State of the Art on Revaporization from RCS Surfaces; IRSN No 2021-00282; IRSN: Fontenay-aux-Roses, France, 2021. [Google Scholar]
- Katata, G.; Chino, M.; Kobayashi, T.; Terada, H.; Ota, M.; Nagai, H.; Kajino, M.; Draxler, R.; Hort, M.C.; Malo, A.; et al. Detailed source term estimation of the atmospheric release for the Fukushima Daiichi Nuclear Power Station accident by coupling simulations of an atmospheric dispersion model with an improved deposition scheme and oceanic dispersion model. Atmos. Chem. Phys. 2015, 15, 1029–1070. [Google Scholar] [CrossRef]
- Terada, H.; Katata, G.; Chino, M.; Nagai, H. Atmospheric discharge and dispersion of radionuclides during the Fukushima Dai-ichi Nuclear Power Plant accident. Part II: Verification of the source term and analysis of regional-scale atmospheric dispersion. J. Environ. Radioact. 2012, 112, 141–154. [Google Scholar] [CrossRef] [PubMed]
- Experiments on Source Term for Delayed Releases (ESTER) Project. 2020. Available online: http://www.oecd-nea.org/jcms/pl_58926/experiments-on-source-term-for-delayed-releases-ester-project (accessed on 31 May 2025).
- Colombani, J.; Pascal, C.; Martinet, L.; Duffieux, C.; Boy, G. AER-11 STEM/EPICUR Test Report; Rapport no PLEIADE PSN-RES/SEREX/2014-00365; Institut de Radioprotection et de Surete Nucleaire: Caradache, France, 2014. [Google Scholar]
- Colombani, J.; Planteur, S. AER-4, AER-5 and AER-6 STEM/EPICUR Test Report Formation and Release of Volatile Iodine Species from CsI Aerosols Under Radiation; Rapport no PLEIADE PSN-RES/SEREX/2013-00616; Institut de Radioprotection et de Surete Nucleaire: Caradache, France, 2013. [Google Scholar]
- Leroy, O. ESTER-EPICUR LOCOV Test Report; Rapport no 2022-00313; Institut de Radioprotection et de Surete Nucleaire: Caradache, France, 2023. [Google Scholar]
- Leroy, O.; Bosland, L. Study of the stability of iodine oxides (IxOy) aerosols in severe accident conditions. Ann. Nucl. Energy 2023, 181, 109526. [Google Scholar] [CrossRef]
- Dickinson, S.; Auvinen, A.; Ammar, Y.; Bosland, L.; Clément, B.; Funke, F.; Glowa, G.; Kärkelä, T.; Powers, D.A.; Tietze, S.; et al. Experimental and modelling studies of iodine oxide formation and aerosol behaviour relevant to nuclear reactor accidents. Ann. Nucl. Energy 2014, 74, 200–207. [Google Scholar] [CrossRef]
- Funke, F.; Langrock, G.; Kanzleiter, T.; Poss, G.; Fischer, K.; Kühnel, A.; Weber, G.; Allelein, H.-J. Iodine oxide in large-scale THAI tests. Nucl. Eng. Des. 2012, 245, 206–222. [Google Scholar] [CrossRef]
- Allelein, H.-J.; Auvinen, A.; Ball, J.; Gűntay, S.; Herranz, L.E.; Hidaka, A.; Jones, A.V.; Kissane, M.; Powers, D.; Weber, G. State-of-the-Art Report on Nuclear Aerosols; NEA/CSNI/R(2009)5; Organisation for Economic Co-operation and Development (OECD) Nuclear Energy Agency (NEA): Boulogne-Billancourt, France, 2009. [Google Scholar]
- Powers, D.A.; Washington, K.E.; Burson, S.B.; Sprung, J.L. A Simplified Model of Aerosol Removal by Natural Processes in Reactor Containments; NUREG/CR-6189; U.S. NRC: Washington, DC, USA, 1996.
- Malicki, M.; Lind, T. Parametric MELCOR 2.2 sensitivity and uncertainty study with a focus on aerosols based on Phebus test FPT1. Prog. Nucl. Energy 2023, 158, 104609. [Google Scholar] [CrossRef]
- Firnhaber, M.; Fischer, K.; Schwarz, S.; Weber, G. International Standard Problem ISP44 KAEVER Experiments on the Behavior of Core-melt Aerosols in a LWR Containment–Comparison Report; NEA/CSNI/R (2003) 5; Nuclear Energy Agency (NEA): Boulogne-Billancourt, France, 2003. [Google Scholar]
- Lee, Y.; Cho, Y.J.; Lim, K. Coupling scheme of multicomponent sectional equations and Mason equations via transition rate matrix of hygroscopic growth applied to international standard problem No. 44. Ann. Nucl. Energy 2019, 127, 437–449. [Google Scholar] [CrossRef]
- Gelbard, F.; Seinfeld, J.H. Simulation of multicomponent aerosol dynamics. J. Colloid Interface Sci. 1980, 78, 485–501. [Google Scholar] [CrossRef]
- Pruppacher, H.R.; Klett, J.D. Microphysics of Clouds and Precipitation; D. Reidel Publishing Co.: Dordrecht, The Netherlands, 1980. [Google Scholar]
- Gauntt, R.O.; Cole, R.K.; Erickson, C.M.; Gido, R.I.; Gasser, R.D.; Rodriguez, S.B.; Young, M.F. MELCOR Computer Code Manuals Vol. 2: Reference Manual, Version 1.8.6; NUREG/CR-6119; Sandia National Laboratories: Albuquerque, NM, USA, 2001. [Google Scholar]
- Gelbard, F. MAEROS User Manual; NUREG/CR-1391, SAND80-0822; Sandia National Laboratories: Albuquerque, NM, USA, 1982. [Google Scholar]
- Rovelli, G.; Miles, R.E.H.; Reid, J.P.; Clegg, S.L. Accurate Measurements of Aerosol Hygroscopic Growth over a Wide Range in Relative Humidity. J. Phys. Chem. A. 2016, 120, 4376–4388. [Google Scholar] [CrossRef] [PubMed]
- Ratner, B. The correlation coefficient: Its values range between +1/−1, or do they? J. Target. Meas. Anal. Market. 2009, 17, 139–142. [Google Scholar] [CrossRef]
- Cohen, J.; Cohen, P.; West, S.G.; Aiken, L.S. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 3rd ed.; Lawrence Erlbaum Associate Inc.: Mahwah, NJ, USA, 2003. [Google Scholar]
- Iman, R.L.; Shortencarier, M.J. A FORTRAN 77 Program and User’s Guide for the Generation of Latin Hypercube and Random Samples for Use with Computer Models; NUREC/CR-3624, SAND83-2365; Sandia National Laboratories: Albuquerque, NM, USA, 1984. [Google Scholar]
- Lee, Y.; Cho, Y.J. Preliminary importance analyses on model for pH in the presence of organic impurities in the aqueous phase for a severe accident of a nuclear power plant. Nucl. Eng. Technol. 2024, 56, 2079–2091. [Google Scholar] [CrossRef]
- Hansson, H.C.; Ahlberg, M.S. Dynamic shape factors of sphere aggregates in an electric-field and their dependence on the Knudsen number. J. Aero. Sci. 1985, 16, 69–79. [Google Scholar] [CrossRef]
- Hochrainer, D.; Hänel, G. Der dynamische formfaktor nicht-kugelf¨ormiger teilchen als funktion des luftdrucks. J. Aero. Sci. 1975, 6, 97–103. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, K.; Lu, X.; Chen, H.; Yang, F.; Li, Q.; Chen, J.; Prather, K.A.; Yang, X.; Wang, X. Online shape and density measurement of single aerosol particles. J. Aero. Sci. 2022, 159, 105880. [Google Scholar] [CrossRef]
- Soffer, L.; Burson, S.B.; Ferrell, C.M.; Lee, R.Y.; Ridgely, J.N. Accident Source Terms for Light-Water Nuclear Power Plants; NUREG-1465; U.S. NRC: Washington, DC, USA, 1995.
- ICRP. Annuals of the ICRP. ICRP Publication 119. Compendium of Dose Coefficients Based on ICRP Publication 60; Elsevier: Amsterdam, The Netherlands, 2012; Volume 41 (Suppl. 1). [Google Scholar]
- Fukushima Daiichi Nuclear Power Station Accident Information Collection and Evaluation (FACE) Project. 2022. Available online: https://www.oecd-nea.org/jcms/pl_70741/fukushima-daiichi-nuclear-power-station-accident-information-collection-and-evaluation-face-project (accessed on 31 May 2025).






| Parameter | Value |
|---|---|
| Van’t Hoff factor | 1.00 |
| Volume of chamber [m3] | 2.86 |
| Temperature [K] | 298 |
| Saturation ratio | 1.00005 |
| Effective saturation ratio | 1.0 |
| Pressure [Pa] | |
| Density of aerosol particle [kg/m3] | 1000 |
| Number of sections (nsection) | 20 |
| Parameters [Units] | Description | Mean | Min. | Max. |
|---|---|---|---|---|
| Sticking efficiency () (P_stick) | Effect of Van der Walls force | 1.0 | 0.1 | 1.0 |
| Slip correction factor () | Deviation from continuum mechanics | 1.37 | 1.1 | 1.3 |
| Diffusion boundary thickness () | Deposition via Brownian diffusion | 10−5 | 10−6 | 10−4 |
| Dynamic shape factor () | Drag force of non-spherical particles | 1.0 | 1.0 | 4.0 |
| Collision shape factor () | Spatial extent of non-spherical particle | 1.0 | 1.0 | 4.0 |
| Thermal accommodation coefficient (αT) | Interaction between gas and particle in terms of temperature | 1.0 | 0.5 | 1.5 |
| Turbulent energy dissipation rate () | Rate at which turbulent kinetic energy is converted into thermal energy | 10−3 | 5 × 10−4 | 1.5 × 10−3 |
| Saturation ratio (S) | Humidity | Experimental condition | 95% | 105% |
| Effective diffusion coefficient of vapor () | Diffusion coefficient for vapor | Experimental condition | 95% | 105% |
| Effective thermal conductivity of the atmosphere in the containment () | Thermal conductivity on the particle | Experimental condition | 93% | 107% |
| Density of aerosol particles () | Mixed particle density | 1000.0 | 1000.0 | 5000.0 |
| Ratio of thermal conductivity of the atmosphere to that of particles () | Ratio of thermal conductivity of gas to that of particle | 0.037 | 0.0002 | 0.055 |
| Experiments | Aerosols | Solubility (Van’t Hoff Factor) |
|---|---|---|
| KAEVER-148 | Ag | 0.08 |
| KAEVER-186 | Ag | 0.08 |
| CsOH | 2.0 | |
| KAEVER-187 | Ag | 0.08 |
| CsI | 1.68 | |
| CsOH | 2.0 |
| Parameter | Value | |
|---|---|---|
| Volume [m3] | 1.00 | |
| Deposition surface [m3] | Ceiling | 5.677 |
| Vertical wall | 26.2665 | |
| Floor | 5.6667 | |
| Parameter | Value | |
|---|---|---|
| Numerical method for solving Equation (29) | Time step size (Δt, s) | Determined by step doubling method (0.05~0.2) |
| Time discretization | Implicit Euler method | |
| Method for solving time discretized equations | Newton method | |
| Section-averaged coefficients | Quadrature | Gaussian quadrature |
| Number of sets of weights and abscissas | 20 | |
| Number of sections | 20 | |
| Case | Average (1) | Standard Deviation (2) |
|---|---|---|
| 10 | 2.45 × 10−3 | 5.79 × 10−2 |
| 50 | 1.54 × 10−3 | 4.68 × 10−3 |
| 100 | 5.10 × 10−4 | 1.94 × 10−3 |
| 500 | 6 × 10−5 | 1.19 × 10−4 |
| 1000 | 2.46 × 10−5 | 7.96 × 10−5 |
| 2000 | 1.27 × 10−6 | 1.42 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y. Importance Analyses on Phenomenological Parameters for the Aerosol Dynamics Models in I-COSTA for a Severe Nuclear Power Plant Accident. Processes 2025, 13, 1935. https://doi.org/10.3390/pr13061935
Lee Y. Importance Analyses on Phenomenological Parameters for the Aerosol Dynamics Models in I-COSTA for a Severe Nuclear Power Plant Accident. Processes. 2025; 13(6):1935. https://doi.org/10.3390/pr13061935
Chicago/Turabian StyleLee, Yoonhee. 2025. "Importance Analyses on Phenomenological Parameters for the Aerosol Dynamics Models in I-COSTA for a Severe Nuclear Power Plant Accident" Processes 13, no. 6: 1935. https://doi.org/10.3390/pr13061935
APA StyleLee, Y. (2025). Importance Analyses on Phenomenological Parameters for the Aerosol Dynamics Models in I-COSTA for a Severe Nuclear Power Plant Accident. Processes, 13(6), 1935. https://doi.org/10.3390/pr13061935





