Analysis of Fluidization Quality in Oscillating Gas–Solid Fluidized Beds with Variable Diameter Structures
Abstract
1. Introduction
2. Simulation Model
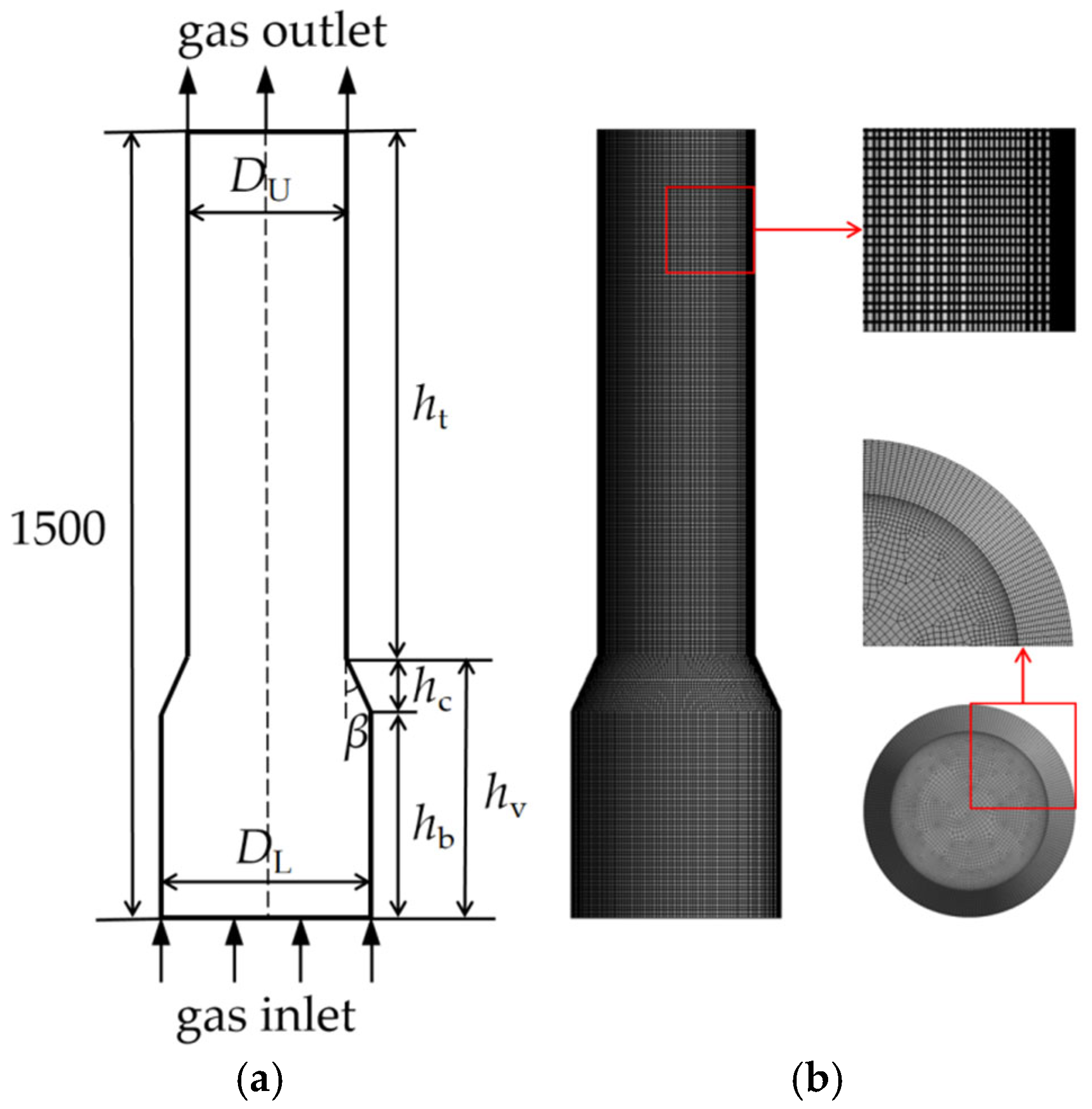
2.1. Geometric Model and Grid Division
2.2. Mathematical Model
2.2.1. Control Equation
2.2.2. Gravity Control Function
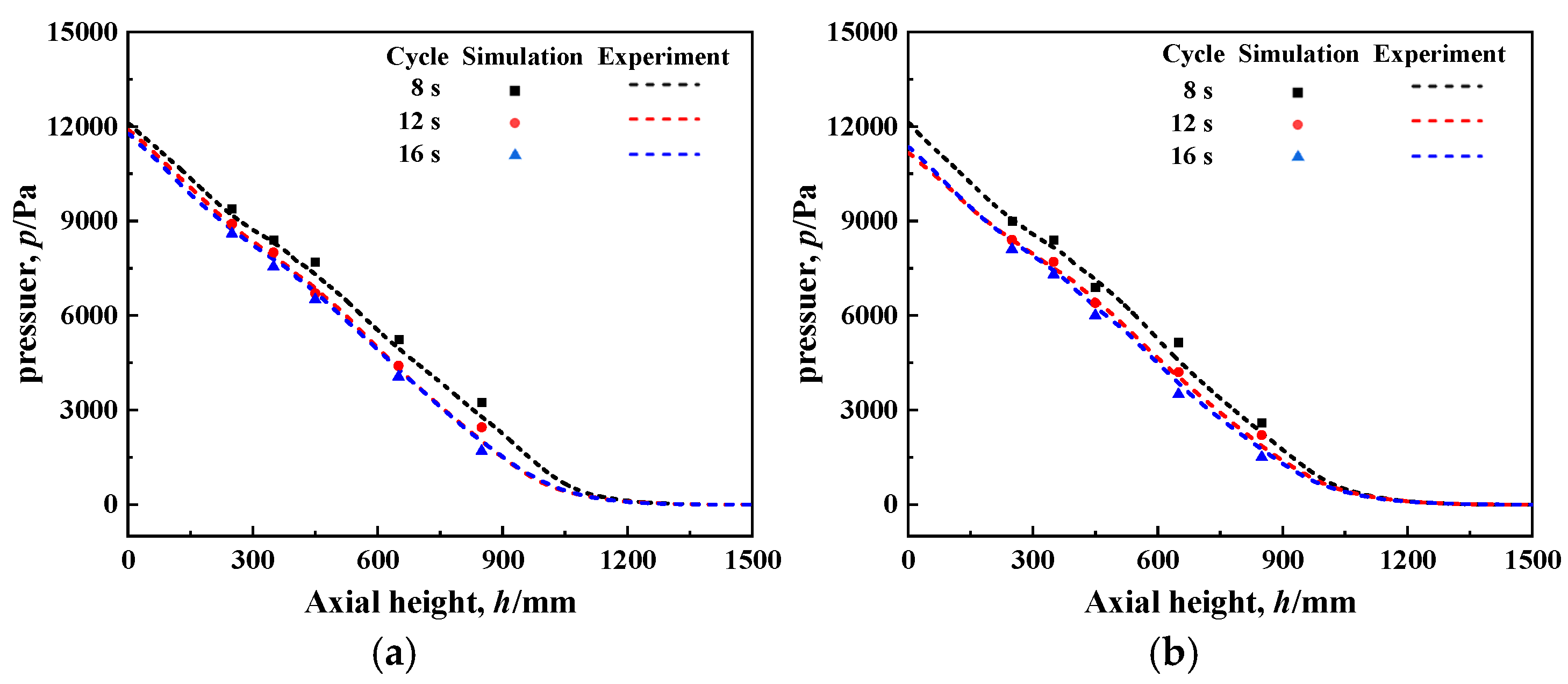
2.3. Grid Independence Verification and Model Validation
2.4. Establishment of Quality Evaluation Indicators for Oscillating Fluidized Bed Fluidization
2.4.1. Method for Determining Bubble Size
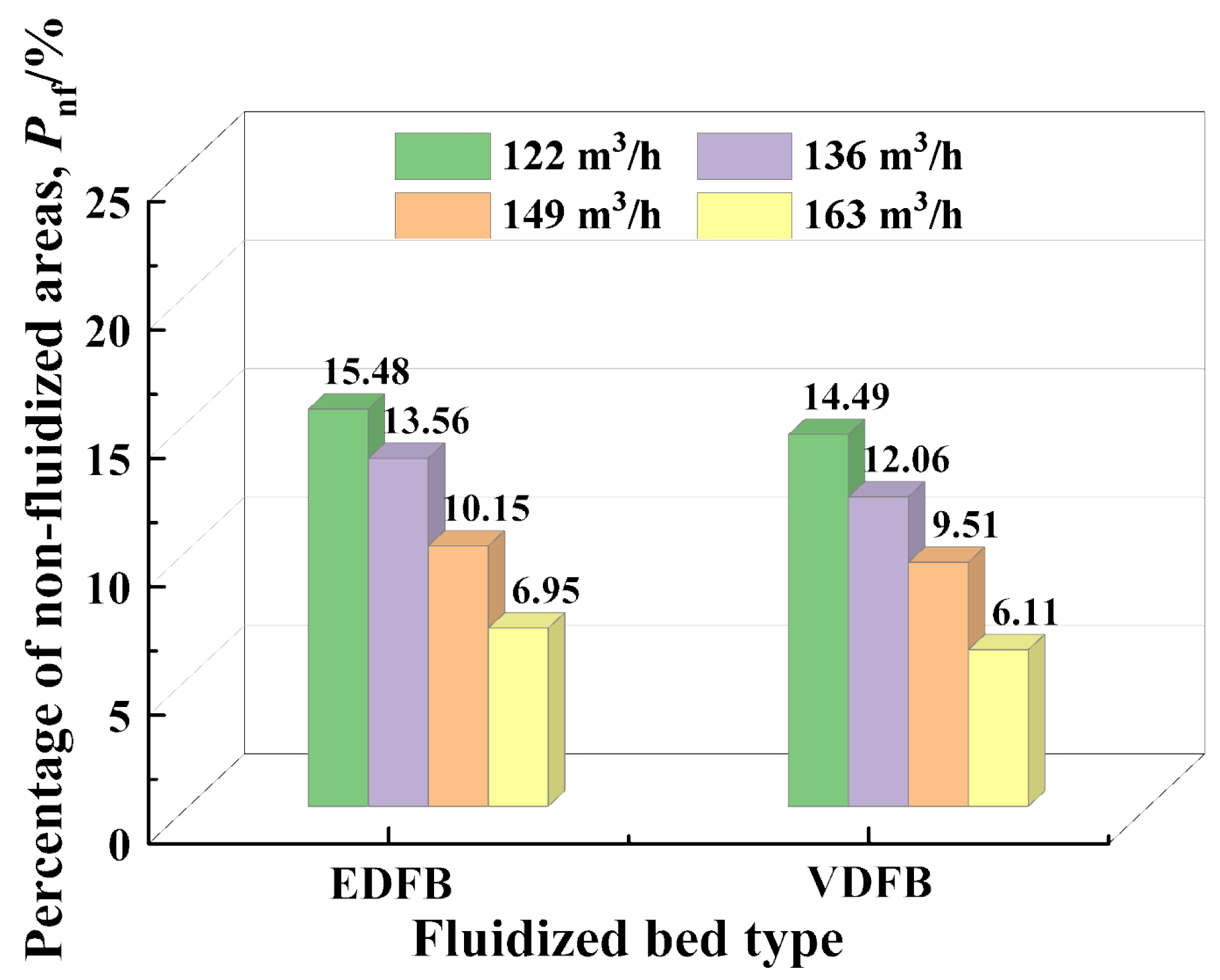
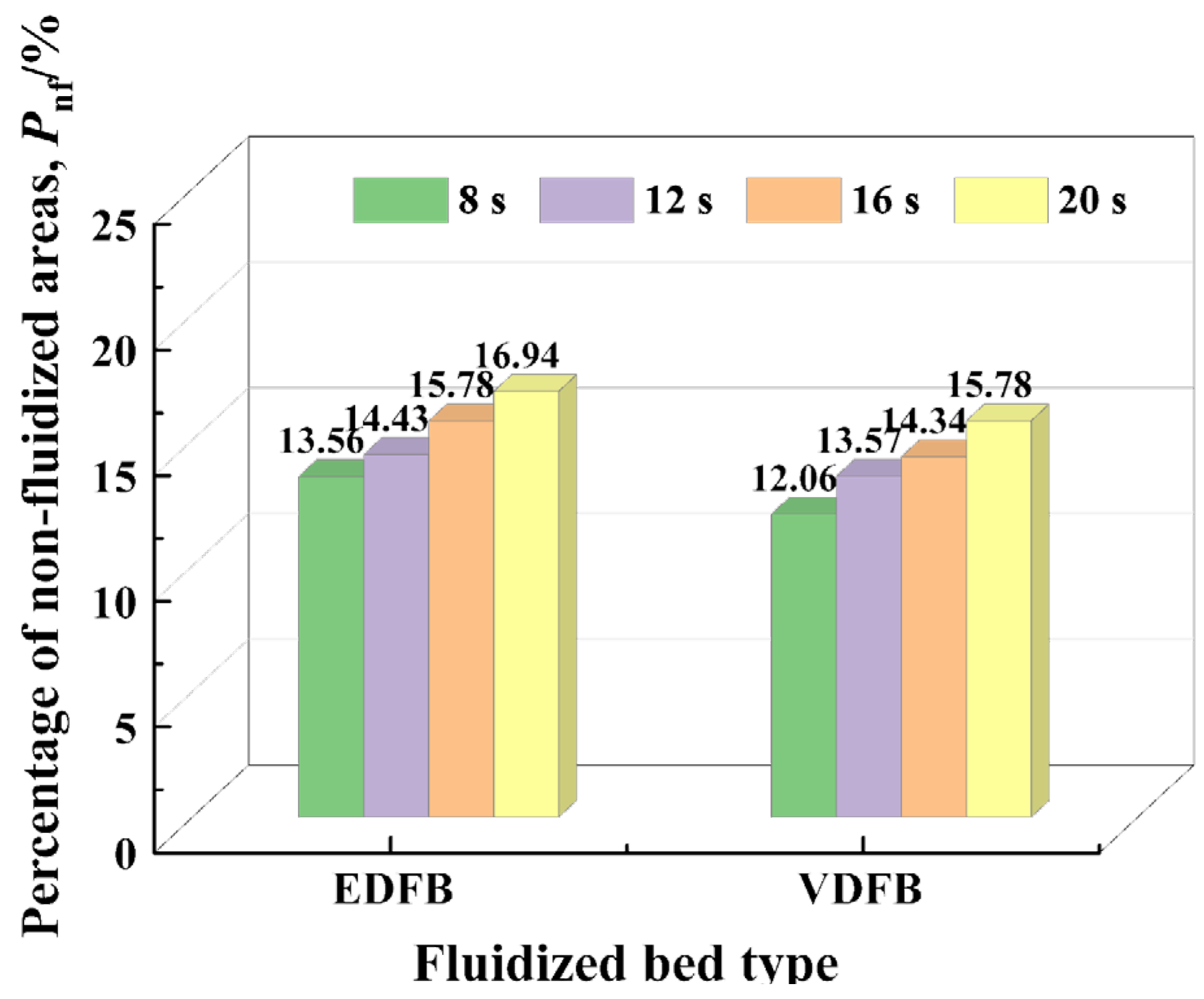
2.4.2. Method for Determining the Percentage of Non-Fluidized Area
3. Results and Discussion
3.1. Determination of Variable-Diameter Oscillating Fluidized Bed Variants
3.2. Influence of Operating Conditions on Fluidization Quality
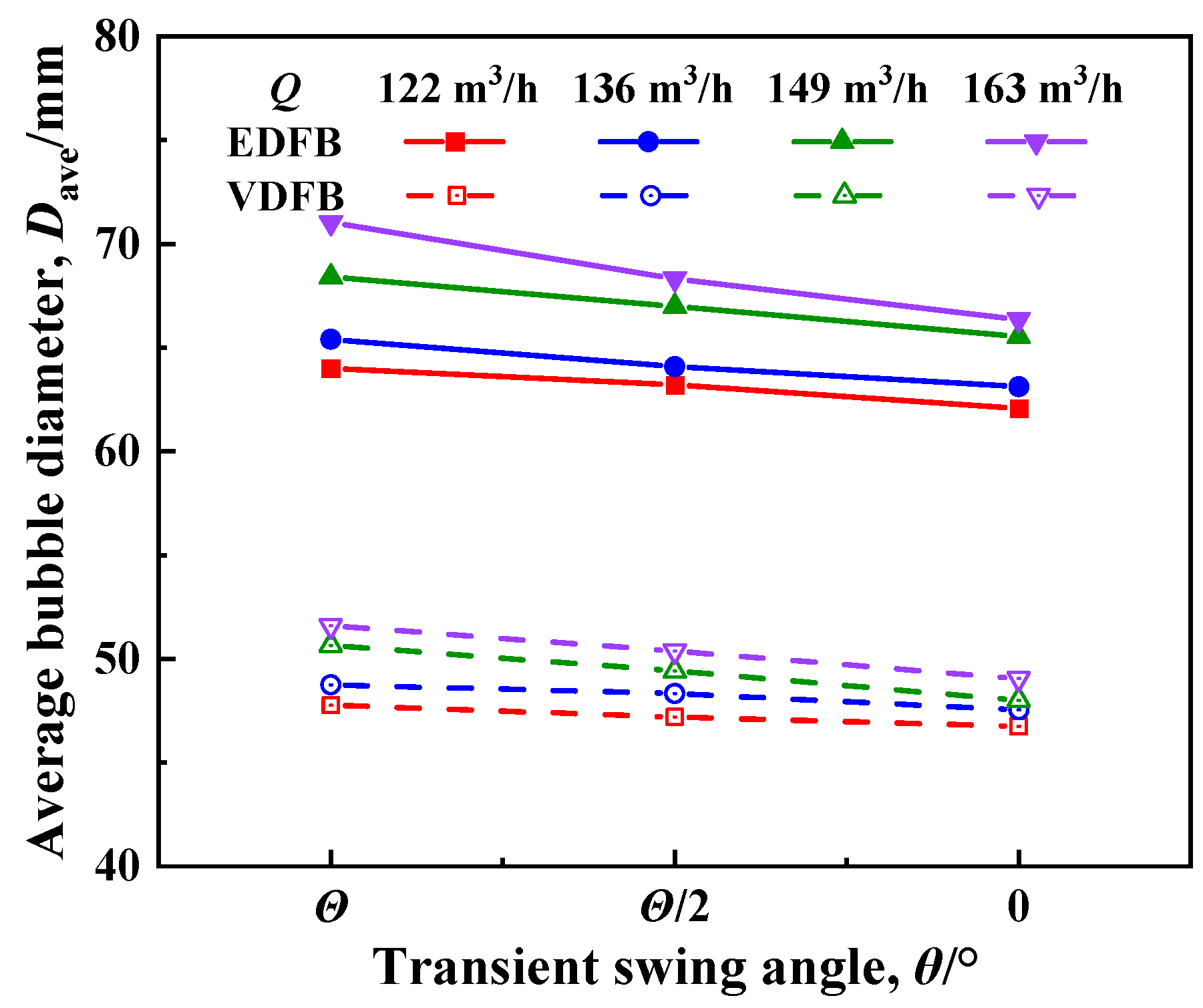
3.2.1. Effect of Gas Flow Rate Q on Fluidization Quality
3.2.2. Effect of Initial Bed Height H on Fluidization Quality
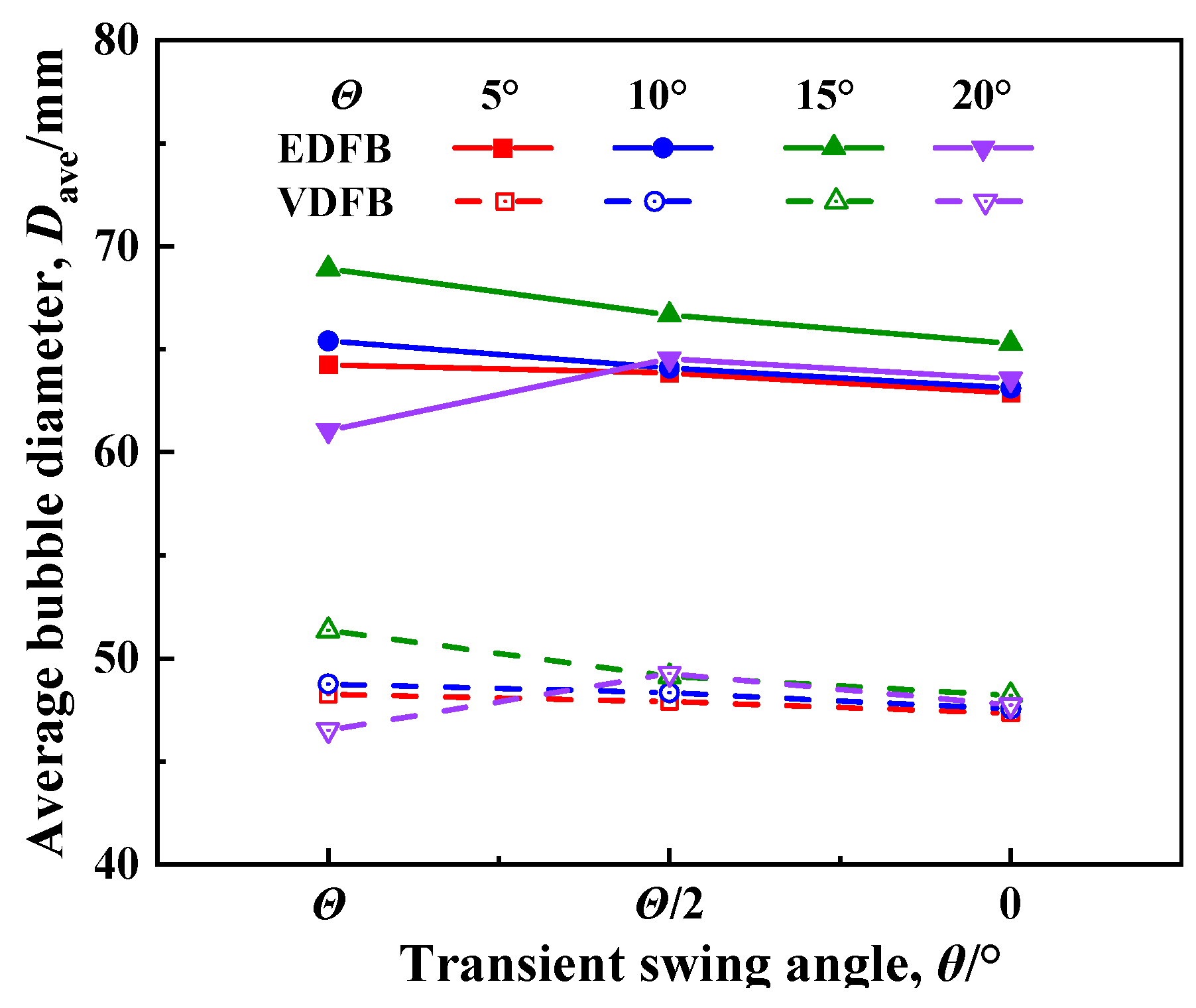
3.2.3. Effect of Oscillation Amplitude Θ on Fluidization Quality
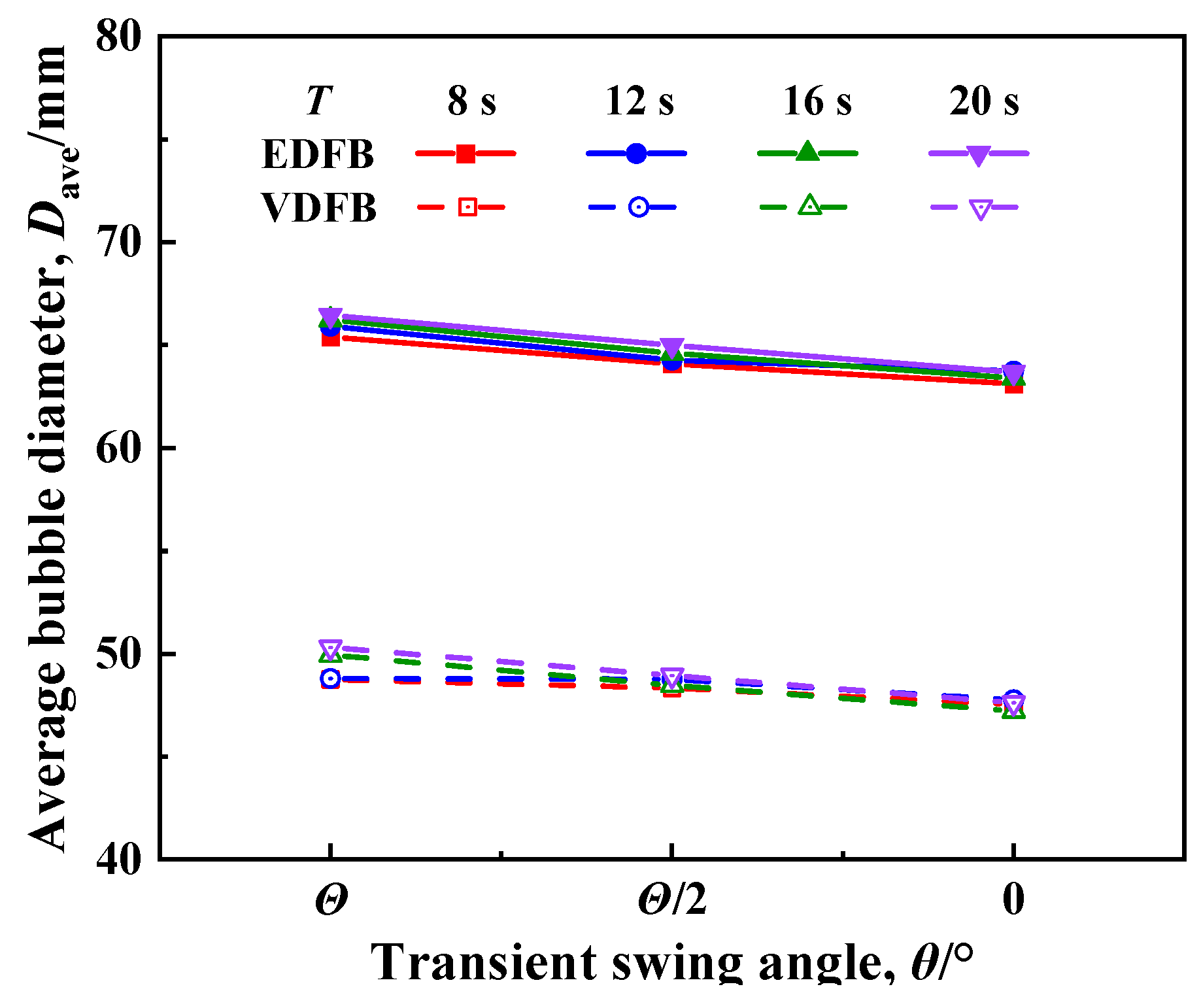
3.2.4. Effect of Oscillation Period T on Fluidization Quality
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| D | Equal-diameter fluidized bed diameter | mm |
| Dave | Average bubble diameter | mm |
| DL | The diameter of the cross-section under the bed | mm |
| DU | The diameter of the cross-section on the bed | mm |
| g | Gravitational acceleration | m/s2 |
| H | The initial loading height of the bed layer | mm |
| h | Axial height of the bed | mm |
| hb | The height of the equal-diameter section under the bed | mm |
| hc | The height of the cone section of the bed | mm |
| ht | The height of the equal-diameter section of the bed | mm |
| Pnf | Percentage of non-fluidized area | % |
| Q | Gas flow rate | m3/h |
| T | Oscillation cycle | s |
| ug | Apparent gas velocity | m/s |
| ugl | Apparent gas velocity in the lower diameter section | m/s |
| ugu | Apparent gas velocity in the upper diameter section | m/s |
| x | The transverse direction of the bed | |
| y | The longitudinal direction of the bed | |
| z | The axial direction of the bed | |
| Θ | Oscillation amplitude | ° |
| θ | Instantaneous swing angle | ° |
| β | The angle between the cone generatrix and the vertical direction | ° |
| ρb | Particle packing density | kg/m3 |
| ρg | Gas density | kg/m3 |
| ρp | Particle density | kg/m3 |
| μg | Gas viscosity | kg/(m∙s) |
| μs | Particle viscosity | kg/(m∙s) |
| εg | Gas volume fraction | |
| εs | Solid volume fraction | |
| ω | Instantaneous swing angular velocity | rad/s |
| αω | Instantaneous angular acceleration of bed swing | rad/s2 |
| Subscript | ||
| g | Gas phase | |
| s | Particle phase |
References
- Zhang, Y.; Lu, D.; Wang, Z.; Wang, J.; Pan, Q.; Su, S. Modeling and simulation of six degrees of freedom marine stable platform. In Proceedings of the International Conference on Mechatronic Engineering and Artificial Intelligence (MEAI 2023), Shenyang, China, 28 February 2024. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, X.; Lv, H.; Zhang, G.; Hou, Z.; Wang, W. Design and Simulation of Measurement and Control System for Six Degree of Freedom Active Wave Compensation Device. Integr. Technol. 2021, 10, 50–62. [Google Scholar] [CrossRef]
- Sarbanha, A.A.; Larachi, F.; Taghavi, S.M. Bubble and particle dynamics in a thin rectangular bubbling fluidized bed under emulated marine instabilities. Chem. Eng. Sci. 2023, 280, 119041. [Google Scholar] [CrossRef]
- Su, B.; Lin, M.; Wang, Q. Study on the flow mixing of hot and cold fluids in the T-junction under rolling motion condition. Nucl. Eng. Des. 2023, 403, 112126. [Google Scholar] [CrossRef]
- Li, Z.; Wang, M.; Fan, G.; Zeng, X.; Yan, Y.; Ma, F. Effects of rolling motion on flow and heat transfer characteristics in a tube bundle channel. Appl. Therm. Eng. 2023, 220, 119696. [Google Scholar] [CrossRef]
- Hao, X.; Tang, M.; Wang, R.; Wang, D.; Zhang, S. Bubble motion characteristics of gas-solid oscillating fluidized bed. J. Process Eng. 2023, 23, 512–522. [Google Scholar] [CrossRef]
- Tian, P.; Wang, D.; Wang, R.; Tang, M.; Hao, X.; Zhang, S. Gas solid flow characteristics of oscillating fluidized bed. J. Chem. Eng. 2021, 72, 5102–5113. [Google Scholar] [CrossRef]
- Huang, J. The Spatiotemporal Dynamic Characteristics of Gas-Solid Flow in Oscillating Fluidized Beds. Master’s Thesis, Hebei University of Technology, Tianjin, China, 2023. [Google Scholar]
- Xu, R.; Wang, R.; Wu, B.; Yuan, X.i.; Wang, D.; Liu, Y.; Zhang, S. Simulation of bubble behavior characteristics in a rolling fluidized bed with the addition of longitudinal internal members. Processes 2024, 12, 1130. [Google Scholar] [CrossRef]
- Sarbanha, A.A.; Larachi, F.; Taghavi, S.M. Strategizing internals’ geometry to improve resilience of marinized bubbling fluidized beds to roll-induced maldistribution. Chem. Eng. Sci. 2025, 302, 120817. [Google Scholar] [CrossRef]
- Jiang, K.; Wang, F.; Kong, Y.; Xu, C.; Du, X. Experimental investigation on the hydrodynamic characteristics of fluidized bed particle solar receiver with gas-solid countercurrent flow pattern. J. Therm. Sci. 2021, 30, 2241–2253. [Google Scholar] [CrossRef]
- Sirisomboon, K.; Arromdee, P. A computational fluid dynamics study of gas-solid distribution of Geldart Group B particles in a swirling fluidized bed. Powder Technol. 2021, 393, 734–750. [Google Scholar] [CrossRef]
- Hu, C. Experimental Study on Cold Model of Circulating Fluidized Bed Variable-Diameter Riser. Master’s Thesis, China University of Petroleum, Beijing, China, 2009. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y. Numerical simulation of gas-solid flow characteristics in the variable-diameter fluidized bed reactor. J. Jinan Univ. (Nat. Sci. Ed.) 2020, 34, 384–389+409. [Google Scholar] [CrossRef]
- Zhao, M. Research progress on conical bubbling fluidized bed. Chem. Eng. Equip. 2022, 10, 207–208. [Google Scholar] [CrossRef]
- Sau, D.C.; Mohanty, S.; Biswal, K.C. Minimum fluidization velocities and maximum bed pressure drops for gas-solid tapered fluidized beds. Chem. Eng. J. 2007, 132, 151–157. [Google Scholar] [CrossRef]
- Gong, W.; Hong, T.; Yan, H. Characteristics of local flow structure with different particle properties in a gas-solid diameter-varying fluidized bed. Powder Technol. 2024, 433, 119202. [Google Scholar] [CrossRef]
- Bahramian, A.; Olazar, M. Multi-stage agglomeration phenomena and properties of titania nanoparticle agglomerates in a lab-scale conical fluidized bed: Evaluation of CFD-DEM simulation by laser-based planar imaging and pressure fluctuation analysis. Powder Technol. 2025, 453, 120621. [Google Scholar] [CrossRef]
- Fang, S. Fluidisation Characterisation and Modelling Based on Pressure Signal Monitoring in a Conical Fluidised Bed. PhD’s Thesis, Zhejiang University, Hangzhou, China, 2021. [Google Scholar] [CrossRef]
- Ma, S. Numerical Simulation of Geldart A-Class Granular Turbulent Bed. Master’s Thesis, Hebei University of Technology, Tianjin, China, 2019. [Google Scholar] [CrossRef]
- Sun, M.; Yu, C.; Lv, D.; Wei, L. Adaptability of different liquid-solid momentum exchange coefficient models for numerical simulation of particle fluidization behavior. J. Cent. South Univ. (Nat. Sci. Ed.) 2019, 50, 1–8. [Google Scholar] [CrossRef]
- Bai, L.; Han, C.; Xu, Y.; Zhou, L.; Zhang, L.; Shi, W. Numerical simulation and experimental study of CFD-DEM for bubbling fluidized bed based on different drag models. J. Irrig. Drain. Mach. Eng. 2022, 40, 49–54. [Google Scholar] [CrossRef]
- Wu, C.; Gao, X.; Cheng, Y.; Wang, L.; Li, X. Experimental and numerical simulation of solid content distribution characteristics in the transition section of a turbulent fluidized bed. J. Chem. Eng. 2013, 64, 858–866. [Google Scholar] [CrossRef]
- Wu, Y.; Peng, L.; Gao, J.; Lan, X. Simulation of gas-solid bubbling bed based on EMMS model and analysis of bubble characteristics. J. Chem. Eng. 2016, 67, 3259–3267. [Google Scholar] [CrossRef]
- Chai, X.; Wang, A.; Fu, Z.; Duan, C.; Bi, X. Identification of the flow structure of dense phase in a gas-solid fluidized bed reactor in bubbling fluidization regime with Geldart B+A particles. Chem. Eng. Sci. 2025, 308, 121424. [Google Scholar] [CrossRef]
- Tu, N.; Wang, C.; Liu, X.; Liu, J.; Fang, J. Numerical simulation of the influence of multi-stage baffles on the residence time distribution of particles in a cross flow bubbling bed. J. Process Eng. 2024, 24, 1047–1057. [Google Scholar] [CrossRef]
- Xu, P. Numerical Simulation and Structural Optimization Design of Two-Phase Flow Characteristics in Gas-Solid Fluidized Beds. Master’s Thesis, Qingdao University of Science and Technology, Qingdao, China, 2020. [Google Scholar] [CrossRef]
- Wu, F.; Yang, C.; Che, X.; Ma, X.; Yan, Y.; Zhou, W. Numerical and experimental study of integral multi-jet structure impact on gas-solid flow in a 3D spout-fluidized bed. Chem. Eng. J. 2020, 393, 124737. [Google Scholar] [CrossRef]
- Wang, S. Euler Lagrange Numerical Simulation Study on Dense Gas-Solid Two-Phase Reactive Flow in Fluidized Bed. PhD Thesis, Zhejiang University, Hangzhou, China, 2019. [Google Scholar] [CrossRef]





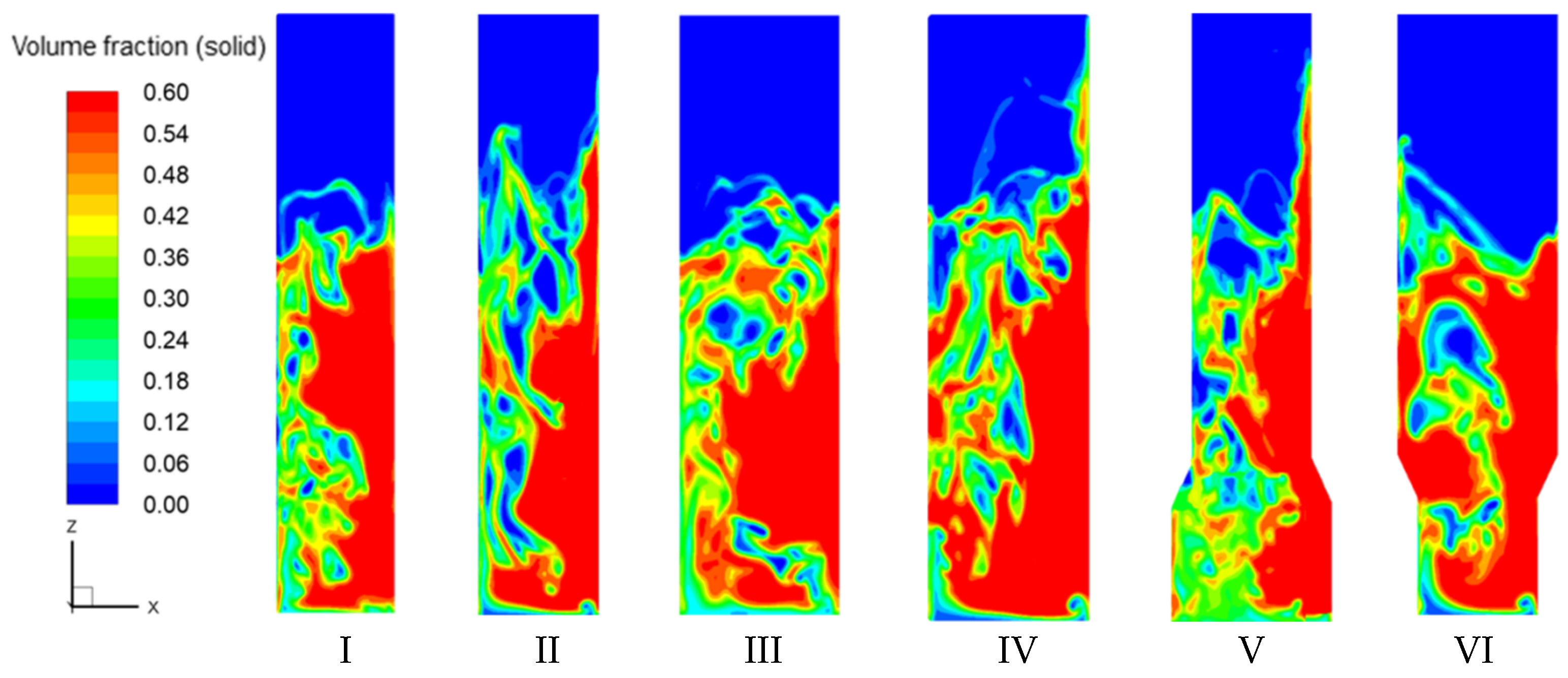

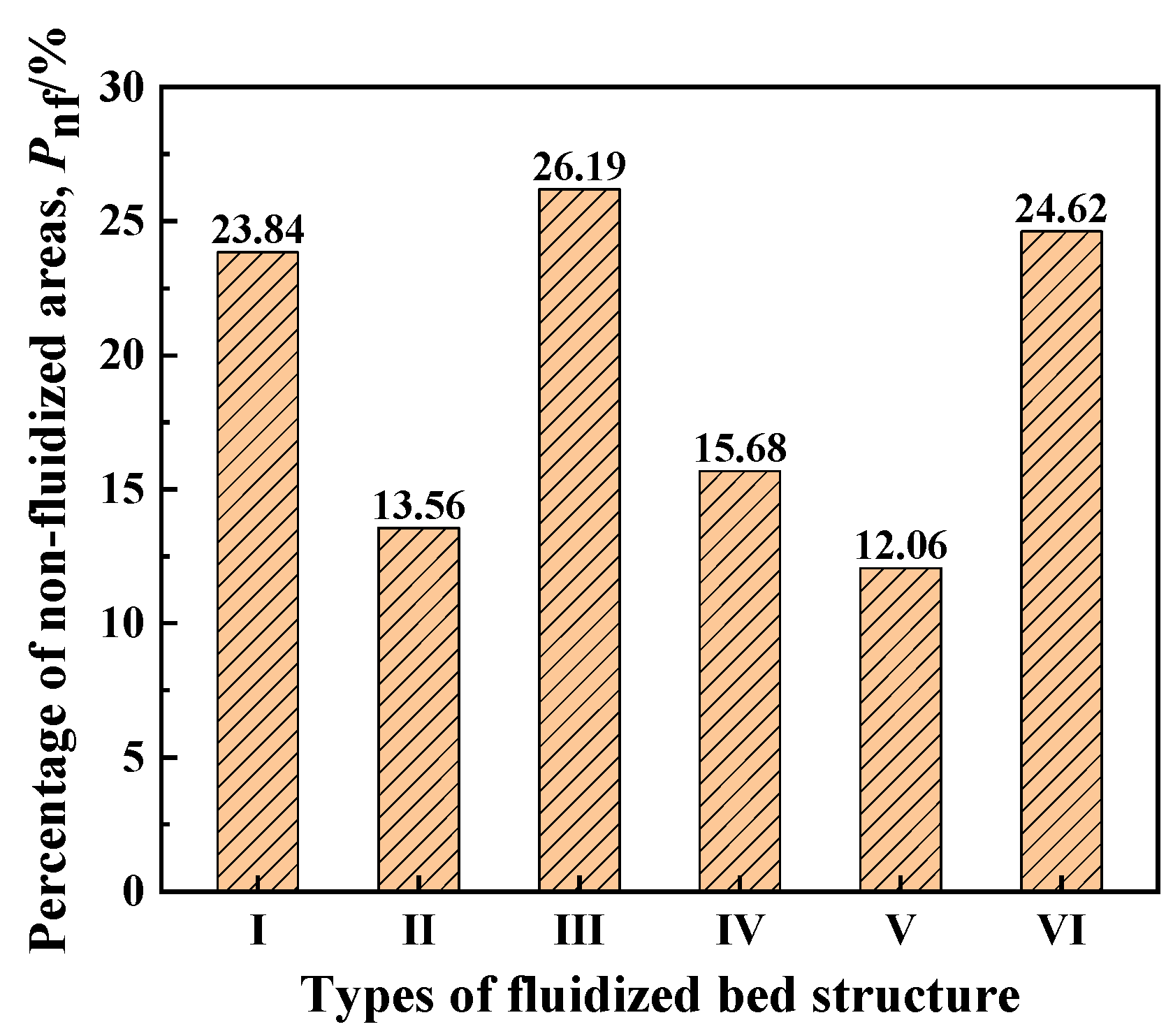

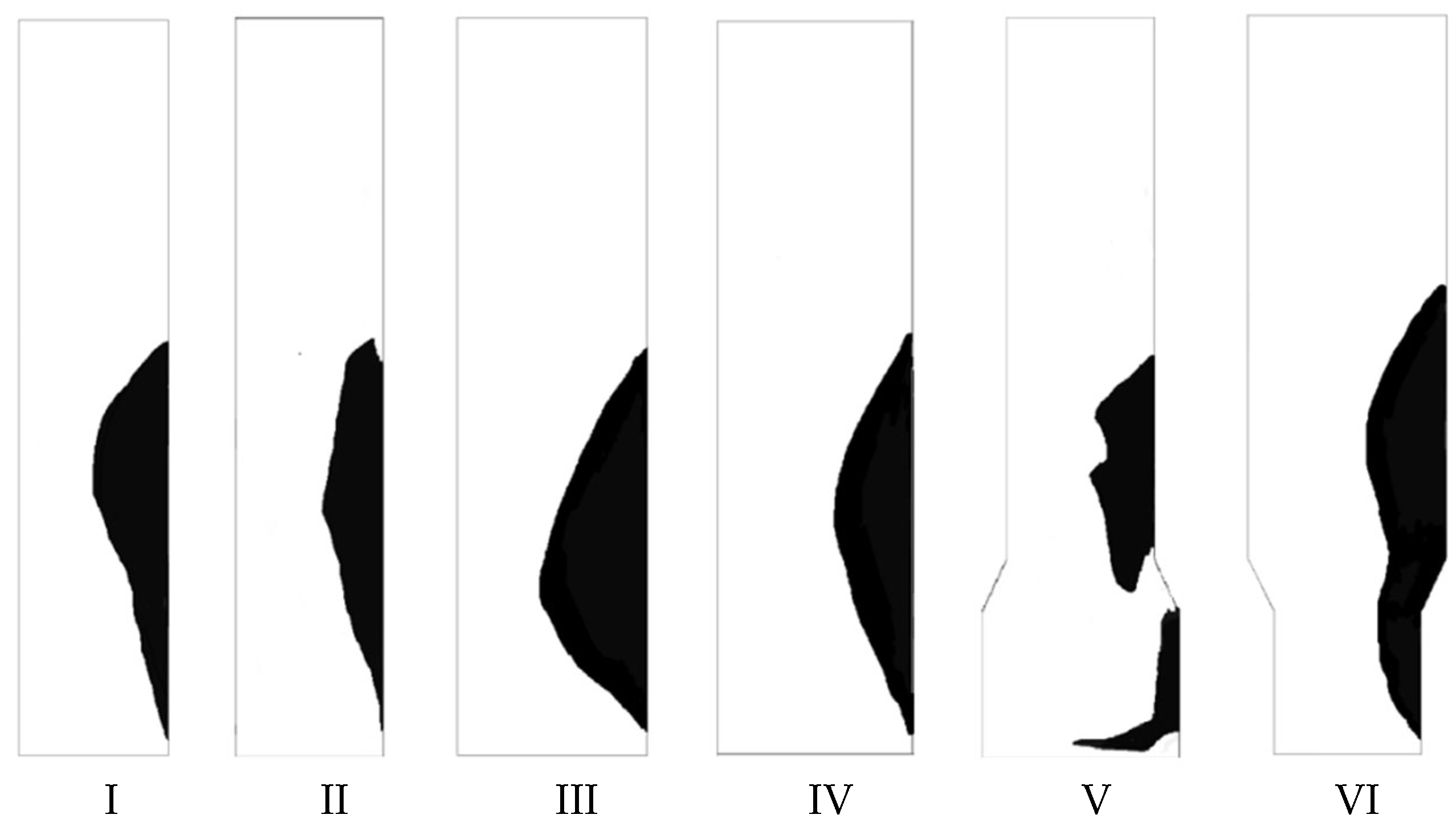




| Serial Number | Fluidized Bed Structure and Diameter | Superficial Gas Velocity (m/s) |
|---|---|---|
| I | EDFB D = 300 mm | ug = 0.30 |
| II | EDFB D = 300 mm | ug = 0.53 |
| III | EDFB D = 400 mm | ug = 0.30 |
| IV | EDFB D = 400 mm | ug = 0.53 |
| V | “cone-contraction” VDFB DL = 400 mm, DU = 300 mm | ugl = 0.30, ugu = 0.53 |
| VI | “cone-expansion” VDFB DL = 300 mm, DU = 400 mm | ugl = 0.53, ugu = 0.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Wang, D.; Zhang, Q.; Yuan, X.; Xu, R.; Zhao, B.; Wang, R.; Zhang, S. Analysis of Fluidization Quality in Oscillating Gas–Solid Fluidized Beds with Variable Diameter Structures. Processes 2025, 13, 1778. https://doi.org/10.3390/pr13061778
Zhang D, Wang D, Zhang Q, Yuan X, Xu R, Zhao B, Wang R, Zhang S. Analysis of Fluidization Quality in Oscillating Gas–Solid Fluidized Beds with Variable Diameter Structures. Processes. 2025; 13(6):1778. https://doi.org/10.3390/pr13061778
Chicago/Turabian StyleZhang, Dan, Dewu Wang, Qinchuan Zhang, Xiaopei Yuan, Ruofeng Xu, Bin Zhao, Ruojin Wang, and Shaofeng Zhang. 2025. "Analysis of Fluidization Quality in Oscillating Gas–Solid Fluidized Beds with Variable Diameter Structures" Processes 13, no. 6: 1778. https://doi.org/10.3390/pr13061778
APA StyleZhang, D., Wang, D., Zhang, Q., Yuan, X., Xu, R., Zhao, B., Wang, R., & Zhang, S. (2025). Analysis of Fluidization Quality in Oscillating Gas–Solid Fluidized Beds with Variable Diameter Structures. Processes, 13(6), 1778. https://doi.org/10.3390/pr13061778





