Multi-Objective Optimization of the Dip-Coating Parameters for Polylactic Acid Plus Bone Screws Using Taguchi Method, Response Surface Methodology, and Non-Dominated Sorting Genetic Algorithm II
Abstract
1. Introduction
2. Materials and Methods
2.1. Design of 3D Model Bone Screws
2.2. Preparation of Nanocomposites
2.3. Compression and Density Tester
2.4. Analysis Methods
3. Results and Discussion
| Ct = 16 − 874 A + 1536 B − 0.3 C + 24.1 D + 20.3 E + 1217 A2 − 442 B2 + 0.051 C2 − 0.193 D2 + 1.382 E2 + 578 A × B + 14.3 A × C + 14.0 A × D − 70.1 A × E − 4.9 B × C − 1.6 B × D − 33.7 B × E − 0.471 C × D − 0.185 C × E + 0.122 D × E | (1) |
| Dt = 1.2433 − 0.181 A + 0.014 B − 0.00288 C − 0.00052 D − 0.00062 E + 0.260 A2 + 0.066 B2 + 0.000015 C2 + 0.000003 D2 + 0.000065 E2 − 0.236 A × B + 0.00292 A × C + 0.00255 A × D − 0.00160 A × E + 0.00153 B × C − 0.00347 B × D + 0.00032 B × E + 0.000035 C × D − 0.000003 C × E − 0.000016 D × E | (2) |
- Construct an evaluation matrix, (aij) A × f, where A represents the 18 non-dominated solution points and f denotes the objective functions.
- To normalize this evaluation matrix, use the formulawhere represents the normalized values of the matrix.
- 3
- Next, calculate the normalized weighted decision matrix, , where , with weights assigned as f1 = 0.60 and f2 = 0.40.
- 4
- Identify the maximum and the minimum of for each criterion, denoted as is a maximum alternative for each criterion, is a minimum alternative for each criterion, respectively.
- 5
- Then, calculate the Euclidean distances between each alternative and the ideal solutions (both positive and negative), where represents the distance from the positive ideal solution and from the negative ideal solution: ,where is the distance of the i-th experiment from the ideal solution (positive ideal solution) has been calculated, and is the distance of the i-th experiment from the ideal solution (negative ideal solution) has been calculated.
- 6
- For each alternative, calculate the similarity to the minimum alternative using the formula , resulting in the TOPSIS scores.where denotes the TOPSIS value, and the highest score indicates the optimal solution.
- 7
- In this case, alternative A3 yields the highest TOPSIS scores of 315.808 and 1.141, identifying it as the optimal single solution.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Langer, R.; Cima, L.G.; Tamada, J.A.; Wintermantel, E. Future directions in biomaterials. Biomaterials 1990, 11, 738–745. [Google Scholar] [CrossRef] [PubMed]
- Biswal, T. Biopolymers for tissue engineering applications: A review. Mater. Today Proc. 2021, 41, 397–402. [Google Scholar] [CrossRef]
- Jiang, Y.; Torun, T.; Maffioletti, S.M.; Serio, A.; Tedesco, F.S. Bioengineering human skeletal muscle models: Recent advances, current challenges and future perspectives. Exp. Cell Res. 2022, 416, 113133. [Google Scholar] [CrossRef] [PubMed]
- Proctor, D.W.; Goodall, R.; Borsky, K.; Salciccioli, J.D.; Marshall, D.C.; Shalhoub, J. Trends in the incidence of rib and sternal fractures: A nationwide study of the global burden of disease database, 1990–2019. Injury 2024, 55, 111404. [Google Scholar] [CrossRef]
- Wasserman, H.; Gordon, C.M. Bone Mineralization and Fracture Risk Assessment in the Pediatric Population. J. Clin. Densitom. Assement Manag. Musculoskelet. Health 2017, 20, 389–396. [Google Scholar] [CrossRef]
- Kanis, J.A.; Johansson, H.; McCloskey, E.V.; Liu, E.; Åkesson, K.E.; Anderson, F.A.; Azagra, R.; Bager, C.; Beaudart, C.; Bischoff-Ferrari, H.A.; et al. Previous fracture and subsequent fracture risk: A meta-analysis to update FRAX. Osteoporos. Int. 2023, 34, 2027–2045. [Google Scholar] [CrossRef] [PubMed]
- Odén, A.; McCloskey, E.V.; Kanis, J.A.; Harvey, N.C.; Johansson, H. Burden of high fracture probability worldwide: Secular increases 2010–2040. Osteoporos. Int. 2015, 26, 2243–2248. [Google Scholar] [CrossRef]
- Nazari, G.; Diep, D.; MacDermid, J.C. The state of trial registrations in the field of Orthopaedics in years 2015–2020. A meta-epidemiological study. Osteoarthr. Cart. Open 2021, 3, 100215. [Google Scholar] [CrossRef]
- Meng, L.; Xie, F.; Zhang, B.; Wang, D.K.; Yu, L. Natural Biopolymer Alloys with Superior Mechanical Properties. ACS Sustain. Chem. Eng. 2018, 7, 2792–2802. [Google Scholar] [CrossRef]
- Yakimets, I.; Paes, S.S.; Wellner, N.; Smith, A.C.; Wilson, R.H.; Mitchell, J.R. Effect of Water Content on the Structural Reorganization and Elastic Properties of Biopolymer Films: A Comparative Study. Biomacromolecules 2007, 8, 1710–1722. [Google Scholar] [CrossRef]
- Brzeziński, M.; Basko, M. Polylactide-Based Materials: Synthesis and Biomedical Applications. Molecules 2023, 28, 1386. [Google Scholar] [CrossRef] [PubMed]
- Arumaiselvan, U.; Kalimuthu, M.; Nagarajan, R.; Mohan, M.; Ismail, S.O.; Mohammad, F.; Al-Lohedan, H.A.; Krishnan, K. Mechanical, physical and thermal properties of polylactic acid filament composite reinforced with newly isolated Cryptostegia grandiflora fiber. BioResources 2024, 2, 3740–3754. [Google Scholar] [CrossRef]
- González-Rodríguez, L.; Pérez-Davila, S.; Lama, R.; López-Álvarez, M.; Serra, J.; Novoa, B.; Figueras, A.; González, P. 3D printing of PLA:CaP:GO scaffolds for bone tissue applications. RSC Adv. 2023, 13, 15947–15959. [Google Scholar] [CrossRef]
- Butt, M.S.; Bai, J.; Xue, F. Biodegradable Mg Strengthened Poly-Lactic Acid Composite through Interfacial Properties. Mater. Sci. Forum 2017, 900, 7–11. [Google Scholar] [CrossRef]
- Kadhum, A.H.; Al-Zubaidi, S.; AlKareem, S.S.A. Optimization of Mechanical Properties and Surface Characteristics of PLA+ 3D Printing Materials. Int. J. Chem. Eng. 2023, 2023, 8887905. [Google Scholar] [CrossRef]
- Sen, M. (Ed.) Nanocomposite Materials. In Nanotechnology and the Environment; IntechOpen: London, UK, 2020; Chapter 6; Volume 1, pp. 1–12. [Google Scholar]
- Basova, T.V.; Vikulova, E.S.; Dorovskikh, S.I.; Hassan, A.; Morozova, N.B. The use of noble metal coatings and nanoparticles for the modification of medical implant materials. Mater. Des. 2021, 204, 109672. [Google Scholar] [CrossRef]
- Dhandapani, R.; Krishnan, P.D.; Zennifer, A.; Kannan, V.; Manigandan, A.; Arul, M.R.; Jaiswal, D.; Subramanian, A.; Kumbar, S.G.; Sethuraman, S. Additive manufacturing of biodegradable porous orthopaedic screw. Bioact. Mater. 2020, 5, 458–467. [Google Scholar] [CrossRef]
- Rouf, S.; Malik, A.; Raina, A.; Haq, M.I.U.; Naveed, N.; Zolfagharian, A.; Bodaghi, M. Functionally graded additive manufacturing for orthopedic applications. J. Orthop. 2022, 33, 70–80. [Google Scholar] [CrossRef]
- Ahirwar, H.; Zhou, Y.; Mahapatra, C.; Ramakrishna, S.; Kumar, P.; Nanda, H.S. Materials for Orthopedic Bioimplants: Modulating Degradation and Surface Modification Using Integrated Nanomaterials. Coatings 2020, 10, 264. [Google Scholar] [CrossRef]
- Ganjali, M.; Asl, S.M.; Alizadeh, M.; Shahlaei, M.; Jam, A.S. Synthesis and characterization of nHA-PLA composite coating on stainless steel 316L by dip-coating process for biomedical applications. J. Interfaces 2017, 2, 57–64. [Google Scholar]
- Uchida, M.; Kim, H.; Kokubo, T.; Nawa, M.; Asano, T.; Tanaka, K.; Nakamura, T. Apatite-forming ability of a zirconia/alumina nano-composite induced by chemical treatment. J. Biomed. Mater. Res. 2002, 60, 277–282. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, D.; Shi, L.; Li, L.; Zhang, J. Novel transparent ternary nanocomposite films of trialkoxysilane-capped poly(methyl methacrylate)/zirconia/titania with incorporating networks. Mater. Chem. Phys. 2008, 110, 463–470. [Google Scholar] [CrossRef]
- Silverajah, V.S.G.; Ibrahim, N.A.; Zainuddin, N.; Yunus, W.M.Z.W.; Hassan, H.A. Mechanical, thermal and morphological properties of poly(lactic acid)/epoxidized palm olein blend. Molecules 2012, 17, 11729–11747. [Google Scholar] [CrossRef]
- Mohan, L.; Babu, P.D.; Kumar, P.; Anandan, C. Influence of zirconium doping on the growth of apatite and corrosion behavior of DLC-coated titanium alloy Ti-13Nb-13Zr. Surf. Interface Anal. 2013, 45, 1785–1791. [Google Scholar] [CrossRef]
- Vaizogullar, A.İ.; Balci, A.; Ugurlu, M.; Karaoglu, M.H. Synthesis of TiO2 and ZrO2/TiO2 Composite Microspheres and Their Photo-Catalytic Degradation of Methylene Blue. Afyon Kocatepe Univ. J. Sci. Eng. 2016, 16, 54–60. [Google Scholar]
- Lung, Y.K. Surface coatings of titanium and zirconia. Adv. Mater. Sci. 2017, 2, 1–3. [Google Scholar] [CrossRef]
- Dini, F.W.; Helmiyati, H.; Krisnandi, Y.K. Cellulose and TiO2–ZrO2 Nanocomposite as a Catalyst for Glucose Conversion to 5-EMF. Bull. Chem. React. Eng. Catal. 2021, 16, 320–330. [Google Scholar] [CrossRef]
- Hari Raj, K.; Gnanavel, S.; Ramalingam, S. Investigation of 3D printed biodegradable PLA orthopedic screw and surface modified with nanocomposites (Ti–Zr) for biocompatibility. Ceram. Int. 2023, 49, 7299–7307. [Google Scholar] [CrossRef]
- Boccaccini, A.R.; Keim, S.; Ma, R.; Li, Y.; Zhitomirsky, I. Electrophoretic deposition of biomaterials. J. R. Soc. Interface 2010, 7, S581–S613. [Google Scholar] [CrossRef]
- Cordero-Arias, L.; Cabanas-Polo, S.; Goudouri, O.; Misra, S.; Gilabert, J.; Valsami-Jones, E.; Sanchez, E.; Virtanen, S.; Boccaccini, A. Electrophoretic deposition of ZnO/alginate and ZnO-bioactive glass/alginate composite coatings for antimicrobial applications. Mater. Sci. Eng. C 2015, 55, 137–144. [Google Scholar] [CrossRef]
- Heimann, R.B. Plasma-Sprayed Osseoconductive Hydroxylapatite Coatings for Endoprosthetic Hip Implants: Phase Composition, Microstructure, Properties, and Biomedical Functions. Coatings 2024, 14, 787. [Google Scholar] [CrossRef]
- Wulandari, R.T.; Triyono, J.; Pujiyanto, E. Multi-response Optimization in Injection Molding Process of PLA Bone Screw using Taguchi Method and Response Surface Methodology. In AIP Conference Proceedings; American Institute of Physics Inc.: College Park, MD, USA, 2023; pp. 1–6. [Google Scholar]
- Tran, C.C.; Nguyen, V.T. Optimization of Filling Time and Volumetric Shrinkage Rate in Simulation of Plastic Product Injection Molding Process Using RSM and NSGA-II. Jordan J. Mech. Ind. Eng. 2024, 19, 67–77. [Google Scholar]
- Pangestu, P.; Pujiyanto, E.; Rosyidi, C.N. Multi-objective cutting parameter optimization model of multi-pass turning in CNC machines for sustainable manufacturing. Heliyon 2021, 7, e06043. [Google Scholar] [CrossRef]
- Rosyidi, C.N.; Budiaji, A.; Pujiyanto, E. Multiresponse optimization on the process of roof tiles manufacture using the taguchi and pcr-topsis method. J. Teknol. 2022, 84, 11–18. [Google Scholar] [CrossRef]
- Naranbat, D.; Phelps, B.; Murphy, J.; Tripathi, A. How to convert a 3D printer to a personal automated liquid handler for life science workflows. SLAS Technol. 2025, 30, 100239. [Google Scholar] [CrossRef] [PubMed]
- Piçarra, S.; Lopes, E.; Almeida, P.L.; De Lencastre, H.; Aires-De-Sousa, M. Novel coating containing molybdenum oxide nanoparticles to reduce Staphylococcus aureus contamination on inanimate surfaces. PLoS ONE 2019, 14, e0213151. [Google Scholar] [CrossRef] [PubMed]
- ASTM D7027; Test Method for Evaluation of Scratch Resistance of Polymeric Coatings and Plastics Using an Instrumented Scratch Machine. ASTM International: West Conshohocken, PA, USA, 2020.
- Redlich, C.; Quadbeck, P.; Thieme, M.; Kieback, B. Molybdenum—A biodegradable implant material for structural applications? Acta Biomater. 2020, 104, 241–251. [Google Scholar] [CrossRef]
- Zhu, Z.; Wu, H.; Ye, C.; Fu, W. Enhancement on Mechanical and Thermal Properties of PLA Biocomposites Due to the Addition of Hybrid Sisal Fibers. J. Nat. Fibers 2017, 14, 875–886. [Google Scholar] [CrossRef]
- Ismail, K.B.M.; Kumar, M.A.; Mahalingam, S.; Kim, J.; Atchudan, R. Recent Advances in Molybdenum Disulfide and Its Nanocomposites for Energy Applications: Challenges and Development. Materials 2023, 16, 4471. [Google Scholar] [CrossRef]
- Castañeda-Rodríguez, S.; González-Torres, M.; Ribas-Aparicio, R.M.; Del Prado, M.L.; Leyva, G.; Gürer, E.S.; Sharifi, J. Recent advances in modified poly (lactic acid) as tissue engineering materials. J. Biol. Eng. 2023, 17, 21. [Google Scholar] [CrossRef]
- Zidan, S.; Silikas, N.; Alhotan, A.; Haider, J.; Yates, J. Investigating the Mechanical Properties of ZrO2-Impregnated PMMA Nanocomposite for Denture-Based Applications. Materials 2019, 12, 1344. [Google Scholar] [CrossRef] [PubMed]
- Mosas, K.K.A.; Chandrasekar, A.R.; Dasan, A.; Pakseresht, A.; Galusek, D. Recent Advancements in Materials and Coatings for Biomedical Implants. Gels 2022, 8, 323. [Google Scholar] [CrossRef] [PubMed]
- Adamiak, S.; Bochnowski, W.; Dziedzic, A.; Szyller, Ł.; Adamiak, D. Characteristics of the structure, mechanical, and tribological properties of a mo-mo2n nanocomposite coating deposited on the ti6al4v alloy by magnetron sputtering. Materials 2021, 14, 6819. [Google Scholar] [CrossRef] [PubMed]
- Zare, Y.; Shabani, I. Polymer/metal nanocomposites for biomedical applications. Mater. Sci. Eng. C 2016, 60, 195–203. [Google Scholar] [CrossRef]
- Zhang, Z.; Peng, F.; Kornev, K.G. The Thickness and Structure of Dip-Coated Polymer Films in the Liquid and Solid States. Micromachines 2022, 13, 982. [Google Scholar] [CrossRef]
- Pujiyanto, E.; Rosyidi, C.N.; Hisjam, M.; Liquddanu, E. Sustainable multi-objective optimization of a machining parameter model for multi-pass turning processes. Cogent Eng. 2022, 9, 2108154. [Google Scholar] [CrossRef]
- Agarwal, R.; Mehtani, H.K.; Singh, J.; Gupta, V. Post-yielding fracture mechanics of 3D printed polymer-based orthopedic cortical screws. Polym. Compos. 2022, 43, 6829–6837. [Google Scholar] [CrossRef]
- Jamari, J.; Fitriyana, D.; Ramadhan, P.S.; Nugroho, S.; Ismail, R.; Bayuseno, A. Interference screws 3D printed with polymer-based biocomposites (HA/PLA/PCL). Mater. Manuf. Process. 2022, 38, 1093–1103. [Google Scholar] [CrossRef]
- Ismail, R.; Fitriyana, D.F.; Bayuseno, A.P.; Munanda, R.; Muhamadin, R.C.; Nugraha, F.W.; Rusiyanto; Setiyawan, A.; Bahatmaka, A.; Firmansyah, H.N.; et al. Design, Manufacturing and Characterization of Biodegradable Bone Screw from PLA Prepared by Fused Deposition Modelling (FDM) 3D Printing Technique. J. Adv. Res. Fluid Mech. Therm. Sci. 2023, 103, 205–215. [Google Scholar] [CrossRef]
- ASTM D3359; Test Methods for Rating Adhesion by Tape Test. ASTM International: West Conshohocken, PA, USA, 2023.
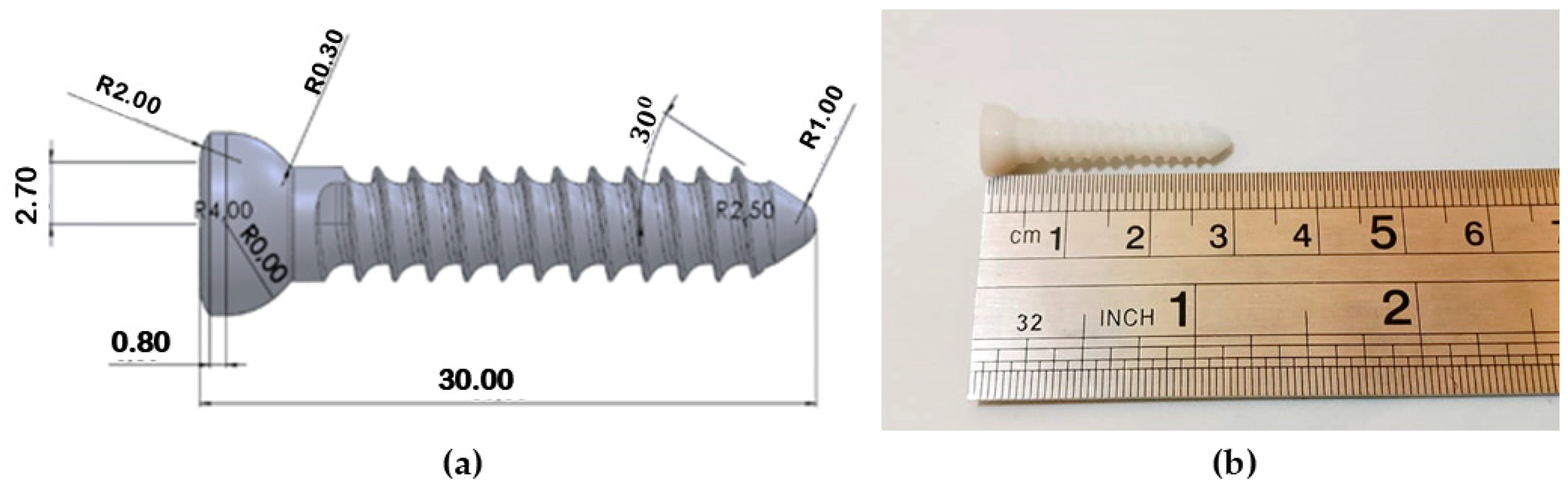


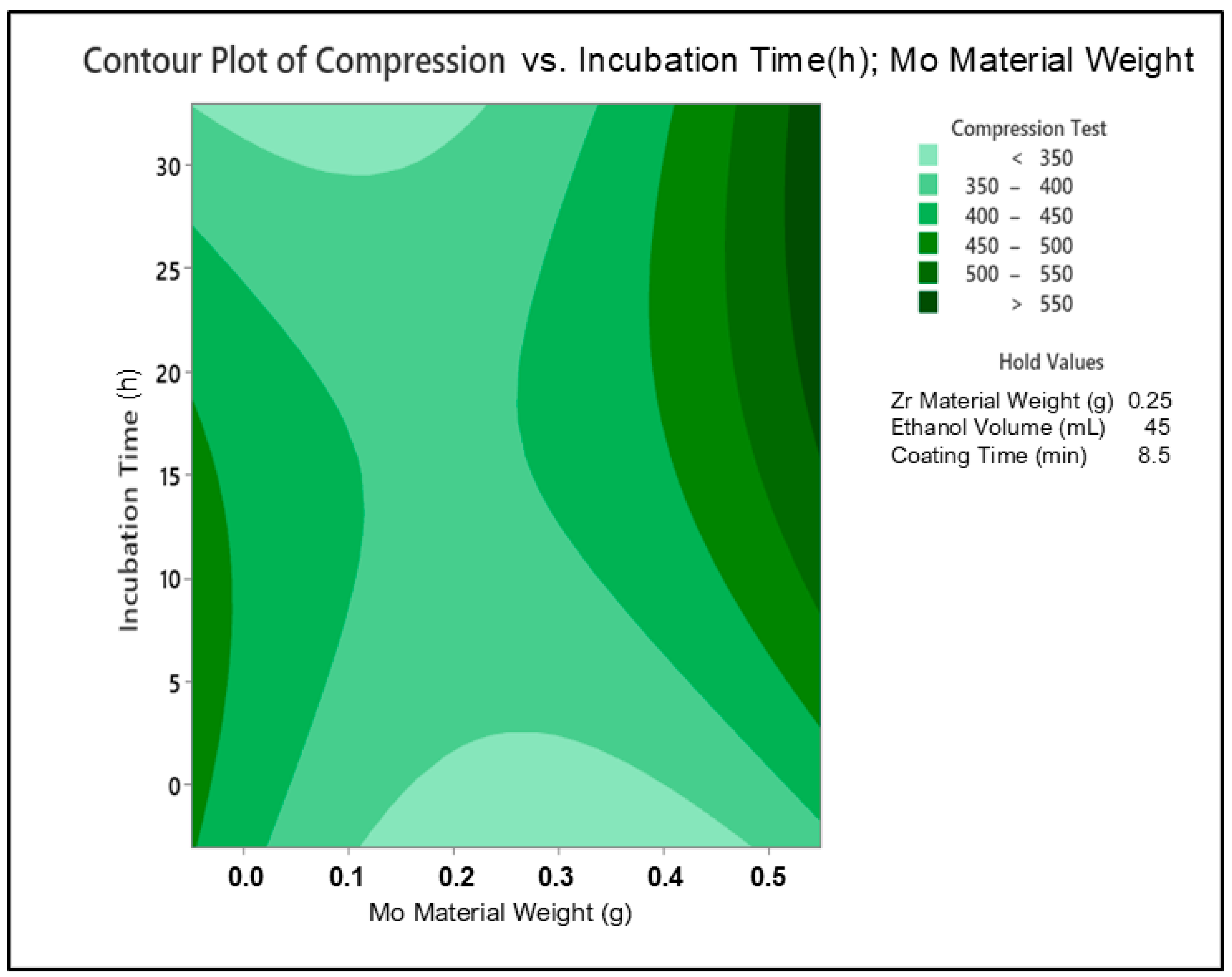


| Parameter | Level | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Molybdenum material weight (g) | 0.1 | 0.2 | 0.3 | 0.4 |
| Zirconia material weight (g) | 0.1 | 0.2 | 0.3 | 0.4 |
| Ethanol volume (mL) | 30 | 40 | 50 | 60 |
| Incubation time (h) | 6 | 8 | 12 | 24 |
| Coating time (min) | 2 | 5 | 10 | 15 |
| Run | A (g) | B (g) | C (mL) | D (h) | E (min) | Compression Test/Ec (Modulus of Elasticity) (MPa) | Density Test (g/cm3) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | SD | 1 | 2 | 3 | 4 | SD | ||||||||
| 1 | 0.1 | 0.1 | 30 | 6 | 2 | 572 | 573 | 571 | 570 | 571.50 | 1.29 | 1.23 | 1.27 | 1.23 | 1.24 | 1.24 | 0.09 |
| 2 | 0.1 | 0.2 | 40 | 8 | 5 | 325 | 324 | 325 | 321 | 323.75 | 1.89 | 1.16 | 1.18 | 1.18 | 1.17 | 1.17 | 0.01 |
| 3 | 0.1 | 0.3 | 50 | 12 | 10 | 1020 | 1023 | 1022 | 1018 | 1020.75 | 2.22 | 1.15 | 1.16 | 1.15 | 1.16 | 1.15 | 0.01 |
| 4 | 0.1 | 0.4 | 60 | 24 | 15 | 502 | 504 | 503 | 502 | 502.75 | 0.96 | 1.14 | 1.13 | 1.15 | 1.16 | 1.14 | 0.01 |
| 5 | 0.2 | 0.1 | 40 | 12 | 15 | 220 | 221 | 222 | 218 | 220.25 | 1.71 | 1.13 | 1.13 | 1.15 | 1.14 | 1.14 | 0.01 |
| 6 | 0.2 | 0.2 | 30 | 24 | 10 | 514 | 512 | 513 | 512 | 512.75 | 0.96 | 1.16 | 1.16 | 1.17 | 1.18 | 1.17 | 0.01 |
| 7 | 0.2 | 0.3 | 60 | 6 | 5 | 241 | 240 | 243 | 239 | 240.75 | 1.71 | 1.16 | 1.16 | 1.16 | 1.16 | 1.16 | 0.00 |
| 8 | 0.2 | 0.4 | 50 | 8 | 2 | 318 | 319 | 320 | 317 | 318.50 | 1.29 | 1.15 | 1.17 | 1.18 | 1.16 | 1.16 | 0.01 |
| 9 | 0.3 | 0.1 | 50 | 24 | 5 | 721 | 720 | 719 | 720 | 720.00 | 0.82 | 1.19 | 1.18 | 1.16 | 1.19 | 1.18 | 0.01 |
| 10 | 0.3 | 0.2 | 60 | 12 | 2 | 621 | 620 | 619 | 618 | 619.50 | 1.29 | 1.17 | 1.21 | 1.19 | 1.18 | 1.18 | 0.01 |
| 11 | 0.3 | 0.3 | 30 | 8 | 15 | 545 | 543 | 544 | 542 | 543.50 | 1.29 | 1.19 | 1.18 | 1.16 | 1.18 | 1.17 | 0.01 |
| 12 | 0.3 | 0.4 | 40 | 6 | 10 | 315 | 314 | 313 | 312 | 313.50 | 1.29 | 1.16 | 1.18 | 1.19 | 1.17 | 1.17 | 0.01 |
| 13 | 0.4 | 0.1 | 60 | 8 | 10 | 220 | 221 | 222 | 219 | 220.50 | 1.29 | 1.16 | 1.21 | 1.18 | 1.19 | 1.18 | 0.02 |
| 14 | 0.4 | 0.2 | 50 | 6 | 15 | 169 | 168 | 167 | 169 | 168.25 | 0.96 | 1.17 | 1.17 | 1.17 | 1.18 | 1.17 | 0.01 |
| 15 | 0.4 | 0.3 | 40 | 24 | 2 | 521 | 522 | 520 | 519 | 520.50 | 1.29 | 1.17 | 1.18 | 1.17 | 1.19 | 1.17 | 0.01 |
| 16 | 0.4 | 0.4 | 30 | 8 | 5 | 378 | 377 | 379 | 376 | 377.50 | 1.29 | 1.20 | 1.19 | 1.19 | 1.18 | 1.19 | 0.01 |
| Factors | DF | SumSqr | MeanSqr | F Value | Prob > F | % Contribution | p-Value |
|---|---|---|---|---|---|---|---|
| Molybdenum material weight (g) | 3 | 817,553 | 272,518 | 140,277 | 0 | 35.40 | 0.000 |
| Zirconia material weight (g) | 3 | 292,141 | 97,380 | 50,126 | 0 | 13.14 | 0.000 |
| Ethanol volume (mL) | 3 | 589,345 | 196,448 | 101,121 | 0 | 15.01 | 0.000 |
| Incubation time (h) | 3 | 810,847 | 270,282 | 139,127 | 0 | 27.72 | 0.000 |
| Coating time (min) | 3 | 257,856 | 85,952 | 44,243.4 | 0 | 8.60 | 0.000 |
| Error | 48 | 93 | 2 | 0.13 | |||
| Total | 63 | 100.00 | |||||
| Model summary | |||||||
| S | R-sq | R-sq (adj) | R-sq (pred) | ||||
| 1.39381 | 98.98% | 96.98% | 94.88% | ||||
| Factors | DF | SumSqr | MeanSqr | F Value | Prob > F | % Contribution | p-Value |
|---|---|---|---|---|---|---|---|
| Molybdenum material weight (g) | 3 | 0.0055 | 0.00183 | 12.9 | 0 | 17.42 | 0.000 |
| Zirconia material weight (g) | 3 | 0.00283 | 0.00094 | 6.64 | 0.001 | 6.76 | 0.001 |
| Ethanol volume (mL) | 3 | 0.00497 | 0.00166 | 11.67 | 0 | 20.65 | 0.000 |
| Incubation time (h) | 3 | 0.00364 | 0.00121 | 8.55 | 0 | 10.20 | 0.000 |
| Coating time (min) | 3 | 0.00913 | 0.00304 | 21.44 | 0 | 25.88 | 0.000 |
| Error | 48 | 0.00682 | 0.00014 | 19.09 | |||
| Total | 63 | 100.00 | |||||
| Model summary | |||||||
| S | R-sq | R-sq (adj) | R-sq (pred) | ||||
| 0.01192 | 80.91% | 74.95% | 66.07% | ||||
| Source | df | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 20 | 8,665,900 | 433,295 | 11.99 | 0.029 |
| Linear | 5 | 2,558,570 | 511,714 | 14.16 | 0.004 |
| Mo material weight (g) | 1 | 381,979 | 381,979 | 10.57 | 0.045 |
| Zr material weight (g) | 1 | 610,371 | 610,371 | 16.89 | 0.012 |
| Ethanol volume (mL) | 1 | 573,510 | 573,510 | 15.87 | 0.020 |
| Incubation time (h) | 1 | 367,523 | 367,523 | 10.17 | 0.018 |
| Coating time (min) | 1 | 625,549 | 625,549 | 17.31 | 0.010 |
| Square | 5 | 2,083,356 | 416,671 | 11.53 | 0.022 |
| Mo material weight (g) × Mo material weight (g) | 1 | 405,468 | 405,468 | 11.22 | 0.026 |
| Zr weight (g) × Zr material weight (g) | 1 | 367,162 | 367,162 | 10.16 | 0.001 |
| Ethanol volume (mL) × Ethanol volume (mL) | 1 | 368,969 | 368,969 | 10.21 | 0.005 |
| Incubation time (h) × Incubation time (h) | 1 | 375,835 | 375,835 | 10.40 | 0.002 |
| Coating time (min) × Coating time (min) | 1 | 561,223 | 561,223 | 15.53 | 0.003 |
| 2-way interaction | 10 | 4,025,773 | 402,577 | 11.14 | 0.035 |
| Mo material weight (g) × Zr material weight (g) | 1 | 366,801 | 366,801 | 10.15 | 0.001 |
| Mo material weight (g) × Ethanol volume (mL) | 1 | 394,627 | 394,627 | 10.92 | 0.004 |
| Mo material weight (g) × Incubation time (h) | 1 | 372,944 | 372,944 | 10.32 | 0.006 |
| Mo material weight (g) × Coating time (min) | 1 | 510,630 | 510,630 | 14.13 | 0.008 |
| Zr material weight (g) × Ethanol volume (mL) | 1 | 397,157 | 397,157 | 10.99 | 0.025 |
| Zr material weight (g) × Incubation time (h) | 1 | 361,380 | 361,380 | 10.00 | 0.048 |
| Zr material weight (g) × Coating time (min) | 1 | 395,711 | 395,711 | 10.95 | 0.004 |
| Ethanol volume (mL) × Incubation time (h) | 1 | 490,754 | 490,754 | 13.58 | 0.015 |
| Ethanol volume (mL) × Coating time (min) | 1 | 371,860 | 371,860 | 10.29 | 0.025 |
| Incubation time (h) × Coating time (min) | 1 | 362,826 | 362,826 | 10.04 | 0.003 |
| Error | 43 | 1,553,938 | 36,138 | ||
| Cor total | 63 | 2,993,383 |
| Source | df | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 20 | 0.185874 | 0.0092937 | 14.32 | 0.000 |
| Linear | 5 | 0.054873 | 0.0109746 | 16.91 | 0.000 |
| Mo material weight (g) | 1 | 0.008054 | 0.0080541 | 12.41 | 0.027 |
| Zr material weight (g) | 1 | 0.015875 | 0.0158745 | 24.46 | 0.000 |
| Ethanol volume (mL) | 1 | 0.014207 | 0.0142066 | 21.89 | 0.000 |
| Incubation time (h) | 1 | 0.016498 | 0.0164976 | 25.42 | 0.000 |
| Coating time (min) | 1 | 0.010384 | 0.0103840 | 16.00 | 0.000 |
| Square | 5 | 0.041082 | 0.0082163 | 12.66 | 0.000 |
| Mo material weight (g) × Mo material weight (g) | 1 | 0.021047 | 0.0210471 | 32.43 | 0.000 |
| Zr weight (g) × Zr material weight (g) | 1 | 0.017873 | 0.0178735 | 27.54 | 0.000 |
| Ethanol volume (mL) × Ethanol volume (mL) | 1 | 0.024123 | 0.0241233 | 37.17 | 0.000 |
| Incubation time (h) × Incubation time (h) | 1 | 0.006769 | 0.0067691 | 10.43 | 0.002 |
| Coating time (min) × Coating time (min) | 1 | 0.006522 | 0.0065225 | 10.05 | 0.032 |
| 2-way interaction | 10 | 0.113705 | 0.0113705 | 17.52 | 0.000 |
| Mo material weight (g) × Zr material weight (g) | 1 | 0.017581 | 0.0175814 | 27.09 | 0.000 |
| Mo material weight (g) × Ethanol volume (mL) | 1 | 0.012188 | 0.0121882 | 18.78 | 0.000 |
| Mo material weight (g) × Incubation time (h) | 1 | 0.013979 | 0.0139795 | 21.54 | 0.000 |
| Mo material weight (g) × Coating time (min) | 1 | 0.017211 | 0.0172115 | 26.52 | 0.000 |
| Zr material weight (g) × Ethanol volume (mL) | 1 | 0.007003 | 0.0070027 | 10.79 | 0.002 |
| Zr material weight (g) × Incubation time (h) | 1 | 0.007191 | 0.0071909 | 11.08 | 0.004 |
| Zr material weight (g) × Coating time (min) | 1 | 0.006490 | 0.0064900 | 10.00 | 0.045 |
| Ethanol volume (mL) × Incubation time (h) | 1 | 0.007191 | 0.0071909 | 11.08 | 0.004 |
| Ethanol volume (mL) × Coating time (min) | 1 | 0.006490 | 0.0064900 | 10.00 | 0.045 |
| Incubation time (h) × Coating time (min) | 1 | 0.006516 | 0.0065160 | 10.04 | 0.036 |
| Error | 43 | 0.027889 | 0.0006490 | ||
| Cor total | 63 | 0.039975 |
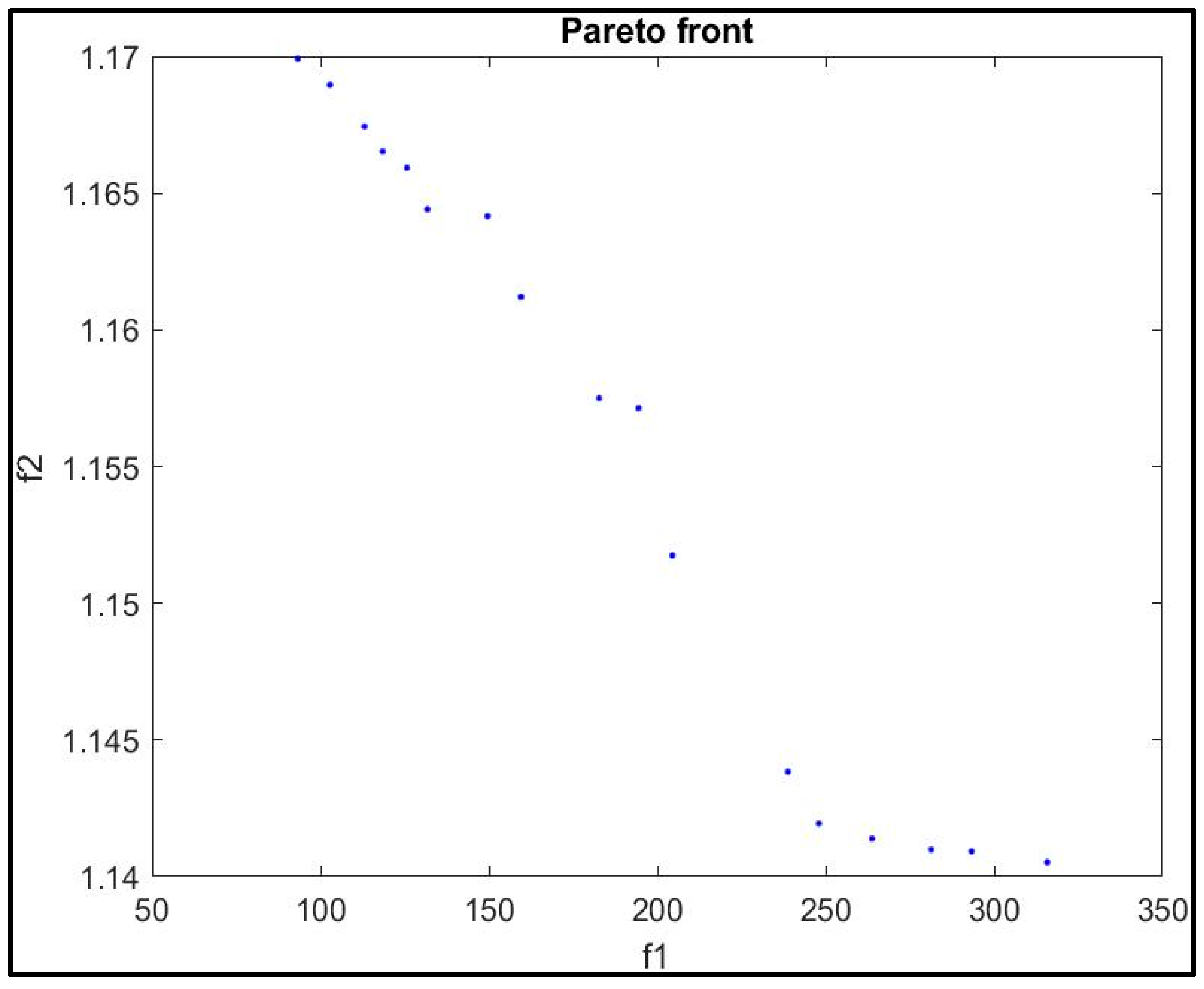
| Pareto Point | Decision Variables | Objective Function | |||||
|---|---|---|---|---|---|---|---|
| Molybdenum Material Weight (g) | Zirconia Material Weight (g) | Ethanol Volume (mL) | Incubation Time (h) | Coating Time (min) | Compression Test/Ec (Modulus of Elasticity) (MPa) | Density Test (g/cm3) | |
| A1 | 0.101 | 0.100 | 59.561 | 23.880 | 2.390 | 93.295 | 1.170 |
| A2 | 0.101 | 0.100 | 59.923 | 6.025 | 7.907 | 316.818 | 1.132 |
| A3 | 0.101 | 0.100 | 59.923 | 6.025 | 7.907 | 315.808 | 1.141 |
| A4 | 0.101 | 0.101 | 59.818 | 6.141 | 4.896 | 263.778 | 1.141 |
| A5 | 0.102 | 0.101 | 59.793 | 12.253 | 2.643 | 204.481 | 1.152 |
| A6 | 0.102 | 0.101 | 59.619 | 23.776 | 3.262 | 102.857 | 1.169 |
| A7 | 0.102 | 0.101 | 59.844 | 6.064 | 3.447 | 248.011 | 1.142 |
| A8 | 0.102 | 0.101 | 59.680 | 20.384 | 2.449 | 131.831 | 1.164 |
| A9 | 0.102 | 0.101 | 59.647 | 21.918 | 2.759 | 118.536 | 1.167 |
| A10 | 0.102 | 0.102 | 59.849 | 6.102 | 6.758 | 293.356 | 1.141 |
| A11 | 0.102 | 0.114 | 59.663 | 16.176 | 4.151 | 194.462 | 1.157 |
| A12 | 0.103 | 0.102 | 59.892 | 6.038 | 6.042 | 281.342 | 1.141 |
| A13 | 0.104 | 0.107 | 59.785 | 16.160 | 3.320 | 182.755 | 1.158 |
| A14 | 0.102 | 0.101 | 59.812 | 7.157 | 3.008 | 238.805 | 1.144 |
| A15 | 0.101 | 0.100 | 59.612 | 22.763 | 3.180 | 113.131 | 1.167 |
| A16 | 0.102 | 0.103 | 59.606 | 21.768 | 3.206 | 125.738 | 1.166 |
| A17 | 0.101 | 0.101 | 59.778 | 21.534 | 5.040 | 149.645 | 1.164 |
| A18 | 0.102 | 0.100 | 59.692 | 19.130 | 3.978 | 159.582 | 1.161 |
| Decision Variables | ||||
|---|---|---|---|---|
| Molybdenum Material Weight (g) | Zirconia Material Weight (g) | Ethanol Volume (mL) | Incubation Time (h) | Coating Time (min) |
| 0.101 | 0.100 | 59.523 | 6.025 | 7.907 |
| Optimal value of objective function | ||||
| Compression Test/Ec (Modulus of elasticity) (MPa) | Density Test (g/cm3) | |||
| 315.808 | 1.141 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luthfianto, S.; Pujiyanto, E.; Rosyidi, C.N.; Laksono, P.W. Multi-Objective Optimization of the Dip-Coating Parameters for Polylactic Acid Plus Bone Screws Using Taguchi Method, Response Surface Methodology, and Non-Dominated Sorting Genetic Algorithm II. Processes 2025, 13, 1690. https://doi.org/10.3390/pr13061690
Luthfianto S, Pujiyanto E, Rosyidi CN, Laksono PW. Multi-Objective Optimization of the Dip-Coating Parameters for Polylactic Acid Plus Bone Screws Using Taguchi Method, Response Surface Methodology, and Non-Dominated Sorting Genetic Algorithm II. Processes. 2025; 13(6):1690. https://doi.org/10.3390/pr13061690
Chicago/Turabian StyleLuthfianto, Saufik, Eko Pujiyanto, Cucuk Nur Rosyidi, and Pringgo Widyo Laksono. 2025. "Multi-Objective Optimization of the Dip-Coating Parameters for Polylactic Acid Plus Bone Screws Using Taguchi Method, Response Surface Methodology, and Non-Dominated Sorting Genetic Algorithm II" Processes 13, no. 6: 1690. https://doi.org/10.3390/pr13061690
APA StyleLuthfianto, S., Pujiyanto, E., Rosyidi, C. N., & Laksono, P. W. (2025). Multi-Objective Optimization of the Dip-Coating Parameters for Polylactic Acid Plus Bone Screws Using Taguchi Method, Response Surface Methodology, and Non-Dominated Sorting Genetic Algorithm II. Processes, 13(6), 1690. https://doi.org/10.3390/pr13061690










