Vibrational Radiative Double Diffusion in Buongiorno’s Nanofluid Model Within Inclined Chambers Filled with Non-Darcy Porous Elements
Abstract
1. Introduction
- How does the inclination angle of the enclosure affect the convective heat transfer and nanoparticle migration in the presence of vibrational forces?
- What are the impacts of radiative heat transfer on the thermal boundary layers and nanoparticle distribution in the nanofluid?
- How does the non-Darcy porous medium influence the overall heat transfer rate compared to a Darcy-based model?
- What is the effect of varying the Brownian motion and thermophoresis parameters on the double-diffusive convection within the enclosure?
- How do different vibration frequencies and amplitudes alter the flow and thermal fields within the nanofluid system?
- How does the combined effect of these factors contribute to the optimization of heat transfer performance in practical engineering applications such as energy systems, thermal insulation, and microfluidic devices?
2. Assumption and Governing System
- All outer boundaries are thermally insulated.
- Two heated fins, each with a length of and a width of 0.2, are attached to the lower boundaries at and .
- Two cold fins, also with a length of and a width of 0.2, are attached to the upper boundaries at x = 0.5 L and x = 1.2 L.
- The flow domain is inclined at an angle .
- A vibration source is modeled as .
- The flow region is filled with a non-Darcy porous medium.
- Two concentrations—one for species and one for nanoparticles—are considered, with Buongiorno’s nanofluid model applied.
- Thermal radiation is accounted for in both the x- and y-directions.
- The flow is assumed to be two-dimensional and laminar.
- : fluid density.
- : porosity of the medium that can be defined as the fraction of void space in the porous material.
- : velocity components in the x-and y- directions, respectively.
- : pressure.
- : effective viscosity, accounting for both fluid and porous medium effects.
- : dynamic viscosity of the fluid.
- : permeability of the porous medium that measures how easily fluid flows through the medium.
- : Forchheimer coefficient that represents non-linear drag effects in high-velocity flows.
- : thermal and solutal expansion coefficients, respectively; those refer to the effect of temperature and concentration variations on fluid density.
- : acceleration due to gravity.
- temperature and concentration of the fluid.
- : nanoparticle volume fraction and its reference value.
- : densities of nanoparticles and fluid, respectively.
- : parameters related to time-dependent oscillations.
- : inclination angle.
3. Numerical Methods
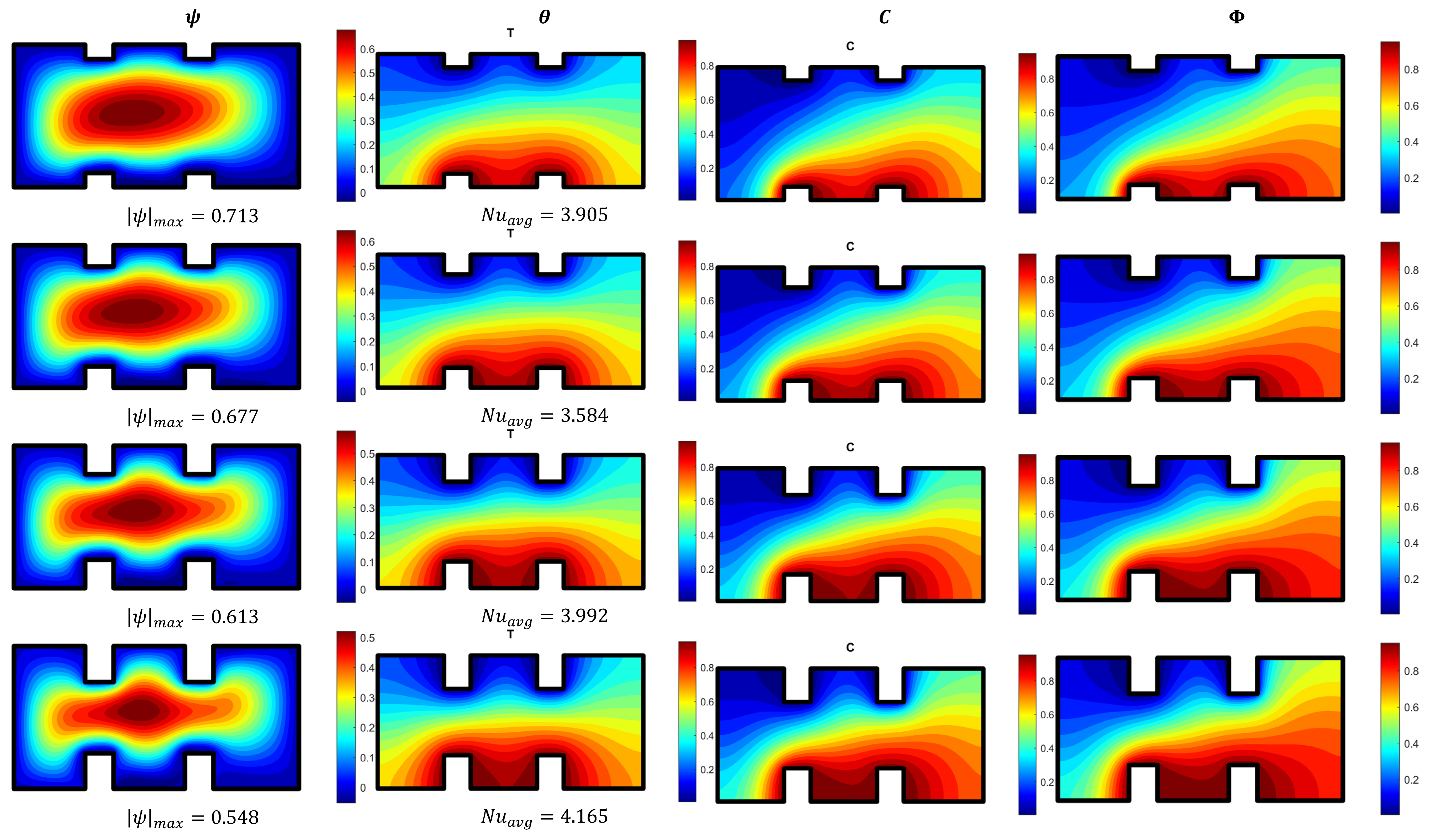
4. Results and Discussion
5. Conclusions
- ➢
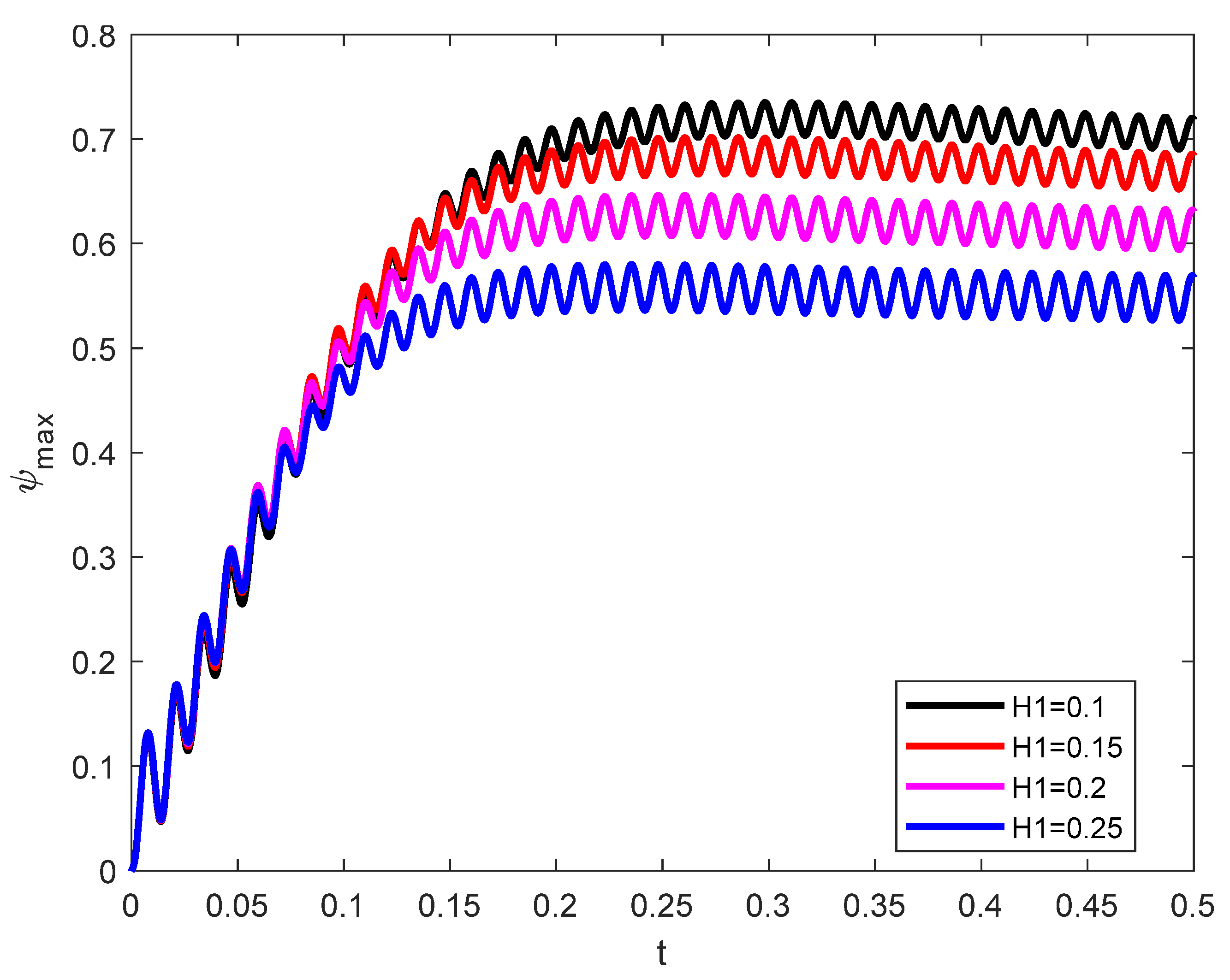
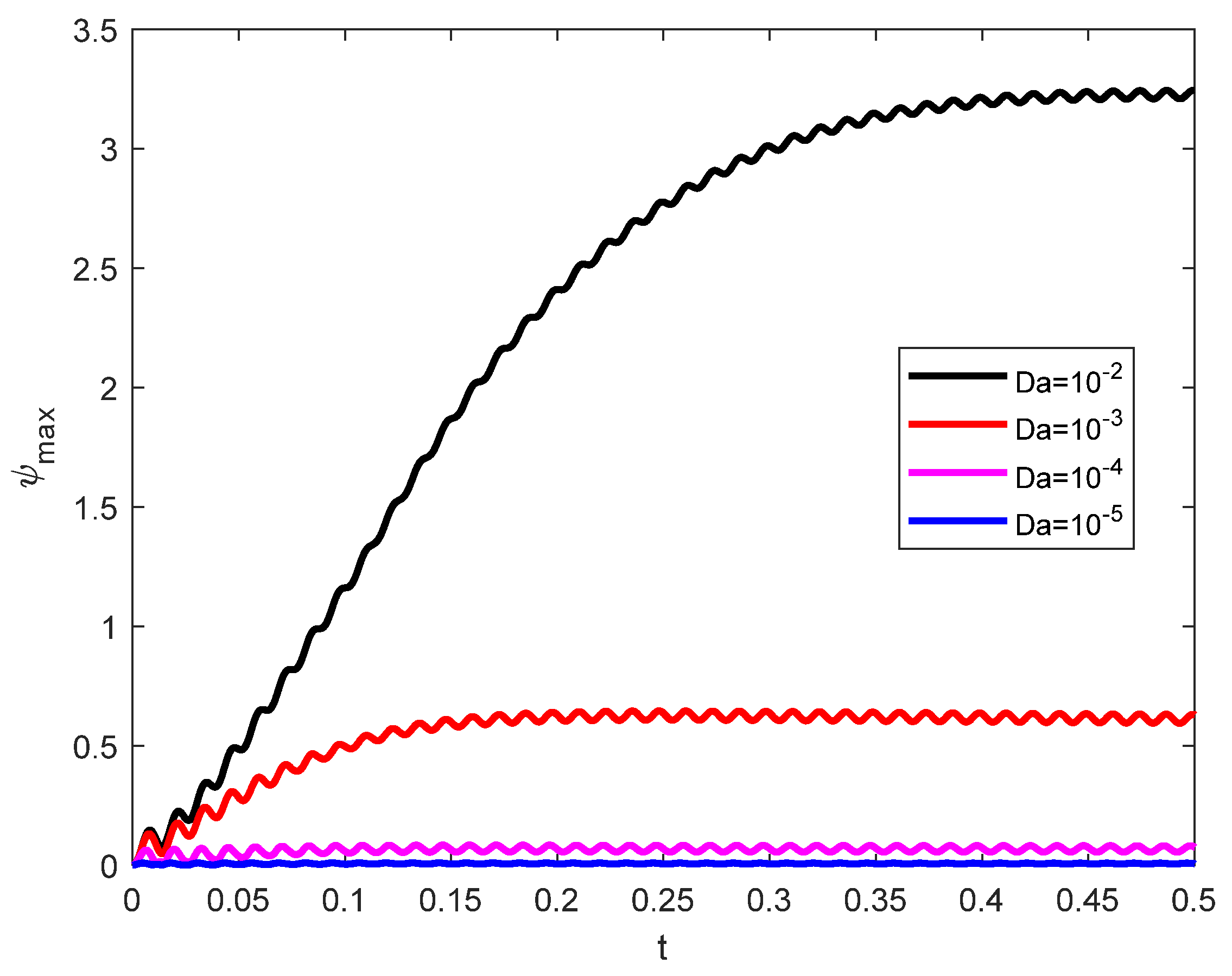
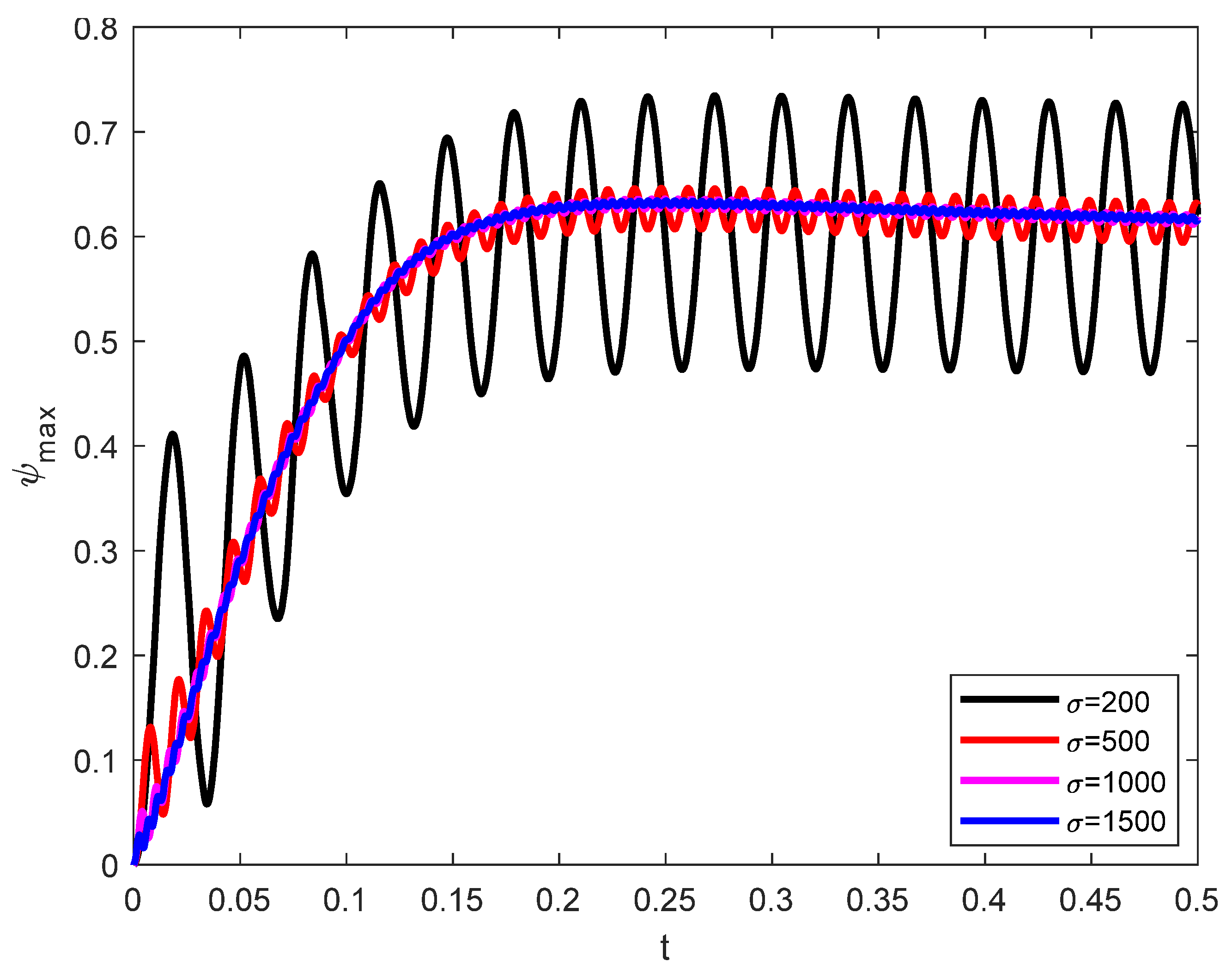
- Harmonic behaviors are obtained for the stream function against the time variations due to the vibrational effects. These behaviors are reduced as either the lengths of the fins increase, or the Darcy number is decreased.
- ➢
- As the vibration frequency rises, the fluctuation in the features of the streamlines is enhanced while their wave’s amplitude is diminishing.
- ➢
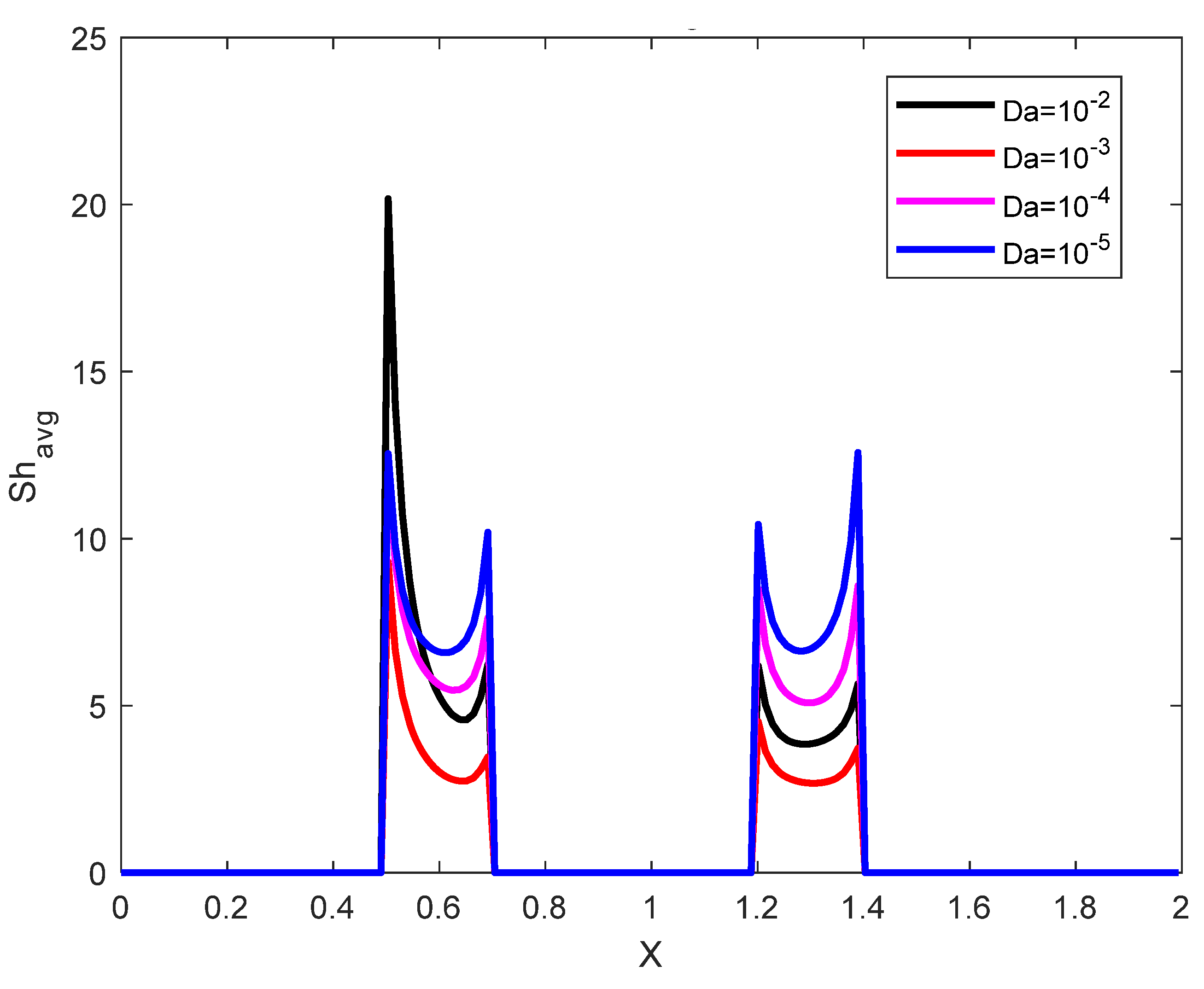
- Higher rates for heat and mass transfer are obtained as the inclination angle is altered.
- ➢
- Due to the higher viscous dissipation effects, the raising in Darcy number enhances gradients of the temperature and concentration.
- ➢
- At fixed values of oscillation amplitude and oscillation frequency increasing the fin lengths from 0.1 to 0.35 results in a reduction in flow activity.
5.1. Practical Industrial Applications:
- Cooling systems in electronics: Vibrational modulation can be used to enhance or control heat transfer in compact heat exchangers filled with porous materials or nanofluids.
- Energy systems and thermal storage: Double-diffusive convection in porous domains is critical in phase-change energy storage, geothermal reservoirs, and solar collectors, where vibrations can occur due to environmental or operational conditions.
- Chemical and biomedical processes: In reactors or separation units filled with porous catalysts or membranes, controlling species transport and temperature profiles using vibration or fin optimization can enhance efficiency and stability.
5.2. Scientific Contributions:
- This study integrates Buongiorno’s nanofluid model with double-diffusive convection in a vibrating porous domain, which has been rarely explored in time-dependent contexts.
- The identification of harmonic flow responses due to vibration adds depth to transient flow dynamics understanding.
- The use of a geometric fin configuration and vibrational control adds a new layer of complexity to previous studies on nanofluid flow in porous cavities.
- This study employs a robust numerical framework (finite volume + geometric domain tracking using inpolygon) that can be extended to more complex geometries.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description | Unit |
| Nomenclature | ||
| Solutal expansion coefficient | 1/(kg/m3) | |
| Thermal expansion coefficient | 1/K | |
| Dimensionless concentration | - | |
| Solute concentration | kg/m3 | |
| Reference solute concentration | kg/m3 | |
| Forchheimer coefficient | - | |
| Brownian diffusion coefficient | m²/s | |
| Solutal diffusivity | m²/s | |
| Thermophoretic diffusion coefficient | m²/s | |
| - | ||
| Gravitational acceleration | m/s2 | |
| Thermal conductivity of the fluid | W/(m·K) | |
| Mean absorption coefficient | 1/m | |
| Permeability of the porous medium | m2 | |
| Characteristic length | m | |
| Lewis number for nanoparticle concentration | - | |
| Lewis number for solute concentration | - | |
| Buoyancy ratio parameter | - | |
| Brownian motion parameter | - | |
| Nanoparticle buoyancy parameter | - | |
| Thermophoresis parameter | - | |
| Nusselt number | - | |
| Pressure | Pa | |
| Prandtl number | - | |
| Radiative heat flux components | W/m2 | |
| Radiation parameter | - | |
| Rayleigh number | - | |
| Heat capacity of fluid | J/(kg·K) | |
| Heat capacity of particles | J/(kg·K) | |
| Temperature | K | |
| Reference temperature | K | |
| Base/reference temperature | K | |
| Velocity components in x and y directions | m/s | |
| Dimensionless velocity components | - | |
| Spatial coordinates | m | |
| Dimensionless spatial coordinates | - | |
| Greek symbols | ||
| Thermal diffusivity of the fluid | m2/s | |
| Porosity of the medium | - | |
| Amplitude of oscillation | - | |
| Dynamic viscosity of the fluid | kg/(m·s) | |
| Effective viscosity | kg/(m·s) | |
| Kinematic viscosity of the fluid | m2/s | |
| Fluid density | kg/m3 | |
| Nanoparticle density | kg/m3 | |
| Stefan–Boltzmann constant | W/(m2·K⁴) | |
| Oscillation frequency | 1/s | |
| Dimensionless temperature | - | |
| - | ||
| Inclination angle | degrees | |
| Dimensionless nanoparticle volume fraction | - | |
| Nanoparticle volume fraction | - | |
| Reference nanoparticle volume fraction | - | |
| Subscript | ||
| Fluid | - | |
| Nanoparticle | - | |
| Local | - | |
| Average | - | |
References
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Rajput, S.; Kumar, R. Influence of vibrations on heat transfer characteristics of nanofluids. Int. J. Therm. Sci. 2021, 164, 106857. [Google Scholar]
- Modest, M.F. Radiative Heat Transfer; Academic Press: New York, NY, USA, 2013. [Google Scholar]
- Gebhart, B.; Pera, L. The nature of vertical natural convection flows resulting from the combined buoyancy effects of thermal and mass diffusion. Int. J. Heat Mass Transf. 1971, 14, 2025–2050. [Google Scholar] [CrossRef]
- Shoaib, M.; Rafia, T.; Raja, M.A.Z.; Khan, W.A.; Waqas, M. Further analysis of double-diffusive flow of nanofluid through a porous medium situated on an inclined plane: AI-based Levenberg–Marquardt scheme with backpropagated neural network. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 227. [Google Scholar] [CrossRef]
- Akram, S.; Athar, M.; Saeed, K.; Imran, M.; Muhammad, T. Slip impact on double-diffusion convection of magneto-fourth-grade nanofluids with peristaltic propulsion through an inclined asymmetric channel. J. Therm. Anal. Calorim. 2022, 147, 8933–8946. [Google Scholar] [CrossRef]
- Humnekar, N.; Srinivasacharya, D. Influence of variable viscosity and double diffusion on the convective stability of a nanofluid flow in an inclined porous channel. Appl. Math. Mech. 2024, 45, 563–580. [Google Scholar] [CrossRef]
- Hussain, S.; Mehmood, K.; Sagheer, M.; Yamin, M. Numerical simulation of double diffusive mixed convective nanofluid flow and entropy generation in a square porous enclosure. Int. J. Heat Mass Transf. 2018, 122, 1283–1297. [Google Scholar] [CrossRef]
- Basak, T.; Roy, S.; Pop, I. Analysis of mixed convection flows within a square cavity with linearly heated side walls inclined at different angles. Int. J. Heat Mass Transf. 2009, 52, 5002–5013. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Asmadi, M.S.; Kasmani, R.M.; Siri, Z.; Saleh, H. Thermal enhancement effects of buoyancy-driven heat transfer of hybrid nanofluid confined in a tilted U-shaped cavity. J. Appl. Fluid Mech. 2022, 15, 337–348. [Google Scholar]
- Alabdulhadi, S.; Waini, I.; Ahmed, S.E.; Ishak, A. Hybrid nanofluid flow and heat transfer past an inclined surface. Mathematics 2021, 9, 3176. [Google Scholar] [CrossRef]
- Mohamed, I.A. Numerical investigation of natural convection in an inclined porous enclosure using non-Darcian flow model. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 1881–1897. [Google Scholar] [CrossRef]
- Luo, W.-J.; Yang, R.-J. Multiple Fluid Flow and Heat Transfer Solutions in a Two-Sided Lid-Driven Cavity. Int. J. Heat Mass Transf. 2007, 50, 3822–3835. [Google Scholar] [CrossRef]
- Luo, W.-J.; Yang, R.-J. Effect of Ionic Concentration on Electrokinetic Instability in a Cross-Shaped Microchannel. Microfluid. Nanofluid. 2009, 6, 619–630. [Google Scholar] [CrossRef]
- Chen, K.-T.; Tsai, C.-C.; Luo, W.-J.; Chen, C.-N. Multiplicity of Steady Solutions in a Two-Sided Lid-Driven Cavity with Different Aspect Ratios. Theor. Comput. Fluid Dyn. 2013, 27, 85–102. [Google Scholar] [CrossRef]
- Luo, W.-J.; Vishwakarma, P.; Panigrahi, B. Hydrodynamic Influence on Thermal Management of Flexible Heatsink Devices Embedded with Out-of-Plane Intricate Microchannel Design. Micromachines 2020, 11, 951. [Google Scholar] [CrossRef]
- Hafed, Z.S.; Arafa, A.A.M.; Hussein, S.A.; Ahmed, S.E.; Morsy, Z. Bioconvective Blood Flow of Tetra Composition Nanofluids Passing Through a Stenotic Artery with Arrhenius Energy. Numer. Heat Transf. Part B Fundam. 2025, 86, 580–603. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Hafed, Z.S.; Mansour, M.A.; Mohamed, E.F.; Bakier, M.A.Y. Role of two isothermal cylinders towards three-dimensional flow and melting of phase-change materials. Case Stud. Therm. Eng. 2024, 63, 105364. [Google Scholar] [CrossRef]
- Hafed, Z.S.; Hussein, S.A.; Alenazi, A.; Arafa, A.A.; Ahmed, S.E. Impacts of Arrhenius energy and viscous dissipation on variable properties of viscoelastic nanofluid flow with slip velocity. Int. J. Model. Simul. 2023, 1–19. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Raizah, Z.; Hafed, Z.S.; Alhazmi, M. Highly mixed convection of micropolar nanofluids in a complex dynamic system with moving walls, a rotating cylinder, and anisotropic porous elements. Int. Commun. Heat Mass Transf. 2025, 164, 108976. [Google Scholar] [CrossRef]
- Sayyou, H.; Belabid, J.; Öztop, H.F.; Allali, K. Vibrational effects on thermosolutal free convection of Cu-Al2O3/water nanofluids in a partially heated and salted square porous enclosure. J. Mol. Liq. 2025, 423, 126990. [Google Scholar] [CrossRef]




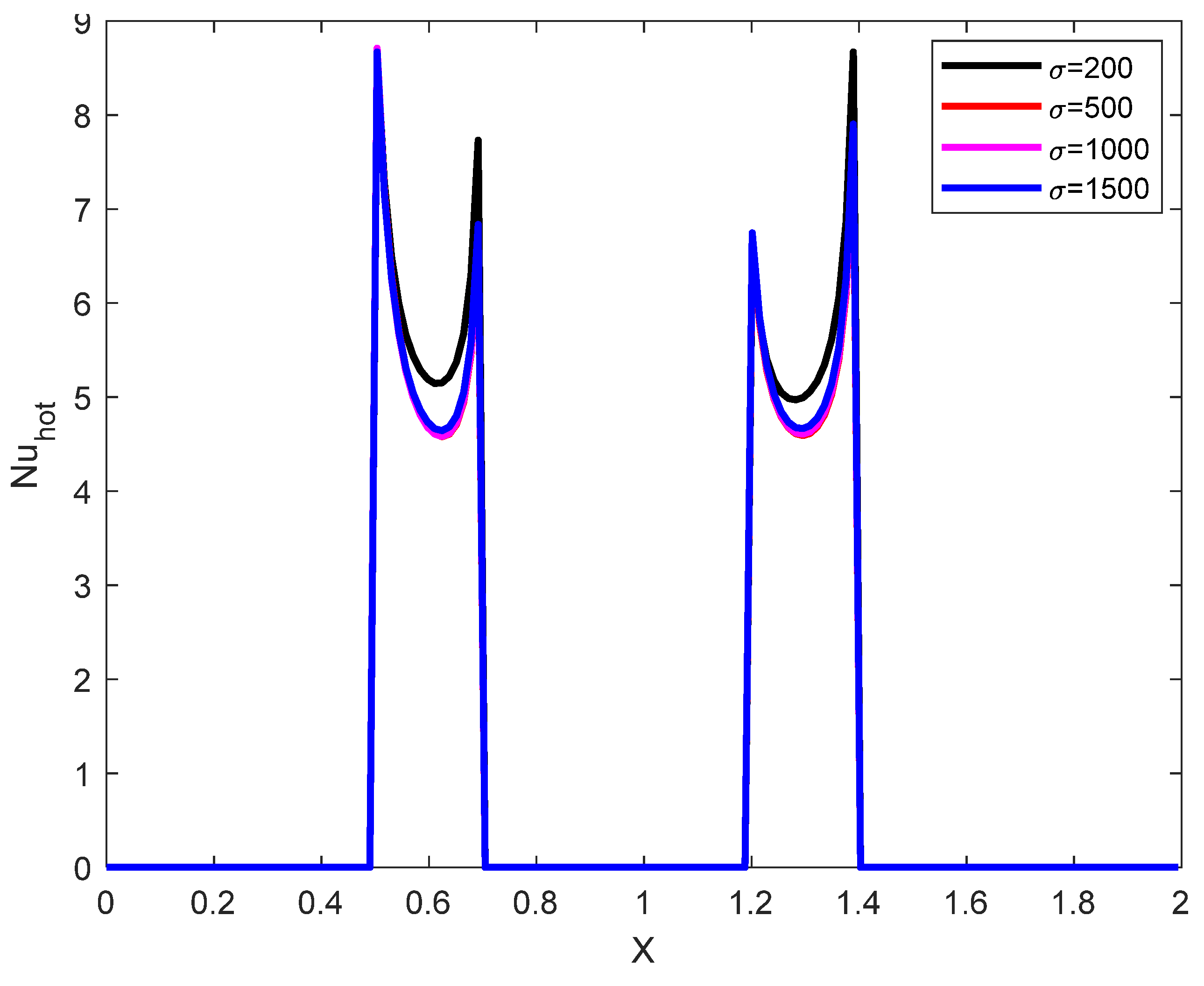
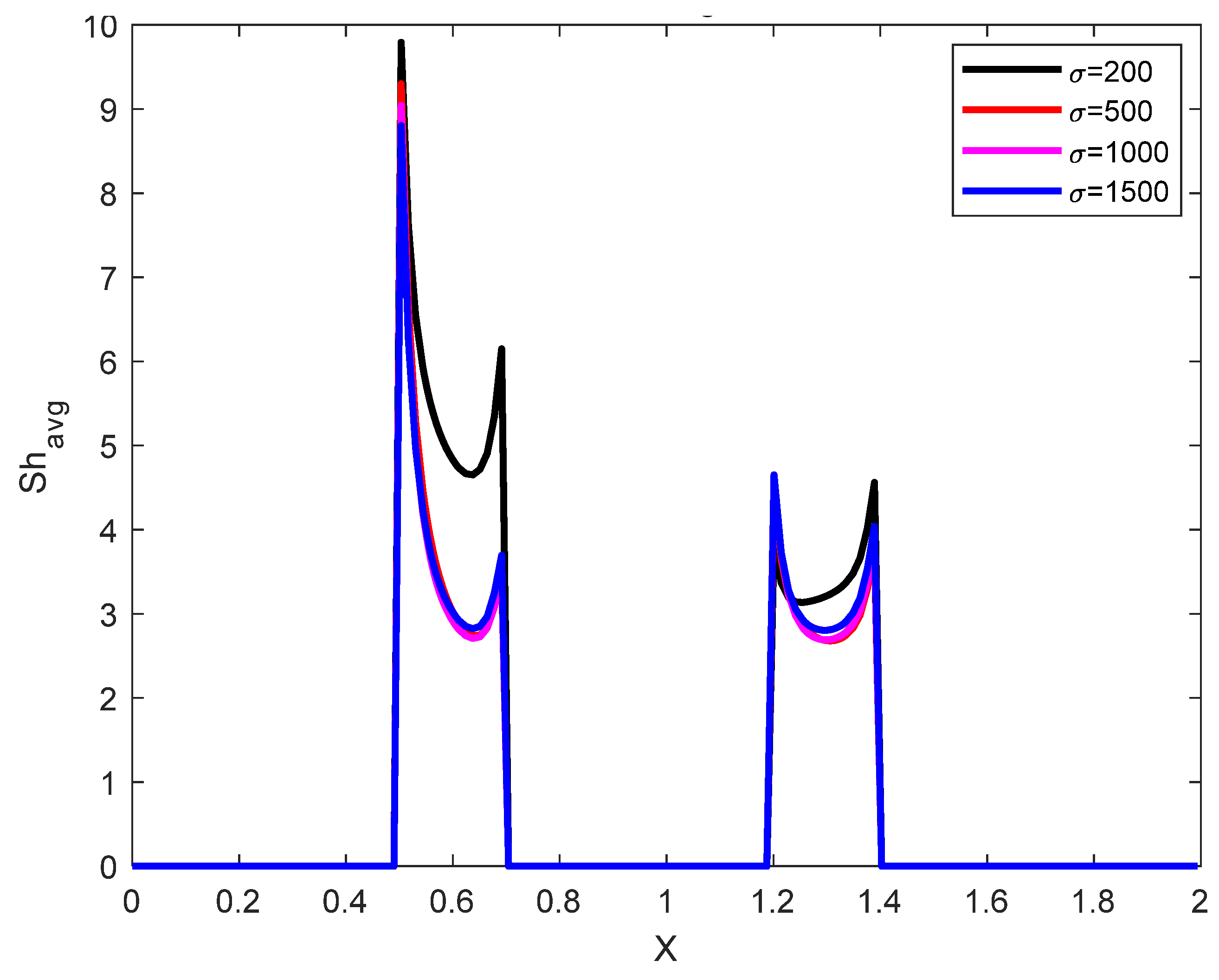
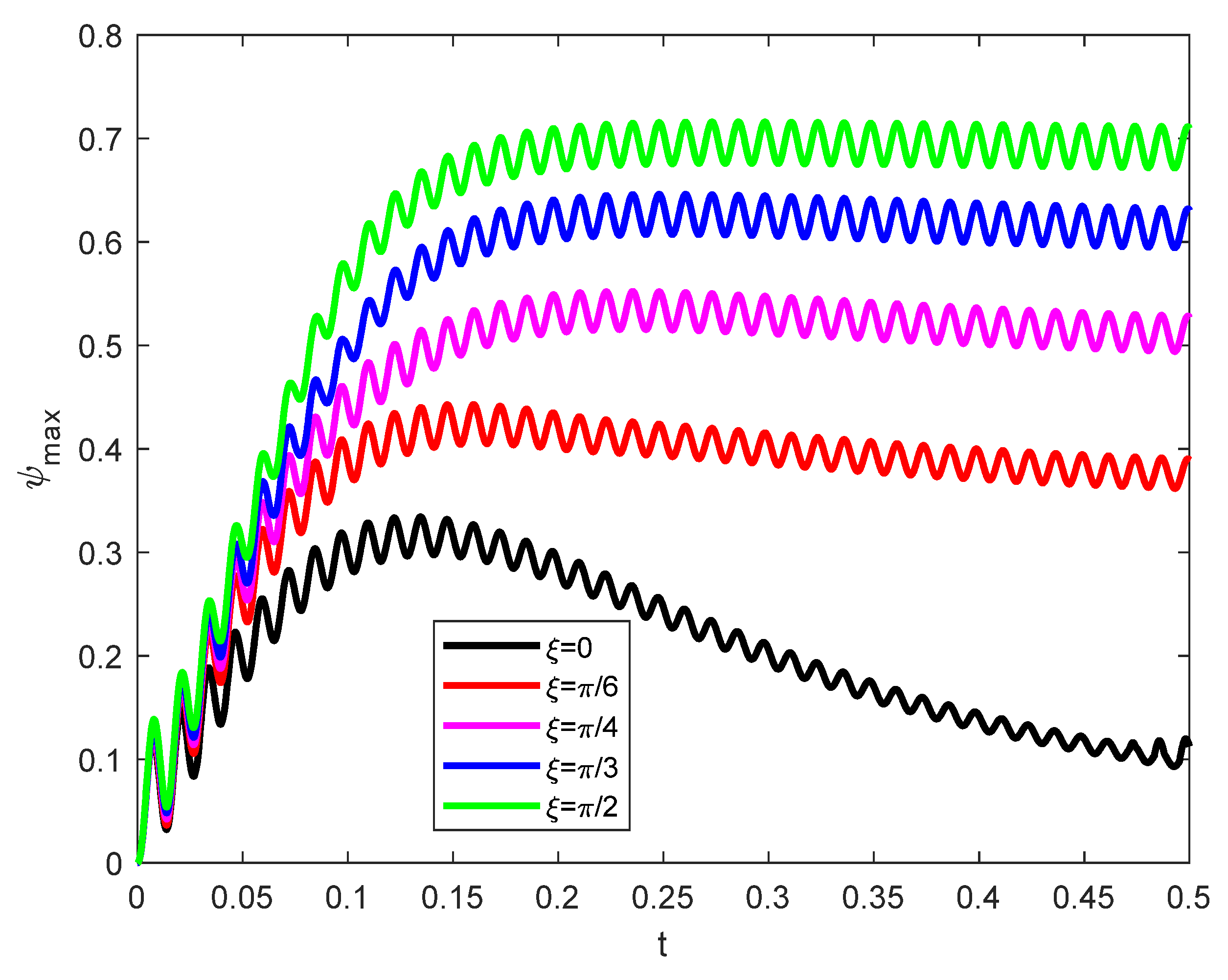


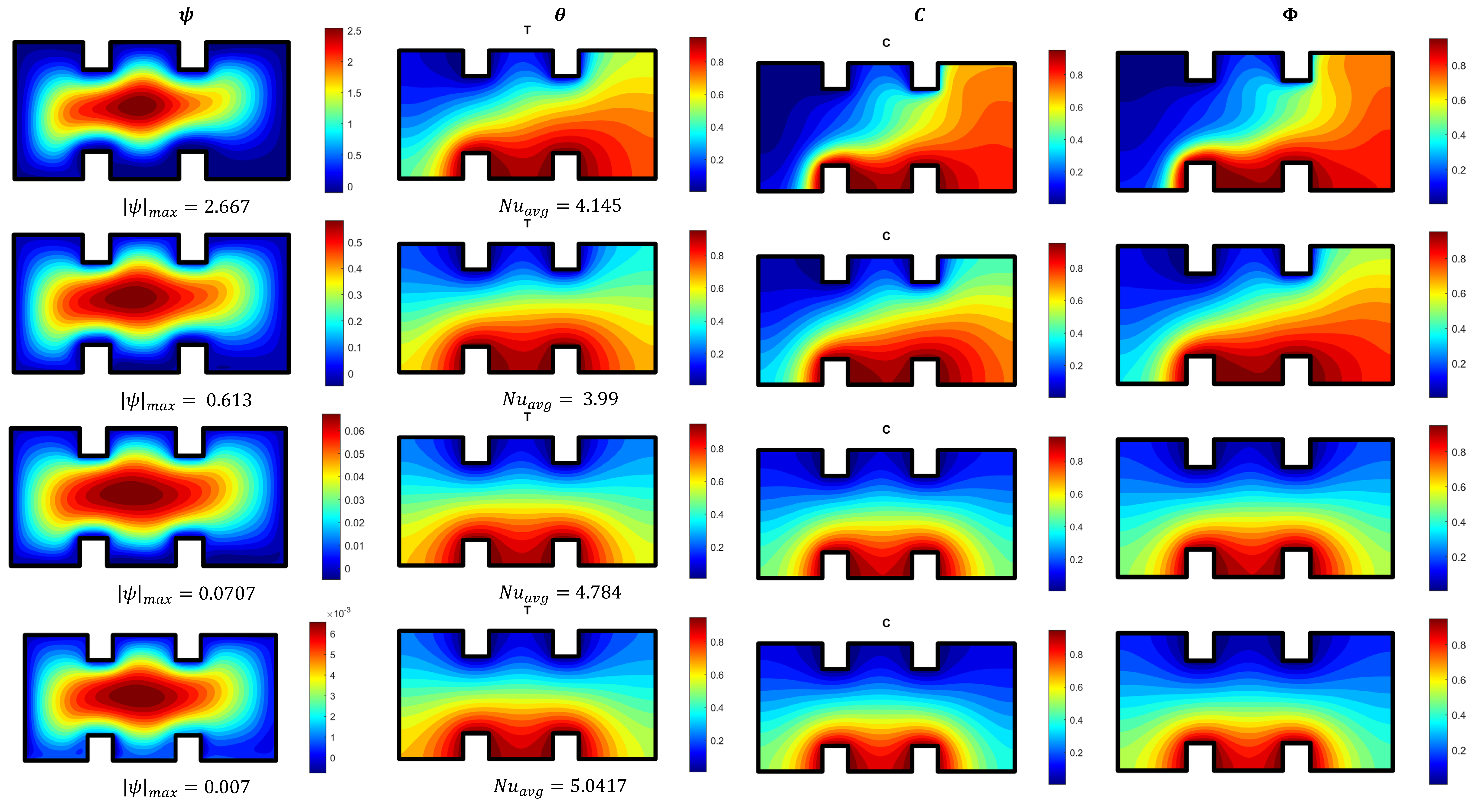

| Grid Size | |
|---|---|
| 0.6501046 | |
| 0.5754108 | |
| 0.5353933 | |
| 0.5206753 | |
| 0.5168692 | |
| 0.5175501 |
| Present Results | Sayyou et al. [23] | ||||
|---|---|---|---|---|---|
| 10 | 3.15 | 13.39 | 3.11 | 13.29 | |
| 10 | 5.01 | 20.82 | 4.96 | 20.29 | |
| 10 | 13.50 | 48.402 | 13.52 | 47.63 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alabdulhadi, S.; Hafed, Z.; Alhazmi, M.; Ahmed, S.E. Vibrational Radiative Double Diffusion in Buongiorno’s Nanofluid Model Within Inclined Chambers Filled with Non-Darcy Porous Elements. Processes 2025, 13, 1551. https://doi.org/10.3390/pr13051551
Alabdulhadi S, Hafed Z, Alhazmi M, Ahmed SE. Vibrational Radiative Double Diffusion in Buongiorno’s Nanofluid Model Within Inclined Chambers Filled with Non-Darcy Porous Elements. Processes. 2025; 13(5):1551. https://doi.org/10.3390/pr13051551
Chicago/Turabian StyleAlabdulhadi, Sumayyah, Zahra Hafed, Muflih Alhazmi, and Sameh E. Ahmed. 2025. "Vibrational Radiative Double Diffusion in Buongiorno’s Nanofluid Model Within Inclined Chambers Filled with Non-Darcy Porous Elements" Processes 13, no. 5: 1551. https://doi.org/10.3390/pr13051551
APA StyleAlabdulhadi, S., Hafed, Z., Alhazmi, M., & Ahmed, S. E. (2025). Vibrational Radiative Double Diffusion in Buongiorno’s Nanofluid Model Within Inclined Chambers Filled with Non-Darcy Porous Elements. Processes, 13(5), 1551. https://doi.org/10.3390/pr13051551







