Chemical Safety Inspection Path Optimization Problems Using Improved Multi-Objective Discrete Growth Optimization Algorithm
Abstract
:1. Introduction
2. Problem Description
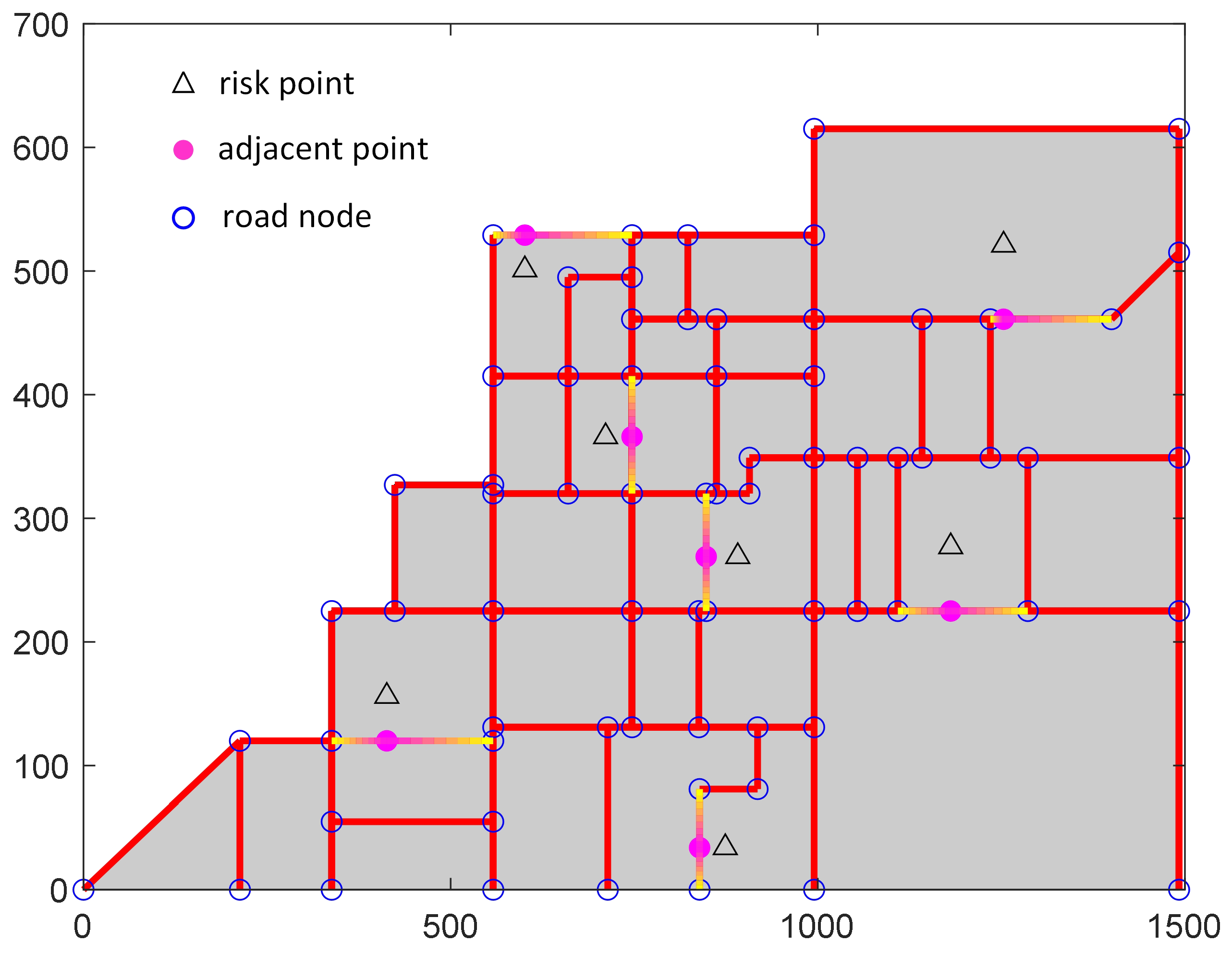
2.1. Problem Statement
2.2. Simulation Model
2.3. Decision Variables and Objective Functions
3. Proposed Algorithm
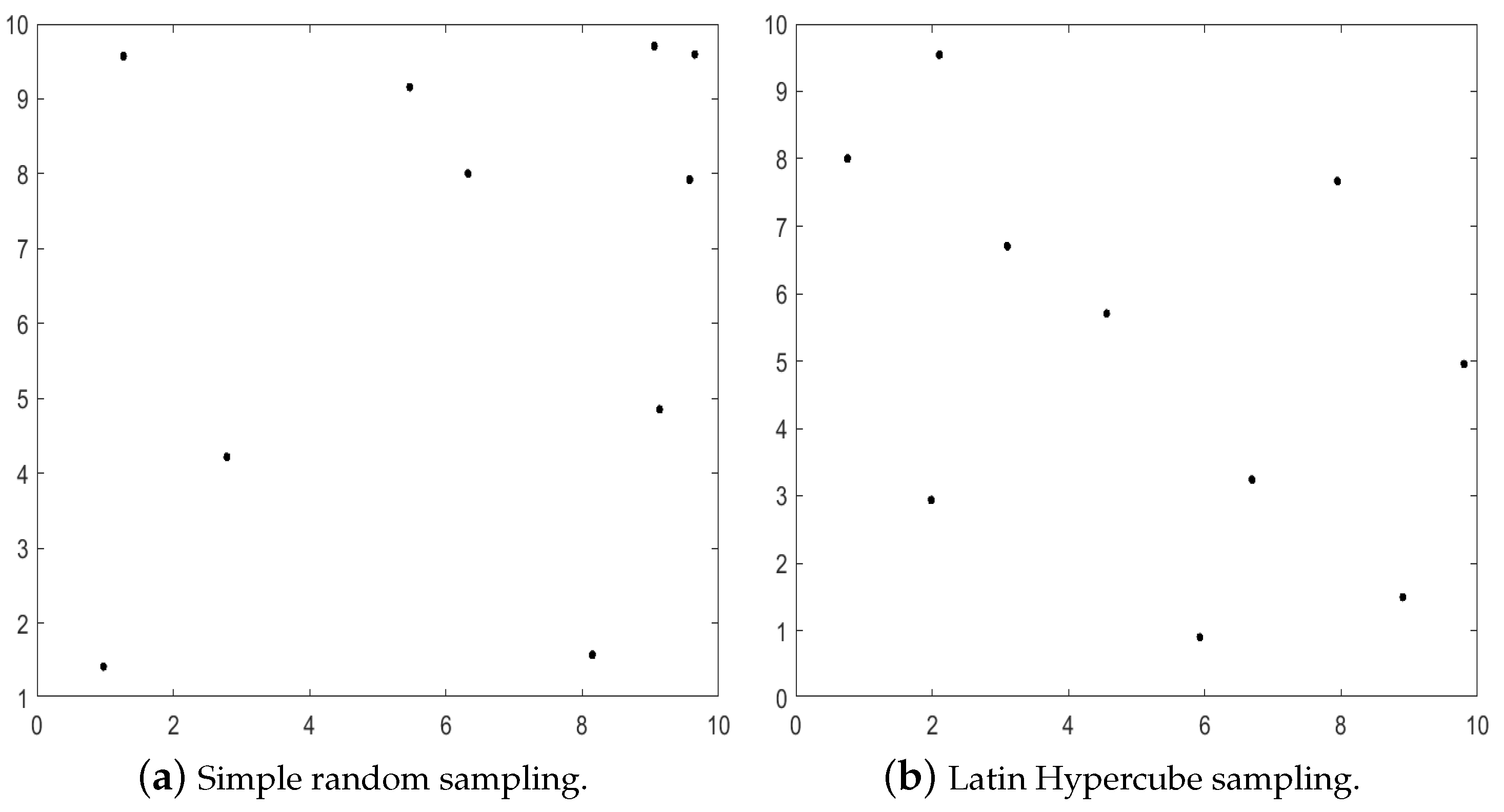
3.1. Population Initialization
3.1.1. Initialization Method
3.1.2. Encoding and Decoding
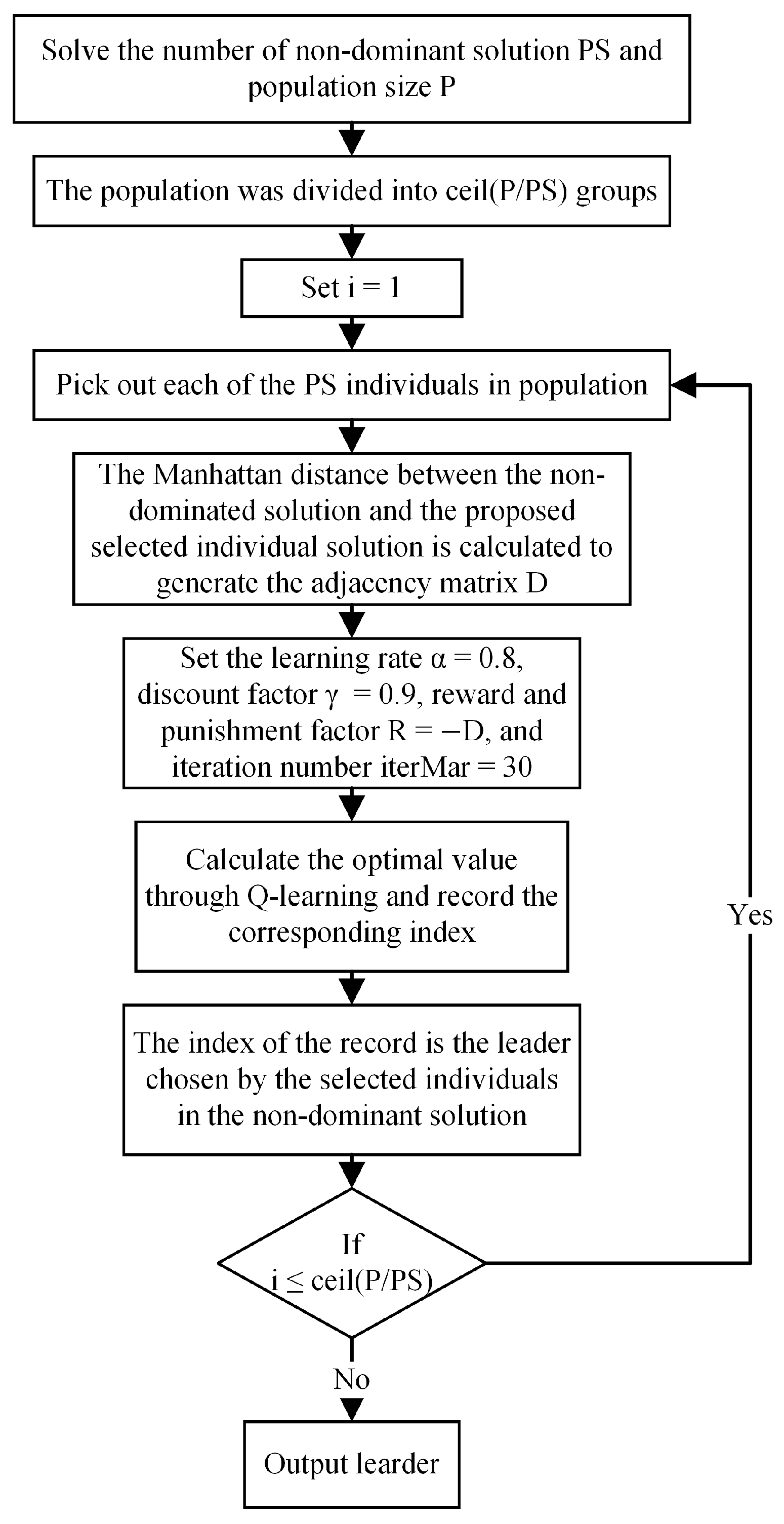
3.2. Leader Selection Strategy
3.3. Algorithm Discretization
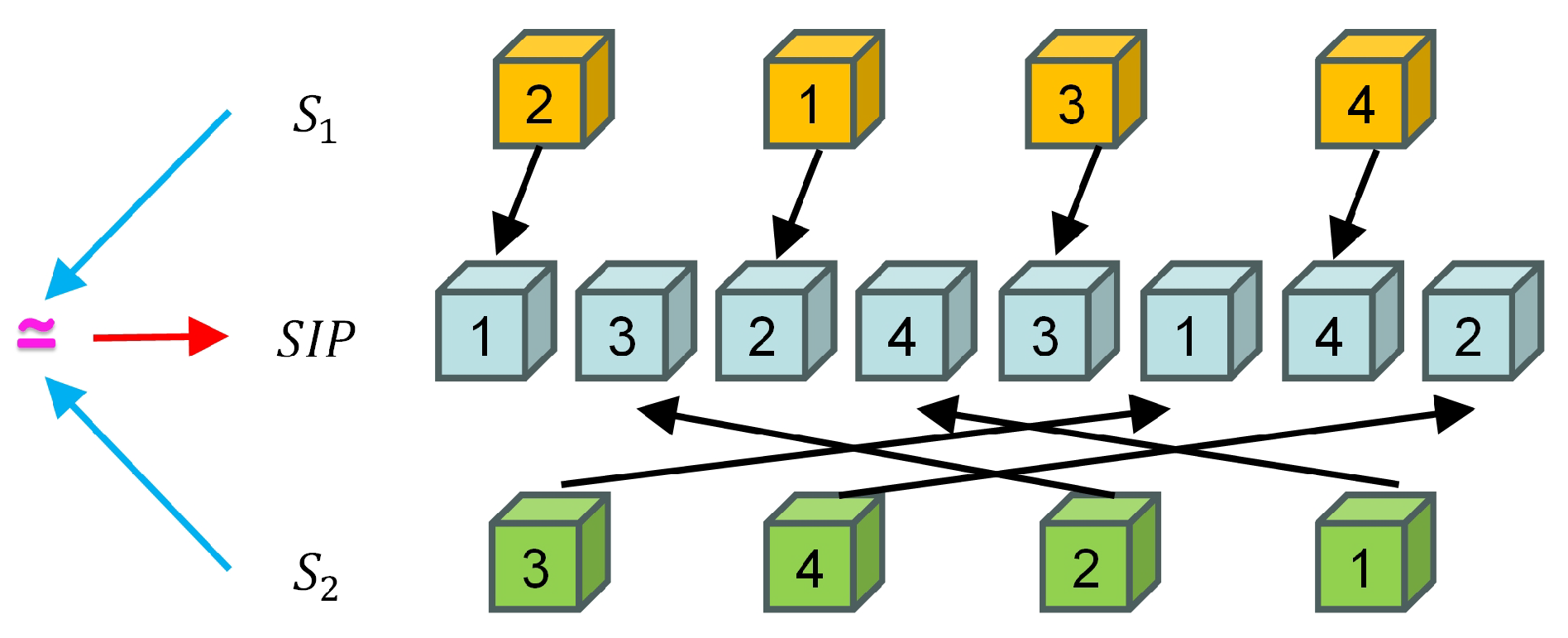
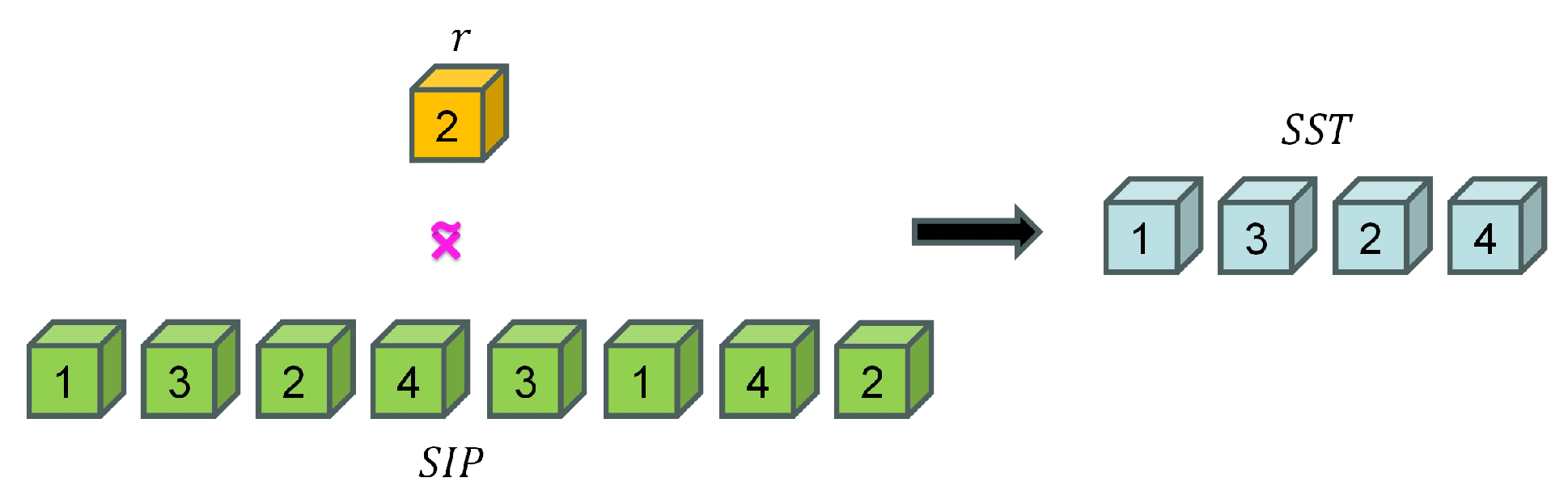
3.3.1. Swap Index Pair ()
3.3.2. Swap Section ()
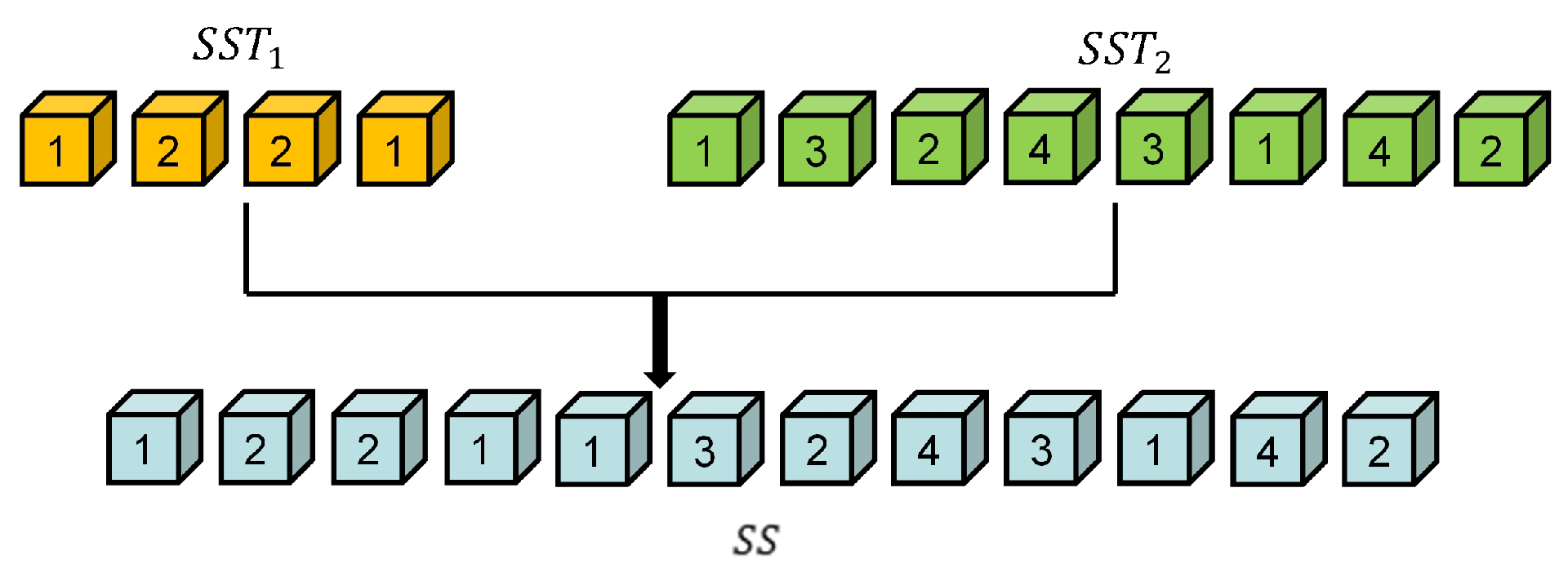
3.3.3. Swap Sequence ()
3.3.4. Swap Operation ()
3.4. Algorithm Implementation
| Algorithm 1 Improved multi-objective growth optimization algorithm |
|
4. Numerical Experiments
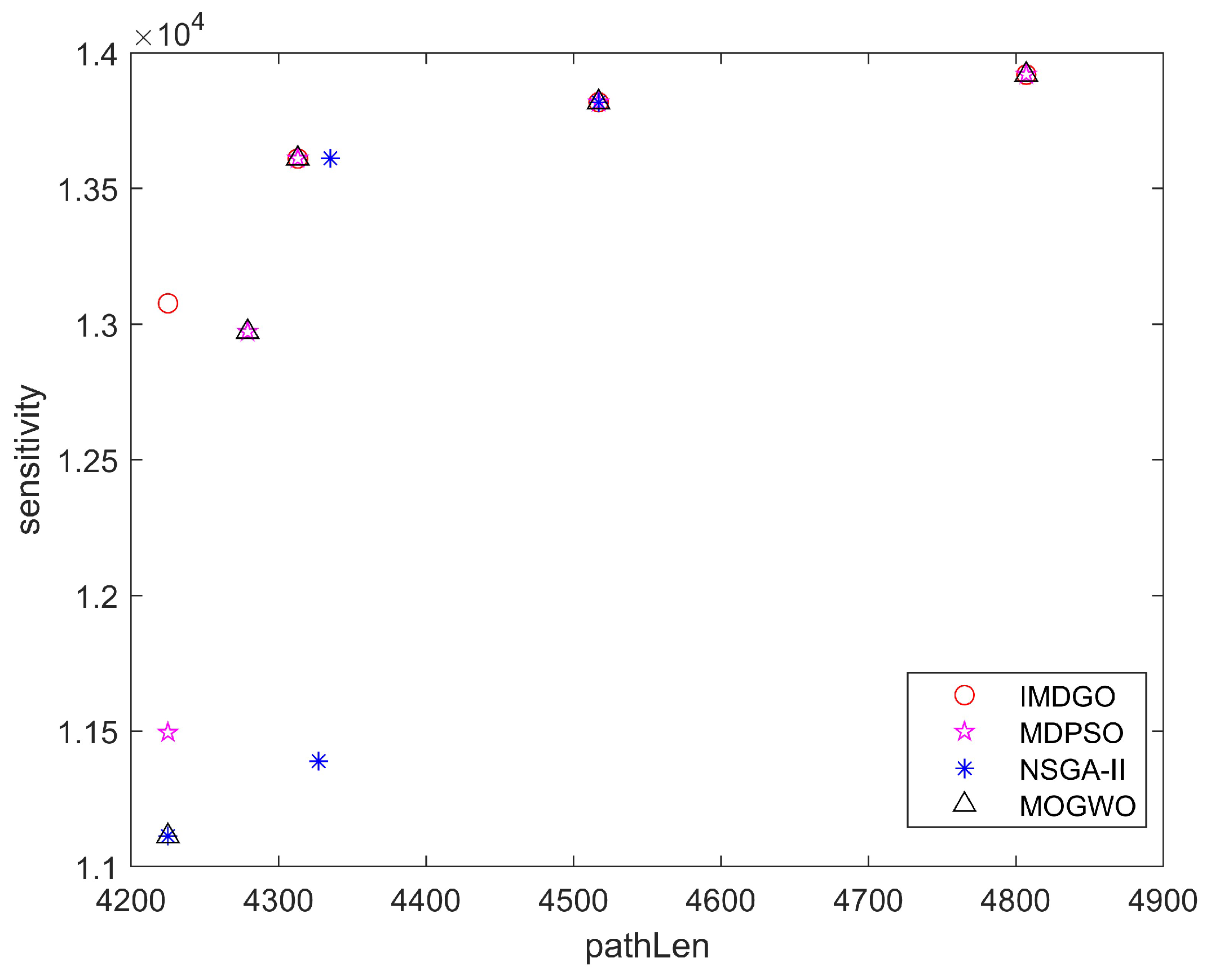
4.1. Numerical Computations
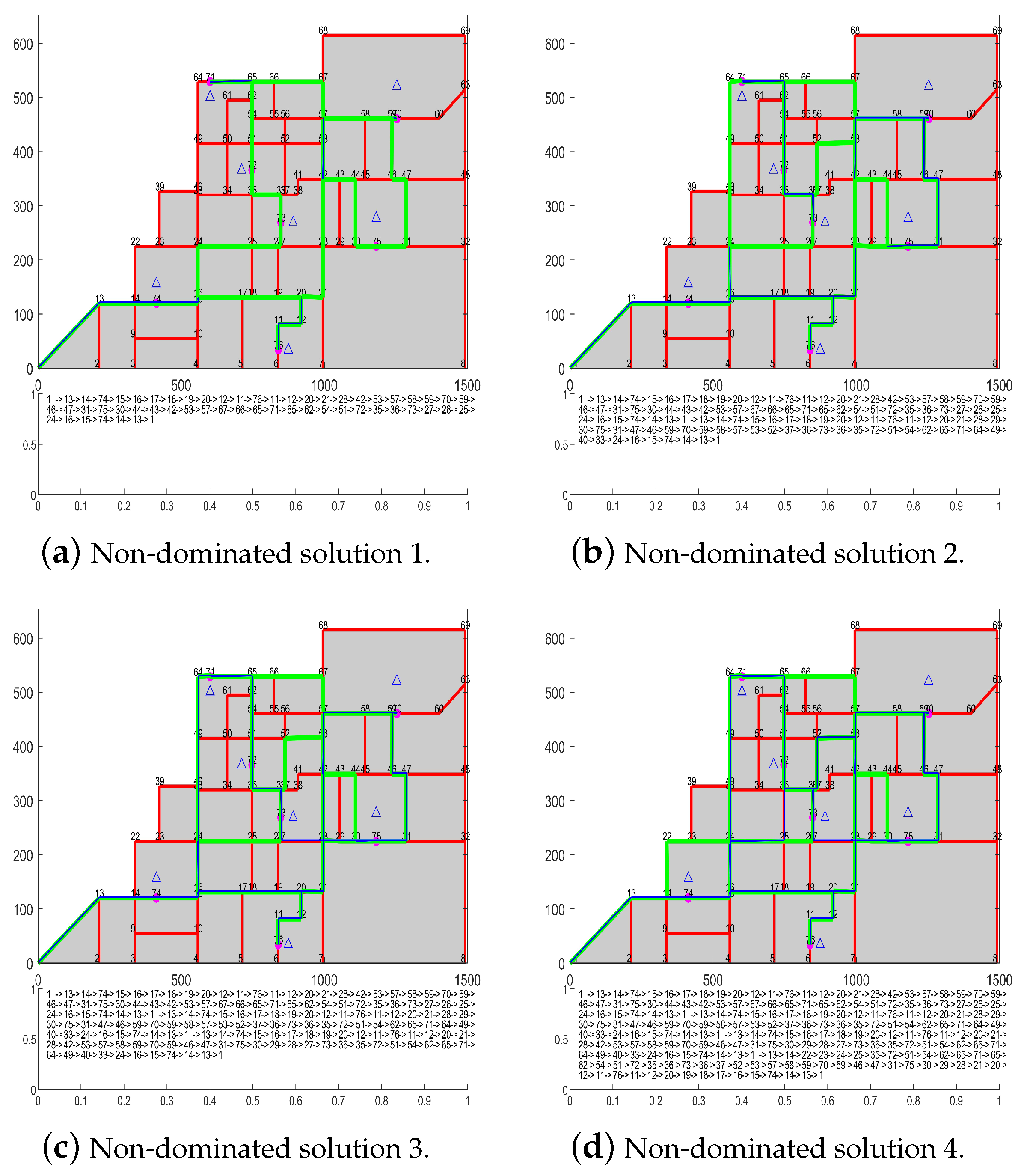
4.2. Inspection Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bai, M.; Qi, M.; Shu, C.; Reniers, G.; Khan, F.; Chen, C.; Liu, Y. Why do major chemical accidents still happen in china: Analysis from a process safety management perspective. Process Saf. Environ. Prot. 2023, 176, 411–420. [Google Scholar] [CrossRef]
- Vesentini, F.; Di, P.; Muradore, R. A Brownian–Markov stochastic model for cart-like wheeled mobile robots. Eur. J. Control 2023, 70, 100771. [Google Scholar] [CrossRef]
- Li, Y.; Chen, S.; Bai, K.; Wang, H. Path planning of patrol robot based on improved discrete electrostatic discharge algorithm. J. Intell. Fuzzy Syst. 2022, 42, 5919–5930. [Google Scholar] [CrossRef]
- Yu, J.; Zeng, Q.; Yu, Y.; Zhang, B.; Ding, H.; Ma, W.; Wu, S.; Li, Z. Safety barrier performance assessment based on multi-phase Markov model and EPN: Application to FPSO gas leakage. Ocean Eng. 2025, 323, 120597. [Google Scholar] [CrossRef]
- Alina, B.; Antonio, C.; Antonino, G.; Jiafu, W.; Maria, F. Evaluating an application aware distributed dijkstra shortest path algorithm in hybrid cloud/edge environments. IEEE Trans. Sustain. Comput. 2022, 7, 289–298. [Google Scholar]
- Liu, Q.; Wang, C. A graph-based pipe routing algorithm in aero-engine rotational space. J. Intell. Manuf. 2015, 26, 1077–1083. [Google Scholar] [CrossRef]
- Dam, T.; Chalvatzaki, G.; Peters, J.; Pajarinen, J. Monte-carlo robot path planning. IEEE Robot. Autom. Lett. 2020, 7, 11213–11220. [Google Scholar] [CrossRef]
- Rousseas, P.; Bechlioulis, C.; Kyriakopoulos, K. Harmonic-based optimal robot motion planning in constrained workspaces using reinforcement learning. IEEE Robot. Autom. Lett. 2021, 6, 2005–2011. [Google Scholar] [CrossRef]
- Chen, G.; Du, Y.; Xi, X.; Zhang, K.; Yang, J.; Xu, L.; Ren, C. Improved genetic algorithm based on bi-level co-evolution for coverage path planning in irregular region. Sci. Rep. 2025, 15, 10047. [Google Scholar] [CrossRef]
- Fang, S.; Deng, Z.; Li, P.; Long, D. Improved strategy of ant colony optimization for path planning via stochastic pheromone updating and cyclic initialization. J. Mech. Sci. Technol. 2025, 39, 2051–2062. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, W.; Zhang, Y.; Huang, N.; Zhang, Y.; Zhu, L. Distributed particle swarm optimization for the planning of time-optimal and interference-free five-axis sweep scanning path. IEEE Trans. Ind. Inform. 2022, 18, 8703–8713. [Google Scholar] [CrossRef]
- Liu, Q.; Jiao, G. A pipe routing method considering vibration for aero-engine using kriging model and NSGA-II. IEEE Access 2018, 6, 6286–6292. [Google Scholar] [CrossRef]
- Xie, X.; Tang, Z.; Cai, J. The multi-objective inspection path planning in radioactive environment based on an improved ant colony optimization algorithm. Prog. Nucl. Energy 2022, 144, 104076. [Google Scholar] [CrossRef]
- Zheng, H.; Lu, Y.; Jie, J.; Hou, B.; Zhang, M.; Zhang, Y. Gaussian adaptive strategy based multi-objective evolutionary optimization for path planning on uneven terrains. IEEE Robot. Autom. Lett. 2024, 9, 539–546. [Google Scholar] [CrossRef]
- Huang, C.; Sun, H.; Liu, C.; Zhang, X.; Gao, T.; Tian, J. Research on Container Multimodal Transportation Multi-Objective Path Optimization From Hinterlands to Shanghai Port. IEEE Access 2025, 13, 32794–32807. [Google Scholar] [CrossRef]
- Guo, X.; Fan, C.; Zhou, M.; Liu, S.; Wang, J.; Qin, S.; Tang, Y. Human-robot collaborative disassembly line balancing problem with stochastic operation time and a solution via multi-objective shuffled frog leaping algorithm. IEEE Trans. Autom. Sci. Eng. 2023, 21, 4448–4459. [Google Scholar] [CrossRef]
- Wei, H.; Zeng, G.; Lu, K.; Geng, G.; Weng, J. MoAR-CNN: Multi-Objective Adversarially Robust Convolutional Neural Network for SAR Image Classification. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 9, 1–18. [Google Scholar] [CrossRef]
- Li, X.; Ma, S. Multiobjective discrete artificial bee colony algorithm for multiobjective permutation flow shop scheduling problem with sequence dependent setup times. IEEE Trans. Eng. Manag. 2017, 64, 149–165. [Google Scholar] [CrossRef]
- Xu, X.; Xie, C.; Ma, L.; Yang, L.; Zhang, T. mMulti-objective evolutionary algorithm with two balancing mechanisms for heterogeneous UAV swarm path planning. Appl. Soft Comput. 2025, 173, 112927. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, H.; Zhan, Z.; Li, J.; Zhang, H. Growth optimizer: A powerful metaheuristic algorithm for solving continuous and discrete global optimization problems. Knowl.-Based Syst. 2023, 261, 110206. [Google Scholar] [CrossRef]
- Ben Aribia, H.; El-Rifaie, A.; Tolba, M.; Shaheen, A.; Moustafa, G.; Elsayed, F.; Elshahed, M. Growth optimizer for parameter identification of solar photovoltaic cells and modules. Sustainability 2023, 15, 7896. [Google Scholar] [CrossRef]
- Fatani, A.; Dahou, A.; Abd Elaziz, M.; Al-qaness, M.; Lu, S.; Alfadhli, S.; Alresheedi, S. Enhancing Intrusion Detection Systems for IoT and Cloud Environments Using a Growth Optimizer Algorithm and Conventional Neural Networks. Sensors 2023, 23, 4430. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Zhang, L.; Yinga, A.; Qiao, J. Adaptive multiple selection strategy for multi-objective particle swarm optimization. Inf. Sci. 2023, 624, 235–251. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Han, H.; Zhang, X.; Shu, X.; Chen, F. A two-stage maintenance and multi-strategy selection for multi-objective particle swarm optimization. Complex Intell. Syst. 2023, 9, 7523–7548. [Google Scholar] [CrossRef]
- Zhou, Y.; Ding, X.; Hu, Y. Research on method for locating ammonia leak source and development of related monitoring. China Saf. Sci. J. 2016, 26, 163–168. [Google Scholar]
- Asef, P.; Denai, M.; Paulides, J.; Marques, B.; Lapthorn, A. A novel multi-criteria local latin hypercube refinement system for commutation angle improvement in IPMSMs. IEEE Trans. Ind. Appl. 2022, 59, 1588–1602. [Google Scholar] [CrossRef]
- Guo, X.; Bi, Z.; Wang, J.; Qin, S. Reinforcement learning for disassembly system optimization problems: A survey. Int. J. Netw. Dyn. Intell. 2023, 2, 1–14. [Google Scholar] [CrossRef]
- Wang, K.; Huang, L.; Zhou, C.; Pang, W. Particle swarm optimization for traveling salesman problem. In Proceedings of the 2003 International Conference on Machine Learning and Cybernetics, Xi’an, China, 5 November 2003; Volume 3, pp. 1583–1585. [Google Scholar]
- Xu, X.; Li, J.; Zhou, M. Bi-objective colored traveling salesman problems. IEEE Trans. Intell. Transp. Syst. 2022, 23, 6326–6336. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Liu, R.; Du, B.; Zhang, L. Multiobjective optimized endmember extraction for hyperspectral image. Remote Sens. 2017, 9, 558. [Google Scholar] [CrossRef]
- Lu, K.; Wu, Z. Multi-Objective False Data Injection Attacks of Cyber–Physical Power Systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3924–3928. [Google Scholar] [CrossRef]
- Wei, L.; Cai, Z.; Zhou, K. Multi-objective Gray Wolf Optimization Algorithm for Multi-agent Pathfinding Problem. In Proceedings of the 2022 IEEE 5th International Conference on Electronics Technology (ICET), Chengdu, China, 13–16 May 2022. [Google Scholar]



| Case | P | |||||||||
| Best | Mean | Worst | Best | Mean | Worst | Best | Mean | Worst | ||
| 10 | 100 | 1 | 0.72917 | 0.3333 | 0.5000 | 0.17818 | 0 | 1 | 0.57695 | 0.1000 |
| 120 | 1 | 0.81970 | 0.3636 | 0.3333 | 0.05492 | 0 | 0.8 | 0.52434 | 0.1111 | |
| 150 | 0.9 | 0.74432 | 0.6000 | 0.3333 | 0.18102 | 0 | 0.8333 | 0.44265 | 0.1250 | |
| 15 | 100 | 1 | 0.95714 | 0.5714 | 0.1667 | 0.01667 | 0 | 1 | 0.55071 | 0.1000 |
| 120 | 1 | 0.86515 | 0.3333 | 0.1667 | 0.01667 | 0 | 1 | 0.74210 | 0.5000 | |
| 150 | 1 | 0.96071 | 0.7500 | 0.0909 | 0.00909 | 0 | 1 | 0.69476 | 0.2500 | |
| 20 | 100 | 1 | 0.95500 | 0.7500 | 0 | 0 | 0 | 1 | 0.65790 | 0.2500 |
| 120 | 1 | 0.94205 | 0.7273 | 0 | 0 | 0 | 1 | 0.71879 | 0.0909 | |
| 150 | 1 | 0.95953 | 0.6667 | 0 | 0 | 0 | 1 | 0.60493 | 0.2000 | |
| Case | P | |||||||||
| Best | Mean | Worst | Best | Mean | Worst | Best | Mean | Worst | ||
| 10 | 100 | 0.6000 | 0.09333 | 0 | 1 | 0.61638 | 0.3000 | 0.7500 | 0.31548 | 0 |
| 120 | 0.5000 | 0.10833 | 0 | 0.8571 | 0.45857 | 0.1818 | 0.7143 | 0.45286 | 0 | |
| 150 | 0.5000 | 0.17333 | 0 | 0.8333 | 0.46781 | 0.1250 | 0.7500 | 0.36523 | 0 | |
| 15 | 100 | 0.8000 | 0.14666 | 0 | 1 | 0.6975 | 0.1250 | 0.8333 | 0.26444 | 0 |
| 120 | 0.2000 | 0.03667 | 0 | 1 | 0.60146 | 0.2500 | 0.3571 | 0.15904 | 0 | |
| 150 | 0.3333 | 0.05333 | 0 | 1 | 0.76547 | 0.2857 | 0.6667 | 0.14667 | 0 | |
| 20 | 100 | 0.6667 | 0.06667 | 0 | 1 | 0.67666 | 0.2857 | 0.5000 | 0.12732 | 0 |
| 120 | 0.5000 | 0.05000 | 0 | 1 | 0.76505 | 0.3750 | 0.2000 | 0.03547 | 0 | |
| 150 | 0.6667 | 0.09167 | 0 | 1 | 0.90051 | 0.6364 | 0 | 0 | 0 |
| Case | P | IMDGO | MDPSO | NSGA-II | MOGWO | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Mean | Worst | Best | Mean | Worst | Best | Mean | Worst | Best | Mean | Worst | ||
| 10 | 100 | 0.0454 | 0.10813 | 0.1983 | 0.0462 | 0.12620 | 0.2709 | 0 | 0.13778 | 0.4113 | 0.0533 | 0.12640 | 0.2562 |
| 120 | 0.0304 | 0.10472 | 0.2191 | 0.0519 | 0.10875 | 0.2329 | 0 | 0.17185 | 0.4928 | 0.0467 | 0.14595 | 0.2670 | |
| 150 | 0.0117 | 0.09871 | 0.1626 | 0.0326 | 0.11701 | 0.2202 | 0.0272 | 0.10854 | 0.3 | 0.0667 | 0.10553 | 0.1636 | |
| 15 | 100 | 0.0282 | 0.06374 | 0.1078 | 0.0545 | 0.15411 | 0.2880 | 0 | 0.12552 | 0.4524 | 0.0482 | 0.08728 | 0.1427 |
| 120 | 0.0038 | 0.07577 | 0.1274 | 0.0480 | 0.11275 | 0.2070 | 0 | 0.07860 | 0.3353 | 0.0275 | 0.08407 | 0.1829 | |
| 150 | 0.0363 | 0.09315 | 0.1790 | 0.0525 | 0.11346 | 0.2094 | 0 | 0.12093 | 0.6115 | 0.0278 | 0.09655 | 0.2297 | |
| 20 | 100 | 0.0094 | 0.07943 | 0.2316 | 0.0321 | 0.12548 | 0.2561 | 0 | 0.13098 | 0.3976 | 0.0225 | 0.15674 | 0.9260 |
| 120 | 0.0284 | 0.07961 | 0.1369 | 0.0545 | 0.10837 | 0.1825 | 0 | 0.11885 | 0.4044 | 0.0345 | 0.08847 | 0.1687 | |
| 150 | 0.0377 | 0.08289 | 0.1655 | 0.0598 | 0.09533 | 0.2194 | 0 | 0.11439 | 0.3981 | 0.0395 | 0.09748 | 0.2134 |
| PS Obtained | ||
|---|---|---|
| Non-dominated solution 1 | 4225 | 13076 |
| Non-dominated solution 2 | 4313 | 13610 |
| Non-dominated solution 3 | 4517 | 13817 |
| Non-dominated solution 4 | 4807 | 13919 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, S.; Liu, Q.; Guo, X.; Yin, M.; Li, Z.; Lang, X. Chemical Safety Inspection Path Optimization Problems Using Improved Multi-Objective Discrete Growth Optimization Algorithm. Processes 2025, 13, 1445. https://doi.org/10.3390/pr13051445
Luo S, Liu Q, Guo X, Yin M, Li Z, Lang X. Chemical Safety Inspection Path Optimization Problems Using Improved Multi-Objective Discrete Growth Optimization Algorithm. Processes. 2025; 13(5):1445. https://doi.org/10.3390/pr13051445
Chicago/Turabian StyleLuo, Shanshan, Qiang Liu, Xiwang Guo, Mingqiang Yin, Zhiwu Li, and Xianming Lang. 2025. "Chemical Safety Inspection Path Optimization Problems Using Improved Multi-Objective Discrete Growth Optimization Algorithm" Processes 13, no. 5: 1445. https://doi.org/10.3390/pr13051445
APA StyleLuo, S., Liu, Q., Guo, X., Yin, M., Li, Z., & Lang, X. (2025). Chemical Safety Inspection Path Optimization Problems Using Improved Multi-Objective Discrete Growth Optimization Algorithm. Processes, 13(5), 1445. https://doi.org/10.3390/pr13051445




