Effect of Process Parameters on Metallurgical Behavior of Liquid Steel in a Thickened Compact Strip Production Mold with Electromagnetic Braking
Abstract
1. Introduction
2. Mathematical Model and Computational Conditions
2.1. Basic Assumptions
- (1)
- Regarding the liquid steel as an incompressible Newtonian fluid with constant physical properties [20].
- (2)
- Disregarding the influence of oscillation and negative taper of the mold [14].
- (3)
- Neglecting the effects of solidification shrinkage and liquid core reduction on flow and heat transfer [25].
- (4)
- Ignoring the effects of mold flux and its surface tension on meniscus flow [26].
2.2. Mathematical Formulation
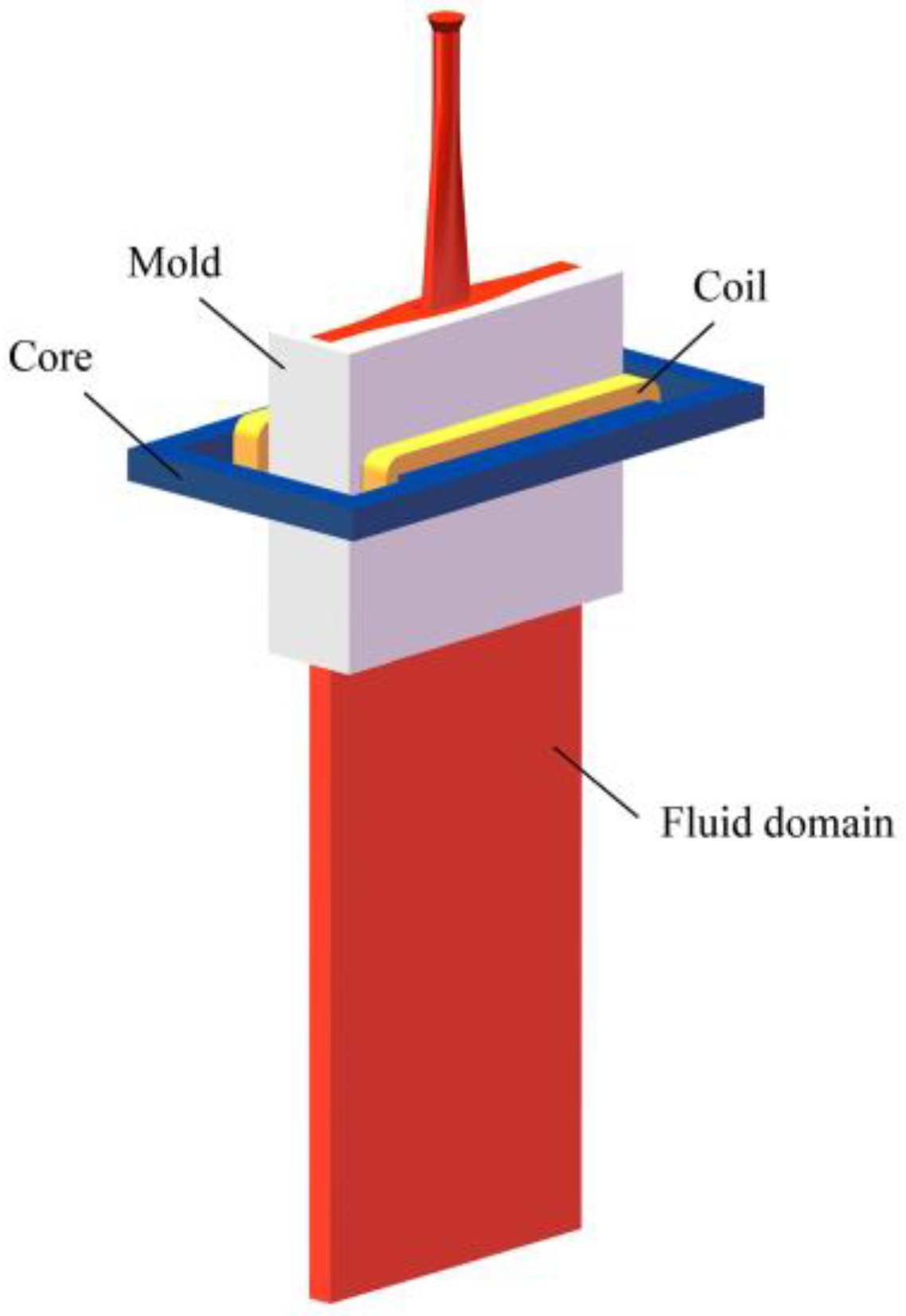
2.3. Geometric Model and Mesh Division
2.4. Boundary Conditions
2.5. Model Validation
3. Results and Discussion
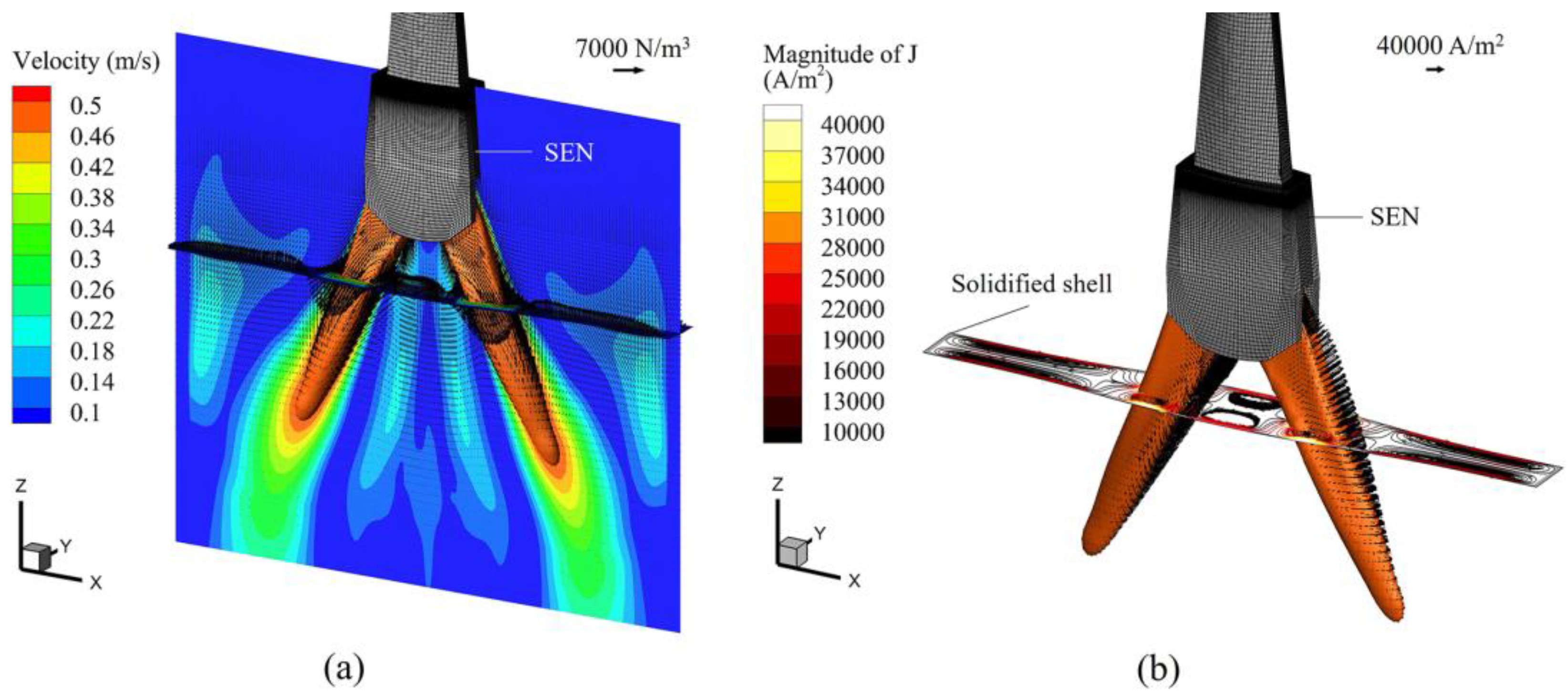
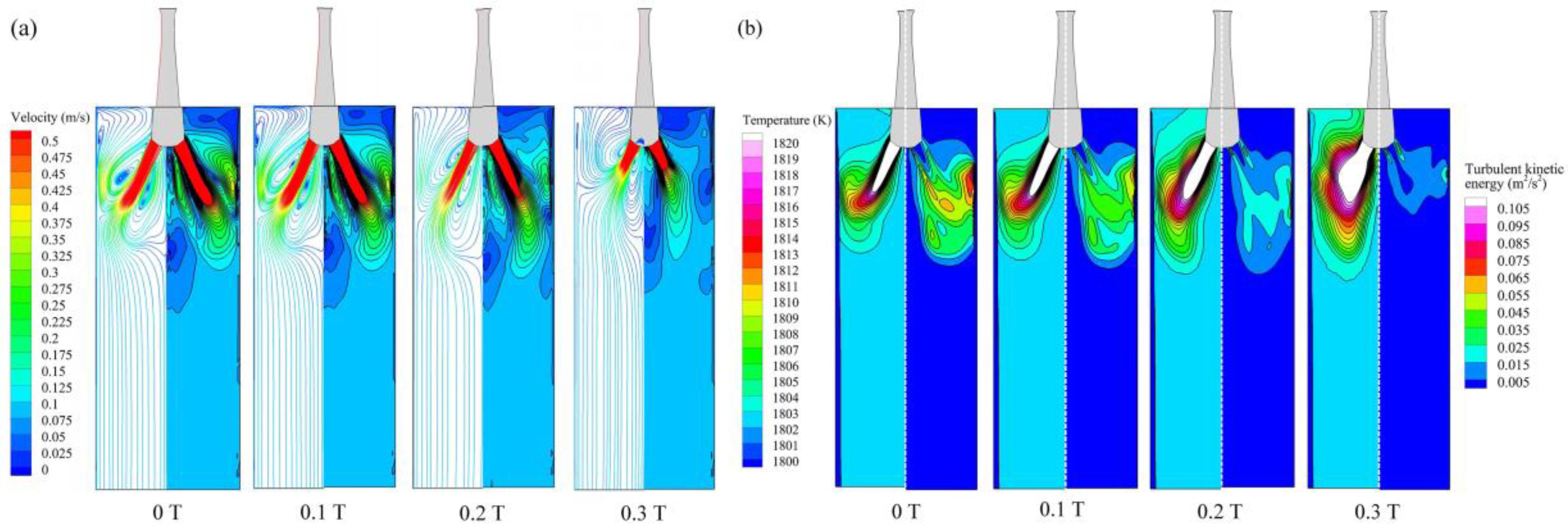
3.1. Electromagnetic Field in CSP Mold with EMBr
3.2. Typical Metallurgical Characteristics of Liquid Steel in CSP Mold with EMBr
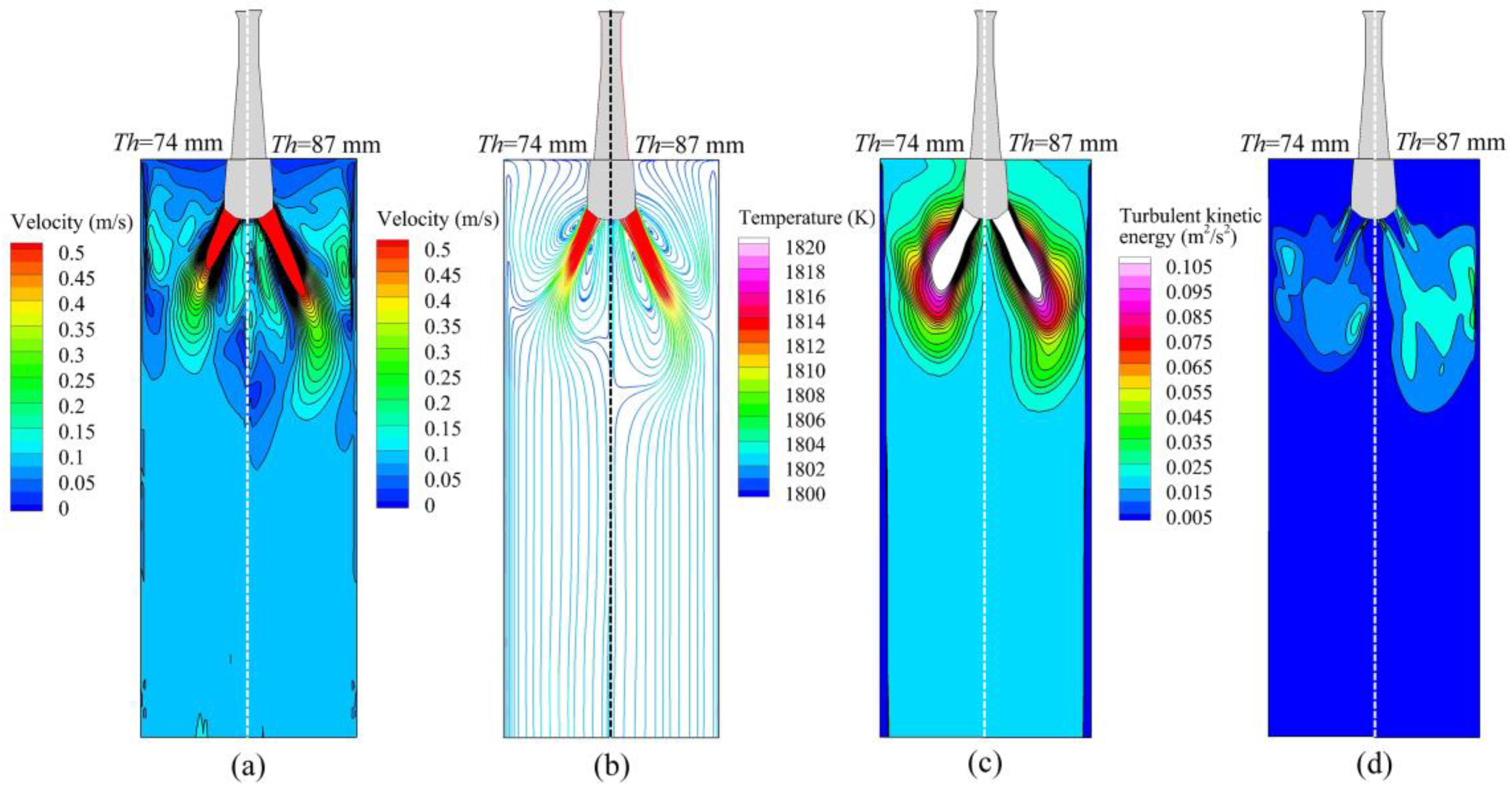
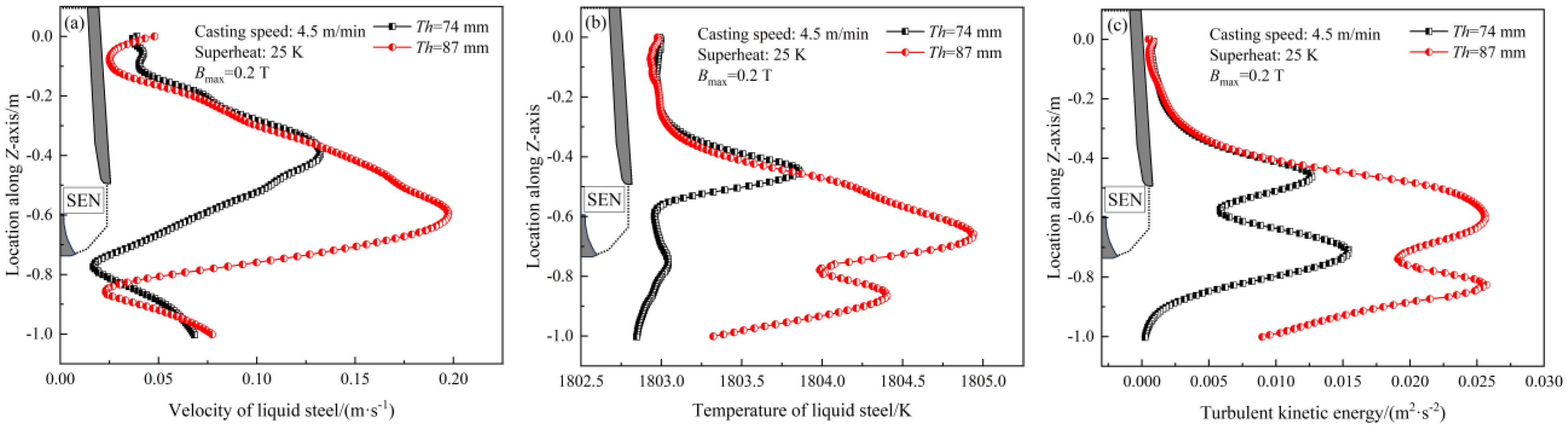
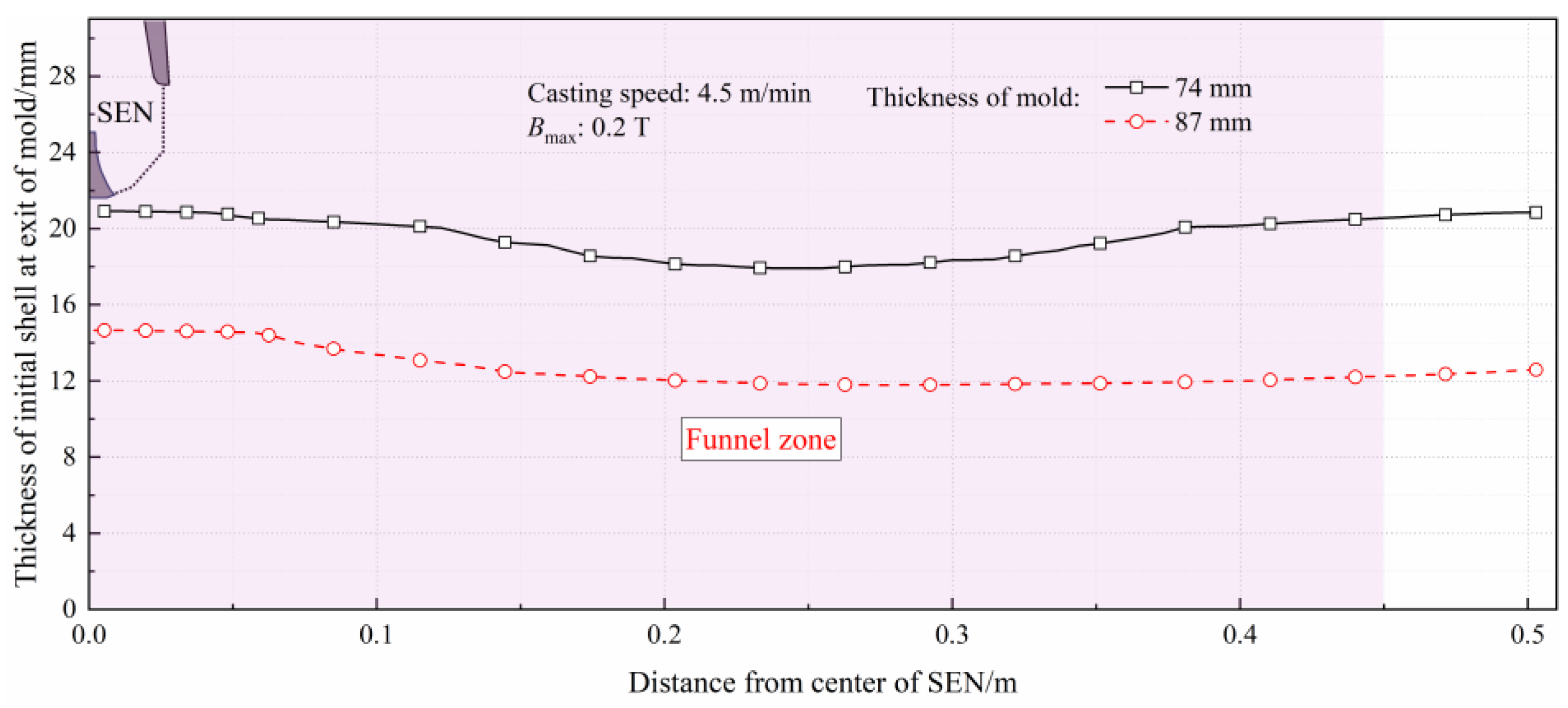
3.3. Comparison of Metallurgical Behavior of Liquid Steel in Thin Slab Molds with Different Thicknesses
3.4. Effect of Process Parameters on Metallurgical Behavior of Liquid Steel in Thin Slab Mold with EMBr
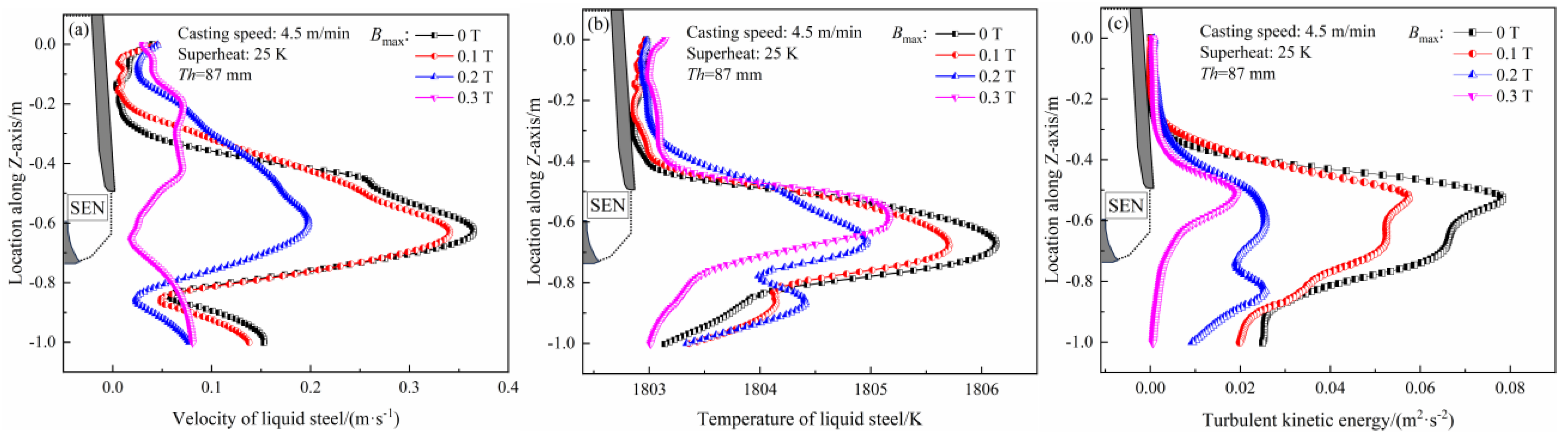
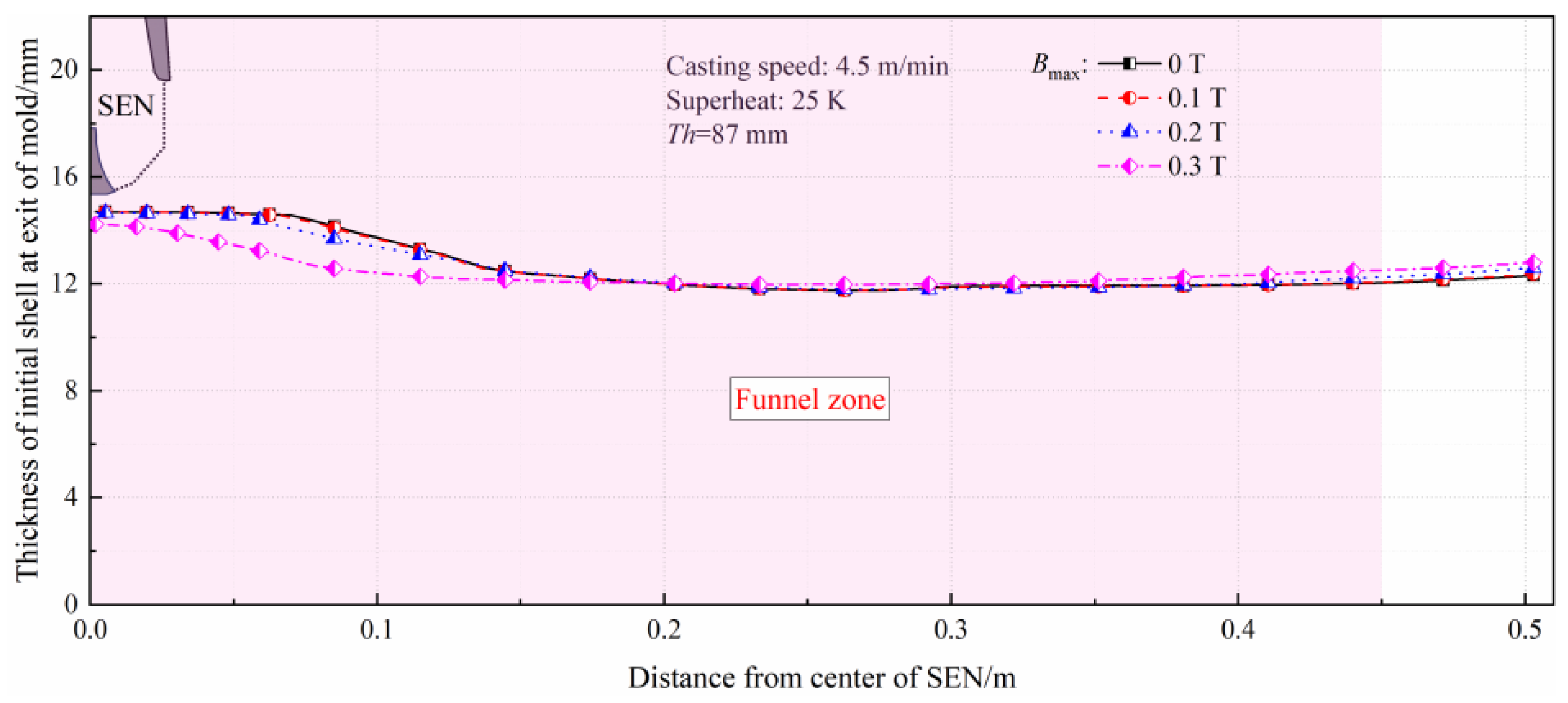
3.4.1. Effect of Electromagnetic Intensity
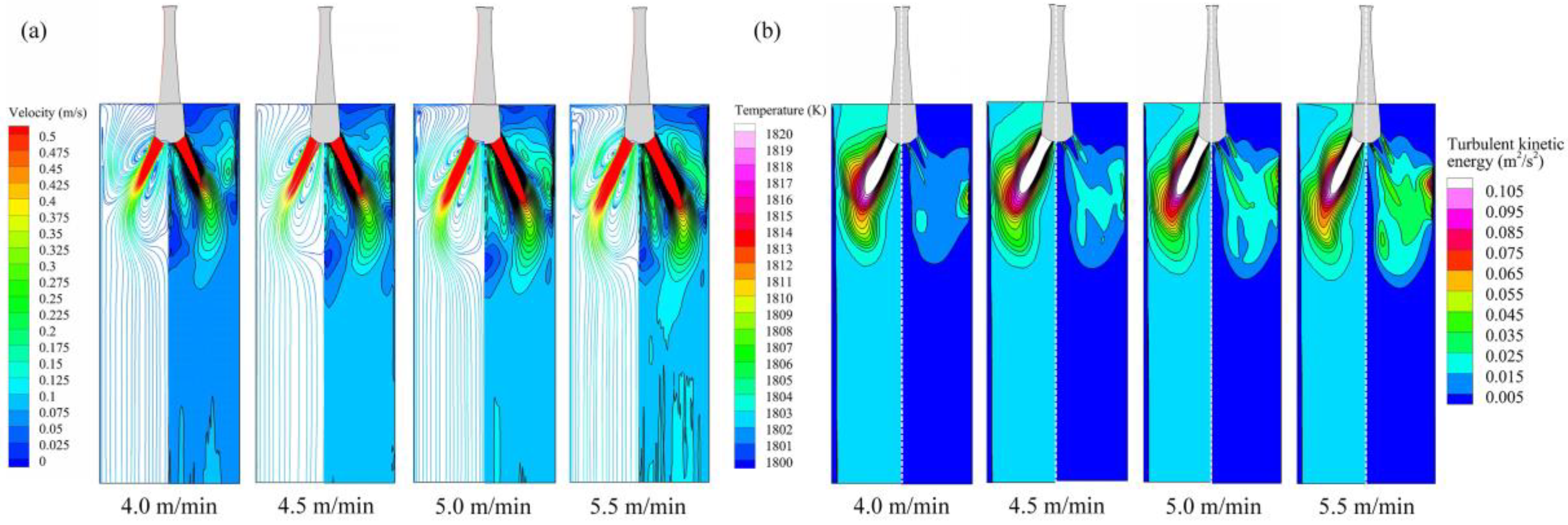
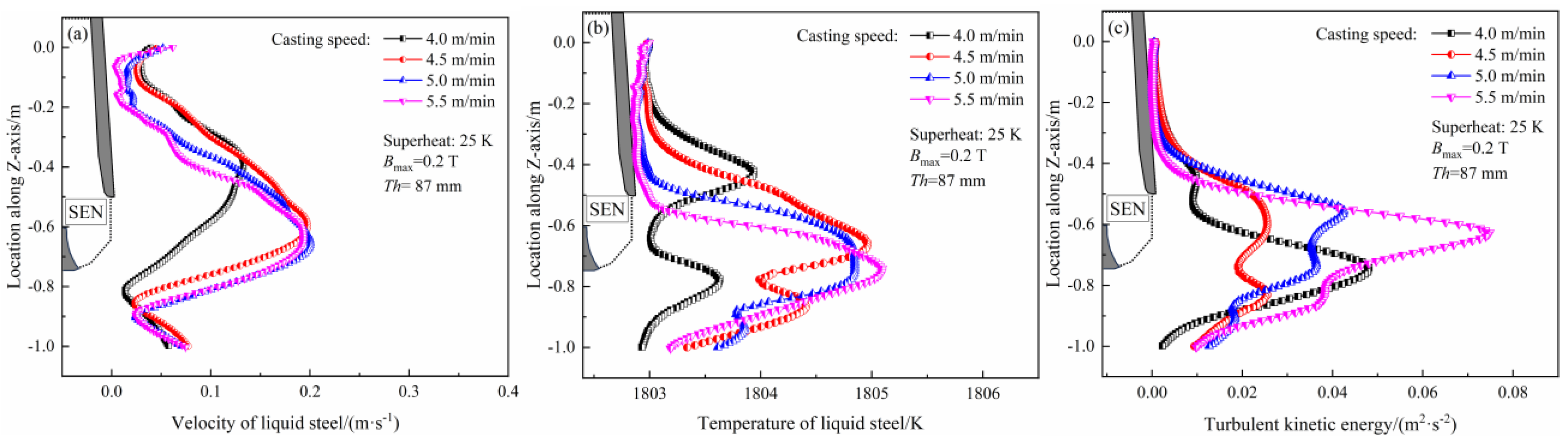
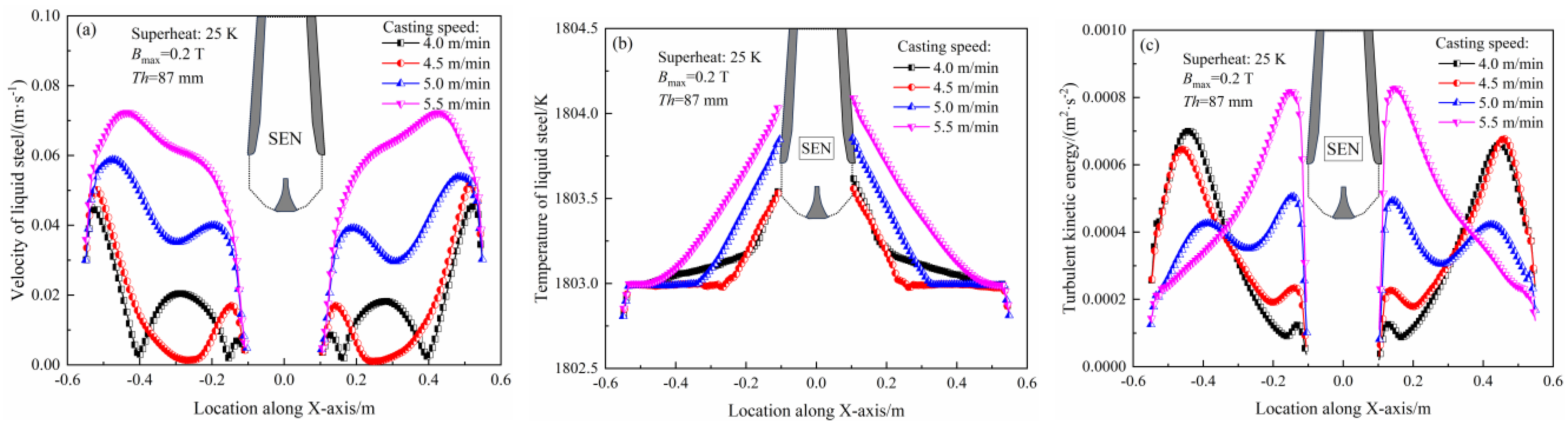
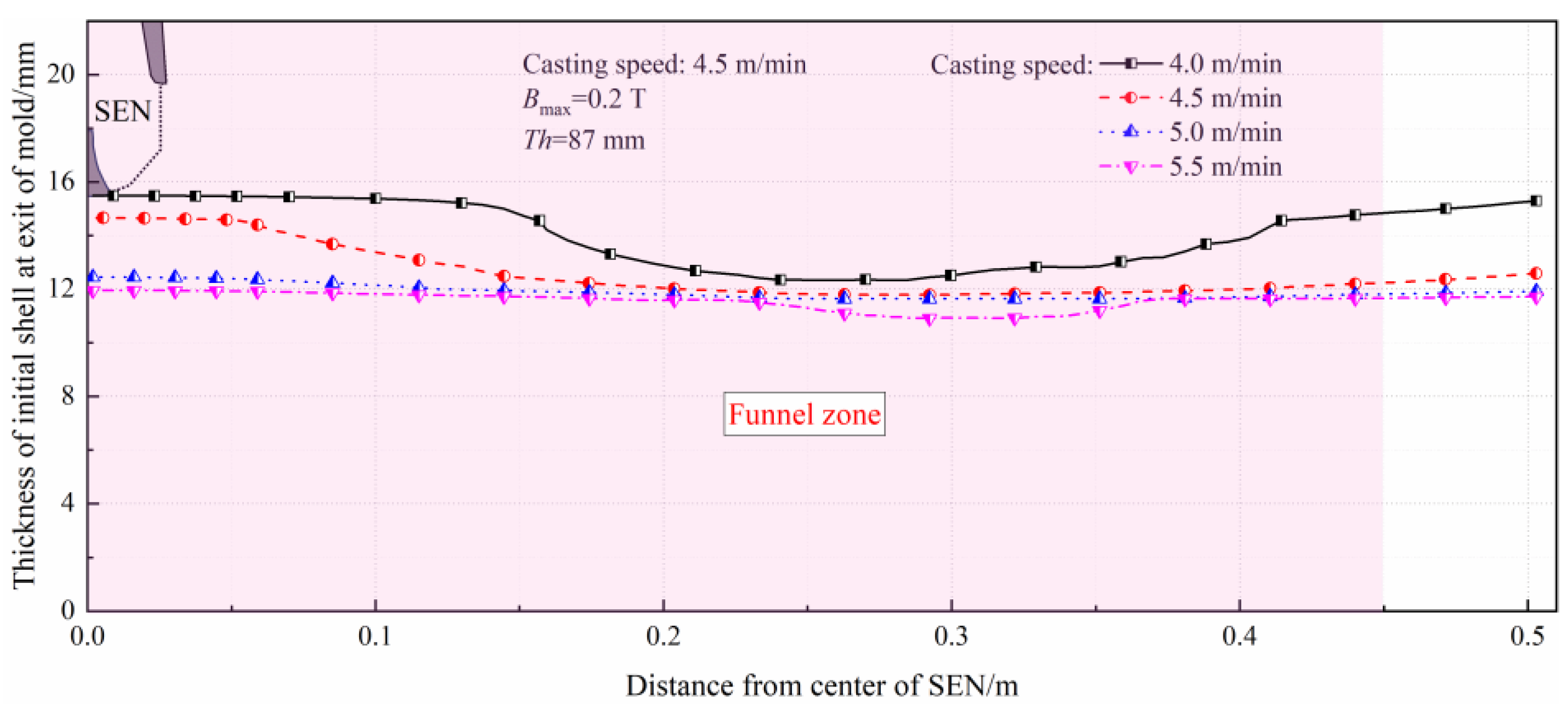
3.4.2. Effect of Casting Speed
4. Conclusions
- (1)
- The solidification shell is thickest near the nozzle center and thinner in the jet penetration region 0.2~0.3 m away from the nozzle. An obvious change in shell thickness is observed within the range of 0.05~0.15 m from the nozzle. In addition, a relatively large Lorentz force opposite to the main jet direction is found near the solidified shell in the jet penetration region, corresponding to a stress magnitude of 38.4 Pa at the solidified front.
- (2)
- When the mold thickness increases from 74 mm to 87 mm, the maximum meniscus velocity and turbulence kinetic energy increase, and the penetration depth increases from 1.12 m to 1.35 m. In addition, the high-temperature penetration zone moves downwards overall, which will increase the superheat at the solidification front and the proportion of columnar crystals. The shell thickness thins, and the average thickness of the solidified shell drops from 19.73 to 12.83 mm, with the non-uniformity coefficient λ increasing from 15.23% to 22.34%.
- (3)
- For the 87 mm-thickened mold, as the magnetic flux density increases, the velocity near the narrow faces and meniscus decreases, and the average thickness of the solidified shell decreases with a more uniform distribution. Increasing the casting speed results in a deeper penetration depth, a larger meniscus velocity and temperature, and a more uniform shell thickness at the mold exit. The lowest non-uniformity coefficient and standard deviation of the solidified shell is obtained at a casting speed of 5.0 m/min, with values of 6.78% and 0.30, respectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, S.; Gao, J.; Wu, G.; Mao, X. Thin slab casting and direct rolling technology: Current status and prospects. Chin. J. Eng. 2022, 44, 534–545. (In Chinese) [Google Scholar]
- Lu, X.; Li, H.; Liu, G.; Yang, W. Influence of different entry nozzle on flow patterns in the CSP mold. J. Iron Steel Res. Int. 2008, 15, 105–109. [Google Scholar]
- Nie, C.; Zhang, X.; Wang, B.; Sun, Y.; Liu, Q. Characteristics of inclusion motion and accumulation in CSP mold. ISIJ Int. 2015, 55, 1677–1683. [Google Scholar] [CrossRef]
- Liu, R.; Blazek, K.; Forman, B.; Fritz, C.; Graham, C. Effect of submerged-entry nozzle (SEN) design on fluid flow and heat transfer in a thin-slab steel caster. Steel Res. Int. 2019, 90, 1800398. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Tao, H.; Zhang, H. Numerical analysis of local heat flux and thin-slab solidification in a CSP funnel-type mold with electromagnetic braking. Metall. Res. Technol. 2020, 117, 602. [Google Scholar] [CrossRef]
- Zong, N.; Liu, Y.; Zhang, H. Application of chamfered narrow face mold technology to reduce longitudinal surface crack defects of hyperperitectic steel generated during flexible thin slab casting process. Metall. Res. Technol. 2017, 114, 413. [Google Scholar] [CrossRef]
- Ramacciotti, A. Thermo-mechanical behaviour of the solidified shell in a “funnel-shaped” mold for continuous casting of thin slabs. Steel Res. 1988, 59, 438–448. [Google Scholar] [CrossRef]
- Garcia-Hernandez, S.; Gonzalez-Guzman, C.H.; Morales, D.R.; Barreto, J.J.; Gutierrez, E.; Calderon-Ramos, I. Modeling study of EMBr effects on the detrimental dynamic distortion phenomenon in a funnel thin slab mold. Crystals 2020, 10, 958. [Google Scholar] [CrossRef]
- Tian, X.; Zou, F.; Li, B.; He, J. Numerical analysis of coupled fluid flow, heat transfer and macroscopic solidification in the thin slab funnel shape mold with a new type EMBr. Metal. Mater. Trans. B. 2010, 41, 112–120. [Google Scholar] [CrossRef]
- Yamamura, H.; Toh, T.; Harada, H.; Takeuchi, E.; Ishii, T. Optimum magnetic flux density in quality control of casts with level DC magnetic field in continuous casting mold. ISIJ Int. 2001, 41, 1229–1235. [Google Scholar] [CrossRef]
- Idogawa, A.; Sugizawa, M.; Takeuchi, S.; Sorimachi, K.; Fujii, T. Control of molten steel flow in continuous casting mold by two static magnetic fields imposed on whole width. Mat. Sci. 1993, 173, 293–297. [Google Scholar] [CrossRef]
- Jayakrishna, P.; Chakraborty, S.; Ganguly, S.; Talukdar, P. Numerical investigation on role of vertical electromagnetic brake system in reducing remelting effect and improving thermal characteristics in thin slab continuous casting. Int. J. Therm. 2023, 192, 108434. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, L.; Bao, Y.; Ma, D.; Wang, E. Numerical simulation of the effects of horizontal and vertical EMBr on jet flow and mold level fluctuation in continuous casting. Metal. Mater. Trans. B 2022, 53, 938–953. [Google Scholar] [CrossRef]
- Xu, L.; Karcher, C.; Wang, E. Numerical simulation of melt flow, heat transfer and solidification in CSP continuous casting mold with vertical-combined electromagnetic braking. Metall. Res. Technol. 2023, 54, 1646–1664. [Google Scholar] [CrossRef]
- Singh, R.; Thomas, B.G.; Vanka, S.P. Large eddy simulations of double-ruler electromagnetic field effect on transient flow during continuous casting. Metal. Mater. Trans. B 2014, 45, 1098–1115. [Google Scholar] [CrossRef]
- Xu, L.; Tang, M.; Lyu, Z.; Li, N.; Liu, C.; Pei, Q. Influence of operating parameters on metal flow and thermal characteristics in an EMBr-single-ruler controlled CSP funnel-shaped mould. Metal. Mater. Trans. B 2024, 121, 316. [Google Scholar] [CrossRef]
- Cui, H.; Sun, J.; Zhang, J.; Ji, C.; Wang, G.; Liu, Q. Large eddy simulation of novel EMBr effect on flow pattern in thin slab casting mold with multi-port SEN and ultra-high casting speed. J. Manuf. Process. 2025, 133, 448–465. [Google Scholar] [CrossRef]
- Liu, H.; Yang, C.; Zhang, H.; Zhai, Q.; Gan, Y. Numerical simulation of fluid flow and thermal characteristics of thin slab in the funnel-type molds of two casters. ISIJ Int. 2011, 51, 392–401. [Google Scholar] [CrossRef]
- Chaudhary, R.; Thomas, B.G.; Vanka, S.P. Effect of electromagnetic ruler braking (EMBr) on transient turbulent flow in continuous slab casting using large eddy simulations. Metal. Mater. Trans. B 2012, 43, 532–553. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, X.; Wang, B.; Liu, Q.; Hu, Z. Numerical analysis of the influences of operational parameters on the braking effect of EMBr in a CSP funnel-type mold. Metal. Mater. Trans. B 2014, 45, 295–306. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Z.; Li, B. Effect of the intensity of single-ruler electromagnetic braking on the flow pattern in a thin-slab funnel mold. Metal. Mater. Trans. B 2023, 54, 3438–3450. [Google Scholar] [CrossRef]
- Greis, B.; Bahrmann, R.; Rueckert, A.; Pfeifer, H. Investigations of flow pattern in the SEN regarding different stopper rod geometries. Steel Res. Int. 2015, 86, 1469–1479. [Google Scholar] [CrossRef]
- Fu, Y.; Yuan, G.; Wang, G.; Mao, Q. Study on the inverse problem of thin slab continuous casting mold based on fluid-solid coupled heat transfer. Case Stud. Therm. Eng. 2024, 63, 105277. [Google Scholar] [CrossRef]
- Sun, Y.; Ni, Y.; Xu, Z.; Cai, K.; Chang, C.; Ma, M.; Du, X.; Jia, X. Longitudinal surface cracks of medium carbon steel on CSP thin slab. J. Iron Steel Res. Int. 2008, 15, 154–164. [Google Scholar]
- Dong, Q.; Zhang, J.; Yin, Y.; Nagaumi, H. Numerical simulation of macrosegregation in billet continuous casting influenced by electromagnetic stirring. J. Iron Steel Res. Int. 2021, 29, 612–627. [Google Scholar] [CrossRef]
- Lu, H.; Xie, X.; Zhong, Y.; Cheng, C.; Ren, W.; Lei, Z. Analysis of Transient Flow and Inclusion Transport in Vertical-Bending Slab Continuous Caster with Mold Electromagnetic Stirring. Metal. Mater. Trans. B 2024, 55, 5052–5067. [Google Scholar] [CrossRef]
- Song, X.; Cheng, S.; Cheng, Z. Numerical computation for metallurgical behavior of primary inclusion in compact strip production mold. ISIJ Int. 2012, 52, 1824–1831. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Z.; Lv, M.; Fang, M.; Liu, K. Numerical simulation of the fluid flow, heat transfer, and solidification in ultrahigh speed continuous casting billet mold. Steel Res. Int. 2022, 93, 2100673. [Google Scholar] [CrossRef]
- Petrus, B.; Zheng, K.; Zhou, X.; Thomas, B.G.; Bentsman, J. Real time, model-based spray-cooling control system for steel continuous casting. Metal. Mater. Trans. B 2011, 42, 87–103. [Google Scholar] [CrossRef]
- Xu, L.; Pei, Q.; Han, Z.; Yang, S.; Wang, J.; Yao, Y. Modeling study on melt flow, heat transfer, and inclusion motion in the funnel-shaped molds for two thin-slab casters. Processes 2022, 10, 2738. [Google Scholar] [CrossRef]
- Lu, H.; Zhong, Y.; Ren, W.; Ren, Z.; Lei, Z. Effect of Electromagnetic brake on transient asymmetric flow, solidification, and inclusion transport in a slab continuous casting. Steel Res. Int. 2022, 93, 2200518. [Google Scholar] [CrossRef]
- Suzuki, M.; Suzuki, M.; Yu, C.; EMI, T. ln-situ measurement of fracture strength of solidifying to predict upper limit of casting speed in continuous oscillating mold. ISIJ Int. 1997, 37, 375–382. [Google Scholar] [CrossRef]







| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Height of iron core/mm | 100 | Relative permeability of mold | 1 |
| Relative permeability of air | 1 | Conductivity of mold (s/m) | 5.81 × 107 |
| Conductivity of air (s/m) | 0 | Relative permeability of liquid steel | 1 |
| Relative permeability of iron core | 4000 | Conductivity of liquid steel (s/m) | 7.14 × 105 |
| Conductivity of iron core (s/m) | 2 × 106 | Relative permeability of coil | 1 |
| Magnetomotive force (a·n) | 19,000, 36,000, 54,000 | Conductivity of coil (s/m) | 5.81 × 107 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Submerged depth of SEN/mm | 175 | Density (kg/m3) | 7020 |
| Superheat/K | 25 | Viscosity (Pa·s) | 0.0062 |
| Casting speed (m/min) | 4.0, 4.5, 5.0, 5.5 | Specific heat (J/kg) | 720 |
| Liquidus temperature/K | 1803 | solidification latent heat (J/(kg·K)) | 275,000 |
| Solidus temperature/K | 1763 | Thermal conductivity (W/(m·K)) | 31 |
| Standard state enthalpy (J/kg mol) | −2,649,000 | Conductivity (S/m) | 7.14 × 105 |
| Inlet temperature (K) | 1828 | Magnetic permeability (H/m) | 1.257 × 10−6 |
| Bmax/T | Thickness Range/mm | Average Thickness/mm | Non-Uniformity Coefficient | Standard Deviation |
|---|---|---|---|---|
| 0 T | 11.76~14.69 | 12.84 | 22.85% | 1.17 |
| 0.1 T | 11.76~14.69 | 12.84 | 22.84% | 1.17 |
| 0.2 T | 11.79~14.66 | 12.83 | 22.34% | 1.10 |
| 0.3 T | 11.97~14.24 | 12.61 | 17.94% | 0.71 |
| Casting Speed (m·min−1) | Thickness Range/mm | Average Thickness/mm | Non-Uniformity Coefficient | Standard Deviation |
|---|---|---|---|---|
| 4.0 | 12.34~15.49 | 14.24 | 22.13% | 1.21 |
| 4.5 | 11.79~14.66 | 12.83 | 22.34% | 1.10 |
| 5.0 | 11.65~12.46 | 11.96 | 6.78% | 0.30 |
| 5.5 | 10.92~11.96 | 11.62 | 8.89% | 0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Qin, X.; Cheng, C.; Zhang, J.; Li, Y. Effect of Process Parameters on Metallurgical Behavior of Liquid Steel in a Thickened Compact Strip Production Mold with Electromagnetic Braking. Processes 2025, 13, 1427. https://doi.org/10.3390/pr13051427
Wang P, Qin X, Cheng C, Zhang J, Li Y. Effect of Process Parameters on Metallurgical Behavior of Liquid Steel in a Thickened Compact Strip Production Mold with Electromagnetic Braking. Processes. 2025; 13(5):1427. https://doi.org/10.3390/pr13051427
Chicago/Turabian StyleWang, Panpan, Xufeng Qin, Changgui Cheng, Jianjun Zhang, and Yang Li. 2025. "Effect of Process Parameters on Metallurgical Behavior of Liquid Steel in a Thickened Compact Strip Production Mold with Electromagnetic Braking" Processes 13, no. 5: 1427. https://doi.org/10.3390/pr13051427
APA StyleWang, P., Qin, X., Cheng, C., Zhang, J., & Li, Y. (2025). Effect of Process Parameters on Metallurgical Behavior of Liquid Steel in a Thickened Compact Strip Production Mold with Electromagnetic Braking. Processes, 13(5), 1427. https://doi.org/10.3390/pr13051427






