Thermally Driven Layered Phase Transition and Decomposition Kinetics of γ-AlH₃: A Multiscale Study Integrating Core-Shell Dynamics and Fluorescence-Guided Analysis

Abstract

In this study, the γ → α phase transition and decomposition of AlH₃ were probed using integrated hot-stage polarized microscopy, in situ XRD, DSC, and fluorescence analysis. Phase coexistence at 100 °C and complete transition at 140 °C were demonstrated by in situ XRD. Meanwhile, synchronized fluorescence decay (ImageJ-quantified) and XRD evolution analysis confirmed the temperature-dependent kinetics, with the isothermal γ → α durations decreasing from 225 min (100 °C) to 5 min (180 °C). The transition involved competing surface nucleation and bulk diffusion, which was accelerated by the reduced diffusion resistance at elevated temperatures. Above 160 °C, α → Al decomposition dominated via interfacial reactions and H₂ release, accompanied by gas-induced crystalline fracturing. DSC analysis revealed heating-rate-dependent core–shell thermal gradients, which caused hysteresis. At the same time, the experiment also shows that the surface oxidation of γ-AlH₃ may have hindered transitions through passivation layer formation. This work validates Gao et al.’s core–shell model, demonstrating that combined fluorescence and conventional techniques elucidate kinetic laws in metastable systems.

1. Introduction

Aluminum hydride (AlH₃) is a high-density hydrogen storage material with a theoretical capacity of 10.1 wt%. Consequently, this material has attracted substantial interest as a precursor for energetic materials and is a promising candidate for solid-state hydrogen storage, fuel applications, and aluminum nanoparticle synthesis [1,2,3,4]. However, the polymorphic diversity of AlH₃ (e.g., α, β, and γ phases) leads to significant variations in thermal stability and decomposition kinetics. To date, by employing different synthesis routes and reaction parameters (particularly time and temperature), at least seven distinct crystalline forms of AlH₃ have been identified [5,6]. Experimental and theoretical studies have consistently confirmed the α-phase as the most thermodynamically stable, followed by the β and γ polymorphs [7]. However, the phase transition dynamics, especially the coupling mechanism between γ → α phase transformation and subsequent α → Al decomposition, remain unresolved. This poses a critical challenge for achieving precise control in advanced applications.

The phase stability of AlH₃ is strongly dependent on the synthesis conditions. Early synthetic methods included the AlH₃-2N(CH₃)₃ preparation reported by Stecher and Wiberg in 1942 as well as Finholt’s ether-based approach [8,9]. Recent breakthroughs include Brower’s room-temperature synthesis of γ-AlH₃ via a LiH-mediated route and Hlova’s mechanochemical synthesis of γ-AlH₃ using LiH and AlCl₃ [10,11]. These strategies have opened new avenues for aluminum hydride preparation and application. Moreover, advances in the development of in situ characterization techniques have revolutionized dynamic behavior studies: Graetz et al. determined the kinetic/thermodynamic properties of AlH₃ polycrystals using thermal analyses (DSC/TG/DTA) and XRD, proposing that the decomposition kinetics are governed by two- and three-dimensional nucleation-growth mechanisms [12,13]. These findings have provided critical kinetic insights for the optimization of AlH₃ as a hydrogen storage material. In contrast, Shichao Gao and Haizhen Liu elucidated the stability and decomposition pathways of γ-AlH₃, revealing distinct hydrogen desorption mechanisms between the outer and inner layers of γ-AlH₃ particles. However, despite these promising results, bulk characterization (e.g., XRD) and thermal analysis methods often fail to correlate surface-bulk reactions with morphological evolution during thermal events.

In this study, γ-AlH₃ phase transitions are systematically investigated under isothermal/non-isothermal conditions through in situ multiscale characterization (hot-stage polarized light microscopy, in situ XRD, and DSC) to uncover the spatiotemporal evolution of γ → α transitions and validate the “hierarchical phase transition model” proposed by Gao and Liu [14,15]. Herein, hot-stage fluorescence microscopy is innovatively integrated with ImageJ-based spatiotemporal analysis to address the technological gap in real-time surface phase transition monitoring. This approach reveals the synergistic effects of temperature gradients and crystal morphology on the reaction kinetics, bridging atomic-scale phase transitions with mesoscopic morphological changes. Promisingly, the established “surface-spherical phase” analytical framework for polycrystalline hydride transitions can be extended to other hydrogen storage systems (e.g., MgH₂ and NaAlH₄). By combining hot-phase polarized fluorescence microscopy with conventional techniques, this work provides a multidimensional strategy for analyzing polycrystalline transitions, offering new perspectives for optimizing kinetic control and decomposition pathways. Furthermore, a semi-quantitative analysis of fluorescence profiles is provided to explore the feasibility of establishing crystal kinetics with minimal raw materials.

2. Materials and Methods

2.1. Materials

Aluminum hydride (γ-phase) with a purity of 97.25% was used without further purification (Hubei Aerospace Chemical Technology Research Institute, Xiangyang, Hubei China).

2.2. Characterization of α and γ Phases

2.2.1. DSC Analysis

DSC analysis of γ-AlH₃ was performed on a METELLR TOLEDO DSC1. Analysis was performed in a gold crucible under a nitrogen flow rate of 50 mL min⁻¹, from 25 to 300 °C using heating rates of 1, 5, 10, and 20 °C/min.

2.2.2. X-ray Powder Diffraction Analysis

X-ray diffraction (XRD) was employed to characterize the crystal structures and phase compositions of the samples. Measurements were performed using a Rigaku SmartLab diffractometer with Cu Kα radiation (λ = 1.5406 Å) operated at 40 kV and 200 mA. Scans were conducted over the 2θ range of 10–80° with a step size of 0.02° and a scanning rate of 7° min⁻¹ [12]. The XRD data were analyzed using MDI Jade 6 software for phase identification and quantification.

2.2.3. SEM Analysis

The crystal morphologies of α- and γ-AlH₃ were analyzed using scanning electron microscopy (SEM; EVO MA 15, Zeiss, Oberkochen, Germany). Samples were prepared by dispersing the powders onto conductive adhesive substrates, followed by sputter-coating with a 5 nm-thick Au layer to mitigate charging artifacts and enhance the surface conductivity.

2.3. In Situ X-Ray Powder Diffraction Analysis

In situ powder X-ray diffraction (PXRD) analyses were conducted on a Bruker D8 Advance diffractometer equipped with a Cu Kα radiation source (λ = 1.5406 Å, 35 kV, 40 mA) without monochromation. Samples were loaded into rotating holders within a temperature-controlled chamber (±1 °C accuracy) and subjected to continuous scans across the 2θ range of 10–80° with a step size of 0.02° and a dwell time of 0.2 s/step. Before data collection, each sample was heated to the target temperature at a heating rate of 10 °C/min and allowed to stabilize for 5 min. Diffraction patterns were then collected after stabilization to ensure thermal equilibrium. The rotating sample holder minimized preferred orientation effects, while the high angular resolution (0.02° step) enabled precise phase identification. As shown in

Table 1. Experimental conditions in the non-isothermal phase.

Name	Temperature Points/(°C)	Heating Rate/(°C min−1)	Residence Time/min
γ-100-180	100, 120, 140, 160, 180	10	10
γ-60-160	60, 80, 90, 100, 110, 120, 130, 140, 150, 160	10	10

, a series of X-ray powder diffraction experiments were carried out at different temperatures in accordance with the non-isothermal phase γ-60-160. The absence of a monochromator enhanced the X-ray flux, which was critical for the rapid in situ tracking of transient phases during thermal decomposition.

2.4. In Situ Thermal Transformation Analysis

2.4.1. Non-Isothermal Hot Stage Analysis

Morphological changes during the heating of AlH₃ were observed using a polarized light microscope (BK-POL, Chongqing Aote Optical Instrument Co. Chongqing Optec Instrument Co., Chongqing China) coupled with a non-isothermal hot stage (HCS621GXY, INSTEC, Boulder, CO, USA; controlled by an mK2000B unit). Samples were heated at 10 °C/min under continuous nitrogen purging to maintain an inert atmosphere. To synchronize with the in situ PXRD acquisition times (10 min per scan), samples were held at each temperature for 10 min, and polarized light images were captured every 2 min to track dynamic changes.

2.4.2. Isothermal Hot Stage Analysis

A hot-stage polarized light microscopy (HSPLM) system was utilized to investigate the phase transition kinetics and morphological evolution of γ-AlH₃ and α-AlH₃. First, γ-AlH₃ and α-AlH₃ powders were uniformly dispersed on microscope slides within a semi-closed chamber under a continuous flow of high-purity nitrogen (regulated via a pressure-reducing valve) to minimize oxidative degradation. To suppress premature decomposition prior to reaching the target temperatures, samples were rapidly heated at 25 °C/min (

Table 2. Experimental conditions in the isothermal phase.

Name	Interval Time/s	Heating Rate/(°C min−1)	Atmosphere
100	300	25	N2
120	180	25	N2
140	50	25	N2
160	20	25	N2
180	20	25	N2

) and isothermally held for 4 h at each temperature. Real-time observations were conducted using a polarizing microscope integrated with a high-resolution CCD camera (2048 × 2048 pixels), which was employed to automatically capture fluorescence images at temperature-specific intervals (Table 2) to optimize the temporal resolution.

2.5. Fluorescence Image Processing Analysis

The fluorescence time-series images acquired during thermal staging were semi-quantitatively analyzed using ImageJ (v1.53) software. The quantification of intensity was dized by converting the raw color images to 8-bit grayscale, which ensured a linear correlation between the pixel values and fluorescence intensity [16,17,18,19]. Background noise, which was caused by ambient thermal fluctuations and hot-stage heating, was subtracted using a 50-pixel radius optical background filter. Overexposure artifacts were mitigated by normalizing all images to the 99th percentile grayscale value (I₀) of the initial frame (t = 0), thereby excluding saturated pixels (Max = 255) from the baseline calculations. To ensure consistent analysis, regions of interest (ROIs) were manually delineated along crystal edges to track the fluorescence intensity (I) versus crystal volume over time. Larger crystals (>20 μm) were prioritized for ROI selection to minimize the fragmentation artifacts observed in smaller crystals (<5 μm) during heating [20]. To mitigate surface sensitivity, fluorescence responses from multiple intact crystals within the same field of view were statistically averaged. Batch-processed grayscale values (Mean) under identical thermal conditions were normalized as I/I₀ to quantify fluorescence decay trends.

3. Results

3.1. Characterization of α and γ Phases

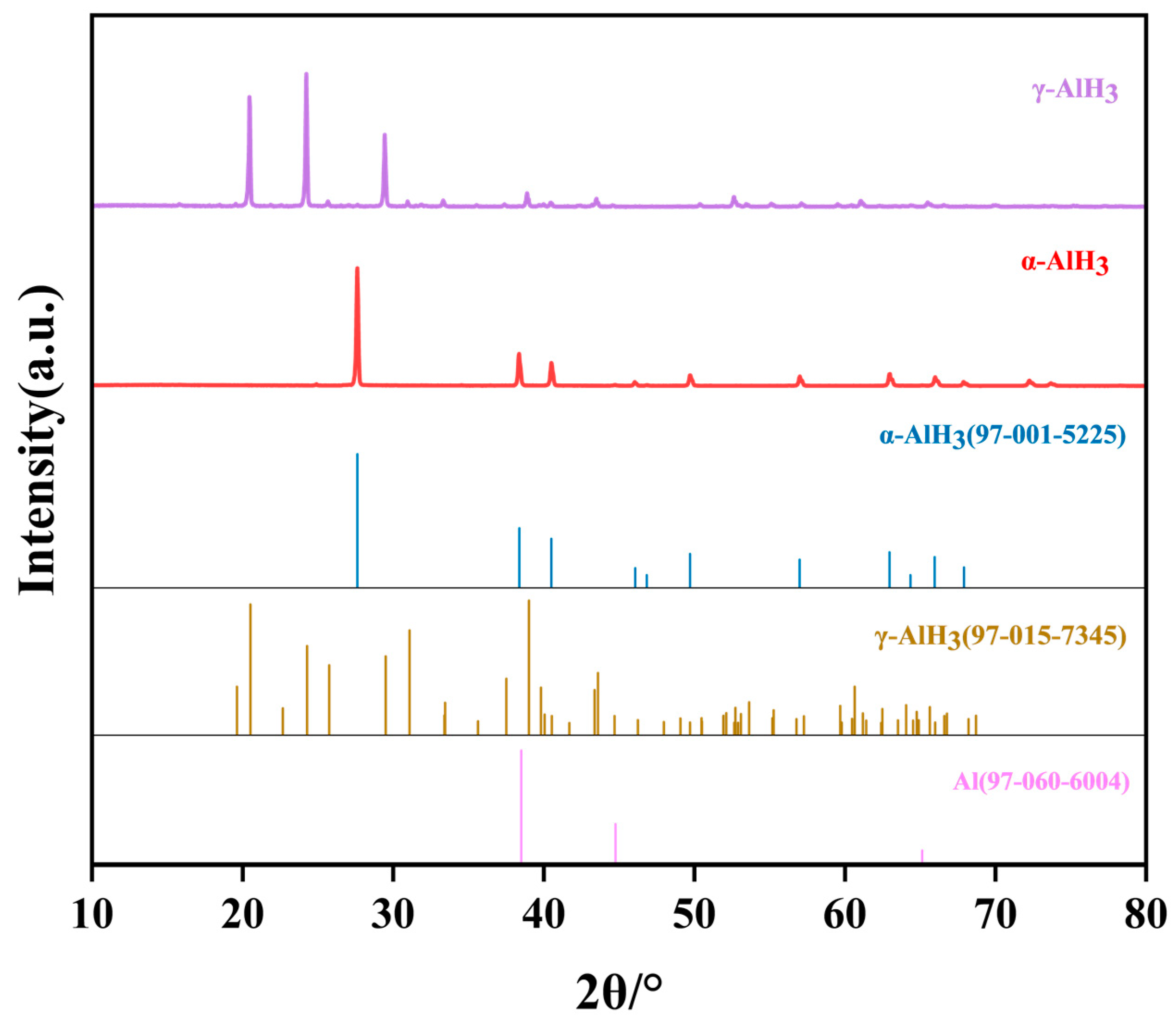
3.1.1. XRD Analysis

The XRD pattern of the γ-AlH₃ raw material is displayed in Figure 1. Characteristic peaks at 2θ = 19.5°, 20.5°, and 29.5° correspond to the γ-phase (PDF#97-015-7345). However, minor α-AlH₃ (2θ = 27.6°) and metallic Al (2θ = 38.5°) phases are also observed, which is consistent with the metastable nature of γ-AlH₃. The presence of α-AlH₃ indicates a partial phase transition from γ-AlH₃ under ambient conditions. This phase transition is driven by thermodynamic instability and surface energy minimization. Meanwhile, the existence of metallic Al is likely due to localized decomposition during sample handling or residual precursor reactions.

3.1.2. SEM Analysis

SEM images of α-AlH₃ and γ-AlH₃ are shown in Figure 2. The α-AlH₃ crystals exhibit a hexagonal prismatic morphology characterized by high crystallographic planarity and well-defined facets, consistent with the thermodynamically stable configuration of this phase [20]. These crystals contain minor surface irregularities, which likely arise from growth defects or partial oxidation during synthesis. In contrast, γ-aluminum hydride (γ-AlH₃) exhibits an acicular (needle-like) morphology with fragmented crystallites, which should be affected by the production process. γ-AlH₃ is in a metastable crystalline form, and its space group is Pnnm, belonging to the orthorhombic crystal system. During the phase transition, these factors promote preferential cleavage along specific crystallographic planes [21,22]. The different morphologies of the two polymorphs, α-aluminum hydride (α-AlH₃) and γ-aluminum hydride, are consistent with their different thermodynamic stabilities and decomposition pathways [23].

3.2. In Situ PXRD

The γ-60-160 experiments were initiated at 60 °C, which was sufficient to activate the γ → α phase transformation. The upper temperature limit of 160 °C was selected based on the reported literature and DSC [12] data, which identify 170 °C as the onset temperature for the decomposition of α-AlH₃ to metallic Al. As shown in Figure 3, negligible phase evolution occurs at 60 °C, 80 °C, or 90 °C. Within the range of 60–90 °C, the characteristic γ-phase XRD peaks (2θ = 19.50°, 20.40°) remain stable, indicating insufficient thermal energy for rapid structural reorganization. The γ → α transition predominantly occurs in the range of 100–120 °C. This phase transition is completed at 140 °C, as evidenced by the disappearance of the exothermic peak in differential scanning calorimetry (DSC) and the attenuation of the fluorescence gradient. At 60 °C, γ-AlH₃ can undergo transformation; however, the phenomenon is not prominent, suggesting that its crystallographic transformation requires a certain threshold of heat accumulation. At 110 °C, the γ-phase peaks exhibit simultaneous attenuation, while distinct signals for the α-phase (2θ = 27.54°) and elemental aluminum (2θ = 38.5°) emerge. The surface γ-aluminum hydride (γ-AlH₃) decomposes via two distinct pathways (Equations (1) and (2)). Between 120 and 160 °C, the α-phase peak intensity reaches its maximum before diminishing, while the Al signals intensify, signifying α → Al decomposition. This process occurs in two stages. First, a gradual reduction in the α-phase signal intensity and growth in the Al signal intensity from 120 to 140 °C reflect interface reaction-controlled decomposition. Second, between 140 and 160 °C, near-complete α-phase decomposition coincides with bulk hydrogen diffusion and the release of H₂ gas, which induces mechanical fragmentation. Post-cooling analysis reveals sample darkening (light gray → dark gray) and residual α-phase signals (<5%) in the XRD patterns. This can be attributed to either the surface oxidation of Al nanoparticles (forming Al₂O₃ passivation layers) or light scattering by submicron fragments. The persistence of the α-phase traces reflects kinetic freezing—a metastable state retained during rapid quenching caused by a lack of sufficient thermal energy for complete phase reversion.

$$\mathrm{\gamma }-\mathrm{A}\mathrm{l}{\mathrm{H}}_3\to \mathrm{\alpha }-\mathrm{A}\mathrm{l}{\mathrm{H}}_3$$

(1)

$$\mathrm{\gamma }-\mathrm{A}\mathrm{l}{\mathrm{H}}_3\to \mathrm{A}\mathrm{l}+{\displaystyle \frac{3}{2}}{\mathrm{H}}_2$$

(2)

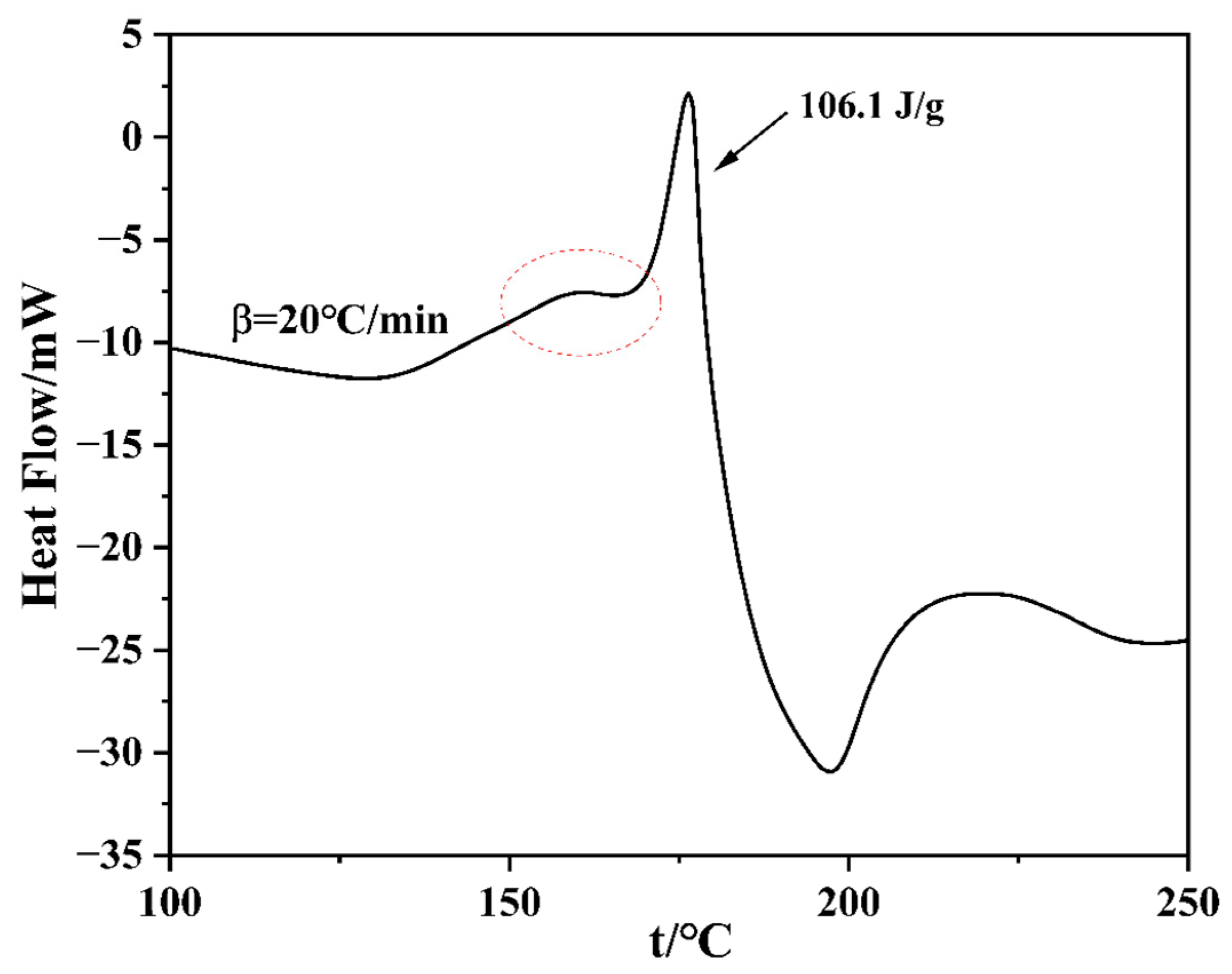
3.3. DSC Analysis

The DSC analysis of γ-AlH₃ (Figure 4) reveals an exothermic peak at 170 °C corresponding to the α → Al decomposition. The initial phase transition temperature is 127.8 °C, which exceeds values reported in the literature (100–110 °C). This difference is attributable to two factors: thermal hysteresis from the heating rate-dependent thermal gradients between the core and shell regions as well as the formation of passivation layers (due to partial surface oxidation) leading to a larger activation energy barrier. The exothermic peak shifts rightward with increasing heating rate [13,24] (1–20 °C/min), which is consistent with delayed heat propagation in the bulk material.

The γ → α transition enthalpy (ΔHγ → α = 3.0 ± 0.2 kJ/mol) aligns with reported values (ΔHγ → α = 2.8 ± 0.4 kJ/mol) [13]. A distinct shoulder peak adjacent to the main exotherm (Figure 4, highlighted region) emerges at higher heating rates (e.g., 20 °C/min), reflecting asynchronous phase transitions between the outer and inner crystal layers. At a heating rate of 1 °C/min, minimal thermal gradients yield smooth DSC curves. In contrast, at 20 °C/min, steep thermal gradients (surface-to-core ΔT ≈ 15 °C) decouple the outer/inner transition kinetics, leading to the generation of resolvable shoulder peaks. The γ → α transition follows a layered core–shell mechanism. First, the outer γ-phase transforms into the α-phase and Al (Equation (1)) due to rapid surface heating. Next, the inner γ-phase subsequently reacts as heat penetrates the bulk (Equation (2)). The temporal separation of these events is caused by hydrogen diffusion limitations through the α-phase shell. The outer-layer transition (main peak) corresponds to rapid surface nucleation, while the delayed inner-layer transition (shoulder peak) reflects mass transfer resistance in the bulk phase.

3.4. On-Line Analysis of Non-Adiabatic Phase Transitions

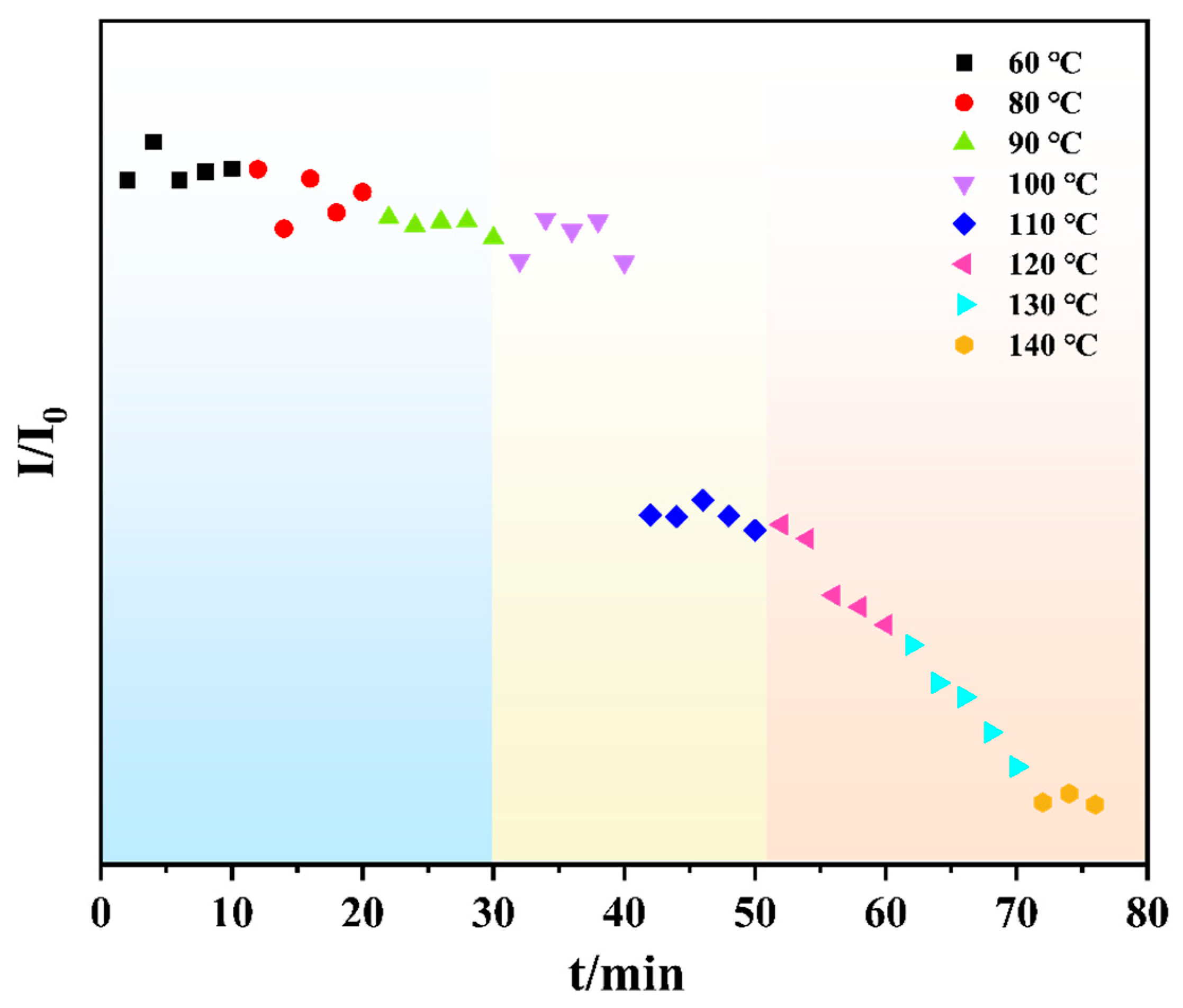
3.4.1. Non-Isothermal Hot Stage Analysis

The crystal morphologies of γ-AlH₃ and α-AlH₃ are illustrated in Figure 5. Real-time observation via hot-stage polarized light microscopy under nitrogen protection was employed to reveal the temperature-dependent morphological and fluorescence evolution. As illustrated in Figure 5, a certain degree of red fluorescence is observable. This phenomenon can be attributed to the presence of defects, including oxygen vacancies, hydrogen vacancies, and dangling bonds, on the surface of AlH₃. These defects introduce deep energy levels within the bandgap, thereby inducing electrons to transition from the valence band to the defect energy levels and subsequently emit long-wavelength (red) fluorescence [25,26]. With an increase in temperature, the migration and recombination of defects are likely to be facilitated, allowing electron transitions to revert to the intrinsic bandgap and resulting in the emission of green fluorescence. Within the 60–100 °C range, the needle-like morphology remains intact and the fluorescence intensity is stable. This indicates the minimal perturbation to the Al–H bonding network and the existence of only minor lattice strain from thermal expansion. Upon heating to 110 °C, abrupt fluorescence quenching occurs in the outer layer within 0–2 min, although no macroscopic deformation is observed. This suggests localized bond reorganization in the lattice, correlating with the in situ XRD data showing reduced γ-phase peaks and emerging α-phase signals at 110 °C—a precursor state of the phase transition. Polarized light micrographs of α-AlH₃, γ-AlH₃, and metallic Al are displayed in Figure 5. The γ-AlH₃ exhibits a needle-like morphology with intense fluorescence, while α-AlH₃ consists of hexagonal crystals with weaker fluorescence. In contrast, metallic Al lacks measurable fluorescence under these conditions. This disparity in fluorescence is caused by fundamental differences in the electronic and crystallographic structures of the different phases [27]. Specifically, γ-AlH₃ has a smaller bandgap (ΔE_γ < ΔE_α), enabling higher electron transition probabilities under polarized light excitation. γ-AlH₃ belongs to the orthorhombic crystal system and α-AlH₃ belongs to the tripartite space group. The lower symmetry of γ-AlH₃ compared to α-AlH₃ introduces additional lattice distortions, enhancing radiative recombination pathways. Meanwhile, the free-electron-dominated electronic structure of metallic Al suppresses fluorescence, making its optical response negligible in practical applications [28].

The distinct fluorescence signatures of γ-AlH₃, α-AlH₃, and metallic Al provide a rapid, non-destructive method for differentiating these phases in mixed-phase systems. This is particularly valuable for the in situ study of decomposition pathways, where real-time phase tracking is critical.

At 130 °C, core fluorescence completely diminishes within 5–10 min. Above 140 °C, fluorescence extinction coincides with progressive crystal fragmentation. This spatiotemporal evolution confirms a diffusion-controlled core–shell mechanism where the phase transition front propagates radially inward from the particle surface [14]. This process is governed by hydrogen diffusion through the bulk rather than interfacial atomic migration, and the kinetics are limited by hydrogen mobility in the lattice. The mechanism of this process can be described as follows: (1) in the precursor stage (≤110 °C), surface-initiated bond relaxation precedes long-range structural rearrangement. (2) In the core–shell transition stage (110–140 °C), the formation of the α-phase shell restricts hydrogen egress from the γ-phase core, causing fluorescence gradient decay. (3) In the fragmentation stage (≥140 °C), the accumulation of mechanical stress via hydrogen release and α → Al decomposition induces crystal disintegration [29,30,31].

Under non-isothermal heating (Figure 6), the fluorescence of the γ-AlH₃ crystals undergoes temperature-dependent evolution. Between 60 and 100 °C, the fluorescence intensity gradually decreases by 15–20%, indicating minor lattice perturbations due to thermal expansion. At 110 °C, the fluorescence intensity abruptly drops to 50% within 0–2 min. This corresponds to the outer-layer γ → α phase transition, while the inner γ-phase persists. Subsequent heating from 110 to 140 °C induces progressive core fluorescence decay, reflecting the inward propagation of the phase boundary. At 140 °C, the fluorescence signals diminish to background noise levels, indicating complete α → Al decomposition. This spatiotemporal fluorescence trajectory validates the core–shell transformation mechanism: the surface-initiated γ → α transition forms an α-phase shell, followed by inward hydrogen diffusion-limited bulk decomposition. The sequential phase evolution (i.e., outer α-phase formation accompanied by Al generation preceding inner γ → α conversion) aligns with the observed fluorescence gradient attenuation. Eventually, the fluorescence is extinguished, which coincides with full α-phase decomposition. This phase decomposition is accompanied by metallic Al accumulation and H₂ gas release, which disrupts the crystal lattice.

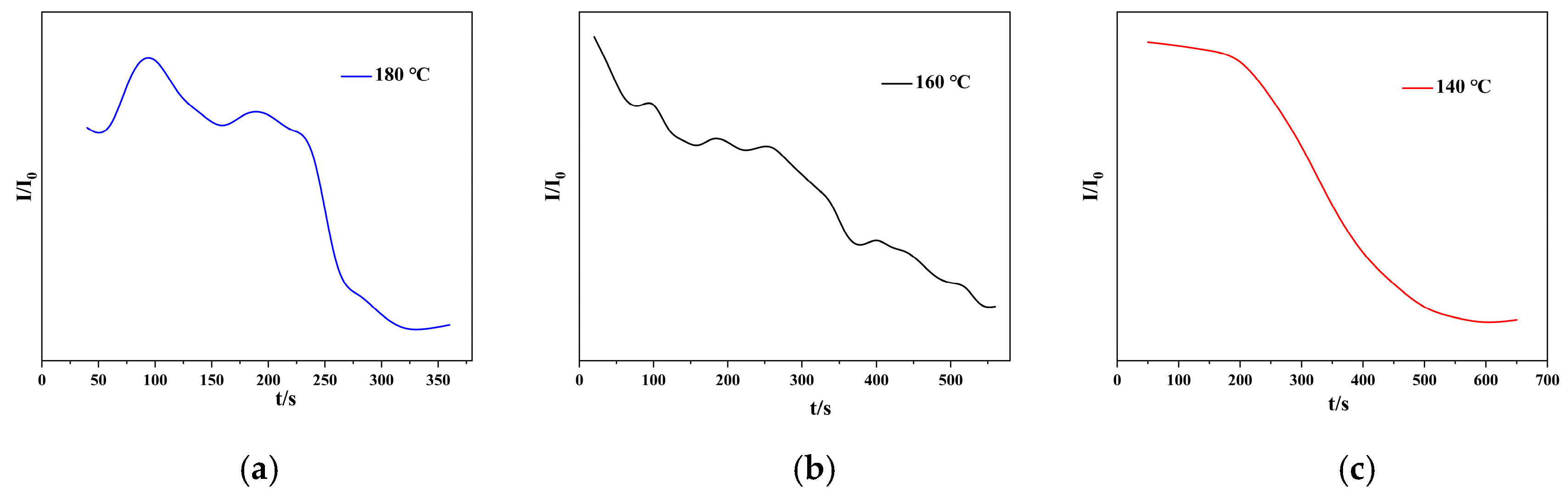
3.4.2. Isothermal Hot Stage Analysis

The isothermal phase transition and decomposition behavior of γ-AlH₃ were systematically investigated using hot-stage polarized microscopy, in situ XRD, and DSC. Figure 7 illustrates the morphological changes before and after heating at different temperatures. At 100 °C and 120 °C (4 h holds), the predominant change is the disappearance of fluorescence from the needle-like γ-AlH₃ crystals, while other structural features remain largely unaffected. The fluorescence extinction times exponentially decrease with increasing temperature: 225 min, 130 min, 14 min, 10 min, and 5 min at 100 °C, 120 °C, 140 °C, 160 °C, and 180 °C, respectively. This temperature-dependent behavior underscores the thermally activated nature of the decomposition process, where elevated temperatures significantly accelerate both the phase transitions (γ → α) and subsequent α → Al decomposition. Figure 8 highlights the spatially resolved fluorescence gradient. Outer-layer quenching precedes core signal loss, which is a signature of the sequential core–shell transformation mechanism. At 180 °C, fluorescence extinction is accompanied by rapid crystal fragmentation, reflecting the mechanical failure induced by the internal hydrogen gas pressure.

Hot-stage microscopy was performed to reveal the kinetic disparities between the small (<5 μm) and large (>20 μm) acicular crystals. The smaller crystals exhibit accelerated decomposition at 160–180 °C due to their high surface-to-volume ratio and defect density, which lower the activation barriers for interfacial reactions. In contrast, the larger crystals demonstrate enhanced stability. This aligns with classical nucleation theory, where a lower interfacial curvature and fewer lattice imperfections suppress nucleation rates. The size dependency of this decomposition process mirrors broader trends in nanomaterial thermodynamics, where the surface energy dominates bulk contributions at reduced dimensions.

The variations in fluorescence intensity with time at different temperatures during isothermal analysis are shown in Figure 9. In general, the fluorescence intensity decreases with increasing time. At all temperatures, a phase involving a rapid decline in intensity is observed, and this phase becomes more pronounced at higher temperatures. At 140 °C, fluorescence attenuation radially propagates from the crystal edges to the cores over ~14 min without morphological collapse. In situ XRD confirms the concurrent emergence of the α-phase (100–120 °C), linking the outer fluorescence decay to the γ → α transition. The diminished fluorescence in α-AlH₃ is due to its lower crystallographic symmetry, which reduces the polarized light response. Delayed core fluorescence disappearance corresponds to the α → Al decomposition, revealing a two-stage process: the initial surface-driven phase transition followed by bulk decomposition. The edge-preferential γ → α transition is initiated via surface energy minimization, forming an α-phase shell that acts as a diffusion barrier. The release of hydrogen from the γ-phase core is thereby constrained by mass transfer through the α-phase shell, causing thermal hysteresis in the inner-layer transitions. At 140 °C, minimal α → Al decomposition (evidenced by the gradual α-phase peak reduction in the XRD analysis) means that gas (H₂) generation is avoided, preserving the crystal integrity. However, at 160 °C, complete α → Al decomposition (XRD) releases H₂ gas. The pressure of this gas exceeds the yield strength of the nascent Al nanoparticles at 180 °C, inducing explosive fragmentation. The detection of an endothermic peak ascribed to α → Al decomposition at 170 °C and an exothermic signal ascribed to self-accelerating reactions in DSC analysis corroborates this mechanism. The surface oxidation of the Al nanoparticles is indicated by the sample darkening observed post-cooling, which is consistent with the residual α-phase (<5%, XRD) attributed to kinetic freezing—a metastable state stabilized by oxide passivation layers blocking reverse transitions. Although fluorescence microscopy provides a critical spatio-temporal resolution, the surface sensitivity of this technique limits the quantification of bulk phases, and crystal size/defect heterogeneity complicates kinetic interpretation.

3.5. Kinetic Analysis of Crystal Phase Transition Mechanisms

The γ → α phase transition kinetics were analyzed using the classical Avrami–Erofeev [12] model, which relates the transformed fraction X(t) to time t as follows:

$$\mathrm{X}\left(\mathrm{t}\right)=1-\exp \left(-\mathrm{k}{\mathrm{t}}^{\mathrm{n}}\right)$$

(3)

where k is the rate constant and n is the Avrami exponent reflecting the dimensionality of growth. The temperature-dependent reaction rate, k(T), can generally be described by the Arrhenius equation:

$$\mathrm{k}\left(\mathrm{t}\right)=\mathrm{A}·\exp \left({\displaystyle \frac{{-\mathrm{E}}_{\mathrm{a}}}{\mathrm{R}\mathrm{T}}}\right)$$

(4)

where A is the preexponential Arrhenius parameter, E_a is the activation energy, and R is the universal gas constant. The activation energy and Arrhenius parameter are determined from the slope and intercept of an Arrhenius plot. The fluorescence intensity decay profiles obtained from isothermal hot-stage microscopy (Figure 9) validate the applicability of the Avrami–Erofeev model for describing the γ → α phase transition kinetics. The normalized fluorescence decay I(t)/I₀ adheres to the following equation:

$$X=1-{\displaystyle \frac{\mathrm{I}\left(\mathrm{t}\right)}{{\mathrm{I}}_0}}$$

(5)

where I(t) is the fluorescence intensity at time t and I₀ is the initial fluorescence intensity. At lower temperatures, the Arrhenius–Avrami model has been modified on the basis of Equations (3)–(5) to obtain Equations (6) and (7):

$${\displaystyle \frac{\mathrm{I}\left(\mathrm{t}\right)}{{\mathrm{I}}_0}}=\exp {\left(-{\displaystyle \frac{\mathrm{t}}{\mathrm{\tau }\left(\mathrm{T}\right)}}\right)}^{\mathrm{n}}$$

(6)

$$\mathrm{\tau }\left(\mathrm{T}\right)={\mathrm{\tau }}_0·\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{{\mathrm{E}}_{\mathrm{a}}}{\mathrm{R}\mathrm{T}}}\right)$$

(7)

where I(t)/I₀ is the normalized fluorescence intensity, τ(T) is the characteristic decay time, and n is the Avrami exponent (n = 1.5). Assuming complete fluorescence quenching at I/I₀ = 0 and substituting the experimental decay times at 100 °C (225 min) and 140 °C (14 min) into Equation (7), the calculated activation energy of E_a = 88.97 kJ/mol agrees with the value reported by Graetz (92.3 ± 8.6 kJ/mol). This demonstrates the validity of the formula for describing phase transformation kinetics in the low-temperature range. However, significant deviations occur when this model is applied to data at 160 °C and 180 °C, revealing the limitations of this model in describing the α-AlH₃ to Al decomposition process at elevated temperatures. Despite its limitations, this model explores the possibility of coupling fluorescence intensity with the kinetic formula for transcrystallization.

4. Discussion

The thermally induced γ → α phase transition in AlH₃ was systematically investigated under both isothermal and non-isothermal conditions through integrated methodologies, including hot-stage polarized light microscopy, in situ XRD, DSC, and semi-quantitative fluorescence analysis. In situ XRD confirms the coexistence of γ-AlH₃ and α-AlH₃ phases at 100 °C, with complete conversion to the α-phase by 140 °C. Non-isothermal experiments (γ-60-160) reveal synchronized fluorescence intensity trends (ImageJ analysis) and phase evolution (in situ XRD). This demonstrates that thermal accumulation, which is modulated by heating rate-dependent core–shell thermal gradients, governs the hysteresis of this phase transformation. Isothermal studies show temperature-dependent fluorescence extinction times: 225 min, 130 min, 14 min, 10 min, and 5 min at 100 °C, 120 °C, 140 °C, 160 °C, and 180 °C, respectively. This temperature dependency highlights a dual-controlled mechanism where γ → α transitions are dominated by surface nucleation kinetics and bulk hydrogen diffusion at lower temperatures (≤140 °C), while α → Al decomposition (160–180 °C) is driven by interfacial reactions and H₂ gas release. Elevated temperatures reduce the diffusion resistance, accelerating synergistic surface nucleation and bulk mass transfer.

Despite these insights, limitations persist. For instance, fluorescence analysis predominantly reflects surface/near-surface responses. Therefore, modeling is needed to correlate this analysis with the bulk phase fractions derived via XRD. Moreover, crystal defect/size heterogeneity introduces fluorescence decay dispersion, which is partially masked by statistical averaging. Finally, the susceptibility of γ-AlH₃ to surface oxidation may kinetically inhibit transitions. These findings validate the layered core–shell transition model proposed by Gao et al., where surface-initiated α-phase nucleation propagates inward. The innovative coupling of hot-stage polarized fluorescence microscopy with conventional techniques described in this work enables the semi-quantitative tracking of phase transitions, demonstrating the potential of cost-effective fluorescence methods for probing metastable material kinetics. This work advances the mechanistic understanding of polymorphic transformations in hydrides, providing a framework for optimizing hydrogen storage systems.