Numerical Study on the Dynamics and Thermal Effects of Bubble Stable Cavitation in Focused Ultrasound Fields
Abstract
1. Introduction
2. Numerical Simulation Method and Bubble Model
2.1. Governing Equation
2.2. Equation of State
2.3. Simulation Setup
2.4. Model Validation
2.5. Numerical Setup
3. Results and Discussion
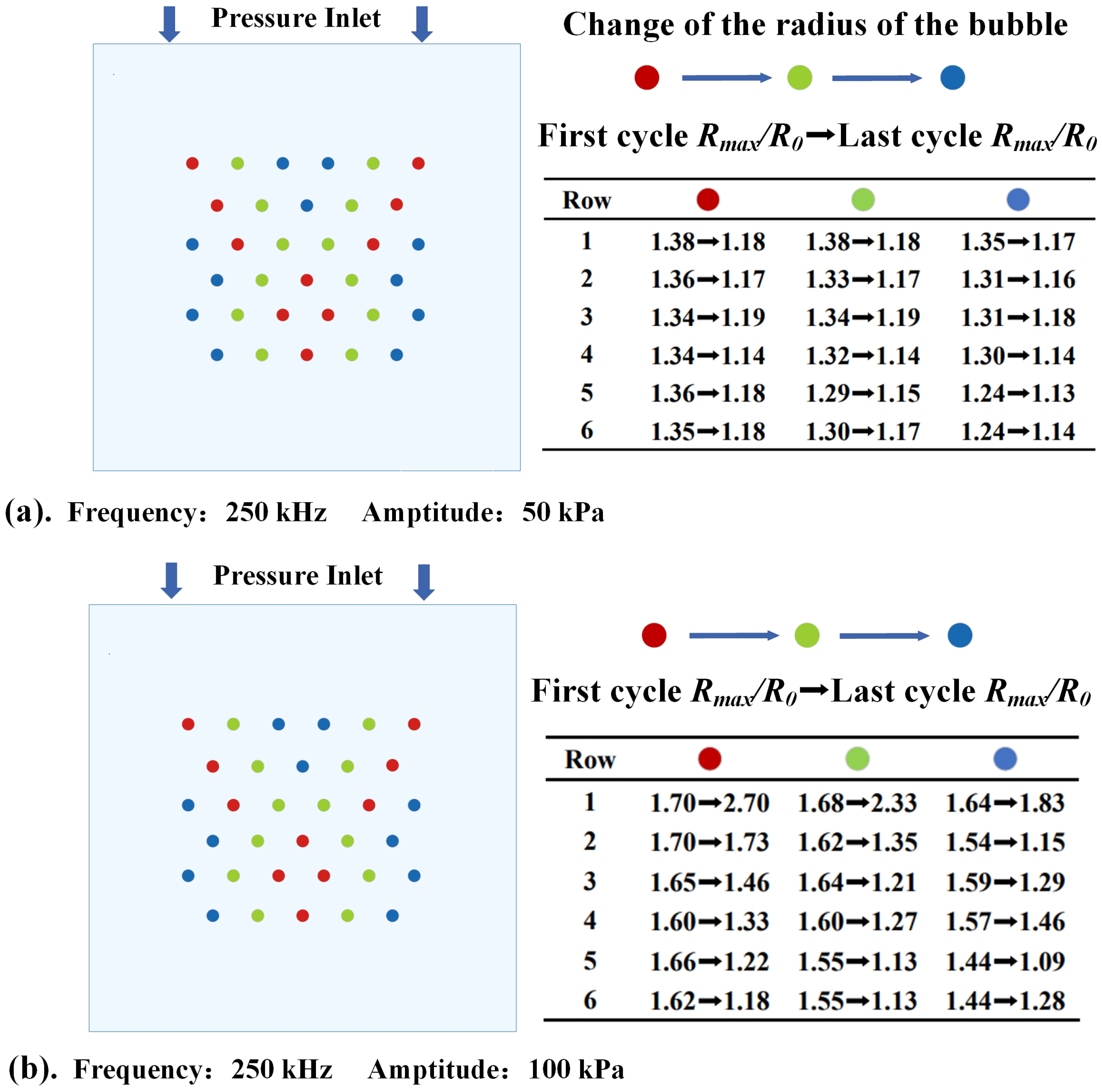
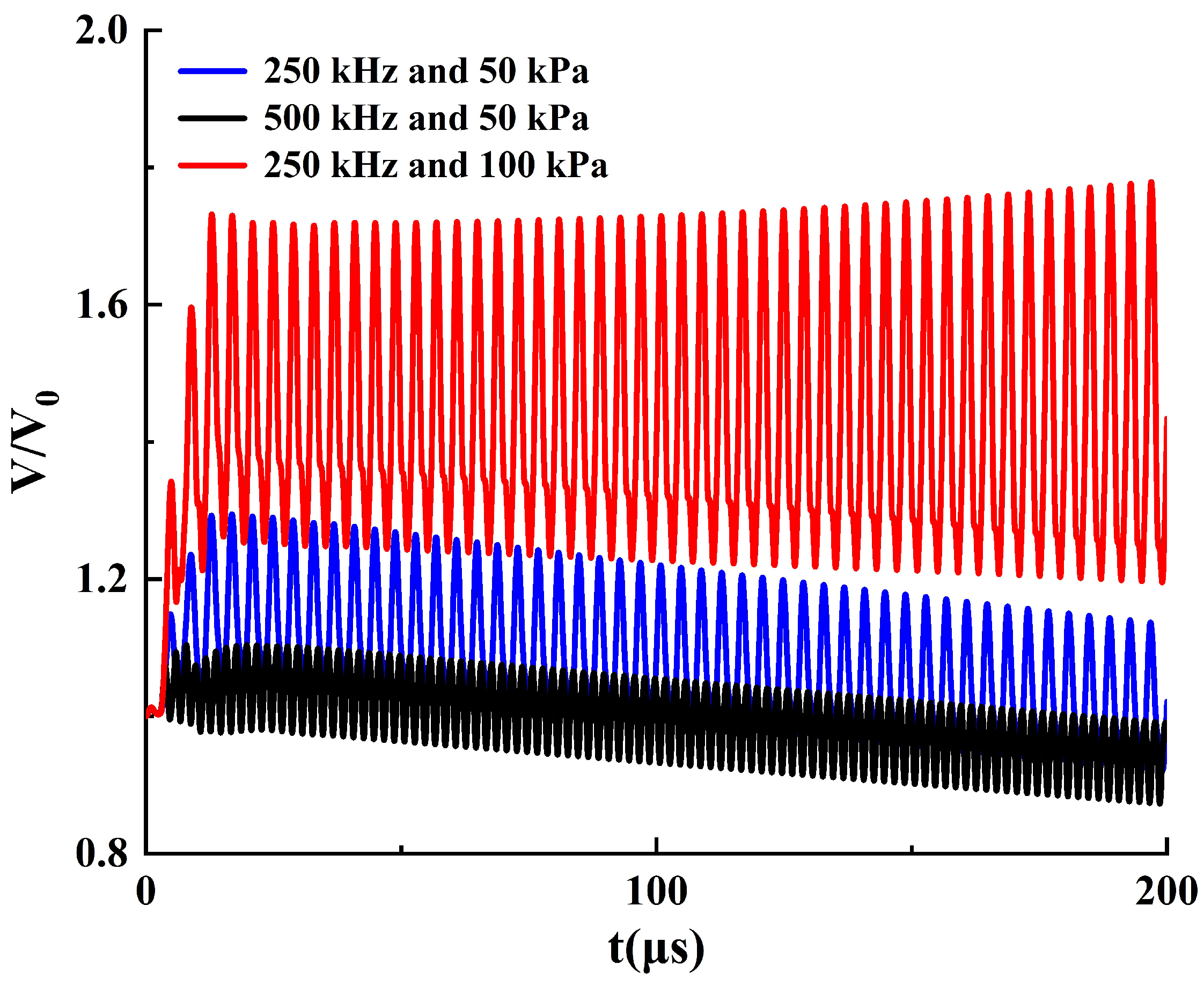
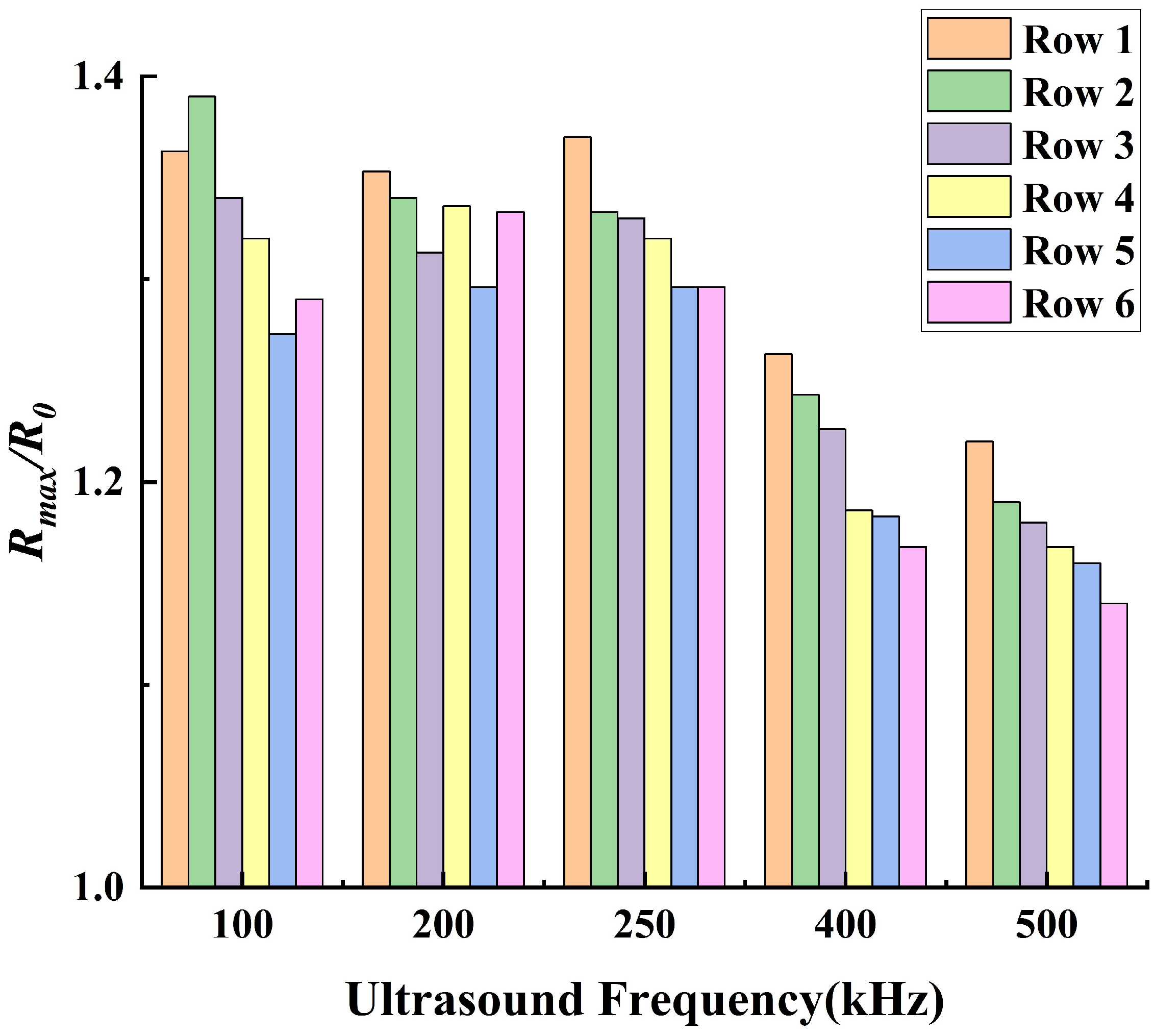
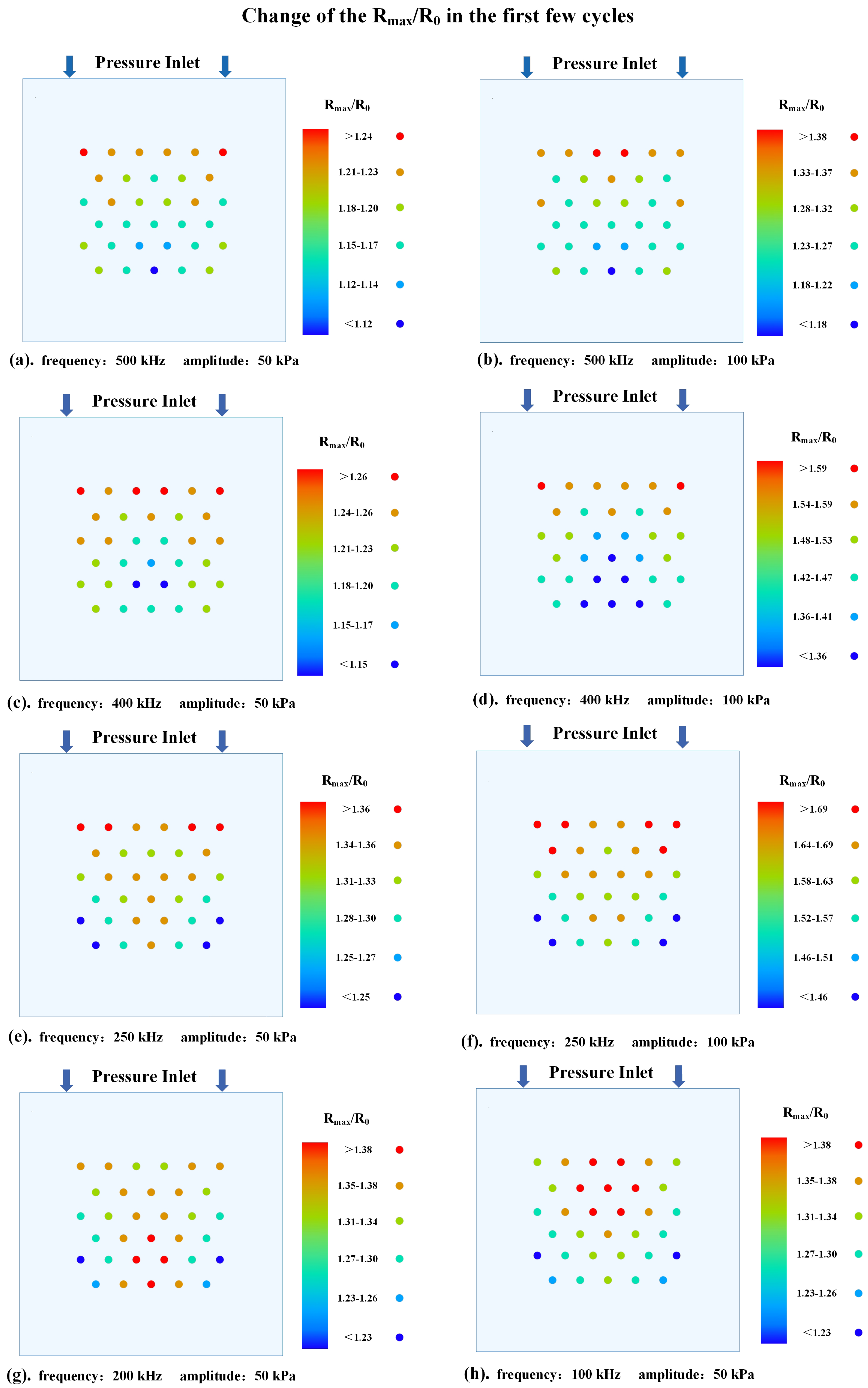
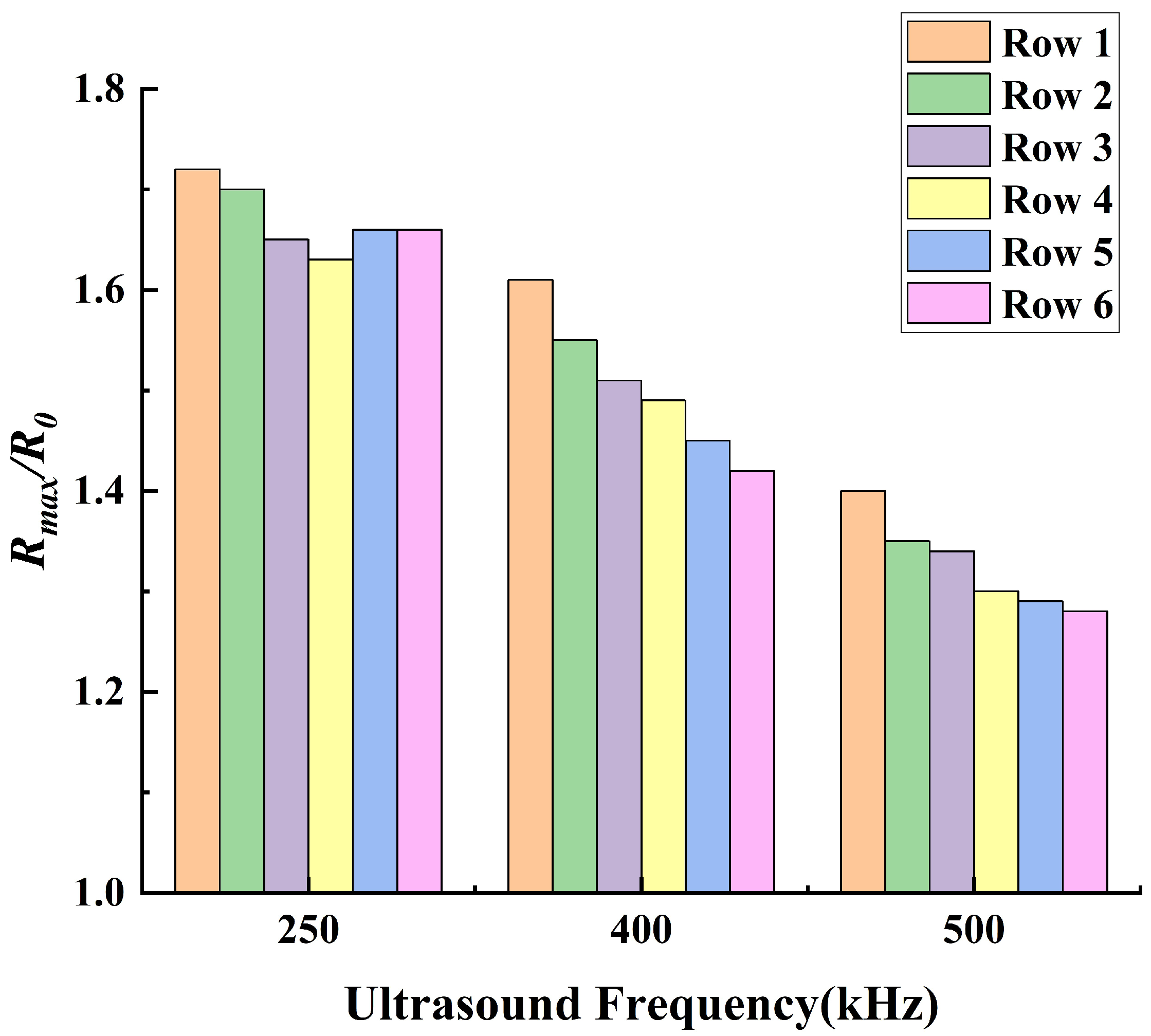
3.1. The Dynamic Behavior of Bubbles in Stable Cavitation
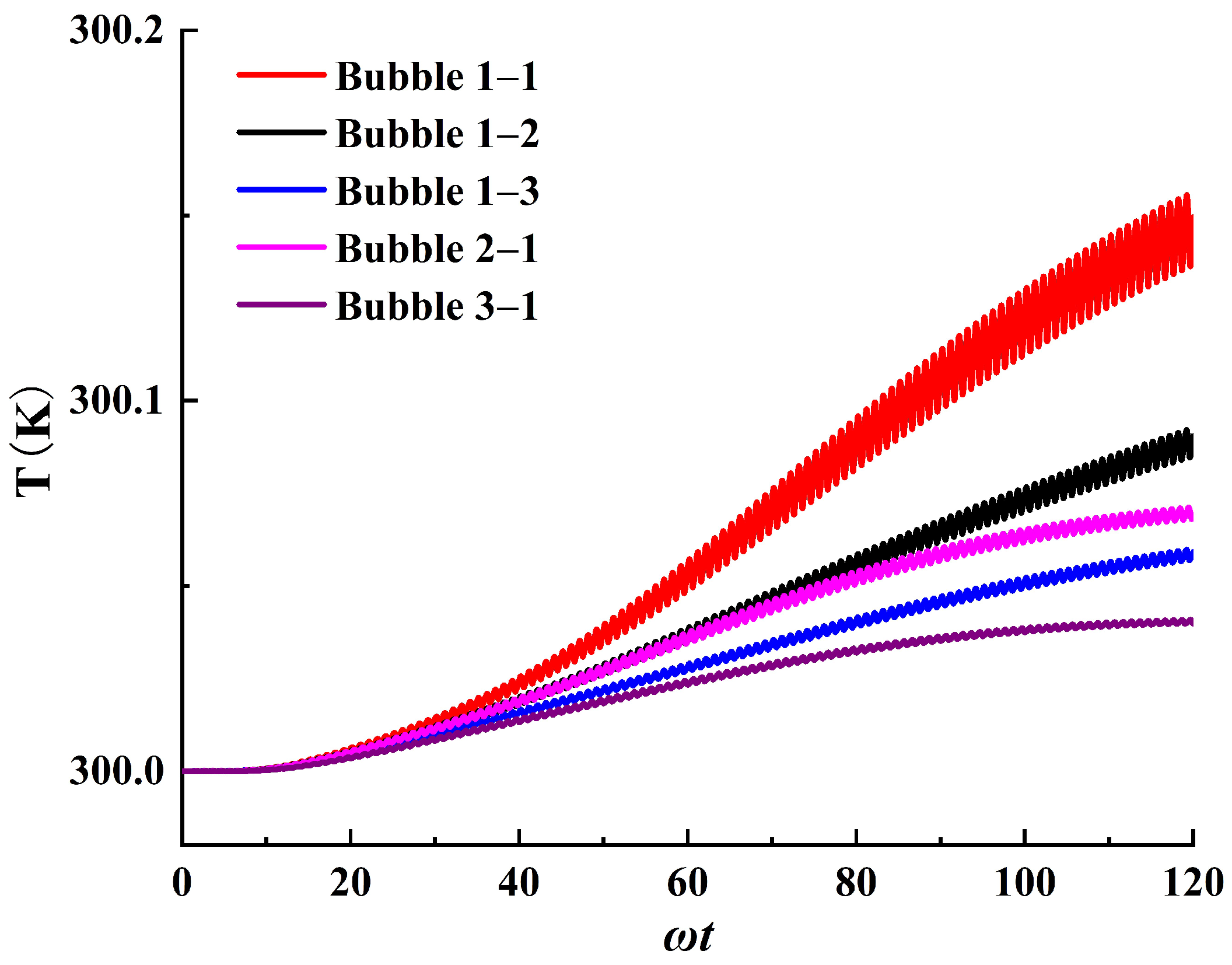
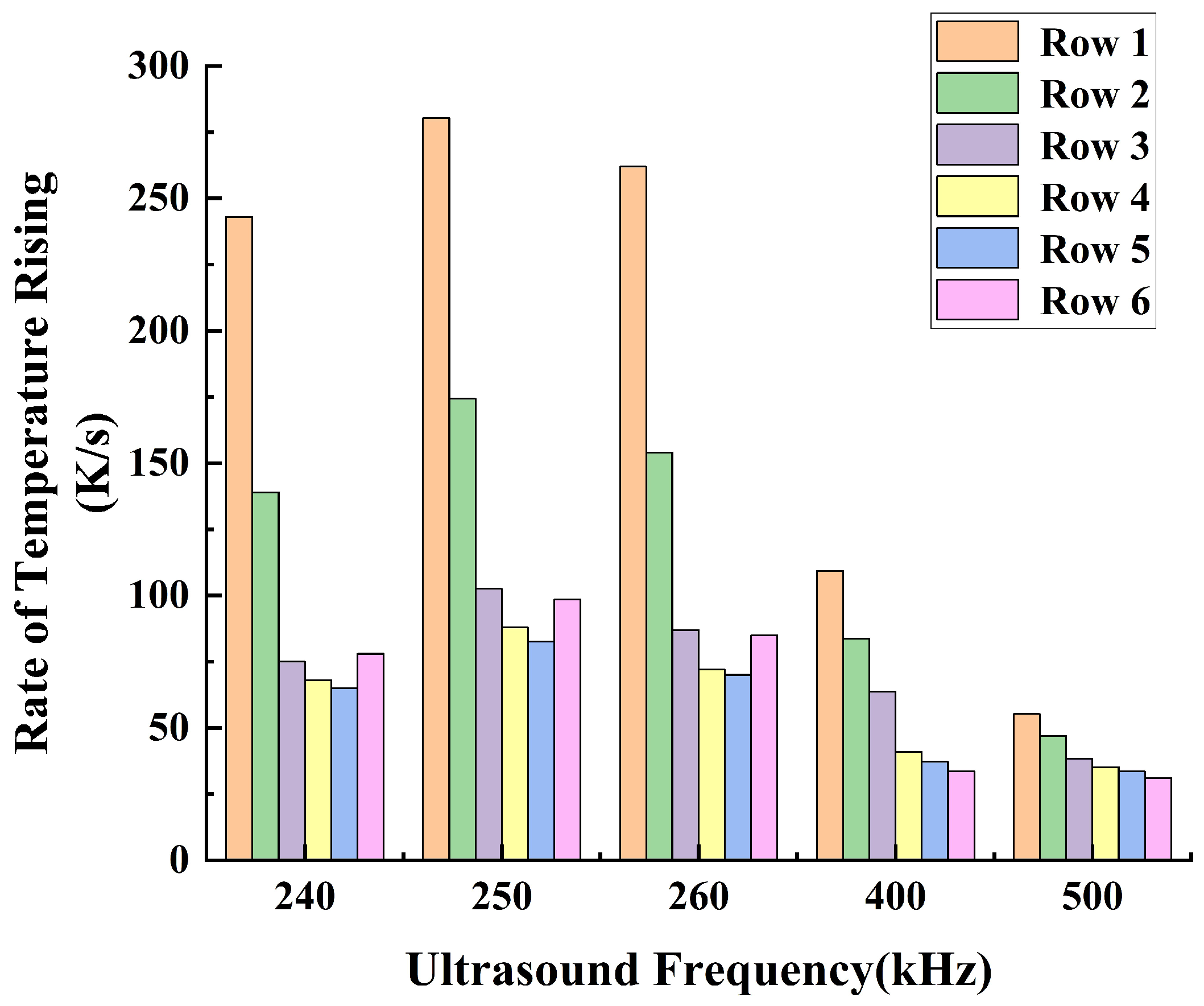
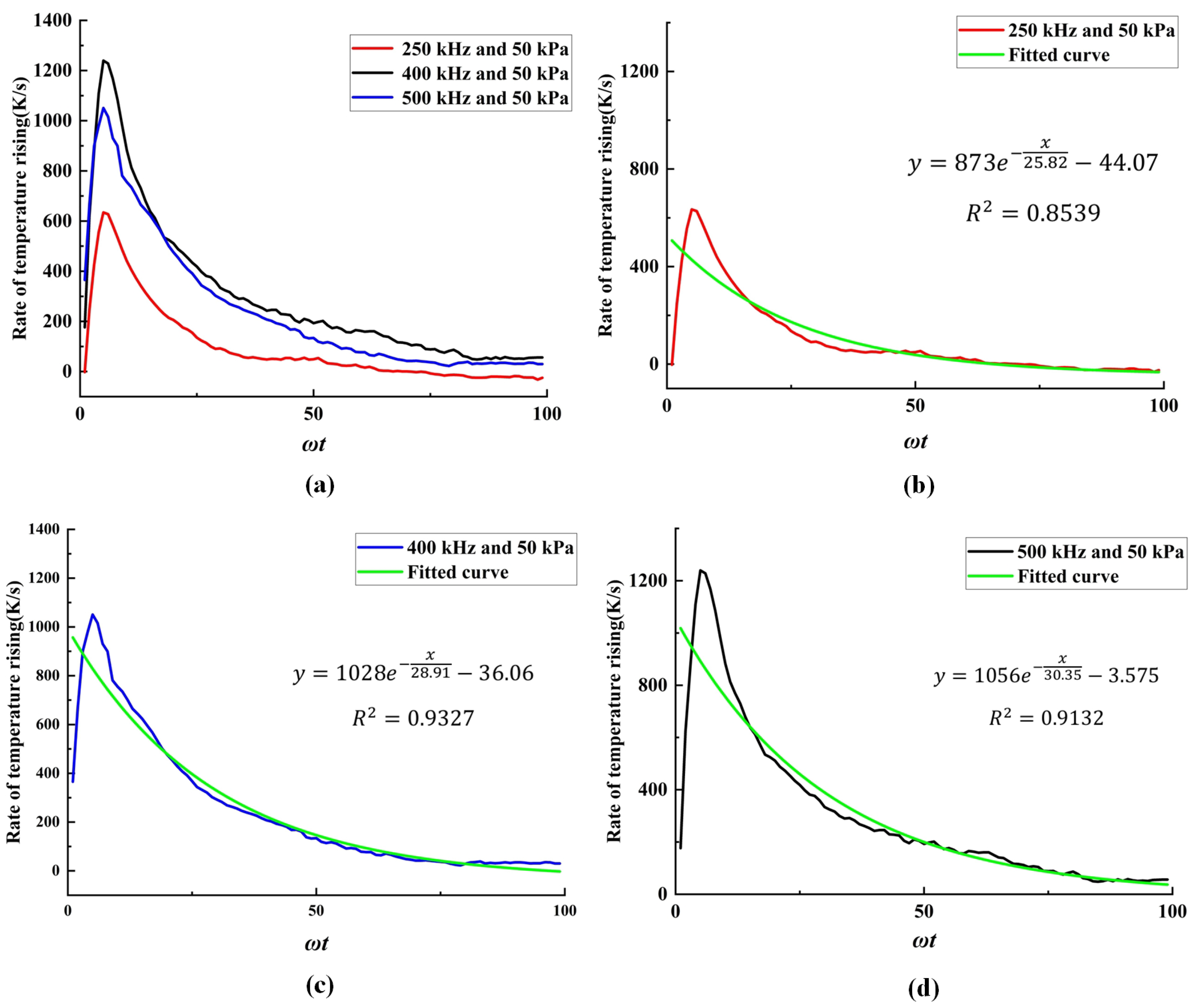
3.2. The Thermal Effects of Stable Cavitation
4. Conclusions
- (i)
- The thermal effect of ultrasound cavitation in bubbles is non−linearly positively correlated with the ultrasound pressure amplitude and the bubbles’ volume change. Additionally, acoustic scattering occurs when ultrasound passes through the bubbles, leading to acoustic focusing in the bubble cluster. Meanwhile, as the ultrasound frequency decreases, the intensity of acoustic focusing increases, with the focal point moving upstream.
- (ii)
- Under the operating conditions discussed in this study, the rate of cavitation thermal effects reaches its maximum at an ultrasound frequency of 250 kHz. At this frequency, the acoustic attenuation in flow and the energy absorption by bubbles reach a balance. When the ultrasound frequency is higher than 250 kHz, the acoustic attenuation is stronger, resulting in a slower temperature rise within the flow domain. Conversely, at a frequency lower than 250 kHz, the acoustic absorption of bubbles becomes weaker, also leading to a slower temperature rise in the flow domain.
- (iii)
- When the acoustic pressure on the bubble’s surface is above 210 kPa, both the bubble oscillation and the thermal effects of ultrasound cavitation are enhanced significantly. Conversely, when the acoustic pressure on the bubble’s surface is below 210 kPa, the bubble oscillation and thermal effects slightly weaken over time. In order to optimize and control the thermal effect of ultrasound therapy, the ultrasound frequency and amplitude should be carefully chosen based on the targeted bubble cluster.
- (iv)
- When bubbles start oscillating, a significant temperature rise occurs in the cavitation region, followed by a sharp decrease in the temperature rise rate, eventually stabilizing at a constant rate. Meanwhile, the temperature rise behavior tends to align with the unsteady heat diffusion model of a cylinder. During the stable cavitation process under long−period ultrasound, the bubble can be considered as a heat source with a constant internal temperature, supplying internal energy outward at a constant rate.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| VOF | Volume of Fluid |
| FVM | Finite Volume Method |
References
- Run-Yang, M.; Shu-Yu, L.; Cheng-Hui, W. Methods of study on sound cavitation. Appl. Acoust. 2009, 28, 389–400. [Google Scholar]
- Zirong, X. A quantitative study on the collapse mechanics of acoustic cavitation bubbles. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2021. [Google Scholar]
- Guédra, M.; Cornu, C.; Inserra, C. A derivation of the stable cavitation threshold accounting for bubble-bubble interactions. Ultrason. Sonochem. 2017, 38, 168–173. [Google Scholar] [PubMed]
- McLaughlan, J.; Rivens, I.; Leighton, T.; Ter Haar, G. A study of bubble activity generated in ex vivo tissue by high intensity focused ultrasound. Ultrasound Med. Biol. 2010, 36, 1327–1344. [Google Scholar] [CrossRef] [PubMed]
- Merouani, S.; Hamdaoui, O.; Rezgui, Y.; Guemini, M. Theoretical estimation of the temperature and pressure within collapsing acoustical bubbles. Ultrason. Sonochem. 2014, 21, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Coussios, C.C.; Roy, R.A. Applications of acoustics and cavitation to noninvasive therapy and drug delivery. Annu. Rev. Fluid Mech. 2008, 40, 395–420. [Google Scholar]
- Vivino, A.A.; Boraker, D.K.; Miller, D.; Nyborg, W. Stable cavitation at low ultrasonic intensities induces cell death and inhibits 3H-TdR incorporation by Con-A-stimulated murine lymphocytes in vitro. Ultrasound Med. Biol. 1985, 11, 751–759. [Google Scholar] [CrossRef]
- Hill, C.R.; Bamber, J.C.; ter Haar, G.R. Physical Principles of Medical Ultrasonics; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Wu, J. Temperature rise generated by ultrasound in the presence of contrast agent. Ultrasound Med. Biol. 1998, 24, 267–274. [Google Scholar] [CrossRef]
- Chavrier, F.; Chapelon, J.; Gelet, A.; Cathignol, D. Modeling of high-intensity focused ultrasound-induced lesions in the presence of cavitation bubbles. J. Acoust. Soc. Am. 2000, 108, 432–440. [Google Scholar] [CrossRef]
- Coussios, C.; Farny, C.; Ter Haar, G.; Roy, R. Role of acoustic cavitation in the delivery and monitoring of cancer treatment by high-intensity focused ultrasound (HIFU). Int. J. Hyperth. 2007, 23, 105–120. [CrossRef]
- Chen, W.S.; Lafon, C.; Matula, T.J.; Vaezy, S.; Crum, L.A. Mechanisms of lesion formation in high intensity focused ultrasound therapy. Acoust. Res. Lett. Online 2003, 4, 41–46. [Google Scholar]
- Holt, R.G.; Roy, R.A. Measurements of bubble-enhanced heating from focused, MHz-frequency ultrasound in a tissue-mimicking material. Ultrasound Med. Biol. 2001, 27, 1399–1412. [Google Scholar] [CrossRef] [PubMed]
- Chapelon, J.; Dupenloup, F.; Cohen, H.; Lenz, P. Reduction of cavitation using pseudorandom signals [therapeutic US]. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1996, 43, 623–625. [Google Scholar] [CrossRef]
- Pond, J.B. The role of heat in the production of ultrasonic focal lesions. J. Acoust. Soc. Am. 1970, 47, 1607–1611. [Google Scholar] [CrossRef]
- Rae, J.; Ashokkumar, M.; Eulaerts, O.; von Sonntag, C.; Reisse, J.; Grieser, F. Estimation of ultrasound induced cavitation bubble temperatures in aqueous solutions. Ultrason. Sonochem. 2005, 12, 325–329. [Google Scholar] [CrossRef]
- Misik, V.; Riesz, P. Free radical formation by ultrasound in organic liquids: A spin trapping and EPR study. J. Phys. Chem. 1994, 98, 1634–1640. [Google Scholar] [CrossRef]
- Zilonova, E.; Solovchuk, M.; Sheu, T. Simulation of cavitation enhanced temperature elevation in a soft tissue during high-intensity focused ultrasound thermal therapy. Ultrason. Sonochem. 2019, 53, 11–24. [Google Scholar] [CrossRef]
- Özsoy, Ç.; Lafci, B.; Reiss, M.; Deán-Ben, X.L.; Razansky, D. Real-time assessment of high-intensity focused ultrasound heating and cavitation with hybrid optoacoustic ultrasound imaging. Photoacoustics 2023, 31, 100508. [Google Scholar] [CrossRef]
- Wu, H.; Zheng, H.; Li, Y.; Ohl, C.D.; Yu, H.; Li, D. Effects of surface tension on the dynamics of a single micro bubble near a rigid wall in an ultrasonic field. Ultrason. Sonochem. 2021, 78, 105735. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.c.; Bai, X.r.; Cheng, H.y.; Ji, B. Temporal and spatial characteristics of monopole acoustic energy dominated by unsteady thermodynamic cavitating flow. J. Hydrodyn. 2021, 33, 867–871. [Google Scholar] [CrossRef]
- Koch, M.; Lechner, C.; Reuter, F.; Köhler, K.; Mettin, R.; Lauterborn, W. Numerical modeling of laser generated cavitation bubbles with the finite volume and volume of fluid method, using OpenFOAM. Comput. Fluids 2016, 126, 71–90. [Google Scholar] [CrossRef]
- Osterman, A.; Dular, M.; Sirok, B. Numerical simulation of a near-wall bubble collapse in an ultrasonic field. J. Fluid Sci. Technol. 2009, 4, 210–221. [Google Scholar]
- Ma, X.; Huang, B.; Li, Y.; Chang, Q.; Qiu, S.; Su, Z.; Fu, X.; Wang, G. Numerical simulation of single bubble dynamics under acoustic travelling waves. Ultrason. Sonochem. 2018, 42, 619–630. [Google Scholar]
- Tian, L.; Zhang, Y.X.; Yin, J.Y.; Lv, L.; Zhang, J.Y.; Zhu, J.J. Study on the liquid jet and shock wave produced by a near-wall cavitation bubble containing a small amount of non-condensable gas. Int. Commun. Heat Mass Transf. 2023, 145, 106815. [Google Scholar]
- Keller, J.B.; Miksis, M. Bubble oscillations of large amplitude. J. Acoust. Soc. Am. 1980, 68, 628–633. [Google Scholar] [CrossRef]
- Rahmatizadeh, B.; Beheshti, M.T.H.; Azadegan, M.; Najafi, M. Stability analysis and sliding mode control of a single spherical bubble described by Keller–Miksis equation. Int. J. Dyn. Control. 2021, 9, 1757–1764. [Google Scholar]
- Stricker, L.; Prosperetti, A.; Lohse, D. Validation of an approximate model for the thermal behavior in acoustically driven bubbles. J. Acoust. Soc. Am. 2011, 130, 3243–3251. [Google Scholar] [PubMed]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1979. [Google Scholar]
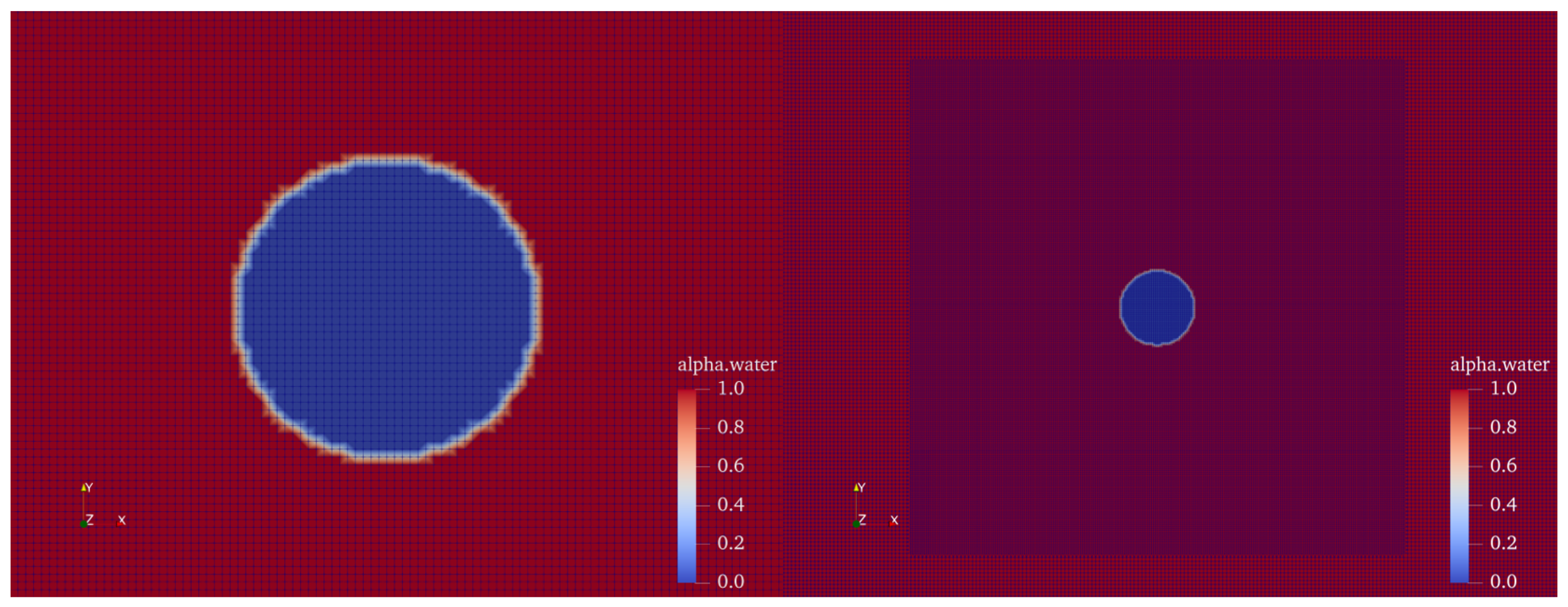

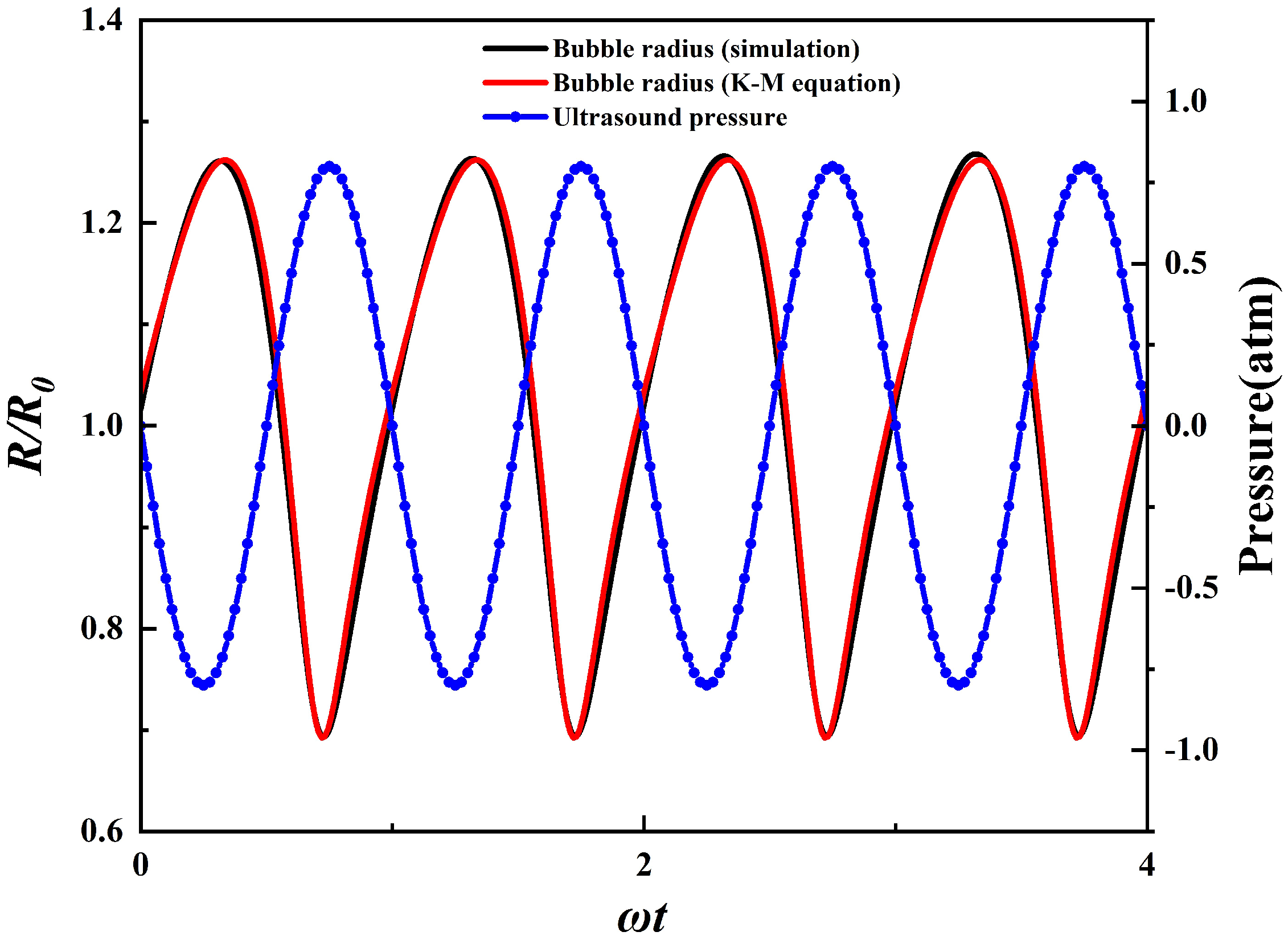
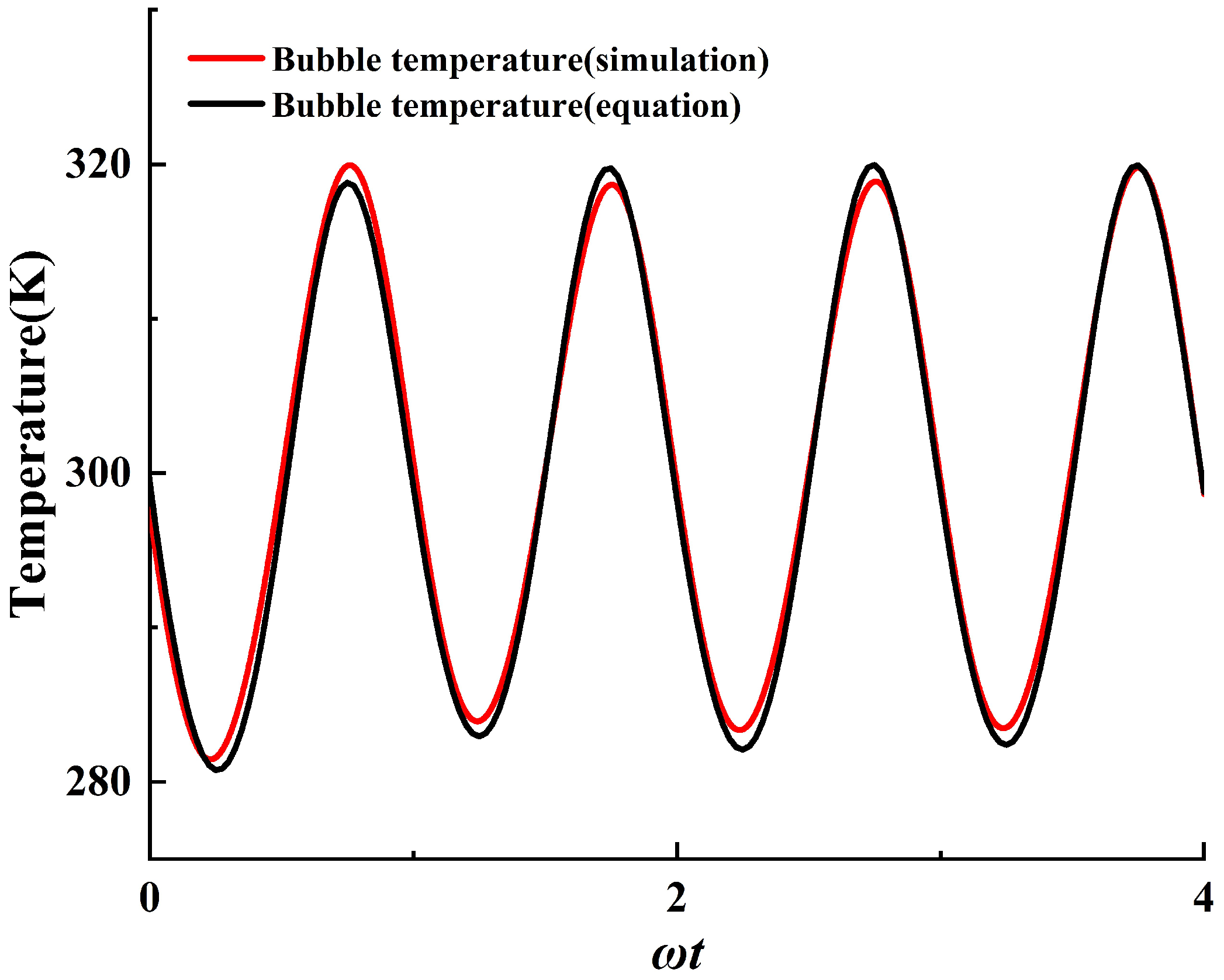
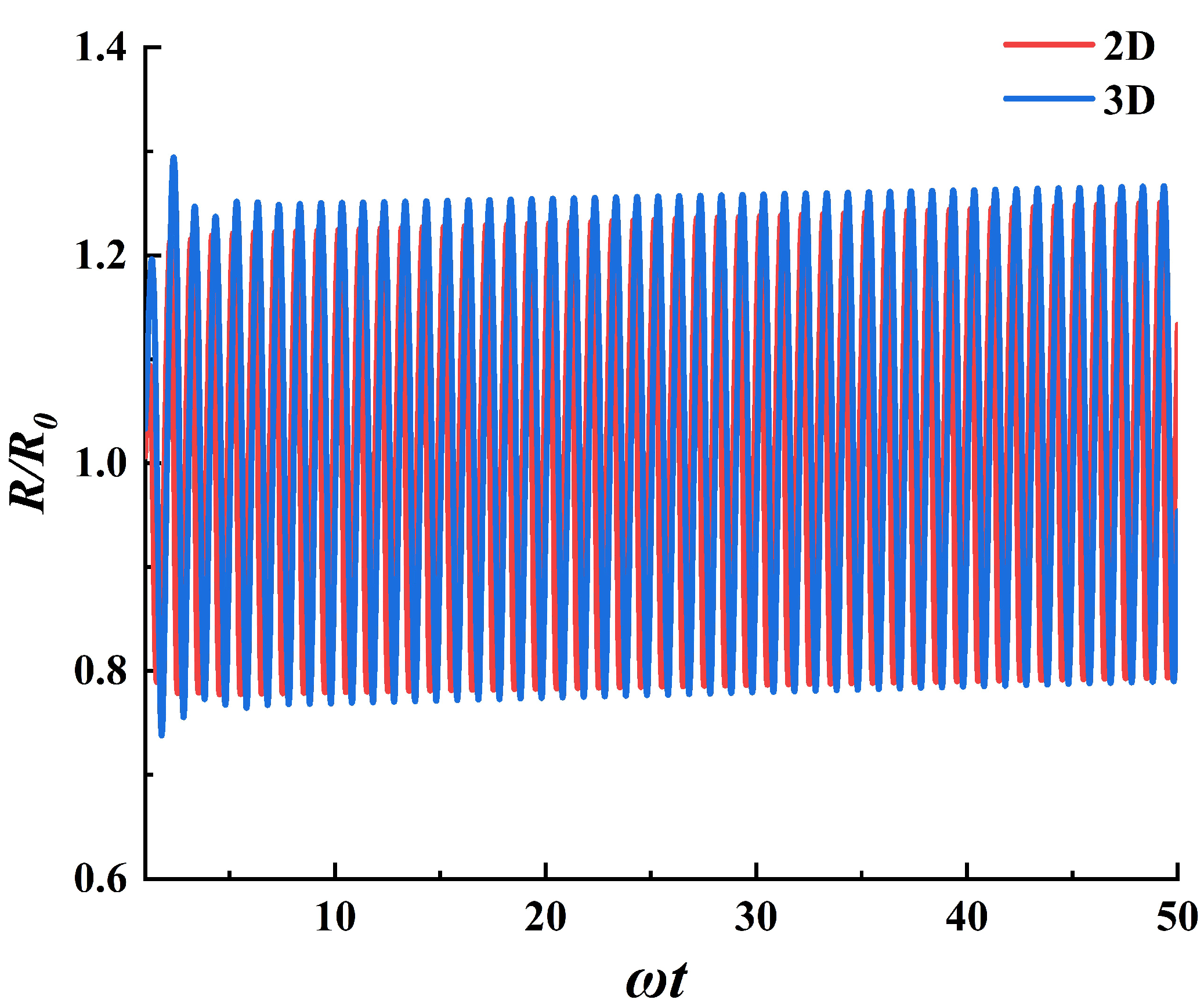
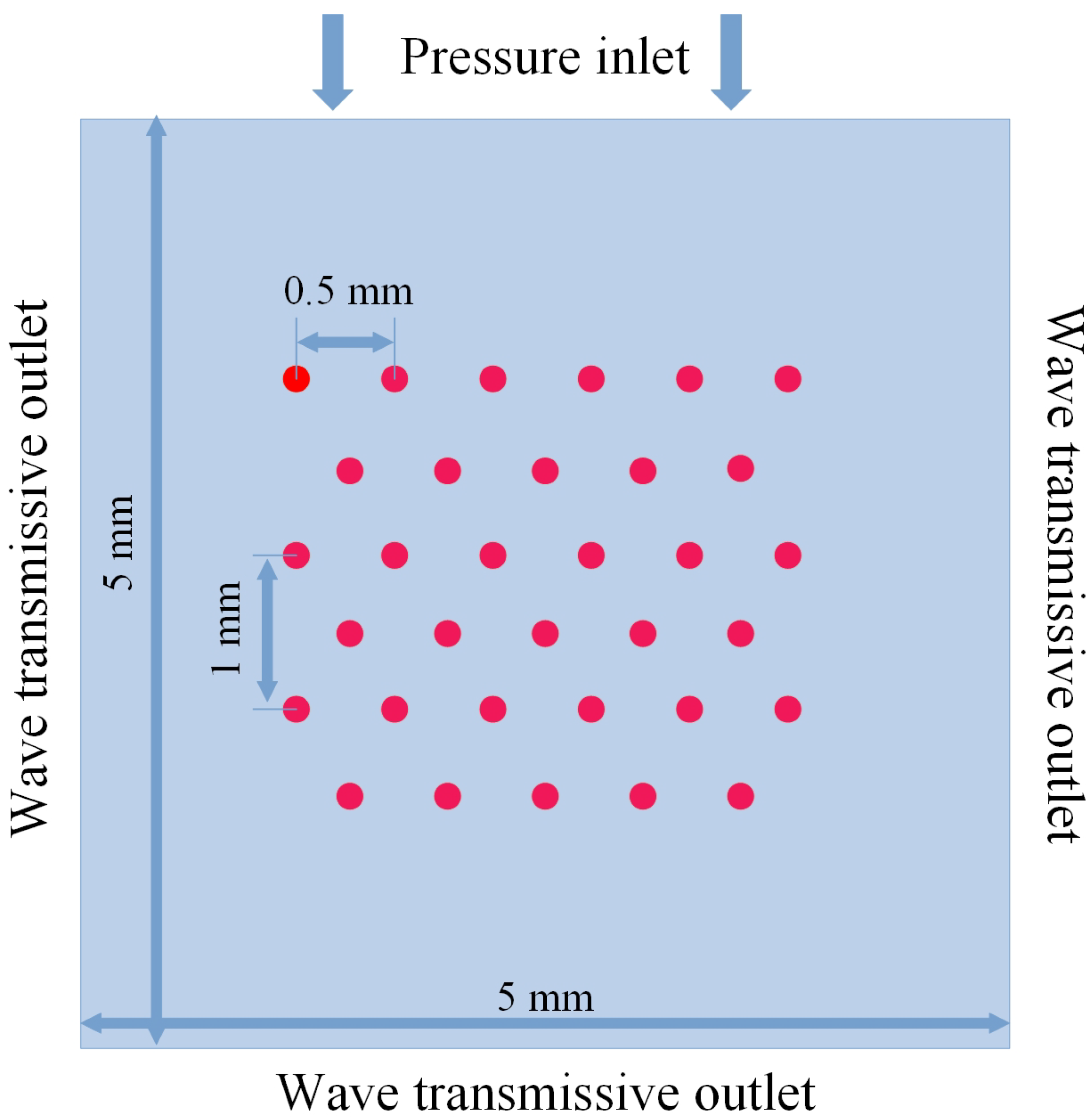





| Model | Total Cell Num | Cell Num in Bubble Radius | Time Step Size |
|---|---|---|---|
| 3D single bubble | 600 w | 20 | |
| 2D bubble cluster | 680 w | 20 |
| Quantity (Unit) | Symbol | Value |
|---|---|---|
| adiabatic exponent (−) | 1.40 | |
| bubble initial radius (μm) | 10 | |
| initial temperature (K) | 300 | |
| liquid phase dynamic viscosity (Pa·s) | μ1 | 0.03645 |
| liquid phase reference density (kg/m3) | 1087 | |
| atmospheric pressure (kPa) | 101.3 | |
| saturated vapor pressure (Pa) | 2440 | |
| surface tension (kg/s2) | 0.076 | |
| pressure amplitude (kPa) | 80 | |
| pressure frequency (kHz) | 250 |
| Parameter | Example |
|---|---|
| Pressure amplitude (kPa) | 50/100 |
| Pressure frequency (kHz) | 100/200/250/400/500 |
| Volume Change | 200 kHz | 250 kHz | 500 kHz |
|---|---|---|---|
| 50 kPa | Decrease 10% | Decrease 8% | Decrease 5% |
| 100 kPa | Increase 5% | Increase 5% | Increase 2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, T.; Zhang, J.; Ye, J.; Gao, Z. Numerical Study on the Dynamics and Thermal Effects of Bubble Stable Cavitation in Focused Ultrasound Fields. Processes 2025, 13, 951. https://doi.org/10.3390/pr13040951
Huang T, Zhang J, Ye J, Gao Z. Numerical Study on the Dynamics and Thermal Effects of Bubble Stable Cavitation in Focused Ultrasound Fields. Processes. 2025; 13(4):951. https://doi.org/10.3390/pr13040951
Chicago/Turabian StyleHuang, Tianyang, Jing Zhang, Jiacheng Ye, and Zhekai Gao. 2025. "Numerical Study on the Dynamics and Thermal Effects of Bubble Stable Cavitation in Focused Ultrasound Fields" Processes 13, no. 4: 951. https://doi.org/10.3390/pr13040951
APA StyleHuang, T., Zhang, J., Ye, J., & Gao, Z. (2025). Numerical Study on the Dynamics and Thermal Effects of Bubble Stable Cavitation in Focused Ultrasound Fields. Processes, 13(4), 951. https://doi.org/10.3390/pr13040951






