Investigation of Surface Quality and Productivity in Precision Hard Turning of AISI 4340 Steel Using Integrated Approach of ML-MOORA-PSO
Abstract
1. Introduction
- (i)
- To look deeper into the influence of wiper geometry and conventional tool inserts on productivity (MRR) and quality (Ra).
- (ii)
- To predict the Ra (after machining by wiper and conventional tool inserts) and MRR after implementation of the ML approach. The results obtained after the above-mentioned approaches will be compared to find the best one, which will be more suitable to adopt the design parameters of for the application of gun barrels.
- (iii)
- To convert the predicted solutions into a single dimensionless quantity known as a performance measure (PM) after normalization using the MOORA method.
- (iv)
- To develop the empirical model for PM and set up a relation between the input parameters and PM.
- (v)
- To apply the PSO on PM for the optimization of input parameters and perform the validation experiments at the suggested setting. Compare the results of the hybrid approach ML-MOORA-PSO with the ML-MOORA.
2. Materials and Methods
2.1. Test Specimen and Cutting Tool Specification
2.2. Surface Roughness Evaluation
2.3. Experiments Configuration
2.4. Methodology
2.4.1. Machine Learning (ML) Methodology
2.4.2. Data Normalization Using MOORA
3. Results and Discussion
3.1. Variation in Ra and MRR
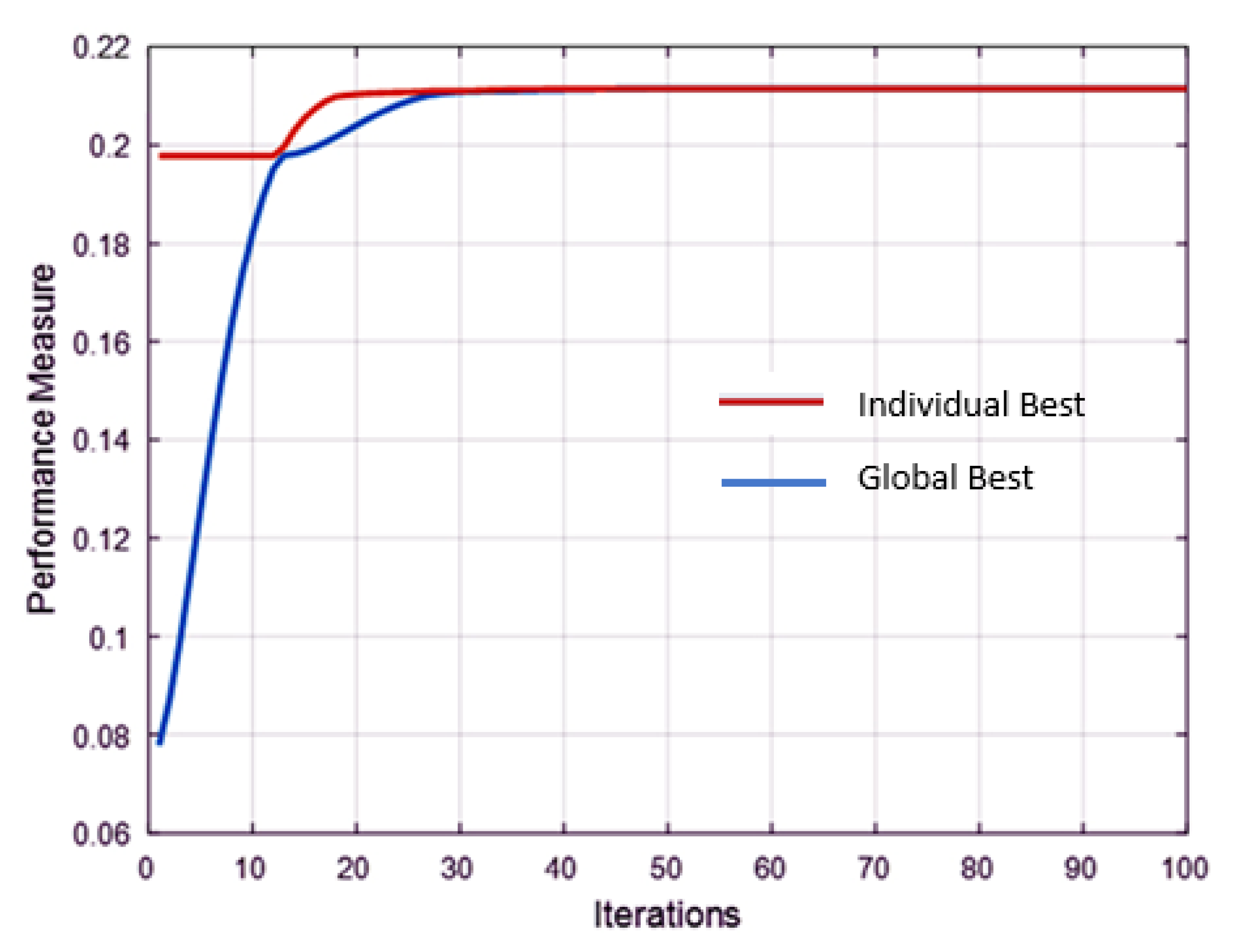
3.2. Implementation of Particle Swarm Optimization (PSO)
4. Computational Experience
5. Conclusions
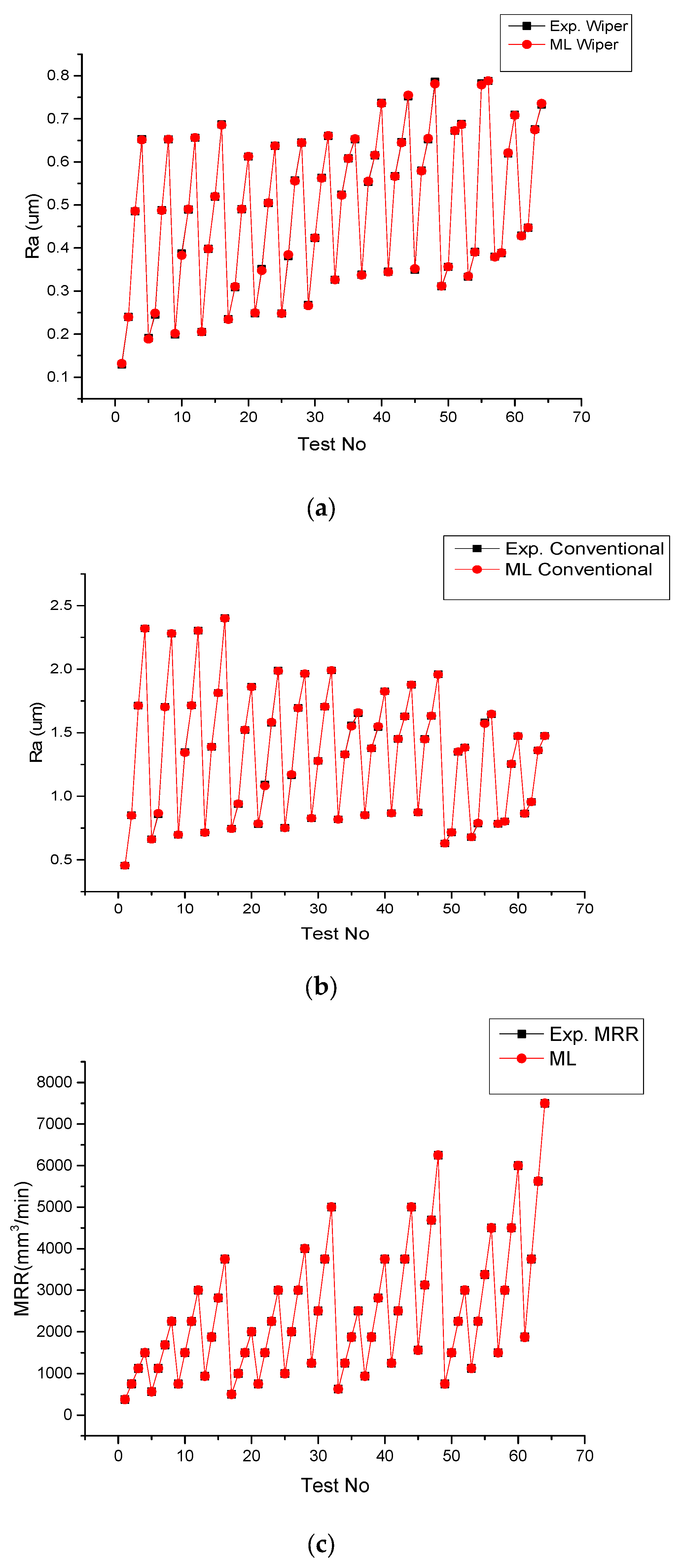
- The findings revealed that the variation in Ra with respect to depth of cut (DoC) was relatively small, increasing from 0.48 µm to 0.52 µm as DoC increased from 0.1 mm to 0.25 mm. This slight increase is attributed to the larger engagement of the tool in the workpiece, which results in the removal of larger craters, thereby marginally increasing surface roughness. Additionally, Ra increased significantly from 0.29 µm to 0.7 µm as the feed rate (f) increased from 0.05 mm/rev to 0.2 mm/rev due to the increased material removal per revolution, leading to larger craters on the machined surface. Conversely, a higher cutting speed (CS) led to a reduction in Ra, likely due to the minimization of built-up edge formation, which enhances surface quality.
- The study also highlighted the effect of machining parameters on MRR. It was observed that MRR increased from 1600 mm3/min to 3400 mm3/min with increasing CS, as a higher cutting speed enables more material removal in a given time. Similarly, MRR increased with increasing DoC and f, which is attributed to the greater volume of material engaged in cutting.
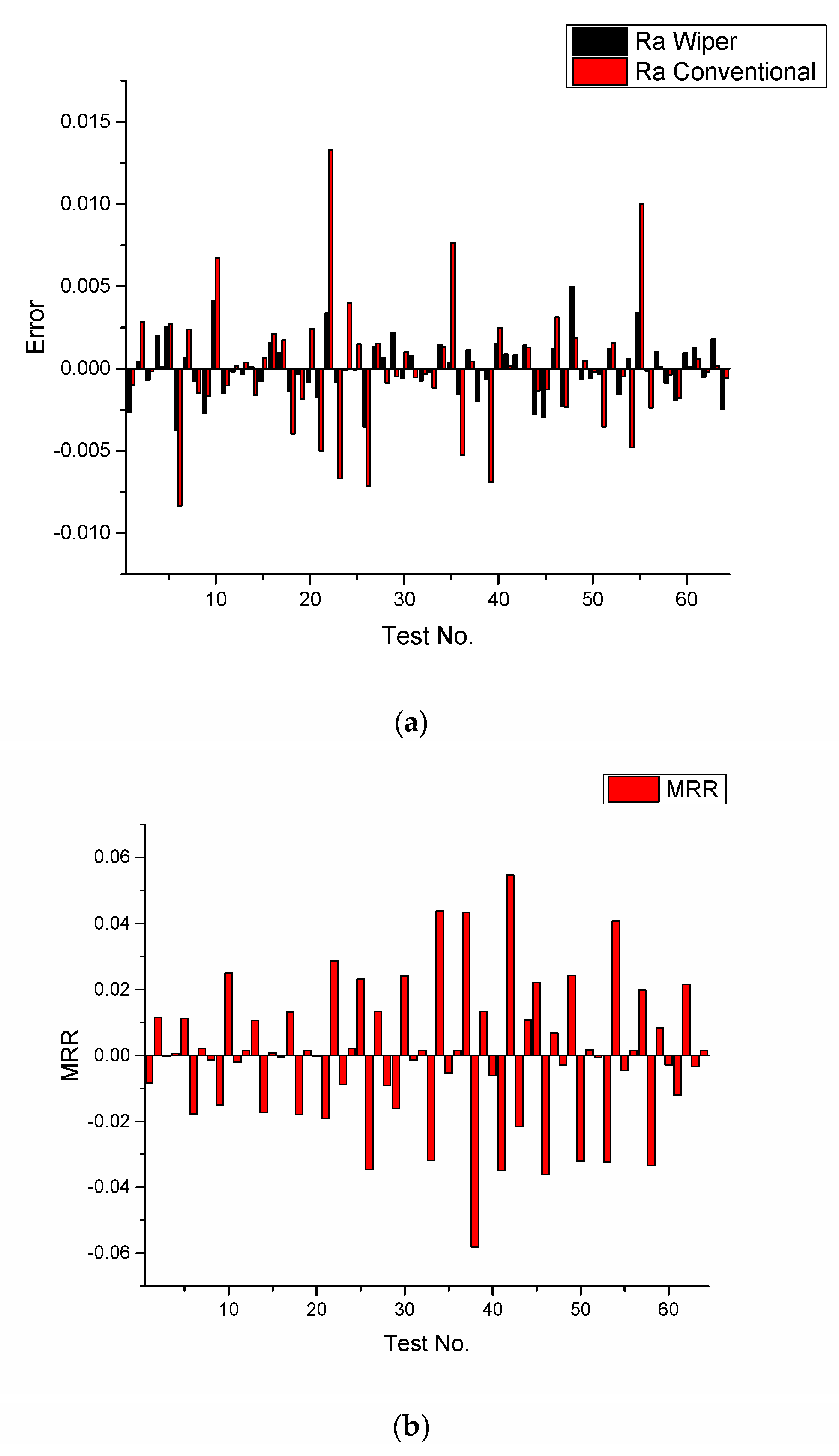
- Statistical analysis confirmed the reliability of the predictive models. The coefficient of determination (R2) values for Ra and MRR exceeded 99%, indicating a high degree of accuracy in ML-based predictions. The analysis of errors revealed minimal deviations between experimental and predicted values, affirming the robustness of the ML model.
- A comparative assessment of wiper and conventional tool inserts demonstrated that wiper geometry provides superior surface quality due to its secondary cutting edge, which eliminates microscopic ridges. The mean square error (MSE) for Ra was found to be lower for wiper inserts compared to conventional inserts, further validating the enhanced performance of wiper geometry in achieving better machining responses.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Test | Speed | Depth of Cut | Feed | Surface Roughness, Ra, (μm) | MRR | Test | Speed | Depth of Cut | Feed | Surface Roughness, Ra, (μm) | MRR | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | (m/min) | (mm) | (mm/rev) | Wiper | Conv. | (mm3/min) | No. | (m/min) | (mm) | (mm/rev) | Wiper | Conv. | (mm3/min) |
| 1 | 75 | 0.1 | 0.05 | 0.129 | 0.454 | 375 | 33 | 125 | 0.1 | 0.05 | 0.326 | 0.817 | 625 |
| 2 | 75 | 0.1 | 0.1 | 0.24 | 0.851 | 750 | 34 | 125 | 0.1 | 0.1 | 0.524 | 1.331 | 1250 |
| 3 | 75 | 0.1 | 0.15 | 0.485 | 1.713 | 1125 | 35 | 125 | 0.1 | 0.15 | 0.608 | 1.558 | 1875 |
| 4 | 75 | 0.1 | 0.2 | 0.653 | 2.32 | 1500 | 36 | 125 | 0.1 | 0.2 | 0.652 | 1.654 | 2500 |
| 5 | 75 | 0.15 | 0.05 | 0.191 | 0.663 | 562.5 | 37 | 125 | 0.15 | 0.05 | 0.338 | 0.852 | 937.5 |
| 6 | 75 | 0.15 | 0.1 | 0.245 | 0.858 | 1125 | 38 | 125 | 0.15 | 0.1 | 0.553 | 1.377 | 1875 |
| 7 | 75 | 0.15 | 0.15 | 0.488 | 1.704 | 1687.5 | 39 | 125 | 0.15 | 0.15 | 0.615 | 1.544 | 2812.5 |
| 8 | 75 | 0.15 | 0.2 | 0.652 | 2.28 | 2250 | 40 | 125 | 0.15 | 0.2 | 0.737 | 1.827 | 3750 |
| 9 | 75 | 0.2 | 0.05 | 0.199 | 0.696 | 750 | 41 | 125 | 0.2 | 0.05 | 0.345 | 0.867 | 1250 |
| 10 | 75 | 0.2 | 0.1 | 0.387 | 1.349 | 1500 | 42 | 125 | 0.2 | 0.1 | 0.567 | 1.451 | 2500 |
| 11 | 75 | 0.2 | 0.15 | 0.489 | 1.714 | 2250 | 43 | 125 | 0.2 | 0.15 | 0.646 | 1.629 | 3750 |
| 12 | 75 | 0.2 | 0.2 | 0.656 | 2.303 | 3000 | 44 | 125 | 0.2 | 0.2 | 0.752 | 1.877 | 5000 |
| 13 | 75 | 0.25 | 0.05 | 0.205 | 0.715 | 937.5 | 45 | 125 | 0.25 | 0.05 | 0.349 | 0.873 | 1562.5 |
| 14 | 75 | 0.25 | 0.1 | 0.398 | 1.388 | 1875 | 46 | 125 | 0.25 | 0.1 | 0.58 | 1.451 | 3125 |
| 15 | 75 | 0.25 | 0.15 | 0.519 | 1.814 | 2812.5 | 47 | 125 | 0.25 | 0.15 | 0.652 | 1.631 | 4687.5 |
| 16 | 75 | 0.25 | 0.2 | 0.687 | 2.402 | 3750 | 48 | 125 | 0.25 | 0.2 | 0.786 | 1.96 | 6250 |
| 17 | 100 | 0.1 | 0.05 | 0.235 | 0.746 | 500 | 49 | 150 | 0.1 | 0.05 | 0.311 | 0.629 | 750 |
| 18 | 100 | 0.1 | 0.1 | 0.309 | 0.938 | 1000 | 50 | 150 | 0.1 | 0.1 | 0.356 | 0.716 | 1500 |
| 19 | 100 | 0.1 | 0.15 | 0.49 | 1.521 | 1500 | 51 | 150 | 0.1 | 0.15 | 0.672 | 1.348 | 2250 |
| 20 | 100 | 0.1 | 0.2 | 0.612 | 1.862 | 2000 | 52 | 150 | 0.1 | 0.2 | 0.688 | 1.384 | 3000 |
| 21 | 100 | 0.15 | 0.05 | 0.248 | 0.78 | 750 | 53 | 150 | 0.15 | 0.05 | 0.333 | 0.678 | 1125 |
| 22 | 100 | 0.15 | 0.1 | 0.351 | 1.094 | 1500 | 54 | 150 | 0.15 | 0.1 | 0.391 | 0.785 | 2250 |
| 23 | 100 | 0.15 | 0.15 | 0.504 | 1.577 | 2250 | 55 | 150 | 0.15 | 0.15 | 0.782 | 1.581 | 3375 |
| 24 | 100 | 0.15 | 0.2 | 0.637 | 1.989 | 3000 | 56 | 150 | 0.15 | 0.2 | 0.788 | 1.645 | 4500 |
| 25 | 100 | 0.2 | 0.05 | 0.248 | 0.752 | 1000 | 57 | 150 | 0.2 | 0.05 | 0.38 | 0.783 | 1500 |
| 26 | 100 | 0.2 | 0.1 | 0.381 | 1.165 | 2000 | 58 | 150 | 0.2 | 0.1 | 0.388 | 0.802 | 3000 |
| 27 | 100 | 0.2 | 0.15 | 0.557 | 1.695 | 3000 | 59 | 150 | 0.2 | 0.15 | 0.619 | 1.253 | 4500 |
| 28 | 100 | 0.2 | 0.2 | 0.645 | 1.964 | 4000 | 60 | 150 | 0.2 | 0.2 | 0.709 | 1.474 | 6000 |
| 29 | 100 | 0.25 | 0.05 | 0.268 | 0.827 | 1250 | 61 | 150 | 0.25 | 0.05 | 0.429 | 0.864 | 1875 |
| 30 | 100 | 0.25 | 0.1 | 0.423 | 1.279 | 2500 | 62 | 150 | 0.25 | 0.1 | 0.447 | 0.956 | 3750 |
| 31 | 100 | 0.25 | 0.15 | 0.563 | 1.704 | 3750 | 63 | 150 | 0.25 | 0.15 | 0.676 | 1.361 | 5625 |
| 32 | 100 | 0.25 | 0.2 | 0.66 | 1.99 | 5000 | 64 | 150 | 0.25 | 0.2 | 0.733 | 1.475 | 7500 |
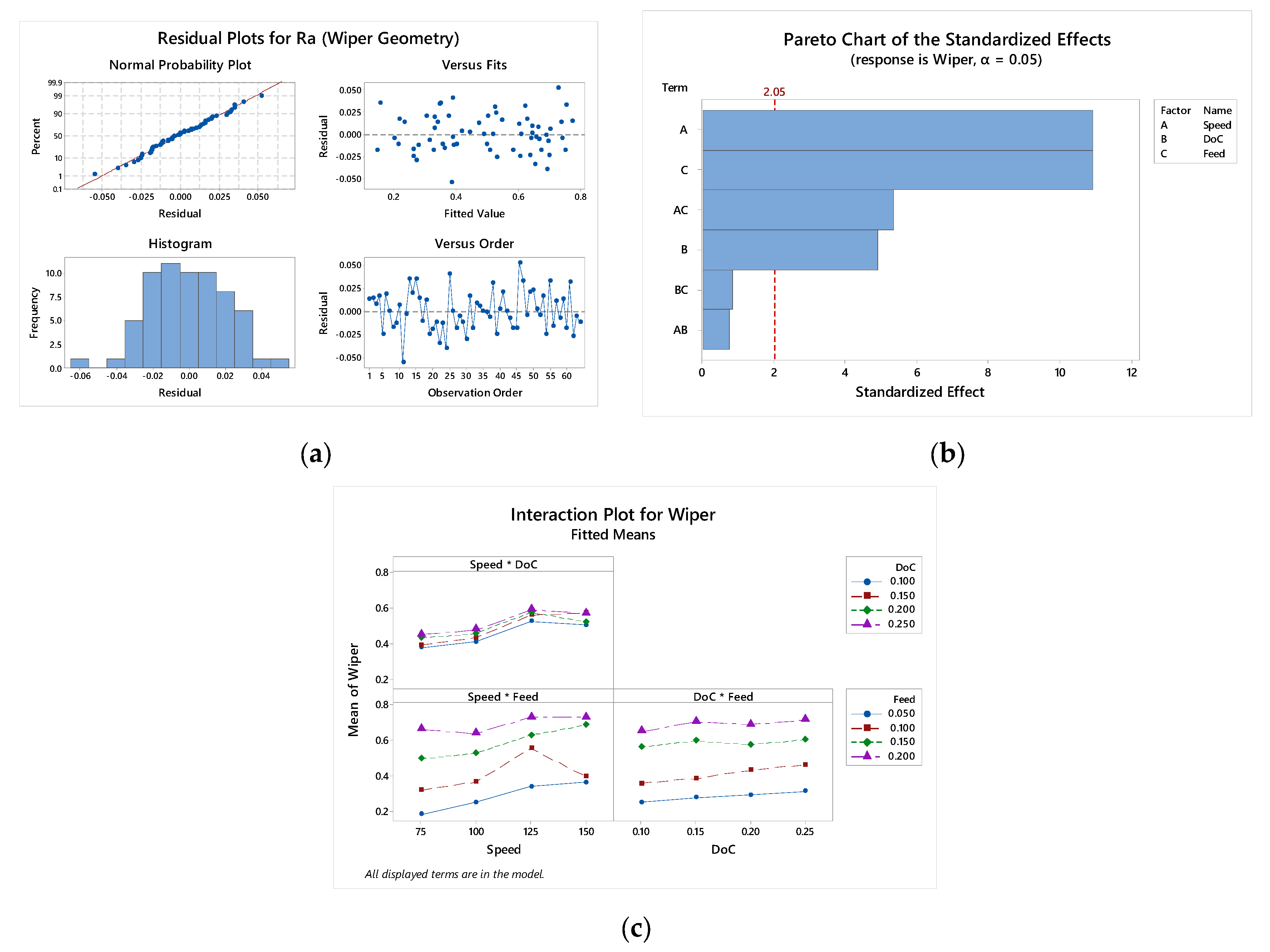
| Ra (Wiper Geometry) | |||||
|---|---|---|---|---|---|
| Source | DF | SS | MS | F-Value | p-Value |
| Model | 36 | 1.96870 | 0.054686 | 51.79 | 0.000 |
| Linear | 9 | 1.87290 | 0.208100 | 197.08 | 0.000 |
| Speed | 3 | 0.25868 | 0.086228 | 81.66 | 0.000 |
| DoC | 3 | 0.03758 | 0.012527 | 11.86 | 0.000 |
| Feed | 3 | 1.57663 | 0.525545 | 497.70 | 0.000 |
| 2-Way Interactions | 27 | 0.09580 | 0.003548 | 3.36 | 0.001 |
| Speed × DoC | 9 | 0.00963 | 0.001070 | 1.01 | 0.454 |
| Speed × Feed | 9 | 0.07588 | 0.008432 | 7.98 | 0.000 |
| DoC × Feed | 9 | 0.01029 | 0.001144 | 1.08 | 0.406 |
| Error | 27 | 0.02851 | 0.001056 | ||
| Total | 63 | 1.99721 | S: 0.0324952; R2: 98.57%; Adj R2: 96.67%; R2 Pred.: 91.98% | ||
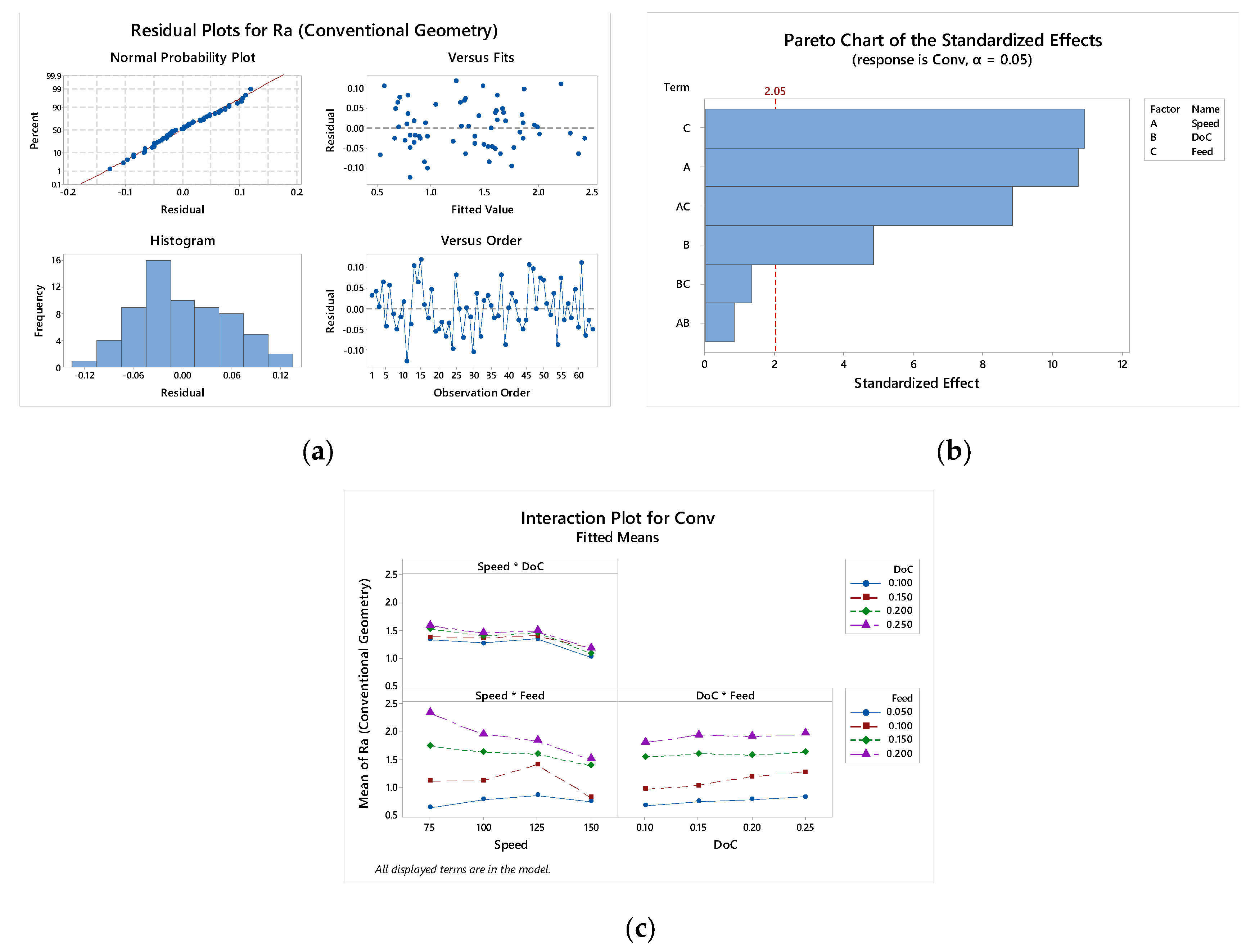
| Ra (Conventional Geometry) | |||||
| Model | 36 | 15.2934 | 0.42482 | 55.63 | 0.000 |
| Linear | 9 | 13.8181 | 1.53535 | 201.06 | 0.000 |
| Speed | 3 | 1.1679 | 0.38930 | 50.98 | 0.000 |
| DoC | 3 | 0.2661 | 0.08871 | 11.62 | 0.000 |
| Feed | 3 | 12.3841 | 4.12804 | 540.58 | 0.000 |
| 2-Way Interactions | 27 | 1.4753 | 0.05464 | 7.16 | 0.000 |
| Speed × DoC | 9 | 0.0746 | 0.00829 | 1.09 | 0.404 |
| Speed × Feed | 9 | 1.2955 | 0.14395 | 18.85 | 0.000 |
| DoC × Feed | 9 | 0.1051 | 0.01168 | 1.53 | 0.188 |
| Error | 27 | 0.2062 | 0.00764 | ||
| Total | 63 | 15.4996 | S: 0.0873863; R2: 98.67%; Adj R2: 96.90%; R2 Pred.: 92.53% | ||
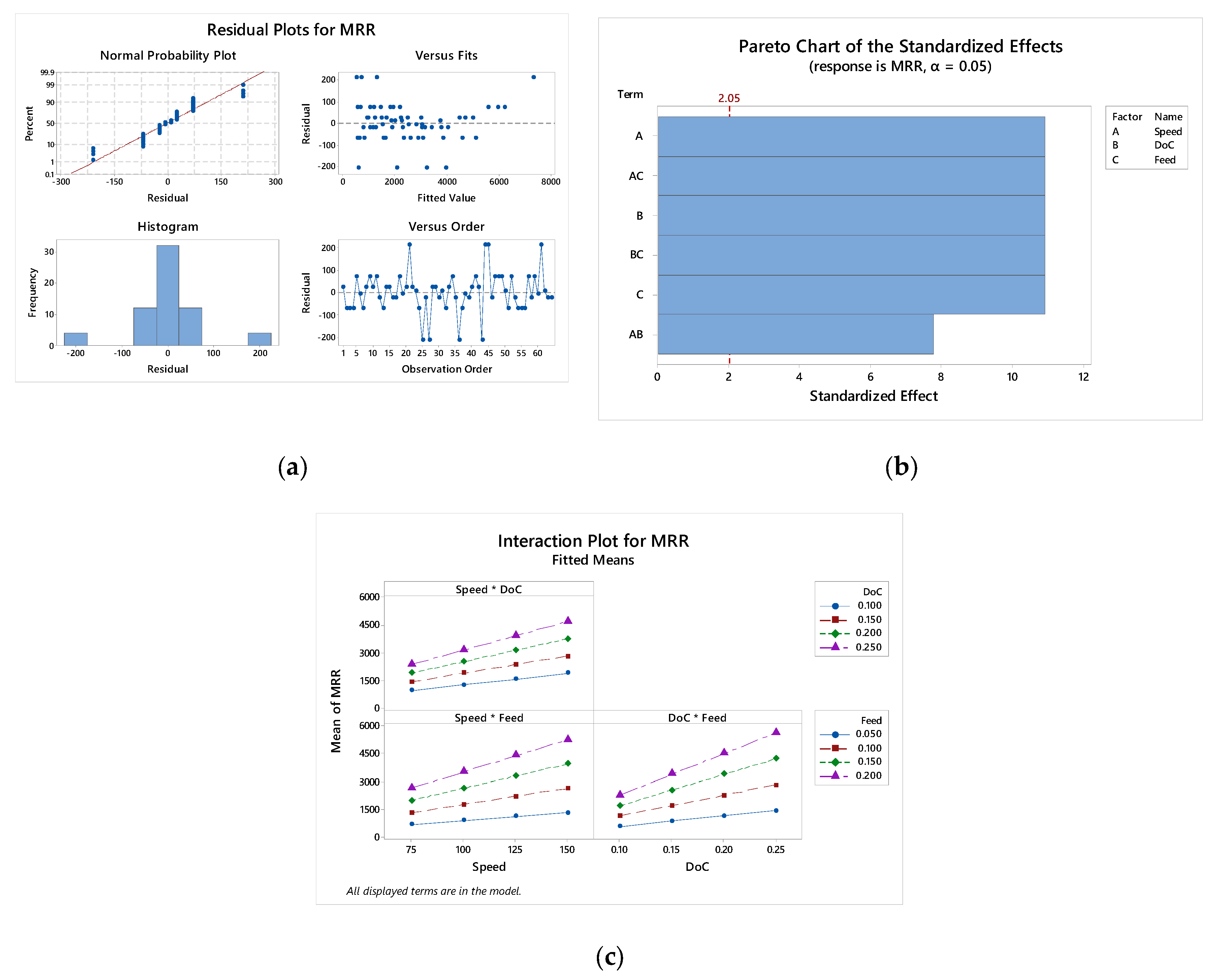
| MRR | |||||
| Model | 36 | 15,61,32,812 | 43,37,023 | 239.82 | 0.000 |
| Linear | 9 | 14,09,96,094 | 15,66,62,33 | 866.28 | 0.000 |
| Speed | 3 | 2,39,25,781 | 79,75,260 | 441.00 | 0.000 |
| DoC | 3 | 3,95,50,781 | 1,31,83,594 | 729.00 | 0.000 |
| Feed | 3 | 7,75,19,531 | 2,58,39,844 | 1428.84 | 0.000 |
| 2-Way Interactions | 27 | 1,51,36,719 | 5,60,619 | 31.00 | 0.000 |
| Speed × DoC | 9 | 24,41,406 | 2,71,267 | 15.00 | 0.000 |
| Speed × Feed | 9 | 47,85,156 | 5,31,684 | 29.40 | 0.000 |
| DoC × Feed | 9 | 79,10,156 | 8,78,906 | 48.60 | 0.000 |
| Error | 27 | 4,88,281 | 18,084 | ||
| Total | 63 | 15,66,21,094 | S: 134.479; R2: 99.69%; Adj R2: 99.27%; R2 Pred.: 98.25% | ||
Appendix B
- Booster Type (‘gbtree’): The ‘gbtree’ booster was selected because it is well-suited for handling structured data with complex interactions among features. Given that machining parameters have non-linear relationships, tree-based models generally perform better than linear models (‘gblinear’).
- Evaluation Metric (RMSE): Root Mean Squared Error (RMSE) was chosen as the primary evaluation metric because it effectively measures prediction accuracy while penalizing large errors, which is crucial in machining optimization, where precise control over parameters is needed.
- Gamma (0): A gamma value of 0 was chosen to allow all splits initially and then fine-tune based on performance. Higher values of gamma would restrict tree splitting, which was not required for the given dataset size and complexity.
- Minimum Child Weight (1): A lower child weight ensures that even smaller subgroups in data are considered while splitting nodes. This helps in capturing variations in machining parameters without overfitting.
- Column Sampling Ratio (1): A full column sample (colsample_bytree = 1) was initially selected to allow the model to consider all features and ensure no relevant information was ignored. However, fine-tuning was conducted using values of 0.9 and 1.
- Subsample Ratio (1): A full subsample was initially chosen to avoid introducing randomness. Further optimization was performed by testing subsample values of 0.9 and 1 to observe its effect on model stability.
- Maximum Depth (6): This value was selected to balance model complexity and performance. A deeper tree might overfit, while a shallower tree might underfit. A tuning grid was tested for depths of 2, 4, 6, and 8 to optimize this tradeoff.
- Learning Rate (Eta = 0.3): A learning rate of 0.3 was selected based on empirical studies, which suggest that for boosting methods, an initial eta in the range of 0.1–0.3 often provides a good balance between convergence speed and performance. Lower values (0.05, 0.1) were also tested for further refinement.
- Early Stopping (20 rounds): The stopping criterion of 20 rounds was used to prevent overfitting. If the validation score did not improve over 20 consecutive rounds, training was stopped to save computational resources.
- Five-Fold Cross-Validation: A 5-fold scheme was used as a standard practice in machine learning to balance computational efficiency and model reliability. Increasing folds (e.g., 10-fold) would increase computation time significantly, while fewer folds (e.g., 3-fold) might not generalize well.
- Tuning Grid Selection: The parameter grid was selected based on prior literature and empirical testing. The chosen ranges ensured a comprehensive search space without excessive computational overhead.
- R2 and MAPE: R2 was chosen as a performance measure to evaluate how well the model explains variance in the machining performance outputs (MRR, Ra). Mean absolute percentage error (MAPE) was used to assess the relative error percentage, ensuring practical significance in real-world applications. The obtained values (R2 > 0.98 and MAPE < 3%) indicate a well-optimized model with high predictive accuracy.
Appendix C
- Population Size (Swarm Size): 40; Maximum Iterations: 100;
- Constriction Coefficients: kappa = 1;
- phi1 = 2.05;
- phi2 = 2.05;
- chi = 2 ∗ kappa/abs (2-phi-sqrt (phi2 − 4 ∗ phi))
- Inertia Coefficient: w = chi
- Damping Ratio of Inertia Weight: wdamp = 1
- Personal and Social Acceleration Coefficients:
- c1 = chi ∗ phi1
- c2 = chi ∗ phi2
- Randomization Factors:
- r1 = 0.9706
- r2 = 0.0318
- Velocity Constraints:
- MaxVelocity = 0.2 ∗ (VarMax − VarMin)
- MinVelocity = −MaxVelocity
References
- He, K.; Gao, M.; Zhao, Z. Soft Computing Techniques for Surface Roughness Prediction in Hard Turning: A Literature Review. IEEE Access 2019, 7, 89556–89569. [Google Scholar] [CrossRef]
- Grzesik, W. Wear Development on Wiper Al2O3–TiC Mixed Ceramic Tools in Hard Machining of High Strength Steel. Wear 2009, 266, 1021–1028. [Google Scholar] [CrossRef]
- D’Addona, D.M.; Raykar, S.J. Thermal Modeling of Tool Temperature Distribution during High Pressure Coolant Assisted Turning of Inconel 718. Materials 2019, 12, 408. [Google Scholar] [CrossRef] [PubMed]
- Abbas, A.T.; Gupta, M.K.; Soliman, M.S.; Mia, M.; Hegab, H.; Luqman, M.; Pimenov, D.Y. Sustainability Assessment Associated with Surface Roughness and Power Consumption Characteristics in Nanofluid MQL-Assisted Turning of AISI 1045 Steel. Int. J. Adv. Manuf. Technol. 2019, 105, 1311–1327. [Google Scholar] [CrossRef]
- Díaz-Álvarez, J.; Díaz-Álvarez, A.; Miguélez, H.; Cantero, J.L. Finishing Turning of Ni Superalloy Haynes 282. Metals 2018, 8, 843. [Google Scholar] [CrossRef]
- Abu Qudeiri, J.E.; Saleh, A.; Ziout, A.; Mourad, A.H.I.; Abidi, M.H.; Elkaseer, A. Advanced Electric Discharge Machining of Stainless Steels: Assessment of the State of the Art, Gaps and Future Prospect. Materials 2019, 12, 907. [Google Scholar] [CrossRef]
- Saleh, B.; Fathi, R.; Tian, Y.; Radhika, N.; Jiang, J.; Ma, A. Fundamentals and Advances of Wire Arc Additive Manufacturing: Materials, Process Parameters, Potential Applications, and Future Trends. Arch. Civ. Mech. Eng. 2023, 23, 96. [Google Scholar] [CrossRef]
- Gaitonde, V.N.; Karnik, S.R.; Figueira, L.; Davim, J.P. Machinability Investigations in Hard Turning of AISI D2 Cold Work Tool Steel with Conventional and Wiper Ceramic Inserts. Int. J. Refract. Met. Hard Mater. 2009, 27, 754–763. [Google Scholar] [CrossRef]
- Kumar, P.; Chauhan, S.R.; Pruncu, C.I.; Gupta, M.K.; Pimenov, D.Y.; Mia, M.; Gill, H.S. Influence of Different Grades of CBN Inserts on Cutting Force and Surface Roughness of AISI H13 Die Tool Steel during Hard Turning Operation. Materials 2019, 12, 177. [Google Scholar] [CrossRef]
- Zhang, S.J.; To, S.; Wang, S.J.; Zhu, Z.W. A Review of Surface Roughness Generation in Ultra-Precision Machining. Int. J. Mach. Tools Manuf. 2015, 91, 76–95. [Google Scholar] [CrossRef]
- Podgornik, B.; Sedlaček, M.; Žužek, B.; Guštin, A. Properties of Tool Steels and Their Importance When Used in a Coated System. Coatings 2020, 10, 265. [Google Scholar] [CrossRef]
- Kishawy, H.A.; Hegab, H.; Umer, U.; Mohany, A. Application of Acoustic Emissions in Machining Processes: Analysis and Critical Review. Int. J. Adv. Manuf. Technol. 2018, 98, 1391–1407. [Google Scholar] [CrossRef]
- Bilal, M.M.; Yaqoob, K.; Zahid, M.H.; Tanveer, W.H.; Wadood, A.; Ahmed, B. Effect of Austempering Conditions on the Microstructure and Mechanical Properties of AISI 4340 and AISI 4140 Steels. J. Mater. Res. Technol. 2019, 8, 5194–5200. [Google Scholar] [CrossRef]
- Astakhov, V.P. Machining of Hard Materials–Definitions and Industrial Applications. In Machining of Hard Materials; Springer: London, UK, 2011; pp. 1–32. [Google Scholar]
- Bhattacharyya, B.; Doloi, B. Modern Machining Technology: Advanced, Hybrid, Micro Machining and Super Finishing Technology; Academic Press: New York, NY, USA, 2019. [Google Scholar]
- Patwari, M.A.U.; Mahmood, M.N.; Noor, S.; Shovon, M.Z.H. Investigation of Machinability Responses during Magnetic Field Assisted Turning Process of Preheated Mild Steel. Procedia Eng. 2013, 56, 713–718. [Google Scholar] [CrossRef]
- Flórez García, L.C.; González Rojas, H.A.; Sánchez Egea, A.J. Estimation of Specific Cutting Energy in an S235 Alloy for Multi-Directional Ultrasonic Vibration-Assisted Machining Using the Finite Element Method. Materials 2020, 13, 567. [Google Scholar] [CrossRef]
- Xu, Y.; Gong, Y.; Zhang, W.; Wen, X.; Xin, B.; Zhang, H. Effect of Grinding Conditions on the Friction and Wear Performance of Ni-Based Singlecrystal Superalloy. Arch. Civ. Mech. Eng. 2022, 22, 102. [Google Scholar] [CrossRef]
- Yap, T.C. Roles of Cryogenic Cooling in Turning of Superalloys, Ferrous Metals, and Viscoelastic Polymers. Technologies 2019, 7, 63. [Google Scholar] [CrossRef]
- Joch, R.; Pilc, J.; Daniš, I.; Drbúl, M.; Krajčoviech, S. Analysis of Surface Roughness in Turning Process Using Rotating Tool with Chip Breaker for Specific Shapes of Automotive Transmission Shafts. Transp. Res. Procedia 2019, 40, 295–301. [Google Scholar] [CrossRef]
- Subbaiah, K.V.; Raju, C.; Pawade, R.S.; Suresh, C. Machinability Investigation with Wiper Ceramic Insert and Optimization during the Hard Turning of AISI 4340 Steel. Mater. Today Proc. 2019, 18, 445–454. [Google Scholar] [CrossRef]
- Chinchanikar, S.; Kore, S.S.; Hujare, P. A Review on Nanofluids in Minimum Quantity Lubrication Machining. J. Manuf. Process. 2021, 68, 56–70. [Google Scholar] [CrossRef]
- Weinert, K.; Inasaki, I.; Sutherland, J.W.; Wakabayashi, T. Dry Machining and Minimum Quantity Lubrication. CIRP Ann. 2004, 53, 511–537. [Google Scholar] [CrossRef]
- De Maddis, M.; Lunetto, V.; Razza, V.; Russo Spena, P. Infrared Thermography for Investigation of Surface Quality in Dry Finish Turning of Ti6Al4V. Metals 2022, 12, 154. [Google Scholar] [CrossRef]
- Sreejith, P.S.; Ngoi, B.K.A. Dry Machining: Machining of the Future. J. Mater. Process. Technol. 2000, 101, 287–291. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Abd Elaziz, M.; Das, S.R.; Muthuramalingam, T.; Lu, S. A New Optimized Predictive Model Based on Political Optimizer for Eco-Friendly MQL-Turning of AISI 4340 Alloy with Nano-Lubricants. J. Manuf. Process. 2021, 67, 562–578. [Google Scholar] [CrossRef]
- Padhan, S.; Das, S.R.; Das, A.; Alsoufi, M.S.; Ibrahim, A.M.M.; Elsheikh, A. Machinability Investigation of Nitronic 60 Steel Turning Using SiAlON Ceramic Tools under Different Cooling/Lubrication Conditions. Materials 2022, 15, 2368. [Google Scholar] [CrossRef]
- Çamlı, K.Y.; Demirsöz, R.; Boy, M.; Korkmaz, M.E.; Yaşar, N.; Giasin, K.; Pimenov, D.Y. Performance of MQL and Nano-MQL Lubrication in Machining ER7 Steel for Train Wheel Applications. Lubricants 2022, 10, 48. [Google Scholar] [CrossRef]
- Etri, H.E.L.; Singla, A.K.; Özdemir, M.T.; Korkmaz, M.E.; Demirsöz, R.; Gupta, M.K.; Krolczyk, J.B.; Ross, N.S. Wear Performance of Ti-6Al-4 V Titanium Alloy through Nano-Doped Lubricants. Arch. Civ. Mech. Eng. 2023, 23, 147. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Charalampous, P. Prediction of Cutting Forces in Milling Using Machine Learning Algorithms and Finite Element Analysis. J. Mater. Eng. Perform. 2021, 30, 2002–2013. [Google Scholar] [CrossRef]
- Gao, S.; Wang, H.; Huang, H.; Dong, Z.; Kang, R. Predictive models for the surface roughness and subsurface damage depth of semiconductor materials in precision grinding. Int. J. Extrem. Manuf. 2025, 7, 035103. [Google Scholar] [CrossRef]
- Korkmaz, M.E.; Gupta, M.K.; Kuntoğlu, M.; Patange, A.D.; Ross, N.S.; Yılmaz, H.; Chauhan, S.; Vashishtha, G. Prediction and classification of tool wear and its state in sustainable machining of Bohler steel with different machine learning models. Measurement 2023, 223, 113825. [Google Scholar] [CrossRef]
- Ross, N.S.; Mashinini, P.M.; Shibi, C.S.; Gupta, M.K.; Korkmaz, M.E.; Krolczyk, G.M.; Sharma, V.S. A new intelligent approach of surface roughness measurement in sustainable machining of AM-316L stainless steel with deep learning models. Measurement 2024, 230, 114515. [Google Scholar] [CrossRef]
- Zhang, P.R.; Liu, Z.Q.; Guo, Y.B. Machinability for Dry Turning of Laser Cladded Parts with Conventional vs. Wiper Insert. J. Manuf. Process. 2017, 28, 494–499. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, D. Finite-Element-Analysis of the Effect of Different Wiper Tool Edge Geometries during the Hard Turning of AISI 4340 Steel. Simul. Model. Pract. Theory 2019, 94, 250–263. [Google Scholar] [CrossRef]
- Kuntoğlu, M.; Sağlam, H. Investigation of signal behaviors for sensor fusion with tool condition monitoring system in turning. Measurement 2021, 173, 108582. [Google Scholar] [CrossRef]
- Asiltürk, İ.; Kuntoğlu, M.; Binali, R.; Akkuş, H.; Salur, E. A comprehensive analysis of surface roughness, vibration, and acoustic emissions based on machine learning during hard turning of AISI 4140 steel. Metals 2023, 13, 437. [Google Scholar] [CrossRef]
- Goyal, K.K.; Sharma, N.; Gupta, R.D.; Gupta, S.; Rani, D.; Kumar, D.; Sharma, V.S. Measurement of Performance Characteristics of WEDM While Processing AZ31 Mg-Alloy Using Levy Flight MOGWO for Orthopedic Application. Int. J. Adv. Manuf. Technol. 2022, 119, 7175–7197. [Google Scholar] [CrossRef]
- Chi, Y.; Dong, Z.; Cui, M.; Shan, C.; Xiong, Y.; Zhang, D.; Luo, M. Comparative study on machinability and surface integrity of γ-TiAl alloy in laser assisted milling. J. Mater. Res. Technol. 2024, 33, 3743–3755. [Google Scholar] [CrossRef]
- Abbas, A.T.; El Rayes, M.M.; Luqman, M.; Naeim, N.; Hegab, H.; Elkaseer, A. On the Assessment of Surface Quality and Productivity Aspects in Precision Hard Turning of AISI 4340 Steel Alloy: Relative Performance of Wiper vs. Conventional Inserts. Materials 2020, 13, 2036. [Google Scholar] [CrossRef]
- Abbas, A.T.; Anwar, S.; Hegab, H.; Benyahia, F.; Ali, H.; Elkaseer, A. Comparative Evaluation of Surface Quality, Tool Wear, and Specific Cutting Energy for Wiper and Conventional Carbide Inserts in Hard Turning of AISI 4340 Alloy Steel. Materials 2020, 13, 5233. [Google Scholar] [CrossRef]
- Brauers, W.K.; Zavadskas, E.K. The MOORA Method and Its Application to Privatization in a Transition Economy. Control Cybern. 2006, 35, 445–469. [Google Scholar]
- Murat, S.; Gupta, M.K.; Tomaz, I.; Pimenov, D.Y.; Kuntoğlu, M.; Khanna, N.; Yıldırım, Ç.V.; Krolczyk, G.M. A state-of-the-art review on tool wear and surface integrity characteristics in machining of superalloys. CIRP J. Manuf. Sci. Technol. 2021, 35, 624–658. [Google Scholar]
- Yu, P.D.; da Silva, L.R.R.; Machado, A.R.; França, P.H.P.; Pintaude, G.; Unune, D.R.; Kuntoğlu, M.; Krolczyk, G.M. A comprehensive review of machinability of difficult-to-machine alloys with advanced lubricating and cooling techniques. Tribol. Int. 2024, 196, 109677. [Google Scholar]
- Machado, A.R.; da Silva, L.R.R.; Pimenov, D.Y.; de Souza, F.C.R.; Kuntoğlu, M.; de Paiva, R.L. Comprehensive review of advanced methods for improving the parameters of machining steels. J. Manuf. Process. 2024, 125, 111–142. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]




| Machining Parameters | Units | Levels of Input Process Parameters | ||||
|---|---|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | Level 4 | |||
| Cutting | Speed | m/min | 75 | 100 | 125 | 150 |
| Depth of cut (DoC) | mm | 0.1 | 0.15 | 0.2 | 0.25 | |
| Feed rate (f) | mm/rev | 0.05 | 0.1 | 0.15 | 0.2 | |
| Predicted | Experimental | |||||||
|---|---|---|---|---|---|---|---|---|
| Method | Setting | PM | MRR | Ra W | Ra C | MRR | Ra W | Ra C |
| ML-MOORA-PSO | CS118DoC0.22F0.2 | 0.2114 | 4996.96 | 0.59 | 1.30 | 5000 | 0.62 | 1.26 |
| MOORA | CS150DoC0.25F0.2 | 0.207 | 7499.999 | 0.735 | 1.476 | 7500 | 0.733 | 1.475 |
| Test No. | Predicted Values ML | Normalized Data | Weighted Normalized Decision Matrix | Grade | Rank | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MRR | Ra (Wiper) | Ra (Conv) | MRR | Ra (Wiper) | Ra (Conv) | MRR | Ra (Wiper) | Ra (Conv) | |||
| 1 | 375.008 | 0.132 | 0.455 | 0.016 | 0.031 | 0.040 | 0.005 | 0.010 | 0.013 | 0.029 | 64 |
| 2 | 749.988 | 0.240 | 0.848 | 0.032 | 0.057 | 0.074 | 0.011 | 0.019 | 0.025 | 0.054 | 57 |
| 3 | 1125.000 | 0.486 | 1.713 | 0.048 | 0.116 | 0.150 | 0.016 | 0.038 | 0.050 | 0.104 | 37 |
| 4 | 1499.999 | 0.651 | 2.320 | 0.064 | 0.156 | 0.204 | 0.021 | 0.051 | 0.067 | 0.140 | 19 |
| 5 | 562.489 | 0.188 | 0.660 | 0.024 | 0.045 | 0.058 | 0.008 | 0.015 | 0.019 | 0.042 | 63 |
| 6 | 1125.018 | 0.249 | 0.866 | 0.048 | 0.059 | 0.076 | 0.016 | 0.020 | 0.025 | 0.061 | 54 |
| 7 | 1687.498 | 0.487 | 1.702 | 0.072 | 0.117 | 0.149 | 0.024 | 0.038 | 0.049 | 0.112 | 33 |
| 8 | 2250.001 | 0.653 | 2.281 | 0.096 | 0.156 | 0.200 | 0.032 | 0.052 | 0.066 | 0.149 | 16 |
| 9 | 750.015 | 0.202 | 0.698 | 0.032 | 0.048 | 0.061 | 0.011 | 0.016 | 0.020 | 0.047 | 62 |
| 10 | 1499.975 | 0.383 | 1.342 | 0.064 | 0.092 | 0.118 | 0.021 | 0.030 | 0.039 | 0.090 | 42 |
| 11 | 2250.002 | 0.490 | 1.715 | 0.096 | 0.117 | 0.151 | 0.032 | 0.039 | 0.050 | 0.120 | 29 |
| 12 | 2999.999 | 0.656 | 2.303 | 0.129 | 0.157 | 0.202 | 0.042 | 0.052 | 0.067 | 0.161 | 12 |
| 13 | 937.489 | 0.205 | 0.715 | 0.040 | 0.049 | 0.063 | 0.013 | 0.016 | 0.021 | 0.050 | 60 |
| 14 | 1875.017 | 0.398 | 1.390 | 0.080 | 0.095 | 0.122 | 0.027 | 0.031 | 0.040 | 0.098 | 38 |
| 15 | 2812.499 | 0.520 | 1.813 | 0.121 | 0.124 | 0.159 | 0.040 | 0.041 | 0.053 | 0.133 | 23 |
| 16 | 3750.000 | 0.685 | 2.400 | 0.161 | 0.164 | 0.211 | 0.053 | 0.054 | 0.070 | 0.177 | 6 |
| 17 | 499.987 | 0.234 | 0.744 | 0.021 | 0.056 | 0.065 | 0.007 | 0.018 | 0.022 | 0.047 | 61 |
| 18 | 1000.018 | 0.310 | 0.942 | 0.043 | 0.074 | 0.083 | 0.014 | 0.025 | 0.027 | 0.066 | 50 |
| 19 | 1499.999 | 0.490 | 1.523 | 0.064 | 0.117 | 0.134 | 0.021 | 0.039 | 0.044 | 0.104 | 36 |
| 20 | 2000.000 | 0.613 | 1.860 | 0.086 | 0.147 | 0.163 | 0.028 | 0.048 | 0.054 | 0.131 | 26 |
| 21 | 750.019 | 0.250 | 0.785 | 0.032 | 0.060 | 0.069 | 0.011 | 0.020 | 0.023 | 0.053 | 59 |
| 22 | 1499.971 | 0.348 | 1.081 | 0.064 | 0.083 | 0.095 | 0.021 | 0.027 | 0.031 | 0.080 | 45 |
| 23 | 2250.009 | 0.505 | 1.584 | 0.096 | 0.121 | 0.139 | 0.032 | 0.040 | 0.046 | 0.118 | 31 |
| 24 | 2999.998 | 0.637 | 1.985 | 0.129 | 0.152 | 0.174 | 0.042 | 0.050 | 0.057 | 0.150 | 15 |
| 25 | 999.977 | 0.248 | 0.751 | 0.043 | 0.059 | 0.066 | 0.014 | 0.020 | 0.022 | 0.055 | 56 |
| 26 | 2000.035 | 0.385 | 1.172 | 0.086 | 0.092 | 0.103 | 0.028 | 0.030 | 0.034 | 0.093 | 41 |
| 27 | 2999.987 | 0.556 | 1.693 | 0.129 | 0.133 | 0.149 | 0.042 | 0.044 | 0.049 | 0.135 | 21 |
| 28 | 4000.009 | 0.644 | 1.965 | 0.171 | 0.154 | 0.172 | 0.057 | 0.051 | 0.057 | 0.164 | 10 |
| 29 | 1250.016 | 0.266 | 0.827 | 0.054 | 0.064 | 0.073 | 0.018 | 0.021 | 0.024 | 0.063 | 52 |
| 30 | 2499.976 | 0.424 | 1.278 | 0.107 | 0.101 | 0.112 | 0.035 | 0.033 | 0.037 | 0.106 | 35 |
| 31 | 3750.001 | 0.562 | 1.705 | 0.161 | 0.134 | 0.150 | 0.053 | 0.044 | 0.049 | 0.147 | 18 |
| 32 | 4999.999 | 0.661 | 1.990 | 0.214 | 0.158 | 0.175 | 0.071 | 0.052 | 0.058 | 0.181 | 5 |
| 33 | 625.032 | 0.326 | 0.818 | 0.027 | 0.078 | 0.072 | 0.009 | 0.026 | 0.024 | 0.058 | 55 |
| 34 | 1249.956 | 0.523 | 1.330 | 0.054 | 0.125 | 0.117 | 0.018 | 0.041 | 0.039 | 0.097 | 39 |
| 35 | 1875.005 | 0.608 | 1.550 | 0.080 | 0.145 | 0.136 | 0.027 | 0.048 | 0.045 | 0.119 | 30 |
| 36 | 2499.999 | 0.654 | 1.659 | 0.107 | 0.156 | 0.146 | 0.035 | 0.052 | 0.048 | 0.135 | 22 |
| 37 | 937.457 | 0.337 | 0.852 | 0.040 | 0.081 | 0.075 | 0.013 | 0.027 | 0.025 | 0.065 | 51 |
| 38 | 1875.058 | 0.555 | 1.377 | 0.080 | 0.133 | 0.121 | 0.027 | 0.044 | 0.040 | 0.110 | 34 |
| 39 | 2812.487 | 0.616 | 1.551 | 0.121 | 0.147 | 0.136 | 0.040 | 0.049 | 0.045 | 0.133 | 24 |
| 40 | 3750.006 | 0.735 | 1.825 | 0.161 | 0.176 | 0.160 | 0.053 | 0.058 | 0.053 | 0.164 | 11 |
| 41 | 1250.035 | 0.344 | 0.867 | 0.054 | 0.082 | 0.076 | 0.018 | 0.027 | 0.025 | 0.070 | 49 |
| 42 | 2499.945 | 0.566 | 1.451 | 0.107 | 0.135 | 0.127 | 0.035 | 0.045 | 0.042 | 0.122 | 28 |
| 43 | 3750.021 | 0.645 | 1.628 | 0.161 | 0.154 | 0.143 | 0.053 | 0.051 | 0.047 | 0.151 | 14 |
| 44 | 4999.989 | 0.755 | 1.878 | 0.214 | 0.181 | 0.165 | 0.071 | 0.060 | 0.054 | 0.185 | 3 |
| 45 | 1562.478 | 0.352 | 0.874 | 0.067 | 0.084 | 0.077 | 0.022 | 0.028 | 0.025 | 0.075 | 46 |
| 46 | 3125.036 | 0.579 | 1.448 | 0.134 | 0.138 | 0.127 | 0.044 | 0.046 | 0.042 | 0.132 | 25 |
| 47 | 4687.493 | 0.654 | 1.633 | 0.201 | 0.156 | 0.143 | 0.066 | 0.052 | 0.047 | 0.165 | 9 |
| 48 | 6250.003 | 0.781 | 1.958 | 0.268 | 0.187 | 0.172 | 0.088 | 0.062 | 0.057 | 0.207 | 2 |
| 49 | 749.976 | 0.312 | 0.629 | 0.032 | 0.075 | 0.055 | 0.011 | 0.025 | 0.018 | 0.053 | 58 |
| 50 | 1500.032 | 0.357 | 0.716 | 0.064 | 0.085 | 0.063 | 0.021 | 0.028 | 0.021 | 0.070 | 48 |
| 51 | 2249.998 | 0.672 | 1.352 | 0.096 | 0.161 | 0.119 | 0.032 | 0.053 | 0.039 | 0.124 | 27 |
| 52 | 3000.001 | 0.687 | 1.382 | 0.129 | 0.164 | 0.121 | 0.042 | 0.054 | 0.040 | 0.137 | 20 |
| 53 | 1125.032 | 0.335 | 0.678 | 0.048 | 0.080 | 0.060 | 0.016 | 0.026 | 0.020 | 0.062 | 53 |
| 54 | 2249.959 | 0.390 | 0.790 | 0.096 | 0.093 | 0.069 | 0.032 | 0.031 | 0.023 | 0.086 | 43 |
| 55 | 3375.005 | 0.779 | 1.571 | 0.145 | 0.186 | 0.138 | 0.048 | 0.061 | 0.046 | 0.155 | 13 |
| 56 | 4499.999 | 0.788 | 1.647 | 0.193 | 0.189 | 0.145 | 0.064 | 0.062 | 0.048 | 0.174 | 7 |
| 57 | 1499.980 | 0.379 | 0.783 | 0.064 | 0.091 | 0.069 | 0.021 | 0.030 | 0.023 | 0.074 | 47 |
| 58 | 3000.033 | 0.389 | 0.802 | 0.129 | 0.093 | 0.070 | 0.042 | 0.031 | 0.023 | 0.096 | 40 |
| 59 | 4499.992 | 0.621 | 1.255 | 0.193 | 0.149 | 0.110 | 0.064 | 0.049 | 0.036 | 0.149 | 17 |
| 60 | 6000.003 | 0.708 | 1.474 | 0.257 | 0.169 | 0.129 | 0.085 | 0.056 | 0.043 | 0.183 | 4 |
| 61 | 1875.012 | 0.428 | 0.863 | 0.080 | 0.102 | 0.076 | 0.027 | 0.034 | 0.025 | 0.085 | 44 |
| 62 | 3749.979 | 0.447 | 0.956 | 0.161 | 0.107 | 0.084 | 0.053 | 0.035 | 0.028 | 0.116 | 32 |
| 63 | 5625.003 | 0.674 | 1.361 | 0.241 | 0.161 | 0.119 | 0.080 | 0.053 | 0.039 | 0.172 | 8 |
| 64 | 7499.999 | 0.735 | 1.476 | 0.321 | 0.176 | 0.130 | 0.106 | 0.058 | 0.043 | 0.207 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, A.T.; Sharma, N.; Alqosaibi, K.F.; Abbas, M.A.; Sharma, R.C.; Elkaseer, A. Investigation of Surface Quality and Productivity in Precision Hard Turning of AISI 4340 Steel Using Integrated Approach of ML-MOORA-PSO. Processes 2025, 13, 1156. https://doi.org/10.3390/pr13041156
Abbas AT, Sharma N, Alqosaibi KF, Abbas MA, Sharma RC, Elkaseer A. Investigation of Surface Quality and Productivity in Precision Hard Turning of AISI 4340 Steel Using Integrated Approach of ML-MOORA-PSO. Processes. 2025; 13(4):1156. https://doi.org/10.3390/pr13041156
Chicago/Turabian StyleAbbas, Adel T., Neeraj Sharma, Khalid F. Alqosaibi, Mohamed A. Abbas, Rakesh Chandmal Sharma, and Ahmed Elkaseer. 2025. "Investigation of Surface Quality and Productivity in Precision Hard Turning of AISI 4340 Steel Using Integrated Approach of ML-MOORA-PSO" Processes 13, no. 4: 1156. https://doi.org/10.3390/pr13041156
APA StyleAbbas, A. T., Sharma, N., Alqosaibi, K. F., Abbas, M. A., Sharma, R. C., & Elkaseer, A. (2025). Investigation of Surface Quality and Productivity in Precision Hard Turning of AISI 4340 Steel Using Integrated Approach of ML-MOORA-PSO. Processes, 13(4), 1156. https://doi.org/10.3390/pr13041156









