1. Introduction
When operating at sea, the hull is subjected to the combined effects of wind, waves, and currents, causing the ship to move in six directions: roll, pitch, bow, sway, surge, and heave. Usually, a dynamic positioning system is installed on a ship, which uses thrusters to resist environmental forces to eliminate the effects of sway, pitch, and bow motion. However, the effect of heave motion on ship operations cannot be eliminated by the dynamic positioning system [
1]. Heave compensation technology is a key technology that ensures the smooth execution of offshore engineering operations. It is mainly used to correct and compensate for motion in the heave direction caused by environmental factors such as wind, waves, and currents during offshore operations. This technology monitors the heave motion of the vessel in real time through sensors installed on the hull, transmitting the measured data to the control system, which then calculates the required displacement or force to be compensated. The corresponding actuators adjust the operation equipment to achieve heave compensation. The application of this technology effectively prevents the impact of heave motion on operational equipment and research personnel, further improving the efficiency and safety of offshore operations [
2,
3].
Since the last century, the application value of the short-term motion prediction of floating platforms in practical engineering has been widely explored, and a large number of prediction models have been developed. According to the theoretical differences of various methods, short-term prediction models can be divided into three types: prediction models based on fluid dynamics, classical time series, and prediction models related to nonlinear and intelligent learning [
4]. In essence, the prediction models related to classical time series and nonlinear intelligent learning are both based on statistical data.
Fluid dynamics-based predictions include convolution-based methods and state-space-based Kalman filter methods. Yanbing Dou aims to solve the problem concerning the difficulty in capturing temporal and spatial features in the ship track sequence data under high sea conditions. It designs and uses convolutional neural networks and long short-term memory neural networks to extract the spatial trend features and time series features in the input, respectively, and finds that this method can improve the prediction effect. Finally, the experimental results on the real ship track data set show that the prediction accuracy and real-time performance of the motion prediction system meet the actual needs [
5]. This method requires accurate response functions and wave inputs. Kalman filtering is another prediction method based on fluid dynamics. Xiaoli WANG and Zhanjie GUO used the Kalman filtering method to establish a random wave model and a ship rolling motion model, and conducted a systematic study on the prediction of ship roll and other postures [
6]. The prediction accuracy of this method depends largely on the wave frequency and noise. However, in practical engineering, accurate state-space equations and noise statistics are difficult to obtain, which makes the Kalman filter difficult to apply.
Compared with the prediction model based on fluid dynamics, the method based on statistical data is easier to model and has lower requirements on computer memory and time. When modeling, time series analysis only needs to consider the historical data of the platform movement. Commonly used classical time series prediction models include autoregressive (AR) and autoregressive moving average (ARMA) models. Although the classical time series model is efficient and adaptive, its prediction results in severe sea conditions are not ideal. Obviously, for drilling platforms operating in the deep sea, the ship platform and the waves are always unstable, so it is difficult to accurately establish the prediction model of the classical time series.
In order to overcome the hidden nonlinearity in real ship motion, prediction models related to nonlinear intelligent learning have been widely studied, such as artificial neural networks, back propagation networks, and wavelet neural networks, which can perform nonlinear modeling without prior knowledge of the relationship between input and output variables. Compared with the traditional BP neural network, the wavelet neural network has obvious advantages. First, the neurons and network topology of the wavelet neural network are determined based on the wavelet analysis theory, which can avoid the arbitrariness of the network structure design. Second, the wavelet neural network has a stronger learning ability. Finally, for the same learning task, the wavelet neural network can converge faster with a simpler network structure. Weiyuan GUO et al. used wavelet neural networks to predict the reliability of ship power systems and improve the service life of ships [
7]. Chuang DAI proposed a ship posture prediction model that integrates wavelet transform and attention. It was verified that this method can effectively improve the stability of the ship platform [
8]. Wenjun ZHANG introduced a wavelet neural network into the field of ship motion control and constructed a ship motion prediction controller based on an improved wavelet neural network. The wavelet neural network was used to perform the online identification and prediction of ship motion dynamics, and ship motion prediction control was performed based on the prediction results. The simulation results verified that the control system has high control accuracy and strong anti-interference ability [
9].
Researchers have conducted a lot of research on floating platform motion prediction, especially focusing on how to improve the accuracy of motion prediction [
10,
11]. However, for the motion prediction of floating platforms that need to be used for real-time compensation control, there is little research on the method of combining platform heave motion prediction with compensation control to ultimately improve the compensation accuracy [
12].
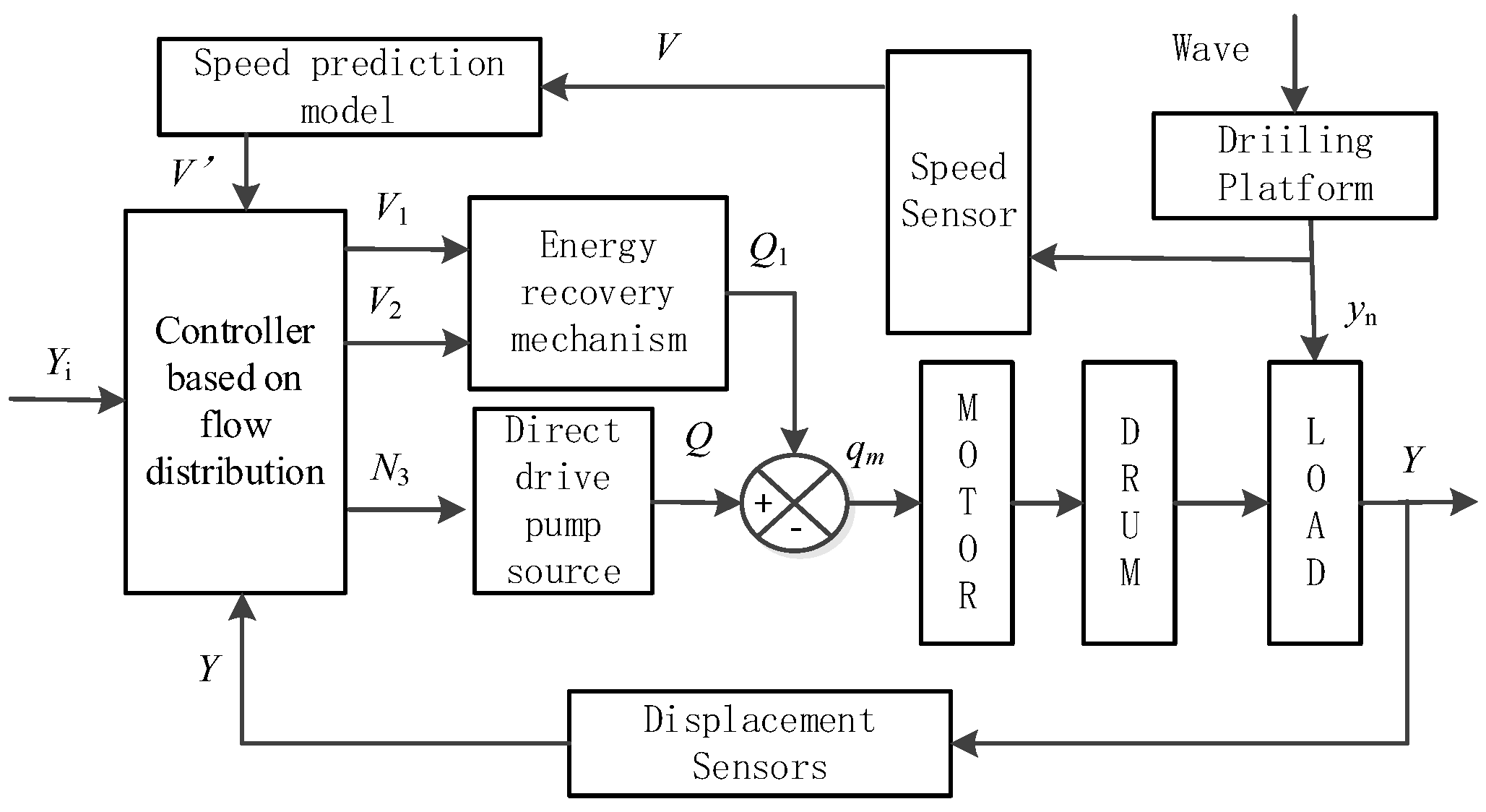
In the winch-type heave compensation system, the conventional feedback control accuracy is not high. The compensation starts only after the error occurs, and the disturbance cannot be eliminated synchronously. The compensation has a lag. Therefore, this paper intends to first perform necessary processing and short-term prediction on the measured platform heave data and use the predicted platform motion velocity for velocity disturbance compensation to achieve a better heave compensation effect [
13].
3. Results
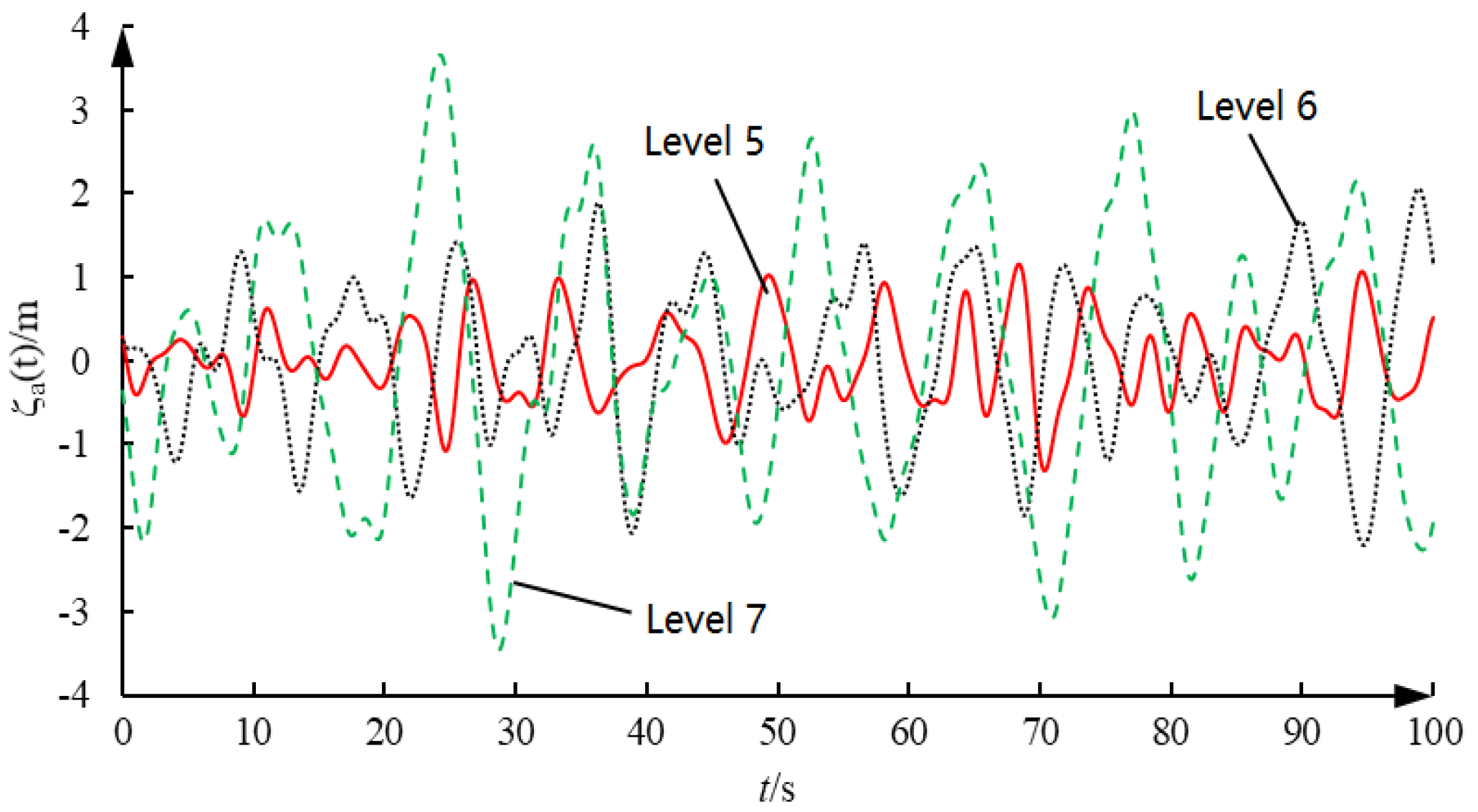
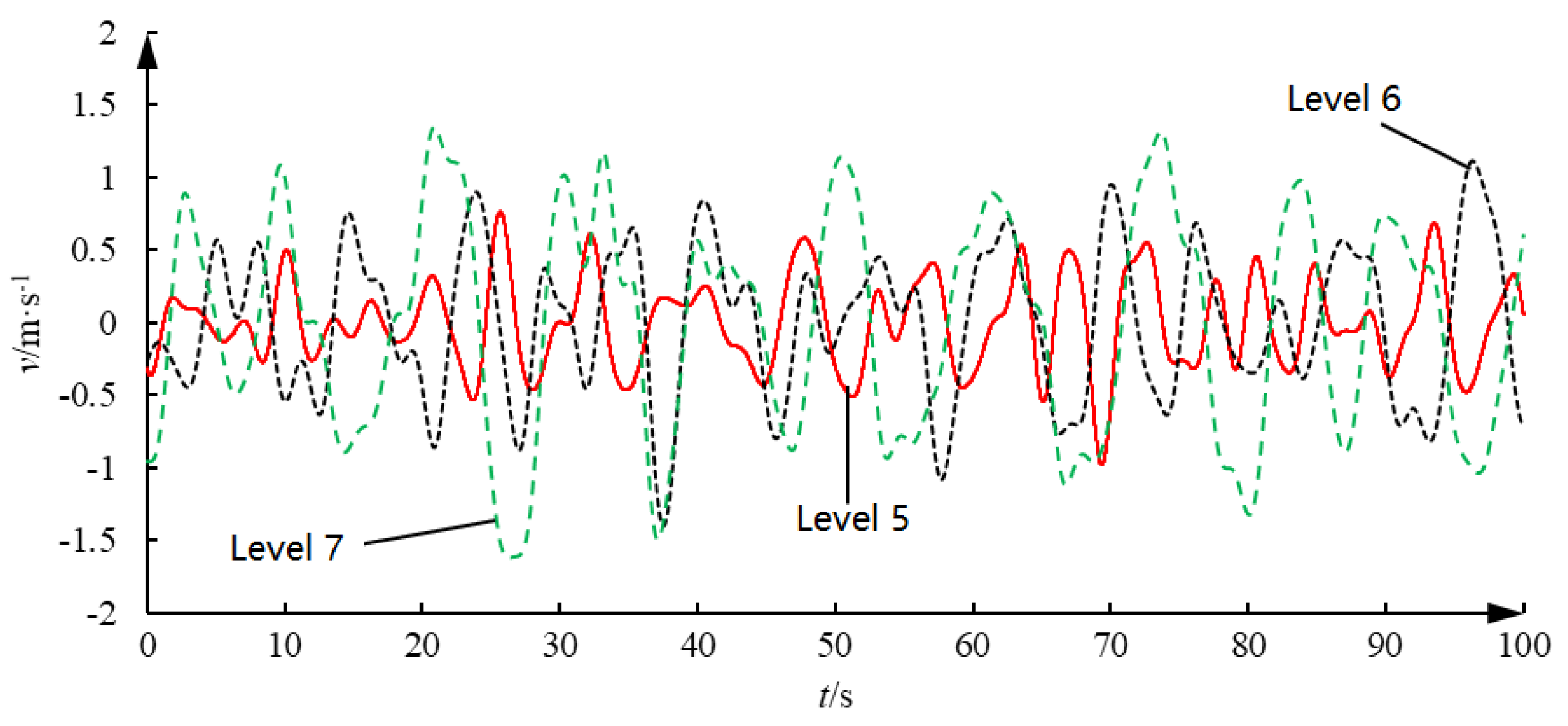
Considering the limit telescopic displacement and velocity of the experimental hydraulic cylinder, it is impossible to fully simulate the heave motion of the floating platform under sea conditions of level 5, 6, and 7. Therefore, in this experiment, the ITTC two-parameter spectrum parameters with a significant wave height
h1/3 of 0.4 m and a characteristic period
T1 of 8 s are taken, as shown in
Figure 14, which is the spectrum diagram of the sea wave and the floating platform. During the experiment, the expected heave displacement is generated in real time in the control software, and then the piston rod is made to track the expected heave displacement through PID control. The control software receives the heave displacement signal, obtains the current piston rod telescopic velocity after differentiation and filtering, and performs real-time velocity prediction.
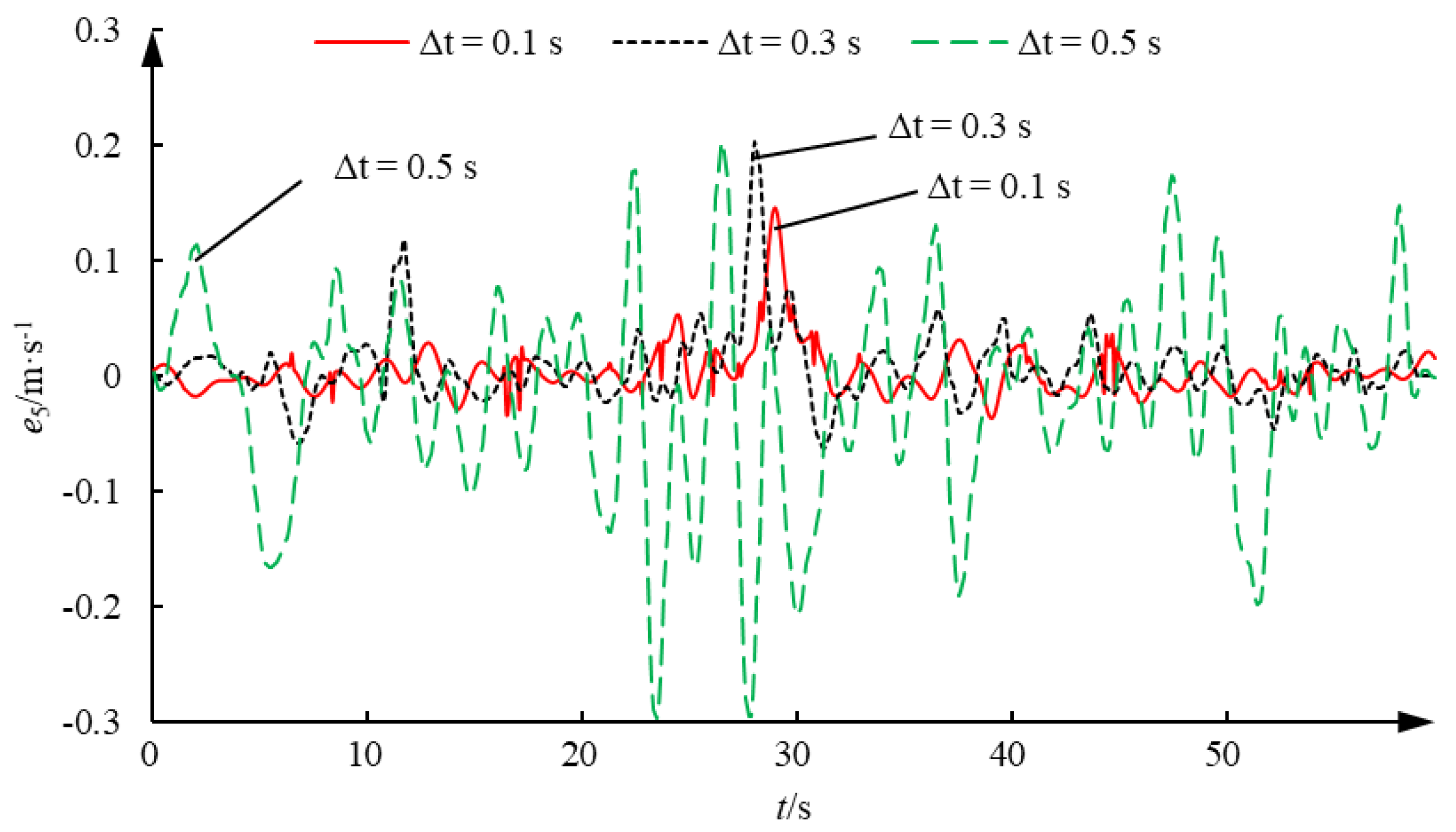
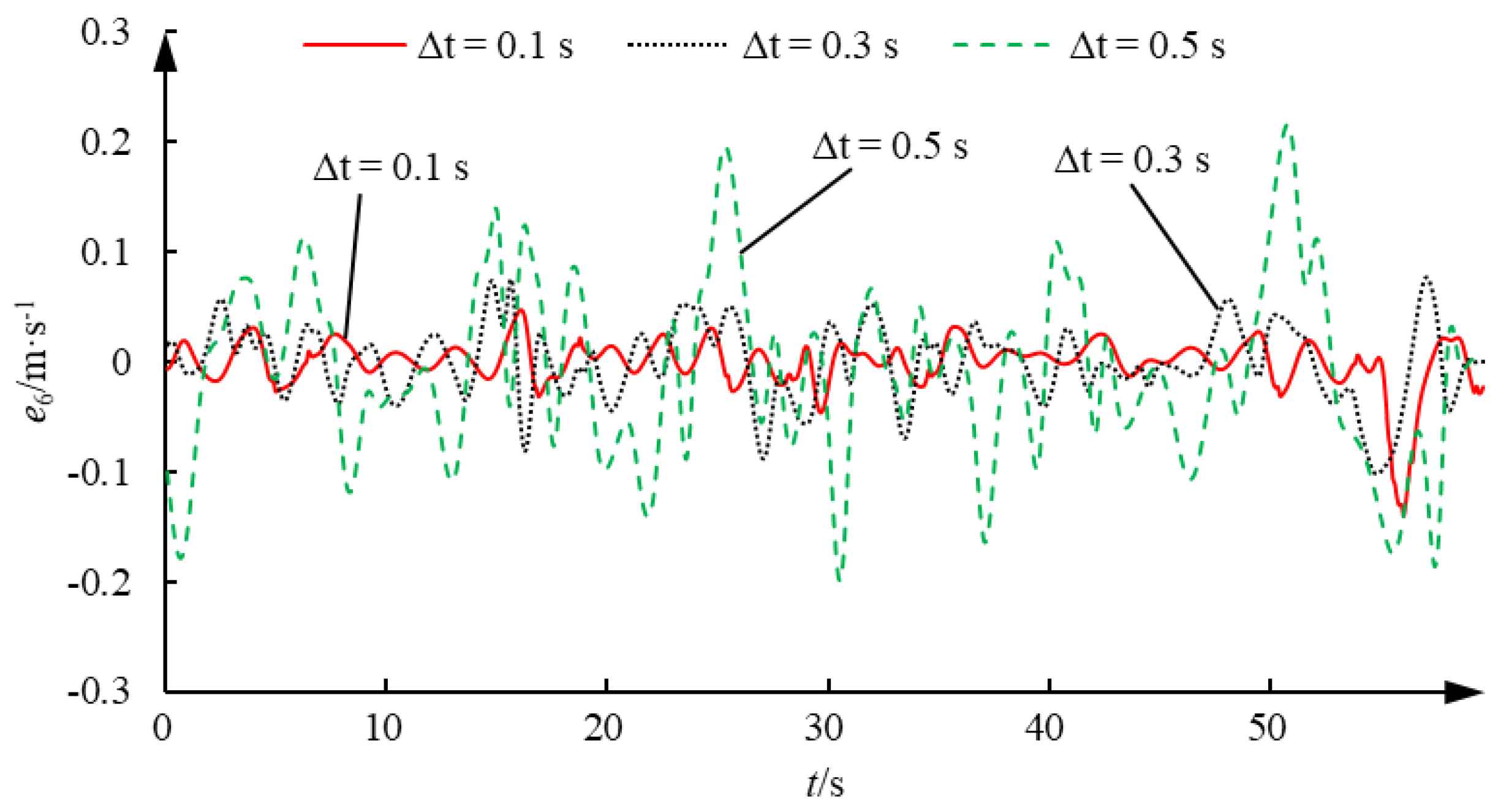
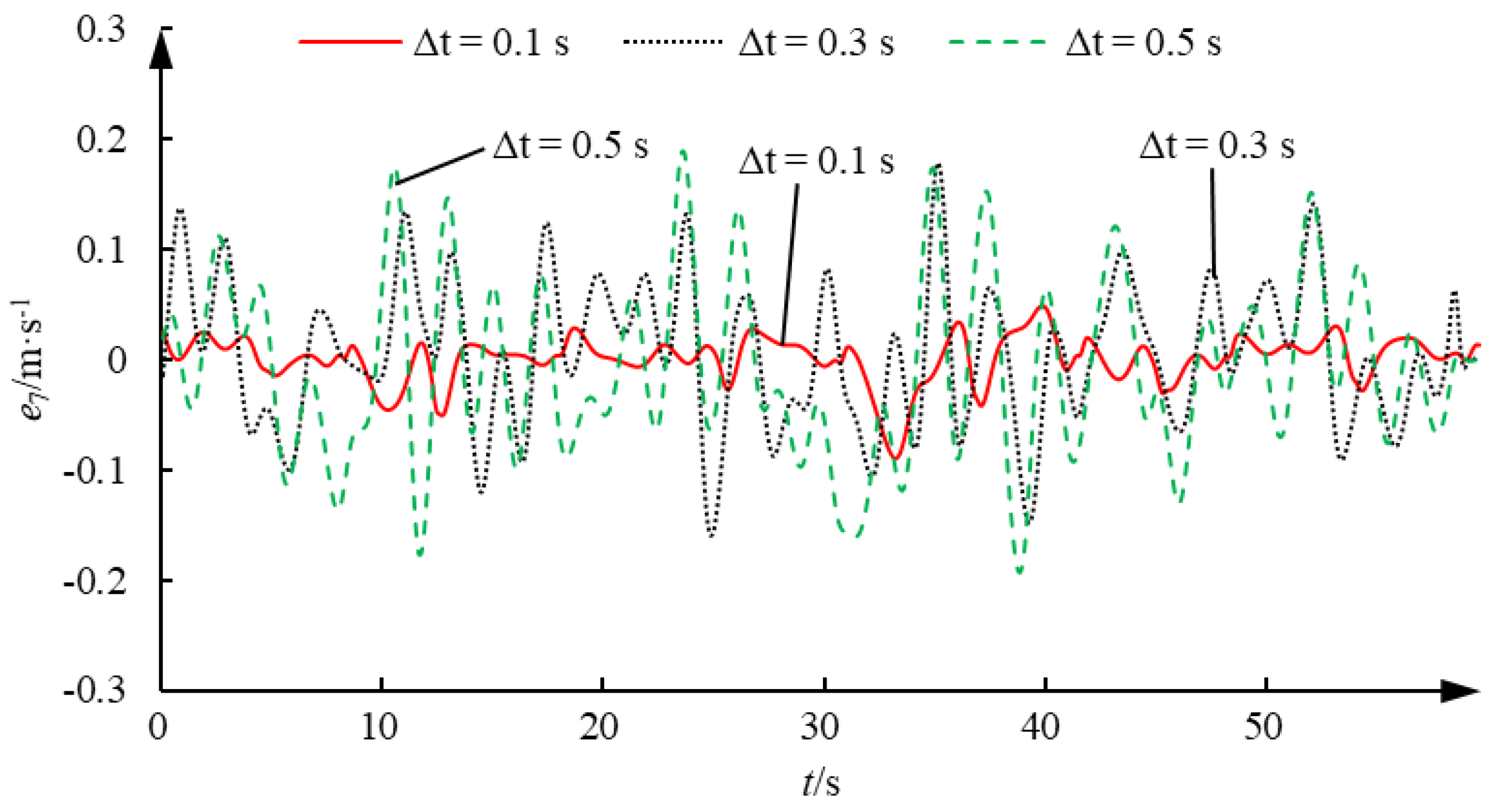
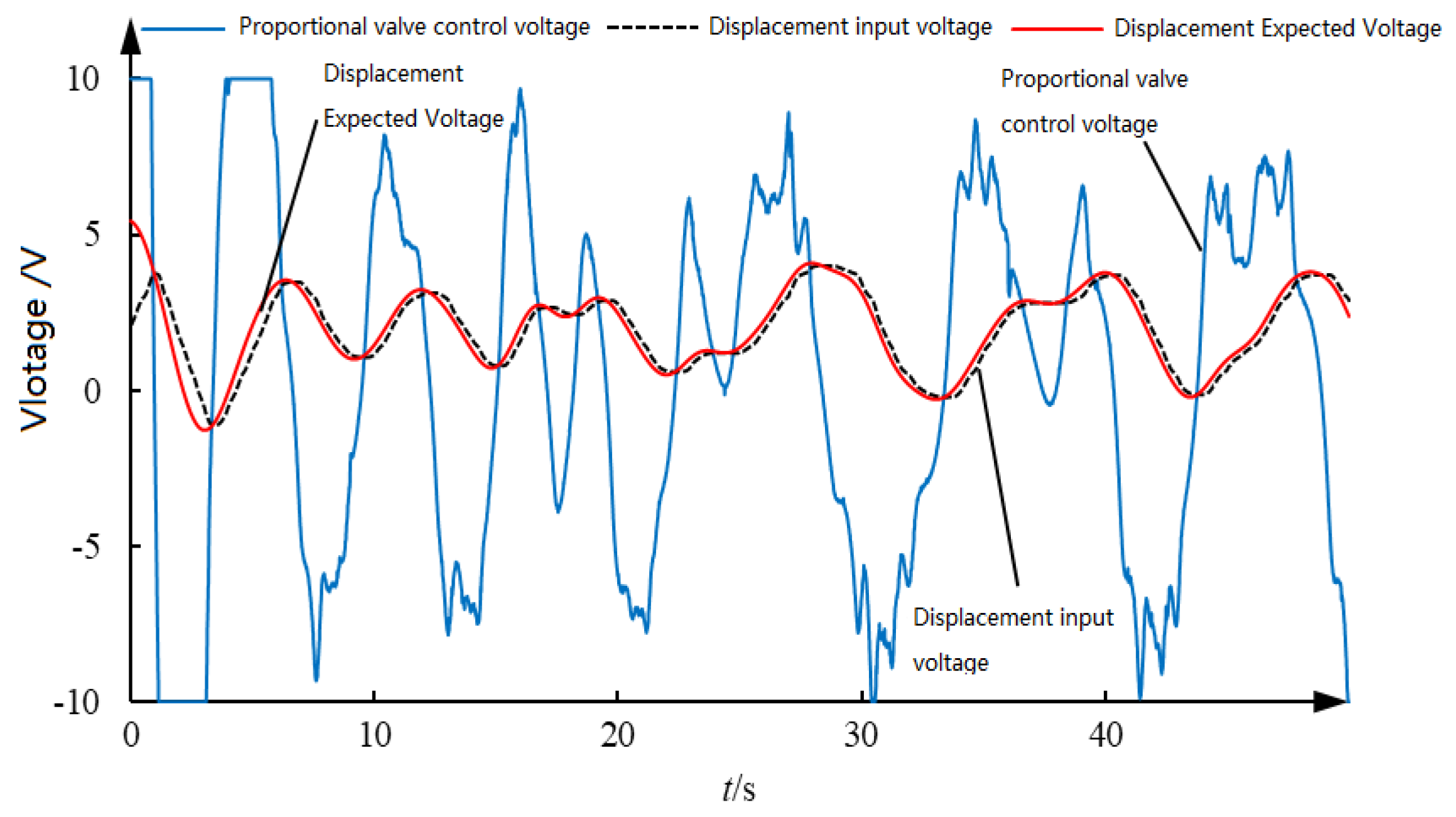
Figure 15 shows the proportional reversing valve-control voltage and displacement voltage signal curves, and
Figure 16 shows the velocity prediction error curves of different prediction steps. From the experimental results, it can be seen that, limited by the piston rod’s maximum extension and retraction velocity and displacement, the heave motion of the floating platform can be simulated in the majority of cases, with only a few scenarios unable to track the target curve effectively. Despite performing operations like low-pass filtering, the obtained piston rod extension and retraction velocity still exhibit some jitter, and in some instances, the velocity even exceeds the actual maximum achievable velocity of the piston rod. This could be due to errors and jitter in the displacement sensor input, which significantly affects the stability of the prediction algorithm. As can be seen from the figure, prediction accuracy is related to the prediction step size, which is consistent with the simulation results. When the prediction step size is 0.1 s, the piston rod velocity prediction error remains within ±10 mm/s, with the maximum error not exceeding 20 mm/s. When the prediction step size is 0.3 s, the maximum prediction error for the piston rod velocity does not exceed 50 mm/s. When the prediction step size is 0.5 s, the local maximum prediction error for the piston rod velocity approaches 100 mm/s. Overall, except for some larger local prediction errors, the time-series-based wavelet neural network velocity prediction method can effectively predict the heave motion velocity of the floating platform.
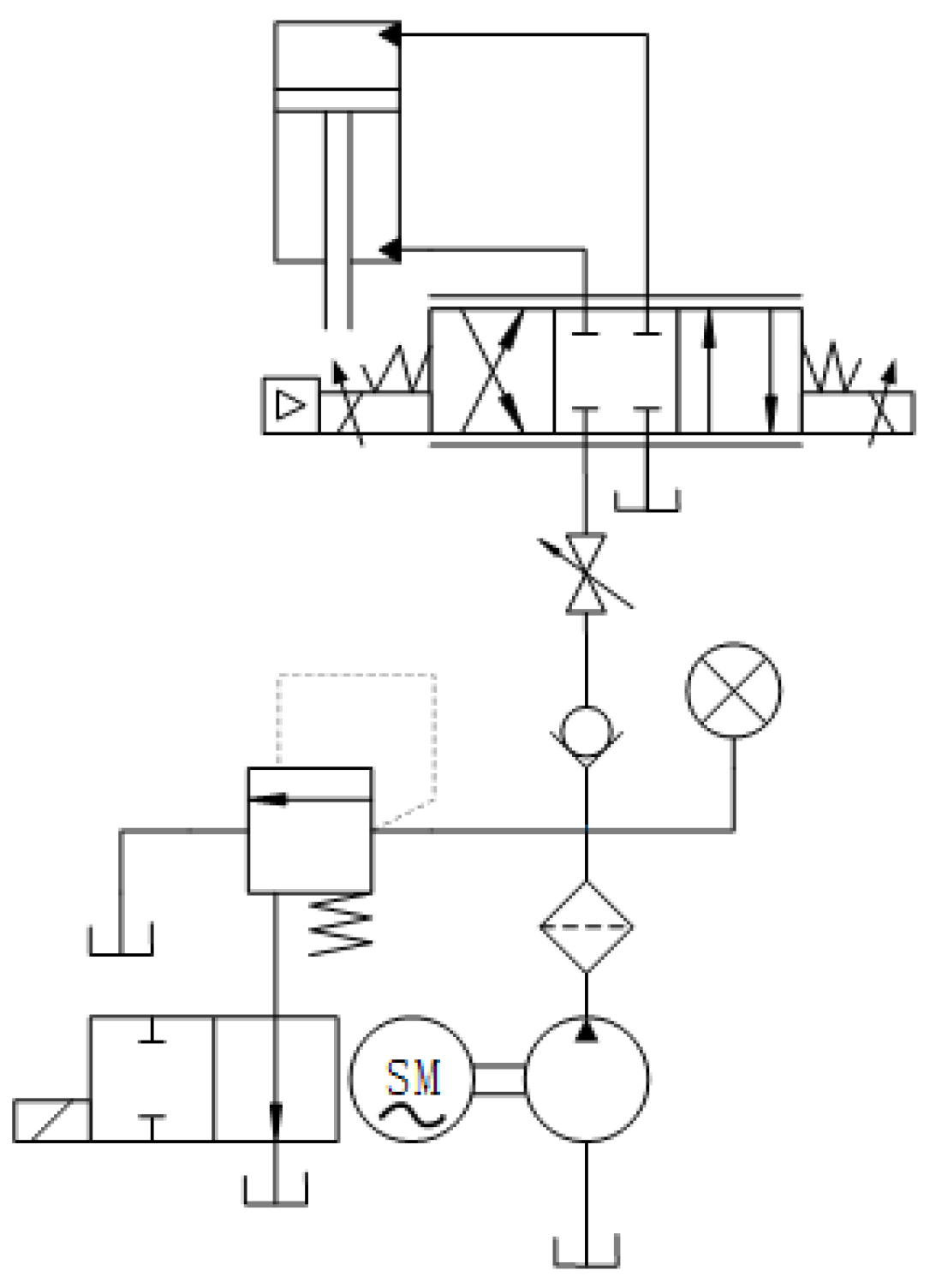
After verifying that the wavelet neural network speed prediction method based on time series can effectively predict the heave velocity of the floating platform, the compensation performance of the system is tested and verified using the winch-type heave compensation simulation test bench built by the research team. As shown in
Figure 17, the laboratory winch-type heave compensation simulation test bench is used. The lower platform, integrated block, variable pump, and servo motor of the six-degree-of-freedom platform are fixed on the bottom plate, and the hydraulic motor, reducer, winch, etc. are fixed on the upper platform of the six-degree-of-freedom platform and will move with the platform. The necessary components such as the electromagnetic ball valve, hydraulically controlled one-way valve, overflow valve, etc. are integrated on the integrated block. In addition, there are speed encoders, grating displacement sensors, tension sensors, pressure sensors, etc. for detecting the operating status of the equipment.
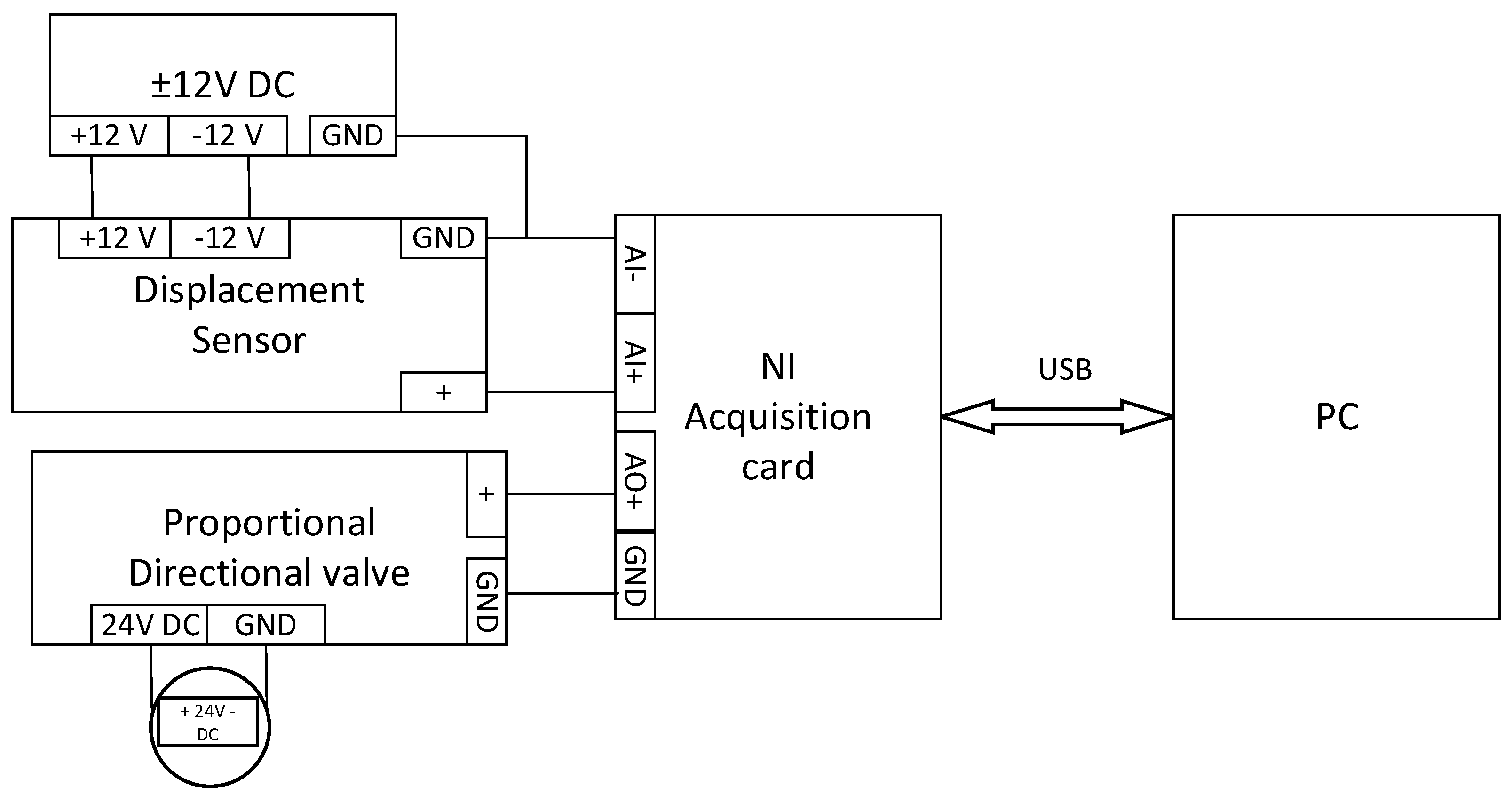
As shown in
Figure 18, the hardware system diagram of the heave compensation simulation test bench is shown. The industrial control computer receives a total of six signals, including the platform, load heave displacement, winch speed, oil circuit pressure, and wire rope tension, through the acquisition card and counting card, and outputs a total of four D/A voltage signals, including relay, variable pump displacement, servo motor speed, and proportional reversing valve, in real time. The industrial control computer is the core of the system, and the real-time acquisition, calculation, and output of all signals are completed here. The control software only needs to add the signal acquisition function. The signal acquisition is carried out using the encapsulation function of the acquisition card.
In the heave compensation experiment, the six-degree-of-freedom platform was uniformly subjected to sinusoidal heave motion with an amplitude of 30 mm and a period of 5 s, and multiple groups of experiments were carried out. After the end, the data were sorted and plotted. In
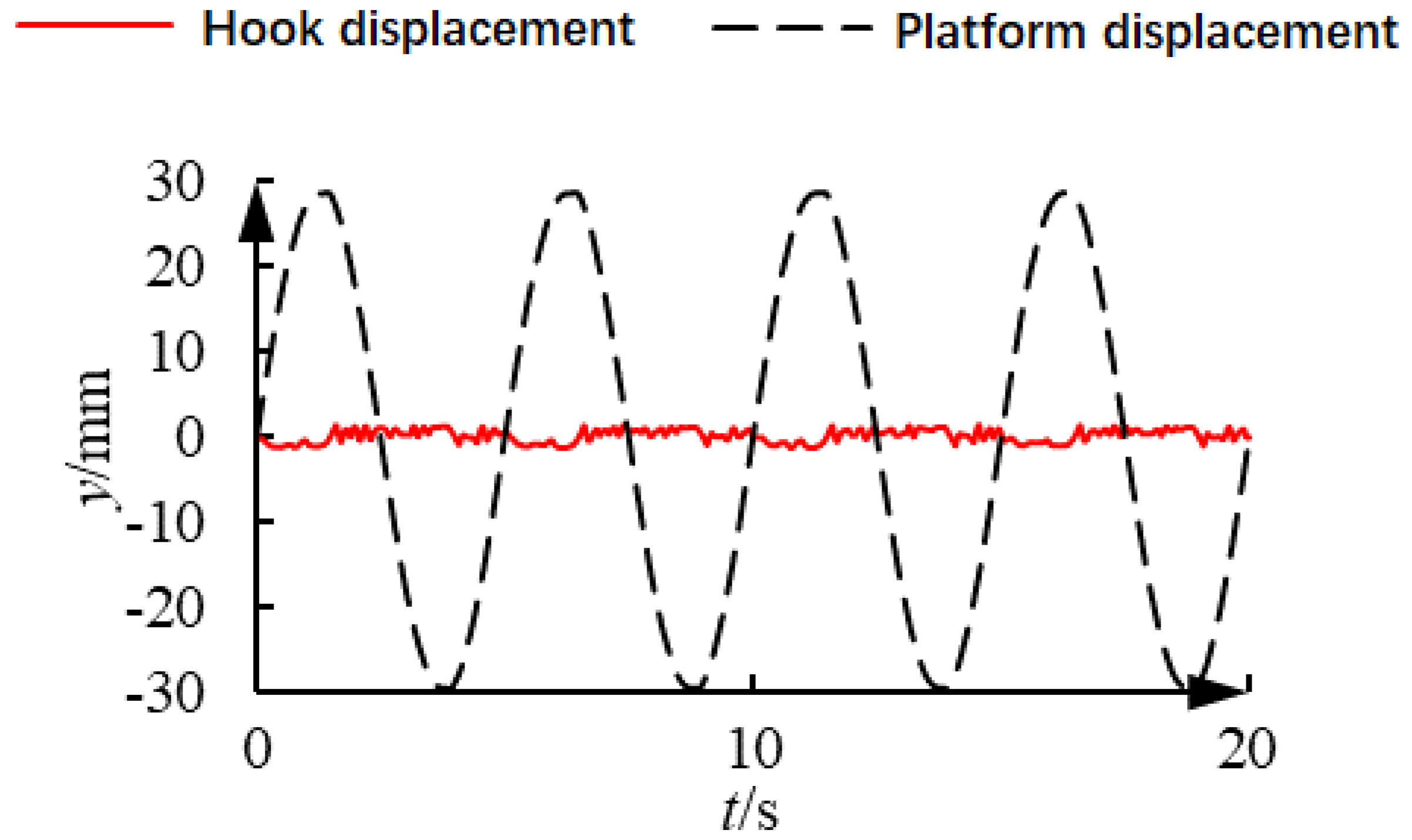
Figure 19, the compensation curve of the simulation test bench when there is no prediction is shown. It can be seen from the figure that when there is no prediction, the experimental curve jitters lightly, and the maximum deviation of the approximate position in the experiment is 2.1 mm. In
Figure 20, the compensation curve of the simulation test bench when the prediction step is 0.1 s is shown; it can be seen from the figure that the introduction of the prediction method aggravates the jitter of the large hook displacement curve, but the maximum deviation of the large hook position in the experiment is slightly reduced. The maximum deviation of the large hook position in the experiment is 1.7 mm. In
Figure 21, the compensation curve of the simulation test bench when the prediction compensation is 0.2 s is shown; as the prediction step increases, the large hook displacement curve in the experiment continues to aggravate the jitter, and the compensation performance becomes worse. The maximum deviation of the large hook position in the experiment is 2.6 mm. When the prediction step is 0.1 s, the compensation accuracy is improved by 19% compared with the case without velocity prediction. After calculation, the RMSE of the load displacement when the prediction is not added is 0.7881, the RMSE of the load displacement when the prediction step is 0.1 s is 0.7702, and the RMSE of the load displacement when the prediction step is 0.2 s is 0.8165. The MAE of load displacement when the prediction is not added is 0.6925, the MAE of load displacement when the prediction step is 0.1 s is 0.6863, and the MAE of load displacement when the prediction step is 0.2 s is 0.7058.
4. Discussion
This paper presents further research on heave compensation winches. First, based on wave spectrum theory and the relationship between sea waves and platform heave motion, offline learning data for sea waves and floating platform heave motion were generated through simulations under sea conditions of level 5, level 6, and level 7 over a period of time. Next, a time-series-based wavelet neural network velocity prediction method was used to predict the heave motion velocity of the platform. Finally, a valve-controlled hydraulic cylinder heave motion simulation system was set up in the laboratory for experimental research. The experimental results show that the hydraulic cylinder can effectively simulate the heave motion of the floating platform, and the time-series-based wavelet neural network prediction method is generally effective. However, as the prediction step size increases, the prediction accuracy decreases.
After verifying that the wavelet neural network velocity prediction method based on time series can effectively predict the speed, the compensation performance of the system was tested and verified using the winch-type heave compensation simulation test bench built in the laboratory. The experiment found that the introduction of the prediction method can improve the compensation performance, but as the prediction step length increases, the compensation performance may deteriorate. However, the movement of the platform in actual sea conditions is also composed of sinusoidal signals with different frequency components. The amplitude and frequency of the sinusoidal signal in this experiment are also consistent with the actual wave conditions; so, we believe that this experiment can represent the actual working conditions under certain circumstances, but the accuracy of the prediction model can be further improved.
The research in this paper further improves the control accuracy of the winch-type heave compensation system. As for the deterioration of compensation performance caused by increasing the prediction step, it is found that when the step size becomes larger, the prediction output of the model will fluctuate. The prediction algorithm needs to be further optimized to improve the accuracy of the prediction model. Compared with the traditional feedback control, which controls after the feedback signal is generated, this paper uses the platform heave velocity of the first four sampling intervals of the prediction time node as the input of the prediction model, and outputs the predicted platform heave velocity, which improves the response time of the control system and avoids the disadvantage of the traditional control method that needs to adjust the control parameters based on experience.
At the same time, further research can be conducted from the following aspects. First, although the method designed in this paper to predict the velocity of the floating platform’s heave motion is effective, its prediction accuracy needs to be further improved, and the prediction algorithm can be further optimized. Secondly, at present, only the laboratory’s hydraulic six-degree-of-freedom motion simulation platform is used to perform the sinusoidal motion of heave to simulate waves. Further research can be conducted to enable it to track any given expected signal, especially to simulate the motion of the offshore floating platform in the heave direction, so as to better verify the effect of this method in actual sea conditions.