Abstract
In engineering fluid dynamics and environmental science, jet concentration prediction is a complex multivariable problem influenced by multiple factors. The accurate simulation and prediction of jet behavior are of significant theoretical and practical importance. However, traditional methods such as theoretical analysis and empirical formulas are applicable in simple or idealized environments and have limited applicability and accuracy in complex multilayered fluids. Computational fluid dynamics (CFD) can simulate more complex flow and concentration distributions but requires substantial computational resources. Therefore, this paper proposes a jet concentration prediction method based on a random forest model in a linear stratified environment. It uses OpenFOAM for flow field simulation to construct a comprehensive dataset, which is divided into training, validation, and test sets in a 6:2:2 ratio, and applies the random forest model for concentration prediction. By comparing it with support vector regression, linear regression, genetic programming, and Adaptive Boosting methods, the superiority of the random forest model in jet concentration prediction is validated. The results show that the overall R2 value of the random forest model reaches 0.99, which is closest to 1, with the lowest RMSE value. It can provide accurate predictions in a short time and has a strong generalization capability. This study offers an efficient and precise alternative method for jet concentration prediction, maintaining a high prediction accuracy while reducing computational resource consumption, and providing strong support for practical engineering applications in fluid dynamics, chemical processes, environmental science, and related fields.
1. Introduction
Understanding the mechanisms and patterns of pollutant dispersion is crucial for chemical processes, protecting ecosystems, safeguarding public health, and optimizing environmental management [1]. The accurate prediction of jet concentration fields helps to better understand the dispersion process of pollutants, supporting the simulation of chemical processes of pollutants, and further optimizing pollution control strategies. However, jet concentration fields involve complex flow characteristics, especially in inclined plane jets, where the velocity distribution of the fluid, shear effects, and boundary effects result in highly nonlinear changes in the concentration field. The handling of high-dimensional data increases the difficulty of modeling and the complexity of predictions. Traditional jet simulation methods, such as physical model experiments, empirical formulas, or semi-empirical models, are suitable for simplified flow models but are limited in their applicability and accuracy in more complex, multi-physics coupled flow phenomena [2]. Numerical simulations can solve the accuracy issues of traditional methods, but they demand high computational resources, especially when dealing with complex geometries and large-scale flow problems, where the computational load can be immense and may require long computation times.
With the rapid development of computer technology, machine learning methods, as an emerging technology, have gradually demonstrated their potential in modeling complex systems. Machine learning methods, which learn patterns automatically from historical data, can effectively capture complex nonlinear relationships, reducing the reliance on physical process modeling. These methods may offer new insights into jet concentration field prediction in complex environments.
To validate the performance of machine learning methods in simulating jet concentration distributions in complex environments, this study uses machine learning techniques to predict the concentration field of inclined plane jets in a linear stratified environment. Inclined plane jets are widely used in environmental pollution control, water quality monitoring, and marine engineering, and predicting their concentration distribution is crucial for pollution control and water resource management. Especially in stratified environments, different layers of fluid have varying physical properties, and accurately describing interlayer interactions is critical for accurate flow simulation. This case also holds significant meaning for the research of machine learning methods. In such complex environments, jet concentration fields are influenced by multiple factors, and the flow process is highly nonlinear, which helps verify the effectiveness of machine learning in flow field simulation and further assess its potential in environmental flow problems.
Traditional methods for jet concentration field prediction mainly rely on physical models, dimensional analysis, and experimental studies. For instance, El-Ghorab et al. [3] constructed a physical model using geometric similarity to investigate the impact of emissions, temperature, and flow state on mixing zone characteristics; Jirka et al. [4] defined the geometry and mixing characteristics of buoyant jets through dimensional analysis and proposed standards for deep-water and shallow-water jets. Furthermore, Knudsen et al. [5] derived dilution and trajectory formulas for buoyant axisymmetric jets, while Kaminski et al. [6] proposed a new theoretical model based on local Richardson numbers to study entrainment behavior in turbulent jets. In experimental studies, Bashitialshaaer et al. [7] conducted experimental research on the behavior of inclined negatively buoyant jets, analyzing the effects of parameters such as nozzle diameter, jet angle, density, and flow rate on the jet trajectory, while Roberts et al. [8] analyzed the behavior of non-buoyant jets discharged horizontally in stratified fluids; Wallace et al. [9] and Lee et al. [10] studied the expansion and mixing behavior of buoyant jets in stratified fluids through experiments. These methods provide theoretical and experimental support for predicting jet concentration fields, but their applicability and accuracy are limited in complex flows and multilayer fluids.
To overcome the accuracy limitations of traditional methods, computational fluid dynamics (CFD) has gradually become a mainstream tool. Jirka et al. [11] proposed an overall model for buoyant jets considering turbulence and resistance mechanisms, validating its accuracy under different flow conditions. Amamou et al. [12] simulated the process of turbulent circular jets entering reverse flow using Reynolds stress models, with results consistent with experiments. Meng et al. [13] explored the impact of density Froude numbers and jet-to-flow velocity ratios on jet behavior through numerical simulations, while Gao et al. [14] used mixture and renormalization group models to simulate jet behavior and studied the effects of density Froude numbers and jet-to-flow velocity ratios on jet behavior. Ishigaki et al. [15] proposed an improved solver to reduce the impact of mesh non-orthogonality on buoyant jet numerical solutions. Additionally, Belcaid et al. [16] validated numerical simulation results for buoyant wall jet turbulence in uniform saline water; Xu et al. [17,18,19] and Chen et al. [20] investigated the effect of waves on jets through large eddy simulation and FLOW-3D. These studies show that numerical simulations can provide more accurate and comprehensive predictions than traditional methods when dealing with complex fluid dynamics and multi-physics coupling problems. However, in a linear stratified environment numerical simulations still require layered grids and high-precision interpolation methods to handle complex boundary effects and concentration diffusion processes, resulting in a high computational cost.
Due to the high computational cost of numerical simulations, researchers have begun exploring more efficient methods, and machine learning, with its data-driven characteristics, has become a potential solution. Currently, machine learning techniques are beginning to be applied to study jet characteristics. Yan et al. [21] proposed a method based on multi-gene genetic programming (MGGP) to predict the trajectory of a rosette momentum jet group in flowing currents. The model outperforms the single-gene genetic programming (SGGP) model. The studies indicate that machine learning methods provide new ideas for studying jet characteristics. Compared to numerical simulations, machine learning can simplify the model-building process, demonstrating a higher adaptability and predictive ability when facing complex physical processes. However, related research is still in its infancy, especially in predicting jet concentration fields under complex flow conditions, with limited application of machine learning methods. Among common machine learning models, such as SVR, linear regression, genetic programming, and AdaBoost, the generalization abilities and computational efficiencies vary, and their applicability to this physical problem is not yet clear. The challenge at present is how to improve computational efficiency while ensuring prediction accuracy.
Random forests, by integrating multiple decision trees, effectively reduce the risk of overfitting, improving both computational efficiency and the accuracy and stability of the model. Compared to the reference machine learning models (SVR, linear regression, genetic programming, and AdaBoost), random forest does not require complex kernel function selection or parameter tuning, and it is less susceptible to noise. It may be better suited to handle the potential nonlinear relationships in the jet concentration field. Hassanzadeh et al. [22] predicted the laminar length and expansion angle of positively buoyant mixing jets using various machine learning methods, and the study showed that the random forest algorithm outperformed other models, providing more accurate predictions of jet expansion behavior under different conditions. However, there has been no study using random forest models to predict jet concentration fields in a linear stratified environment with inclined plane jets.
Therefore, this study explores the application of random forest models under complex flow conditions. Specifically, this study uses OpenFOAM to simulate jet concentration fields under different operating conditions, constructs a comprehensive dataset, and applies the random forest model to predict the concentration distribution. By comparing the prediction performance of random forest with other machine learning models, the superiority of random forests in nonlinear, high-dimensional flow problems is verified. To the best of the author’s knowledge, this is the first study to apply the random forest algorithm to predict the concentration field of inclined plane jets in a linear stratified environment. The method effectively captures nonlinear relationships and high-dimensional features in complex flows, demonstrating a robust performance and accuracy. This research provides a new approach for understanding and predicting concentration changes in linear stratified environments and offers valuable references for further optimizing fluid dynamics models.
2. Materials and Methods
2.1. Overall Research Approach
This study simulates the inclined plane jet in a linear stratified environment using the random forest method. The overall research approach is illustrated in Figure 1. First, OpenFOAM (version 11) is used for numerical simulation of the inclined plane jet. Twenty cases are designed, and sixteen cases are randomly selected from the twenty to construct a comprehensive dataset (a total of 435,200 data points). This dataset is then divided into training, validation, and test sets in a 6:2:2 ratio for model training. The remaining four cases are used to test the model’s prediction performance (a total of 108,800 data points). Through prior research accumulation and numerical simulation experiments, the inherent correlation characteristics between various physical parameters in layered jets have been understood, clarifying the nonlinear coupling effects between the concentration field, velocity, and spatial coordinates in the layered jet [23]. Other unnecessary variables have a minimal impact on the model in this study and are therefore not considered. Based on this, this study constructs a random forest model and other machine learning models with the x-coordinate, y-coordinate, and their velocity components as input features, and the concentration field as the target variable. Through error analysis, the random forest model is compared with other machine learning models to assess the performance of each model, compare their generalization ability on unseen data, and verify the prediction accuracy and applicability of the random forest model.
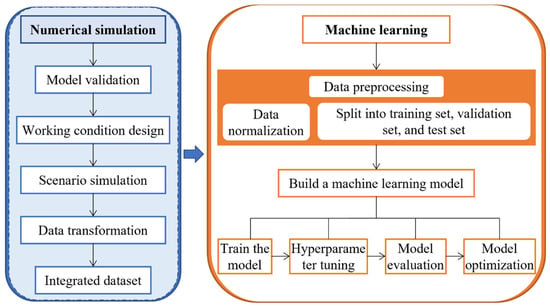
Figure 1.
Schematic of research methods.
2.2. Physical Phenomenon
The inclined plane jet in a linear stratified environment is shown in Figure 2 [10,23]. Here, ρt is the initial density of the receiving water at the water surface, ρb is the initial density of the receiving water at the bottom wall, Za is the flow depth, hs is the spreading layer thickness, and Zm is the terminal level. The jet is discharged at a certain angle into the receiving water body with a channel width of Bj. The jet initially sinks vertically due to sedimentation, and then gradually spreads in the horizontal direction. During propagation, it generates shear forces with the surrounding water, leading to turbulence and exhibiting a complex vortex structure.
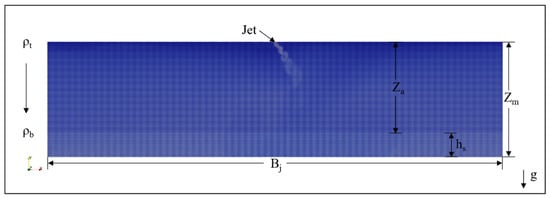
Figure 2.
Schematic diagram of an inclined plane jet in a linear stratified environment.
2.3. Physical Representation
The numerical model is constructed within the OpenFOAM framework, which is an open-source computational fluid dynamics software library that provides various tools and solvers to simulate jet behavior. Yan et al. [23] modified the multiphase solver “twoLiquidMixingFoam” to simulate the liquid mixing process in stratified environments. In this study, this model is used for numerical simulation. The model solves the standard 3D Navier–Stokes equations and the diffusion equation. The 3D Navier–Stokes equations are as follows:
With:
where t denotes time, U is velocity, and ρ is density. The term prgh represents static pressure minus hydraulic pressure, and h is the height of the fluid column. The variable α represents the volume fraction, and is used in this study to quantify the volume fraction of the two liquids. The symbol μ represents dynamic viscosity, and μt represents turbulent viscosity. The subscript i denotes either salt water or fresh water.
To compute the distribution of α, a transport equation was utilized:
where Dab denotes the molecular diffusivity, νt represents the turbulent eddy viscosity, and SC represents the turbulent Schmidt number.
OpenFOAM provides various turbulence models to describe the turbulent characteristics of jets, such as k-ε, k-ω, LES, etc. In this study, the renormalization group (RNG) k-ε turbulence model is used, which has been shown to be more accurate than the standard k-ε turbulence model. The turbulence model equations are as follows:
With:
where k and ε represent the turbulent kinetic energy and turbulent energy dissipation rate, respectively. G denotes the production of turbulence due to shear, and σk, σε, c1ε, c2ε, cμ, η0, and β are model constants, and their values are 0.71942, 0.71942, 1.42, 1.68, 0.0845, 4.38, and 0.012, respectively.
2.4. Numerical Experiments
The computational domain for this study is defined to cover the flow region of the inclined plane jet, allowing for the capture of the jet’s development and its interaction with the surrounding environment. A structured mesh is used for discretization, and the mesh resolution is determined through preliminary simulations with mesh sensitivity analysis. In this study, the simulation uncertainty caused by the grid mesh is kept below 3%. If the difference in prediction results exceeds 3% when using two different grids, a finer grid will be used. If reducing the grid size has no significant impact on the prediction results, the grid mesh will be considered satisfactory, and no further optimization will be necessary. The grid is uniformly distributed in both the horizontal and vertical directions to ensure an accurate resolution of the velocity and concentration fields. Mesh refinement is applied in the spreading layer region to improve the resolution and capture detailed flow features. For more model setup information, such as boundary conditions and parameter settings, please refer to the paper by Yan et al. [23]. This study is based on the case P2 from the research of Yan et al. [23] (slot width of 0.01 m, initial jet velocity of 0.0511 m/s, modified initial gravitational acceleration of 0.2305 m/s2, stratification parameter of 0.1392 s−2, densimetric Froude number of 1.0644, and stratification length scale of 0.0464 m). The initial jet velocity is varied, and 20 different operating conditions are generated using Latin hypercube sampling. These conditions are based on variations in the velocity components in both horizontal and vertical directions, and their corresponding initial turbulence characteristics are mainly represented by two parameters: turbulent kinetic energy (k) and turbulence dissipation rate (ε). Specific values are provided in Table 1.

Table 1.
Operating conditions design.
2.5. Random Forest Algorithm
Random forest (RF) is an ensemble learning method that improves model accuracy and robustness by combining the prediction results of multiple decision trees. It has efficient predictive capabilities and strong robustness, making it particularly suitable for handling large-scale and high-dimensional data. In this study, a random forest regression model is used to predict the concentration field of inclined plane jets. The overall process of the model is shown in Figure 3. Multiple regression trees are trained, and the prediction results of all trees are averaged to obtain the final concentration field prediction. To enhance the accuracy of the model, 100 decision trees are used, and random seeds are adjusted to ensure the reproducibility of the results. During the training process, a normalized training dataset is used, and the model is trained through the fit() method. This approach demonstrates good handling capabilities for large-scale data, improving model accuracy while effectively avoiding overfitting issues.
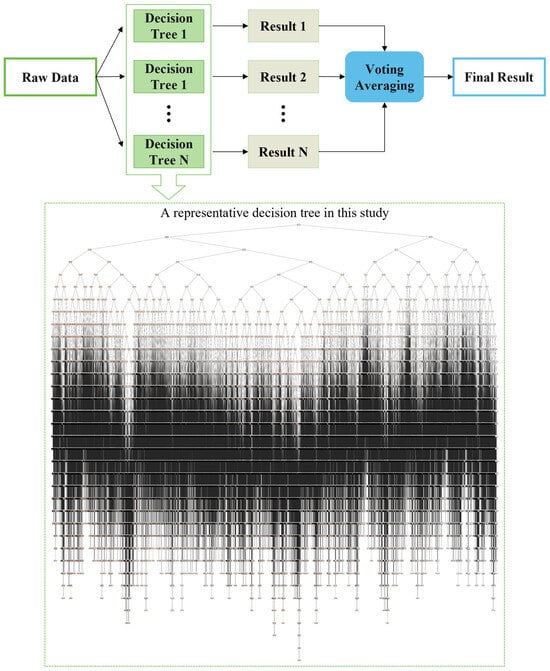
Figure 3.
Flowchart of the random forest algorithm.
2.6. Reference Methods
2.6.1. Support Vector Regression
Support vector regression (SVR) is a regression analysis method based on support vector machines (SVMs), and is aimed at establishing the relationship between input features and target variables by minimizing training errors and controlling model complexity. The core idea of SVR is to map the data into a high-dimensional space and construct an optimal hyperplane such that most data points are as close as possible to this hyperplane, enabling precise prediction of the target variable. In this study, an SVR model based on a radial basis function (RBF) kernel is used to predict the concentration field of inclined plane jets. During the model training process, the penalty parameter is set to 100 to balance model complexity and training errors, while epsilon is set to 0.1 to control the allowable prediction error range, thus determining the tolerance for support vectors.
2.6.2. Linear Regression
Linear regression is a classic regression analysis method, where the core idea is to establish a linear relationship between input features and the target variable by fitting a straight line or hyperplane. The model assumes that the target variable is a weighted sum of the input features, and these weights are determined by minimizing the prediction error. In this study, the linear regression model predicts the target variable, the concentration field, based on input features such as x- and y-coordinates and velocity components. During the training process, the model learns the optimal linear relationship by minimizing the error on the training data.
2.6.3. Genetic Programming
Genetic programming (GP) is an evolutionary algorithm that simulates the process of natural selection, aiming to find solutions to problems by continuously generating and optimizing programs. Unlike traditional optimization algorithms, GP not only optimizes numerical parameters but also automatically generates model structures, thereby enhancing the flexibility and adaptability of the model. In this study, GP is used to optimize the parameters of a linear regression model to predict the concentration field in an inclined plane jet. First, a population is initialized, where each individual consists of four floating-point weight values representing the weights of the input features. Through genetic operations such as crossover, mutation, and selection, the algorithm iteratively optimizes individuals, progressively minimizing the prediction error (RMSE). The algorithm runs for 50 generations, where in each generation the fitness of the individuals is evaluated by calculating the error between the predicted and actual values, selecting the optimal solution, and continuing until the model parameters that minimize the error are found.
2.6.4. Adaptive Boosting
Adaptive Boosting (AdaBoost) constructs a strong learner by combining multiple weak learners. The core idea is to improve the model’s predictive ability by a weighted combination of several weak classifiers. In each iteration, AdaBoost increases the weight of the misclassified samples, encouraging subsequent base learners to focus more on these difficult-to-predict samples, thereby improving the overall accuracy of the model. In this study, the base learner for the AdaBoost regression model is a decision tree regressor with a depth of 4. By setting max_depth = 4, the complexity of each base learner is limited to avoid overfitting. Setting n_estimators = 100 defines the number of base learners in the model, i.e., training 100 decision tree models. Finally, the model is optimized by calling the fit() method to train on the training data.
2.6.5. Algorithm Comparison and Analysis
Among the aforementioned machine learning methods, each algorithm has its unique advantages and disadvantages. Random forest and AdaBoost, through ensemble learning strategies, can significantly enhance model accuracy, especially when handling spatial coordinates and velocity components of jets in a linear stratified environment. However, AdaBoost is sensitive to noise, which could lead to overfitting. Support vector regression, relying on kernel functions, is capable of capturing complex relationships in linear stratified environments, but it is sensitive to parameters and requires fine-tuning. Genetic programming can automatically adjust model structures and optimize parameters, potentially capturing more complex patterns in the prediction of inclined plane jet concentration fields, but it may suffer from overfitting to noise, reducing its generalization ability. Linear regression, while simple, assumes strict linearity, which may struggle to describe the nonlinear characteristics of stratified flow fields. This study will systematically evaluate these algorithms to gain a clearer understanding of their applicability in predicting the inclined plane jet concentration field in linear stratified environments.
3. Results
3.1. Numerical Results
Yan et al. [23] have validated this numerical model, and the model showed excellent performance in simulations. The R2 value for simulating the terminal level Zm was 0.986 with an RMSE value of 0.015 m; for simulating the bottom flow depth Za, the R2 value was 0.982 with an RMSE value of 0.009 m; and for simulating the expansion layer thickness hs, the R2 value was 0.895 with an RMSE value of 0.019 m. The prediction errors for the terminal level, under-flow depth, and spreading layer thickness are approximately 4%, 9%, and 9%, respectively. These results demonstrate that the model can effectively and accurately predict key variables, showing a high reliability, and can be used for scenario simulation.
The results of the numerical experiments are shown in Figure 4. From the figure, it can be observed that in a linear stratified environment, due to the presence of density stratification, vertical diffusion is significantly suppressed, leading to horizontal diffusion dominating the process. For C01–C05, the Ux and Uy values are small, and both horizontal and vertical diffusion are limited. For C06–C15, the Ux values increase, and the sinking rate accelerates, leading to significant diffusion and a wider jet spread. For C16–C20, both Ux and Uy values are larger, causing the jet to gradually dilute and the jet boundary to spread, with the core region becoming more diffuse. Furthermore, the density gradient in the stratified environment enhances the buoyancy effect of the jet, leading to accelerated diffusion in the low-density layer and decelerated diffusion in the high-density layer. Overall, the diffusion range of the jet in the stratified environment exhibits clear directional characteristics, with a broader horizontal diffusion range and a relatively narrower vertical diffusion range, forming a “fan-shaped” diffusion pattern. These results are consistent with existing theoretical knowledge and can provide a reliable comprehensive dataset for subsequent machine learning algorithms (hereinafter referred to as the ground truth).
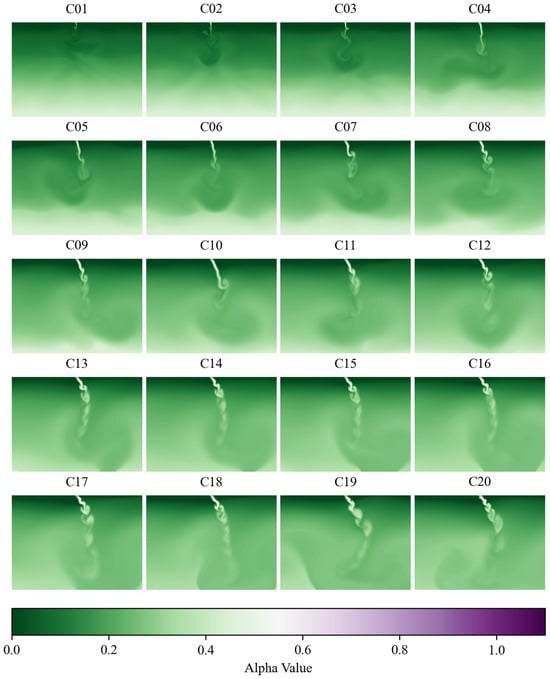
Figure 4.
Spatial distribution map of numerical simulation results.
3.2. Performance of the Random Forest Method
In the comprehensive dataset, four cases were randomly selected to compare the random forest’s prediction results with the ground truth, as shown in Figure 5. The results show that in cases C05–C20, as the velocity increases, the diffusion range of the jet gradually expands. The high-concentration region (close to 1.0) is mainly concentrated in the core of the jet and diffuses along the inclined direction, while the low-concentration region gradually extends to the periphery. The random forest model’s prediction results are highly consistent with the ground truth in terms of overall trends, accurately capturing the main features of concentration distribution, including the location of the high-concentration core and the overall trend of concentration diffusion.
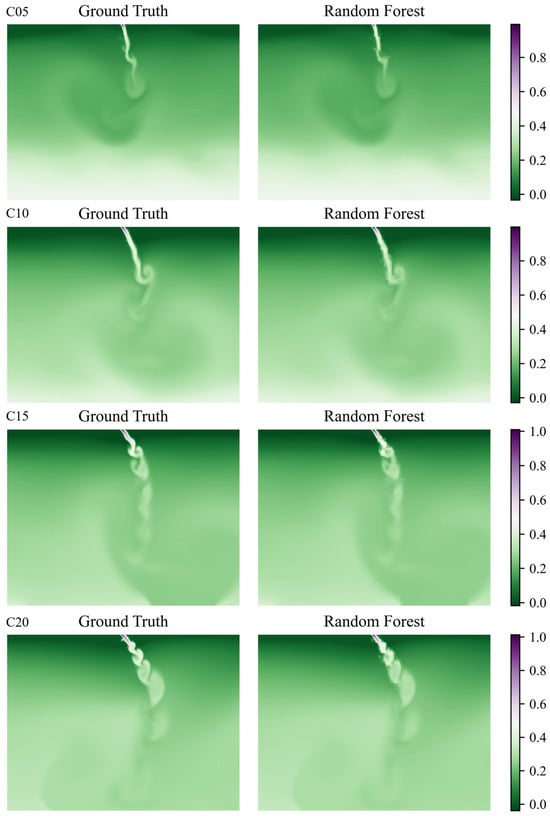
Figure 5.
Comparison chart of the random forest model with the ground truth concentration field distribution in the integrated dataset.
To evaluate the prediction performance of the random forest model on unseen data, the prediction results of the remaining four cases were compared with the ground truth, as shown in Figure 6. It can be seen that the random forest model’s concentration field prediction results are generally accurate in cases C04, C06, C12, and C16. The model is able to reproduce the trend of an increasing diffusion range with velocity change and reflects the spatial distribution characteristics of the ground truth well, demonstrating a high consistency. Overall, the random forest model’s prediction performance is stable and effectively predicts the concentration field distribution of the inclined planar jet in a linear stratified environment.
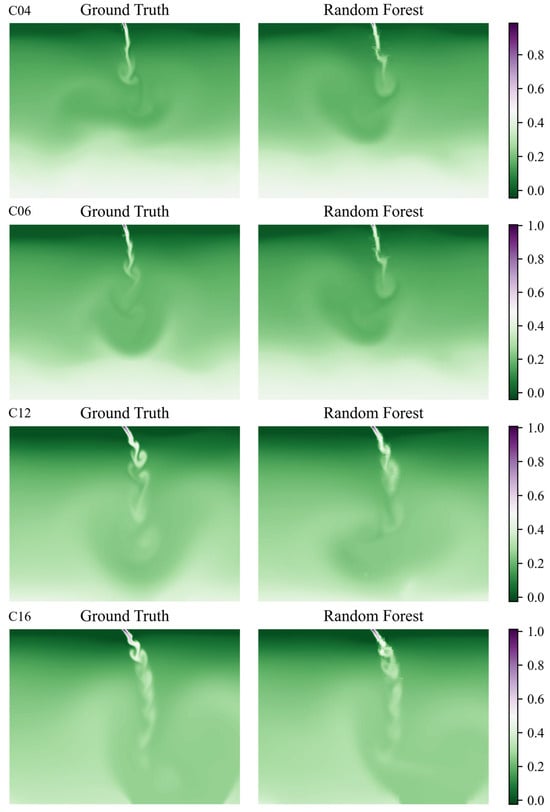
Figure 6.
Comparison chart of the random forest model with the ground truth concentration field distribution in the unseen data.
To further analyze the prediction accuracy of the random forest model, contour scatter plots were created, as shown in Figure 7 and Figure 8. It can be observed that the random forest model exhibits a high prediction accuracy in the comprehensive dataset (C05, C10, C15, C20), with the predicted values closely fitting the ground truth along the 1:1 diagonal in the scatter plot, indicating that the model has a strong capability in reconstructing the actual data. The R2 values for all cases are close to 1, and the root mean square error (RMSE) is extremely low. In particular, for case C05 the R2 value reaches 0.999 and the RMSE is 0.004, further validating the model’s stability and accuracy. In the unseen cases (C04, C06, C12, C16), although random forest reduces the risk of overfitting through ensemble learning, it still relies on the representativeness and diversity of the training data, and may perform slightly worse when facing new situations. Therefore, the prediction accuracy is slightly lower compared to the seen data, but it still demonstrates a high accuracy. From the results of the scatter plots, the R2 values range from 0.974 to 0.958, indicating that the model has a strong fitting ability for the overall trend of the concentration field distribution. The RMSE values range from 0.017 to 0.021, which are relatively low, indicating that the model’s prediction error is small and the prediction accuracy is high. In conclusion, the random forest model demonstrates a high stability and reliability in capturing the distribution and variation trends of the jet concentration field, showcasing an excellent prediction performance and application potential.
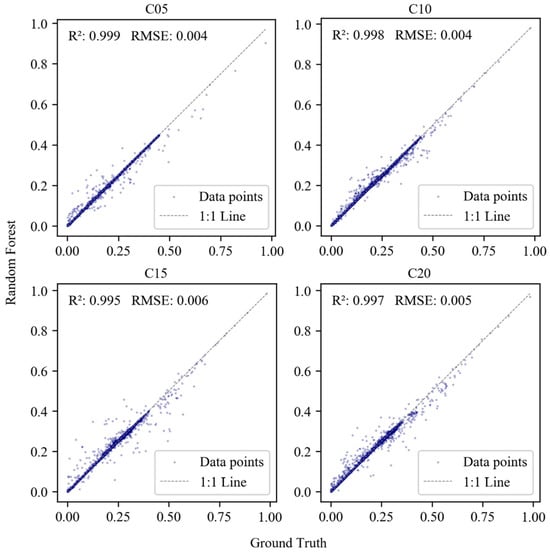
Figure 7.
Contour plot of the random forest model and ground truth in the comprehensive dataset.
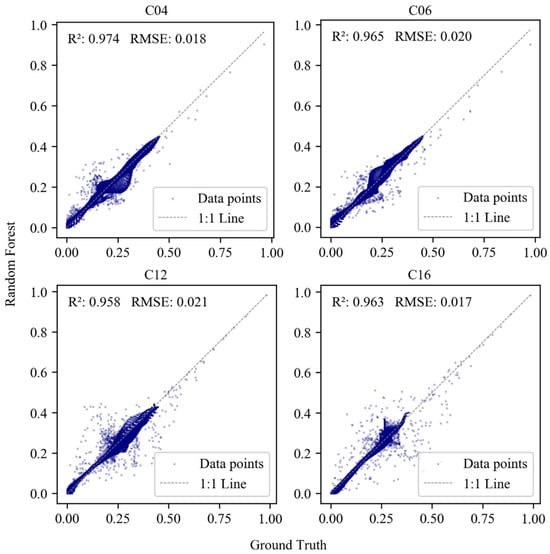
Figure 8.
Contour plot of the random forest model and ground truth in the unseen data.
3.3. Performance of the Reference Methods
To evaluate the performance of the support vector regression, linear regression, genetic programming, and Adaptive Boosting algorithms, the R2 and RMSE values for each algorithm were calculated for different cases. The results are shown in Figure 9 and Figure 10. From the figures, it is clear that all four algorithms performed well, but there were notable differences. Among them, the AdaBoost algorithm performed the best. Compared to the other three algorithms, its R2 values were relatively stable across all cases, with most cases falling between 0.8 and 0.9, and the RMSE values consistently remained low, around 0.04 to 0.045. The genetic programming and linear regression algorithms showed a similar performance to AdaBoost in cases C01–C08, with high R2 values and low RMSE values, but their fitting performance declined in cases C13–C20. In contrast, the support vector regression algorithm performed the worst, with its R2 and RMSE values being the least favorable across all cases, showing a poor predictive performance and higher errors.

Figure 9.
Heatmap of the R2 matrix for other algorithms.

Figure 10.
Heatmap of the RMSE matrix for other algorithms.
4. Discussion
This study is the first to introduce the random forest algorithm to the prediction of the concentration field of inclined plane jets in a linear stratified environment, filling the gap in the application of machine learning in complex stratified flow modeling. Unlike previous studies that mainly focus on traditional fluid mechanics methods or simple analytical models, this research leverages the ensemble feature of multiple decision trees in the random forest model, which can effectively and efficiently reproduce the phenomena. Based on the consideration of fluid physical processes, the model accurately simulates the concentration distribution at different layers in stratified water bodies. The model demonstrates a strong environmental adaptability and generalization ability, providing fast and accurate predictions under varying conditions. This study thoroughly validates the robustness of the random forest model in predicting the concentration field of inclined planar jets in a linear stratified environment, using both comprehensive datasets (with a total of 435,200 data points) and unseen datasets (with a total of 108,800 data points). The results show that the model can construct an accurate and efficient predictive model even under limited data training conditions. Preliminary tests indicate that, for this physical problem, the random forest algorithm outperforms support vector regression, linear regression, genetic programming, and Adaptive Boosting algorithms.
To further evaluate the performance of each machine learning model, the R2 and RMSE values for each case were calculated, as shown in Figure 11 and Figure 12. The error lines in the figures represent the 90% confidence intervals. The results indicate that random forest performed the best across all cases, with its R2 value being the closest to 1, its RMSE value being the lowest, and its error lines being shorter, suggesting excellent fitting capability and error control, with stable results. Genetic programming and linear regression demonstrated some fitting capability in cases C01–C06, but as the velocity increased their R2 values significantly decreased and RMSE values rose, indicating limitations in handling complex nonlinear problems. The performance of AdaBoost was similar to that of genetic programming and linear regression, but with slightly less stability. In contrast, support vector regression had lower R2 values, higher RMSE values, and larger error ranges, showing a poor fitting capability and error control. In terms of computational efficiency and resource consumption, the models were trained on a computer equipped with a 13th generation Intel(R) Core(TM) i5 processor and 16 GB of memory. The running times of random forest, linear regression, genetic programming, and Adaptive Boosting algorithms are all below 90 s, with linear regression having the fastest training speed. However, its predictive performance is limited by the model assumptions. On the other hand, SVR takes the longest time (7 min 32 s) due to the high complexity of kernel function calculations. Therefore, random forest strikes a good balance between accuracy and efficiency. In summary, the random forest algorithm exhibited a superior stability and high performance in predicting complex jet concentration fields compared to other machine learning algorithms. This can be attributed to the advantages of ensemble learning in random forest, where multiple decision trees are constructed and their predictions are combined, effectively reducing overfitting risks and handling complex nonlinear relationships in the data. Compared to other algorithms, random forest automatically adapts to the interactions between data features and excels in handling nonlinear data.
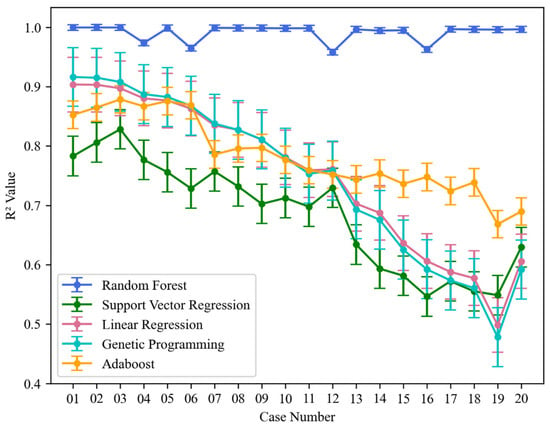
Figure 11.
R2 error line chart.
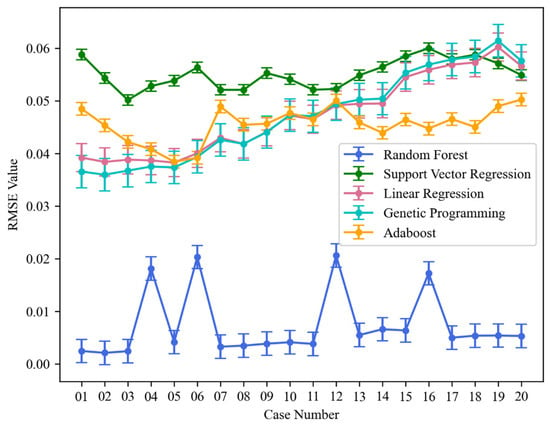
Figure 12.
RMSE error line chart.
In predicting the concentration field of complex jet processes, the machine learning method proposed in this study significantly improves computational efficiency and prediction accuracy compared to traditional methods. Traditional jet simulation methods include empirical formulas and numerical simulations. Empirical formulas or semi-empirical models are based on specific experimental conditions or simplified assumptions, making their applicability limited. For complex flow phenomena, particularly the complex diffusion process of inclined plane jets in a stratified environment, these methods cannot provide sufficiently accurate results. While numerical simulation methods can describe fluid dynamics processes more precisely, they often rely on complex physical equations. These equations are difficult to solve when dealing with complex systems and require detailed modeling of various aspects of the system. Furthermore, when faced with high-dimensional and complex data, numerical simulations are often constrained by computational resources and model assumptions, resulting in a low computational efficiency. In predicting the concentration field of inclined plane jets in a linear stratified environment, the computation time is several hours. In contrast, machine learning methods learn patterns automatically from historical data in a data-driven manner, without the need to explicitly model physical processes. This reduces the complexity and dependency on assumptions during the modeling process. In this study, the computation time is reduced to the minute level. The machine learning model currently being developed is not intended to surpass the prediction accuracy of numerical simulations, but rather to serve as an efficient alternative. While maintaining a prediction accuracy comparable to numerical simulations, the computation time is reduced from the order of hours to the order of minutes, achieving a two-order-of-magnitude improvement in efficiency and significantly enhancing computational efficiency. Compared to traditional simulation methods, especially in simulating the concentration field of inclined jets in complex environments, machine learning can handle multiple input variables, such as flow velocity, temperature, pressure, etc., thus avoiding the tedious repetition of calculations for each specific scenario required by traditional methods. Once trained, machine learning models can make rapid predictions, significantly improving computational efficiency and reducing resource consumption, with a strong generalization ability. Therefore, machine learning methods are more flexible, efficient, and adaptable than traditional methods when simulating the concentration field of complex jet processes.
In practical applications, taking the example of predicting pollutant diffusion concentration fields for an inclined jet at a coastal sewage outlet, the specific implementation steps are as follows: First, obtain the coordinates (x, y) and their corresponding velocity components (u, v) at each point in the region. These data are organized into a four-column Excel table (the first two columns are u and v, and the last two columns are x- and y-coordinates). The data are then normalized, and the normalized dataset is input into the pre-trained random forest model, which outputs the normalized concentration values. These are then inverse-normalized to obtain the actual concentration field distribution. Finally, the concentration field can be visualized using heatmaps or contour plots, providing an intuitive display of the concentration distribution in the region, which serves as a decision-making basis for optimizing the sewage discharge plan. The entire process from data input to result output takes only a few seconds, improving the efficiency by two orders of magnitude compared to traditional CFD simulations, and does not require complex grid partitioning and iterative calculations, highlighting the unique advantages of machine learning models in practical engineering applications.
This study tested the performance of random forest, support vector regression, linear regression, genetic programming, and AdaBoost algorithms in simulating the concentration field of inclined planar jets in a linear stratified environment. However, this study did not account for complex scenarios involving multi-scale and multi-physical process coupling. In practical applications, physical phenomena in water bodies may be more complex, involving turbulence, sedimentation, thermodynamics, and other factors. Future research can enhance the modeling of these complex physical processes and incorporate them into machine learning models to further improve prediction accuracy and applicability.
5. Conclusions
This study predicts the concentration field of inclined planar jets in a linear stratified environment using the random forest algorithm and compares its performance with support vector regression, linear regression, genetic programming, and AdaBoost algorithms. Numerical simulations were conducted using OpenFOAM to extract data under different operating conditions to construct a comprehensive dataset, which was then divided into training, validation, and test sets for model training. This study demonstrates that random forest consistently outperforms all other models, exhibiting the highest R2 value, the lowest RMSE, and a smaller error range. It effectively handles nonlinear relationships and high-dimensional features in the flow concentration field, outperforming other machine learning models. This research verifies that the random forest algorithm has a strong adaptability and stability in predicting complex jet concentration fields, offering new insights and technical support for fields such as water pollution diffusion in environmental engineering and marine engineering. Future research could focus on enhancing the modeling of multi-physical processes to further improve model performance.
Author Contributions
X.Y. reviewed and edited the manuscript, X.C. and S.L. prepared the original draft, Z.S. and L.L. processed the data. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Open Fund of Anhui Province Key Laboratory of Intelligent Mining Equipment and Technology [Grant number ZKSYS202202], the National Natural Science Foundation of China [Grant number 52309079], and the National Key Research and Development Program of China [Grant number 2022YFC3702300].
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Symbols and Abbreviations
| Symbols | |
| ρt | Initial density of the receiving water at the water surface |
| ρb | Initial density of the receiving water at the bottom wall |
| Za | Flow depth |
| hs | Spreading layer thickness |
| Zm | Terminal level |
| Bj | Channel width |
| U | Velocity |
| ρ | Density |
| prgh | Static pressure minus hydraulic pressure |
| h | Height of the fluid column |
| α | Volume fraction |
| μ | Dynamic viscosity |
| μt | Turbulent viscosity |
| i | Salt water or fresh water |
| Dab | Molecular diffusivity |
| νt | Turbulent eddy viscosity |
| SC | Turbulent Schmidt number |
| k | Turbulent kinetic energy |
| ε | Turbulent energy dissipation rate |
| G | Production of turbulence due to shear |
| σk | 0.71942 |
| σε | 0.71942 |
| c1ε | 1.42 |
| c2ε | 1.68 |
| cμ | 0.0845 |
| η0 | 4.38 |
| β | 0.012 |
| Ux | Velocity component in the x direction |
| Uy | Velocity component in the y direction |
| Abbreviations | |
| RF | Random Forest |
| SVR | Support Vector Regression |
| SVM | Support Vector Machine |
| RBF | Radial Basis Function |
| GP | Genetic Programming |
| AdaBoost | Adaptive Boosting |
| MGGP | Multi-Gene Genetic Programming |
| SGGP | Single-Gene Genetic Programming |
| RMSE | Root Mean Square Error |
| R2 | R-squared |
References
- Drami, D.; Yacobi, Y.Z.; Stambler, N.; Kress, N. Seawater quality and microbial communities at a desalination plant marine outfall. A field study at the Israeli Mediterranean coast. Water Res. 2011, 45, 5449–5462. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A. Numerical modeling of vertical buoyant jets subjected to lateral confinement. J. Hydraul. Eng. 2017, 143, 04017016. [Google Scholar] [CrossRef]
- El-Ghorab, E.A.S. Physical model to investigate the effect of the thermal discharge on the mixing zone (Case Study: North Giza Power Plant, Egypt). Alex. Eng. J. 2013, 52, 175–185. [Google Scholar] [CrossRef]
- Jirka, G.H.; Stolzenbach, K.D.; Adams, E.E. Buoyant surface jets. J. Hydraul. Div. 1981, 107, 1467–1487. [Google Scholar] [CrossRef]
- Knudsen, M. Buoyant Horizontal Jets in an Ambient Flow. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 1988. [Google Scholar]
- Kaminski, E.; Tait, S.; Carazzo, G. Turbulent entrainment in jets with arbitrary buoyancy. J. Fluid Mech. 2005, 526, 361–376. [Google Scholar] [CrossRef]
- Bashitialshaaer, R.; Larson, M.; Persson, K.M. An experimental investigation on inclined negatively buoyant jets. Water 2012, 4, 720–738. [Google Scholar] [CrossRef]
- Roberts, P.J.W.; Matthews, P.R. Dynamics of jets in two-layer stratified fluids. J. Hydraul. Eng. 1984, 110, 1201–1217. [Google Scholar] [CrossRef]
- Wallace, R.B.; Wright, S.J. Spreading layer of two-dimensional buoyant jet. J. Hydraul. Eng. 1984, 110, 813–828. [Google Scholar] [CrossRef]
- Lee, J.H.W.; Cheung, V.W.L. Inclined plane buoyant jet in stratified fluid. J. Hydraul. Eng. 1986, 112, 580–589. [Google Scholar] [CrossRef]
- Jirka, G.H. Integral model for turbulent buoyant jets in unbounded stratified flows. Part I: Single round jet. Environ. Fluid Mech. 2004, 4, 1–56. [Google Scholar] [CrossRef]
- Amamou, A.; Habli, S.; Saïd, N.M.; Bournot, P.; Le Palec, G. Numerical study of turbulent round jet in a uniform counterflow using a second order Reynolds stress model. J. Hydro-Environ. Res. 2015, 9, 482–495. [Google Scholar] [CrossRef]
- Meng, G.; Wenxin, H. Numerical simulation of a round buoyant jet in a counterflow. Procedia Eng. 2016, 154, 943–950. [Google Scholar] [CrossRef]
- Gao, M.; Huai, W.-X.; Li, Y.-T.; Wang, W.-J. Numerical study of the flow and dilution behaviors of round buoyant jet in counterflow. J. Hydrodyn. Ser. B 2017, 29, 172–175. [Google Scholar] [CrossRef]
- Ishigaki, M.; Abe, S.; Sibamoto, Y.; Yonomoto, T. Influence of mesh non-orthogonality on numerical simulation of buoyant jet flows. Nucl. Eng. Des. 2017, 314, 326–337. [Google Scholar] [CrossRef]
- Belcaid, A.; Le Palec, G.; Draoui, A. Numerical and experimental study of Boussinesq wall horizontal turbulent jet of fresh water in a static homogeneous environment of salt water. J. Hydrodyn. 2015, 27, 604–615. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, Y.; Tao, J.; Pan, Y.; Sowa, D.M.A.; Li, C.-W. Three-dimensional flow structure of a non-buoyant jet in a wave-current coexisting environment. Ocean Eng. 2016, 116, 42–54. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, Y.; Wang, Y.; Zhang, C. Near-field dilution of a turbulent jet discharged into coastal waters: Effect of regular waves. Ocean Eng. 2017, 140, 29–42. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, Y.; Pan, Y. Initial dilution equations for wastewater discharge: Example of non-buoyant jet in wave-following-current environment. Ocean Eng. 2018, 164, 139–147. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Hsiao, S.-C. Numerical modeling of a buoyant round jet under regular waves. Ocean Eng. 2018, 161, 154–167. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A. Evolutionary prediction of the trajectory of a rosette momentum jet group in flowing currents. J. Coast. Res. 2020, 36, 1059–1067. [Google Scholar] [CrossRef]
- Hassanzadeh, H.; Joshi, S.; Taghavi, S.M. Predicting buoyant jet characteristics: A machine learning approach. Chem. Prod. Process Model. 2024, 19, 163–177. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.; Mohammadian, A.; Chen, X. Numerical modeling of inclined plane jets in a linearly stratified environment. Alex. Eng. J. 2020, 59, 1857–1867. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).