Acoustic Emission/Mine Microseismic Sensor Network Optimization Based on Grid Loop Search and Particle Swarm Source Location
Abstract
1. Introduction
2. Methodology
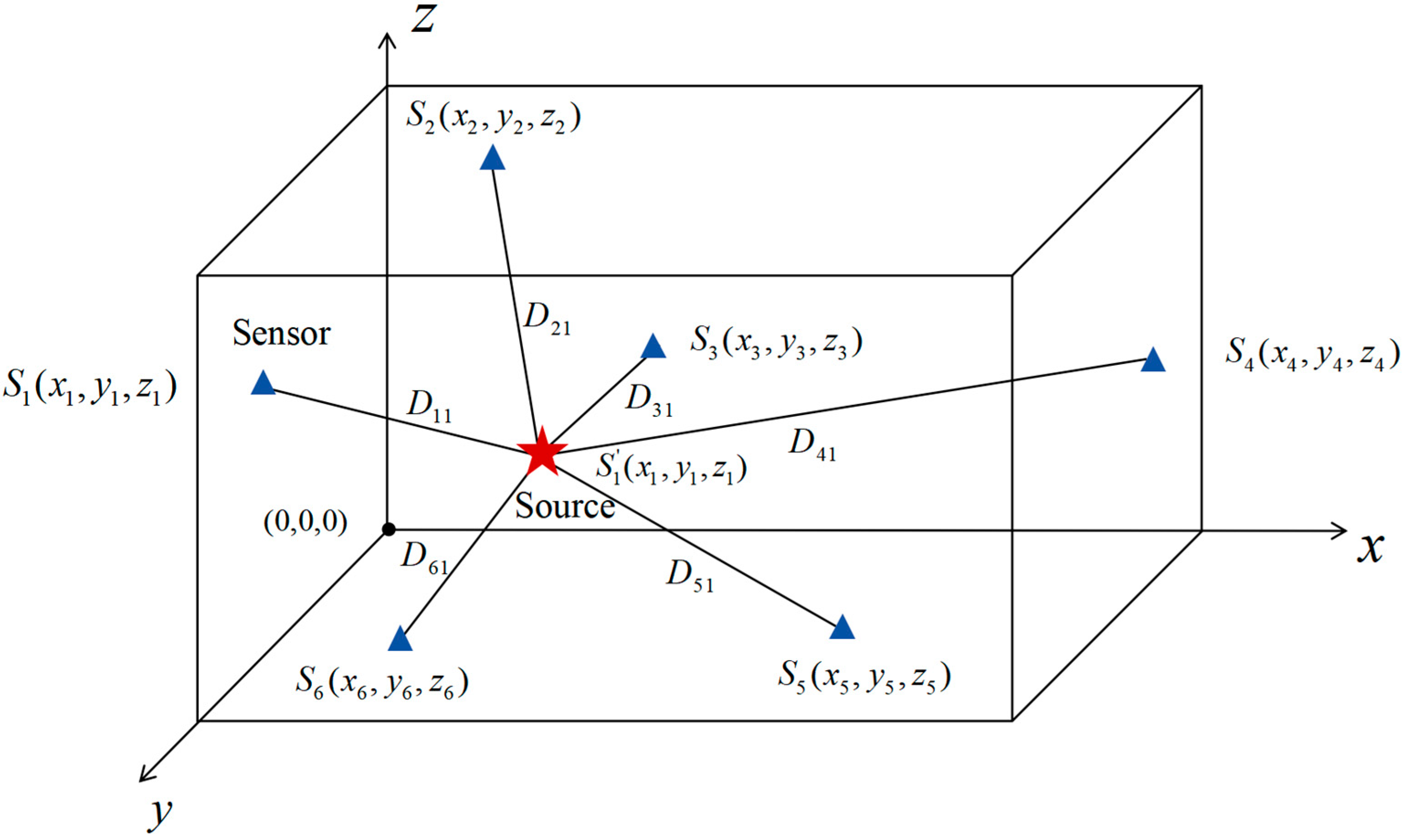
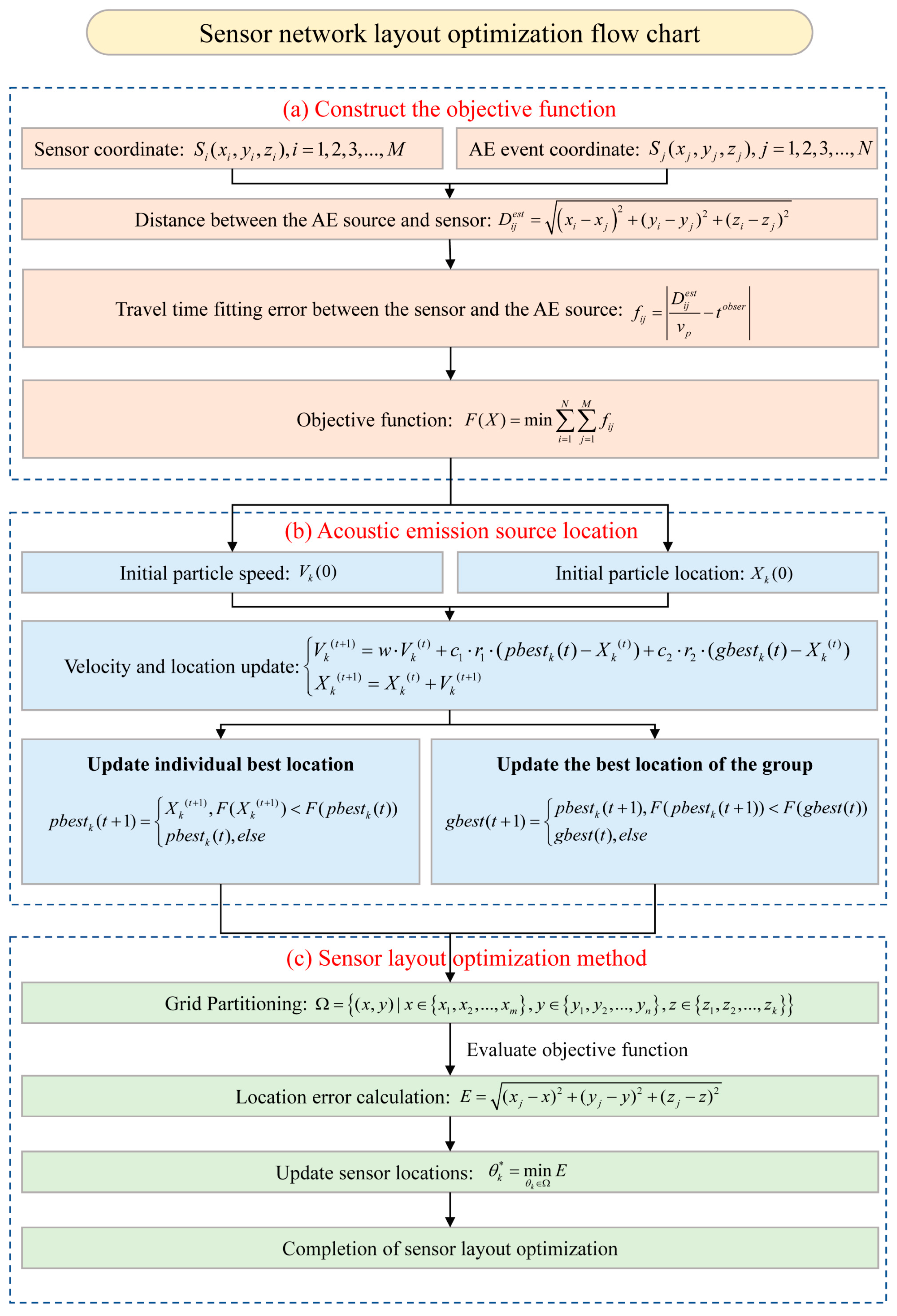
2.1. Sensor Location Objective Function
2.2. PSO-Based Location Algorithm
- Parameter initialization: Multi-particles are randomly generated, and each particle represents a potential AE event location. Each particle is assigned a random velocity and location , where represents the index of different particles.Then, these initial parameters of each particle are substituted into the objective function Equation (3) to calculate the initial fitness , which is then set as each particle’s personal best .
- Velocity and location update: The velocity of each particle is updated according to Equation (4):where represents the velocity of particle at time , and is set to 30; is the inertia weight, which determines the particle’s tendency to maintain its current velocity; is the velocity of particle at time ; and separately are learning factors that control the particle’s attraction to its personal best and the global best location, and they are both set to 1.49; and are random numbers within the range [0, 1].Then, the particle’s location is updated based on the updated velocity:where represents the location of particle at time , and is the location of particle at time .
- Fitness evaluation: After updating each particle’s location , the parameters represented by this location are substituted into the objective function . The is used to update the individual historical best location of particle at time and the global best location of the swarm.
- Updating and : The fitness function is used as a criterion, where lower values indicate higher accuracy in determining the optimal location. For each particle , if the new fitness is smaller than the fitness of its historical best location, the historical best location is updated as . Otherwise, the historical best location remains unchanged. Among the historical best locations of all particles, the location with the best fitness is selected as the global best location of the swarm. The updated equations are as follows:
- Iteration and convergence: By iteratively updating each particle’s velocity and location, updated and are generated until the maximum number of iterations is reached. Ultimately, the global best location is considered as the optimal coordinate for the AE event. This location represents the solution that minimizes the error of the objective function.
2.3. Sensor Layout Optimization Method
- Grid Partitioning: Within the sensor deployment area, a regular grid is generated based on predefined spacing. The density of the grid points is determined by the required optimization accuracy. Assuming the target area is mm2, the set of grid points can be expressed aswhere , , and represent the coordinates of the grid points.
- Objective function evaluation: For each sensor , the location is moved to each candidate location . For each candidate location, the AE source location is calculated using Equation (3).
- Location error calculation: For each candidate location , the location error is calculated as the distance between the AE source location and the actual source location :where is the source location and is the actual source location.
- Update sensor locations: In each iteration, the candidate location with the minimum location error for each sensor is selected. This location is then updated as the new sensor layout configuration:If the error at this location is smaller than the current global minimum error , the global optimal location and the corresponding error are updated.
- Completion of sensor layout optimization: During the optimization process, the optimal sensor locations and the corresponding location errors for each iteration are recorded. The final optimization results are validated to ensure the rationality of the sensor layout and the improvement in location accuracy.
3. Synthetic Test
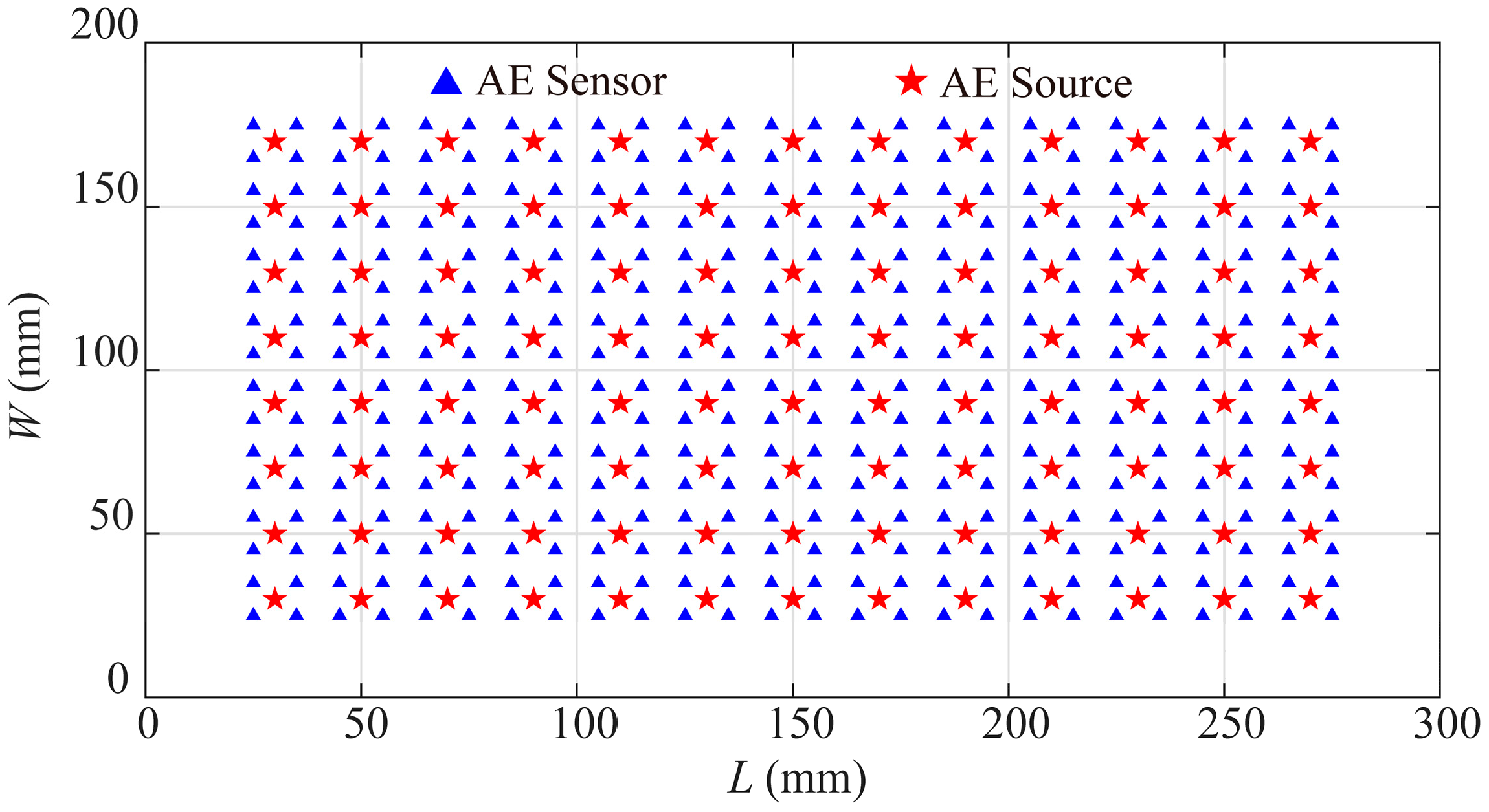
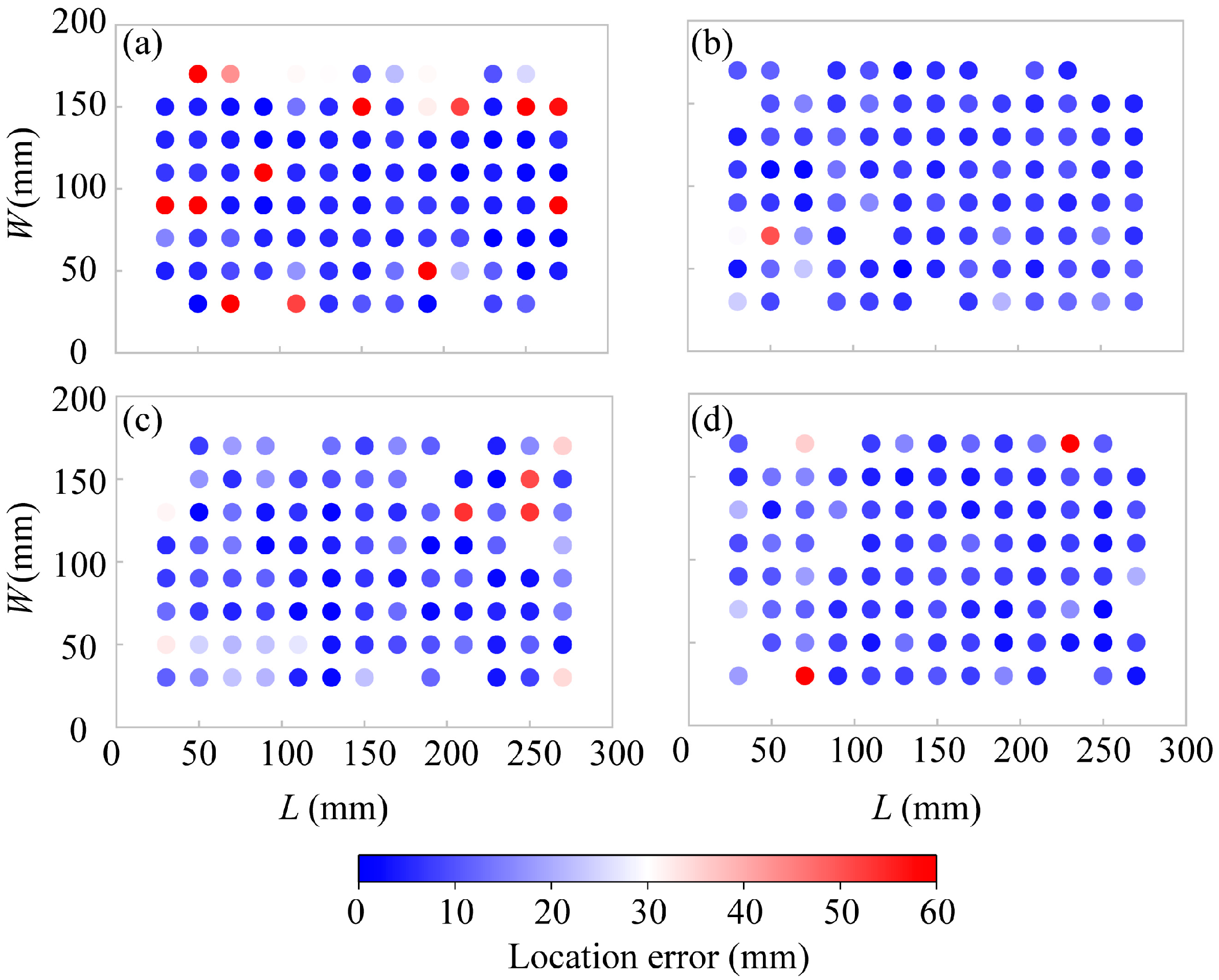
3.1. Sensor Network Optimization
3.2. Location Results
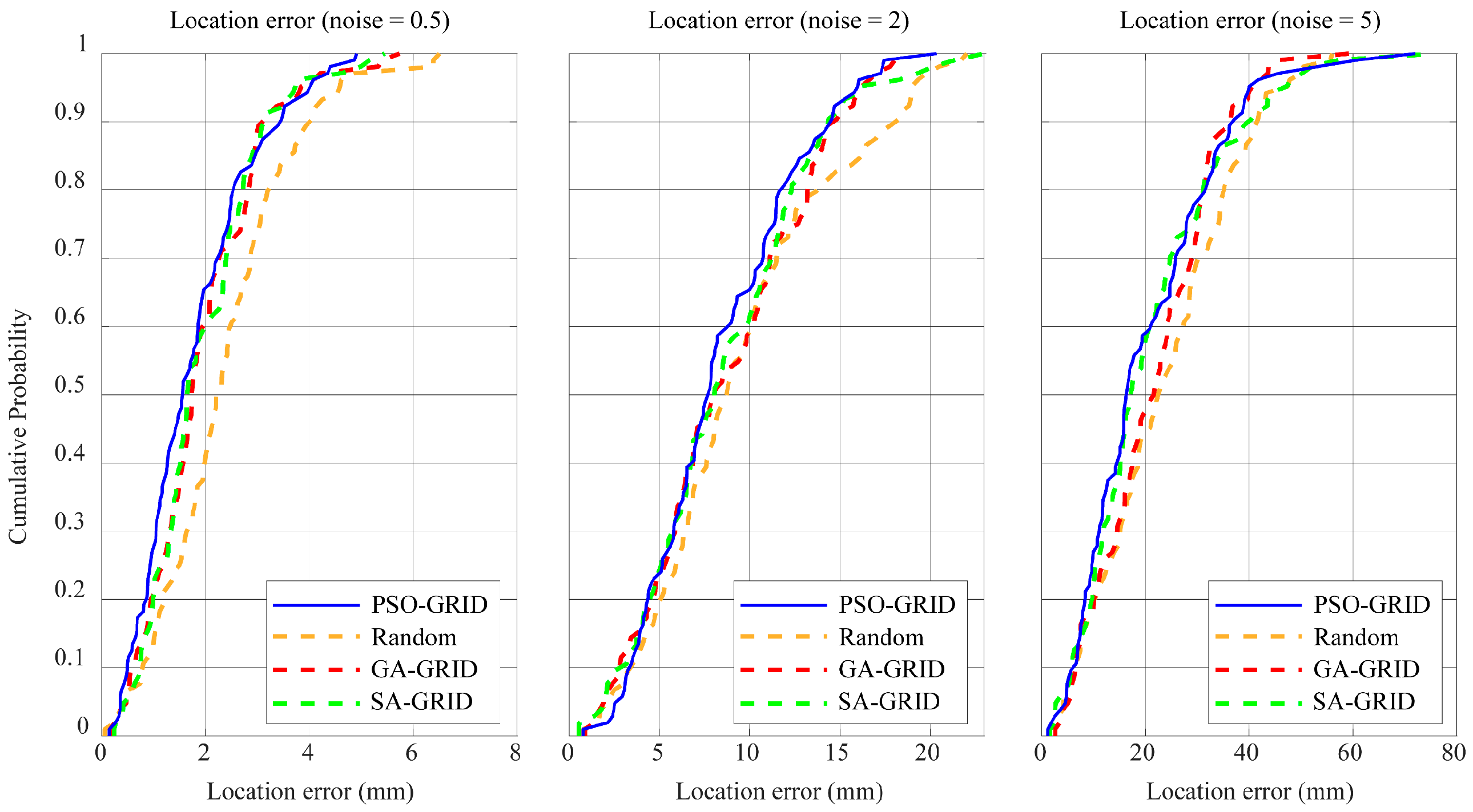
3.3. Noise Resistance Testing of the Synthetic Model
4. Experimental Test
4.1. Experimental Setup
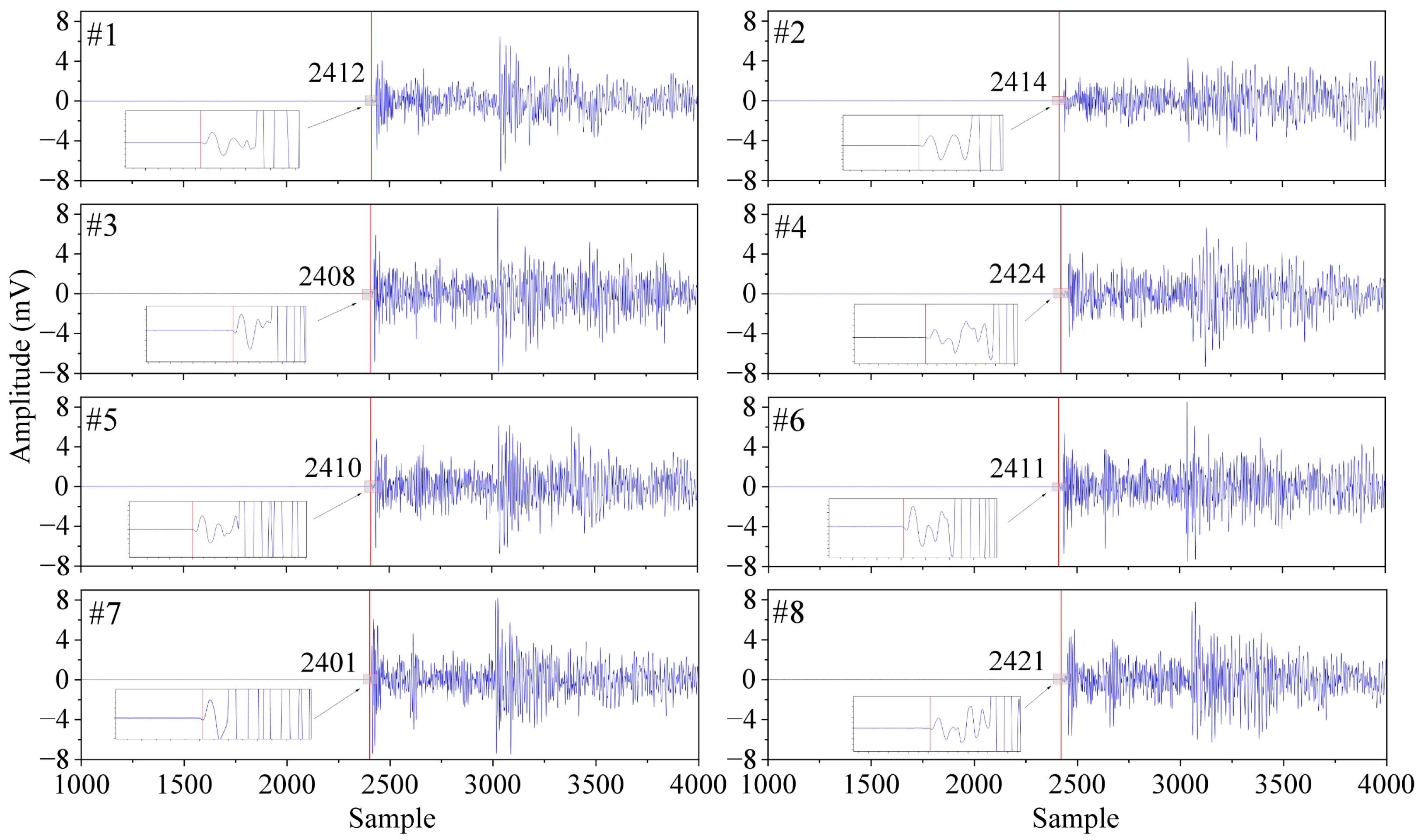
4.2. Experimental Data Processing
4.3. Location Test
5. Discussions
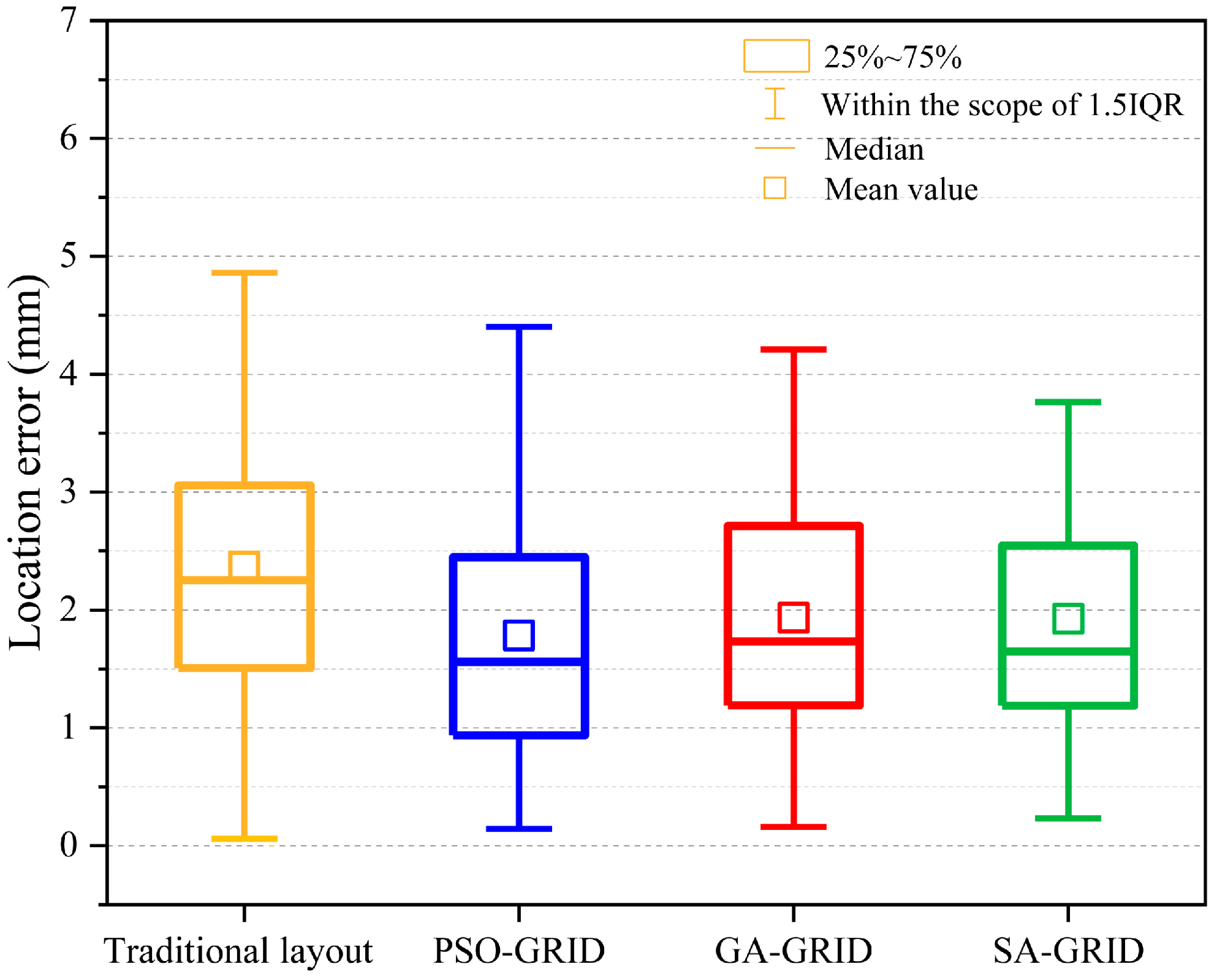
5.1. Influence of Sensor Layouts
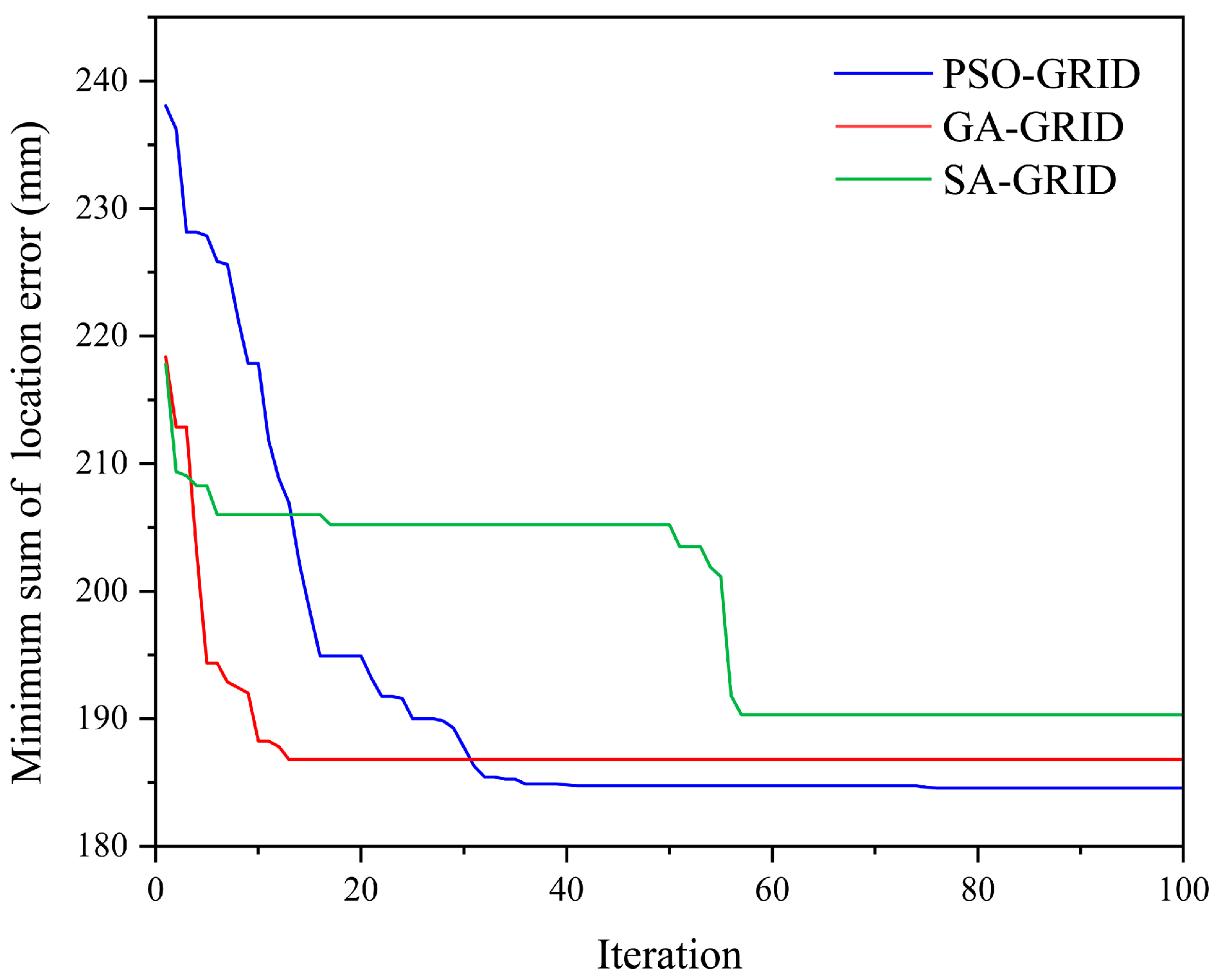
5.2. Influence of Optimization Algorithms
5.3. Influence of the Number of Sensors
6. Conclusions
- A sensor network layout optimization method based on the minimum travel-time difference is developed by combining the PSO method with the grid search methods. The method establishes a location objective function based on source travel-time theory and optimizes the function by PSO. It integrates grid search to systematically examine potential sensor locations, thereby determining the optimal sensor layout. This approach focuses on optimizing source location and is easy to understand.
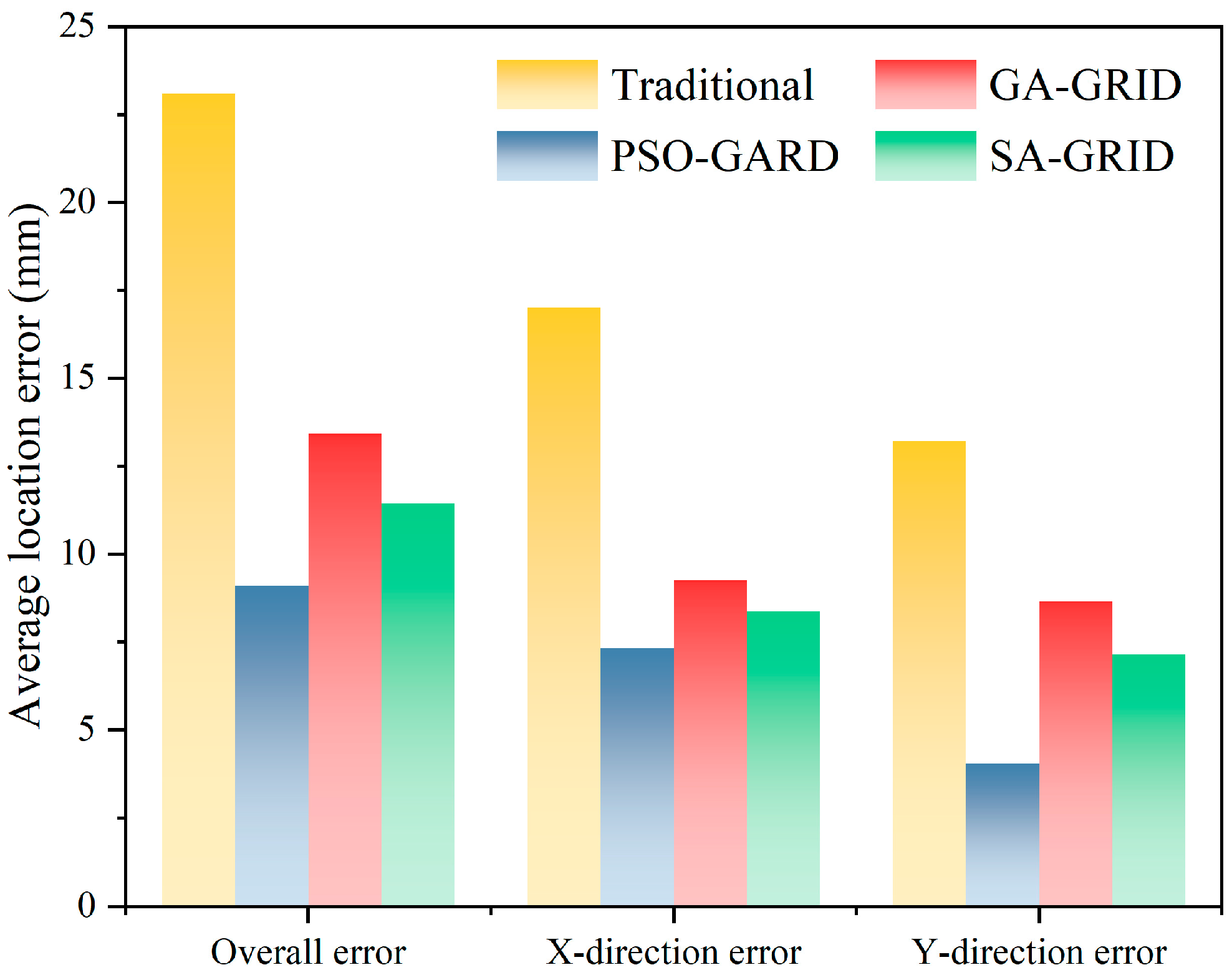
- The optimization method proposed in this study demonstrated excellent location accuracy and strong noise resistance in synthetic tests. In the synthetic test, the PSO-GRID method, GA-GRID method, and SA-GRID method, improving location accuracy by 24.89%, 7.81%, and 7.39%, respectively. Furthermore, under varying noise levels the PSO-GRID method maintained high location accuracy, achieving improvements of 24.89%, 12.59%, and 15.06% across three noise conditions. These results validate the effectiveness and robustness of the proposed method in synthetic scenarios.
- The proposed optimization method performed well in laboratory AE experiments. In AE experiments, the PSO-GRID method improved location accuracy by 59.15%, 31.76%, and 20.46% compared to the traditional layout, GA-GRID method, and SA-GRID method, respectively. It also demonstrated high computational efficiency, minimal error fluctuations, and optimal performance under various noise conditions, requiring minimal parameter adjustment. These results confirm PSO-GRID as the most reliable and practical choice for location optimization.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lockner, D. The Role of Acoustic-Emission in the Study of Rock Fracture. Int. J. Rock Mech. Min. Sci. 1993, 30, 883–899. [Google Scholar] [CrossRef]
- Recoquillay, A.; Pénicaud, M.; Serey, V.; Lefeuve, C. Source Reconstruction for Acoustic Emission Signals Clustering and Events Nature Identification. Application to a Composite Pipe Bending Test. Mech. Syst. Signal Process. 2025, 224, 111954. [Google Scholar] [CrossRef]
- Huang, L.Q.; Wu, X.; Li, X.B.; Wang, S.F. Influence of Sensor Array on Ms/Ae Source Location Accuracy in Rock Mass. Trans. Nonferrous Met. Soc. China 2023, 33, 254–274. [Google Scholar] [CrossRef]
- Kijko, A. Algorithm for Optimum Distribution of a Regional Seismic Network—I. Pure Appl. Geophys. 1977, 115, 999–1009. [Google Scholar] [CrossRef]
- Kijko, A. Algorithm for Optimum Distribution of a Regional Seismic Network—II. Analysis of Accuracy of Location of Local Earthquakes Depending on Number of Seismic Stations. Pure Appl. Geophys. 1977, 115, 1011–1021. [Google Scholar] [CrossRef]
- Rabinowitz, N.; Steinberg, D.M. Optimal Configuration of a Seismographic Network—A Statistical Approach. Bull. Seismol. Soc. Am. 1990, 80, 187–196. [Google Scholar] [CrossRef]
- Jones, R.H.; Rayne, C.M.; Ulf, L. The Use of a Genetic Algorithm for the Optimal Design of Microseismic Monitoring Networks. In Proceedings of the Rock Mechanics in Petroleum Engineering, Delft, The Netherlands, 29–31 August 1994. [Google Scholar]
- Kraft, T.; Mignan, A.; Giardini, D. Optimization of a Large-Scale Microseismic Monitoring Network in Northern Switzerland. Geophys. J. Int. 2013, 195, 474–490. [Google Scholar] [CrossRef]
- Rosa-Cintas, S.; Galiana-Merino, J.J.; Alfaro, P.; Rosa-Herranz, J. Optimizing the Number of Stations in Arrays Measurements: Experimental Outcomes for Different Array Geometries and the F-K Method. J. Appl. Geophys. 2014, 102, 96–133. [Google Scholar] [CrossRef]
- De Landro, G.; Picozzi, M.; Russo, G.; Adinolfi, G.M.; Zollo, A. Seismic Networks Layout Optimization for a High-Resolution Monitoring of Induced Micro-Seismicity. J. Seismol. 2020, 24, 953–966. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Zhao, C.C.; Huang, Y.H. An Optimization Method for the Station Layout of a Microseismic Monitoring System in Underground Mine Engineering. Sensors 2022, 22, 4775. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Ge, M.C.; Wang, E.Y.; Zhang, S.H. The Influence Mechanism and Optimization of the Sensor Network on the Ms/Ae Source Location. Shock Vib. 2020, 2020, 2651214. [Google Scholar] [CrossRef]
- Li, G.; Chen, J.; Han, M.; Gajraj, A.; Xing, Y.; Wu, F.; Liu, H.; Yin, C. Accurate Microseismic Event Location Inversion Using a Gradient-Based Method. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–10 October 2012. [Google Scholar]
- Thurber, C.H. Nonlinear Earthquake Location—Theory and Examples. Bull. Seismol. Soc. Am. 1985, 75, 779–790. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Basu, A.; Frazer, L.N. Rapid Determination of the Critical Temperature in Simulated Annealing Inversion. Science 1990, 249, 1409–1412. [Google Scholar] [CrossRef] [PubMed]
- Dhiman, G.; Kumar, V. Spotted Hyena Optimizer: A Novel Bio-Inspired Based Metaheuristic Technique for Engineering Applications. Adv. Eng. Softw. 2017, 114, 48–70. [Google Scholar] [CrossRef]
- Pace, F.; Santilano, A.; Godio, A. A Review of Geophysical Modeling Based on Particle Swarm Optimization. Surv. Geophys. 2021, 42, 505–549. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Feng, X.; Li, S.; Yuan, J.; Xu, S. Microseism Source Location with Hierarchical Strategy Based on Particle Swarm Optimization. Chin. J. Rock Mech. Eng. 2009, 28, 740–749. [Google Scholar]
- Raorane, S.; Ercan, T.; Papadimitriou, C.; Packo, P.; Uhl, T. Bayesian Optimal Sensor Placement for Acoustic Emission Source Localization with Clusters of Sensors in Isotropic Plates. Mech. Syst. Signal Process. 2024, 214, 111342. [Google Scholar] [CrossRef]
- Dong, L.J.; Cao, H.; Hu, Q.C.; Zhang, S.; Zhang, X.H. Error Distribution and Influencing Factors of Acoustic Emission Source Location for Sensor Rectangular Network. Measurement 2024, 225, 113983. [Google Scholar] [CrossRef]
- Rui, Y.C.; Zhu, C.J.; Chen, J.; Zhou, Z.L.; Pu, Y.Y. Study on Sensor Network Optimization for Ms/Ae Monitoring System Using Fisher Information and Improved Encoding Framework. IEEE Sens. J. 2024, 24, 22958–22973. [Google Scholar] [CrossRef]
- Sleeman, R.; van Eck, T. Robust Automatic P-Phase Picking: An on-Line Implementation in the Analysis of Broadband Seismogram Recordings. Phys. Earth Planet. Inter. 1999, 113, 265–275. [Google Scholar] [CrossRef]
- Gomes, G.F.; De Almeida, F.A.; Lopes Alexandrino, P.D.S.; Da Cunha, S.S., Jr.; De Sousa, B.S.; Ancelotti, A.C., Jr. A Multiobjective Sensor Placement Optimization for Shm Systems Considering Fisher Information Matrix and Mode Shape Interpolation. Eng. Comput. 2019, 35, 519–535. [Google Scholar] [CrossRef]
- Kord, S.; Taghikhany, T.; Madadi, A.; Hosseinbor, O. A Novel Triple-Structure Coding to Use Evolutionary Algorithms for Optimal Sensor Placement Integrated with Modal Identification. Struct. Multidiscip. Optim. 2024, 67, 58. [Google Scholar] [CrossRef]
- Chen, Y.L.; Zhang, M.W.; Wu, H.S.; Zhang, K.; Qian, D.Y. Improving the Positioning Accuracy of Acoustic Emission Events by Optimizing the Sensor Deployment and First Arrival Signal Picking. IEEE Access 2020, 8, 71160–71172. [Google Scholar] [CrossRef]


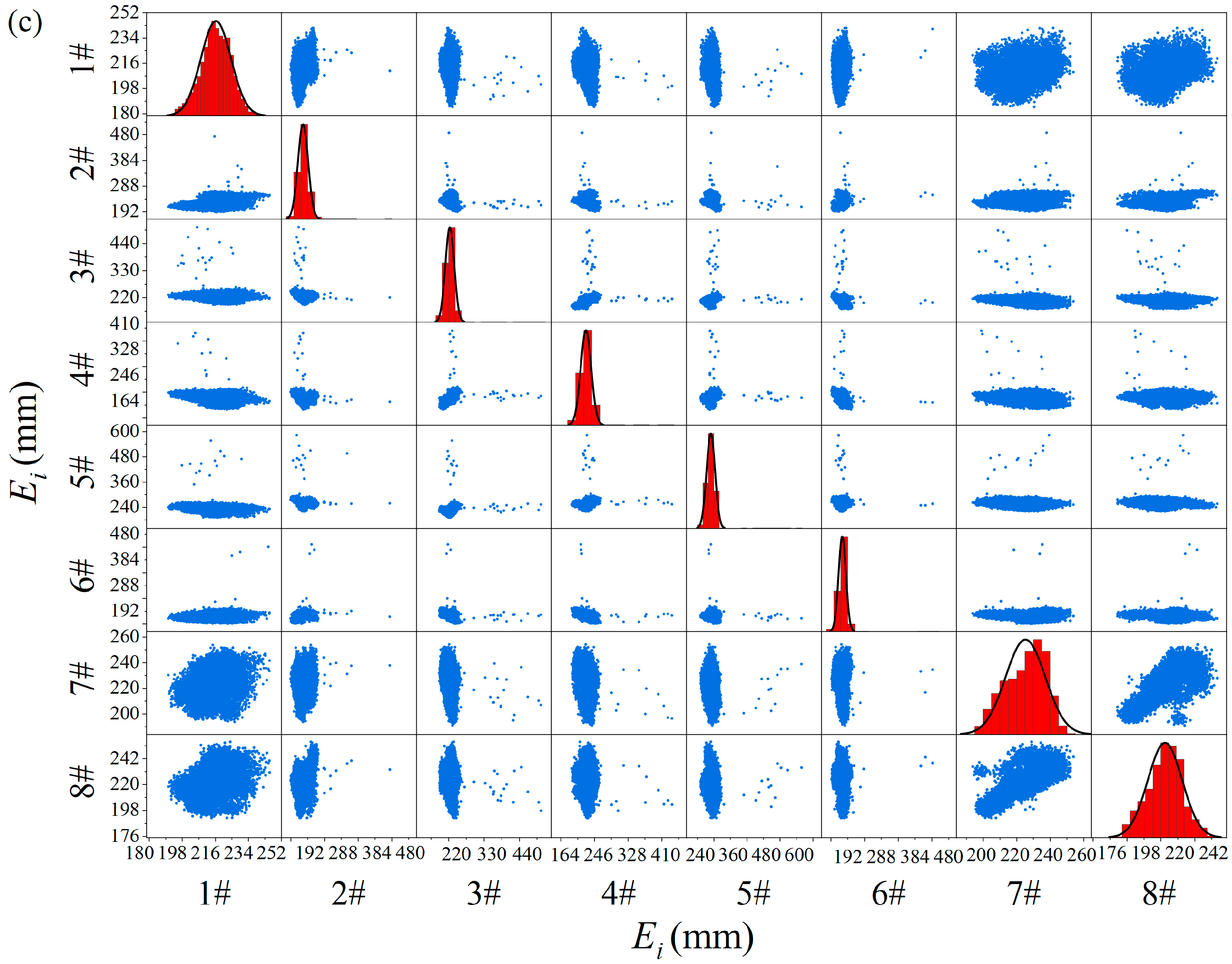





| Sensor ID | Radom-GRID | PSO-GRID | GA-GRID | SA-GRID | ||||
|---|---|---|---|---|---|---|---|---|
| x (mm) | y (mm) | x (mm) | y (mm) | x (mm) | y (mm) | x (mm) | y (mm) | |
| 1 | 25 | 25 | 275 | 165 | 35 | 155 | 95 | 105 |
| 2 | 95 | 25 | 75 | 25 | 185 | 145 | 25 | 45 |
| 3 | 205 | 25 | 105 | 75 | 205 | 25 | 275 | 75 |
| 4 | 275 | 25 | 25 | 145 | 175 | 25 | 235 | 25 |
| 5 | 275 | 175 | 255 | 165 | 255 | 105 | 275 | 175 |
| 6 | 205 | 175 | 185 | 175 | 205 | 175 | 55 | 25 |
| 7 | 95 | 175 | 155 | 25 | 105 | 175 | 55 | 175 |
| 8 | 25 | 175 | 65 | 165 | 35 | 175 | 85 | 165 |
| Method | Location Error of 8 Sensors (mm) | Location Error 12 Sensors (mm) | Location Error 16 Sensors (mm) |
|---|---|---|---|
| Tradition layout | 2.37 | 2.00 | 1.61 |
| PSO-GRID | 1.78 | 1.60 | 1.42 |
| GA-GRID | 1.93 | 1.78 | 1.46 |
| SA-GRID | 1.92 | 1.81 | 1.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Shang, X.; Ren, Y.; Liu, L.; Li, X.; Zhang, Y.; Wu, X.; Li, Z.; Tai, Y.; Pu, Y.; et al. Acoustic Emission/Mine Microseismic Sensor Network Optimization Based on Grid Loop Search and Particle Swarm Source Location. Processes 2025, 13, 496. https://doi.org/10.3390/pr13020496
Chen Y, Shang X, Ren Y, Liu L, Li X, Zhang Y, Wu X, Li Z, Tai Y, Pu Y, et al. Acoustic Emission/Mine Microseismic Sensor Network Optimization Based on Grid Loop Search and Particle Swarm Source Location. Processes. 2025; 13(2):496. https://doi.org/10.3390/pr13020496
Chicago/Turabian StyleChen, Yiling, Xueyi Shang, Yi Ren, Linghao Liu, Xiaoying Li, Yu Zhang, Xiao Wu, Zhuqing Li, Yang Tai, Yuanyuan Pu, and et al. 2025. "Acoustic Emission/Mine Microseismic Sensor Network Optimization Based on Grid Loop Search and Particle Swarm Source Location" Processes 13, no. 2: 496. https://doi.org/10.3390/pr13020496
APA StyleChen, Y., Shang, X., Ren, Y., Liu, L., Li, X., Zhang, Y., Wu, X., Li, Z., Tai, Y., Pu, Y., & Xiang, G. (2025). Acoustic Emission/Mine Microseismic Sensor Network Optimization Based on Grid Loop Search and Particle Swarm Source Location. Processes, 13(2), 496. https://doi.org/10.3390/pr13020496








