Flow and Corrosion Analysis of CO2 Injection Wells: A Case Study of the Changqing Oilfield CCUS Project
Abstract
1. Introduction
2. Mathematical Model
2.1. Fluid Property Model
- (1)
- Density equation
- (2)
- Viscosity equation
- (3)
- Thermal conductivity equation
- (4)
- Heat capacity equation
- (5)
- Compression factor equation
2.2. Wellbore Pressure Drop Model
2.3. Wellbore Heat Transfer Model
2.4. Wellbore Corrosion Model
3. Model Solution
3.1. Initial Conditions
3.2. Boundary Conditions
3.3. Solution Method
4. Model Verification
5. Model Applications
5.1. Effect of Injection Temperature
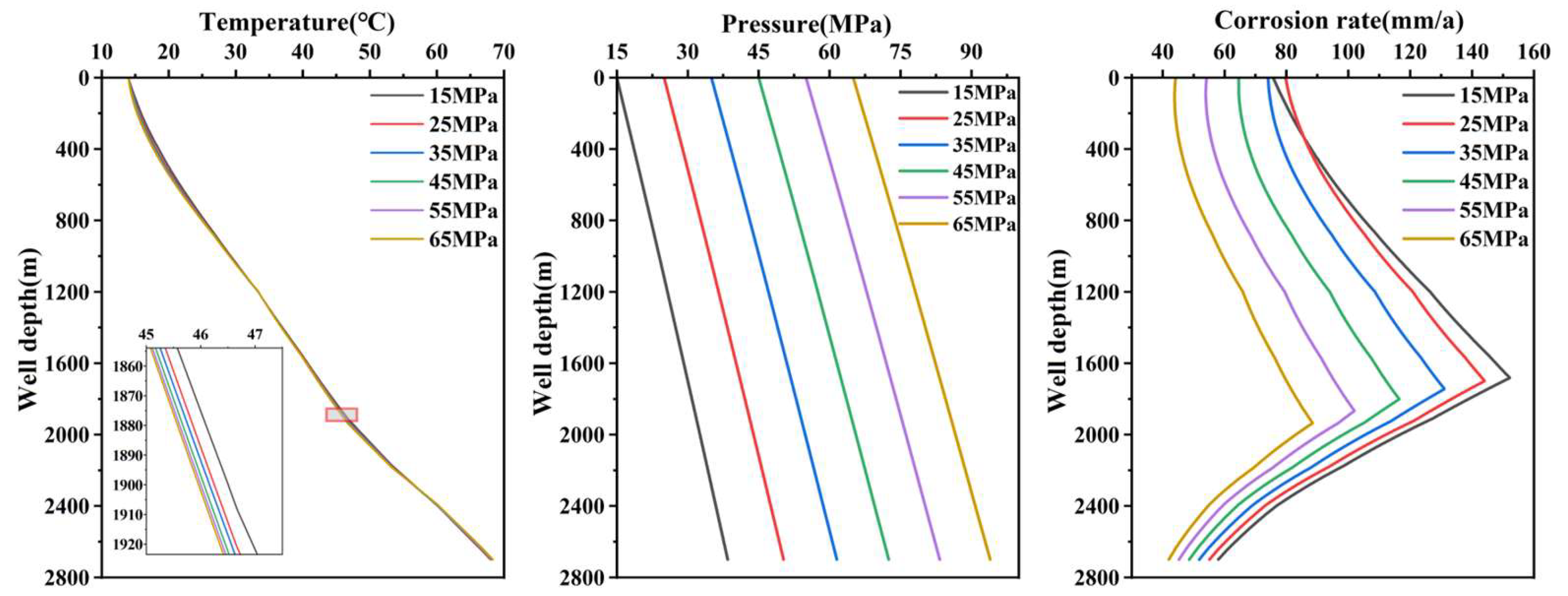
5.2. Effects of Injection Pressure
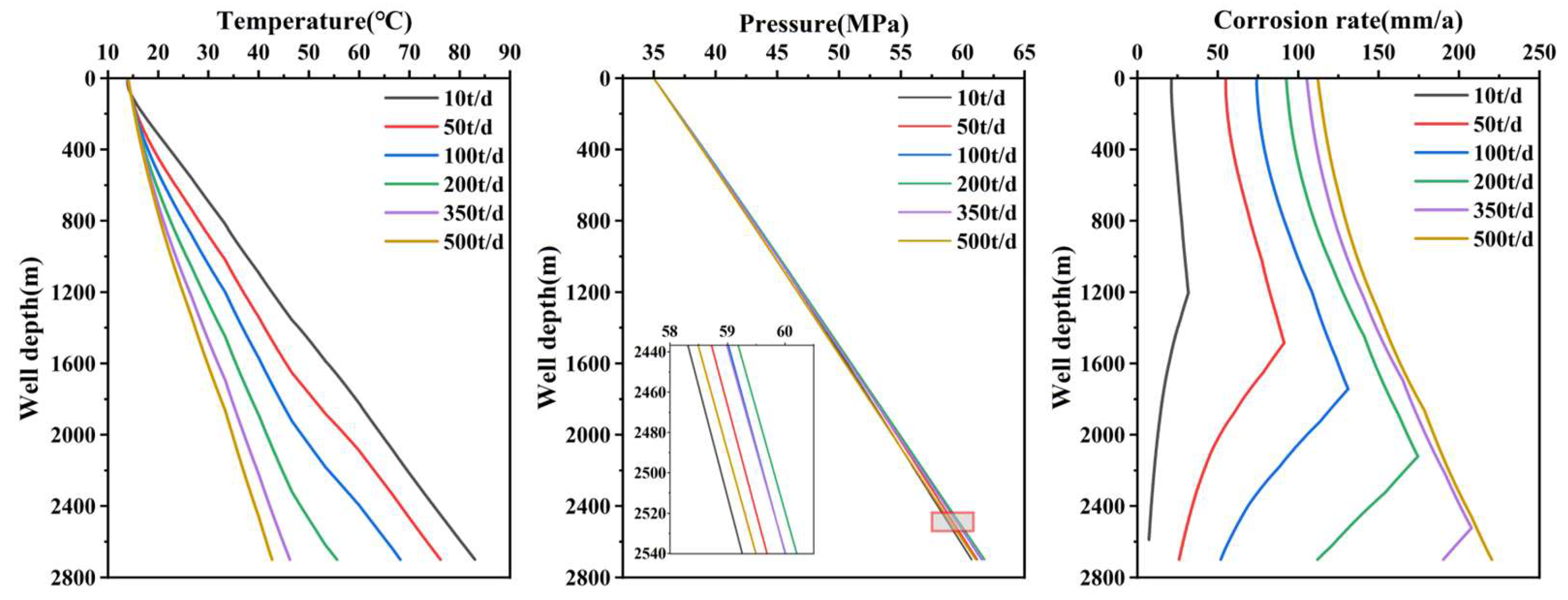
5.3. Effect of Injection Volume
5.4. Effect of CO2 Injection Concentration
6. Discussion and Conclusions
- (1)
- Wellbore temperature is highly sensitive to injection temperature and injection flow rate. It increases with higher injection temperature and decreases with larger injection flow rates. Wellbore pressure is more sensitive to injection pressure and CO2 injection concentration, increasing linearly with higher injection pressure and rising with increased CO2 injection concentration. Wellbore corrosion rate is highly sensitive to injection temperature, injection pressure and injection flow rate. It increases with higher injection temperature, decreases with higher injection pressure and increases with higher injection flow rate.
- (2)
- The wellbore corrosion rate curve exhibits a turning point, where it initially increases and then decreases with increasing well depth. In the upper and middle sections of the wellbore, the corrosion rate increases due to factors such as elevated temperature, increased CO2 solubility and higher flow velocity. However, in the lower section of the wellbore, the corrosion rate decreases.
- (3)
- The coupled model proposed in this study can be used to optimize injection parameters and develop an appropriate injection strategy. Special attention should be given to the changes in corrosion rate in the upper and middle sections of the wellbore at the site, with timely corrosion control measures implemented to ensure the safety of CO2 injection.
- (4)
- The simulation results in this study are based on specific injection parameters; however, in actual field conditions, wellbore flow may be influenced by factors such as multiphase flow and heterogeneous formations. These factors were not considered in this study, which may limit the applicability of the findings. It is recommended that future research take these factors into account to enhance the model’s applicability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency Paris. Transforming Industry Through CCUS; OECD: Paris, France, 2019. [Google Scholar]
- Li, Q.; Li, Q.; Wang, F.; Wu, J.; Wang, Y. The carrying behavior of water-based fracturing fluid in shale reservoir fractures and molecular dynamics of sand-carrying mechanism. Processes 2024, 12, 2051. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Han, Y. A numerical investigation on kick control with the displacement kill method during a well test in a deep-water gas reservoir: A case study. Processes 2024, 12, 2090. [Google Scholar] [CrossRef]
- Gasda, S.E.; Bachu, S.; Celia, M.A. Spatial characterization of the location of potentially leaky wells penetrating a deep saline aquifer in a mature sedimentary basin. Environ. Geol. 2004, 46, 707–720. [Google Scholar] [CrossRef]
- Pan, L.; Oldenburg, C.M.; Wu, Y.-S.; Pruess, K. Wellbore flow model for carbon dioxide and brine. Energy Procedia 2009, 1, 71–78. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Pouladi, B.; Barghi, T. Numerical modeling of CO2 injection scenarios in petroleum reservoirs: Application to CO2 sequestration and EOR. J. Nat. Gas Sci. Eng. 2016, 30, 38–49. [Google Scholar] [CrossRef]
- Lu, M.; Connell, L.D. Transient, thermal wellbore flow of multispecies carbon dioxide mixtures with phase transition during geological storage. Int. J. Multiph. Flow 2014, 63, 82–92. [Google Scholar] [CrossRef]
- Lu, M.; Connell, L.D. Non-isothermal flow of carbon dioxide in injection wells during geological storage. Int. J. Greenh. Gas Control. 2008, 2, 248–258. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Span, R.; Wagner, W. A new equation of state for carbon dioxide covering the fluid region from the triple-point temperature to 1100 K at pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. [Google Scholar] [CrossRef]
- Al-Adwani, F.; Langlinais, J.; Hughes, R. Modeling of an underbalanced-drilling operation using supercritical carbon dioxide. SPE Drill. Complet. 2009, 24, 599–610. [Google Scholar] [CrossRef]
- Ruan, B.; Xu, R.; Wei, L.; Ouyang, X.; Luo, F.; Jiang, P. Flow and thermal modeling of CO2 in injection well during geological sequestration. Int. J. Greenh. Gas Control. 2013, 19, 271–280. [Google Scholar] [CrossRef]
- Aursand, P.; Hammer, M.; Lavrov, A.; Lund, H.; Munkejord, S.T.; Torsæter, M. Well integrity for CO2 injection from ships: Simulation of the effect of flow and material parameters on thermal stresses. Int. J. Greenh. Gas Control. 2017, 62, 130–141. [Google Scholar] [CrossRef]
- Shingo, A.; Emmanuel, H.; Olivier, P. Well integrity: Modeling of thermo-mechanical behavior and gas migration along wells-application to ketzin injection well. Energy Procedia 2012, 23, 462–471. [Google Scholar]
- Roy, P.; Morris, J.P.; Walsh, S.D.; Iyer, J.; Carroll, S. Effect of thermal stress on wellbore integrity during CO2 injection. Int. J. Greenh. Gas Control. 2018, 77, 14–26. [Google Scholar] [CrossRef]
- Dong, X.; Duan, Z.; Gao, D. Assessment on the cement integrity of CO2 injection wells through a wellbore flow model and stress analysis. J. Nat. Gas Sci. Eng. 2020, 74, 103097. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.J.; Zhang, C.; Huang, Y.; Guo, Y.; Luo, L.; Shi, T. Wellbore integrity design of high-temperature gas wells containing CO2. Nat. Gas Ind. 2013, 33, 79–86. [Google Scholar]
- De Waard, C.; Milliams, D.E. Carbonic acid corrosion of steel. Corrosion 1975, 31, 177–181. [Google Scholar] [CrossRef]
- De Waard, C.; Lotz, U.; Milliams, D.E. Predictive model for CO2 corrosion engineering in wet natural gas pipelines. Corrosion 1991, 47, 976–985. [Google Scholar] [CrossRef]
- Xiao, G.; Tan, S.; Yu, Z.; Dong, B.; Yi, Y.; Tian, G.; Yu, H.; Shi, S. CO2 corrosion behaviors of 13Cr steel in the high-temperature steam environment. Petroleum 2020, 6, 106–113. [Google Scholar] [CrossRef]
- Yin, Z.F.; Feng, Y.R.; Zhao, W.Z.; Bai, Z.Q.; Lin, G.F. Effect of temperature on CO2 corrosion of carbon steel. Surf. Interface Anal. 2009, 41, 517–523. [Google Scholar] [CrossRef]
- Moreira, R.; Franco, C.; Joia, C.; Giordana, S.; Mattos, O. The effects of temperature and hydrodynamics on the CO2 corrosion of 13Cr and 13Cr5Ni2Mo stainless steels in the presence of free acetic acid. Corros. Sci. 2004, 46, 2987–3003. [Google Scholar] [CrossRef]
- Nazari, M.H.; Allahkaram, S.R.; Kermani, M.B. The effects of temperature and pH on the characteristics of corrosion product in CO2 corrosion of grade X70 steel. Mater. Des. 2010, 31, 3559–3563. [Google Scholar] [CrossRef]
- Li, D.; Han, D.; Zhang, L.; Ma, W.; Lu, M.; Wang, L. Effects of temperature on CO2 corrosion of tubing and casing steel. Corrosion 2013, 2013, 85. [Google Scholar]
- Weiqiang, S.O.; Hongjian, N.I.; Yinghua, J.I. Study on wellbore flow field of supercritical carbon dioxide drilling. J. China Univ. Pet. 2017, 41, 101–107. [Google Scholar]
- Lu, J.; Hu, Q.; Zhang, D.; Yan, F.; Li, Y.; Nie, C. Numerical simulation of impurity-containing supercritical CO2 pipeline transport in CCUS. Int. J. Greenh. Gas Control. 2024, 138, 104236. [Google Scholar] [CrossRef]
- Chapman, S.; Cowling, T.G. The Mathematical Theory of Non-Uniform Gases. An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases; Cambridge University Press: Cambridge, UK, 1970. [Google Scholar]
- Fang, T.; Liu, Y.; Bai, J.; Chen, H.; Zhao, S.; Li, Y.; Pang, M.; Wang, Y.; Dong, P. Transient heat transfer model for wellbore and formation of shut-in offshore oil wells. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Virtual, 17–19 November 2020, D022S006R008.
- Zhang, S.; Fu, J.; Peng, C.; Su, Y.; Zhang, H.; Yang, M. The Analysis of Transient Temperature in the Wellbore of a Deep Shale Gas Horizontal Well. Processes 2024, 12, 1402. [Google Scholar] [CrossRef]
- Papavinasam, S. Corrosion Control in the Oil and Gas Industry; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Ahmadi, S.; Khormali, A. Development of an RSM-based predictive model for evaluation of corrosion efficiency of ATMP in one molar HCl for carbon steel samples. Pet. Sci. Technol. 2023, 42, 4537–4555. [Google Scholar] [CrossRef]

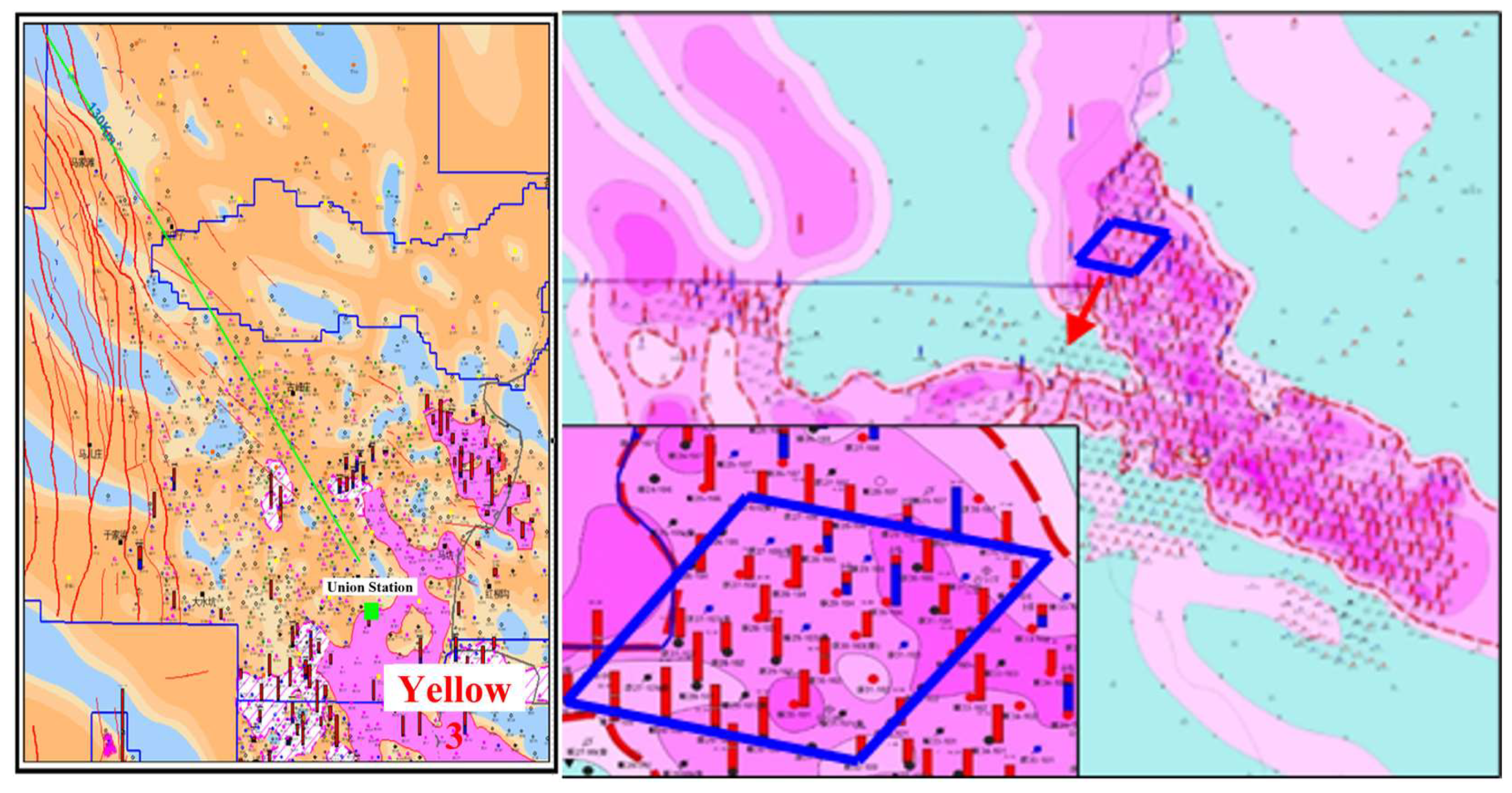
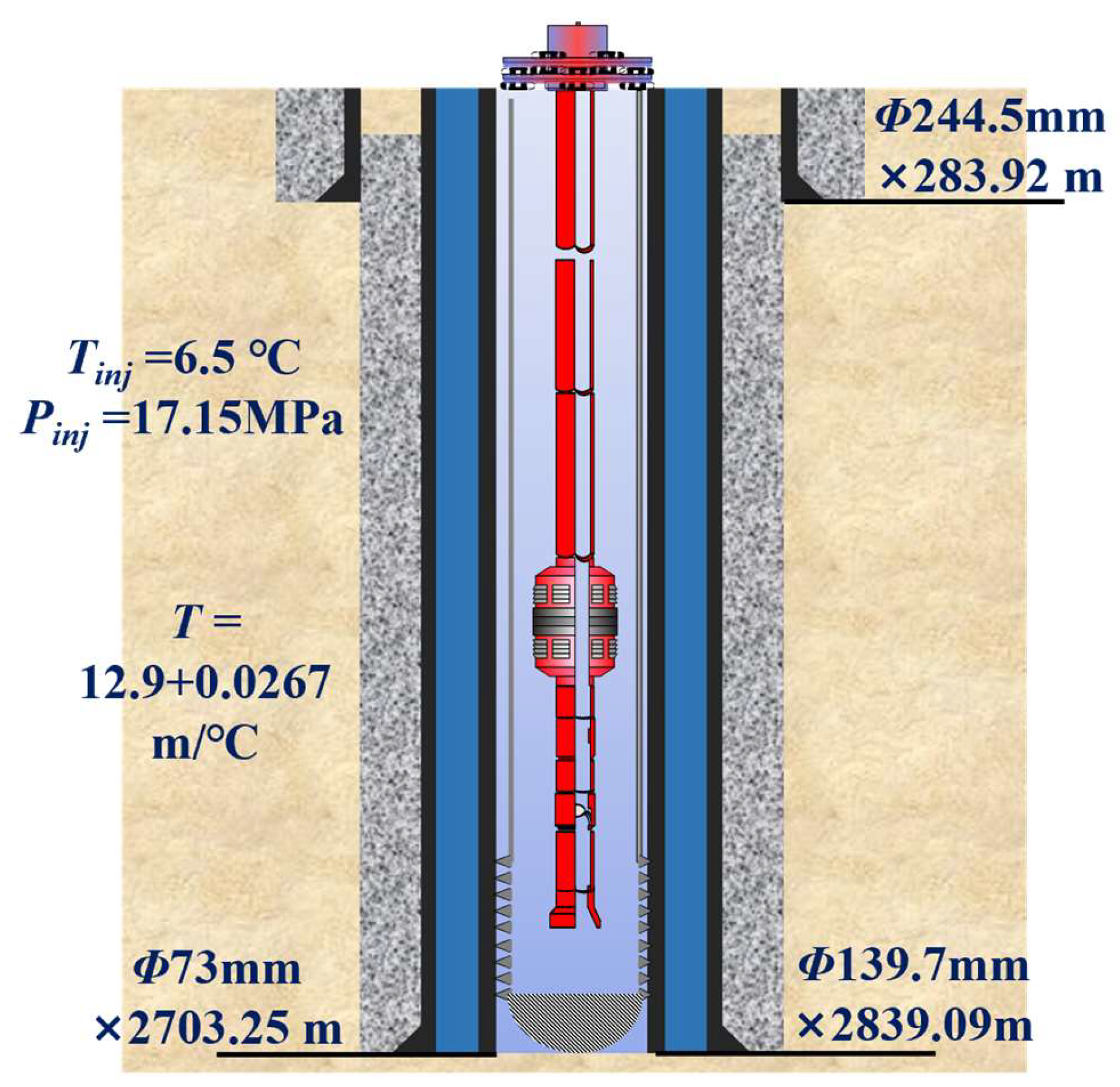



| Parameter | Value |
|---|---|
| Fluid component | Impure CO2 |
| Injection temperature | 14 °C |
| Injection pressure | 35 MPa |
| Injection rate | 100 t/d |
| Parameter | Value |
|---|---|
| Depth of surface casing | 283.92 m |
| Depth of oil sleeve | 2660 m |
| Depth of tubing | 2703.25 m |
| Cement return height | 87.6 m |
| Perforated interval | 2698–2703 m |
| Packer | 2660 m |
| Casing grade | J55 |
| Tubing material | P110 |
| Parameter | Value |
|---|---|
| Ground temperature | 12.91 °C |
| Geothermal gradient | 2.67 °C/100 m |
| Formation pressure | 19.74 MPa |
| Reservoir depth | 2700 m |
| Reservoir temperature | 85 °C |
| Reservoir thickness | 5.3 m |
| Permeability | 0.34 mD |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, W.; Liang, T.; Lu, C.; Li, M.; Zhou, P.; Yu, X.; Wang, B.; Wang, H. Flow and Corrosion Analysis of CO2 Injection Wells: A Case Study of the Changqing Oilfield CCUS Project. Processes 2025, 13, 439. https://doi.org/10.3390/pr13020439
Lv W, Liang T, Lu C, Li M, Zhou P, Yu X, Wang B, Wang H. Flow and Corrosion Analysis of CO2 Injection Wells: A Case Study of the Changqing Oilfield CCUS Project. Processes. 2025; 13(2):439. https://doi.org/10.3390/pr13020439
Chicago/Turabian StyleLv, Wei, Tongyao Liang, Cheng Lu, Mingxing Li, Pei Zhou, Xing Yu, Bin Wang, and Haizhu Wang. 2025. "Flow and Corrosion Analysis of CO2 Injection Wells: A Case Study of the Changqing Oilfield CCUS Project" Processes 13, no. 2: 439. https://doi.org/10.3390/pr13020439
APA StyleLv, W., Liang, T., Lu, C., Li, M., Zhou, P., Yu, X., Wang, B., & Wang, H. (2025). Flow and Corrosion Analysis of CO2 Injection Wells: A Case Study of the Changqing Oilfield CCUS Project. Processes, 13(2), 439. https://doi.org/10.3390/pr13020439







