A Numerical Analysis of the Descending Behaviors of Clusters at the Wall of the Circulating Fluidized Bed Riser
Abstract
1. Introduction
2. Materials and Methods
2.1. Eulerian–Lagrangian Model
2.1.1. Gas Phase
2.1.2. Particle Phase
2.1.3. Initial and Boundary Conditions
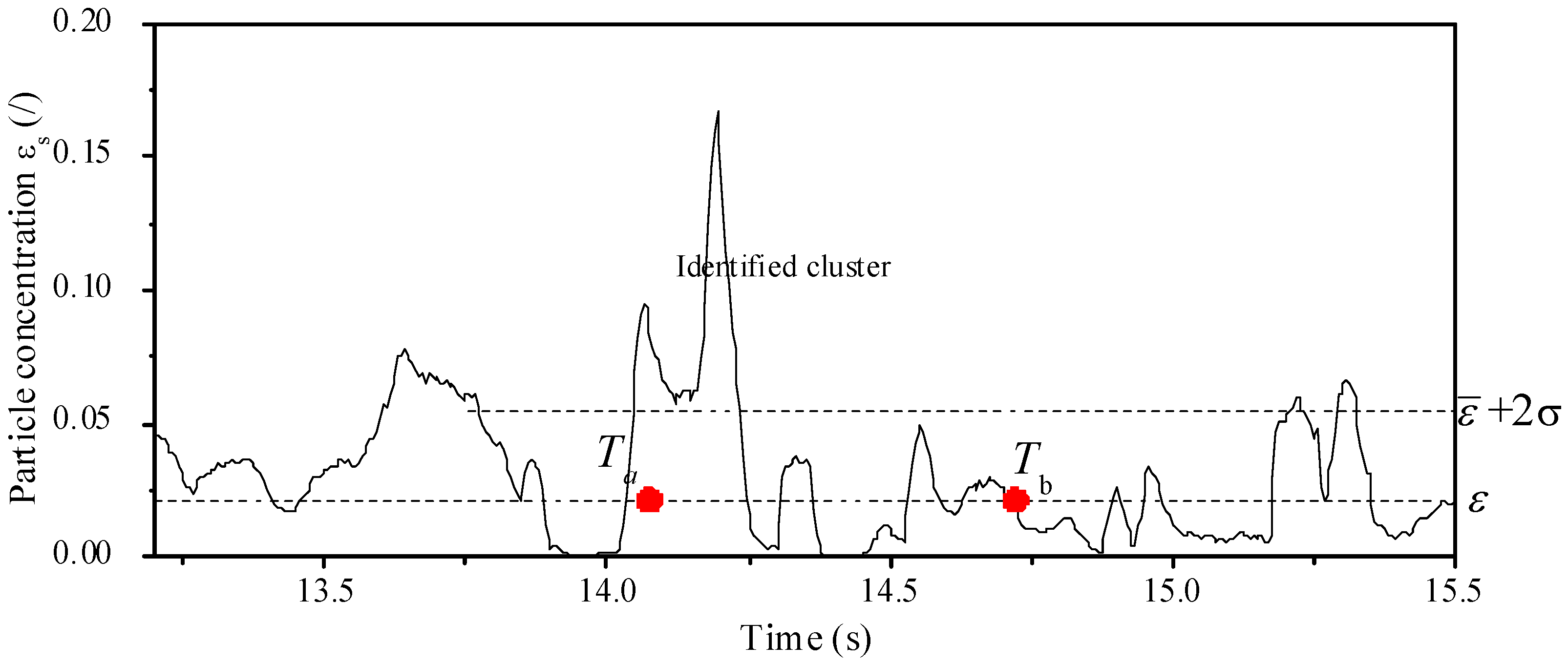
2.2. The Method for Identifying Clusters at the Wall of CFB Riser
3. Results
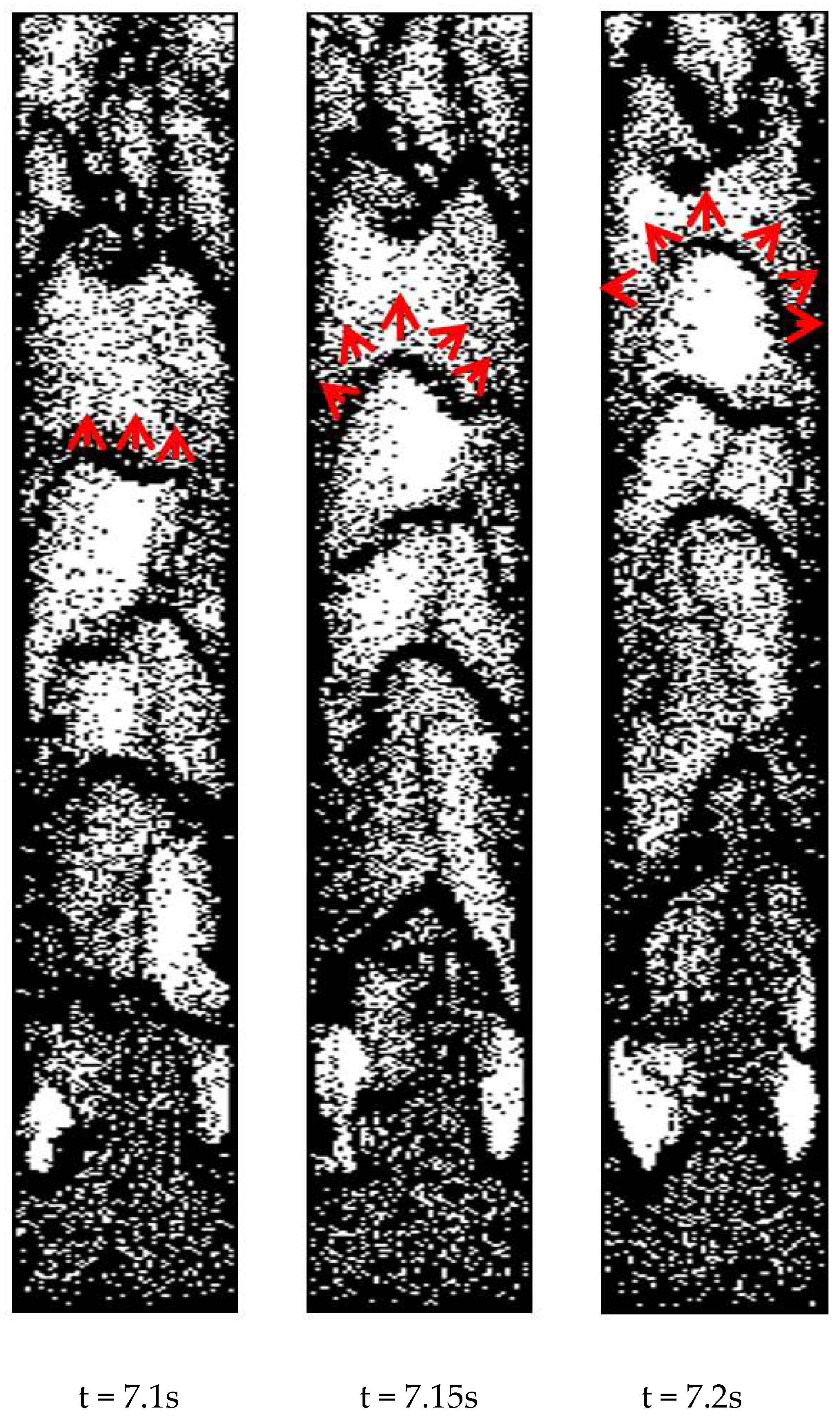
3.1. The Flow Regime of a Descending Cluster at the Wall of the CFB Riser
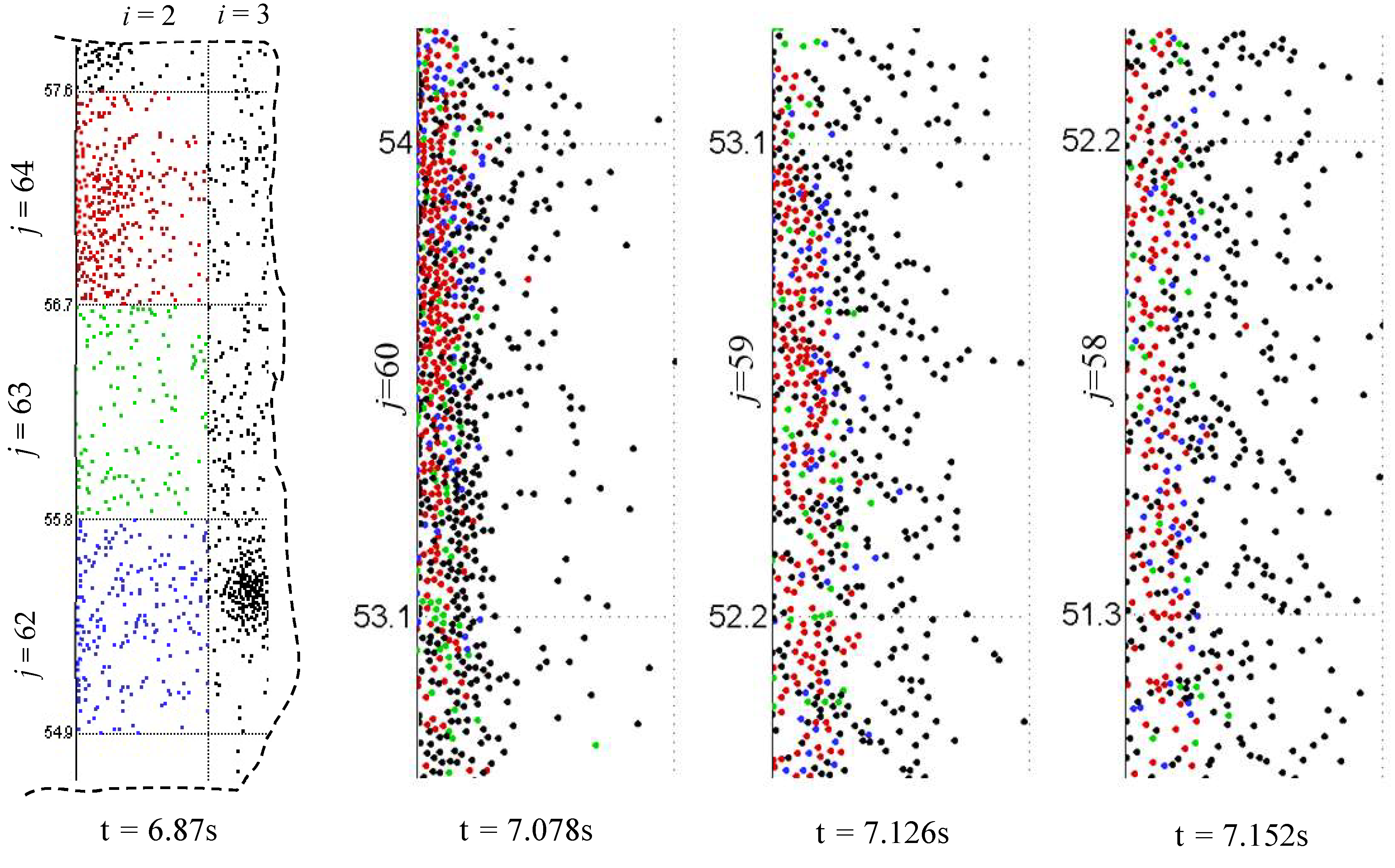
3.2. Transient Flow Behavior of a Particle Within the Descending Cluster
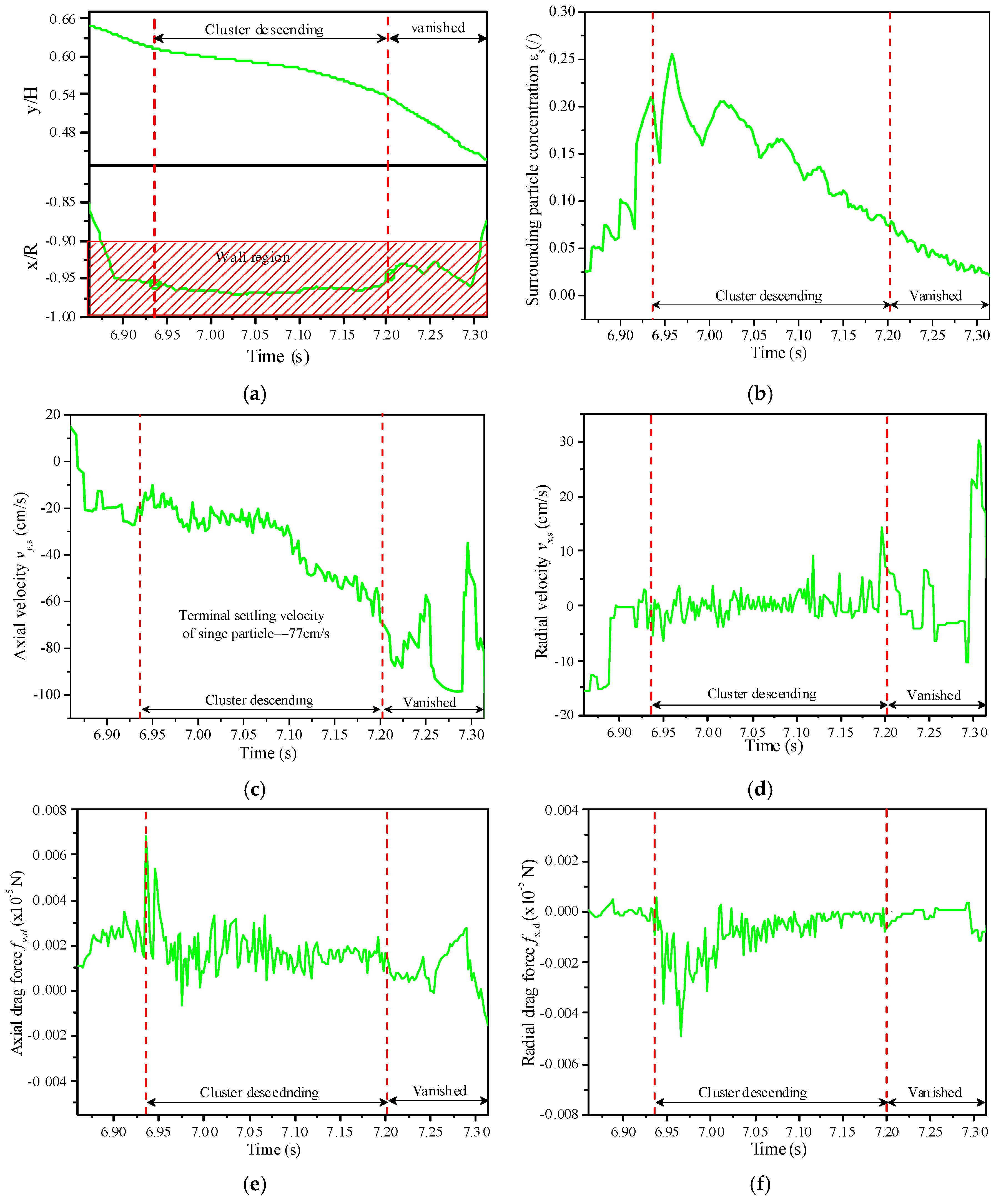
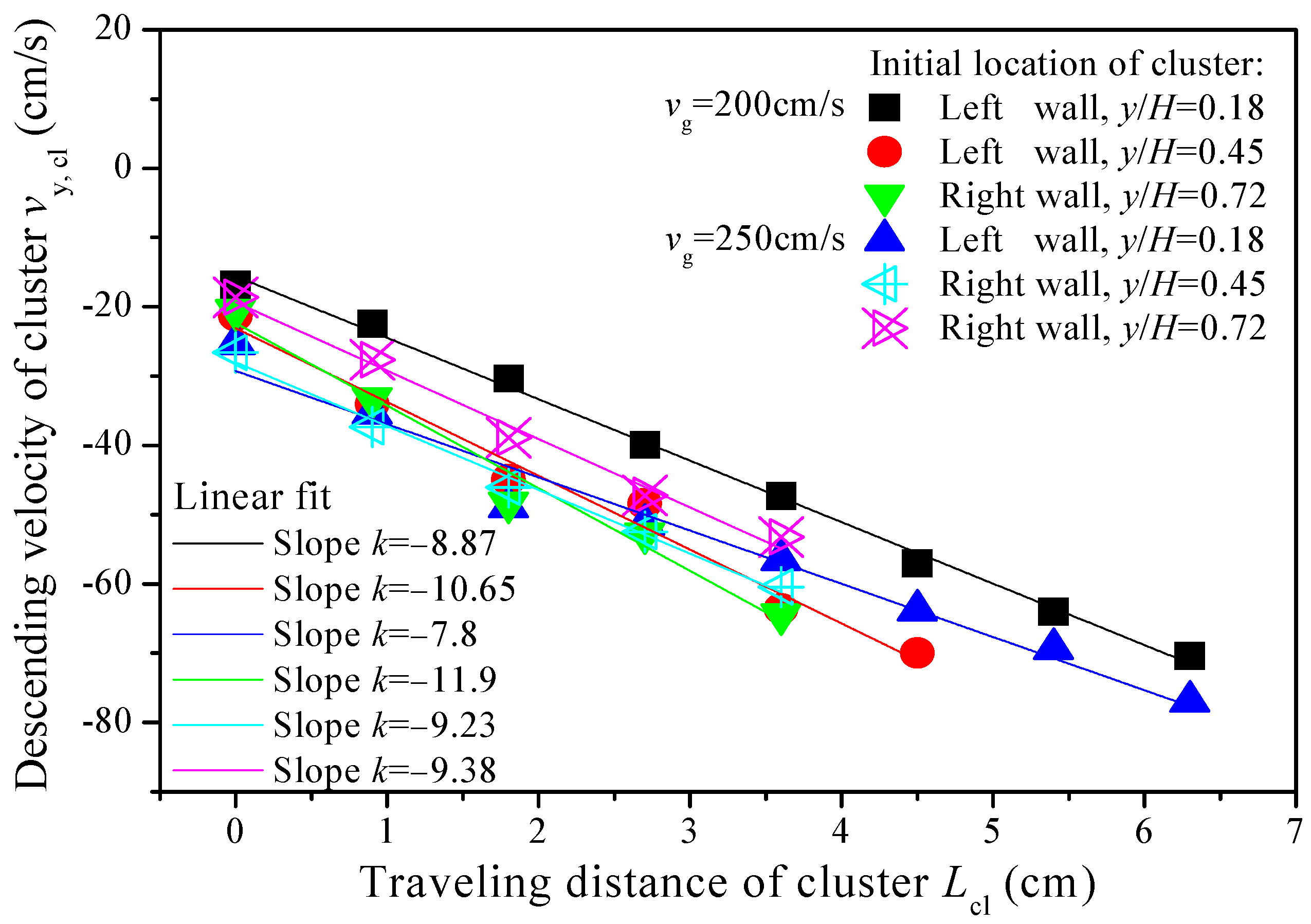
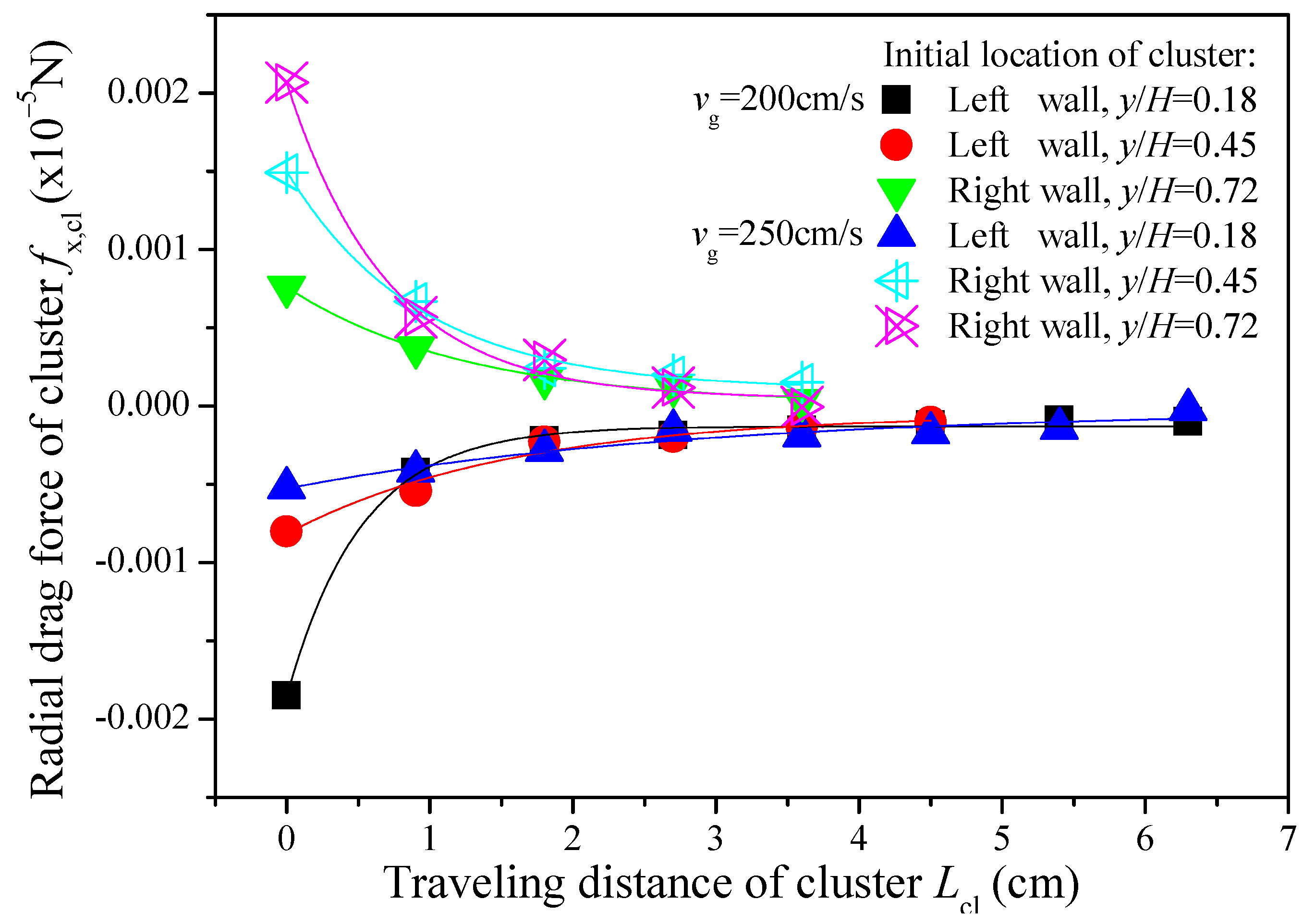
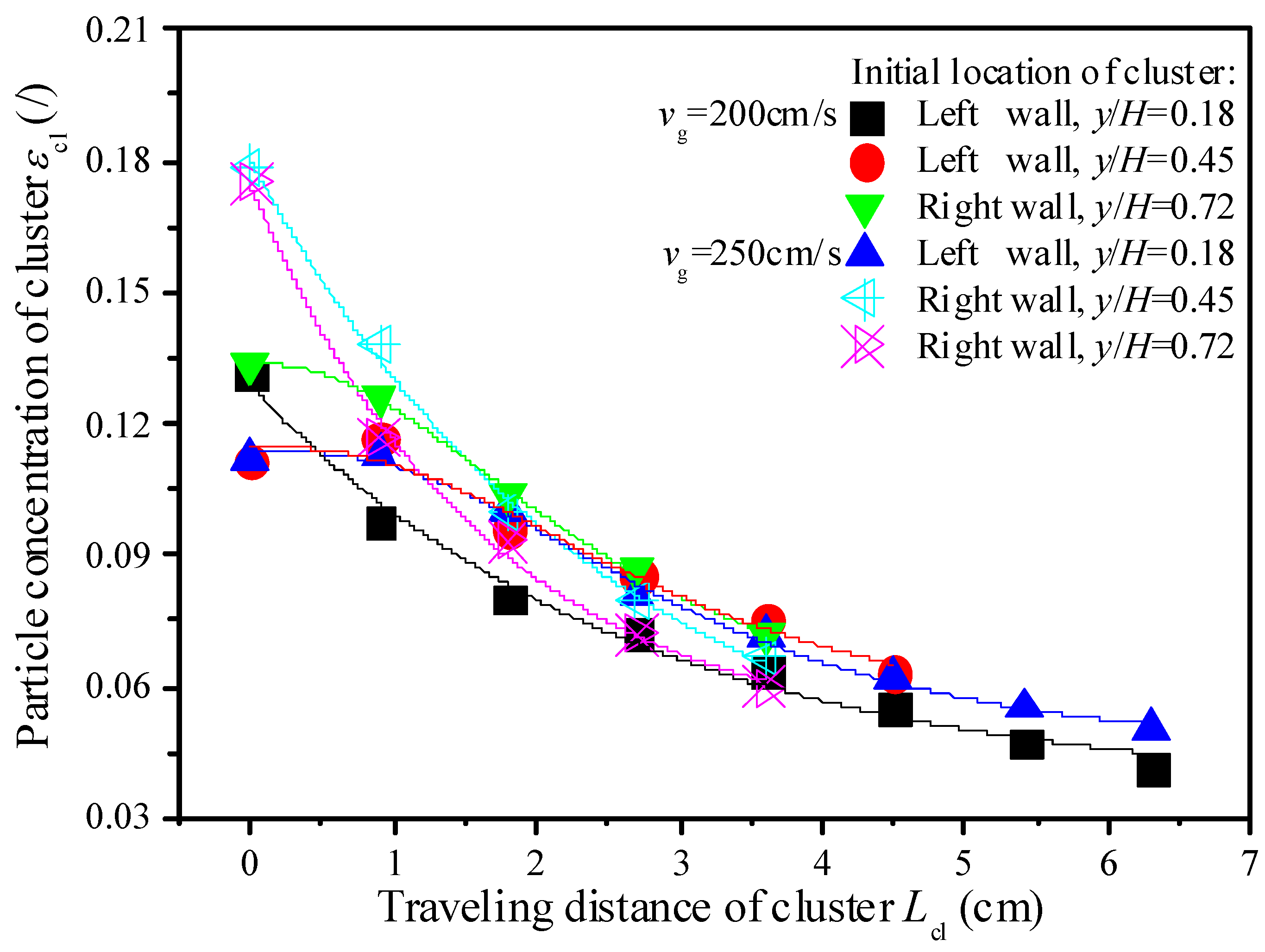
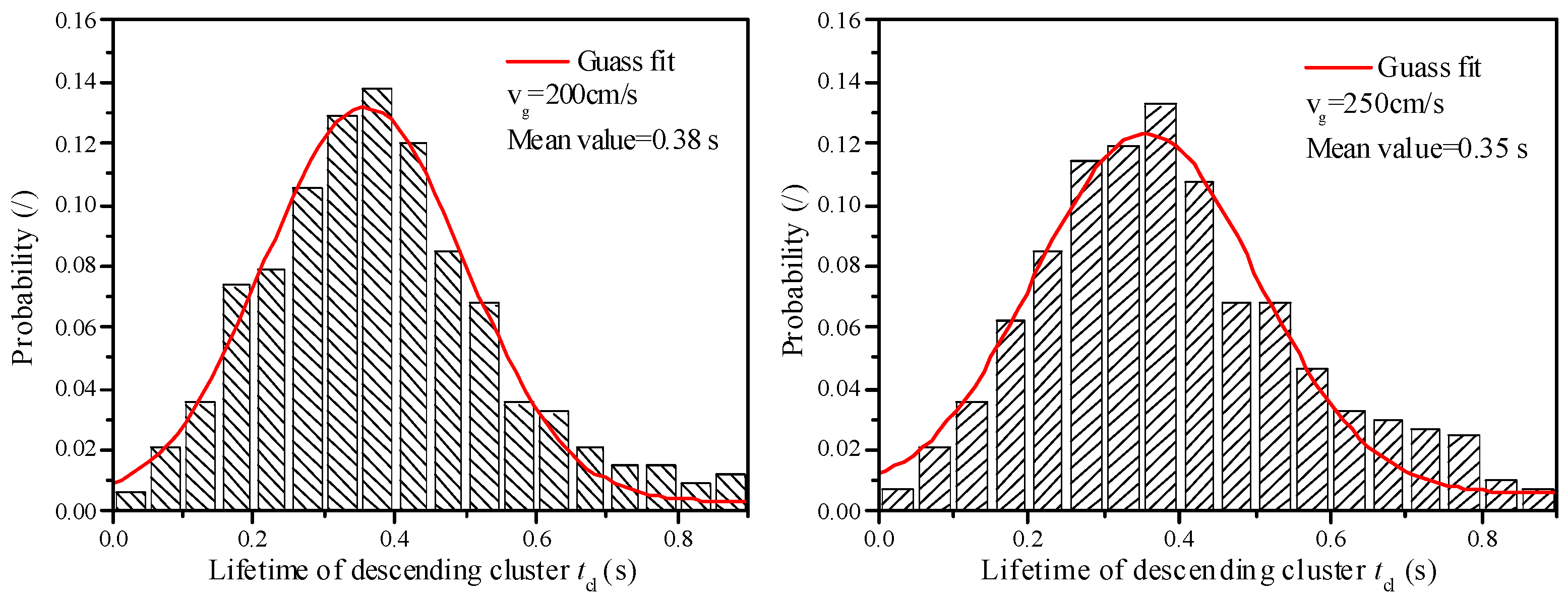
3.3. Transient Behavior of Descending Cluster
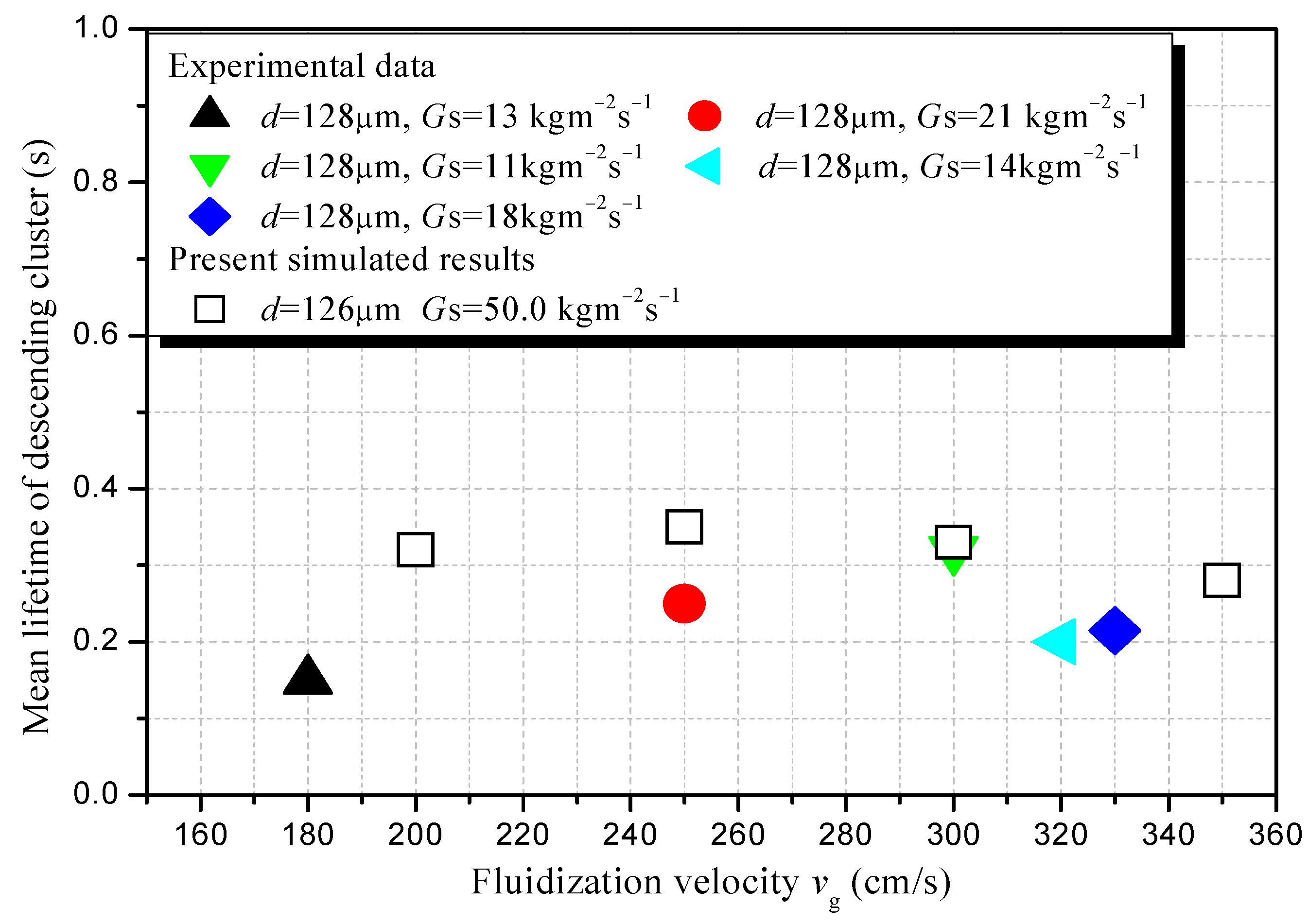
3.4. Comparison Between Present Simulation Result and Reported Experimental Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, G.; Li, Y. CFD-DEM Simulation of slugging and non-slugging fast fluidization of fine particles in a micro riser. Processes 2023, 11, 2977. [Google Scholar] [CrossRef]
- Aditya, A.; Allan, I.; Reddy, K.; John, F.; Christine, M.H.; Ray, A.C.; Chew, J. Annulus flow behavior of Geldart Group B particles in a pilot-scale CFB riser. Powder Technol. 2017, 305, 816–828. [Google Scholar]
- Liu, X.; Wang, S.; Yang, S.; Wang, H. Investigation of cluster property in the riser of circulating fluidized bed with a wide particle size distribution. Powder Technol. 2021, 390, 273–291. [Google Scholar] [CrossRef]
- Noymer, P.D.; Glicksman, L.R. Cluster motion and particle-convective heat transfer at the wall of a circulating fluidized bed. Int. J. Heat Mass Transf. 1998, 41, 147–158. [Google Scholar] [CrossRef]
- Kong, L.; Xu, J.; Wang, J.; Ge, W. Characterizing particle clustering behavior in dense gas-solid suspensions. Ind. Eng. Chem. Res. 2023, 62, 19145–19160. [Google Scholar] [CrossRef]
- Liu, X.; Gao, S.; Li, J. Characterizing particle clustering behavior by PDPA measurement for dilute gas-solid flow. Chem. Eng. J. 2005, 108, 193–202. [Google Scholar] [CrossRef]
- Manyele, S.V.; Parssinen, J.; Zhu, J. Characterizing particle aggregates in a high-density and high-flux CFB riser. Chem. Eng. J. 2002, 88, 151–161. [Google Scholar] [CrossRef]
- Medina-Pedraza, C.; de Lasa, H. Cluster acceleration and stabilization in a downflow circulating fluidized bed unit. Ind. Eng. Chem. Res. 2020, 59, 12360–12370. [Google Scholar] [CrossRef]
- Ishii, H.; Nakajima, T.; Horio, M. The clustering annular flow model of circulating fluidized beds. J. Chem. Eng. Jpn. 1989, 22, 484–490. [Google Scholar] [CrossRef]
- Guo, Y.; Yin, S.; Lu, S.; Song, T.; Ge, H.; Lu, P. An image processing method for feature extraction and dynamic tracking of particle clusters in CFBs. Particuology 2023, 77, 1–13. [Google Scholar] [CrossRef]
- Jia, X.; Yu, Y.; Liu, J.; Min, C.; Liu, F.; Zhang, N.; Chen, S.; Zhu, Z. Changes in surface hydrophobicity of coal particles and the formation of coarse particle–bubble clusters in the process of high-intensity conditioning. Processes 2023, 11, 1723. [Google Scholar] [CrossRef]
- Wang, C.; Lan, X.; Sun, Z.; Han, M.; Gao, J.; Ye, M.; Zhu, J. Cluster identification by a k-means algorithm-assisted imaging method in a laboratory-scale circulating fluidized bed. Ind. Eng. Chem. Res. 2022, 61, 942–956. [Google Scholar] [CrossRef]
- Rhodes, M.J.; Mineo, H.; Hirama, T. Particle motion at the wall of a circulating fluidized bed. Powder Technol. 1992, 70, 207–214. [Google Scholar] [CrossRef]
- Lim, K.S.; Zhou, J.; Finlay, C.; Grace, J.R.; Lim, C.J.; Griffith, C.M.H. Cluster descending velocity at the wall of circulating fluidised bed risers. In Circulating Fluidised Bed Technology V; Kwauk, M., Li, J., Eds.; Pergamon: Oxford, UK, 1995; pp. 218–223. [Google Scholar]
- Horio, M.; Morishita, K.; Tachibana, O.; Murata, N. Solid distribution and movement in circulating fluidized beds. In Circulating Fluidized Bed Technology II; Basu, P., Large, J.F., Eds.; Pergamon: Oxford, UK, 1988; pp. 147–154. [Google Scholar]
- Noymer, P.D.; Glicksman, L.R. Descent velocities of particle clusters at the wall of a circuating fluidized bed. Chem. Eng. Sci. 2000, 55, 5283–5289. [Google Scholar] [CrossRef]
- Griffith, A.E.; Louge, M.Y. The scaling of cluster velocity at the wall of circulating fluidized bed risers. Chem. Eng. Sci. 1998, 53, 2475–2477. [Google Scholar] [CrossRef]
- Horio, M.; Kuroki, H. Three-dimensional flow visualisation of dilutely dispersed solids in bubbling and circulating fluidised beds. Chem. Eng. Sci. 1994, 49, 2413–2421. [Google Scholar] [CrossRef]
- Harris, A.T.; Davidson, J.F.; Thorpe, R.B. The prediction of particle cluster properties in the near wall region of a vertical riser. Powder Technol. 2002, 127, 128–143. [Google Scholar] [CrossRef]
- Sharma, A.K.; Tuzla, K.; Matsen, J.; Chen, J.C. Parametric effects of particle size and gas velocity on cluster characteristics in fast fluidized beds. Powder Technol. 2000, 11, 114–122. [Google Scholar] [CrossRef]
- Wang, J. Continuum theory for dense gas-solid flow: A state-of-the-art review. Chem. Eng. Sci. 2019, 215, 115428. [Google Scholar]
- Yuu, S.; Ueno, T.; Umekage, T. Numerical simulation of the high Reynolds number slit nozzle gas-particle jet using subgrid-scale coupling large eddy simulation. Chem. Eng. Sci. 2001, 56, 4293–4307. [Google Scholar] [CrossRef]
- Bird, G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; CRC Press: Oxford, UK, 1994. [Google Scholar]
- Nanbu, K. Probablity theory of Electron-molecule, ion-molecule, molecule-molecule, and coulomb collision for particle modeling of materials processing plasmas and gas. IEEE Trans. Plasma Sci. 2000, 28, 971–990. [Google Scholar] [CrossRef]
- Wang, S.; Liu, H.; Lu, H.; Liu, W.; Ding, J.; Li, W. Flow behavior of clusters in a riser simulated by direct simulation Monte Carlo method. Chem. Eng. J. 2005, 106, 197–211. [Google Scholar]
- Hoomans, B.P.B.; Kuipers, J.A.M.; Briels, W.J.W.; Swaaij, P.M.V. Discrete particle simulation of bubble and slug formation in a two-dimensional gas-fluidized bed: A hard-sphere approach. Chem. Eng. Sci. 1996, 51, 99–118. [Google Scholar] [CrossRef]
- Soong, C.; Tuzla, K.; Chen, J. Experimental determination of clusters size and velocity in circulating fluidizeds. In Fluidization VIII, Proceedings of the Eighth Engineering Foundation Conference on Fluidization, Tours, France, 14–19 May 1995; Amer Inst of Chemical Engineers: New York, NY, USA, 1995; pp. 219–227. [Google Scholar]
- Helland, E.; Occelli, R.; Tadrist, L. Computational study of fluctuating motions and cluster structures in gas-particle flows. Int. J. Multiphase Flow. 2002, 28, 199–223. [Google Scholar] [CrossRef]
- Brereton, C.M.H.; Grace, J.R. Microstructural aspects of the behaviour of circulating fluidized beds. Chem. Eng. Sci. 1993, 48, 2565–2572. [Google Scholar] [CrossRef]
- Wang, S.; Liu, H.; Yang, C. Structure and drag characteristics of fluidized nanoparticle agglomerates at the bottom of the bed. Ind. Eng. Chem. Res. 2019, 58, 19693–19701. [Google Scholar] [CrossRef]
- Lints, M.C.; Glicksman, L.R. The structure of particle clusters near the wall of a circulating fluidized bed. In AIChE Symposium Series; American Institute of Chemical Engineers: New York, NY, USA, 1993; p. 35. [Google Scholar]
- Noymer, P.D.; Glicksman, L.R. Near-wall hydrodynamics in a scale-model circulating fluidized bed. Int. J. Heat. Mass. Transf. 1999, 42, 1389–1403. [Google Scholar] [CrossRef]



| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Particle shape | Sphere | Gas viscosity | 1.5 × 10−5 (Pa·s) |
| Particle diameter | 0.0126 (cm) | Solid flux | 50 kg/m2 s |
| Particle density | 2400 (kg/m3) | CFB riser size | 9 × 100 (cm) |
| Restitution coefficient between particles | 0.9 | Fluidization velocity | 200~300 (cm/s) |
| Coefficient of restitution between particle and wall | 0.8 | Gas density | 1.2 (Kg/m3) |
| Tangential restitution coefficient | 0.3 | Cell number | 20 × 111 |
| Friction coefficient | 0.1 | Sub-cell number per cell | 2 × 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, N.; Wang, S.; Zhang, H.; Cao, Q. A Numerical Analysis of the Descending Behaviors of Clusters at the Wall of the Circulating Fluidized Bed Riser. Processes 2025, 13, 409. https://doi.org/10.3390/pr13020409
Liu N, Wang S, Zhang H, Cao Q. A Numerical Analysis of the Descending Behaviors of Clusters at the Wall of the Circulating Fluidized Bed Riser. Processes. 2025; 13(2):409. https://doi.org/10.3390/pr13020409
Chicago/Turabian StyleLiu, Niannian, Shaowei Wang, Heng Zhang, and Qingxi Cao. 2025. "A Numerical Analysis of the Descending Behaviors of Clusters at the Wall of the Circulating Fluidized Bed Riser" Processes 13, no. 2: 409. https://doi.org/10.3390/pr13020409
APA StyleLiu, N., Wang, S., Zhang, H., & Cao, Q. (2025). A Numerical Analysis of the Descending Behaviors of Clusters at the Wall of the Circulating Fluidized Bed Riser. Processes, 13(2), 409. https://doi.org/10.3390/pr13020409






