Distribution Model of Wellbore Collapse Pressure in Deviated Wells Considering Fracture Development and Engineering Applications
Abstract
1. Introduction
2. Methodology
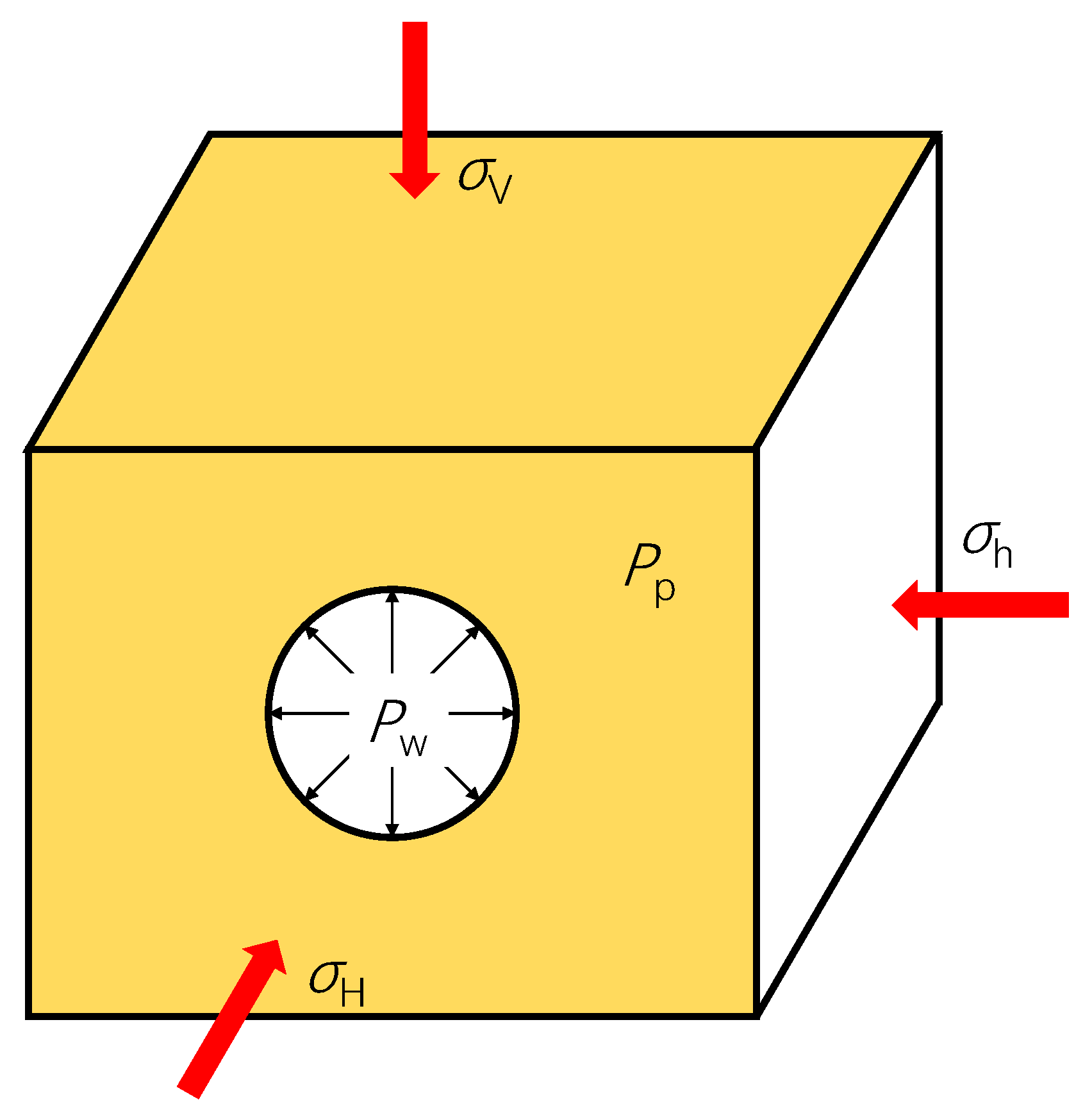
2.1. Stress Distribution Model Around Deviated Wellbores
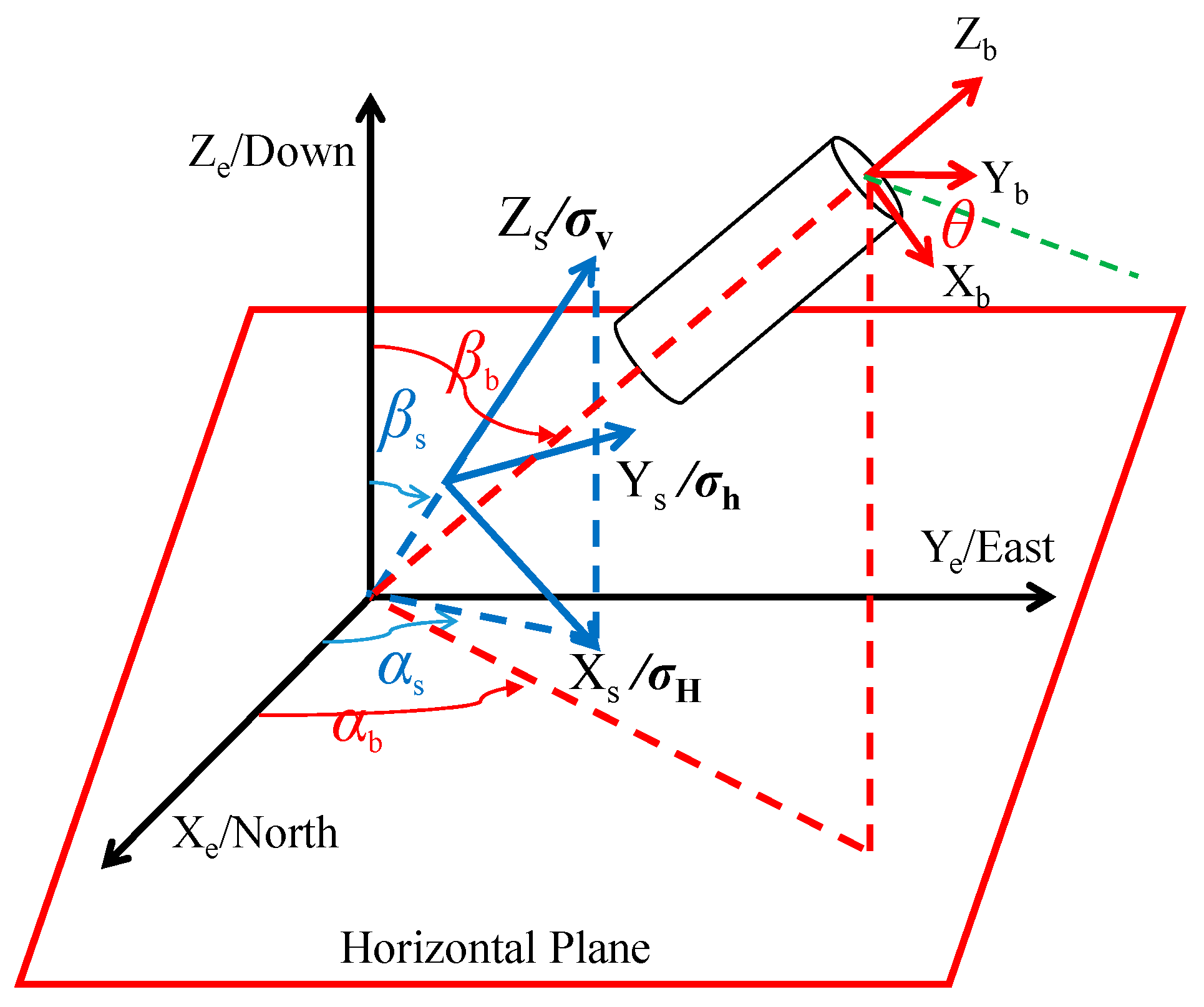
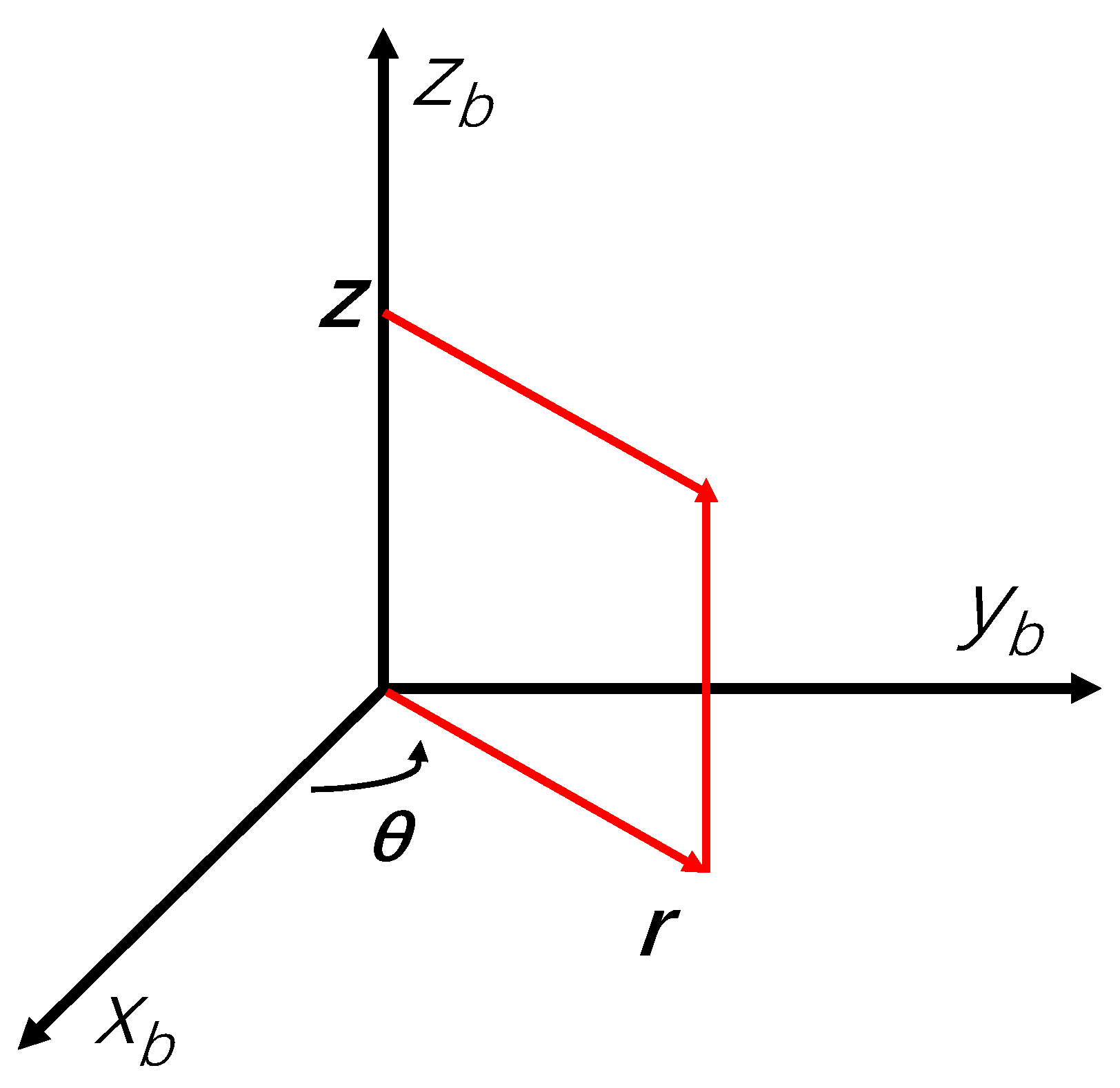
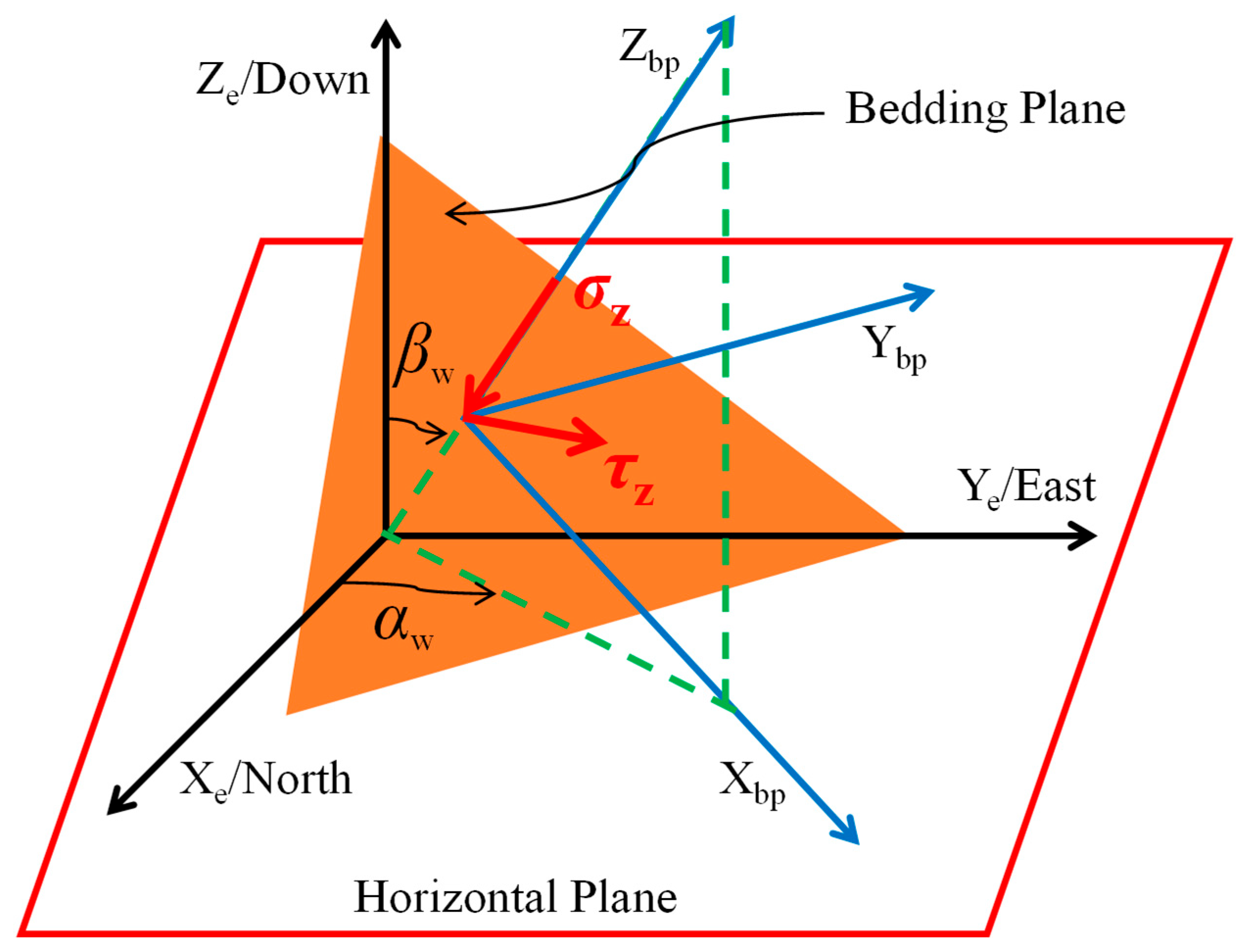
2.1.1. Coordinate Transformation
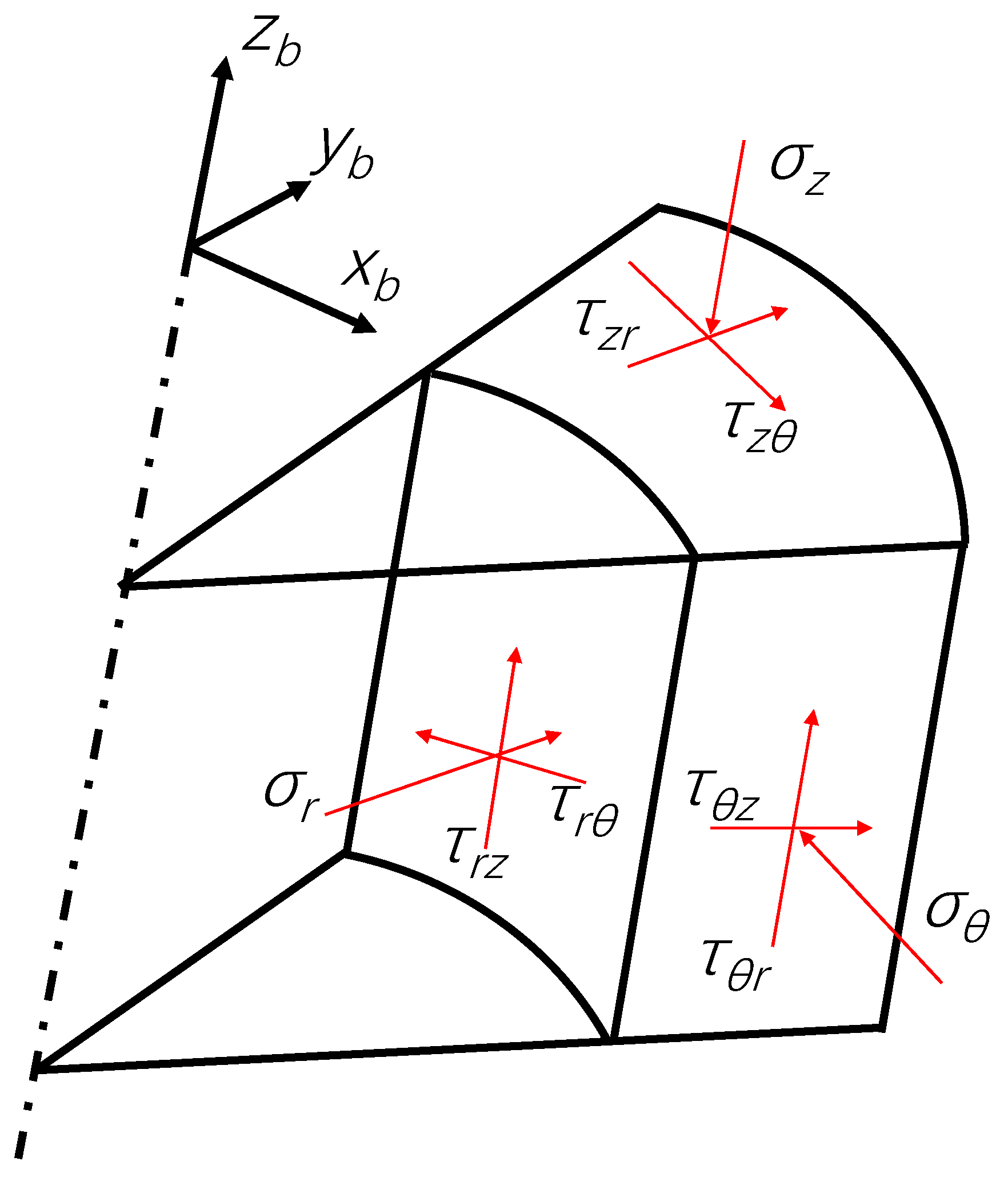
2.1.2. Wellbore Stress Distribution Model
2.2. Strength Criteria
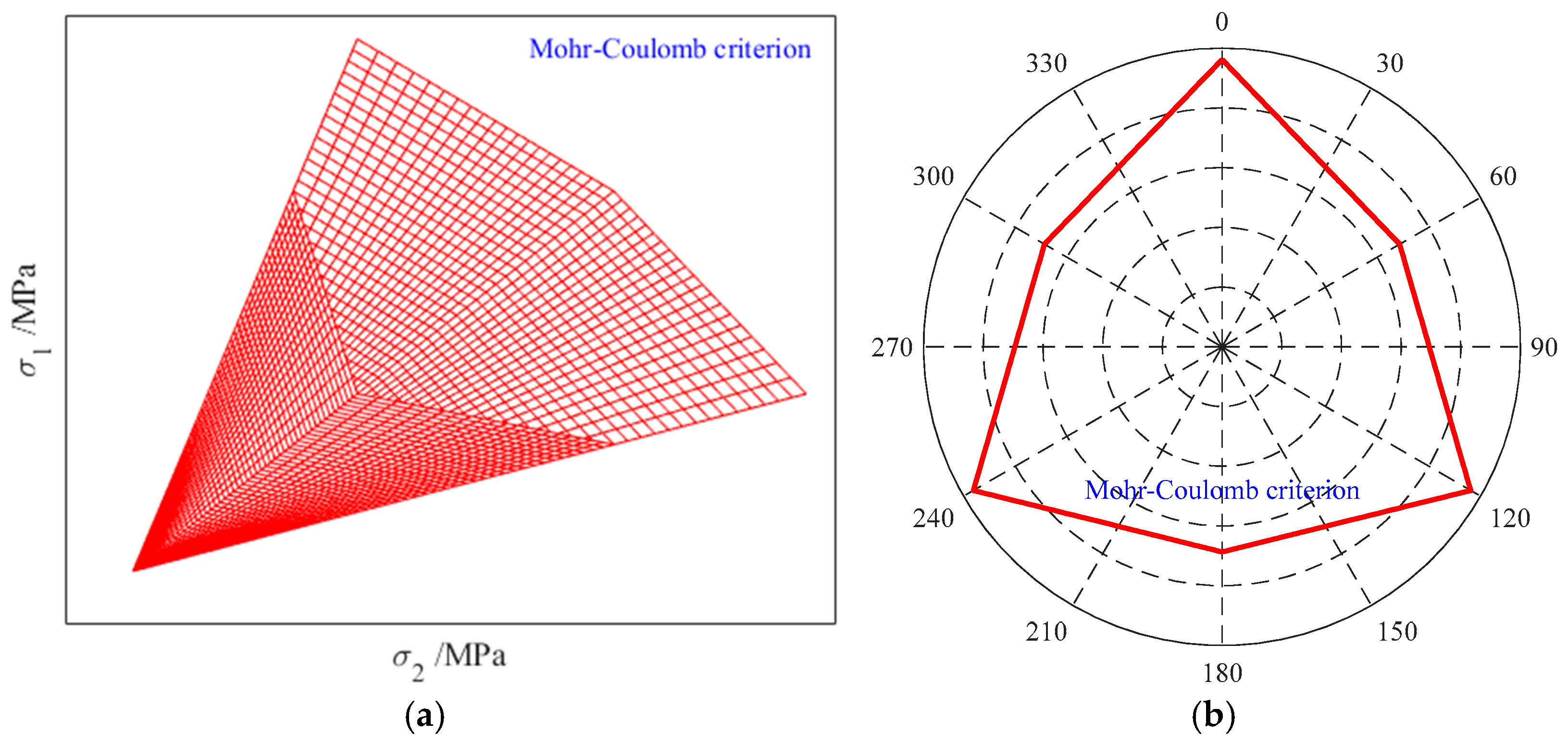
2.2.1. Mohr–Coulomb Strength Criterion
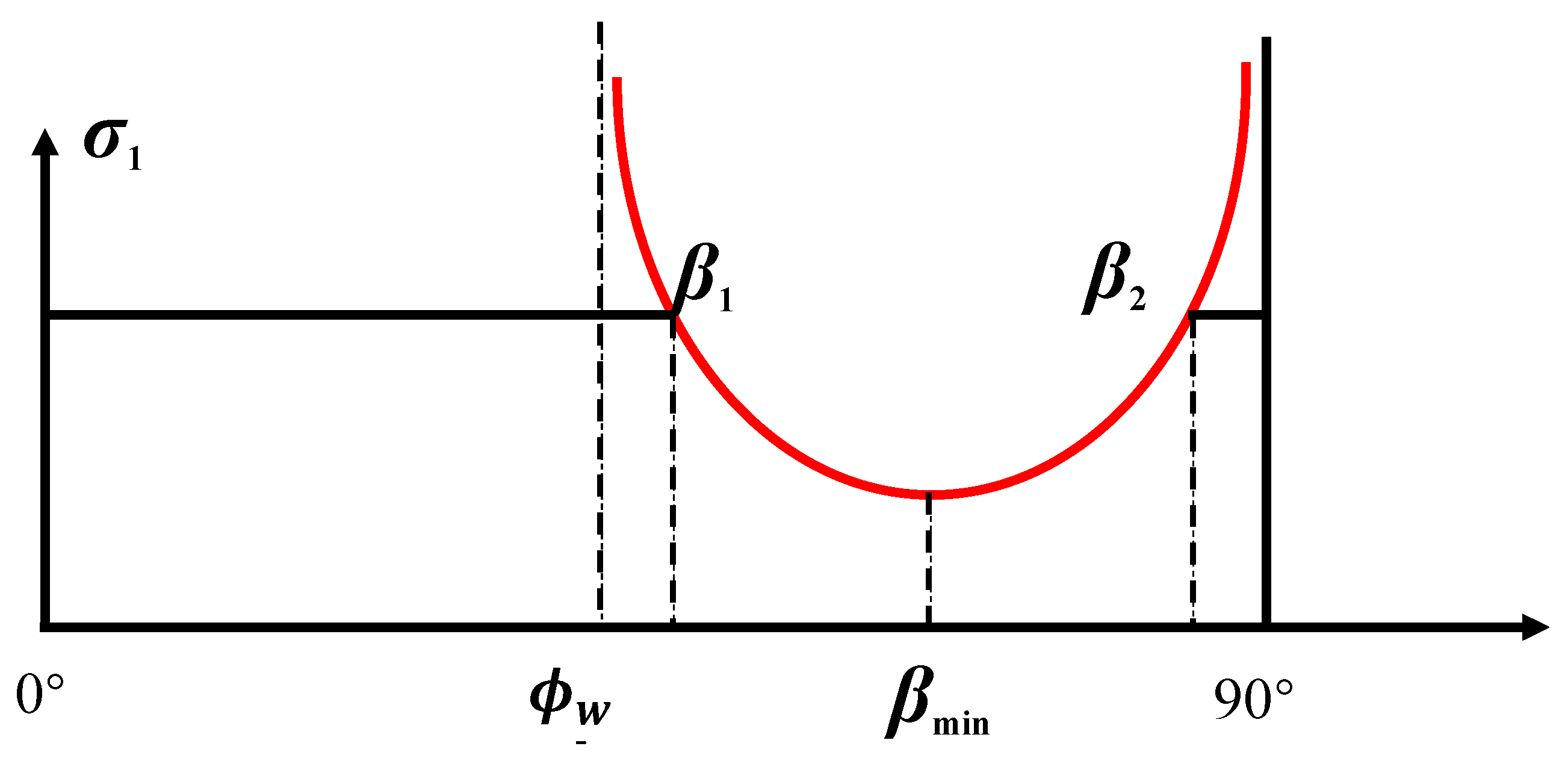
2.2.2. Single Plane of Weakness Criterion
2.3. Collapse Pressure Solution Model
2.3.1. Transformation of Wellbore Principal Stresses
2.3.2. Stress Distribution on Fracture Planes Around the Wellbore
- Input basic model parameters, such as in situ stresses and their orientations, the orientation and strength parameters of fracture plane i, wellbore trajectory, and wellbore radius r.
- Determine the wellbore azimuth angle θ, increasing from 0° to 360° in increments of 2°. Set the initial bottomhole pressure Pw = 0 MPa and calculate the wellbore stress components at a specific point in the wellbore Cartesian coordinate system.
- Transform the stress components into polar coordinates and convert them into principal stresses using Equation (14). Substitute the principal stresses into the Single Plane of Weakness Criterion. Gradually increase the bottomhole pressure until the point reaches critical equilibrium. The corresponding bottomhole pressure is the collapse pressure for rock matrix shear failure.
- Transform the stresses onto fracture plane i using coordinate conversion and obtain the normal and shear stresses. Substitute these into the 3D Weak Plane Strength Criterion (Equations (5)–(14)). Gradually increase the bottomhole pressure until the point reaches critical equilibrium. The corresponding bottomhole pressure is the collapse pressure for shear failure along fracture plane i.
- Determine the maximum collapse pressure at the point. The maximum collapse pressure value along the wellbore wall is identified as the wellbore collapse pressure for the specified trajectory. The procedure is repeated by varying the well inclination from 0° to 90° in 10° increments and the azimuth from 0° to 360° in 10° increments to generate a comprehensive polar plot of wellbore collapse pressure.
2.3.3. Model Validation
3. Results and Discussion
4. Conclusions
- (1)
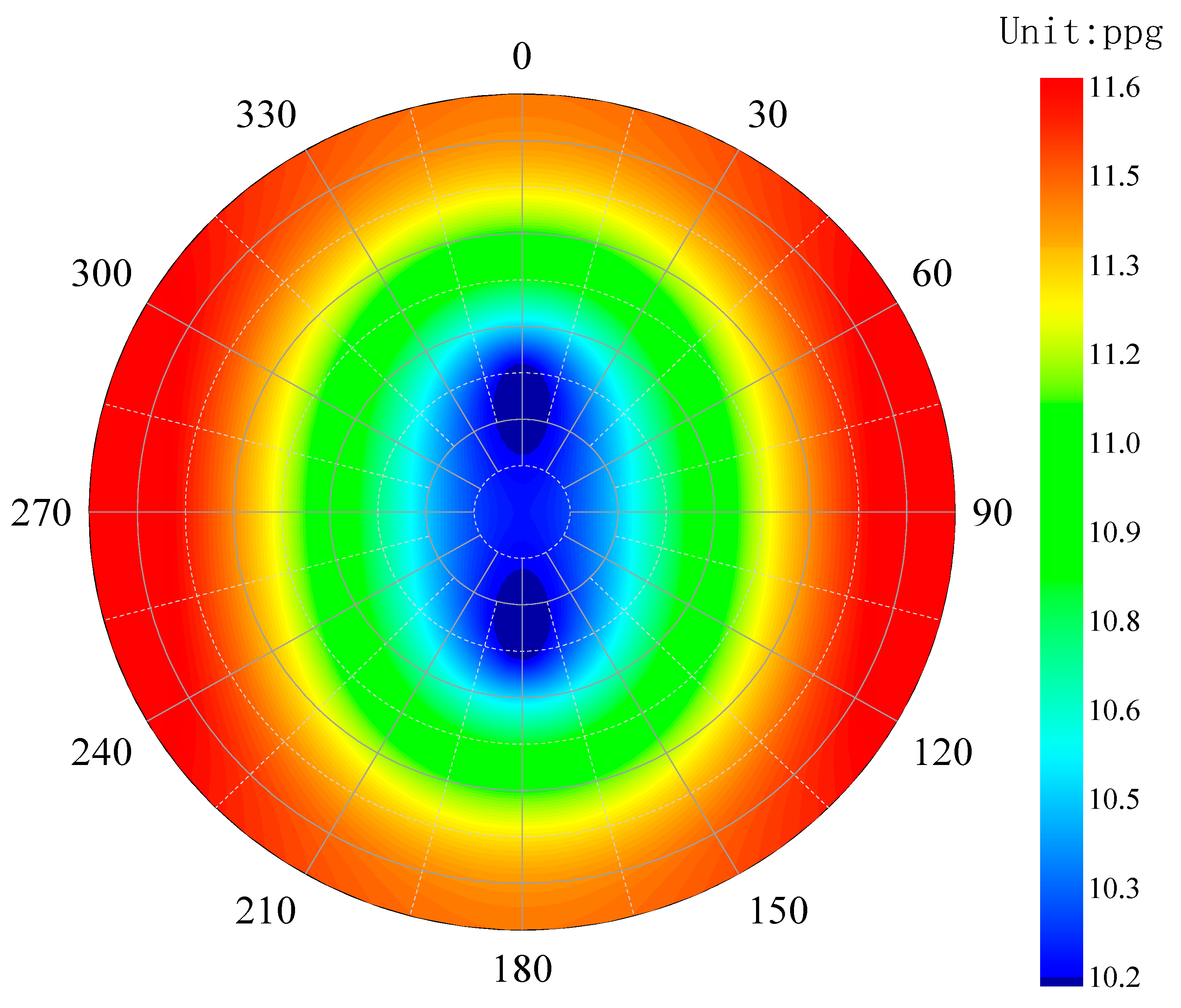
- In highly fractured formations, wellbore collapse pressure is strongly influenced by fracture orientation and density. The traditional Mohr–Coulomb criterion significantly underestimates the required mud density due to its inability to account for fracture effects. When fractures are considered, the collapse pressure range widens to 1.40–2.10 g/cm3, with the most stable wellbore azimuth falling between 220° and 260°. This confirms that fractures reduce rock integrity and modify stress distribution, thereby elevating instability risks.
- (2)
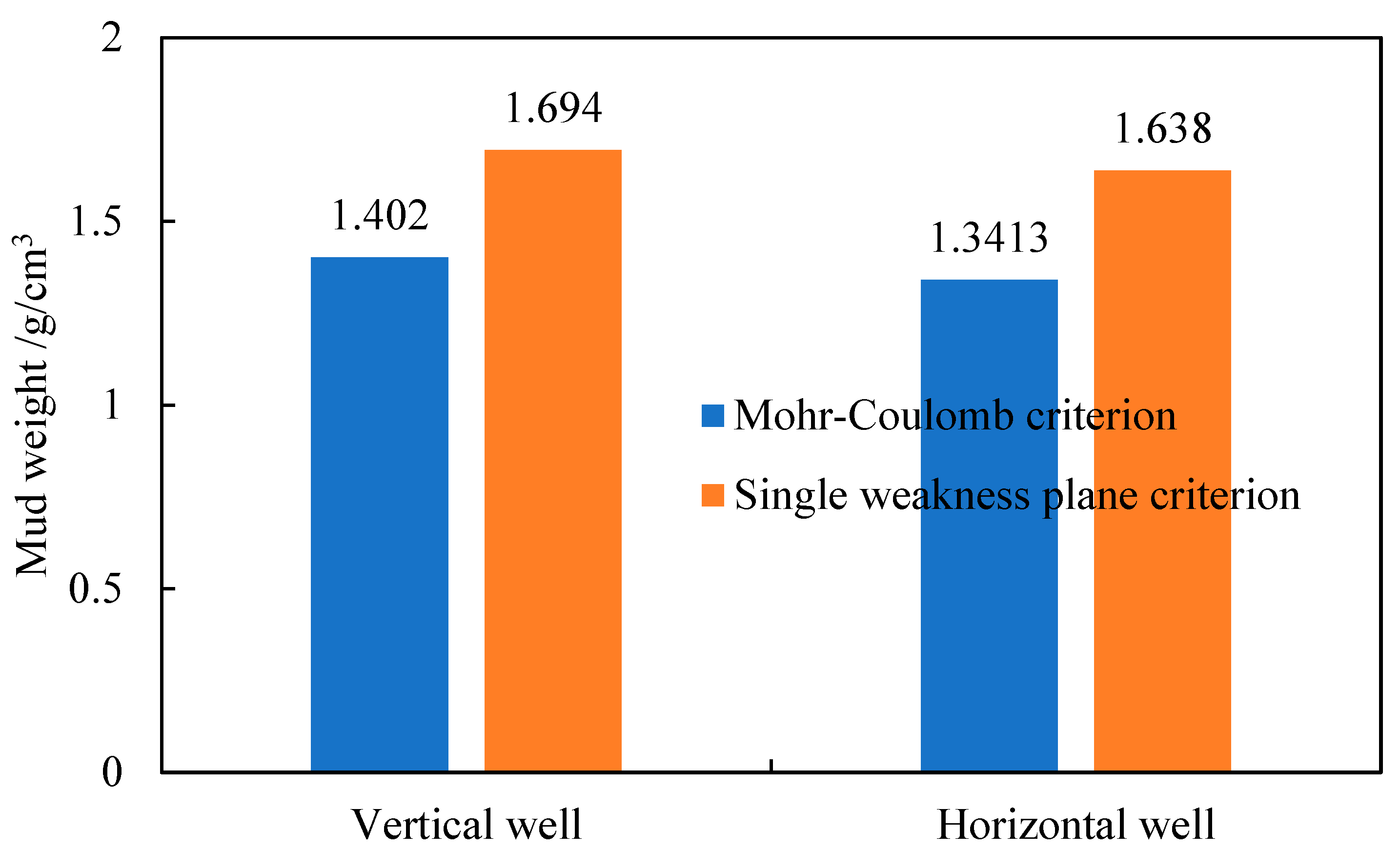
- A mud density of 1.55 g/cm3, as derived from the Mohr–Coulomb criterion, is insufficient in fractured formations. The proposed model recommends a density of at least 1.638 g/cm3 for horizontal sections, which aligns with actual drilling experience in Well THX—where wellbore instability occurred at 1.55 g/cm3, validating the model’s accuracy.
- (3)
- Sensitivity analysis identifies fracture orientation as the dominant factor influencing collapse pressure. Collapse pressure increases significantly when the angle between the fracture plane and the maximum principal stress approaches the internal friction angle of the fracture. Furthermore, the interaction between in situ stress direction and wellbore trajectory results in asymmetric stress distribution. A 10° deviation in azimuth can lead to a 15% increase in prediction error.
- (4)
- To mitigate collapse risk, the wellbore trajectory should be optimized within the azimuth range of 220–260°, and drilling fluid density should be maintained at or above 1.638 g/cm3. In extensively fractured intervals, additional measures such as improved bridging or cement plugging are recommended to counteract hydration-induced softening.
- (5)
- These conclusions are primarily based on data from Well THX; thus, generalizability may be limited. Future work should incorporate true triaxial strength criteria to consider the influence of the intermediate principal stress and apply machine learning methods to address uncertainties in fracture parameters. Such enhancements will improve the model’s applicability in complex shale gas reservoirs, such as those in the Sichuan Basin, supporting safe and efficient development of unconventional resources under the “Dual Carbon” framework.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, A.; Rao, K.S.; Ayothiraman, R. An analytical solution to wellbore stability using Mogi-Coulomb failure criterion. J. Rock Mech. Geotech. Eng. 2019, 11, 1211–1230. [Google Scholar] [CrossRef]
- Aubertin, M.; Li, L.; Simon, R. A multiaxial stress criterion for short- and long-term strength of isotropic rock media. Int. J. Rock Mech. Min. Sci. 2000, 37, 1169–1193. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, J.; Zhang, Q.; Hu, X. A new closed-form solution for circular openings modeled by the Unified Strength Theory and radius-dependent Young’s modulus. Comput. Geotech. 2012, 42, 118–128. [Google Scholar] [CrossRef]
- Haimson, B.; Chang, C. A new true triaxial cell for testing mechanical properties of rock, and its use to determine rock strength and deformability of Westerly granite. Int. J. Rock Mech. Min. Sci. 2000, 37, 285–296. [Google Scholar] [CrossRef]
- Zhang, W.; Gao, J.; Lan, K.; Liu, X.; Feng, G.; Ma, Q. Analysis of borehole collapse and fracture initiation positions and drilling trajectory optimization. J. Pet. Sci. Eng. 2015, 129, 29–39. [Google Scholar] [CrossRef]
- Xu, K.; Liu, Z.; Chen, Q.; Zhang, Q.; Ling, X.; Cai, X.; He, Q.; Yang, M. Application of machine learning in wellbore stability prediction: A review. Geoenergy Sci. Eng. 2024, 232, 212409. [Google Scholar] [CrossRef]
- Muller, A.L.; do Amaral Vargas, E., Jr.; Vaz, L.E.; Gonçalves, C.J. Borehole stability analysis considering spatial variability and poroelastoplasticity. Int. J. Rock Mech. Min. Sci. 2009, 46, 90–96. [Google Scholar] [CrossRef]
- Zare-Reisabadi, M.R.; Kaffash, A.; Shadizadeh, S.R. Determination of optimal well trajectory during drilling and production based on borehole stability. J. Pet. Sci. Eng. 2012, 77–87. [Google Scholar] [CrossRef]
- Cao, W.; Liu, W.; Liu, H.; Lin, H. Effect of formation strength anisotropy on wellbore shear failure in bedding shale. J. Pet. Sci. Eng. 2012, 90–91, 107–118. [Google Scholar] [CrossRef]
- Dokhani, V.; Yu, M.; Miska, S.Z.; Takach, N.E.; Ozbayoglu, E.; Bloys, B. Effects of adsorptive characteristics of shale on wellbore stability. In Proceedings of the 49th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 28 June–1 July 2015; American Rock Mechanics Association: Alexandria, VA, USA, 2015. [Google Scholar]
- Singh, A.; Kumar, C.; Kannan, L.G.; Rao, K.S.; Ayothiraman, R. Engineering properties of rock salt and simplified closed-form deformation solution for circular opening in rock salt under the true triaxial stress state. Eng. Geol. 2018, 243, 218–230. [Google Scholar] [CrossRef]
- Xiang, Z.; Kang, W.-H.; Ji, Y.; Si, G.; Canbulat, I.; Lin, H.; Oh, J. Estimation of in-situ horizontal stresses based on multiscale borehole breakout data via machine learning: Model development, validation and application. Geophys. J. Int. 2025, 242, ggaf144. [Google Scholar] [CrossRef]
- Ma, X.; Haimson, B.C. Failure characteristics of two porous sandstones subjected to true triaxial stresses. J. Geophys. Res. Solid Earth 2016, 121, 6477–6498. [Google Scholar] [CrossRef]
- Charlez, P.A. The impact of constitutive laws on wellbore stability: A general review. SPE Drill. Complet. 1997, 12, 123–134. [Google Scholar] [CrossRef]
- Mehrabian, A. The stability of inclined and fractured wellbores. SPE J. 2016, 21, 1050–1068. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, H. Three-dimensional Hoek-Brown strength criterion for rocks. J. Geotech. Geoenviron. Eng. 2007, 133, 1128–1135. [Google Scholar] [CrossRef]
- Zhou, X.P.; Shou, Y.D.; Qian, Q.H. Three-dimensional nonlinear dynamic strength criterion for rock. J. Mater. Civ. Eng. 2015, 27, 04015047. [Google Scholar] [CrossRef]
- Zhou, X.P.; Bao, X.R.; Yu, M.H.; Xie, Q. Triaxial stress state of cylindrical openings for rocks modeled by elastoplasticity and strength criterion. Theor. Appl. Fract. Mech. 2010, 53, 65–73. [Google Scholar] [CrossRef]
- Chang, C.; Haimson, B. True triaxial strength and deformability of the German Continental Deep Drilling Program (KTB) deep hole amphibolite. J. Geophys. Res. Solid Earth 2000, 105, 18999–19013. [Google Scholar] [CrossRef]
- Oku, H.; Haimson, B.; Song, S.-R. True triaxial strength and deformability of the siltstone overlying the Chelungpu fault (Chi-Chi earthquake), Taiwan. Geophys. Res. Lett. 2007, 34, L09306. [Google Scholar] [CrossRef]
- Lee, H.; Haimson, B.C. True triaxial strength, deformability, and brittle failure of granodiorite from the San Andreas Fault Observatory at Depth. Int. J. Rock Mech. Min. Sci. 2011, 48, 894–901. [Google Scholar] [CrossRef]
- Sriapai, T.; Walsri, C.; Fuenkajorn, K. True-triaxial compressive strength of Maha Sarakham salt. Int. J. Rock Mech. Min. Sci. 2013, 61, 256–265. [Google Scholar] [CrossRef]
- Chen, S.L.; Abousleiman, Y.N. Wellbore stability analysis using strain hardening and/or softening plasticity models. J. Pet. Sci. Eng. 2012, 86–87, 109–119. [Google Scholar] [CrossRef]
- Kang, Y.; Yu, M.; Miska, S.; Takach, N.E. Wellbore stability: A critical review and introduction to DEM. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009; SPE: Richardson, TX, USA, 2009. SPE-124364. [Google Scholar]
- McLean, M.R.; Addis, M.A. Wellbore stability analysis: A review of current methods of analysis and their field application. In Proceedings of the IADC/SPE Drilling Conference, Houston, TX, USA, 27 February–2 March 1990; SPE: Richardson, TX, USA, 1990. IADC/SPE-19941. [Google Scholar]
- Plazas Niño, F.A. Wellbore stability analysis based on sensitivity and uncertainty analysis. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 26–28 September 2016; SPE: Richardson, TX, USA, 2016. SPE-184480-STU. [Google Scholar]
- Zhang, H.; Ren, Y.; Zhang, Y.; Zheng, S. Intelligent prediction method for fracture pressure based on stacking ensemble algorithm. J. Pet. Explor. Prod. Technol. 2023, 9, 149. [Google Scholar] [CrossRef]
- Barsanescu, P.; Sandovici, A.; Serban, A. Mohr-Coulomb criterion with circular failure envelope, extended to materials with strength-differential effect. J. Rock Mech. Geotech. Eng. 2018, 10, 647–669. [Google Scholar] [CrossRef]
- Detournay, E.; Cheng, A.H.-D. Poroelastic response of a borehole in a non-hydrostatic stress field. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1988, 25, 171–182. [Google Scholar] [CrossRef]
- Zhang, M.M.; Liang, L.X.; Liu, X.J. Analysis of the Influence of Different Rock Shear Failure Criteria on Wellbore Collapse Pressure. Chin. J. Rock Mech. Eng. 2017, 36, 3485–3491. [Google Scholar]
- Zhang, M.; Fan, X.; Zhang, Q.; Yang, B.; Zhao, P.; Yao, B.; He, L. Influence of multi-planes of weakness on unstable zones near wellbore wall in a fractured formation. J. Nat. Gas Sci. Eng. 2021, 93, 104026. [Google Scholar] [CrossRef]
- Zhang, M.; Fan, X.; Zhang, Q.; Yang, B.; Zhao, P.; Yao, B.; Ran, J. Parametric sensitivity study of wellbore stability in transversely isotropic medium based on poly-axial strength criteria. J. Pet. Sci. Eng. 2021, 197, 108078. [Google Scholar] [CrossRef]
- Zhang, M.; Li, D.; Liu, J.; Zhang, D.; Zhang, Y.; Cui, K. The modification of Mohr-Coulomb criteria based on shape function and determination method of undetermined parameters. Mech. Mater. 2023, 185, 104772. [Google Scholar] [CrossRef]
- Zhang, M.; Wen, J.; Xu, Z.; Feng, J.; Zhao, X. Study of borehole stability of volcanic rock formation with the influence of multiple factors. J. Pet. Explor. Prod. Technol. 2024, 14, 3367–3382. [Google Scholar] [CrossRef]
- Abousleiman, Y.; Cui, L. Poroelastic solutions in transversely isotropic media for wellbore and cylinder. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1998, 35, 171–182. [Google Scholar] [CrossRef]
- Tiwari, R.P.; Rao, K.S. Post failure behaviour of a rock mass under the influence of triaxial and true triaxial confinement. Eng. Geol. 2006, 84, 112–129. [Google Scholar] [CrossRef]
- Gao, J.; Chen, F.; Zhao, Y.; Meng, M.; Peng, H.; Bian, G.; Huang, L. Quantitative risk analysis and parameter sensitivity evaluation of wellbore instability in poroelastic media considering uncertainty of geomechanical parameters. Comput. Geotech. 2024, 170, 106234. [Google Scholar] [CrossRef]
- Lei, G.; Ren, J.; Liu, B.; Xiong, J.; Liu, X.; Cheng, W.; Liang, L.; Li, Z. Evolution of physical properties of Longmaxi Formation shale under scCO2-water-rock interaction and its influence on wellbore stability. Nat. Gas Ind. 2025, 45, 136–149. [Google Scholar] [CrossRef]
- Liu, X.; Ding, Y.; Cao, G.; Yue, Z.; Zhang, Z.; Zhang, W.; Liang, L.; Yu, X. The investigation on wellbore stability of large size borehole of upper part of ultradeep well. Coal J. 2025. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, B.; Geng, Y.; Xiao, R. Prediction model of rock mechanics parameters in ultra-deep fractured formations based on big data. Pet. Drill. Tech. 2024, 52, 91–96. [Google Scholar] [CrossRef]
- Gao, S.; Bo, K.; Zhang, Y.; Gao, H.; Huangfu, J. Study on wellbore instability mechanism of continental shale reservoir in Northeastern Sichuan Basin. Drill. Fluid Complet. Fluid 2025, 42, 217–224. [Google Scholar] [CrossRef]
- Bai, Y.; Yang, Z.; Bai, H.; Wang, C.; Zhang, X.; Chen, Y.; Wu, H. Study on the mechanism of borehole instability in Wujiaping Formation in Hongxing area and countermeasures of drilling fluid. Fault Block Oil Gas Field 2025, 32, 685–691. Available online: https://link.cnki.net/urlid/41.1219.TE.20250425.1513.002 (accessed on 27 September 2025).
- Shi, X.; Zhang, Q.; Gao, L.; Zhang, H. Evaluation model and application of wellbore stability based on an improved three-dimensional Hoek-Brown strength criterion. Pet. Sci. Bull. 2025, 10, 762–777. Available online: https://link.cnki.net/urlid/10.1405.te.20250709.1509.002 (accessed on 27 September 2025).
- Chu, Q.; Mu, G.; Ge, C.; Zhang, T.; Yang, M.; Liu, C. Preparation and properties of a drilling fluid non-fluorescent flexible plugging. Drill. Fluid Complet. Fluid 2025, 42, 290–295. [Google Scholar] [CrossRef]
- He, M.; Wang, L.; Zhou, B.; Xu, M. Multi-field coupling model of wellbore stability in gas drilling horizontal wells. World Pet. Ind. 2025, 32, 82–92. [Google Scholar] [CrossRef]
- Yang, S.; Feng, C.; Guo, L. Experiments on the expansion, spallation and mechanical deterioration in coal rocks immersed into water-based drilling fluid. Nat. Gas Technol. Econ. 2025, 19, 15–22. [Google Scholar] [CrossRef]
- Zhai, K.; Dang, Z.; Chen, X.; Yang, W.; Zhao, X. Numerical analysis of in-situ stress inversion and main controlling factors of wellbore stability in the mudstone section of the Tahe Block. Chin. Q. Mech. 2024, 45, 1088–1096. [Google Scholar] [CrossRef]
- Fan, Z.; Song, X.; Wang, D.; Ayasrah, M.; Li, S. Poroelastic Solutions of a Semi-Permeable Borehole Under Non-Hydrostatic in Situ Stresses Within Transversely Isotropic Media. Int. J. Geomech. 2025, 25, 04024342. [Google Scholar] [CrossRef]
- Gao, R.; Kuang, T.; Meng, X.; Huo, B. Effects of ground fracturing with horizontal fracture plane on rock breakage characteristics and mine pressure control. Rock Mech. Rock Eng. 2021, 54, 3229–3243. [Google Scholar] [CrossRef]
- Gao, R.; Dou, B.; Yu, B.; Yang, T.; Meng, X.; Zhang, W. Ground fracturing of multi-strata for strong ground pressure control in extra-thick coal seams with hard roofs: Numerical simulation and case study. Eng. Fract. Mech. 2024, 303, 110129. [Google Scholar] [CrossRef]
- Jiang, S.; Zhang, J.; Diao, K.; Liu, X.; Ding, Z. Research Advances in Solvent Extraction of Lithium: The Potential of Ionic Liquids. Adv. Funct. Mater. 2025, 35, 2423566. [Google Scholar] [CrossRef]
- Yang, M.; Si, S.; Zhang, K.; Xi, M.; Zhang, W. Bridging the relationship between physical exercise and mental health in adolescents based on network analysis. PsyCh J. 2024, 13, 835–848. [Google Scholar] [CrossRef]
- Mehrabi, A.; Bagheri, M.; Bidhendi, M.N.; Delijani, E.B.; Behnoud, M. Improved porosity estimation in complex carbonate reservoirs using hybrid CRNN deep learning model. Earth Sci. Inf. 2024, 17, 4773–4790. [Google Scholar] [CrossRef]
- Moosavi, N.; Bagheri, M.; Nabi-Bidhendi, M. Hydrocarbon reservoir parameter estimation using a fuzzy Gaussian based SVR method. Bull. Geophys. Oceanogr. 2024, 65, 70. [Google Scholar] [CrossRef]
- Lee, H.; Ong, S.H.; Azeemuddin, M.; Goodman, H. A wellbore stability model for formations with anisotropic rock strengths. J. Pet. Sci. Eng. 2012, 96, 109–119. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J. Advancements and challenges of high-speed active flow control: Plasma actuators. Int. J. Heat Mass Transf. 2025, 252, 127481. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X. Active flow control for supersonic aircraft: A novel hybrid synthetic jet actuator. Sens. Actuators A Phys. 2020, 302, 111770. [Google Scholar] [CrossRef]
- Gao, X.; Wang, M.; Shi, X.; Li, C.; Zhang, M. Risk Assessment Method for Analyzing Borehole Instability Considering Formation Heterogeneity. Processes 2024, 12, 70. [Google Scholar] [CrossRef]
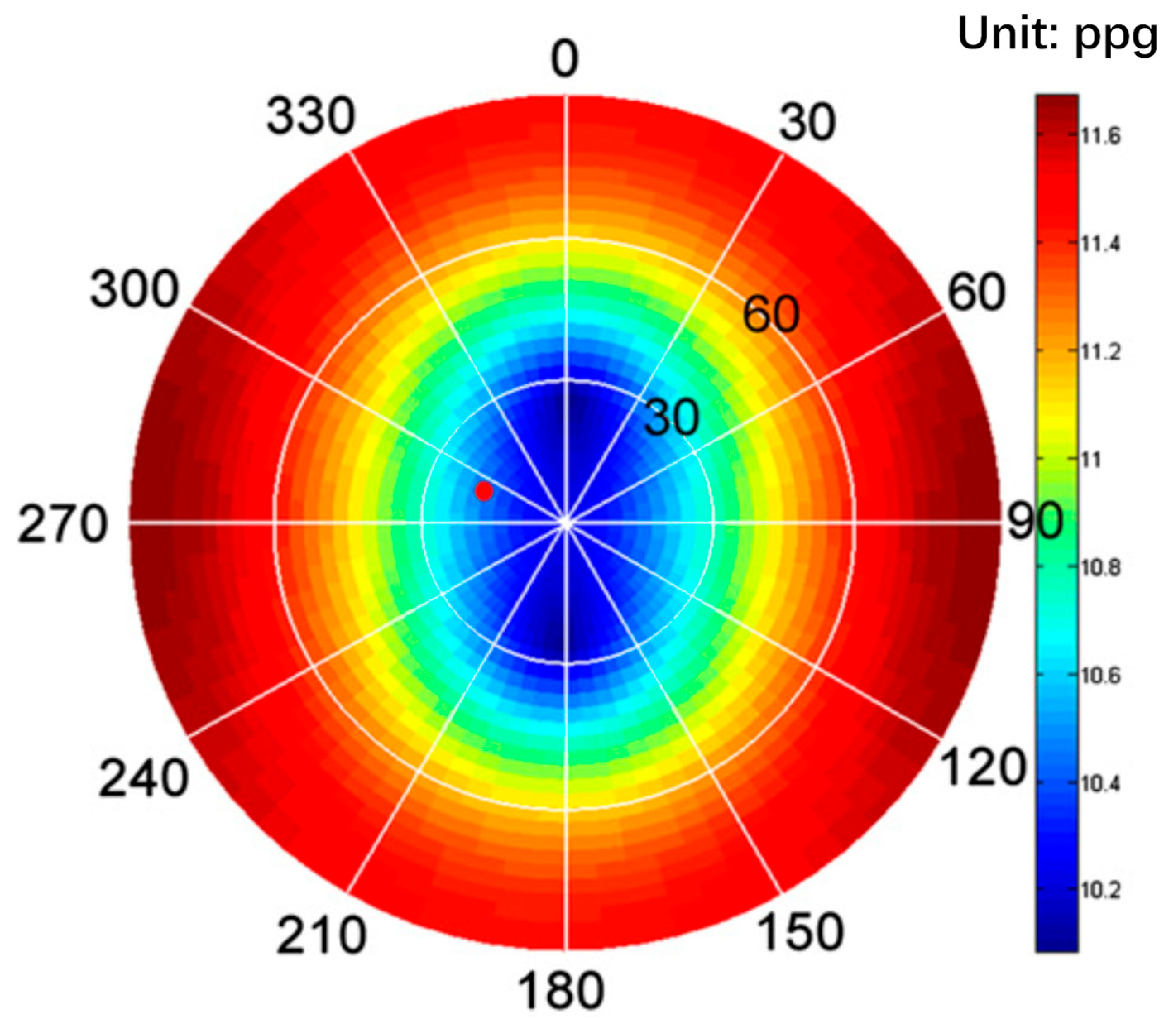
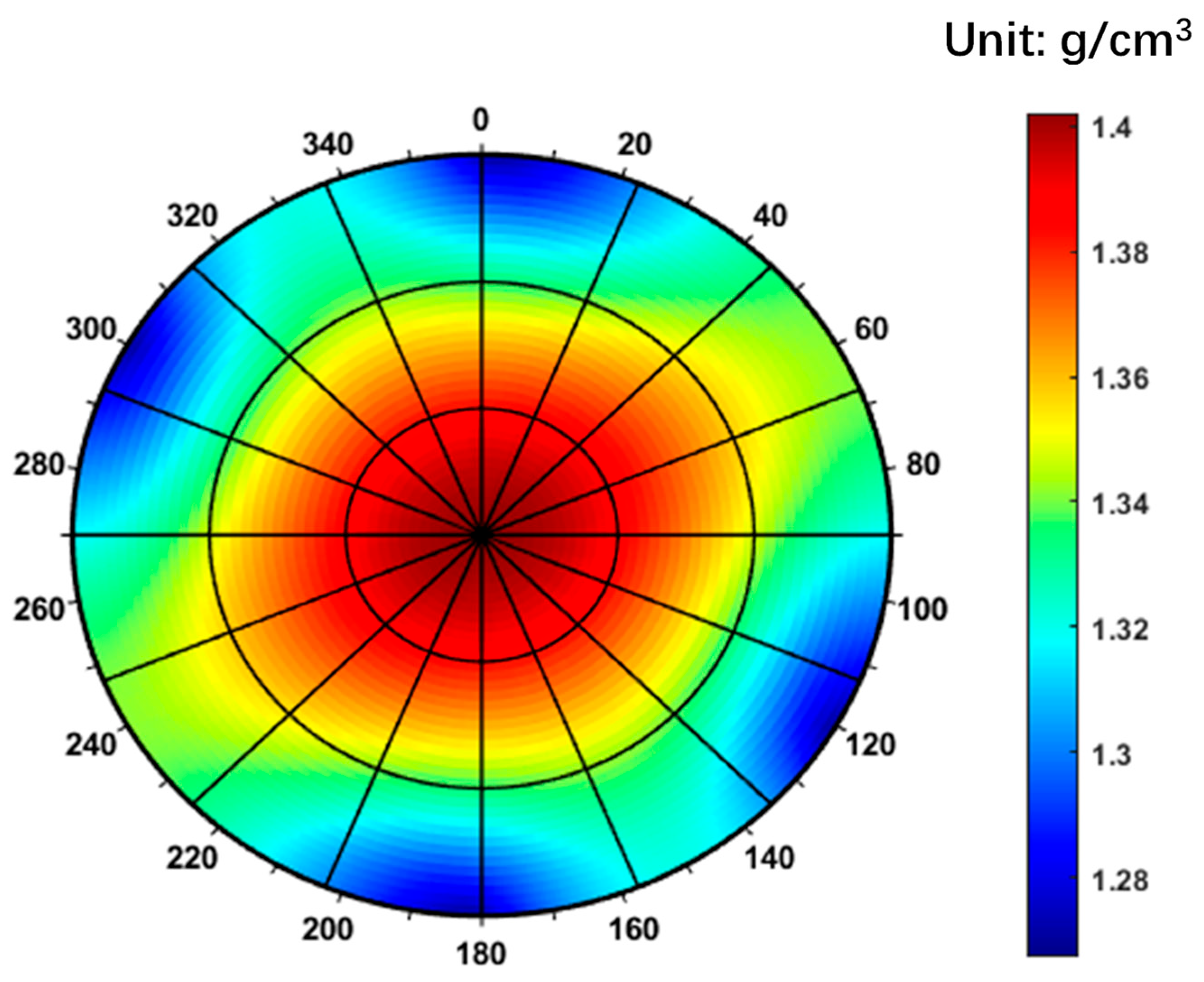
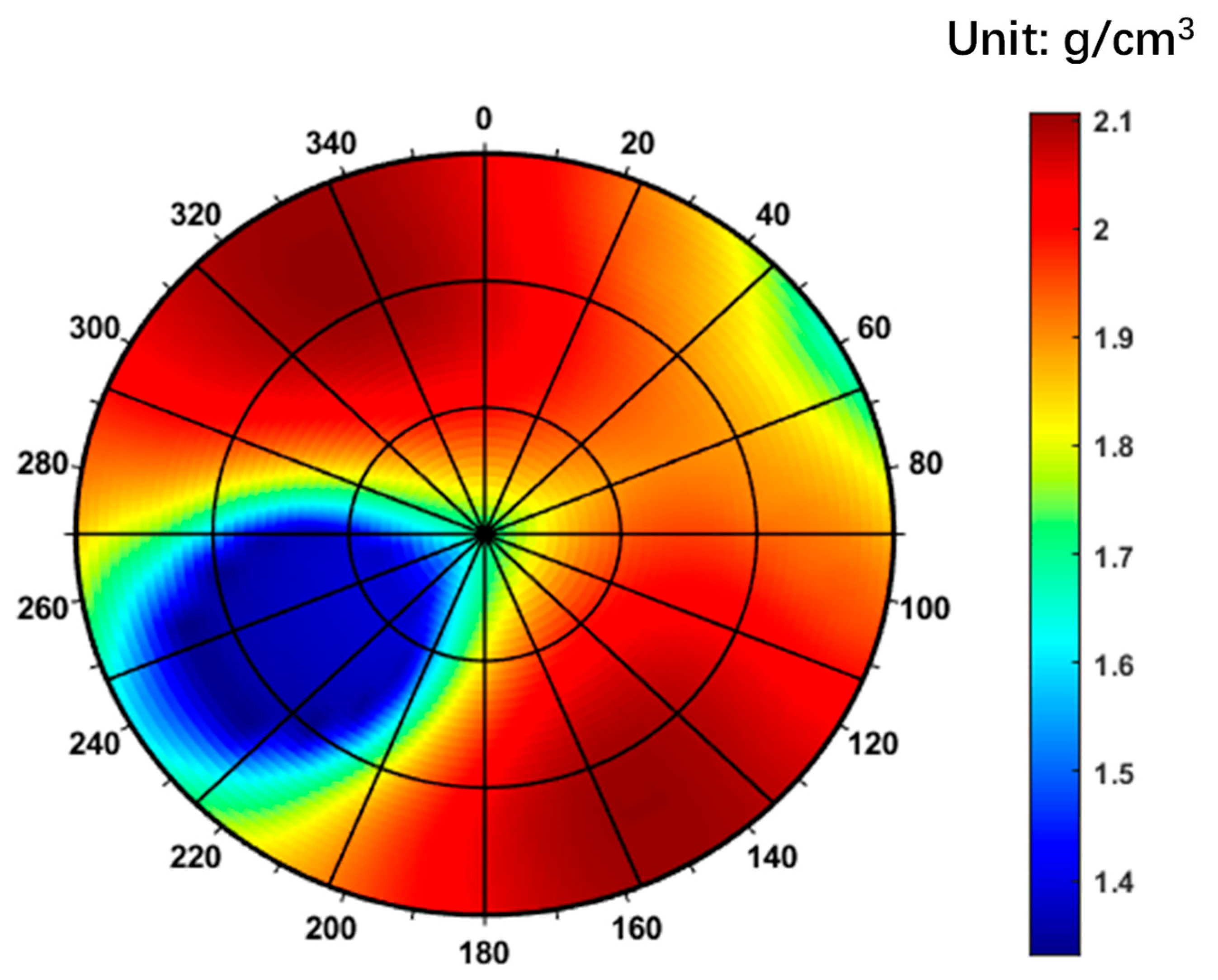
| Well depth, m | 4800 | Maximum horizontal in situ stress, MPa | 97.05 |
| Minimum horizontal in situ stress, MPa | 83.45 | Overburden pressure, MPa | 94.35 |
| Formation pressure, MPa | 52.7 | In situ stress orientation, ° | 60 |
| Biot’s coefficient | 0.8 | Poisson’s ratio | 0.22 |
| Intact rock friction angle, ° | 30.8 | Intact rock cohesion, MPa | 25.06 |
| Fracture friction angle, ° | 12.9 | Fracture cohesion, MPa | 9.03 |
| Fracture plane dip direction, ° | 60 | Fracture plane dip angle, ° | 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Zhao, Y.; Fu, Y.; Yue, P. Distribution Model of Wellbore Collapse Pressure in Deviated Wells Considering Fracture Development and Engineering Applications. Processes 2025, 13, 3769. https://doi.org/10.3390/pr13123769
Li L, Zhao Y, Fu Y, Yue P. Distribution Model of Wellbore Collapse Pressure in Deviated Wells Considering Fracture Development and Engineering Applications. Processes. 2025; 13(12):3769. https://doi.org/10.3390/pr13123769
Chicago/Turabian StyleLi, Lu, Yang Zhao, Yafei Fu, and Ping Yue. 2025. "Distribution Model of Wellbore Collapse Pressure in Deviated Wells Considering Fracture Development and Engineering Applications" Processes 13, no. 12: 3769. https://doi.org/10.3390/pr13123769
APA StyleLi, L., Zhao, Y., Fu, Y., & Yue, P. (2025). Distribution Model of Wellbore Collapse Pressure in Deviated Wells Considering Fracture Development and Engineering Applications. Processes, 13(12), 3769. https://doi.org/10.3390/pr13123769





