Research and Experimentation on Pneumatic Particle Transport in Confined Spaces of Offshore Oil and Gas Wells Based on DEM-CFD Coupling Method
Abstract
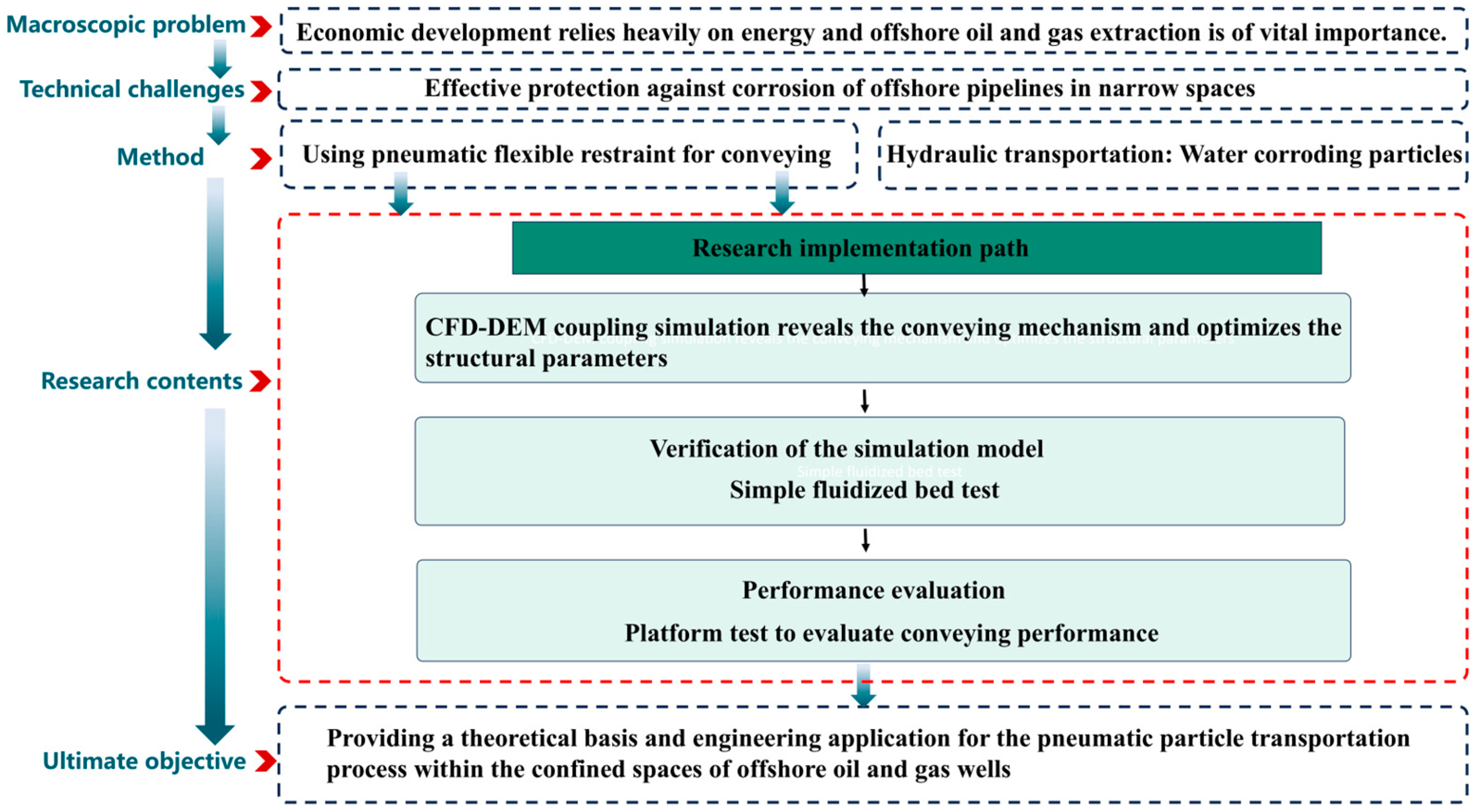
1. Introduction
2. Materials and Methods
2.1. Working Principle
2.2. Mathematical Model for Pill Particles Transport
2.2.1. Gas–Solid Coupled Simulation Mathematical Model
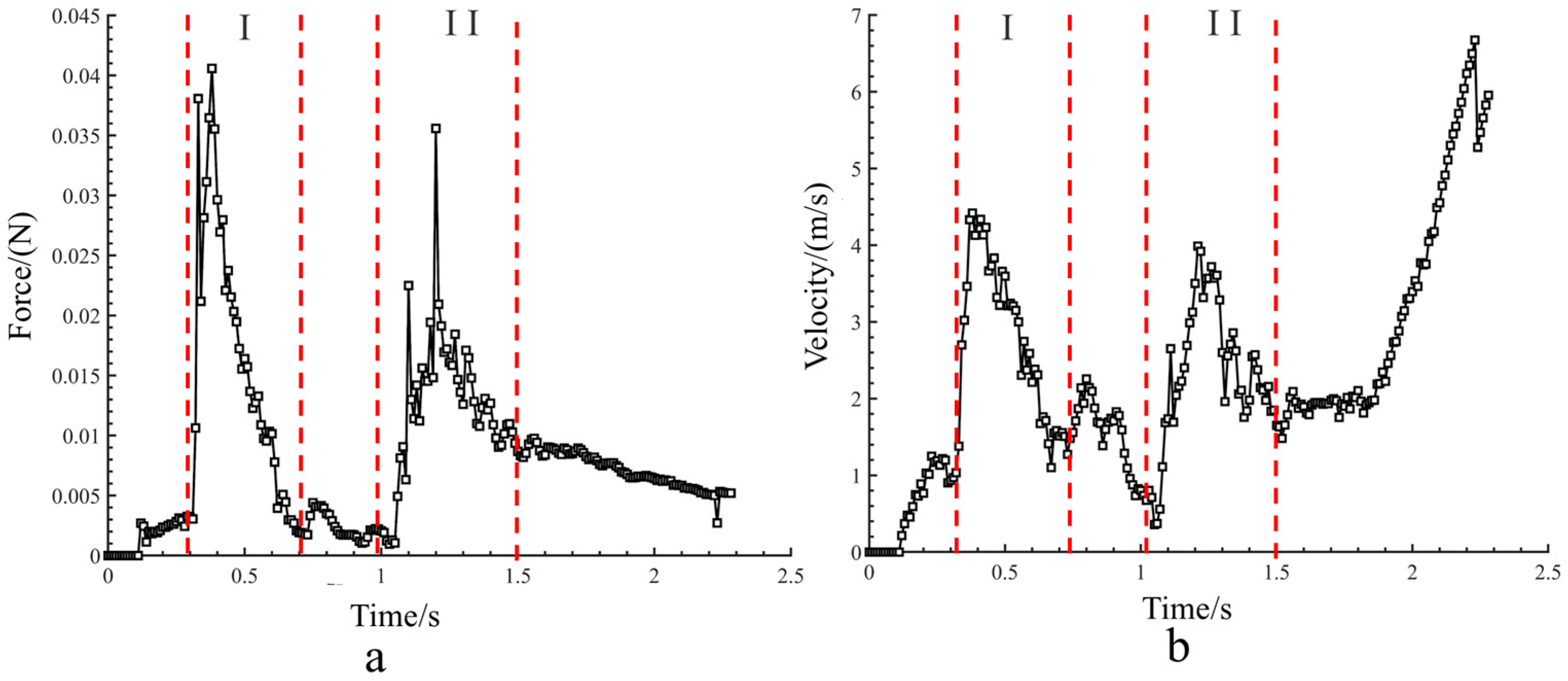
2.2.2. Analysis of the Pill Particles Acceleration Process in the Pipeline
2.3. Verification of the Simulation Model
3. Numerical Simulation Analysis of a Pneumatic Feeding Device for Pill Particles
3.1. Model Processing and Boundary Conditions Definition
- (1)
- Mesh Generation for the Pneumatic Conveying Device
- (2)
- Determination of Boundary Conditions for DEM-CFD Simulation
3.2. Simulation Test Contents and Methods
3.3. Validation of the Discrete Element Model for Pill Particles
4. Results and Discussion
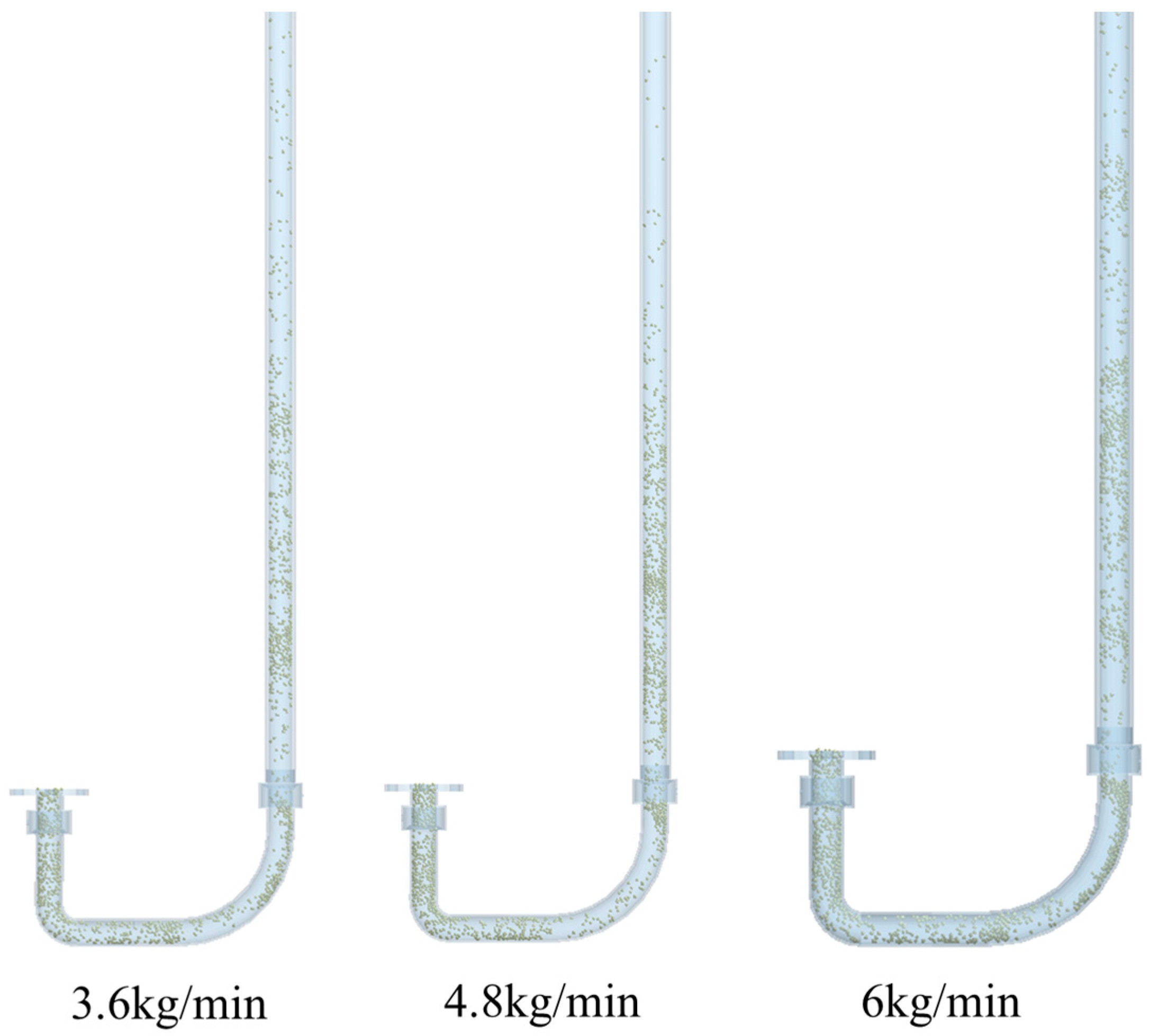
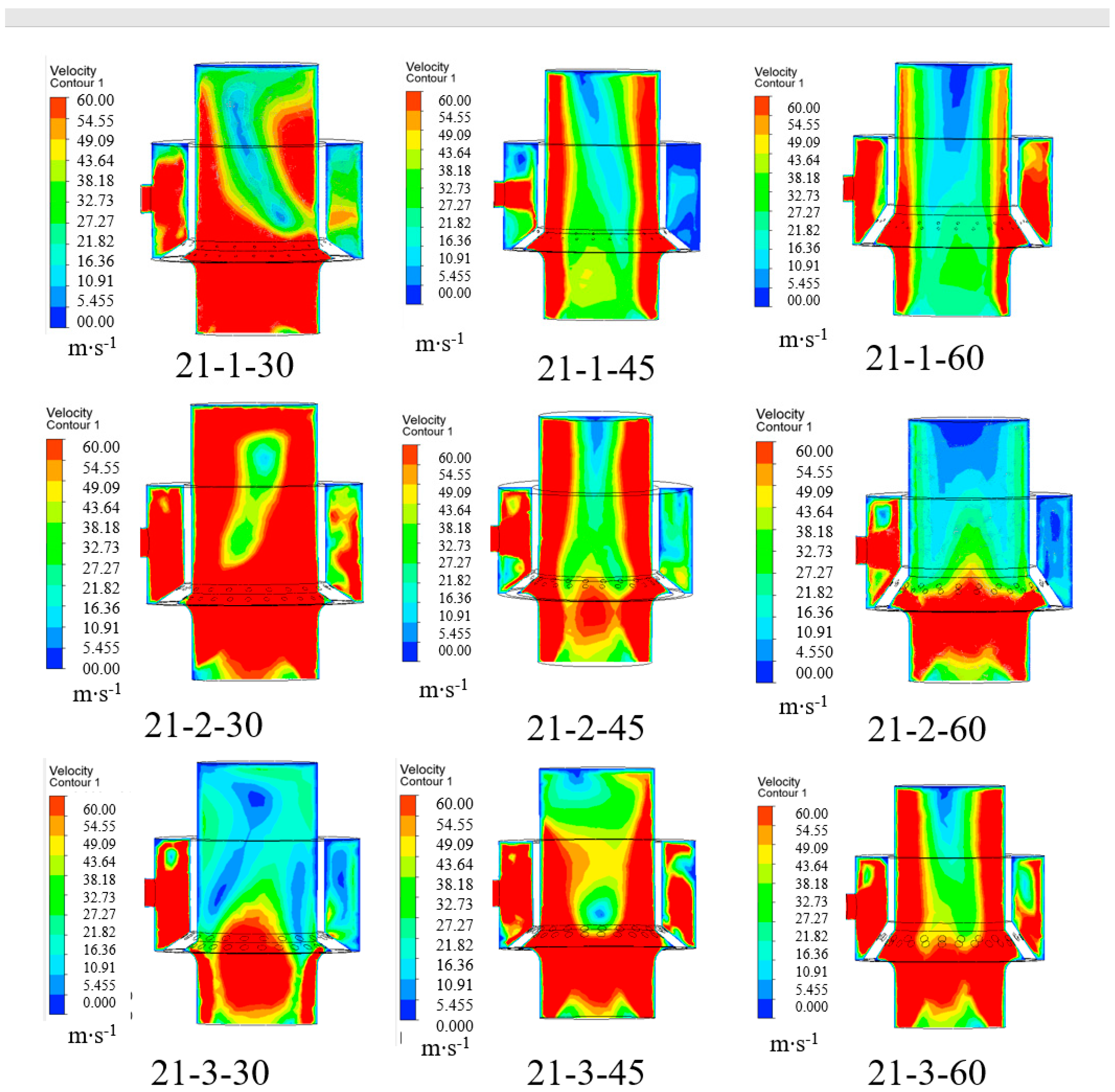
4.1. Single-Factor Simulation Analysis of Conveying Pressure
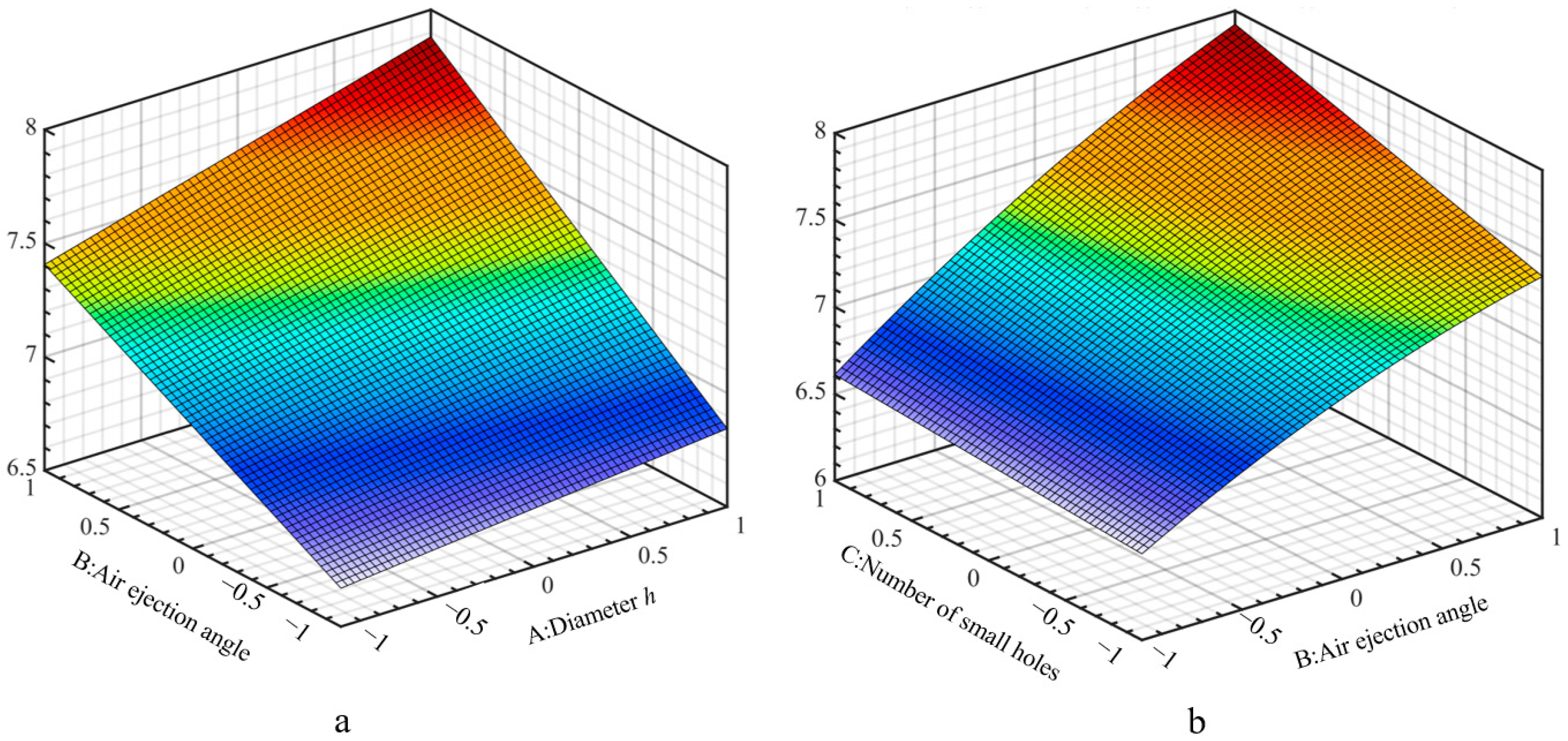
4.2. Multi-Factor Coupled Simulation Analysis
4.3. Bench Test Results
5. Conclusions
- Theoretical Analysis and Single-Factor Experiments: Theoretical analysis revealed that particle acceleration is positively correlated with airflow velocity in the stable acceleration zone. Single-factor experiments on feeding rate and minimum conveying pressure demonstrated that particles were transported stably at feeding rates of 3.6 kg/min and 4.8 kg/min with a conveying pressure of 0.20 MPa. However, at a feeding rate of 6.0 kg/min, particle accumulation and disordered collisions occurred at bends. The minimum pressure required for stable transport was determined to be 0.25 MPa.
- Response Surface Methodology (RSM) Optimization: A Box–Behnken three-factor, three-level experimental design was conducted based on response surface methodology, with airflow orifice diameter (Φh2) and injection angle (θ) as variables, and the particle exit velocity at the outlet (N) as the evaluation index. The main and secondary factors affecting the performance of the discharging device were evaluated, and the optimal parameter combination was identified. Parameter optimization using Design Expert 8.0.6 software determined the optimal values for the orifice diameter (Φh2), injection angle (θ), and number of orifices (N).
- Simulation and Physical Model Validation: Through simulation-based design and optimization, a physical model was constructed. No clogging occurred during the test, and the discharge behavior of the pill particles met practical production requirements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DEM | Discrete Element Method |
| EDEM | DEM Software |
| CFD | Computational Fluid Dynamics |
| CFD–DEM | Computational Fluid Dynamics–Discrete Element Method |
| PU | Polyurethane |
References
- Wang, F.; Kobina, F. The Influence of Geological Factors and Transmission Fluids on the Exploitation of Reservoir Geothermal Resources: Factor Discussion and Mechanism Analysis. Reserv. Sci. 2025, 1, 3–18. [Google Scholar] [CrossRef]
- Wu, J.; Ansari, U. From CO2 Sequestration to Hydrogen Storage: Further Utilization of Depleted Gas Reservoirs. Reserv. Sci. 2025, 1, 19–35. [Google Scholar] [CrossRef]
- Li, Q. Reservoir Science: A Multi-Coupling Communication Platform to Promote Energy Transformation, Climate Change and Environmental Protection. Reserv. Sci. 2025, 1, 1–2. [Google Scholar] [CrossRef]
- Chasemi, M.F.; Mehrpooya, M.; Chiasi, M.M.; Mohammadi, A.H.; Zendehboudi, S. Regional tectonic state and poro-thermolasticity analysis of near wellbore zone in field development plan: Utilization of an uncoupled approach. J. Nat. Gas Sci. Eng. 2017, 46, 615–636. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, D.; Song, J.; Xiao, Q.; Du, K.; Wei, X.; Dang, L.; Yu, Y.; Zhao, H. Coating Process of Oil and Gas Well Pipeline Preventive Repair Materials Inspired by Remora Suckerfish Structure. Biomimetics 2025, 10, 436. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Chen, Y.; Li, H.; Xu, Z.; Dong, H.; Wang, W. Effect of particles micro characteristics destroyed by ball milling on fly ash electrostatic separation. Adv. Powder Technol. 2022, 33, 103449. [Google Scholar] [CrossRef]
- Liu, D.; Lu, Y.; Lin, H.; Qiao, C.; Song, J.; Chen, S.; Yao, Z.; Du, K.; Yu, Y. Study on the Discharge Process and Mechanism of Anti-Corrosion Pill Particles in the Oil and Gas Field Wellbore Casing Annulus Based on the Discrete Element Method. Processes 2022, 10, 1737. [Google Scholar] [CrossRef]
- Lavrinec, A.; Orozovic, O.; Rajabnia, H.; Williams, K.; Jones, M.G.; Klinzing, G. Velocity and porosity relationships within dense phase pneumatic conveying as studied using coupled CFD-DEM. Powder Technol. 2020, 375, 89–100. [Google Scholar] [CrossRef]
- Musango, L.; John, S.; Lloyd, M. Comparison of CFD-DEM and TFM approaches for the simulation of the small scale challenge problem. Powder Technol. 2021, 378, 85–103. [Google Scholar] [CrossRef]
- Kuang, S.B.; Li, K.; Zou, R.P.; Pan, R.H.; Yu, A.B. Application of periodic boundary conditions to CFD-DEM simulation of gas-solid flow in pneumatic conveying. Chem. Eng. Sci. 2013, 93, 214–228. [Google Scholar] [CrossRef]
- Yang, L.; Luo, L.; Chen, X.; Wu, X.; Jing, F. Hydraulic transportation of non-spherical coarse particles in deep-sea mining: Impact of particle shape on flow dynamics. Ocean. Eng. 2025, 323, 120652. [Google Scholar] [CrossRef]
- Ren, W.; Zhang, X.; Zhang, Y.; Lu, X. The impact of particle size and concentration on the characteristics of solid–fluid two-phase flow in vertical pipe under pulsating flow. Chem. Eng. J. 2024, 500, 156398. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, H.; Wen, C. Sand Transport and Deposition Behaviour in Subsea Pipelines for Flow Assurance. Energies 2019, 12, 4070. [Google Scholar] [CrossRef]
- Xu, H.; Chen, W.; Li, L.; Yang, F. Morphology of Deep-Sea Mining Hydraulic Conveying Pipeline and Its Influencing Laws in Marine Dynamic Environment. J. Cent. South Univ. 2023, 30, 3790–3807. [Google Scholar] [CrossRef]
- Schnorr Filho, E.A.; Lima, N.C.; Franklin, E.M. Resolved CFD–DEM Simulations of the Hydraulic Conveying of Coarse Grains through a Very-Narrow Elbow. Powder Technol. 2022, 385, 811–821. [Google Scholar] [CrossRef]
- Nossair, A.; Rodgers, P.; Goharzadeh, A. Influence of Pipeline Inclination on Hydraulic Conveying of Sand Particles. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition 2012, Houston, TX, USA, 9–15 November 2012; ASME: New York, NY, USA; pp. 1–9. [Google Scholar] [CrossRef]
- Huang, C.; van Oijen, J.; Deen, N.; Tang, Y. Incorporation of flamelets generated manifold method in coarse-grained Euler-Lagrange simulations of pulverized coal combustion. Chem. Eng. Sci. 2022, 260, 117838. [Google Scholar] [CrossRef]
- Leporini, M.; Marchetti, B.; Corvaro, F.; Giovine, G.; Polonara, F.; Terenzi, A. Sand transport in multiphase flow mixtures in a horizontal pipeline: An experimental investigation. Petroleum 2019, 5, 161–170. [Google Scholar] [CrossRef]
- Yao, R.; Wang, Z.; Huang, X. Design Parameters Investigation on Sand Transportation Characteristics of V-Inclined Pipe Based on Eulerian–Eulerian Two-Phase Flow Model. Water 2023, 15, 4266. [Google Scholar] [CrossRef]
- Lei, X.; Liao, Y.; Zhang, Q.; Wang, L.; Liao, Q. Numerical simulation of seed motion characteristics of distribution head for rapeseed and wheat. Comput. Electron. Agric. 2018, 150, 98–109. [Google Scholar] [CrossRef]
- Gu, F.; Zhao, Y.; Wu, F.; Hu, Z.; Shi, L. Simulation analysis and experimental validation of conveying device in uniform rushed straw throwing and seed-sowing Machines using CFD-DEM coupled approach. Comput. Electron. Agric. 2022, 193, 106720. [Google Scholar] [CrossRef]
- Zhou, F.; Hu, S.; Liu, Y.; Liu, C.; Xia, T. CFD-DEM simulation of the pneumatic conveying of fine particles through a horizontal slit. Particuology 2014, 16, 196–205. [Google Scholar] [CrossRef]
- Zhang, S.; Tekeste, M.; Li, Y.; Gaul, A.; Zhu, D.; Liao, J. Scaled-up rice grain modelling for DEM calibration and the validation of hopper flow. Biosyst. Eng. 2020, 194, 196–212. [Google Scholar] [CrossRef]
- Mansourpour, Z.; Karimi, S.; Zarghami, R.; Mostoufi, N.; Sotudeh-Gharebagh, R. Insights in hydrodynamics of bubbling fluidized beds at elevated pressure by DEM–CFD approach. Particuology 2010, 8, 407–414. [Google Scholar] [CrossRef]
- Gu, C.; Zhao, H.; Xu, B.; Yang, J.; Zhang, J.; Du, M.; Liu, Y.; Tikhankin, D.; Yuan, Z. CFD-DEM simulation of distribution and agglomeration characteristics of bendable chain-like biomass particles in a fluidized bed reactor. Fuel 2023, 340, 127570. [Google Scholar] [CrossRef]
- Saidi, M.; Tabrizi, H.B.; Grace, J.R.; Lim, C.J. Hydrodynamic investigation of gas-solid flow in rectangular spout-fluid bed using CFD-DEM modeling. Powder Technol. 2015, 284, 355–364. [Google Scholar] [CrossRef]
- El-Emam, M.; Zhou, L.; Shi, W.; Han, C.; Bai, L.; Agarwal, R. Theories and Applications of CFD–DEM Coupling Approach for Granular Flow: A Review. Arch. Comput. Methods Eng. 2021, 28, 4979–5020. [Google Scholar] [CrossRef]
- Wang, Z.; Teng, Y.; Liu, M. A semi-resolved CFD–DEM approach for particulate flows with kernel-based approximation and Hilbert curve-based searching strategy. J. Comput. Phys. 2019, 384, 151–169. [Google Scholar] [CrossRef]
- Nan, X.; Hou, J.; Shen, Z.; Tong, Y.; Li, G.; Wang, X.; Kang, Y. CFD-DEM coupling with multi-sphere particles and application in predicting dynamic behaviors of drifting boats. Ocean Eng. 2022, 247, 110368. [Google Scholar] [CrossRef]
- Brazhenko, V.; Mochalin, I. Terminal Velocity and Drag Coefficient of a Smooth Steel Sphere Moving in Water-Filled Vertical and Inclined Glass Pipes (Newton Regime). Powder Technol. 2024, 446, 120120. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, H.; Huang, J.; Lou, C.; Chen, Y.; Liu, L.; Zhang, T.; Chen, L. Design and parameter optimization of air-delivery auxiliary seed guide for pneumatic plate precision rapeseed metering device. Comput. Electron. Agric. 2025, 230, 109840. [Google Scholar] [CrossRef]
- Liu, D.; Qiao, C.; Wan, J.; Lu, Y.; Song, J.; Yao, Z.; Wei, X.; Yu, Y. Modelling method and application of anti-corrosion pill particles in oil and gas field wellbore casing annulus based on the discrete element method. Processes 2022, 10, 1164. [Google Scholar] [CrossRef]



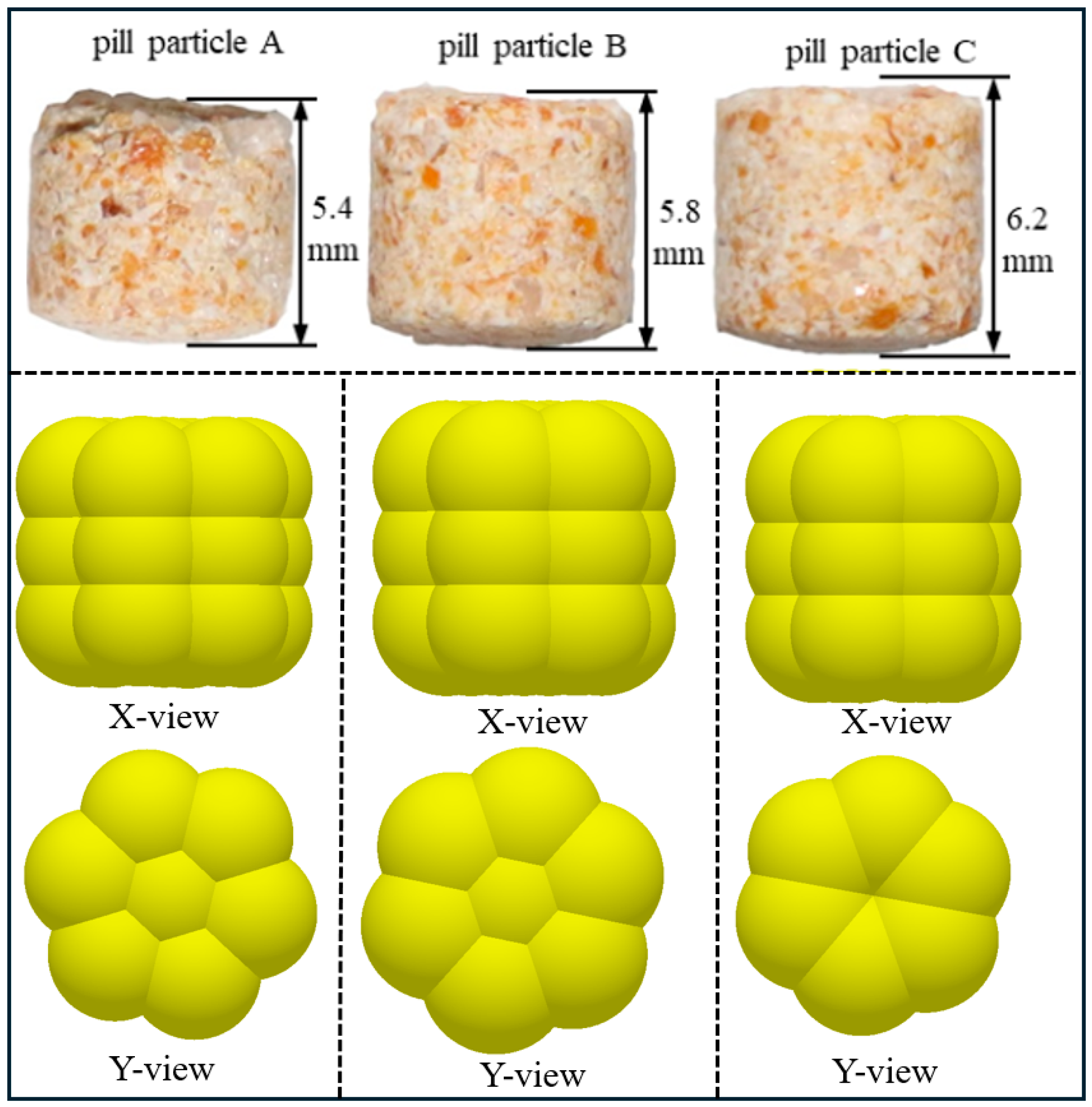





| Material | Parameter | Value |
|---|---|---|
| Pill particles | Density of Pill particles (kg/m3) | 1380 |
| Poisson’s ratio of pill particles | 0.25 | |
| Engineering plastics | Shear modulus of pill particles (Pa) | 2500.00 |
| Density of engineering plastics (kg/m3) | 1350 | |
| Poisson’s ratio of engineering plastics | 1 × 108 | |
| Pill particles and Pill particles | Shear modulus of engineering plastics (Pa) | 0.50 |
| Coefficient of restitution | 0.50 | |
| Coefficient of static friction | 0.05 | |
| Pill particles to engineering plastics | Coefficient of rolling friction | 0.5 |
| Coefficient of restitution | 0.5 | |
| Coefficient of static friction | 0.01 | |
| Gas phase | Coefficient of rolling friction | Air |
| Fluid/air | 1.225 | |
| Density (kg/m3) | 1.7894 × 10−5 | |
| Viscosity (kg/(m·s)) | 9.81 | |
| Gravitational acceleration (m/s2) | 9 × 10−6 | |
| Fixed time step of EDEM (s) | 9 × 10−4 | |
| Fixed time step of Fluent (s) | 9 |
| Factor | Level | ||
|---|---|---|---|
| −1 | 0 | 1 | |
| Airflow conveying orifice diameter h2 | 1 | 2 | 3 |
| Injection angle θ | 30 | 45 | 60 |
| Number of orifices N | 16 | 20 | 24 |
| NO | Airflow Conveying Orifice Diameter h1 (mm) | Injection Angle θ (°) | Number of Orifices N | Outlet Velocity (m/s) |
|---|---|---|---|---|
| 1 | 1 | 30 | 20 | 6.52 |
| 2 | 3 | 30 | 20 | 7.43 |
| 3 | 2 | 45 | 20 | 7.22 |
| 4 | 2 | 30 | 24 | 7.36 |
| 5 | 1 | 45 | 24 | 6.98 |
| 6 | 1 | 60 | 20 | 6.58 |
| 7 | 2 | 45 | 20 | 7.24 |
| 8 | 2 | 60 | 16 | 6.78 |
| 9 | 1 | 45 | 16 | 6.12 |
| 10 | 3 | 45 | 16 | 7.25 |
| 11 | 3 | 60 | 20 | 7.91 |
| 12 | 2 | 30 | 16 | 6.55 |
| 13 | 2 | 60 | 24 | 7.89 |
| 14 | 2 | 45 | 20 | 7.19 |
| 15 | 3 | 45 | 24 | 8.02 |
| 16 | 2 | 45 | 20 | 7.26 |
| 17 | 2 | 45 | 20 | 7.28 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 4.32 | 6 | 0.7205 | 164.07 | <0.0001 | significant |
| A-Airflow conveying orifice diameter | 2.43 | 1 | 2.43 | 553.60 | <0.0001 | |
| B- Injection angle | 0.2112 | 1 | 0.2112 | 48.11 | <0.0001 | |
| C-Number of orifices | 1.58 | 1 | 1.58 | 358.74 | <0.0001 | |
| AB | 0.0441 | 1 | 0.0441 | 10.04 | 0.0100 | |
| BC | 0.0225 | 1 | 0.0225 | 5.12 | 0.0471 | |
| A2 | 0.0386 | 1 | 0.0386 | 8.78 | 0.0142 | |
| Residual | 0.0439 | 10 | 0.0044 | |||
| Lack of Fit | 0.0390 | 6 | 0.0065 | 5.33 | 0.0636 | not significant |
| Pure Error | 0.0049 | 4 | 0.0012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Lu, Y.; Liu, D.; Xiao, Q.; Du, K.; Wei, X.; Yu, Y.; Zhang, H. Research and Experimentation on Pneumatic Particle Transport in Confined Spaces of Offshore Oil and Gas Wells Based on DEM-CFD Coupling Method. Processes 2025, 13, 3599. https://doi.org/10.3390/pr13113599
Song J, Lu Y, Liu D, Xiao Q, Du K, Wei X, Yu Y, Zhang H. Research and Experimentation on Pneumatic Particle Transport in Confined Spaces of Offshore Oil and Gas Wells Based on DEM-CFD Coupling Method. Processes. 2025; 13(11):3599. https://doi.org/10.3390/pr13113599
Chicago/Turabian StyleSong, Jiming, Yuliang Lu, Dongtao Liu, Qiaogang Xiao, Kezheng Du, Xinjie Wei, Yajun Yu, and Heng Zhang. 2025. "Research and Experimentation on Pneumatic Particle Transport in Confined Spaces of Offshore Oil and Gas Wells Based on DEM-CFD Coupling Method" Processes 13, no. 11: 3599. https://doi.org/10.3390/pr13113599
APA StyleSong, J., Lu, Y., Liu, D., Xiao, Q., Du, K., Wei, X., Yu, Y., & Zhang, H. (2025). Research and Experimentation on Pneumatic Particle Transport in Confined Spaces of Offshore Oil and Gas Wells Based on DEM-CFD Coupling Method. Processes, 13(11), 3599. https://doi.org/10.3390/pr13113599






