Spherical Fuzzy CRITIC–ARAS Framework for Evaluating Flow Experience in Metaverse Fashion Retail

Abstract

The Metaverse—an evolving convergence of virtual and physical realities—has emerged as a transformative platform, particularly within the fashion and retail industries. Its immersive nature aligns closely with the principles of flow theory, which describes the optimal psychological state of deep engagement and enjoyment. This study investigates the dynamics of fashion retail shopping in the Metaverse through a novel multi-criteria decision-making (MCDM) framework. Specifically, it integrates the CRITIC and ARAS methods within a spherical fuzzy environment to address decision-making under uncertainty. Flow theory is employed as the theoretical lens, with its dimensions serving as evaluation criteria. By incorporating spherical fuzzy sets, the model accommodates expert uncertainty more effectively. The findings provide empirical insights into the relative importance of flow constructs in shaping immersive consumer experiences in Metaverse-based retail environments. This study offers both theoretical contributions to the literature on digital consumer behavior and practical implications for fashion brands navigating immersive virtual ecosystems. Sensitivity analyses and comparative validation further demonstrate the robustness of the proposed framework.

1. Introduction

The rapid development of digital technologies has fundamentally transformed how consumers engage with brands. Among the most disruptive forces in this landscape is the Metaverse—an emerging paradigm derived from the fusion of “Meta,” denoting virtual transcendence, and “Universe,” representing the real world. According to Hollensen et al. [1], the Metaverse comprises a series of interconnected digital spaces where individuals navigate and interact through customized avatars using virtual and augmented reality.

The Metaverse is best described as a persistent and shared network of virtual environments that enable interaction, akin to real-world experiences [2,3]. It transcends simple virtual reality platforms, functioning as a nexus that bridges the physical and digital realms [4]. It is more precisely understood as a “network of interconnected experiences and applications, devices and products, tools and infrastructure” [5]. As a concept, it represents the evolution of 3D digital worlds that synthesize elements from both physical and virtual realities [3,6].

Forward-thinking platforms and major fashion brands have begun leveraging the Metaverse as a strategic marketing tool [7,8]. Recognizing its long-term significance, Facebook rebranded as Meta with a mission to “bring the Metaverse to life” [9]. Similarly, Microsoft announced initiatives to build its own immersive ecosystems [10].

With projections indicating growth from USD 68.49 billion in 2022 to USD 1.3 trillion by 2030, fashion retail stands as the third most impacted vertical, following media and finance. Brands such as Gucci, Ralph Lauren, and H&M have already launched virtual stores in the Metaverse [11]. These initiatives signal a transformative phase for the fashion and retail sectors, driven by immersive digital technologies [4,12].

Among the Metaverse’s defining traits is its capacity to deliver immersive customer experiences that closely align with the characteristics of flow theory. Flow is a psychological state of deep engagement, wherein individuals become so absorbed in an activity that they lose awareness of time and space. This state is particularly relevant in Metaverse environments, where users often report experiencing heightened levels of enjoyment and presence.

Despite increased industry interest, academic research remains limited on how the Metaverse shapes consumer engagement and brand strategy. Although studies by Park et al. [13] and Yi and Lee [14] have initiated dialog in this area, significant gaps remain. This paper addresses that gap by examining consumer experiences in fashion retail within the Metaverse, using flow theory as the conceptual lens and applying a fuzzy evaluation framework to analyze the relative impact of different flow dimensions.

2. Literature Review

Previous studies have indicated notable disparities in the objectives and actions of consumers in physical and virtual settings [15]. This implies that the existing knowledge and insights pertaining to consumer behaviors in real-life situations may not possess sufficient adequacy or applicability in the realm of the Metaverse. Conversely, there has been a lack of empirical investigation thus far that has examined the concept of flow as a framework for engagement within the Metaverse environment. This environment presents itself as a rich subject for examination due to its distinct characteristics. The utilization of avatars may elicit an enhanced sense of identification, the capabilities of the Metaverse environment may evoke a heightened sense of immersion, and the direct manipulation of objects may foster an increased sense of control—all of which are fundamental dimensions of flow theory.

This study provides multiple theoretical contributions. Firstly, owing to the recent emergence of the Metaverse, there exists a scarcity of research on it, particularly concerning the intersection between the fashion retail industry and the Metaverse, with the exception of the studies undertaken by Park et al. [13] and Yi and Lee [14]. The flow experience epitomizes the optimal state across consumption behaviors; hence, when consumers encounter flow, it effectively stimulates the actual act of purchasing [16]. Therefore, it makes sense to investigate the aforementioned phenomenon with flow theory because the immersive nature of the Metaverse makes flow theory a perfect fit for studying it in combination with this context. As such, using flow theory, which has received considerable interest among scholars, is an interesting research topic which has not been studied yet.

The flow experience encompasses various subconstructs, such as clear goals and feedback, a balance between challenges and skills, a distorted sense of time and place, autotelic and self-rewarding experiences, etc. This paper uses flow constructs to create an MCDM model. As such, this paper is also significant in that it is the first to develop a practical and ready-to-use MCDM model to assess the relative importance and weight of different flow subconstructs to help brands and decision makers in designing immersive brand experiences in the Metaverse context.

The objective of this research is to assess the relative importance of flow experience subconstructs within the context of fashion retail shopping in the Metaverse using a fuzzy approach. In doing so, this study aims to identify the key dimensions of flow theory that significantly influence consumer engagement and satisfaction in Metaverse-based fashion retail.

The problem statement can be formulated as follows: What is the relative importance of various dimensions of flow theory in the context of the Metaverse. Specifically, which aspects of flow theory, such as the challenge–skill balance, immediate feedback, etc., significantly impact consumer engagement and satisfaction in the Metaverse-based fashion retail setting?

This paper makes a notable contribution to the existing body of knowledge in that it represents a novel application of flow theory to the Metaverse, shedding light on the dynamics of consumer experiences in this emerging digital realm. This study also quantifies the relative importance of specific flow dimensions through empirical analysis and fuzzy modeling in the context of fashion retail shopping in the Metaverse. In sum, this paper enriches the academic discourse by bridging the domains of flow theory, the Metaverse, and fuzzy decision-making, yielding both theoretical contributions and actionable insights for businesses. It advances our understanding of how consumers interact with the Metaverse and offers guidance for adapting marketing strategies to meet the demands of this transformative digital environment.

2.1. Augmented Reality, Virtual Reality, and Metaverse Concepts

Augmented Reality (AR): The advancement of technology has brought a transformation in consumers’ engagement with brands. One notable technology in this realm is augmented reality (AR), which facilitates novel forms of interaction between consumers and brands [17]. The utilization of AR applications has experienced a surge in popularity, particularly with respect to virtual try-on experiences offered by prestigious brands like Zara, Nike, Sephora, Gucci, and the furniture brand IKEA. Papagiannis [18] discovered that products incorporating AR features exhibit a 94% higher rate of consumer interaction compared to those lacking such features.

Virtual Reality (VR): Virtual reality (VR) is a concept that denotes a digitally produced setting that an individual can navigate through employing specialized electronic equipment. The primary objective of VR is to induce a sense of actual presence in the user by immersing them within the simulated environment.

In recent years, there has been growing interest in the use of VR for fashion retail shopping. VR can be used to create a more immersive and interactive shopping experience for customers, allowing them to try on clothes and accessories virtually before making a purchase. Being able to interact with the products using the simulated sense of touch can make it possible to perceive the product’s usefulness [19].

The extant literature has found out that consumer entertainment, realistic atmospheres, a feeling of presence, and perceived control increase buying intentions, and price sensitivity is perceived to be less important in VR contexts [20,21,22,23,24]. Based on the technological developments, some VR characteristics, such as a heightened sense of presence and higher user control, increase technology acceptance and courage to try VR [25]. These characteristics also start a pleasurable state of flow in which consumers perceive that time passes fast, which as a result contributes to the overall entertainment related to the experience.

Metaverse: The Metaverse, in its broadest sense, refers to a collective virtual shared space that is created by the convergence of multiple digital platforms, technologies, and interactions. It is envisioned as a fully immersive and interactive virtual reality space where users can engage with each other and the environment in various ways. The Metaverse is a concept that extends beyond the scope of both augmented reality (AR) and virtual reality (VR) individually. While AR and VR technologies can contribute to the development and realization of the Metaverse, the Metaverse itself encompasses a broader concept.

The imminent years are expected to witness the disruption of various industries by the Metaverse. The fashion industry is definitely not excluded from this phenomenon. In the year 2021, Nike completed the acquisition of RTFKT, a company renowned for its creation of virtual sneakers and digital artifacts, with the aim of expediting its digital transformation within the Metaverse. According to a recent report, leading brands such as Nike, Dolce & Gabbana, and Tiffany have amassed a substantial revenue of 232 million through non-fungible tokens [26]. Additionally, esteemed brands including Gucci, Ralph Lauren, and H&M have introduced virtual stores on the gaming platform Roblox, wherein they sell exclusively digital clothing and accessories [11]. Consequently, the fashion and retail sectors are capitalizing on the Metaverse to advance their marketing strategies, primarily by offering digital products and immersive brand experiences.

Although it has been foreseen that the Metaverse will bring forth notable transformations in the realm of fashion and retail [4,12], a consensus regarding its essence and its manifestation within the fashion industry remains elusive. Moreover, there exists a scarcity of scholarly investigations into the effects of the Metaverse on the marketing strategies and brand experiences of fashion labels. Recognizing the urgent demand for research pertaining to Metaverse-related matters in the fashion industry, this study endeavors to elucidate the scope of the Metaverse by concentrating on its function within the fashion domain and proposes a research agenda aimed at scrutinizing the concept of the Metaverse within the field of fashion.

2.2. Flow Experience

Flow theory, initially formulated by Csikszentmihalyi [27], has garnered considerable attention from scholars in various fields, particularly in recent times. The flow experience, which entails a mental state characterized by complete concentration, absorption, and engagement in an activity, is also commonly referred to as flow state. This phenomenon can be described as a comprehensive sensation individuals experience when they are fully engrossed in an activity. In the state of flow, individuals are fully engrossed and driven to pursue the given activity, which has been associated with a diminished self-awareness, intense focus on the task at hand, and an overall sense of enjoyment according to Csikszentmihalyi’s work [27]. Those in a state of flow have reported being deeply interested, experiencing profound pleasure, and perceiving time to pass at an accelerated pace [28].

According to Hoffman and Novak [29], the pivotal element of the flow concept is the complete concentration and immersion in an activity. Chen et al. [30] argue that people experiencing flow often describe deep joy, intense interest, focused attention, and a sense that time is passing quickly.

The captivating experience known as “flow” has been shown to influence consumer behavior [31]. According to earlier research [32,33,34], being in a state of flow produces particular behavioral results. Hoffman and Novak [35] hypothesized that people who engage in flow states would be more satisfied and loyal than non-users. According to Koufaris’s theory [36], customers who experience flow when shopping online are more inclined to make impulsive purchases.

There is little research on the experience of flow in the Metaverse environment in the extant literature. Holdack et al. [37] argued that immersive technologies generally aim to provide users with a pleasant and engaging experience.

Parker et al. [13] investigated the role of mediators of Metaverse flow experiences in fashion products and found, among other things, that telepresence (referring to the feeling of being in a virtual environment) has a significant effect on users’ flow experience.

2.3. Spherical Fuzzy Sets

Spherical fuzzy sets [38], an extension of ordinary fuzzy sets, introduce a three-dimensional spherical geometry that enables the independent assignment of membership, non-membership, and hesitancy parameters within a large domain. This unique feature has garnered significant attention from scholars, making spherical fuzzy sets increasingly popular for addressing various decision-making problems across diverse domains.

Several researchers have applied spherical fuzzy sets to well-established decision-making methods in order to solve an advertisement strategy selection problem [39], prioritize expert evaluations in the context of a public transport business model [40], address prioritization problems in career management activities [41], evaluate building contractors [42], and select suppliers [43].

Spherical fuzzy sets have also been integrated with various other MCDM methods. Mathew et al. combined the AHP with TOPSIS to address a manufacturing system selection problem [44]. Ayyildiz and Taskin Gumus [45], as well as Otay et al. [46], presented AHP WASPAS models for applications in petrol station location and outsource manufacturer selection problems. Atak et al. [47] tackled a vessel engine selection problem by integrating interval-valued spherical fuzzy AHPs with TOPSIS. Additionally, Oztaysi et al. [48] combined the AHP with VIse KriterijumsaOptimiz acija I Kompromisno Resenje (VIKOR) for an advertisement selection problem.

2.4. The CRITIC Method

In MCDM problems, determining the weights of criteria is a crucial step that significantly influences the model’s outcome. The CRITIC method [49] is commonly employed to calculate the objective weights of criteria. This method relies on the analysis of an evaluation matrix, capturing all preference information inherent in the criteria. CRITIC quantifies the intrinsic information of each criterion to achieve its objective weight. The contrast intensity of the criteria, approximated as the standard deviation, is used to evaluate the objective weight, while conflicts between criteria are calculated using the correlation coefficient. This method has proven successful in various real-world MCDM applications.

Researchers have extended and adapted the CRITIC method for specific applications, such as software selection [50], prequalification for construction contractors [51], and block-chain evaluations [52].

In addition to crisp environments, researchers have applied CRITIC in fuzzy and probabilistic contexts, including for determining investment alternative weights [53], evaluating sustainable supply chain risk management [54], logistics provider selection [55,56], ranking supplier selection criteria [57], smartphone addiction assessment [58], the selection of additive manufacturing processes for automotive industry [59] to assess agriculture crops [60], and green building energy-saving solutions [61].

These studies collectively showcase the versatility and applicability of the CRITIC method across diverse domains, providing effective solutions to complex decision-making problems in uncertain and fuzzy environments.

2.5. ARAS Method

ARAS [62] is an MCDM technique designed to evaluate the performance of predetermined alternatives by comparing each with the ideal alternative using a utility function. Fuzzy ARAS techniques have gained popularity among scholars for handling decision-making problems in uncertain environments. Fuzzy ARAS methods have been applied in various contexts, such as selecting a location for a recycling facility [63], evaluating the seismic vulnerability of buildings [64,65], the selection of e-learning courses [66], choosing a COVID-19 testing laboratory [67], and assessing logistics performances of countries [68] and digital maturity levels of companies [69].

Heidary Dahooie et al. [70] took a different approach by integrating data envelopment analysis with ARAS in a triangular fuzzy environment to prioritize human resource practices, showcasing the flexibility of the ARAS method in combination with other techniques for various applications [70]. These diverse applications illustrate the effectiveness of the ARAS method and its fuzzy extensions in handling decision-making problems across different domains and levels of uncertainty.

Upon reviewing the existing literature, it becomes evident that the integration of the CRITIC and ARAS methods within a spherical fuzzy context has not been previously introduced. This research uniquely combines the CRITIC and ARAS methods within a spherical fuzzy framework, highlighting the synergies between these two approaches and leveraging the benefits offered by spherical fuzzy sets.

3. Materials and Methods

3.1. Spherical Fuzzy Set

The definition, basic operators, aggregation operator, normalized Euclidean distance [38], and defuzzification operator [71] of spherical fuzzy sets are provided below:

Definition 1.

A spherical fuzzy set [38] $\widetilde{A_S}$ of the universe of discourse ∪ is given in Equation (1).

$$\widetilde{A_S}=\{\mathrm{u},{\mathsf{\mu }}_{\widetilde{A_S}}\left(u\right),{\mathsf{\nu }}_{\widetilde{A_S}}\left(u\right),{\mathsf{\pi }}_{\widetilde{A_S}}\left(u\right)\mid u\in \cup \}$$

(1)

where

$$0\le {\mathsf{\mu }}_{\widetilde{{\mathrm{A}}_{\mathrm{S}}}}^2\left(\mathrm{u}\right)+{\mathsf{\nu }}_{\widetilde{{\mathrm{A}}_{\mathrm{S}}}}^2\left(\mathrm{u}\right)+{\mathsf{\pi }}_{\widetilde{{\mathrm{A}}_{\mathrm{S}}}}^2\left(\mathrm{u}\right)\le 1;\forall \mathrm{u}\in$$

(2)

Equation (2) is presented below for the surface of the sphere:

$${\mathsf{\mu }}_{\widetilde{A_S}}^2\left(u\right)+{\mathsf{\nu }}_{\widetilde{A_S}}^2\left(u\right)+{\mathsf{\pi }}_{\widetilde{A_S}}^2\left(u\right)=1;\forall u\in \cup$$

(3)

Definition 2.

The addition, multiplication, multiplication by a scalar, and power of spherical fuzzy sets are given as follows:

• The addition of two spherical fuzzy sets [38] is given in Equation (4).

  $$\begin{array}{c}\widetilde{A_S}\oplus \widetilde{B_S}=\{({\mu }_{\widetilde{A_S}}^2+{\mu }_{\widetilde{B_S}}^2-{\mu }_{\widetilde{A_S}}^2{\mu }_{\widetilde{B_S}}^2{)}^{1/2},{\nu }_{\widetilde{A_S}}^2{\nu }_{\widetilde{B_S}}^2,\\ ((1-{\mu }_{\widetilde{B_S}}^2){\pi }_{\widetilde{A_S}}^2+(1-{\mu }_{\widetilde{A_S}}^2){\pi }_{\widetilde{B_S}}^2-{\pi }_{\widetilde{A_S}}^2{\pi }_{\widetilde{B_S}}^2{)}^{1/2}\}\end{array}$$

  (4)
• The multiplication of two spherical fuzzy sets [38] is given in Equation (5).

  $$\begin{array}{c}\widetilde{A_S}\otimes \widetilde{B_S}={\{\mu }_{\widetilde{A_S}}{\mu }_{\widetilde{B_S}},({\nu }_{\widetilde{A_S}}^2+{\nu }_{\widetilde{B_S}}^2-{\nu }_{\widetilde{A_S}}^2{\nu }_{\widetilde{B_S}}^2{)}^{1/2},\\ ((1-{\nu }_{\widetilde{B_S}}^2){\pi }_{\widetilde{A_S}}^2+(1-{\nu }_{\widetilde{A_S}}^2){\pi }_{\widetilde{B_S}}^2-{\pi }_{\widetilde{A_S}}^2{\pi }_{\widetilde{B_S}}^2{)}^{1/2}\}\end{array}$$

  (5)
• The multiplication of a spherical fuzzy number by a scalar (λ > 0) [38] is given in Equation (6).

  $$\begin{array}{c}\lambda \cdot \widetilde{A_S}=\{\{(1-(1-{\mu }_{\widetilde{A_S}}^2{)}^{\lambda }{)}^{1/2},{\nu }_{\widetilde{A_S}}^{\lambda },\\ ((1-{\mu }_{\widetilde{A_S}}^2{)}^{\lambda }-(1-{\mu }_{\widetilde{A_S}}^2-{\pi }_{\widetilde{A_S}}^2{)}^{\lambda }{)}^{1/2}\}\end{array}$$

  (6)
• The λ th power of $\widetilde{A˜S}$ (λ > 0) for a spherical fuzzy number [38] is given in Equation (7).

  $$\begin{array}{c}{\widetilde{A_S}}^{\lambda }=\{\{{\mu }_{\widetilde{A_S}}^{\lambda },(1-(1-{\nu }_{\widetilde{A_S}}^2{)}^{\lambda }{)}^{1/2},\\ ((1-{\nu }_{\widetilde{A_S}}^2{)}^{\lambda }-(1-{\nu }_{\widetilde{A_S}}^2-{\pi }_{\widetilde{A_S}}^2{)}^{\lambda }{)}^{1/2}\}\end{array}$$

  (7)

It is important to ensure that operations on spherical fuzzy numbers do not violate the fundamental constraint μ2 + ν2 + π2 ≤ 1μ² + ν² + π²\leq 1μ² + ν² + π² ≤ 1.

Therefore, in this study, we restrict scalar values of λ to λ ≥ 1 during scalar multiplication (Equation (6)) and exponentiation (Equation (7)) to guarantee constraint preservation. This follows the guidance of Akdag et al. [72], where lower values of λ may lead to values exceeding the unit sphere boundary, especially when μ, ν, or π are close to 1.

Definition 3.

The aggregation operation is a function that is used in those situations when we need to find a single value representing the set of various numbers. An aggregation operator converts a number of input data into a single value. In this study, a geometric mean operator (GM) [38] is used for aggregating the matrices. The geometric mean of n spherical fuzzy numbers is given in Equation (8).

$$\begin{array}{c}{\widetilde{G{M}_w}(\widetilde{A_{S1}},\dots ,\widetilde{A_{Sn}})=\widetilde{A_{S1}}}^{w_1}+{\widetilde{A_{S2}}}^{w_2}+\dots .+\\ {\widetilde{A_{Sn}}}^{w_n}=\{{\prod }_{i=1}^n{\mu }_{\widetilde{A_{Si}}}^{w_j},[1-{\prod }_{i=1}^n(1-{\nu }_{\widetilde{A_{Si}}}^2{)}^{w_j}{]}^{1/2},\\ [{\prod }_{i=1}^n(1-{\nu }_{\widetilde{A_{Si}}}^2{)}^{w_j}-{\prod }_{i=1}^n(1-{\nu }_{\widetilde{A_{Si}}}^2-{\pi }_{\widetilde{A_{Si}}}^2{)}^{w_j}{]}^{1/2}\}\end{array}$$

(8)

where w = (w₁, w₂, …, w_n); w_j ∈ [0, 1]; and ∑ⁿ_i=1 w_j = 1.

Definition 4.

Fuzzification refers to the process of converting a precise numerical value into its corresponding fuzzy representation, while defuzzification is the reverse operation that involves transforming a fuzzy number back into a crisp, precise form [73]. The defuzzification operator, i.e., score function for spherical fuzzy sets [71], is given in Equation (9).

$$\mathrm{S}(\mathrm{A}~\mathrm{S})=\mathsf{\mu }-\mathsf{\nu }(1-\mathsf{\pi })$$

(9)

Definition 5.

The normalized Euclidean distance is a distance measure used for calculating the differences between two elements, two sets, etc. In fuzzy set theory, it can be useful, for example, for the calculation of distances between fuzzy sets [74]. The normalized Euclidean distance between two spherical fuzzy numbers [38] is given in Equation (10).

$$D\left(\widetilde{A_S},\widetilde{B_S}\right)=\sqrt{{\displaystyle \frac{1}{2n}}{\sum }_{i=1}^n\left({\left({\mathsf{\mu }}_{\widetilde{A_S}}-{\mathsf{\mu }}_{\widetilde{B_S}}\right)}^2+{\left({\mathsf{\nu }}_{\widetilde{A_S}}-{\mathsf{\nu }}_{\widetilde{B_S}}\right)}^2+{\left({\mathsf{\pi }}_{\widetilde{A_S}}-{\mathsf{\pi }}_{\widetilde{B_S}}\right)}^2\right)}$$

(10)

3.2. Proposed Spherical Fuzzy CRITIC ARAS

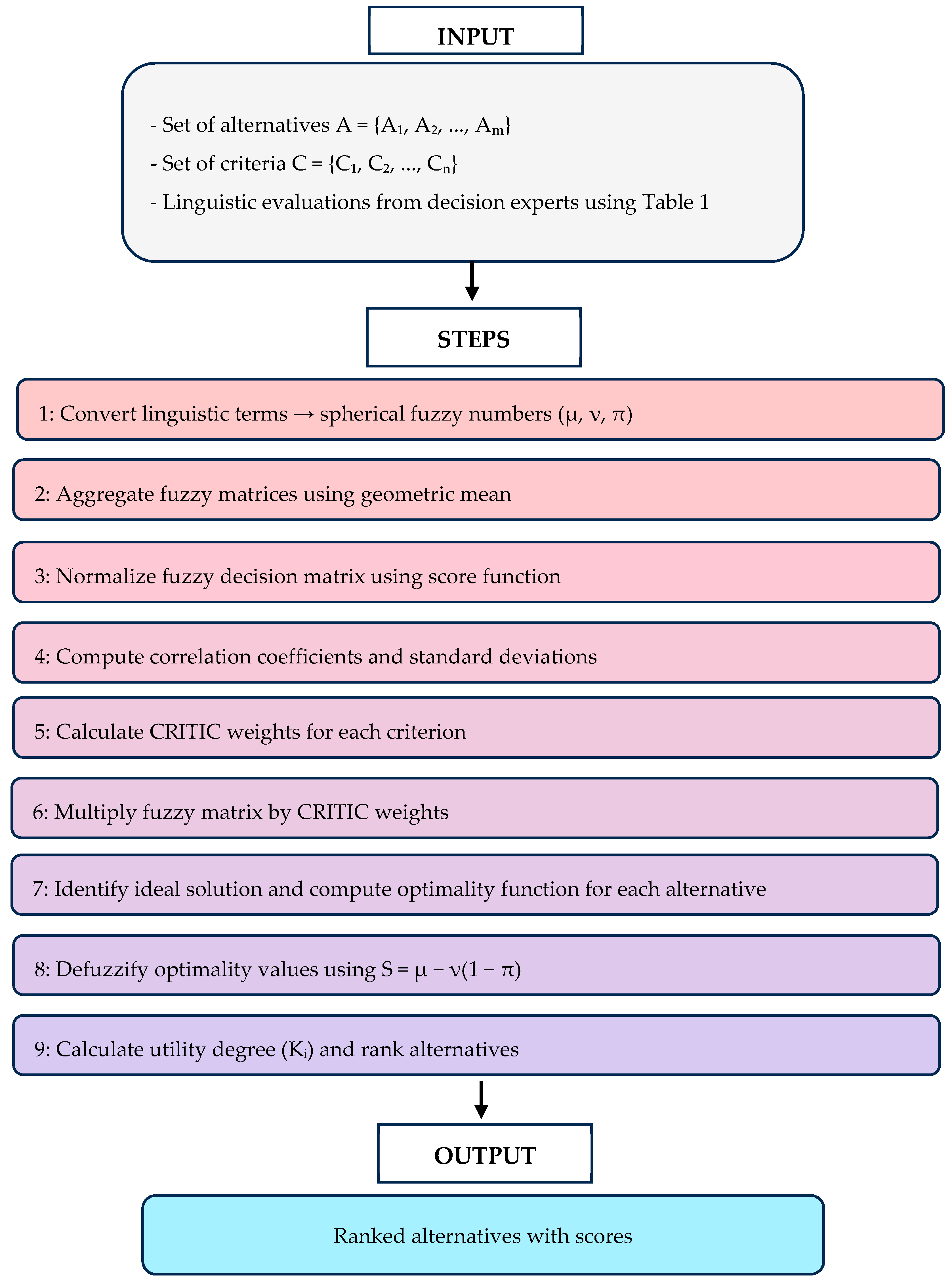
This section provides a systematic presentation of the proposed spherical fuzzy CRITIC ARAS, outlining each step in a clear and organized manner. Prior to providing the details, an overview of each step can be seen collectively in Figure 1.

Stage 1. Obtaining criterion weights through spherical fuzzy CRITIC method.

Step 1.1 The decision experts evaluate the alternatives with respect to the criteria by utilizing the linguistic terms that are developed for spherical fuzzy sets [38], as in

Table 1. Linguistic terms and their corresponding spherical fuzzy numbers [38].

Linguistic Term	µ	ν	π
Absolutely more importance (AMI)	0.9	0.1	0.1
Very high importance (VHI)	0.8	0.2	0.2
High importance (HI)	0.7	0.3	0.3
Slightly more importance (SLI)	0.6	0.4	0.4
Equally importance (EI)	0.5	0.4	0.5
Slightly low importance (SLI)	0.4	0.6	0.4
Low importance (LI)	0.3	0.7	0.3
Very low importance (VLI)	0.2	0.8	0.2
Absolutely low importance (ALI)	0.1	0.9	0.1

.

In Table 1, µ, ν, and π represent the membership, non-membership, and hesitancy degrees, respectively.

Step 1.2 As can be seen in Figure 2, the linguistic evaluations of each decision expert are transformed into spherical fuzzy numbers in matrix form. The linguistic scale that is given in Table 1 is used for the conversion operation. Then, all matrices are aggregated to obtain one unique collective matrix, which is called spherical fuzzy alternative evaluation matrix $\tilde{K}$. The geometric aggregation operator, $\tilde{G}$, provided in Equation (8) is used for aggregating the matrices obtained from the decision experts. The structure of this matrix is given in Equation (11).

$$\tilde{K}=C_j(A_i{)}_{mxn}=\left[\begin{array}{cccc}{\tilde{k}}_{11}& {\tilde{k}}_{12}& \dots & {\tilde{k}}_{1n}\\ {\tilde{k}}_{21}& {\tilde{k}}_{22}& \dots & {\tilde{k}}_{2n}\\ \dots & \dots & \dots & \\ {\tilde{k}}_{m1}& {\tilde{k}}_{m2}& \dots & {\tilde{k}}_{mn}\end{array}\right]$$

(11)

where $k˜ij=\mathsf{\mu }ij,\nu ij,\pi ij$ is the spherical fuzzy element of the evaluation matrix; the evaluation of alternative $Ai(i=1,2,\dots ,m)$ with respect to criterion $Cj(j=1,2,\dots ,n)$ is donated by $\tilde{K}=\left(Cj\right(Ai\left)\right)mxn$ in a spherical fuzzy matrix, and µ_ij, ν_ij, and π_ij are the membership, non-membership, and hesitancy degrees for the ith alternative and jth criterion.

While the spherical fuzzy CRITIC method employs expert assessments using linguistic terms, the transformation of these evaluations into crisp weights is performed through statistical measures—standard deviation and correlation—embedded within the CRITIC approach. This reduces subjectivity significantly. The aggregated fuzzy evaluation matrix is first normalized and then processed to compute the contrast intensity and conflict via correlation coefficients. Hence, although initial inputs involve subjective linguistic evaluations, the CRITIC method translates these into objective weights through a mathematically grounded process that minimizes human bias.

Step 1.3 $\tilde{K}$ is normalized by utilizing Equations (12) and (13) for positive and negative attributes, respectively.

$$x_{ij}={\displaystyle \frac{\sqrt{\frac{1}{2}\{({\mu }_{{\tilde{k}}_{ij}}-{\mu }_{{\tilde{k}}_i^{-}}{)}^2+({\nu }_{{\tilde{k}}_{ij}}-{\nu }_{{\tilde{k}}_i^{-}}{)}^2+({\pi }_{{\tilde{k}}_{ij}}-{\pi }_{{\tilde{k}}_i^{-}}{)}^2)\}}}{\sqrt{\frac{1}{2}\{({\mu }_{{\tilde{k}}_i^{+}}-{\mu }_{{\tilde{k}}_i^{-}}{)}^2+({\nu }_{{\tilde{k}}_i^{+}}-{\nu }_{{\tilde{k}}_i^{-}}{)}^2+({\pi }_{{\tilde{k}}_i^{+}}-{\pi }_{{\tilde{k}}_i^{-}}{)}^2)\}}}}$$

(12)

$$x_{ij}={\displaystyle \frac{\sqrt{\frac{1}{2}\{({\mu }_{{\tilde{k}}_{ij}}-{\mu }_{{\tilde{k}}_i^{+}}{)}^2+({\nu }_{{\tilde{k}}_{ij}}-{\nu }_{{\tilde{k}}_i^{+}}{)}^2+({\pi }_{{\tilde{k}}_{ij}}-{\pi }_{{\tilde{k}}_i^{+}}{)}^2)\}}}{\sqrt{\frac{1}{2}\{({\mu }_{{\tilde{k}}_i^{-}}-{\mu }_{{\tilde{k}}_i^{+}}{)}^2+({\nu }_{{\tilde{k}}_i^{-}}-{\nu }_{{\tilde{k}}_i^{+}}{)}^2+({\pi }_{{\tilde{k}}_i^{-}}-{\pi }_{{\tilde{k}}_i^{+}}{)}^2)\}}}}$$

(13)

where i = 1, 2, …, m; j = 1, 2, …, n; x_ij is the normalized value of k˜i j; k˜+ = max(k˜1, k˜2, …, k˜m), and k˜− = min(k˜1, k˜2, …, k˜m).

k˜+ and k˜− are found by comparing the crisp values of the attributes. The score function in Equation (9), S = μ − ν(1 − π)S = μ − ν(1 − π)S = μ − ν(1 − π), is used to obtain the crisp values for normalization.

Step 1.4 The correlation coefficient ρ_jk between each attribute pair is calculated by utilizing Equation (14).

$${\rho }_{jk}={\displaystyle \frac{\sum _{i=1}^m(x_{ij}-{\overline{x}}_j)(x_{ik}-{\overline{x}}_k)}{\sqrt{\sum _{i=1}^m(x_{ij}-{\overline{x}}_j{)}^2\sum _{i=1}^m(x_{ik}-{\overline{x}}_k{)}^2}}}$$

(14)

where ${\overline{x}}_j$ and ${\overline{x}}_k$ are the mean values of jth and kth attributes, and ${\overline{x}}_j$ is obtained by utilizing Equation (15). ${\overline{x}}_k$ is also obtained in the same way.

$$\overline{x_j}={\displaystyle \frac{1}{n}}{\sum }_{j=1}^n{x}_{ij},i=\mathrm{1,2},\dots ,m$$

(15)

Step 1.5 The standard deviation σ_j of each criterion is calculated as given in Equation (16).

$${\sigma }_j=\sqrt{{\displaystyle \frac{1}{m}}\sum _{i=1}^m(x_{ij}-{\overline{x}}_j{)}^2}$$

(16)

where

“m: number of alternatives”;

“x_ij: normalized value of alternative A_i under criterion C_j”;

“${\overline{x}}_j$: mean of criterion j across all alternatives”.

Step 1.6 The C index is obtained in the same way as in Equation (17).

$$C_j={\mathsf{\sigma }}_{j{\sum }_{k=1}^n\left(1-{\mathsf{\rho }}_{jk}\right)},j=\mathrm{1,2},\dots ,n$$

(17)

Step 1.7 Criterion weights are obtained as given in Equation (18).

$$w_j={\displaystyle \frac{C_j}{{\sum }_{j=1}^n{C}_j}}$$

(18)

Stage 2 Ranking of alternatives by utilizing spherical fuzzy ARAS.

Step 2.1 Spherical fuzzy decision matrix is obtained by multiplying spherical fuzzy alternative evaluation matrix by criterion weights. Multiplication by a scalar operator that is given in Equation (6) is used for the multiplication operation.

Step 2.2 Determine the spherical fuzzy ideal solution based on score and accuracy values of attributes in spherical fuzzy decision matrix. The score values are calculated using the standard defuzzification formula S = μ − ν(1 − π)S = μ − ν(1 − π)S = μ − ν(1 − π), and the accuracy values are derived from Euclidean distance (Equation (10)).

Step 2.3 Determine the spherical fuzzy optimality function values ($\widetilde{O_i}$) for all alternatives, as well as for the spherical fuzzy ideal solution $\widetilde{O_o}$ as given in Equations (19) and (20).

$$\widetilde{O_i}=\left({\mathsf{\mu }}_{i1},{\mathsf{\nu }}_{i1},{\mathsf{\pi }}_{i1}\right)+\left({\mathsf{\mu }}_{i2},{\mathsf{\nu }}_{i2},{\mathsf{\pi }}_{i2}\right)+\dots +\left({\mathsf{\mu }}_{in},{\mathsf{\nu }}_{in},{\mathsf{\pi }}_{in}\right)$$

(19)

where $\widetilde{O_i}$ gives the optimality function value for the ith alternative, and n is the number of criteria. Thus µ_i1, ν_i1, and π_i1 are the membership, non-membership, and hesitancy for the first criterion of the ith alternative and so on.

$$\widetilde{O_i}=\left({\mathsf{\mu }}_{o1},{\mathsf{\nu }}_{o1},{\mathsf{\pi }}_{o1}\right)+\left({\mathsf{\mu }}_{o2},{\mathsf{\nu }}_{o2},{\mathsf{\pi }}_{o2}\right)+\dots +\left({\mathsf{\mu }}_{on},{\mathsf{\nu }}_{on},{\mathsf{\pi }}_{on}\right)$$

(20)

where $\widetilde{O_O}$ gives the optimality function value for the ideal solution, and n is the number of criteria. Thus µ_1∗, ν_2∗, and π_3∗ are the membership, non-membership, and hesitancy for the first criterion of the ideal solution.

Spherical fuzzy addition operator that is given in Equation (4) is used for calculating $\widetilde{O_i}$ and $\widetilde{O_o}$.

Step 2.4 Defuzzify and obtain crisp form of O~iÕ_iO~i and O~0Õ₀O~0. Then calculate the utility degree KiK_iKi of an alternative AiA_iAi by comparing the score values.

The defuzzification uses the updated score function S = μ − ν(1 − π)S = μ − ν(1 − π)S = μ − ν(1 − π) from Equation (9) to ensure consistency and interpretability.

$$K_i={\displaystyle \frac{O_i}{O_o}}$$

(21)

where O_i and O_o are the optimality criterion values for ith and ideal alternatives.

Step 2.5 Rank the alternatives according to utility degrees (K_i) of the alternatives. The higher the utility value, the better the alternative.

4. Application and Results

4.1. The Criteria Set of the Problem

This study uses flow constructs as the criteria set. Many authors used a set of different related constructs in different contexts [36,75]. Although different scholars use slightly different yet similar constructs, a unified measurement of flow has not been established within the extant literature, see [29,35,76,77].

For the sake of this study, the following flow constructs have been taken into con-sideration, which also serve as the criteria set in the MCDM model developed in this study: 1. There is direct and immediate feedback during the activity. (FDBK) 2. There is a balance between the activity challenge and individual skill. (CHSK) 3. An individual exhibits complete concentration on the task with focused attention. (CTRN) 4. The merging of action and awareness, a temporary Loss of Place, is experienced. (LPLC) 5. There is an Altered Sense of Time; one’s experience of time is altered. (LTIM) 6. The individual has a temporary Loss of Self-Consciousness or ego. (LSLF) 7. A feeling of control over the situation or activity. (CTRL) 8. The activity is an autotelic, intrinsically rewarding experience. (AUTO)

The criteria set is defined in detail below:

C1 Clear goals: Clear goals refer to the extent to which the individual knows what they are trying to achieve and what the rewards are for achieving it. A clear goal provides a sense of direction and purpose, which can help to focus attention and motivation [27].

C2 Immediate feedback: Immediate feedback denotes the extent to which an individual receives feedback on their performance. The provision of immediate feedback aids in sustaining individuals’ engagement and motivation by enabling them to comprehend their performance and effectuate adjustments when deemed necessary [78]. This phenomenon encompasses an individual’s capacity to receive prompt feedback pertaining to their conduct.

C3 Challenge–skill balance: The challenge–skill balance refers to the degree to which a task is challenging but not too difficult. If the task is too simple, flow will not be experienced by the person, and stimulation will not take place. If the task is too difficult, the individual will become frustrated and give up [27].

C4 Complete concentration on the task: Complete concentration on the task refers to the extent to which a person is fully focused on the task at hand. When an individual is in a state of flow, they are so engrossed in a task that they are not aware of their surroundings or other distractions [27].

C5 Loss of Place: Loss of Place refers to an individual’s experience of losing time and space when one is fully focused on a task. It can be defined as “the degree to which an individual loses awareness of his surroundings and his body”. This definition appears to be the centerpiece of the Metaverse idea [27].

C6 Altered Sense of Time: Altered Sense of Time (transformation of time, speeding up/slowing down) refers to an individual’s different experience of the passage of time as it flows. It can be defined as “the degree to which a person experiences time passing more quickly or more slowly than usual” [27].

C7 Losing self-consciousness: Losing self-consciousness (the seamless merging of actions and awareness) is the experience of an individual losing their sense of self and full focus on a task. It can be defined as “the degree to which an individual loses awareness of himself as an independent entity” [27].

C8 Feeling of control over the task: The feeling of control over the task refers to a person’s feeling that they are in control of a task and can achieve their goals. It can be defined as “the extent to which a person feels that he or she is in control of a situation and able to achieve goals” [27].

C9 Autotelic: An autotelic, intrinsically rewarding experience is when a person perceives an activity as intrinsically rewarding, regardless of any extrinsic benefits. It can be defined as “the extent to which individuals believe that activities are intrinsically rewarding and do not require any external reward to motivate them” [27].

Step 1.1 The alternatives are evaluated as in

Table 2. Linguistic evaluations of alternatives.

Decision Expert	Alternative	C1	C2	C3	C4	C5	C6	C7	C8	C9
DM1	A1	SMI	VHI	EI	SMI	VHI	VHI	VHI	VHI	VHI
	A2	EI	SMI	SMI	VLI	E	VHI	VHI	VHI	VHII
	A3	HI	VHI	VLI	VHI	SMI	VHI	VHI	VHI	VHI
	A4	HI	VHI	VLI	VHI	SMI	VHI	VHI	VHI	VHI
	A5	SMI	EI	SLI	SMI	SLI	VHI	VHI	VHI	VHI
DM2	A1	VHI	VHI	SMI	SMI	SMI	VHI	VHI	VHI	VHI
	A2	SLI	HI	SMI	SLI	EI	VHI	VHI	VHI	VHI
	A3	VHI	HI	SLI	HI	HI	VHI	VHI	VHI	VHI
	A4	HI	VHI	VLI	VHI	SMI	VHI	VHI	VHI	VHI
	A5	SMI	SMI	SLI	SLI	SMI	VHI	VHI	VHI	VHI
DM3	A1	SMI	AMI	EI	SMI	HI	VHI	VHI	VHI	VHI
	A2	EI	SMI	VHI	LI	SLI	VHI	VHI	VHI	VHI
	A3	AMI	SLI	EI	SMI	SMI	VHI	VHI	VHI	VHI
	A4	HI	VHI	VLI	VHI	SMI	VHI	VHI	VHI	VHI
	A5	EI	SLI	VLI	SMI	SLI	VHI	VHI	VHI	VHI

.

Step 1.2 The spherical fuzzy alternative evaluation matrix is obtained as in

Table 3. Spherical fuzzy alternative evaluation matrix.

	C1	C2	C3	C4	C5	C6	C7	C8	C9
A1	(0.58;0.44;0.35)	(0.80;0.20;0.20)	(0.68;0.30;0.36)	(0.50;0.40;0.50)	(0.46;0.48;0.47)	(0.70;0.30;0.30)	(0.38;0.63;0.33)	(0.40;0.60;0.40)	(0.52;0.48;0.40)
A2	(0.43;0.55;0.43)	(0.70;0.31;0.32)	(0.29;0.71;0.30)	(0.40;0.60;0.40)	(0.25;0.75;0.26)	(0.52;0.46;0.42)	(0.29;0.71;0.30)	(0.49;0.48;0.44)	(0.36;0.64;0.37)
A3	(0.70;0.31;0.32)	(0.83;0.19;0.20)	(0.65;0.31;0.37)	(0.83;0.19;0.20)	(0.65;0.31;0.37)	(0.83;0.19;0.20)	(0.90;0.10;0.10)	(0.90;0.10;0.10)	(0.80;0.20;0.20)
A4	(0.70;0.30;0.30)	(0.59;0.37;0.42)	(0.80;0.20;0.20)	(0.70;0.30;0.30)	(0.73;0.29;0.29)	(0.70;0.30;0.30)	(0.63;0.37;0.37)	(0.63;0.34;0.39)	(0.49;0.48;0.44)
A5	(0.83;0.17;0.17)	(0.80;0.20;0.20)	(0.73;0.27;0.27)	(0.43;0.58;0.32)	(0.73;0.27;0.27)	(0.69;0.34;0.35)	(0.70;0.30;0.30)	(0.70;0.30;0.30)	(0.80;0.20;0.20)

.

Steps 1.3 and 1.4 The correlation coefficient ρjk between each attribute pair is calculated as in

Table 4. Correlation coefficients.

	C1	C2	C3	C4	C5	C6	C7	C8	C9
C1	1.00	0.25	0.79	0.29	0.92	0.54	0.75	0.56	0.83
C2	0.25	1.00	0.09	0.04	0.14	0.41	0.29	0.23	0.64
C3	0.79	0.09	1.00	0.57	0.94	0.72	0.60	0.30	0.57
C4	0.29	0.04	0.57	1.00	0.58	0.90	0.73	0.65	0.43
C5	0.92	0.14	0.94	0.58	1.00	0.75	0.81	0.57	0.76
C6	0.54	0.41	0.72	0.90	0.75	1.00	0.83	0.67	0.72
C7	0.75	0.29	0.60	0.73	0.81	0.83	1.00	0.94	0.87
C8	0.56	0.23	0.30	0.65	0.57	0.67	0.77	1.00	0.77
C9	0.83	0.64	0.57	0.43	0.76	0.72	0.87	0.77	1.00

.

Steps 1.5–1.7 The standard deviation σ_j, C index, and criterion weights wj are calculated as in

Table 5. Standard deviation σ_j, C index, and criterion weights w_j.

	C1	C2	C3	C4	C5	C6	C7	C8	C9
σj	0.282	0.331	0.296	0.309	0.318	0.270	0.305	0.288	0.336
C index	1.022	2.037	1.100	1.379	2.568	2.281	2.515	0.952	0.808
wj	0.070	0.139	0.075	0.094	0.175	0.156	0.172	0.065	0.055

.

The fifth criterion, C5 Loss of Place, is identified as the most significant criterion in the assessment of alternative retail stores. C7 Losing self-consciousness and C6 Altered Sense of Time are obtained as the second and third critical criteria, respectively. Stage 2 is the ranking of alternatives by utilizing spherical fuzzy ARAS.

Step 2.1 The spherical fuzzy decision matrix is obtained as in

Table 6. Spherical fuzzy final decision matrix.

	C1	C2	C3	C4	C5	C6	C7	C8	C9
A1	(0.17;0.94;0.12)	(0.36;0.80;0.12)	(0.21;0.91;0.14)	(0.16;0.92;0.19)	(0.20;0.88;0.23)	(0.32;0.83;0.16)	(0.16;0.92;0.15)	(0.11;0.97;0.12)	(0.13;0.96;0.12)
A2	(0.12;0.96;0.13)	(0.30;0.85;0.17)	(0.08;0.98;0.09)	(0.13;0.95;0.14)	(0.11;0.95;0.12)	(0.22;0.89;0.20)	(0.12;0.94;0.13)	(0.13;0.95;0.14)	(0.09;0.98;0.10)
A3	(0.21;0.92;0.12)	(0.39;0.80;0.12)	(0.20;0.92;0.14)	(0.32;0.86;0.11)	(0.31;0.82;0.21)	(0.41;0.77;0.13)	(0.50;0.67;0.08)	(0.32;0.86;0.06)	(0.23;0.92;0.08)
A4	(0.21;0.92;0.11)	(0.24;0.87;0.20)	(0.27;0.89;0.09)	(0.25;0.89;0.13)	(0.35;0.80;0.17)	(0.32;0.83;0.16)	(0.29;0.84;0.20)	(0.18;0.93;0.13)	(0.12;0.96;0.12)
A5	(0.28;0.89;0.08)	(0.36;0.80;0.12)	(0.24;0.91;0.11)	(0.14;0.95;0.11)	(0.35;0.80;0.16)	(0.31;0.84;0.19)	(0.33;0.81;0.17)	(0.21;0.92;0.11)	(0.23;0.92;0.08)

.

Steps 2.2 and 2.3 Spherical fuzzy optimality function values (O˜i) for all alternatives are calculated as in

Table 7. Optimality criterion values of alternatives.

Alternative	Optimality Criterion Values
S1	(0.60;0.40;0.36)
S2	(0.36;0.00;0.27)
S3	(0.81;0.19;0.22)
S4	(0.68;0.32;0.33)
S5	(0.73;0.28;0.27)
Ideal best S0	(0.83;0.18;0.18)

.

Steps 2.4 and 2.5 Appraisal scores and final rankings of alternatives are obtained as in

Table 8. Appraisal scores and final rankings of alternatives.

Alternative	Appraisal Score	Final Ranking
A1	0.401	4
A2	0.132	5
A3	0.925	1
A4	0.564	3
A5	0.690	2

.

4.1.1. Implementation Notes on Fuzzy Number Handling

The implementation of the proposed model was carried out using Python (Version: 3.12.2). Spherical fuzzy numbers were represented as Python dictionaries containing keys for membership (μ), non-membership (ν), and hesitancy (π) values. These fuzzy triplets were stored in structured NumPy arrays or Pandas DataFrames for matrix-based operations.

For the comparison and sorting of fuzzy numbers, the score function S = μ − ν(1 − π) was used to compute crisp values. These values enabled direct comparisons of alternatives and criteria. The accuracy function was also calculated to resolve ties or close values.

Aggregation operations (such as the geometric mean used in expert aggregation) were applied element-wise to μ, ν, and π components independently, ensuring that the spherical constraint (μ² + ν² + π² ≤ 1) was preserved.

During normalization, fuzzy values were temporarily converted to crisp scores using the score function, allowing scalar operations (e.g., max, min, and normalization) to proceed in a computationally efficient manner.

This implementation structure ensures modularity, ease of extension, and reproducibility and is suitable for integration with user interaction data in future real-time adaptations of the model.

4.1.2. Operationalization and Expert Evaluation Process

Each of the nine flow dimensions—drawn from the foundational work of Csikszentmihalyi [27]—was used as a criterion in evaluating the consumer experience across five Metaverse fashion retail alternatives. The expert panel consisted of three academics with expertise in consumer behavior and immersive technologies.

To ensure consistent interpretation, the experts were provided with a structured evaluation form, which included the following:

• A clear definition of each flow construct (e.g., “Loss of Self-Consciousness”, defined as “the extent to which users lose awareness of themselves during virtual interaction”).
• A 9-point linguistic scale (Table 1) ranging from “Absolutely Low Importance” to “Absolutely More Importance”.
• Instructions to evaluate each alternative against each flow dimension based on perceived effectiveness in inducing that flow component.

To reduce bias, all experts completed their evaluations independently. After collection, the linguistic terms were converted to spherical fuzzy triplets using Table 1, and geometric mean aggregation was applied to generate a collective matrix.

Inter-rater consistency was evaluated using Fleiss’ Kappa, which yielded a moderate agreement score of κ = 0.61 across all items. This indicates an acceptable consistency among expert judgments, lending reliability to the collective decision matrix.

Example Mapping of Linguistic Term to Spherical Fuzzy Triplet:

For instance, if a decision expert assigns the term “Very High Importance” (VHI) to the criterion “Loss of Self-Consciousness” for Alternative A3, this is mapped to its corresponding spherical fuzzy number from Table 1:

VHI → (μ,ν,π) = (0.8,0.2,0.2)

These values represent the following:

• μ: Degree of membership (support for high importance);
• ν: Degree of non-membership (opposition);
• π: Degree of hesitancy (uncertainty).

The resulting triplet is entered into the fuzzy evaluation matrix for further aggregation and analysis.

4.2. Sensitivity Analysis

Sensitivity analysis is a common technique to assess the efficacy of MCDM procedures, evaluating how variations in inputs impact the output. This study provides two distinct sensitivity analyses for the weights of criteria and decision makers. To conduct sensitivity analysis on criterion weights, different scenarios are created based on the original scenario. Specifically, the initial scenario w1 undergoes systematic shifts, resulting in the generation of six additional scenarios (w2, w3, w4, w6, and w7), as outlined in

Table 9. Criterion weight distribution scenarios.

	C1	C2	C3	C4	C5	C6	C7	C8	C9
w1	0.070	0.139	0.075	0.094	0.175	0.156	0.172	0.065	0.055
w2	0.139	0.075	0.094	0.175	0.156	0.172	0.065	0.055	0.070
w3	0.075	0.094	0.175	0.156	0.172	0.065	0.055	0.070	0.139
w4	0.094	0.175	0.156	0.172	0.065	0.055	0.070	0.139	0.075
w5	0.175	0.156	0.172	0.065	0.055	0.070	0.139	0.075	0.094
w6	0.156	0.172	0.065	0.055	0.070	0.139	0.075	0.094	0.175
w7	0.172	0.065	0.055	0.070	0.139	0.075	0.094	0.175	0.156
w8	0.065	0.055	0.070	0.139	0.075	0.094	0.175	0.156	0.172
w9	0.055	0.070	0.139	0.075	0.094	0.175	0.156	0.172	0.065

.

Based on the varying criterion weight distribution scenarios, the alternatives are ranked as in

Table 10. Appraisal scores and final rankings of alternatives for different criterion weight distribution scenarios.

	C1	C2	C3	C4	C5	C6	C7	C8	C9
A1	0.401 (4)	0.400 (4)	0.397 (4)	0.423 (4)	0.431 (4)	0.447 (4)	0.313 (4)	0.291 (4)	0.356 (4)
A2	0.132 (5)	0.111 (5)	0.121 (5)	0.166 (5)	0.152 (5)	0.156 (5)	0.088 (5)	0.070 (5)	0.077 (5)
A3	0.925 (1)	0.890 (1)	0.878 (1)	0.909 (1)	0.877 (1)	0.914 (1)	0.904 (1)	0.949 (1)	0.927 (1)
A4	0.564 (3)	0.618 (3)	0.623 (3)	0.565 (3)	0.565 (3)	0.512 (3)	0.520 (3)	0.494 (3)	0.554 (3)
A5	0.690 (2)	0.697 (2)	0.729 (2)	0.686 (2)	0.752 (2)	0.776 (2)	0.737 (2)	0.649 (2)	0.644 (2)

.

Additionally, in order to conduct a more comprehensive sensitivity analysis, the effects of varying the weight distributions of decision experts on the results are investigated. Ten distinct weight distribution scenarios are generated in this configuration, and alternative rankings are derived in the manner shown in

Table 11. Sensitivity analysis results for varying decision expert (DE) weight distributions.

DE 1;	0.33;	0.20;	0.20;	0.60;	0.20;	0.40;	0.40;	0.90;	0.05;	0.05;
DE 2;	0.33;	0.20;	0.60;	0.20;	0.40;	0.20;	0.40;	0.05;	0.90;	0.05;
DE 3	0.33	0.60	0.20	0.20	0.40	0.40	0.20	0.05	0.05	0.90
A1	0.401 (4)	0.444 (4)	0.358 (4)	0.386 (4)	0.413 (4)	0.421 (4)	0.371 (4)	0.384 (4)	0.316 (4)	0.481 (4)
A2	0.132 (5)	0.173 (5)	0.128 (5)	0.091 (5)	0.159 (5)	0.132 (5)	0.110 (5)	0.054 (5)	0.126 (5)	0.228 (5)
A3	0.925 (1)	0.899 (1)	0.916 (1)	0.947 (1)	0.910 (1)	0.929 (1)	0.933 (1)	0.961 (1)	0.913 (1)	0.869 (1)
A4	0.564 (3)	0.56 (3)2	0.535 (3)	0.582 (3)	0.550 (3)	0.577 (3)	0.560 (3)	0.599 (3)	0.505 (3)	0.550 (3)
A5	0.690 (2)	0.755 (2)	0.660 (2)	0.636 (2)	0.718 (2)	0.699 (2)	0.651 (2)	0.577 (2)	0.640 (2)	0.833 (2)

.

The current model operates on a static decision matrix derived from expert evaluations at a single time point. While this setup ensures methodological clarity, it does not directly accommodate real-time changes inherent in Metaverse platforms. To enhance adaptability, future versions of the model could be extended with real-time data integration by connecting behavioral analytics or user interaction logs with the fuzzy evaluation framework. This would allow the model to dynamically update weights or re-rank alternatives as user behavior shifts, ensuring responsiveness in evolving digital environments.

4.3. Comparative Study

To validate the suggested methodology, a comparative study is conducted with an alternative MCDM method. In this context, the problem at hand was resolved using the spherical fuzzy TOPSIS [38] approach by using the decision matrix obtained in the problem. The appraisal scores of alternatives and final rankings calculated in this manner are presented in

Table 12. Comparative analysis results.

Alternative	Spherical Fuzzy CRITIC ARAS	Spherical Fuzzy TOPSIS
A1	0.481 (4)	0.438 (4)
A2	0.228 (5)	0.220 (5)
A3	0.869 (1)	0.765 (1)
A4	0.550 (3)	0.508 (3)
A5	0.833 (2)	0.696 (2)

.

The proposed method yields consistent rankings with the TOPSIS approach, despite variations in appraisal scores. This suggests that the proposed approach is effective and produces valid results, establishing its reliability in comparison to the well-established TOPSIS approach.

Statistical Validation of Ranking Consistency:

To validate the consistency between the rankings produced by the proposed spherical fuzzy CRITIC–ARAS method and the benchmark spherical fuzzy TOPSIS method, we computed Spearman’s rank correlation coefficient and Kendall’s tau coefficient.

The results are as follows:

• Spearman’s ρ = 1.0;
• Kendall’s τ = 1.0.

These values indicate a perfect positive correlation, confirming that the two methods yield identical rankings. This statistical confirmation supports the reliability and robustness of the proposed approach.

5. Discussion

This study ventured into uncharted territory by applying flow theory to the Metaverse context, specifically within the domain of fashion retail shopping. The Metaverse’s immersive nature aligns seamlessly with the principles of flow theory, where individuals experience complete involvement and engagement. Our findings validate the relevance of flow theory in understanding consumer behavior and experiences within the Metaverse. By dissecting the various dimensions of flow theory and quantifying their influence, this study contributed to the theoretical framework that underpins research in this domain.

In the Metaverse environment, customers can shop in virtual stores, businesses can collect data about customer experiences, and brands can use this data to develop their physical stores. However, businesses are still in their early stages of adopting Metaverse applications, and the availability of ultra-fast internet is crucial for their success in this space. The Metaverse offers opportunities for businesses to market both physical and digital products and services, reduce production costs in creative activities, generate income through alternative sources, and increase brand awareness.

The results are in line with the findings of Park et al. [13] in that flow experiences are more likely to occur on Metaverse platforms that offer a sense of telepresence and social interaction.

Among the nine flow dimensions evaluated, “Loss of Place” and “Loss of Self-Consciousness” emerged as the most significant criteria based on the CRITIC weights. This finding aligns closely with the immersive nature of the Metaverse, which enables users to enter environments where conventional spatial and personal boundaries are temporarily suspended.

“Loss of Place” reflects a user’s disconnection from physical space, often referred to as spatial presence in virtual reality research. Similarly, “Loss of Self-Consciousness” de-notes ego dissolution or deep absorption, where users no longer think about themselves as separate entities but become fully engrossed in the activity. These dimensions are heightened in Metaverse environments due to rich visual stimuli, avatar-based social interactions, and high levels of interactivity.

This suggests that for fashion brands aiming to foster strong consumer engagement in the Metaverse, enhancing these immersive aspects—such as avatar embodiment, virtu-al store realism, and seamless interaction—could be more effective than focusing solely on traditional cues like goals or feedback mechanisms.

Therefore, while choosing which platform to enter, marketers may take these various Metaverse platform characteristics into account.

This study underscores the transformative impact of the Metaverse on fashion brands’ marketing strategies and brand experiences. As brands increasingly explore the Metaverse as a marketing platform, it becomes imperative to adapt and innovate. The Metaverse demands a shift from traditional marketing paradigms to more interactive and experiential approaches.

In addressing the challenge of decision uncertainty in the Metaverse context, this study introduced a novel spherical fuzzy CRITIC-integrated ARAS model. The provided approach proved effective in modeling and managing the inherent uncertainty associated with decision-making in this complex environment. By incorporating these techniques, we have expanded the methodological toolkit available to researchers and decision makers in the field, offering a more nuanced understanding of the Metaverse’s dynamics.

6. Conclusions

This study introduces an innovative approach called the spherical fuzzy CRITIC ARAS methodology for evaluating retail shop alternatives. The criteria set is developed based on the dimensions of flow theory. In this particular context, the evaluation of five retail shop alternatives is conducted through the suggested spherical fuzzy CRITIC ARAS methodology, considering nine criteria. The CRITIC method is employed to objectively determine criteria weights. While the traditional ARAS methodology is a robust multi-criteria decision-making (MCDM) tool, it falls short in handling the inherent vagueness in MCDM problems. To address this limitation, spherical fuzzy sets are utilized, allowing the independent modeling of membership, non-membership, and hesitancy parameters. Following the numerical solution, sensitivity analysis was conducted, demonstrating the stability of the proposed method against variations in decision expert weights and different criteria weight distribution scenarios. Additionally, a comparative analysis validates the results by contrasting the proposed approach with another prominent MCDM method.

Another source of originality for this study lies in its novel application of flow theory to the Metaverse, shedding light on the dynamics of consumer experiences in this emerging digital realm. Furthermore, the development of a practical and ready-to-use MCDM model based on flow constructs adds significance to this research. By quantifying the relative importance of specific flow dimensions through empirical analysis and fuzzy modeling, this study provides actionable insights for businesses and enriches the academic discourse on consumer interactions in the Metaverse.

For future applications, the methodology proposed here can be extended to address a diverse range of problems in fields such as health, engineering, and management. Re-searchers can analyze the stability of this methodology against rank reversal phenomena using appropriate analytic methods. Additionally, exploring the integration of other fuzzy sets, such as neutrosophic sets, with the CRITIC ARAS approach could provide further insights. Various modifications, such as integrating CRITIC with WASPAS or DEMATEL, may also be explored for different decision-making scenarios.

However, it is important to acknowledge some limitations in the current study. The CRITIC approach relies on calculating correlation coefficients, which, due to the nature of spherical fuzzy environments, are transferred to a crisp environment through normalization, potentially leading to information loss. Furthermore, this study heavily depends on subjective assessments and does not leverage existing datasets. Future research could incorporate machine learning techniques, such as logistic regression, linear discriminant analysis, and decision trees, to create MCDM models that integrate real-world data.