Displacement Efficiency Under Pulsatile Injection: The Roles of Frequency, Amplitude, and Porosity
Abstract
1. Introduction
2. Materials and Methods
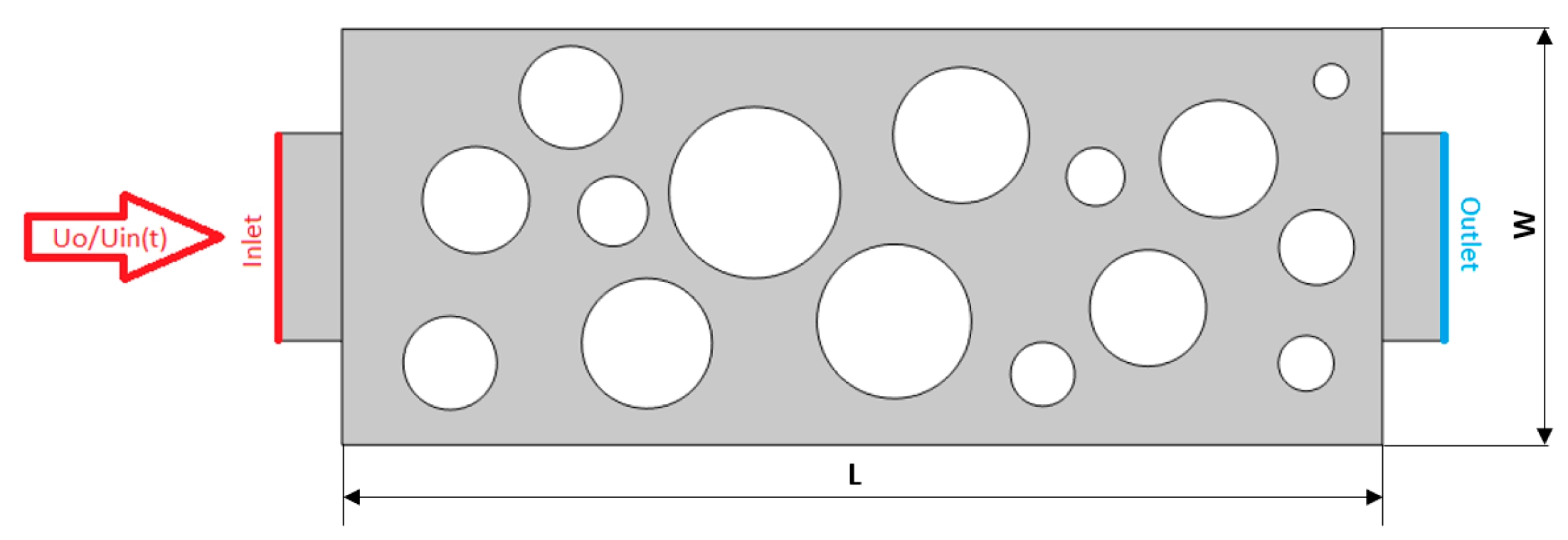
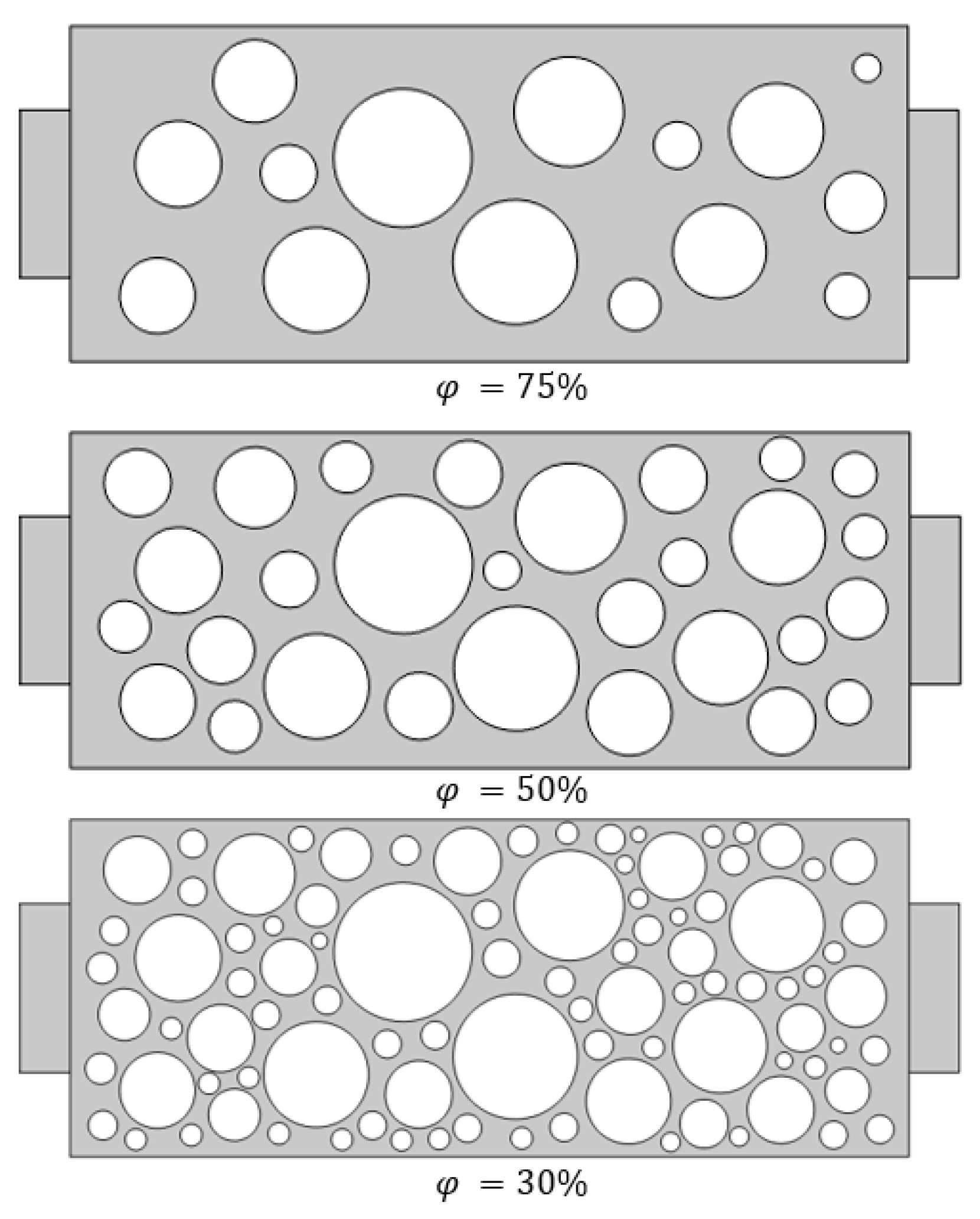
2.1. Geometry Model and Boundary Condition
2.2. Numerical Setup
2.3. Pulsatile Injection
2.4. Dimensional Framework
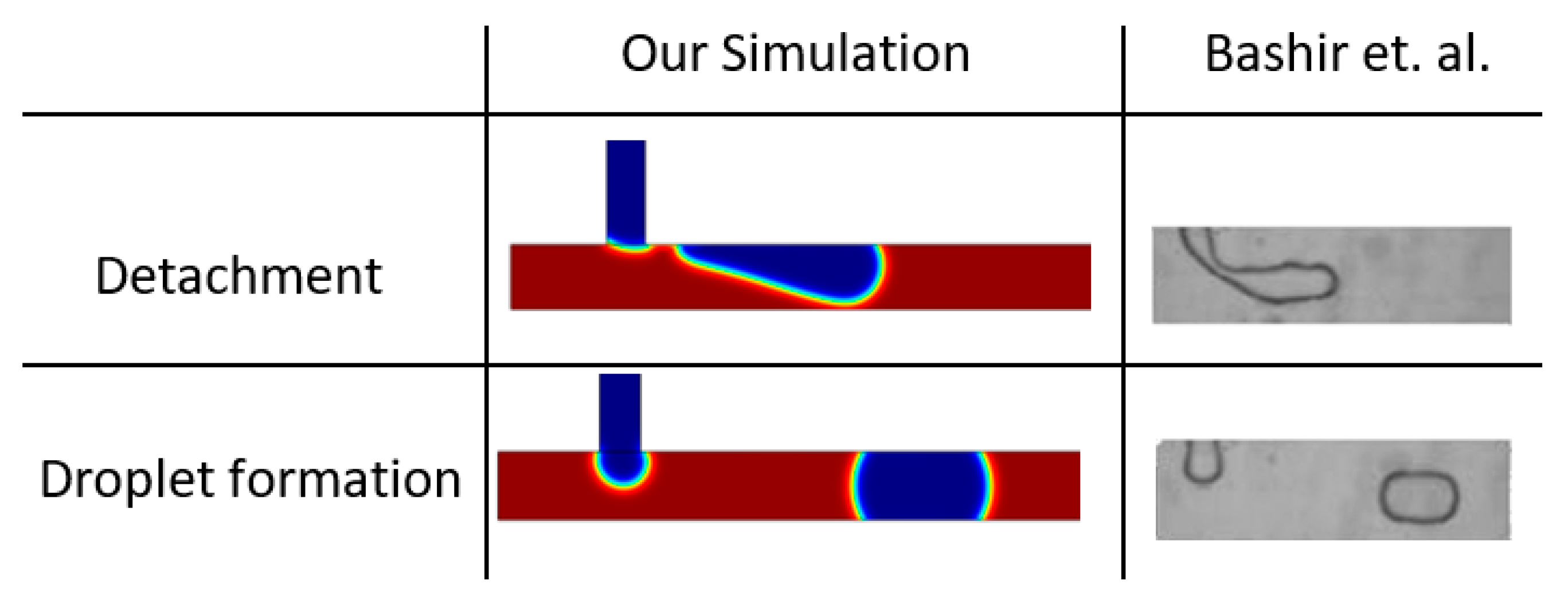
2.5. Validation
2.6. Mesh Sensitivity Analysis
3. Results and Discussion
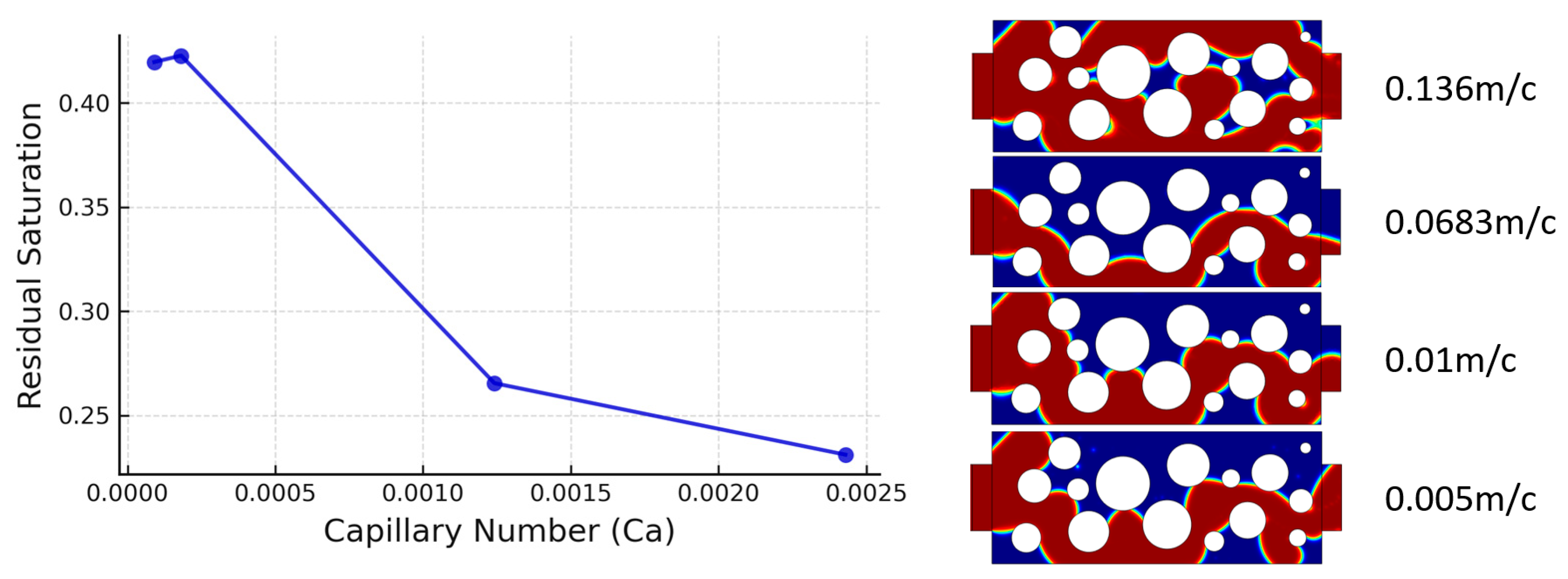
3.1. Baseline Regime
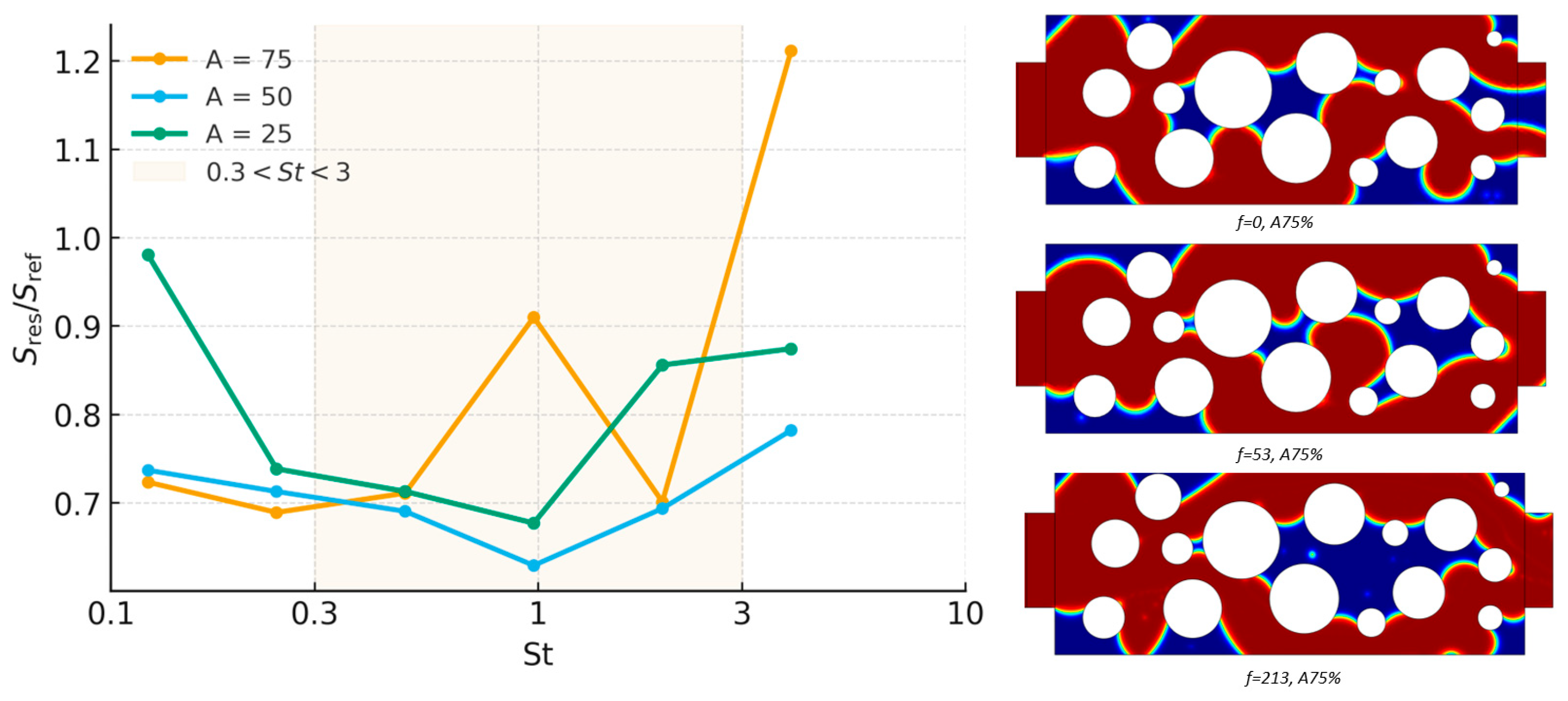
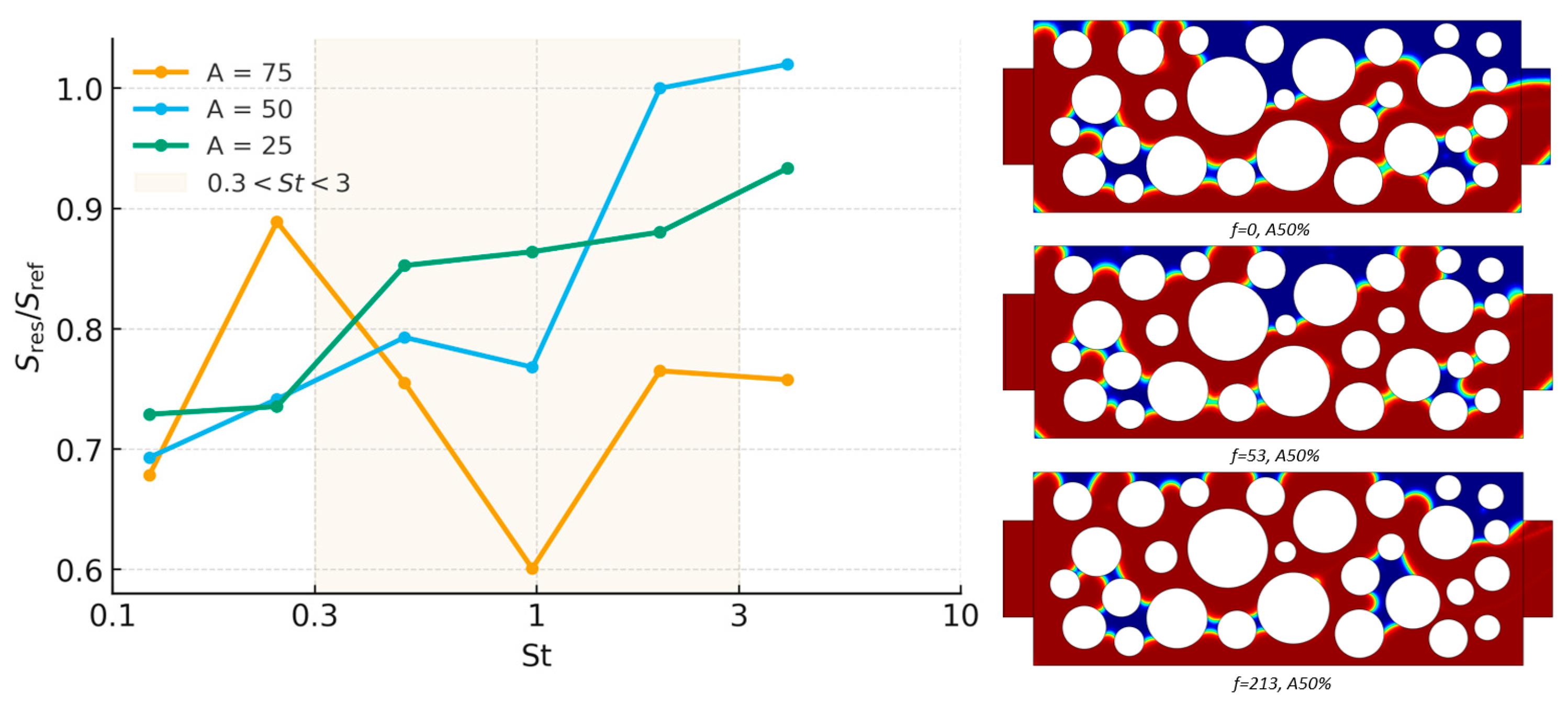
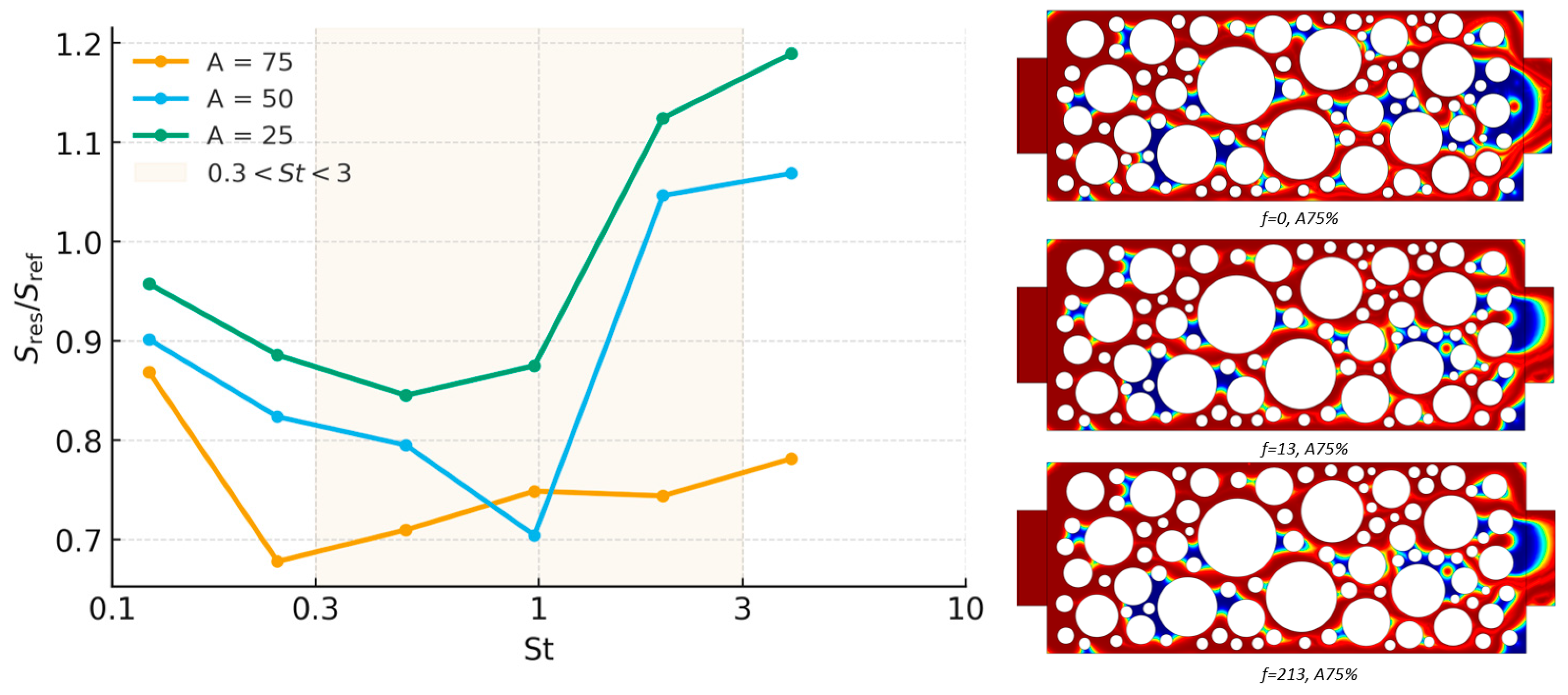
3.2. Effect of Amplitude and Frequency at Different Porosity Levels
3.3. Velocity Fields and Flow Reorganization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dincau, B.; Savin, T.; Sauret, A. Pulsatile flow in microfluidic systems. Small 2020, 16, 1904032. [Google Scholar] [CrossRef]
- Mudugamuwa, A.; Roshan, U.; Hettiarachchi, S.; Cha, H.; Musharaf, H.; Kang, X.; Trinh, Q.T.; Xia, H.M.; Nguyen, N.T.; Zhang, J. Periodic flows in microfluidics. Small 2024, 20, e2404685. [Google Scholar] [CrossRef]
- Mutlu, B.R.; Edd, J.F.; Toner, M. Oscillatory inertial focusing in infinite microchannels. Proc. Natl. Acad. Sci. USA 2018, 115, 7682–7687. [Google Scholar] [CrossRef]
- Vázquez–Vergara, P.; Torres-Herrera, U.; Olguin, L.F.; Poiré, E.C. Singular behavior of microfluidic pulsatile flow due to dynamic curving of air–fluid interfaces. Phys. Rev. Fluids 2021, 6, 024003. [Google Scholar] [CrossRef]
- Tan, Y.; Zhang, Y.; Hui, C.; Yu, C.; Tian, S.; Wang, T.; Wang, F. Resonance-enhanced pulsing water injection for improved oil recovery: Micromodel experiments and analysis. Processes 2023, 11, 957. [Google Scholar] [CrossRef]
- Ji, B.; He, Y.; Tang, Y.; Yang, S. Inertial property of oscillatory flow for pulse injection in porous media. Energy Explor. Exploit. 2021, 39, 1184–1194. [Google Scholar] [CrossRef]
- Holtzman, R. Effects of pore-scale disorder on fluid displacement in partially-wettable porous media. Sci. Rep. 2016, 6, 36221. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Chauhan, K.; Pereira, J.–M.; Gan, Y. Disorder characterization of porous media and its effect on fluid displacement. Phys. Rev. Fluids 2019, 4, 034305. [Google Scholar] [CrossRef]
- Wu, D.S.; Hu, R.; Lan, T.; Chen, Y. Role of pore-scale disorder in fluid displacement. Water Resour. Res. 2021, 57, e2020WR028004. [Google Scholar] [CrossRef]
- Yiotis, A.; Karadimitriou, N.K.; Zarikos, I.; Steeb, H. Pore-scale effects during the transition from capillary- to viscosity-dominated flow dynamics within microfluidic porous-like domains. Sci. Rep. 2021, 11, 3891. [Google Scholar] [CrossRef] [PubMed]
- Jahanbakhsh, A.; Wlodarczyk, K.L.; Hand, D.P.; Maier, R.R.J.; Maroto-Valer, M.M. Review of microfluidic devices and imaging techniques for fluid flow study in porous geomaterials. Sensors 2020, 20, 4030. [Google Scholar] [CrossRef]
- Massimiani, A.; Panini, F.; Marasso, S.L.; Cocuzza, M.; Quaglio, M.; Pirri, C.F.; Verga, F.; Viberti, D. 2D microfluidic devices for pore-scale phenomena investigation: A review. Water 2023, 15, 1222. [Google Scholar] [CrossRef]
- Olsson, E.; Kreiss, G. A conservative level set method for two–phase flow. J. Comput. Phys. 2005, 210, 225–246. [Google Scholar] [CrossRef]
- Olsson, E.; Kreiss, G. A conservative level set method for two–phase flow. II. J. Comput. Phys. 2007, 225, 785–807. [Google Scholar] [CrossRef]
- Cifani, P.; Kuerten, J.G.M.; van der Vegt, J.J.W. A comparison between the surface-compression method and an interface reconstruction method for VOF. Comput. Fluids 2016, 136, 421–435. [Google Scholar] [CrossRef]
- Boniou, V.; Schmitt, T.; Vié, A. Comparison of interface-capturing methods for two-phase flow in a unified low-Mach framework. Int. J. Multiph. Flow 2022, 149, 103957. [Google Scholar] [CrossRef]
- Amini, Y.; Ghazanfari, V.; Heydari, M.; Shadman, M.M.; Khamseh, A.G.; Khani, M.H.; Hassanvand, A. Computational fluid dynamics simulation of two-phase flow patterns in a serpentine microfluidic device. Sci. Rep. 2023, 13, 9483. [Google Scholar] [CrossRef]
- Tekseth, K.R.; Breiby, D.W. 4D imaging of two-phase flow in porous media using laboratory-based micro-computed tomography. Water Resour. Res. 2024, 60, e2023WR036514. [Google Scholar] [CrossRef]
- Ben-Noah, I.; Friedman, S.P.; Berkowitz, B. Dynamics of air flow in partially water-saturated porous media. Rev. Geophys. 2023, 61, e2022RG000798. [Google Scholar] [CrossRef]
- Kuljabekov, A.; Segalini, A.; Wang, L.; Monaco, E.; Royer, J.-J.; Rojas-Solórzano, L.R. Isothermal CO2 injection into water–saturated porous media: Lattice–Boltzmann modelling of pulsatile flow with porosity, tortuosity and optimal–frequency characterization. Petroleum 2023, 43, 101949. [Google Scholar] [CrossRef]
- Whelan, B.K.; Woods, A.W. The periodic injection and extraction of fluid in a porous medium for hydrogen storage. J. Fluid Mech. 2025, 1002, R2. [Google Scholar] [CrossRef]
- Liu, C.; Chen, T.; Yu, Z.; Yang, Z.; Yin, J. Pressure attenuation law of low-frequency pulse pressure flooding and its influence on oil recovery. ACS Omega 2021, 6, 35272–35283. [Google Scholar] [CrossRef]
- Unglehrt, L.; Manhart, M. Assessment of models for nonlinear oscillatory flow through a hexagonal sphere pack. Transp. Porous Media 2024, 151, 2183–2213. [Google Scholar] [CrossRef]
- Yao, C.; Zhao, Y.; Ma, H.; Liu, Y.; Zhao, Q.; Chen, G. Two–Phase flow and mass transfer in microchannels: A review from local mechanism to global models. Chem. Eng. Sci. 2021, 229, 116017. [Google Scholar] [CrossRef]
- Zacharoudiou, I.; Boek, E.S.; Crawshaw, J. Pore-scale modeling of drainage displacement patterns in association with geological sequestration of CO2. Water Resour. Res. 2020, 56, e2019WR026332. [Google Scholar] [CrossRef]
- Kunz, P.; Zarikos, I.M.; Karadimitriou, N.K.; Huber, M.; Nieken, U.; Hassanizadeh, S.M. Study of multi-phase flow in porous media: Comparison of SPH simulations with micro-model experiments. Transp. Porous Media 2016, 114, 581–600. [Google Scholar] [CrossRef]
- Bashir, S.; Rees, J.M.; Zimmerman, W.B.J. Simulations of microfluidic droplet formation using the two–phase level set method. Chem. Eng. Sci. 2011, 66, 4733–4741. [Google Scholar] [CrossRef]
- COMSOL AB. Two–Phase Flow Modeling Guidelines. COMSOL Learning Center. Available online: https://www.comsol.com/support/learning-center/article/Two-Phase-Flow-Modeling-Guidelines-46471 (accessed on 5 October 2025).
- COMSOL AB. Level Set and Phase Field Equations. COMSOL Multiphysics® v6.0 Documentation. Available online: https://doc.comsol.com/6.0/doc/com.comsol.help.cfd/cfd_ug_fluidflow_multi.09.122.html (accessed on 5 October 2025).
- COMSOL AB. The Wetted Wall Coupling Feature. COMSOL Multiphysics® v6.0 Documentation. Available online: https://doc.comsol.com/6.0/doc/com.comsol.help.cfd/cfd_ug_fluidflow_multi.09.011.html (accessed on 5 October 2025).

| Symbol | Definition | Formula | Range (This Study) |
|---|---|---|---|
| Ca | Capillary number | 2.5 × 10−3 | |
| Re | Reynolds number | ≈0.34 | |
| St | Strouhal number | 0–39 | |
| Capillary time | 2.2–5.5 × 10−4 s | ||
| Dimensionless frequency | 0–0.12 |
| Mesh Type | Number of Elements | ΔS (%) Compared to Fine Mesh | |
|---|---|---|---|
| Coarse | 5571 | 0.412 | 2.6% |
| Fine | 7063 | 0.423 | 0.2% |
| Extra Fine (ref) | 10,224 | 0.424 | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bolysbek, D.; Kuljabekov, A.; Uzbekaliyev, K.; Zhantayev, Z. Displacement Efficiency Under Pulsatile Injection: The Roles of Frequency, Amplitude, and Porosity. Processes 2025, 13, 3553. https://doi.org/10.3390/pr13113553
Bolysbek D, Kuljabekov A, Uzbekaliyev K, Zhantayev Z. Displacement Efficiency Under Pulsatile Injection: The Roles of Frequency, Amplitude, and Porosity. Processes. 2025; 13(11):3553. https://doi.org/10.3390/pr13113553
Chicago/Turabian StyleBolysbek, Darezhat, Alibek Kuljabekov, Kenbai Uzbekaliyev, and Zhumabek Zhantayev. 2025. "Displacement Efficiency Under Pulsatile Injection: The Roles of Frequency, Amplitude, and Porosity" Processes 13, no. 11: 3553. https://doi.org/10.3390/pr13113553
APA StyleBolysbek, D., Kuljabekov, A., Uzbekaliyev, K., & Zhantayev, Z. (2025). Displacement Efficiency Under Pulsatile Injection: The Roles of Frequency, Amplitude, and Porosity. Processes, 13(11), 3553. https://doi.org/10.3390/pr13113553






