Experimental and Modeling Study of the Thermodynamic Behavior and Solubility of the NH4NO3–D-Sucrose–Water Ternary System at 298.15 K
Abstract
1. Introduction
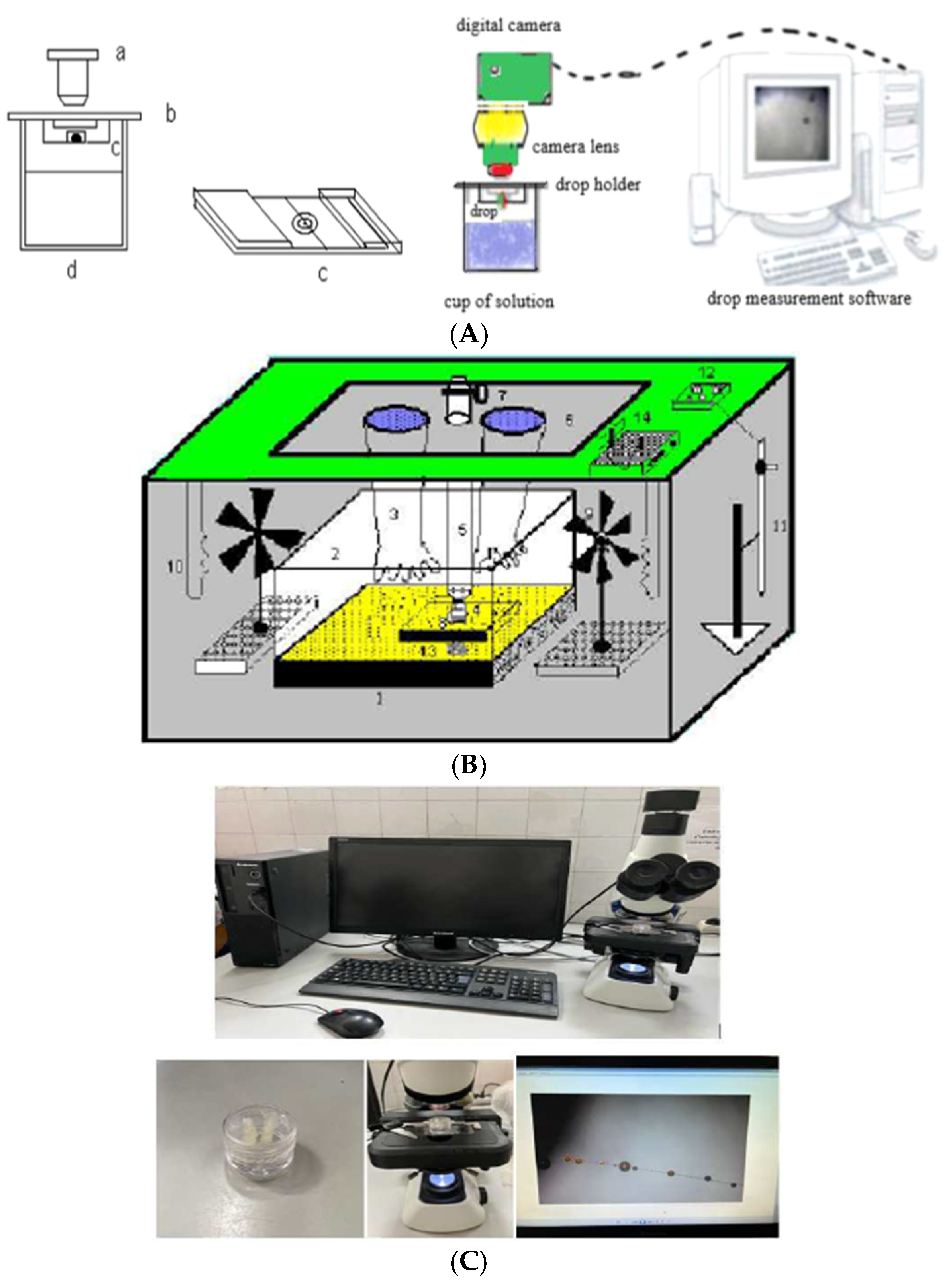
2. Experimental Section
Hygrometric Method
3. Thermodynamic Formwork
3.1. Estimation of Thermodynamic Properties
3.2. Estimation of Solubility Data
3.2.1. D-Sucrose Solubility
3.2.2. Electrolyte Solubility
3.3. Optimization of Model Parameters
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
List of Symbols
| a | Activity |
| Ax | Debye–Hückel parameter |
| Parameter of single electrolyte | |
| D | Diameter of the drop |
| gex | Excess Gibbs energy per mole of particles |
| Gex | Excess Gibbs energy |
| hr | Relative humidity |
| K | Ratio of drops |
| Ks | Solubility product |
| M | Molality |
| n | Mole number |
| nr | Index of refraction |
| R | Gas constant, J·mol−1·K−1 |
| T | Absolute temperature |
| P | Pressure |
| x | Mole fraction |
| u(p) | Standard uncertainty of parameter p |
| W12, U12 | Parameters of PSC model |
| , , | Short-range parameters between molecule j and salt MX |
| Short-range ternary parameters molecule-molecule-Salt MX | |
| Greek letters | |
| α | Constant |
| ρ | Closest approach distance |
| ϕ | Osmotic coefficient |
| γ | Activity coefficient |
| σaw | Uncertainty of measured water activity |
| σϕ | Uncertainty of measured osmotic coefficient |
| Subscripts | |
| Calc | Calculated |
| Exp | Experimental |
| ref | Reference |
| i, 1,2 | Indicate component |
| PSC | Pitzer–Simonson–Clegg |
| PDH | Pitzer–Debye–Hückel |
| Superscripts | |
| Ex | Excess |
Appendix A. Calculation of Uncertainties
Appendix B. ECA Equation [25]
Appendix C. The Lin et al. Equation [16]
Appendix D. The LS Model [27,28]
References
- Azov, V.A.; Egorova, K.S.; Seitkalieva, M.M.; Kashin, A.S.; Ananikov, V.P. “Solvent-in-salt” systems for design of new materials in chemistry, biology and energy research. Chem. Soc. Rev. 2018, 47, 1250–1284. [Google Scholar] [CrossRef]
- Yin, H.; Li, B.; Wang, X.; Xi, Z. Effect of ammonium and nitrate supplies on nitrogen and sucrose metabolism of cabernet sauvignon (Vitis vinifera cv.). J. Sci. Food Agric. 2020, 100, 5239–5250. [Google Scholar] [CrossRef]
- Liu, J.; Lyu, M.; Xu, X.; Liu, C.; Qin, H.; Tian, G.; Zhu, Z.; Ge, S.; Jiang, Y. Exogenous sucrose promotes the growth of apple rootstocks under high nitrate supply by modulating carbon and nitrogen metabolism. Plant Physiol. Biochem. 2022, 192, 196–206. [Google Scholar] [CrossRef]
- Sjolin, C. The influence of moisture on the structure and quality of ammonium nitrate prills. J. Agric. Food Chem. 1971, 19, 83–95. [Google Scholar] [CrossRef]
- Sihag, R.K.; Guha-Mukherjee, S.; Sopory, S.K. Effect of ammonium, sucrose and light on the regulation of nitrate reductase level in Pisum sativum. Physiol. Plant. 1979, 45, 281–287. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Zhou, S.L.; Huang, Q.; Leng, G.H.; Xue, Q.W.; Stewart, B.A.; Wang, Z.M. Effects of sucrose and ammonium nitrate on phosphoenolpyruvate carboxylase and ribulose-1, 5-bisphosphate carboxylase activities in wheat ears. Aust. J. Crop Sci. 2012, 6, 822–827. [Google Scholar]
- Seuvre, A.M.; Mathlouthi, M. Solutions properties and solute–solvent interactions in ternary sugar–salt–water solutions. Food Chem. 2010, 122, 455–461. [Google Scholar] [CrossRef]
- Hernández-Luis, F.; Amado-González, E.; Esteso, M.A. Activity coefficients of NaCl in trehalose–water and maltose–water mixtures at 298.15 K. Carbohydr. Res. 2003, 338, 1415–1424. [Google Scholar] [CrossRef]
- Abderafi, S.; Bounahmidi, T. Measurement and modeling of atmospheric pressure vapor-liquid equilibrium data for binary, ternary and quaternary mixtures of sucrose, glucose, fructose and water components. Fluid Phase Equilibria 1994, 93, 337–351. [Google Scholar] [CrossRef]
- Messnaoui, B.; Mounir, A.; Dinane, A.; Samaouali, A.; Mounir, B. Determination of water activity, osmotic coefficients, activity coefficients, solubility and excess gibbs free energies of NaCl-sucrose-H2O mixture at 298.15 K. J. Mol. Liq. 2019, 284, 492–501. [Google Scholar] [CrossRef]
- Hu, Y.; Guo, T. Thermodynamics of electrolytes in aqueous systems containing both ionic and nonionic solutes, Application of the Pitzer–Simonson–Clegg equations to activity coefficients and solubilities of 1:1 electrolytes in four ternary systems at 298.15 K electrolyte–non-electrolyte–H2O. Phys. Chem. Chem. Phys. 1999, 1, 3303–3308. [Google Scholar] [CrossRef]
- Robinson, R.A.; Stokes, R.H.; Marsh, K.N. Activity coefficients in theternarysystem: Water + Sucrose + sodiumchloride. J. Chem. Thermodyn. 1985, 2, 745–750. [Google Scholar] [CrossRef]
- Wang, J.; Liu, W.; Bai, T.; Lu, J. Standard Gibbs Energies of Transfer ofsomeElectrolytesfromWatertoAqueousSucrose Solutions at 298.15 K. J. Chem. Soc. Faraday Trans. 1993, 89, 1741–1744. [Google Scholar] [CrossRef]
- Mounir, A.; Messnaoui, B.; Dinane, A.; Samaouali, A. Determination of water activity, osmotic coefficient, activity coefficient, solubility, excess Gibbs energy and transfer Gibbs energy of KCl-D−sucrose-water mixture at 298.15 K. J. Chem. Thermodyn. 2020, 142, 105962. [Google Scholar] [CrossRef]
- El Fadel, W.; El Hantati, S.; Nour, Z.; Dinane, A.; Samaouali, A.; Messnaoui, B. Experimental Determination of Osmotic Coefficient and Salt Solubility of System NH4NO3−NH4H2PO4−H2O and Their Correlation and Prediction with the Pitzer−Simonson−Clegg Model. J. Ind. Eng. Chem. Res. 2023, 62, 17986–17996. [Google Scholar] [CrossRef]
- Clegg, S.L.; Pitzer, K.S. Thermodynamics of Multicomponent, Miscible, Ionic Solutions: Generalized Equations for Symmetrical Electrolytes. J. Phys. Chem. 1992, 96, 3513–3520. [Google Scholar] [CrossRef]
- Clegg, S.L.; Pitzer, K.S.; Brimblecombe, P. Thermodynamics of Multicomponent, Miscible, Ionic solutions. 2. Mixtures Including Unsymmetrical Eelectrolytes. J. Phys. Chem. 1992, 96, 9470–9479. [Google Scholar] [CrossRef]
- Clegg, S.L.; Pitzer, K.S.; Brimblecombe, P. Thermodynamics of Multicomponent, Miscible, Ionic Solutions: Generalized Equations for Symmetrical Electrolytes. J. Phys. Chem. 1992, 96, 9472, Erratum in J. Phys. Chem. 1994, 98, 1368. [Google Scholar] [CrossRef]
- Perron, G.; Joly, D.; Desnoyers, J.E.; Avedikian, L.; Morel, J.P. Thermodynamics of the salting effect; free energies, enthalpies, entropies, heat capacities, and volumes of the ternary systems electrolyte–alcohol–water at 25 °C. Can. J. Chem. 1978, 56, 552–559. [Google Scholar] [CrossRef]
- Morel, J.P.; Lhermet, C.; Desrosiers, N.M. Interactions between cations and sugars. Part 4. Free energy of interaction of the calcium ion with some aldopentoses and aldohexoses in water at 298.15 K. J. Chem. Soc. Faraday Trans. 1988, 184, 567–2571. [Google Scholar] [CrossRef]
- Dagade, D.H.; Patil, K.J. Thermodynamic studies for aqueous solutions involving 18-crown-6 and alkali bromides at 298.15 K. Fluid Phase Equilibria 2005, 231, 44–52. [Google Scholar] [CrossRef]
- Robinson, R.A.; Stokes, R.H. Activity coefficients in aqueous solutions of D-Sucrose, mannitol and their mixtures at 25°. J. Phys. Chem. 1961, 65, 1954–1958. [Google Scholar] [CrossRef]
- Song, J.; Meng, Y.; Yuan, F.; Guo, Y.; Xie, Y.; Deng, T. Phase diagrams for the ternary system (NH4NO3 + CsNO3 + H2O) at 298.15 and 348.15 K and its application to cesium nitrate recovery from the eluent aqueous solution of ammonium nitrate. J. Mol. Liq. 2021, 338, 117079. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Dinane, A.; El Guendouzi, M.; Mounir, A. Hygrometric determination of water activities, osmotic and activity coefficients of (NaCl + KCl)(aq) at T = 298.15 K. J. Chem. Thermodyn. 2002, 34, 423–441. [Google Scholar] [CrossRef]
- Lin, D.Q.; Zhu, Z.Q.; Mei, L.H.; Yang, L.R. Isopiestic determination of the water activities of poly(ethyleneglycol) salt water systems at 25 °C. J. Chem. Eng. Data 1996, 41, 1040–1042. [Google Scholar] [CrossRef]
- Lietzke, M.H.; Stoughton, R.W. Simple empirical equation for the prediction of the activity coefficients value of each component in aqueous electrolyte mixtures containing a common ion. J. Solut. Chem. 1972, 1, 299–308. [Google Scholar] [CrossRef]
- Lietzke, M.H.; Stoughton, R.W. A simple method for predicting the osmoticcoefficient of aqueous solutions containing more than one electrolyte. J. Inorg. Nucl. Chem. 1974, 36, 1315–1317. [Google Scholar] [CrossRef]
- Hamer, W.J.; Wu, Y.-C. Osmotic Coefficients and Mean Activity Coefficients of Uniunivalent Electrolytes in Water at 25 °C. J. Phys. Chem. Ref. Data 1972, 11, 1047–1100. [Google Scholar] [CrossRef]
- Partanen Jaakko, I. Mean Activity Coefficients and Osmotic Coefficients in Aqueous Solutions of Salts of Ammonium Ions with Univalent Anions at 25 °C. J. Chem. Eng. Data 2012, 57, 2654–2666. [Google Scholar] [CrossRef]


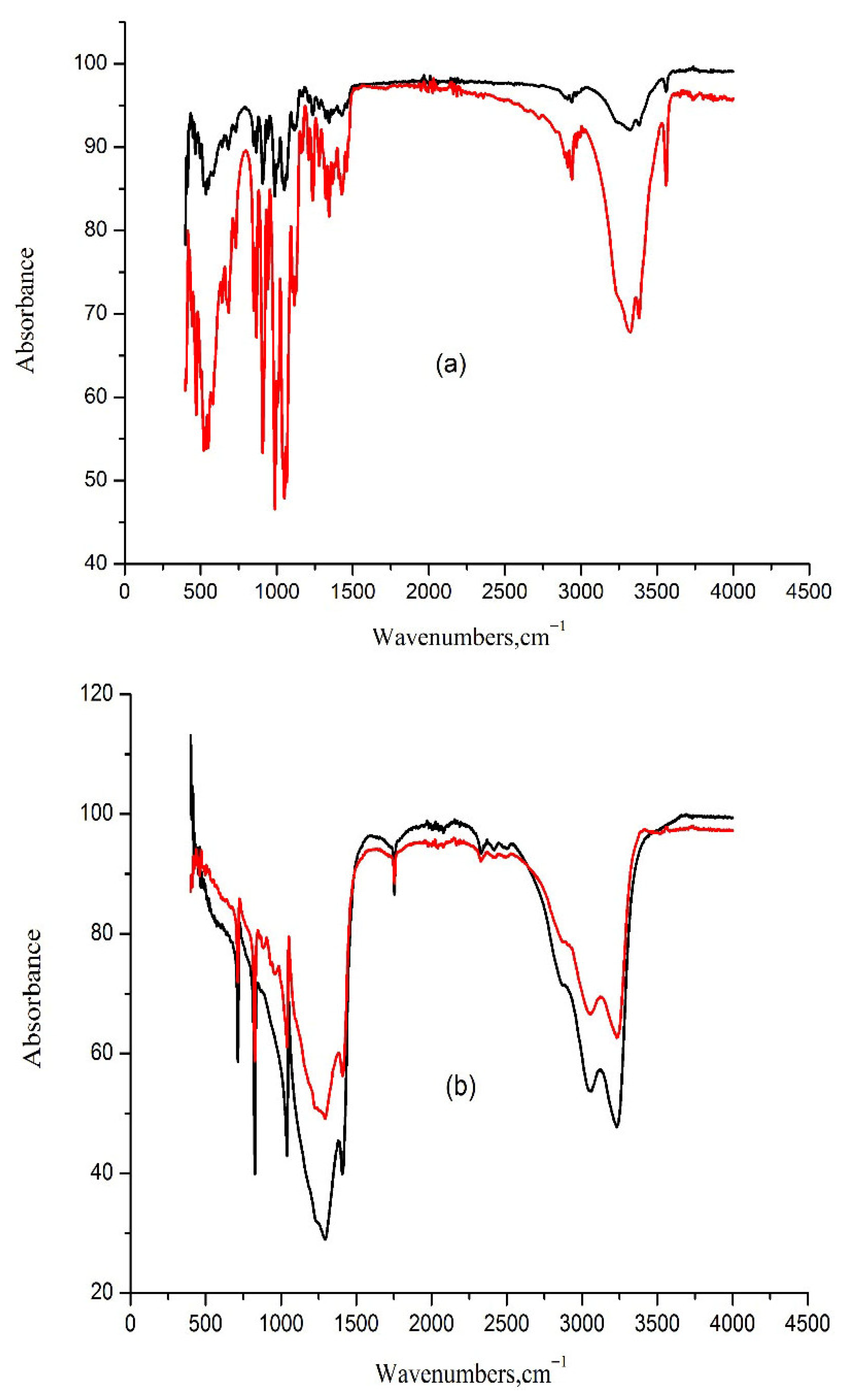

| Compound | Form | Source | Fraction Purity |
|---|---|---|---|
| NaCl | Anhydrous | Fluka | ≥0.995 |
| Sucrose | Anhydrous | Panreac | ≥0.990 |
| NH4NO3 | Anhydrous | Merck | ≥0.995 |
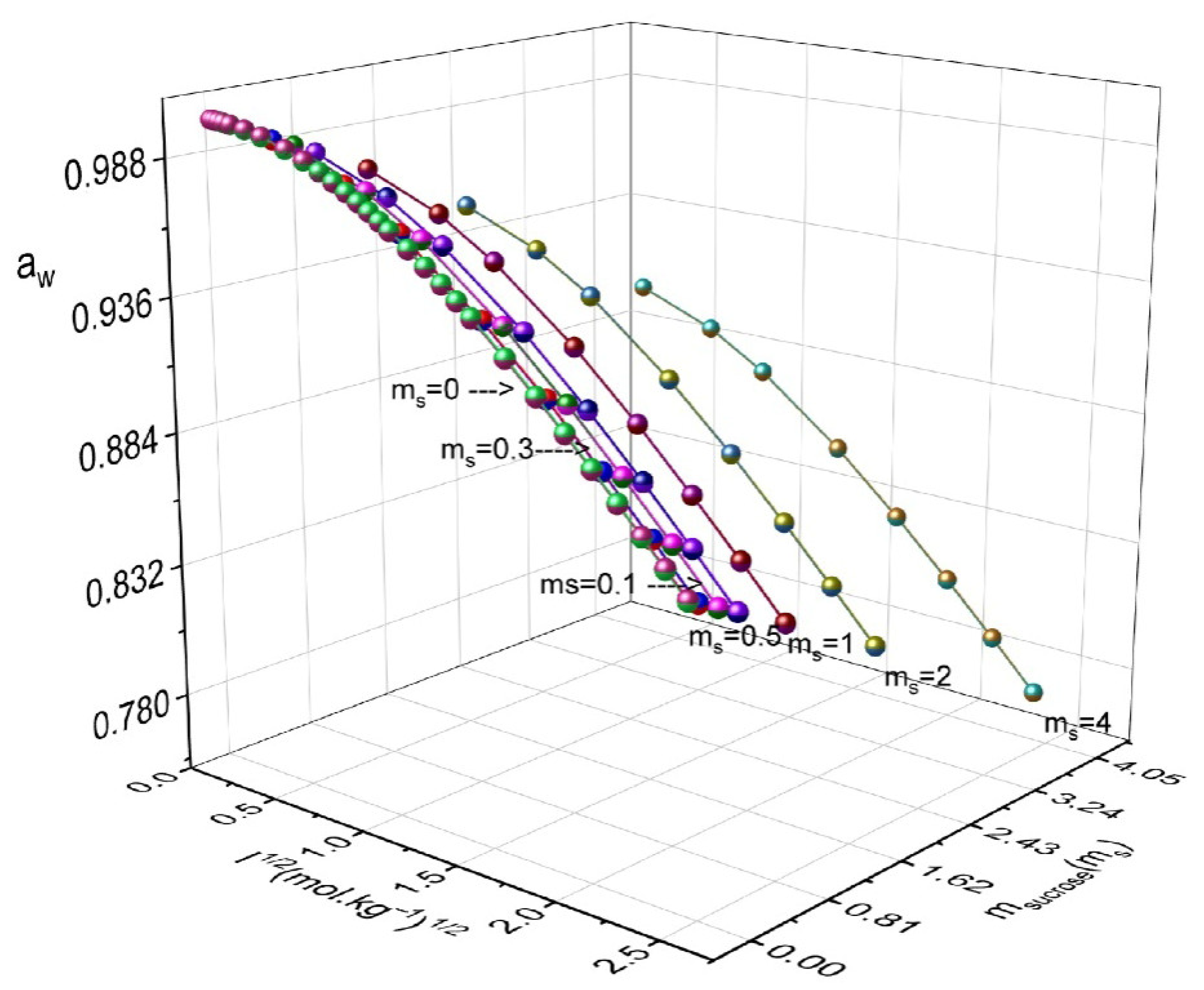
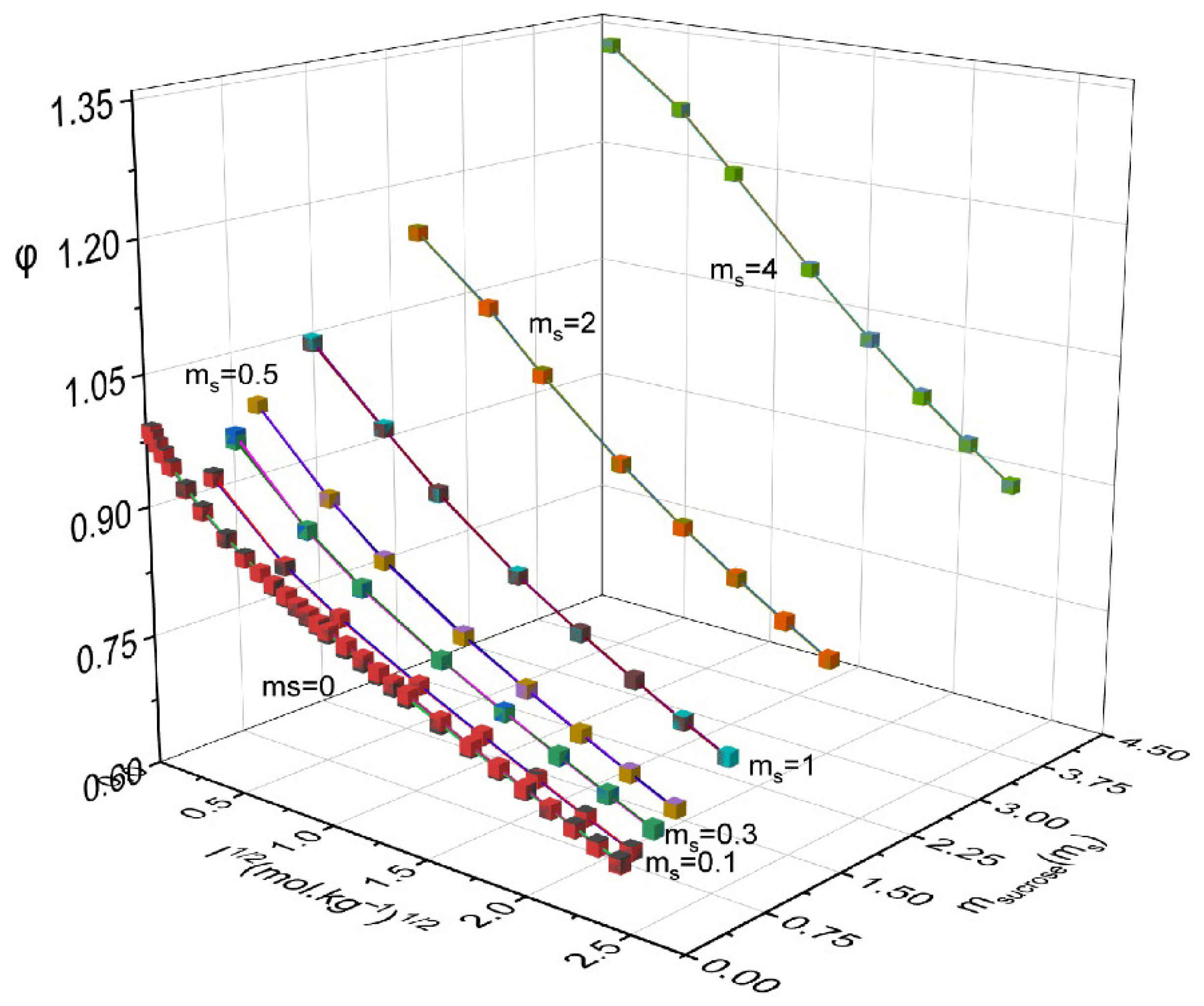
| msucrose | mNH4NO3 | aw | ϕ | msucrose | mNH4NO3 | aw | ϕ |
|---|---|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.9949 | 0.946 | 1.0 | 3.0 | 0.9019 | 0.819 |
| 0.1 | 0.5 | 0.9829 | 0.870 | 1.0 | 4.0 | 0.8805 | 0.785 |
| 0.1 | 1.0 | 0.9691 | 0.830 | 1.0 | 5.0 | 0.8609 | 0.756 |
| 0.1 | 2.0 | 0.9438 | 0.783 | 1.0 | 6.0 | 0.8425 | 0.732 |
| 0.1 | 3.0 | 0.9209 | 0.750 | 2.0 | 0.1 | 0.9549 | 1.164 |
| 0.1 | 4.0 | 0.8999 | 0.723 | 2.0 | 0.5 | 0.9426 | 1.094 |
| 0.1 | 5.0 | 0.8804 | 0.700 | 2.0 | 1.0 | 0.9285 | 1.029 |
| 0.1 | 6.0 | 0.8622 | 0.680 | 2.0 | 2.0 | 0.9025 | 0.949 |
| 0.3 | 0.1 | 0.9912 | 0.981 | 2.0 | 3.0 | 0.8791 | 0.894 |
| 0.3 | 0.5 | 0.9791 | 0.902 | 2.0 | 4.0 | 0.8576 | 0.853 |
| 0.3 | 1.0 | 0.9652 | 0.855 | 2.0 | 5.0 | 0.8377 | 0.819 |
| 0.3 | 2.0 | 0.9398 | 0.801 | 2.0 | 6.0 | 0.8193 | 0.790 |
| 0.3 | 3.0 | 0.9168 | 0.765 | 3.0 | 0.1 | 0.9295 | 1.268 |
| 0.3 | 4.0 | 0.8957 | 0.737 | 3.0 | 0.5 | 0.9176 | 1.193 |
| 0.3 | 5.0 | 0.8761 | 0.713 | 3.0 | 1.0 | 0.9032 | 1.130 |
| 0.3 | 6.0 | 0.8578 | 0.692 | 3.0 | 2.0 | 0.8776 | 1.035 |
| 0.5 | 0.1 | 0.9873 | 1.014 | 3.0 | 3.0 | 0.8547 | 0.968 |
| 0.5 | 0.5 | 0.9752 | 0.929 | 3.0 | 4.0 | 0.8363 | 0.902 |
| 0.5 | 1.0 | 0.9613 | 0.876 | 3.0 | 5.0 | 0.8175 | 0.860 |
| 0.5 | 2.0 | 0.9358 | 0.818 | 3.0 | 6.0 | 0.8003 | 0.824 |
| 0.5 | 3.0 | 0.9126 | 0.781 | 4.0 | 0.1 | 0.9036 | 1.340 |
| 0.5 | 4.0 | 0.8914 | 0.751 | 4.0 | 0.5 | 0.8916 | 1.274 |
| 0.5 | 5.0 | 0.8718 | 0.725 | 4.0 | 1.0 | 0.8777 | 1.207 |
| 0.5 | 6.0 | 0.8536 | 0.703 | 4.0 | 2.0 | 0.8523 | 1.109 |
| 1.0 | 0.1 | 0.9772 | 1.067 | 4.0 | 3.0 | 0.8293 | 1.039 |
| 1.0 | 0.5 | 0.965 | 0.989 | 4.0 | 4.0 | 0.8084 | 0.984 |
| 1.0 | 1.0 | 0.9509 | 0.932 | 4.0 | 5.0 | 0.7889 | 0.940 |
| 1.0 | 2.0 | 0.9252 | 0.863 | 4.0 | 6.0 | 0.7708 | 0.903 |
| NH4NO3-H2O | mmax (mol·kg−1) | BMX | U1MX | V1MX | W1MX | SDϕ × 03 | SDγ × 103 |
|---|---|---|---|---|---|---|---|
| 7.405 | −9.9030 | −0.7388 | 0.3779 | 0.2568 | 3.397 a | 1.65 a | |
| Sucrose–H2O | mmax (mol·kg−1) | w12 | u12 | SDφ × 102 | SDγ × 102 | ||
| 6.00 | −11.013 | 1.753 | 1.2124 | 2.0183 | |||
| NH4NO3–sucrose-H2O | N a | UNMX | VNMX | WNMX | Y0MNMX | Y1MNMX | SD × 103 |
| 57 | 2.306 | 0 | −7.317 | 3.006 | 0 | 1.003 |
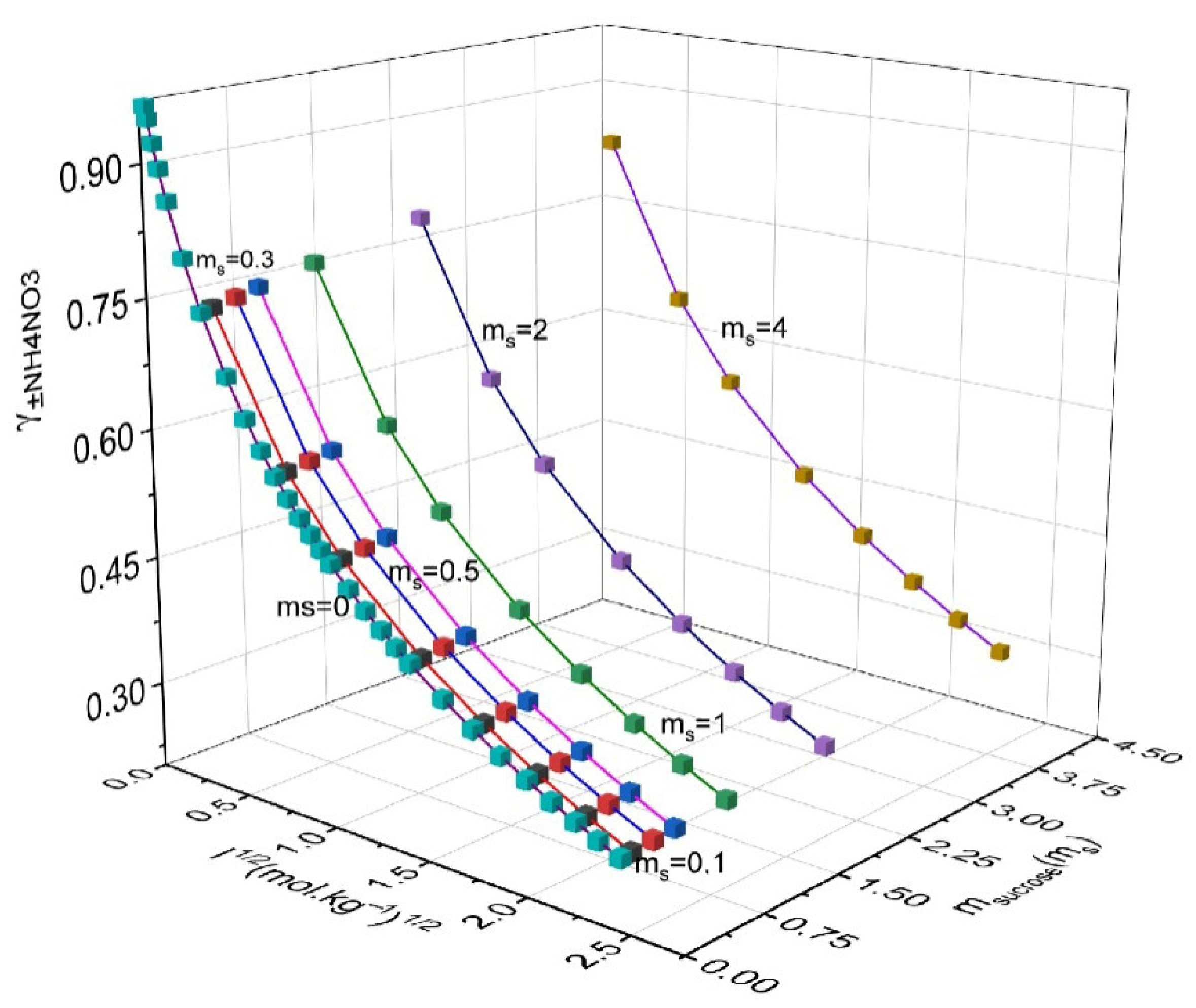
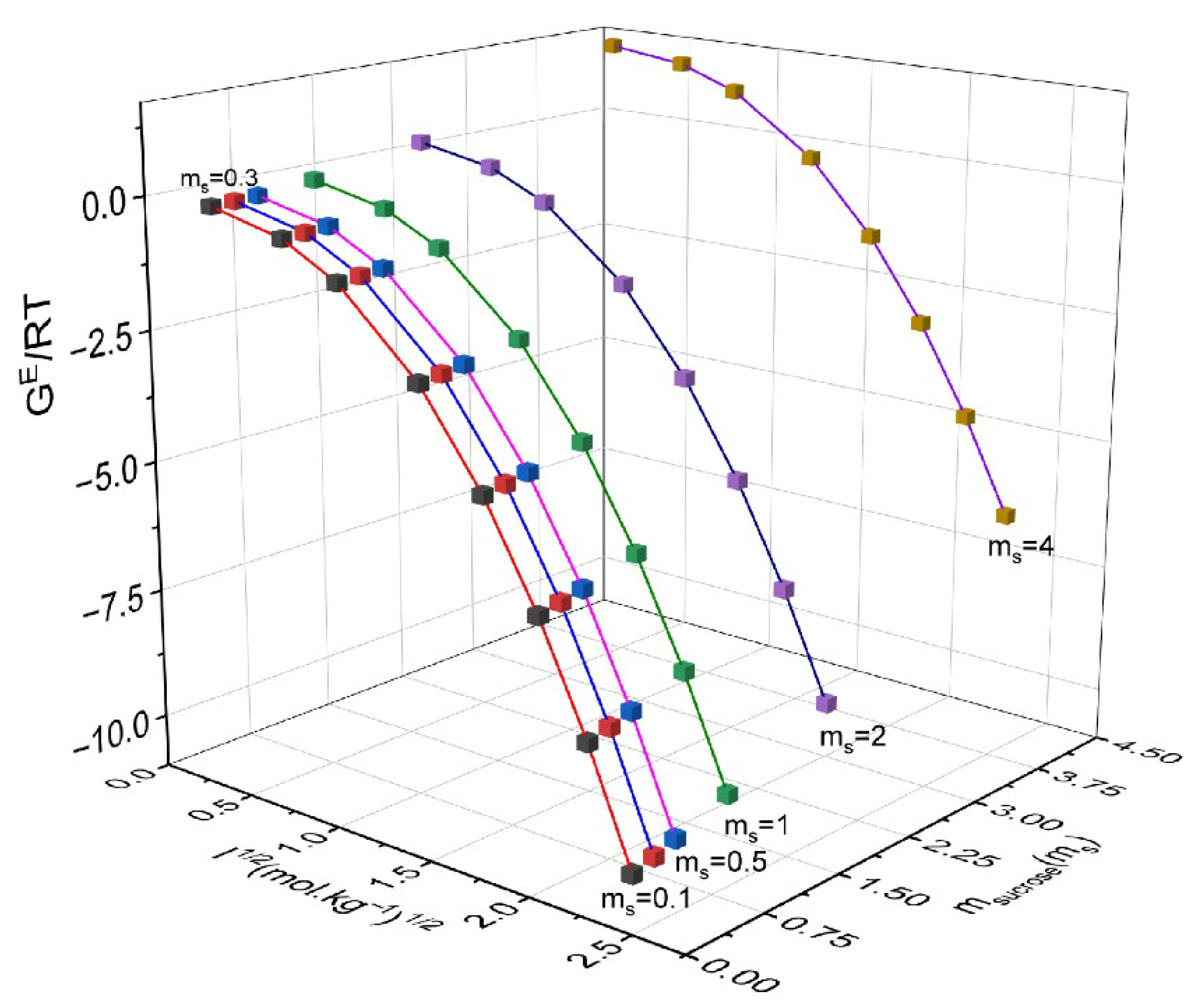
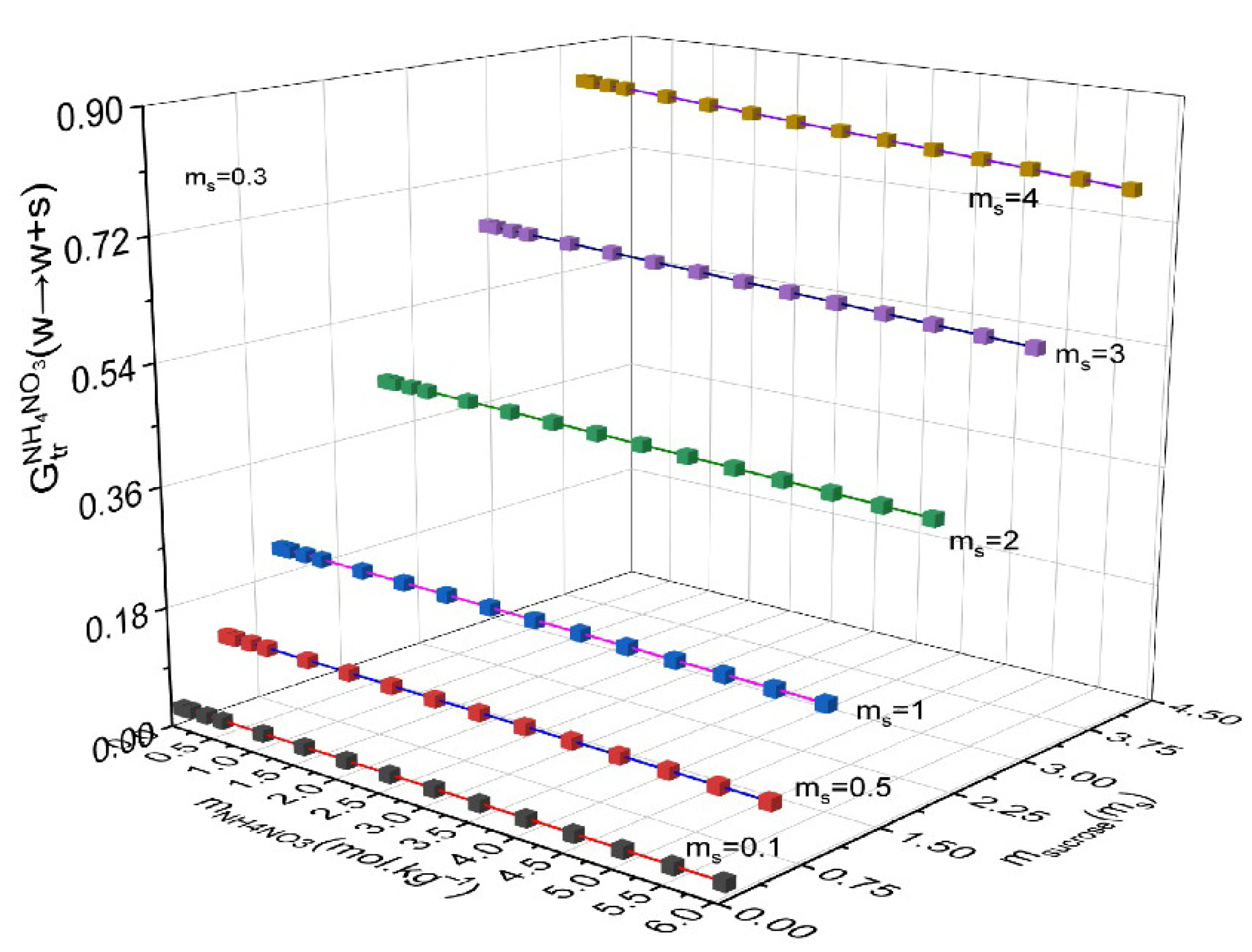
| msucrose/mol·kg−1 | mNH4NO3/mol·kg−1 | γ ± NH4NO3 | γsucrose | GE/RT | msucrose/mol·kg−1 | mNH4NO3/mol·kg−1 | γNH4NO3 | γsucrose | GE/RT |
|---|---|---|---|---|---|---|---|---|---|
| 0.10 | 0.10 | 0.751 | 0.783 | −0.038 | 1.00 | 0.10 | 0.774 | 0.927 | 0.073 |
| 0.10 | 0.50 | 0.586 | 0.662 | −0.373 | 1.00 | 0.50 | 0.605 | 0.783 | −0.224 |
| 0.10 | 1.00 | 0.504 | 0.620 | −0.959 | 1.00 | 1.00 | 0.520 | 0.731 | −0.763 |
| 0.10 | 2.00 | 0.419 | 0.598 | −2.416 | 1.00 | 2.00 | 0.432 | 0.699 | −2.128 |
| 0.10 | 3.00 | 0.368 | 0.601 | −4.112 | 1.00 | 3.00 | 0.379 | 0.699 | −3.734 |
| 0.10 | 4.00 | 0.332 | 0.614 | −5.974 | 1.00 | 4.00 | 0.341 | 0.710 | −5.510 |
| 0.10 | 5.00 | 0.304 | 0.633 | −7.964 | 1.00 | 5.00 | 0.312 | 0.728 | −7.416 |
| 0.10 | 6.00 | 0.281 | 0.655 | −10.058 | 1.00 | 6.00 | 0.289 | 0.750 | −9.429 |
| 0.30 | 0.10 | 0.756 | 0.813 | −0.027 | 2.00 | 0.10 | 0.799 | 1.114 | 0.388 |
| 0.30 | 0.50 | 0.590 | 0.687 | −0.354 | 2.00 | 0.50 | 0.624 | 0.939 | 0.130 |
| 0.30 | 1.00 | 0.508 | 0.643 | −0.929 | 2.00 | 1.00 | 0.537 | 0.873 | −0.360 |
| 0.30 | 2.00 | 0.422 | 0.619 | −2.366 | 2.00 | 2.00 | 0.445 | 0.831 | −1.630 |
| 0.30 | 3.00 | 0.371 | 0.621 | −4.041 | 2.00 | 3.00 | 0.390 | 0.825 | −3.143 |
| 0.30 | 4.00 | 0.334 | 0.634 | −5.883 | 2.00 | 4.00 | 0.351 | 0.833 | −4.829 |
| 0.30 | 5.00 | 0.306 | 0.653 | −7.854 | 2.00 | 5.00 | 0.321 | 0.848 | −6.648 |
| 0.30 | 6.00 | 0.283 | 0.675 | −9.929 | 2.00 | 6.00 | 0.296 | 0.869 | −8.577 |
| 0.50 | 0.10 | 0.761 | 0.844 | −0.009 | 4.00 | 0.10 | 0.841 | 1.589 | 1.607 |
| 0.50 | 0.50 | 0.594 | 0.713 | −0.327 | 4.00 | 0.50 | 0.658 | 1.333 | 1.418 |
| 0.50 | 1.00 | 0.512 | 0.667 | −0.892 | 4.00 | 1.00 | 0.566 | 1.232 | 1.013 |
| 0.50 | 2.00 | 0.425 | 0.641 | −2.307 | 4.00 | 2.00 | 0.469 | 1.157 | −0.087 |
| 0.50 | 3.00 | 0.373 | 0.643 | −3.963 | 4.00 | 3.00 | 0.411 | 1.134 | −1.436 |
| 0.50 | 4.00 | 0.336 | 0.655 | −5.785 | 4.00 | 4.00 | 0.369 | 1.132 | −2.962 |
| 0.50 | 5.00 | 0.307 | 0.674 | −7.737 | 4.00 | 5.00 | 0.336 | 1.140 | −4.627 |
| 0.50 | 6.00 | 0.285 | 0.696 | −9.795 | 4.00 | 6.00 | 0.310 | 1.156 | −6.405 |
| gEN J.kg.mol−2 | gEEN J.kg.mol−3 | gENN J.kg.mol−3 | R2% | ηs |
|---|---|---|---|---|
| 137.89 | −7.73561 | −5.93842 | 99.99 | 0.2225 |
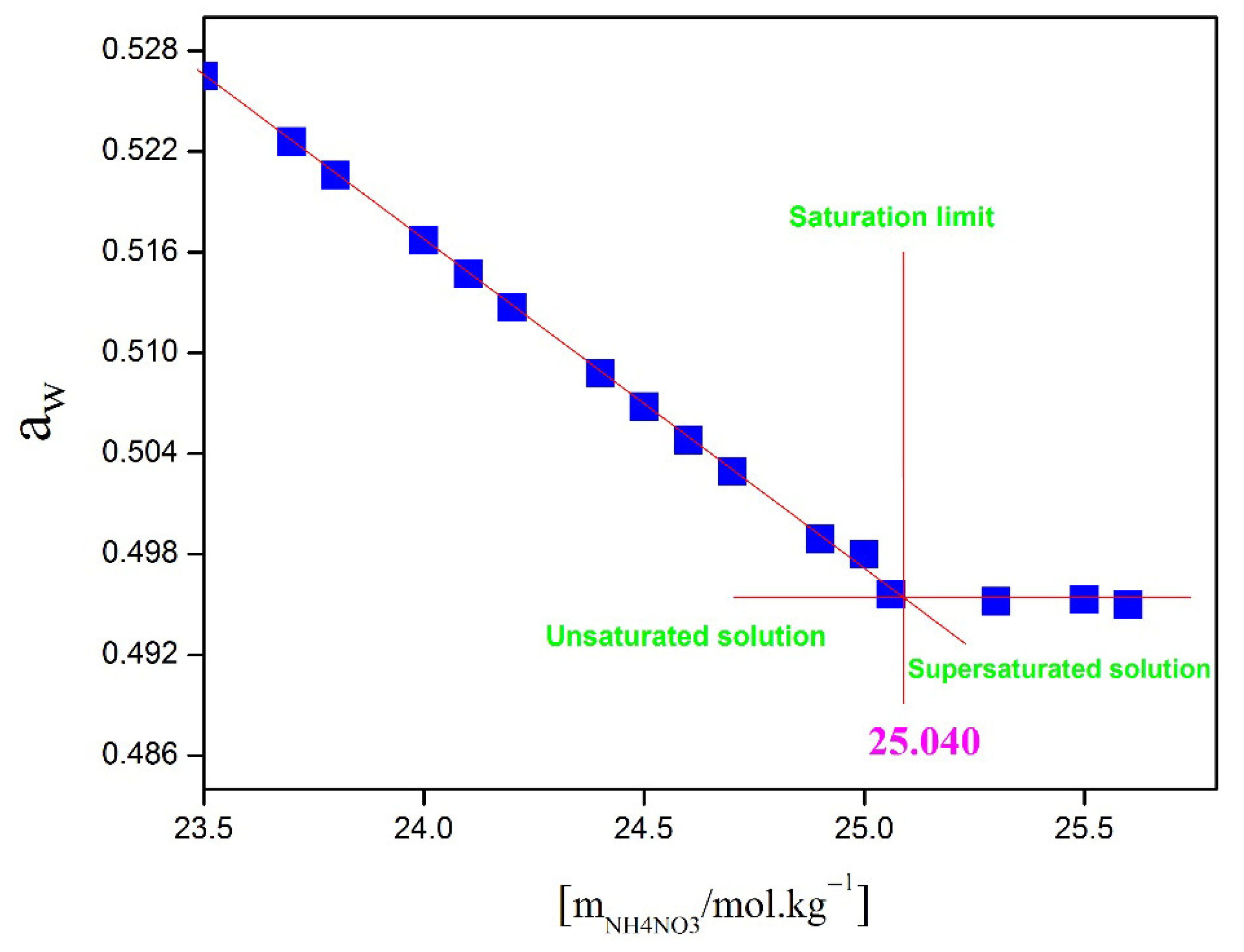
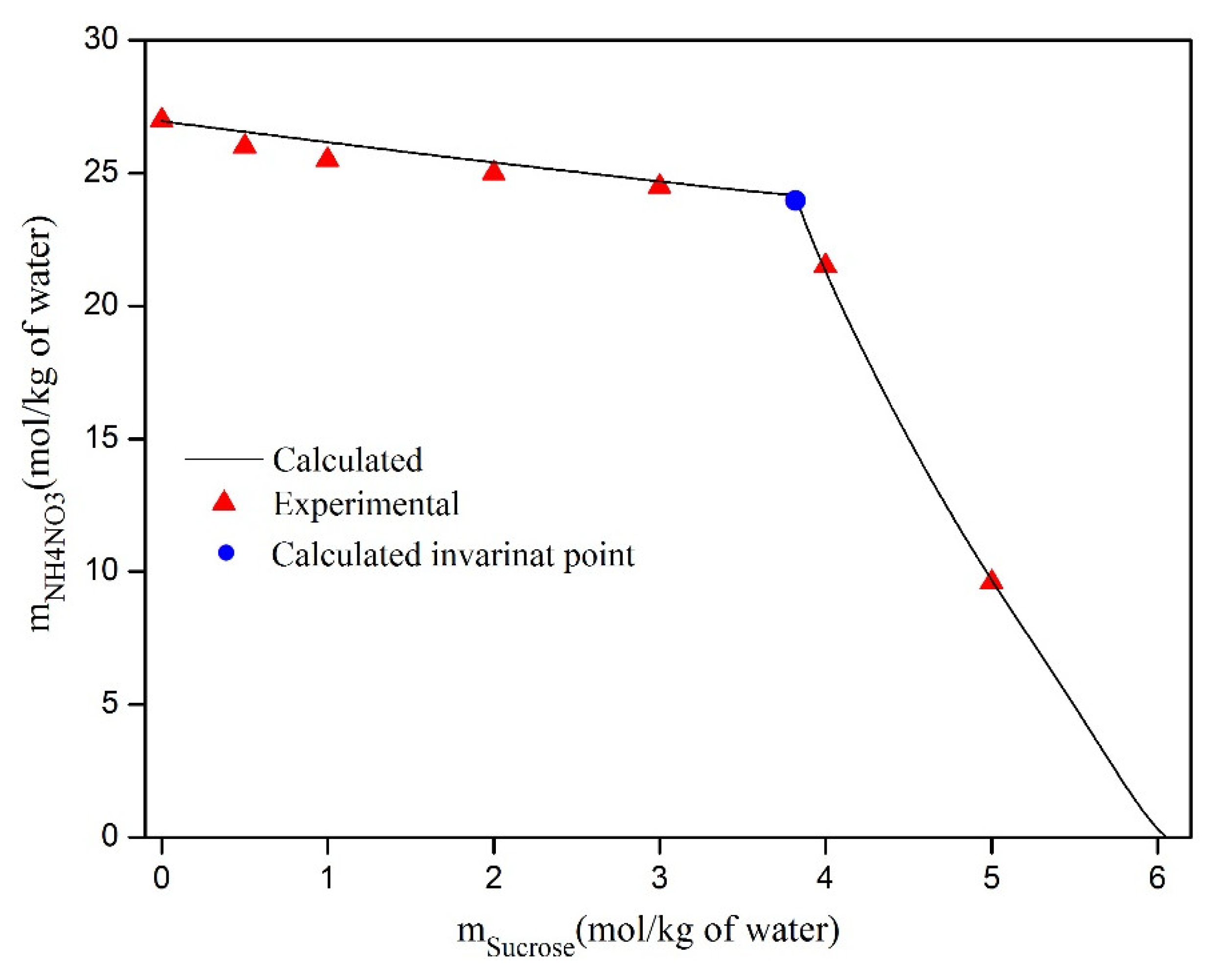
| msucrose (mol·kg−1) | Solubility of NH4NO3 (mol·kg−1) | Uncertainty | Crystalline Solid |
|---|---|---|---|
| 0.00 | 26.955 | 0.527 | NH4NO3(S) |
| 2.50 | 25.040 | 0.415 | NH4NO3(S) |
| 2.80 | 24.828 | 0.634 | NH4NO3(S) |
| 3.10 | 24.620 | 0.293 | NH4NO3(S) |
| 3.40 | 24.416 | 0.591 | NH4NO3(S) |
| Solubility of sucrose (mol·kg−1) | mNH4NO3 (mol·kg−1) | Uncertainty | Crystalline Solid |
| 5.98 | 0.200 | 0.120 | Sucrose(S) |
| 4.19 | 18.700 | 0.108 | Sucrose(S) |
| 6.00 | 0.000 | 0.152 | Sucrose(S) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Fadel, W.; El Hantati, S.; Nour, Z.; Dinane, A.; Messnaoui, B.; Mounir, A.; Samaouali, A.; Arbaoui, A. Experimental and Modeling Study of the Thermodynamic Behavior and Solubility of the NH4NO3–D-Sucrose–Water Ternary System at 298.15 K. Processes 2025, 13, 3438. https://doi.org/10.3390/pr13113438
El Fadel W, El Hantati S, Nour Z, Dinane A, Messnaoui B, Mounir A, Samaouali A, Arbaoui A. Experimental and Modeling Study of the Thermodynamic Behavior and Solubility of the NH4NO3–D-Sucrose–Water Ternary System at 298.15 K. Processes. 2025; 13(11):3438. https://doi.org/10.3390/pr13113438
Chicago/Turabian StyleEl Fadel, Wiam, Soukaina El Hantati, Zineb Nour, Abderrahim Dinane, Brahim Messnaoui, Abdelfetah Mounir, Abderrahim Samaouali, and Asmae Arbaoui. 2025. "Experimental and Modeling Study of the Thermodynamic Behavior and Solubility of the NH4NO3–D-Sucrose–Water Ternary System at 298.15 K" Processes 13, no. 11: 3438. https://doi.org/10.3390/pr13113438
APA StyleEl Fadel, W., El Hantati, S., Nour, Z., Dinane, A., Messnaoui, B., Mounir, A., Samaouali, A., & Arbaoui, A. (2025). Experimental and Modeling Study of the Thermodynamic Behavior and Solubility of the NH4NO3–D-Sucrose–Water Ternary System at 298.15 K. Processes, 13(11), 3438. https://doi.org/10.3390/pr13113438






