Polymerization Reaction Kinetics of Poly α-Olefin and Numerical Simulation of a Continuous Polymerization Reactor

Abstract

The hydrodynamic and reaction characteristics of poly-alpha-olefin (PAO) polymerization in a continuous stirred tank reactor (CSTR) under Eulerian–Eulerian multiphase flow and a finite-rate chemical kinetics model were studied in this paper. A mathematical framework correlating 1-decene conversion with operational and structural parameters was established. Numerical simulations revealed an axial circulation flow pattern driven by combined impellers, with internal coils enhancing heat exchange and flow guidance. The gaseous catalyst, injected below the turbine impeller, achieved rapid dispersion and low gas holdup. The results demonstrated that 1-decene conversion exhibited insensitivity to impeller speed under fully turbulent mixing (mixing time <0.15% of space time), suggesting limited mass transfer benefits from further speed increases. Conversion positively correlated with temperature and space time, albeit with diminishing returns at prolonged durations. Series reactor configurations improved conversion efficiency, though incremental gains decreased with additional units. Optimal reactor design should balance conversion targets with economic factors, including energy consumption and capital investment. These findings provide critical insights into scaling PAO polymerization processes, emphasizing the interplay between reactor geometry, mixing dynamics, and reaction kinetics for industrial applications.

1. Introduction

With the development of modern industry, the use of various new energy vehicles and high-precision mechanical equipment has led to a growing demand for high-grade lubricating oils, which plays a crucial role in reducing friction, maintaining the efficient operation of machinery, and minimizing wear and tear, thereby extending the service life of mechanical components.

Lubricating oils are composed of base oils and various additives, where the main component base oil generally determines the quality of the lubricant. Among various base oils, fully synthetic poly-alpha-olefin (PAO) is recognized as an ideal high-quality base oil. Compared with traditional mineral oils, PAO can meet the increasingly stringent performance requirements and usage demands for lubricants. PAO exhibits a regular molecular structure, high viscosity index, low pour point, low low-temperature viscosity, and excellent thermal and oxidative stability. In addition to its applications in advanced technological fields, PAO has also found widespread usages in various industries. The most commonly used type of PAO is low-viscosity oil, which accounts for approximately 90% of the total PAO consumption. It is primarily employed in engine oils, hydraulic oils, automatic transmission fluids, gear oils, offshore drilling fluids, and fiber-optic filling oils.

Many current studies, including those employing experimental methods [1,2] and numerical simulations [3,4], have been able to effectively elucidate the relationship between mixing processes and polymerization reactions. However, in experimental research, obtaining parameters related to the mixing process within the reactor (such as mixing time and space time) and enhancing the spatial accuracy of experimental results are both challenging [5,6]. Moreover, the complex physical properties and spatial distribution characteristics of polymerization reaction systems make quantitative measurements and flow visualization studies even more difficult and time-consuming [7]. Therefore, developing a model that can relate the polymerization reactions with the transport processes is not only necessary and important but also highly challenging.

Computational fluid dynamics (CFD) serves as a powerful tool capable of effectively characterizing the intricate details between transport and reaction processes. CFD studies primarily focused on the flow and mixing within reactors [8,9], while the coupling of polymerization reaction kinetics to solve for species concentration distributions has been less frequently reported [10]. The complex interplay among flow mixing, heat transfer, and reactions during polymerization processes further complicates CFD investigations.

Although many attempts have been made in CFD studies coupled with polymerization reactions [11,12,13], there are still some shortcomings that require further research. Current studies mainly focus on laboratory-scale reactors [14,15], with few investigations extending to industrial-scale polymerization reactors. As is well known, during the scale-up from the laboratory to industrial scale, the non-idealities within the reactor become more pronounced on the polymerization process, making relevant scale-up studies more challenging. More importantly, research should pay greater attention to the impact between the mixing process during the reaction and the quality of the polymer product, which would be conducive to accurately guiding industrial production.

In this work, firstly, the flow characteristics within a PAO polymerization reactor were elucidated by numerical simulation. Subsequently, through theoretical analysis, the relationship between the conversion rate of 1-decene in a continuous stirred tank reactor (CSTR) and the operating and structural parameters was established. Finally, the principal aim of this study is to examine the influence of operating conditions and structural parameters on the conversion rate of 1-decene in an industrial-scale PAO polymerization reactor.

Therefore, the structure of this paper is organized as follows: in Section 2, we introduce the flow systems of the polymerization reactor. Following that, an overview of the numerical methods and a discussion of the numerical strategy employed are provided. In Section 4, we analyze the flow pattern and phase distribution in the reactor. After that, a mathematical model for the conversion rate in an idealized PAO polymerization reactor is derived through theoretical analysis. Subsequently, we examine the conversion rate of 1-decene under various operating conditions and reactor configurations, which aids in identifying and controlling the flow characteristics in the industrial-scale PAO polymerization reactor. Finally, the paper concludes with a summary of the key findings.

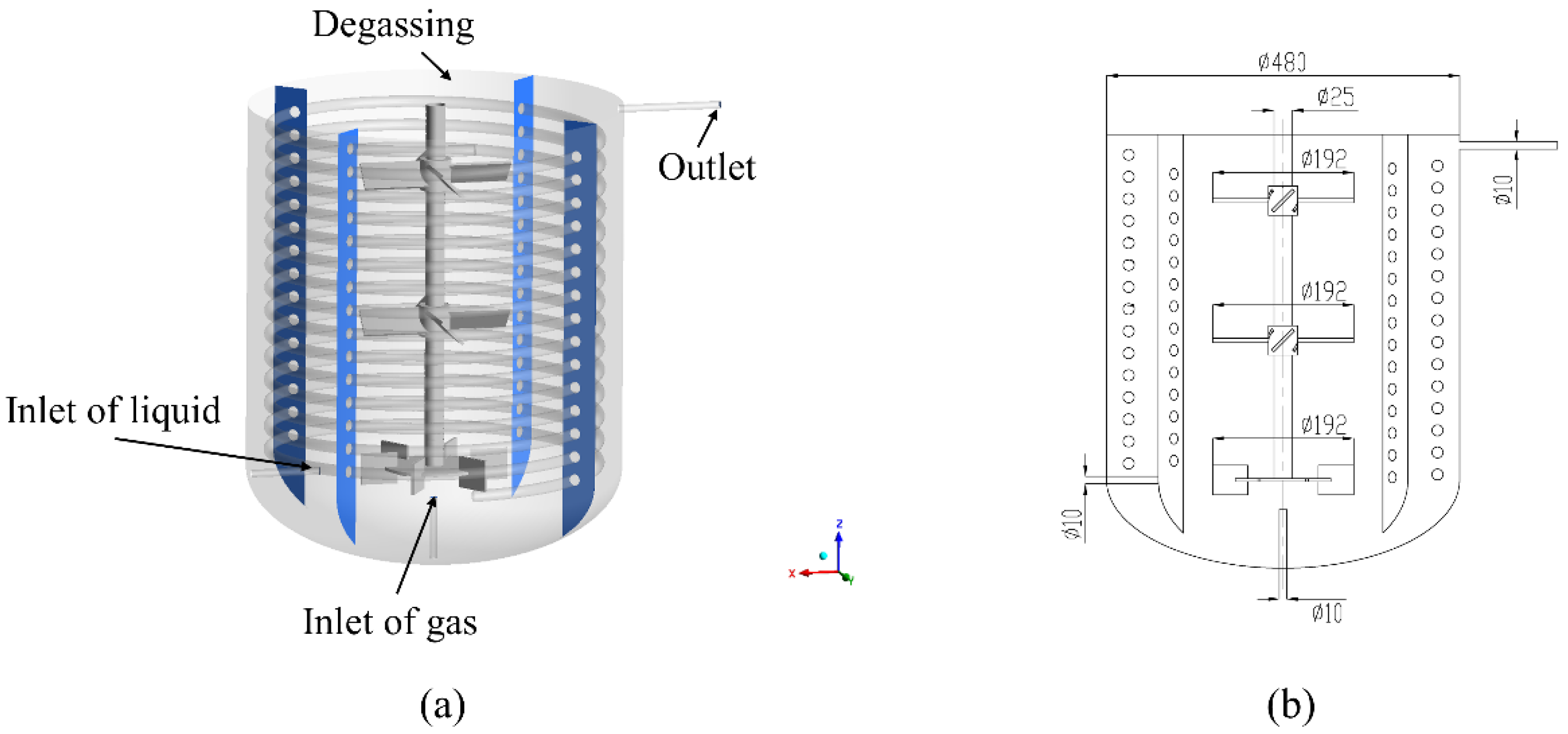
2. Polymerization Reactor System

The schematic diagram of the flow system is depicted in Figure 1. The reactor is a standard elliptical-bottom stirred tank with an internal diameter of 480 mm. Four standard baffles are installed within the reactor, oriented at a 45° angle relative to the direction of the material outlet. A coil with an outer diameter of 15 mm is positioned inside the reactor. The impeller assembly consists of three stages: the upper two stages are pitched-blade turbines (PBT), while the bottom is a standard Rushton turbine (RT). The diameter of each impeller is 192 mm, with a spacing of 190 mm between two adjacent impellers. The impellers are driven by a shaft with a diameter of 25 mm. Liquid material feed enters the reactor horizontally through a 10 mm diameter pipe, whereas the gaseous material feed is introduced axially through a 10 mm diameter pipe from the bottom of the reactor. The reactor is equipped with a degassing port at the top, which permits only the gas phase to escape. The liquid product is withdrawn through an outlet on the side of the reactor head, with an outlet pipe diameter of 10 mm.

The simulation scheme in the present work is listed in

Table 1. Numerical simulation schemes.

Case	Temperature (°C)	Impeller Speed (rpm)	Number of Reactors (-)	Liquid Space Time (h)
1	30	50	1	4.2
2	30	100	1	4.2
3	30	150	1	4.2
4	30	200	1	4.2
5	10	100	1	4.2
6	50	100	1	4.2
7	70	100	1	4.2
8	30	100	1	2.1
9	30	100	1	6.3
10	30	100	1	8.4
11	30	100	2	4.2
12	30	100	3	4.2

. Cases 1 to 4 investigate the influence of the impeller speed on the polymerization process. Case 2 and Cases 5 to 7 examine the impact of temperature on the reaction. Case 2 and Cases 8 to 10 assess the effects of liquid space time on the reaction. Case 2, Case 11, and Case 12 compare the influence of the number of reactors in series on the reaction.

Table 2. Physical properties of material.

Material	Density/kg m−3	Viscosity/Pa s
BF3	6.575	1.789 × 10−5
1-decene	740	9 × 10−4
PAO	830	8.4 × 10−3

gives the properties of BF₃, 1-decene, and PAO used in this work.

3. Numerical Simulation Method

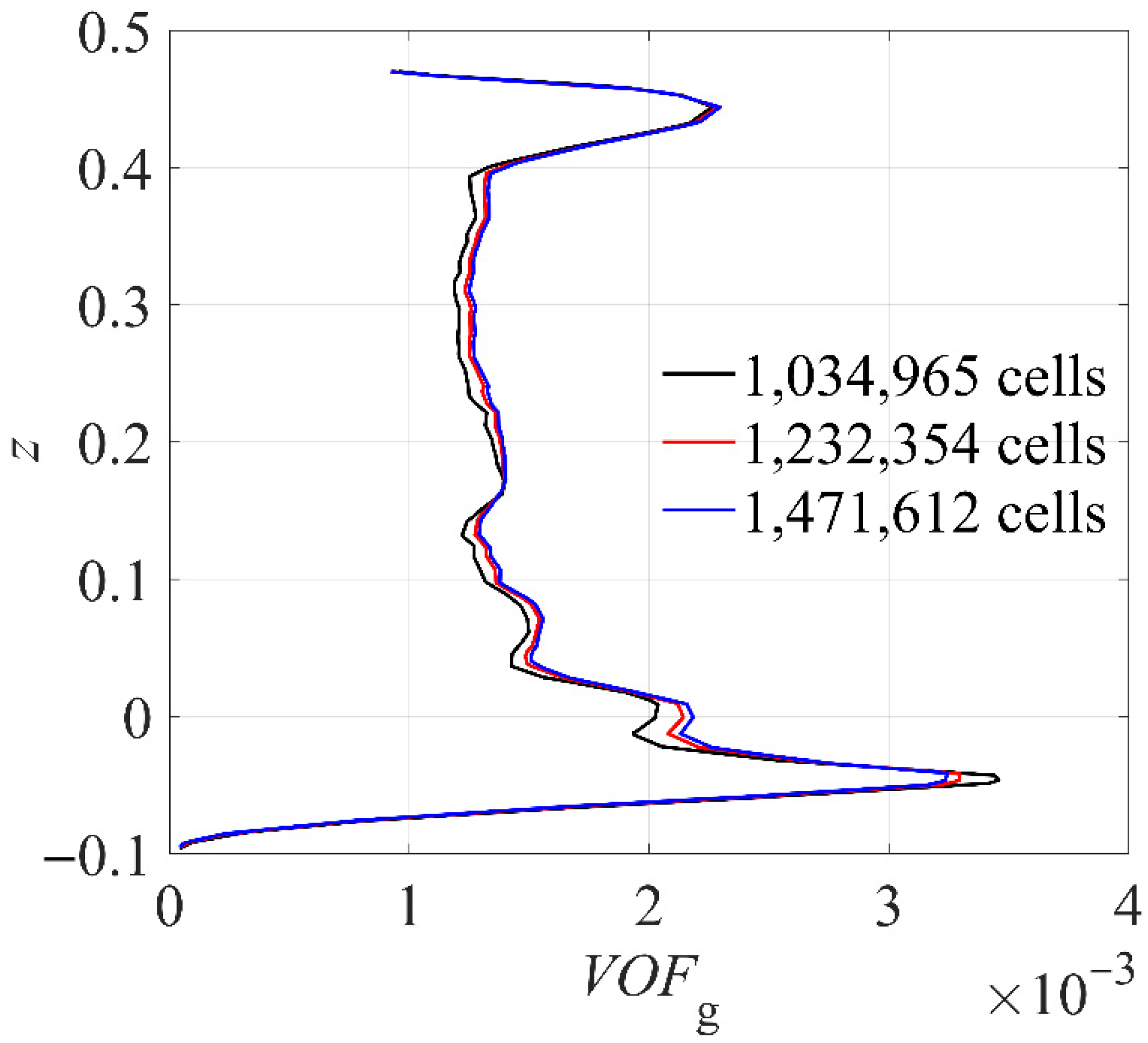
3.1. Numerical Method

In this study, the Eulerian–Eulerian two-fluid model was used to characterize the gas–liquid two-phase flow. Here, the gas phase is the dispersed phase, whereas the liquid phase serves as the continuous phase. Each phase adheres to its own continuity and momentum equations, which are presented as follows:

$${\displaystyle \frac{𝜕\left({\alpha }_q{\rho }_q\right)}{𝜕t}}+\nabla \cdot \left({\alpha }_q{\rho }_q{\mathit{v}}_q\right)=0$$

(1)

$${\displaystyle \frac{𝜕\left({\alpha }_q{\rho }_q{\mathit{v}}_q\right)}{𝜕t}}+\nabla \cdot \left({\alpha }_q{\rho }_q{\mathit{v}}_q\right)=-{\alpha }_q\nabla p+\nabla \cdot \left({\alpha }_q{\tau }_q\right)+{\alpha }_q{\rho }_{q}g+{\mathit{M}}_q$$

(2)

where $t$, $p$, and $g$ represent time, pressure, and gravity, respectively. ${\alpha }_q$, $p$, ${\mathit{v}}_q$, ${\tau }_q$, and $M_q$ denote the phase fraction, phase density, phase velocity vector, stress tensor, and interphase momentum transfer term of phase q, respectively. Here, q represents either the gas phase (g) or the liquid phase (l).

In this work, we treat the polymerization reaction under isothermal conditions, so that the energy equation was not applied. Additionally, the simulation of the reactive flow encompasses solving the transport equations for each component involved in the copolymerization reaction. As the PAO polymerization process involves a gas–liquid two-phase system and includes a significant number of reactive components, for ease of description, these components are classified into the following three categories:

① The gaseous component (catalyst BF₃). Its concentration change is primarily due to convective mass transfer from the gas phase to the liquid phase. The corresponding species equation is as follows:

$${\displaystyle \frac{𝜕\left({\alpha }_g{\rho }_g{Y}_g\right)}{𝜕t}}+\nabla \cdot \left({\alpha }_g{\rho }_g{\mathit{v}}_q{Y}_g\right)=\nabla \cdot \left({\alpha }_g{\rho }_g{D}_g\nabla Y_g\right)-m_{g\to l}$$

(3)

where ${\mathit{m}}_{g\to l}$ represents the mass transfer rate of BF₃ per unit volume from the gas phase (g) to the liquid phase (l) (kg/(m³·s)).

② The catalyst BF₃ dissolving in the liquid phase. Its concentration change is sourced from convective mass transfer from the gas phase to the liquid phase. The corresponding species equation is as follows:

$${\displaystyle \frac{𝜕\left({\alpha }_l{\rho }_l{Y}_{l,j}\right)}{𝜕t}}+\nabla \cdot \left({\alpha }_l{\rho }_l{\mathit{v}}_q{Y}_{l,i}\right)=\nabla \cdot \left({\alpha }_l{\rho }_l{D}_{l,i}\nabla Y_{l,i}\right)+m_{g\to l}$$

(4)

③ Other reactive components in the liquid phase. These components include the feedstock 1-decene, PAO, etc. The changes in their concentrations are primarily due to the polymerization reactions. The corresponding species equations are as follows:

$${\displaystyle \frac{𝜕\left({\alpha }_l{\rho }_l{Y}_{l,j}\right)}{𝜕t}}+\nabla \cdot \left({\alpha }_l{\rho }_l{\mathit{v}}_q{Y}_{l,i}\right)=\nabla \cdot \left({\alpha }_l{\rho }_l{D}_{l,i}\nabla Y_{l,i}\right)+{\alpha }_l{S}_i$$

(5)

where $Y_{l,j}$ is the mass fraction of species i, $D$ is the diffusion coefficient and is set as 1.3 × 10⁻¹⁰ m²/s according to the work of Schmitt et al. for 1-decene [16], and S represents the reaction rate source term for component i (kg/(m³·s)). The density of the mixture follows the volume-weighted mixture law. The effective viscosity of the mixture is calculated by using the mass-weighted mixing law.

The hydrodynamic behavior in agitated vessels typically exhibits complex turbulence characteristics. To resolve this challenge, the standard k-ε model was employed in this study. This turbulence closure scheme presumes fully developed turbulence. The governing equation for turbulent kinetic energy transport is expressed as follows:

$${\displaystyle \frac{𝜕}{𝜕t}}\left(\rho k\right)+{\displaystyle \frac{𝜕}{𝜕x_j}}\left(\rho k{u}_j\right)={\displaystyle \frac{𝜕}{𝜕x_j}}\left(\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\right){\displaystyle \frac{𝜕k}{𝜕x_j}}\right)+\mu {\displaystyle \frac{𝜕u_i}{𝜕x_j}}\left({\displaystyle \frac{𝜕u_i}{𝜕x_j}}+{\displaystyle \frac{𝜕u_j}{𝜕x_i}}\right)-\rho e$$

(6)

$${\displaystyle \frac{𝜕}{𝜕t}}\left(\rho e\right)+{\displaystyle \frac{𝜕}{𝜕x_j}}\left(\rho e{u}_j\right)={\displaystyle \frac{𝜕}{𝜕x_j}}\left(\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_e}}\right){\displaystyle \frac{𝜕e}{𝜕x_j}}\right)+{\displaystyle \frac{c_1\epsilon }{k}}{\mu }_i{\displaystyle \frac{𝜕u_i}{𝜕x_k}}\left({\displaystyle \frac{𝜕u_i}{𝜕x_k}}+{\displaystyle \frac{𝜕u_k}{𝜕x_i}}\right)-{\displaystyle \frac{c_2\rho e^2}{k}}$$

(7)

where

$${\mu }_t={\displaystyle \frac{c_{\mu }\rho k^2}{\epsilon }}$$

(8)

The empirical constants in the model are as follows: $c_1$= 1.44, $c_2$ = 1.92, $c_{\mu }$= 0.09, ${\sigma }_k$= 1.0, and ${\sigma }_e$= 1.3.

3.2. Numerical Setup

In the present work, simulations were conducted using the reactor configuration introduced previously. The mesh, comprising approximately 1.2 million polyhedral elements, was constructed in Fluent Meshing. As shown in Figure 2, this grid type was selected to enhance both computational efficiency and numerical accuracy relative to traditional tetrahedral-cell schemes.

The Ansys Fluent 19.0 software was employed with a pressure-based solver. The gravitational acceleration was 9.81 m/s² in the negative z-direction. The simulation of rotor motion employed the multiple reference frame technique. The spatial discretization for species conservation equations used the third-order MUSCL scheme. Coupling of pressure and velocity was achieved through the SIMPLE algorithm. The second-order implicit scheme was used for time advancement. All the wall boundaries were maintained as no-slip. The initial conditions for the simulation were set as follows: all fluid velocities were zero, the gas volume fraction was zero, the material conversion rate inside the reactor was zero, and the temperature was set according to the value specified in Section 4.3.1.

In this study, all simulations were carried out using a steady-state solver, except for the mixing time analysis, which was performed with a transient solver. For the transient simulation, a time step of 0.01 s was applied, and the Courant number was 0.01. Convergence was achieved when the normalized residuals of the continuity, mass fraction, and velocities were lower than 10⁻⁴.

A grid independence study was systematically conducted to ensure result reliability. As shown in Figure 3, the gas volume fraction distribution along a vertical line in the reactor exhibits negligible differences once the mesh size exceeds 1.23 million cells. Therefore, to achieve an optimal balance between computational cost and numerical accuracy, all subsequent simulations were carried out using the grid model with approximately 1.23 million elements.

4. Results and Discussion

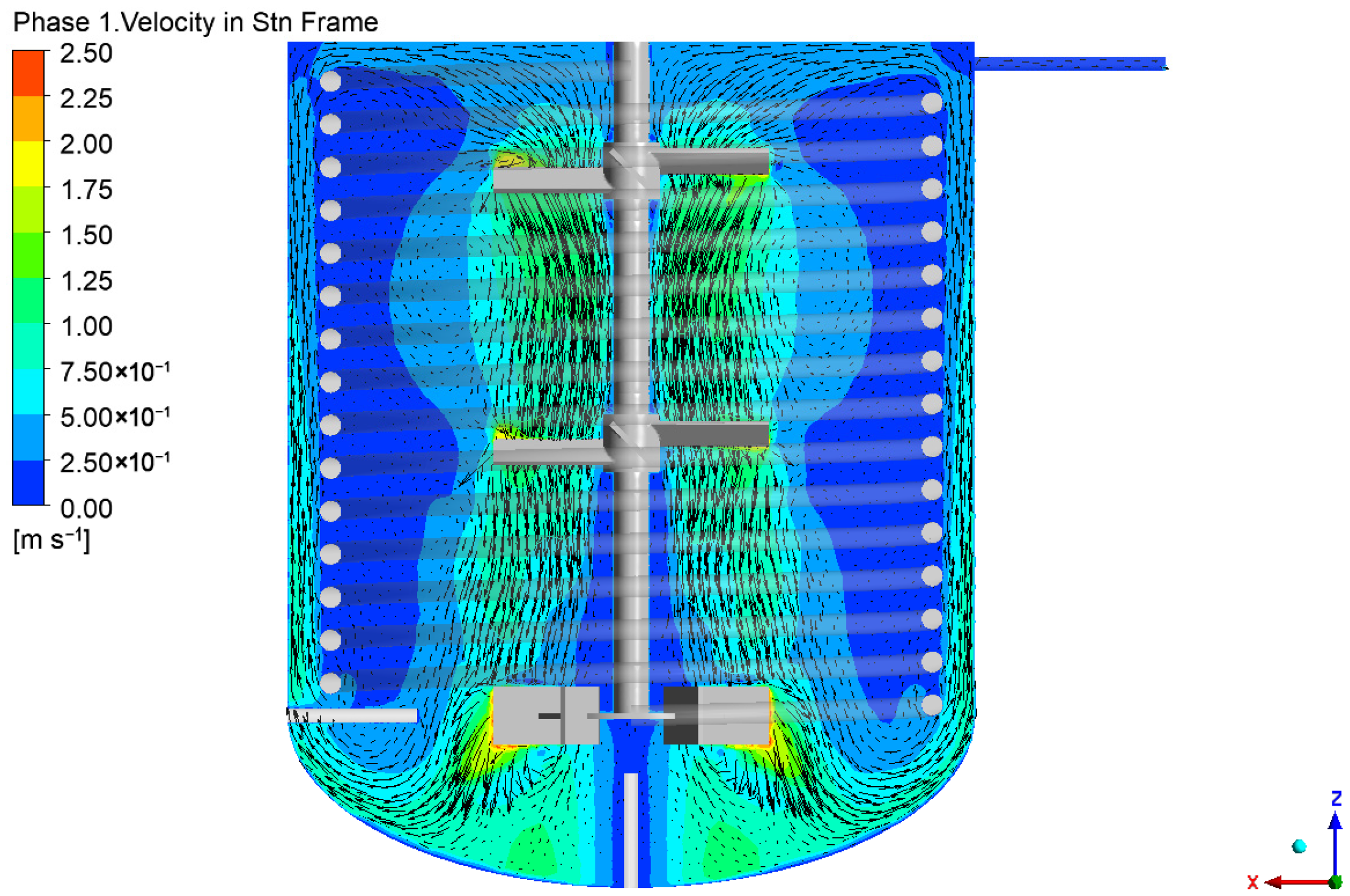
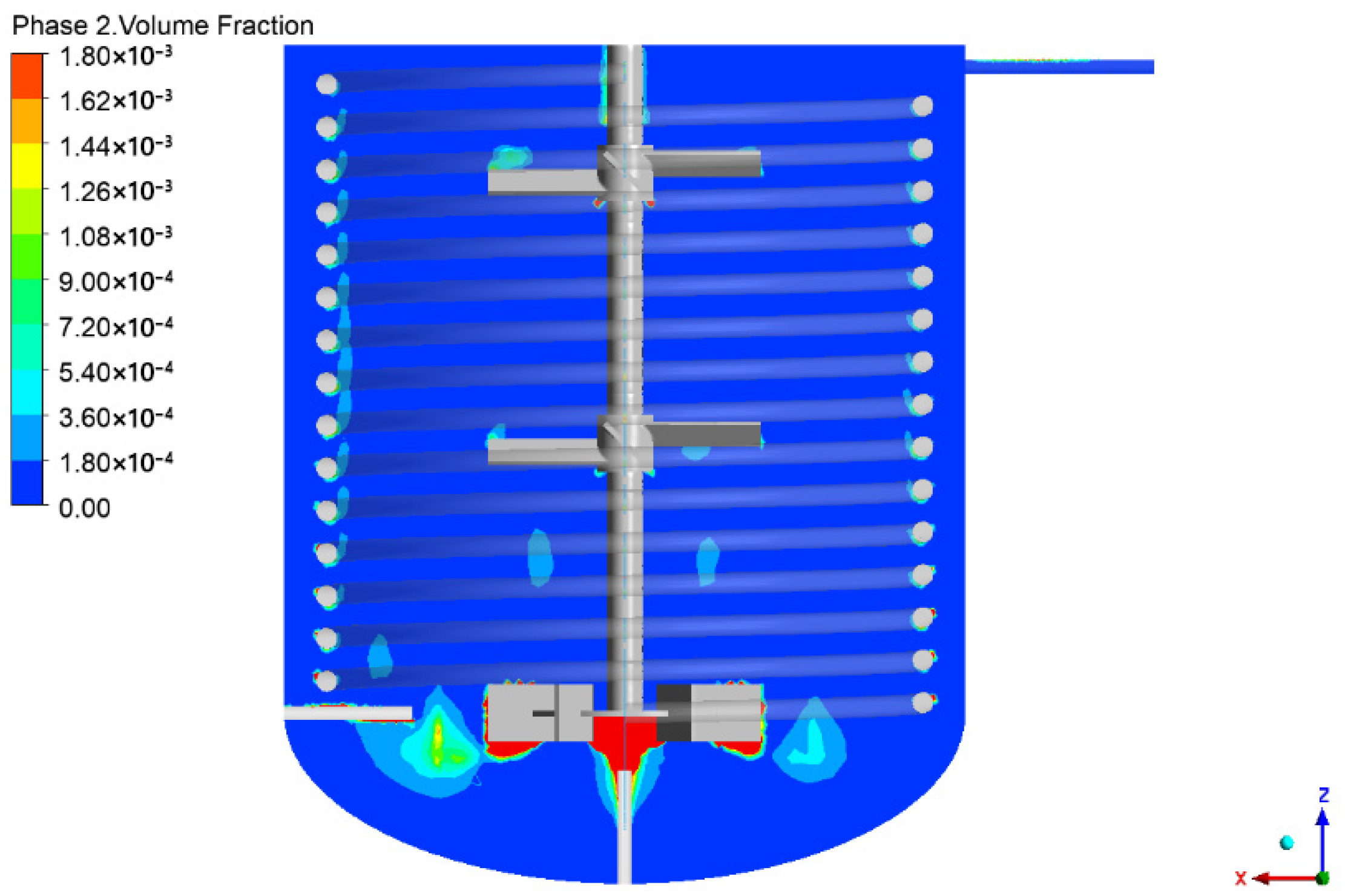
4.1. Flow Field in the Reactor

The hydrodynamic characteristics within the reactor remain similar under the operating conditions. To demonstrate the hydrodynamic behavior within the reactor, Figure 4 presents the liquid velocity and gas holdup distributions under the following specific conditions: impeller rotational speed of 50 rpm, liquid space time of 4.2 h, and reaction temperature of 30 °C.

As shown in Figure 4, the multiple impellers generate an axial circulation flow pattern from top to the bottom of the reactor, with the flow field being axially symmetrical on both sides of the shaft. Additionally, the presence of the coil in the reactor can significantly influence the fluid dynamics. The coil guides the fluid, promoting an overall axial circulation within the reactor. This flow configuration is highly beneficial for achieving a rapid mixing of materials within the reactor.

Figure 5 illustrates the distribution of gas holdup within the reactor. The overall gas holdup in the reactor is relatively low due to the small amount of gaseous catalyst BF₃ required for the PAO polymerization reaction. In terms of distribution, the gaseous components are imported through the gas inlet, drawn in by the bottom impeller, and then discharged radially. After the quick dispersion, the catalyst is involved in the gas–liquid mass transfer process. Some of the gases are confined near the bottom of the reactor by the lower circulation, where they can further dissolve. This type of flow field is conducive to the efficient utilization of the gaseous catalyst BF₃.

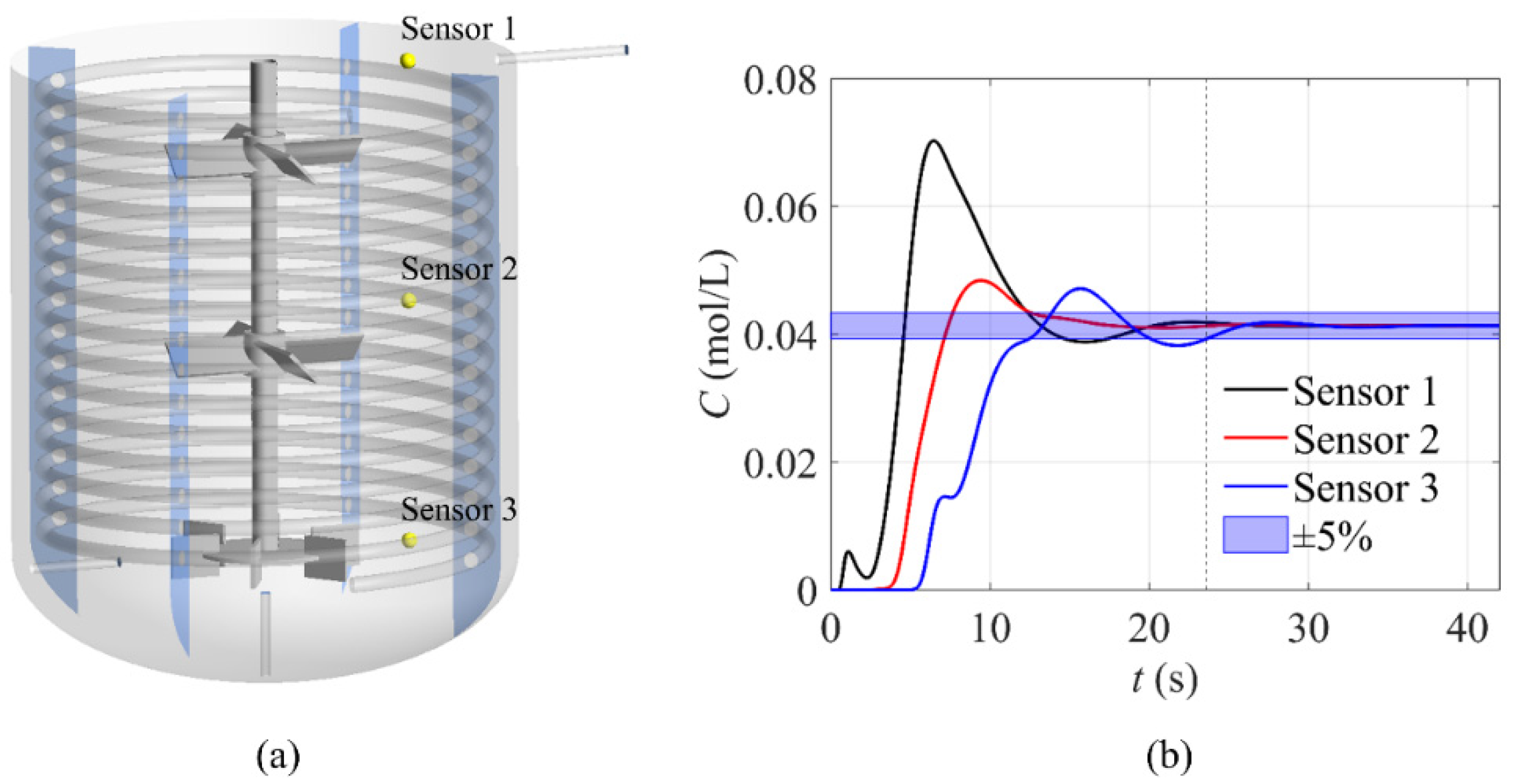
4.2. Analysis of Reaction and the Mixing Time in the Reactor

The reaction rate mainly depends on the olefin concentration, the catalyst concentration, and the reaction temperature. The kinetic equation of reaction can be expressed as follows:

$$r_A=A{e}^{-E_a/RT}{C}_{ca}^a{C}_m^b$$

(9)

where $r_A$ is the reaction rate based on the reduction rate of olefin monomer (mol/(L·s)), A is the pre-exponential factor, E_a is the activation energy (J/mol), R is the gas constant (8.314 J/(mole·K)), T is the reaction temperature (K), C_ca is the concentration of catalyst (mol/L), and C_m is the olefin concentration (mol/L). a and b are, respectively, the order of catalyst concentration and olefin concentration. Based on the previous research [17], the reaction kinetic equation is as follows:

$$r_A=0.63e^{-16817/RT}{C}_{cat}{C_A}^2$$

(10)

Now, the material balance in the continuous stirred tank reactor (CSTR) is as follows:

$$F_{A0}=F_{Af}+\left(-r_A\right)V_R+0$$

(11)

where $F_{A0}$ is the amount of material A entering the reactor per unit time, and $F_{Af}$ is the amount of material discharged from the reactor per unit time,

$$F_{Af}=F_{A0}\left(1-x_A\right)$$

(12)

where $\left(-r_A\right)V_R$ is the amount of material A consumed per unit time, and 0 means that there is no accumulation of material a per unit time.

Rearranging the above equation, there is the follows:

$${\displaystyle \frac{V_R}{F_{A0}}}={\displaystyle \frac{x_A-x_{A0}}{\left(-r_A\right)}}$$

(13)

As

$$F_{A0}=V_0{c}_{A0}$$

(14)

So

$$\tau ={\displaystyle \frac{V_R}{V_0}}=c_{A0}{\displaystyle \frac{x_A-x_{A0}}{\left(-r_A\right)}}$$

(15)

When the inlet conversion is 0 and the reactor volume is constant,

$$\tau ={\displaystyle \frac{c_{A0}-c_A}{\left(-r_A\right)}}$$

(16)

Substituting the macroscopic reaction kinetics, we get

$$\tau ={\displaystyle \frac{c_{A0}-c_A}{A{e}^{-E_a/RT}{C}_{cat}{C_A}^2}}={\displaystyle \frac{x_A}{A{e}^{-E_a/RT}{C}_{cat}{C}_{A0}{\left(1-x_A\right)}^2}}$$

(17)

From the equation above, it can be found that when the temperature, space time, and feed concentration are known, the theoretical conversion of 1-decene in a CSTR can be calculated based on Equation (17).

Figure 6 illustrates the simulated conversion of 1-decene in the reactor at various impeller speeds based on a finite-rate chemical kinetics model. The results indicate that when the speed ranges from 50 rpm to 200 rpm, the conversion of 1-decene closely aligns with the theoretical conversion for a continuous stirred tank reactor (CSTR), as represented by the black dashed line. This consistency confirms the accuracy of the previously mentioned theoretical analysis.

Moreover, Figure 7 shows that the conversion of 1-decene remains almost unchanged with variations in impeller speed. Since different impeller speeds correspond to different mixing times in the reactor, when the mixing time within the reactor is considerably shorter than the space time, the polymerization products can remain consistent. Therefore, we subsequently performed a transient simulation of the mixing time at an impeller speed of 50 rpm and a space time of 4.2 h at 30 °C. Initially, the continuity and momentum equations were solved under steady-state conditions to establish a stable flow field. Subsequently, a tracer was introduced at the feed inlet, and the component transport equation was solved. The concentration of the tracer at various spatial locations within the reactor was monitored over time, and then the instantaneous tracer concentration curves at different monitoring points could be derived, as shown in Figure 7.

After the tracer was added in 23.4 s, the concentration changes at each monitoring point were less than ±5% of the average value, indicating that 95% uniform mixing had been achieved within the reactor. At this point, the mixing time was approximately 0.15% of the space time, where the mixing time was significantly shorter than the space time. In this situation, the mixing process within the reactor would not affect the polymerization reaction conversion rate.

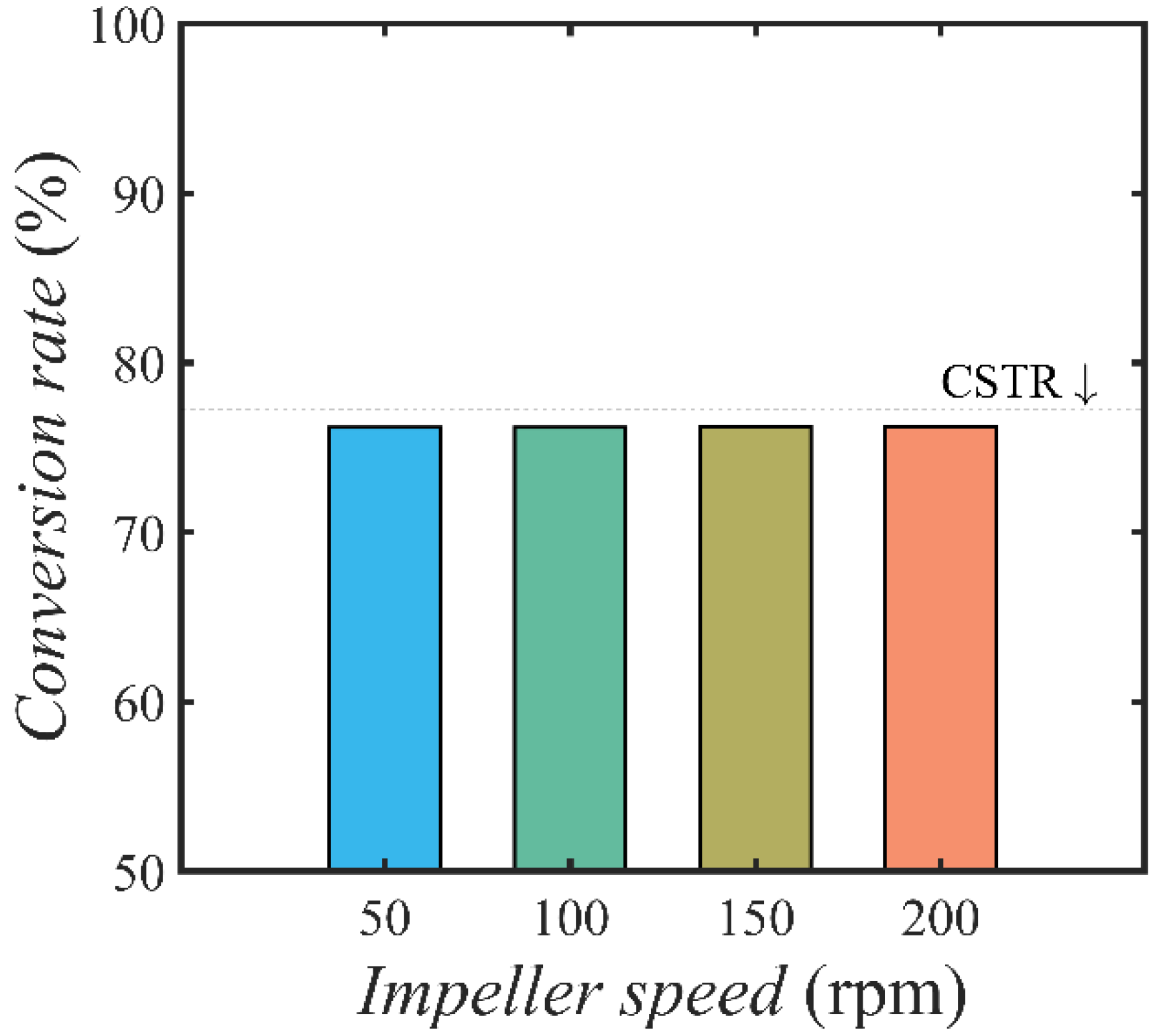
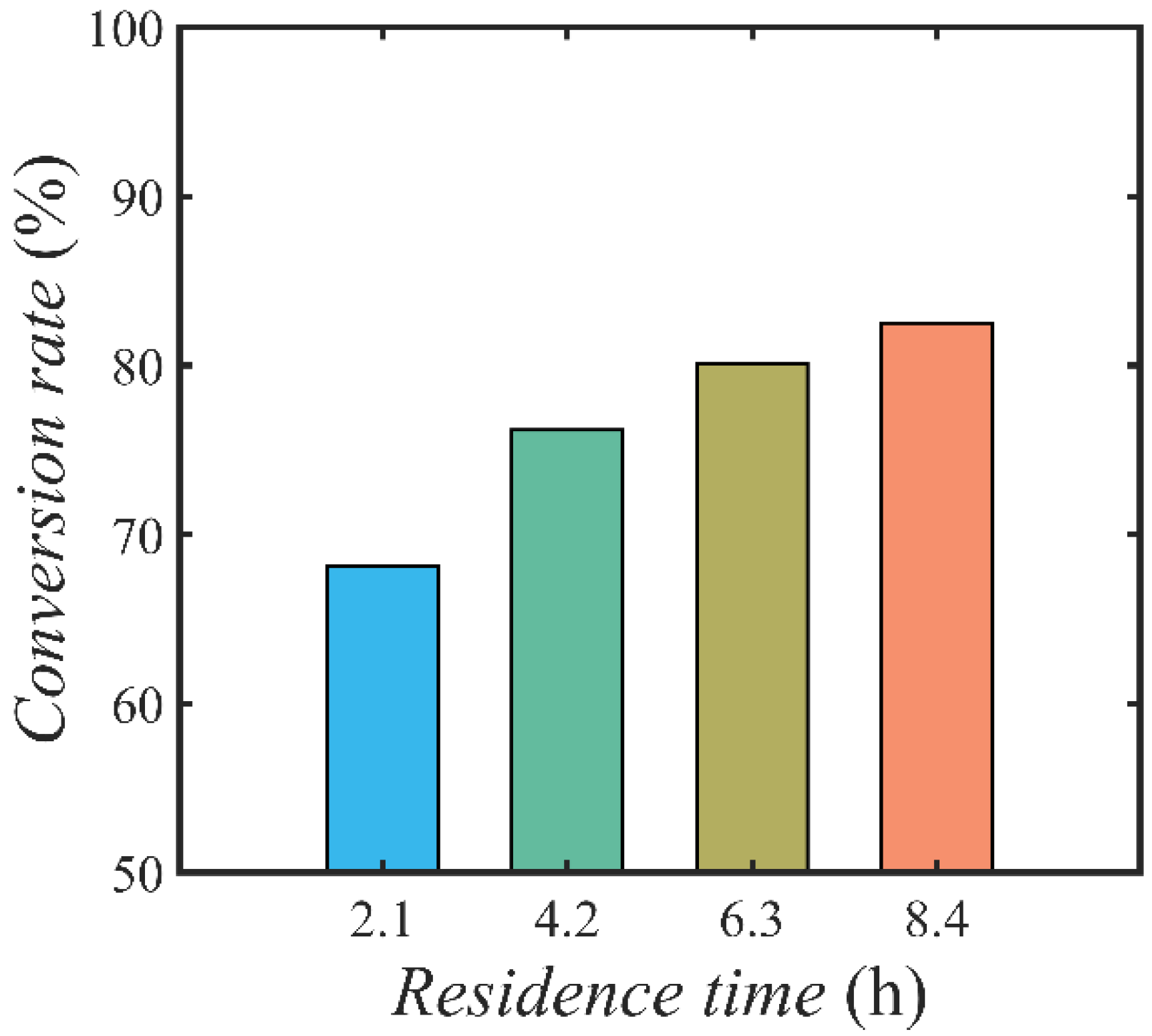
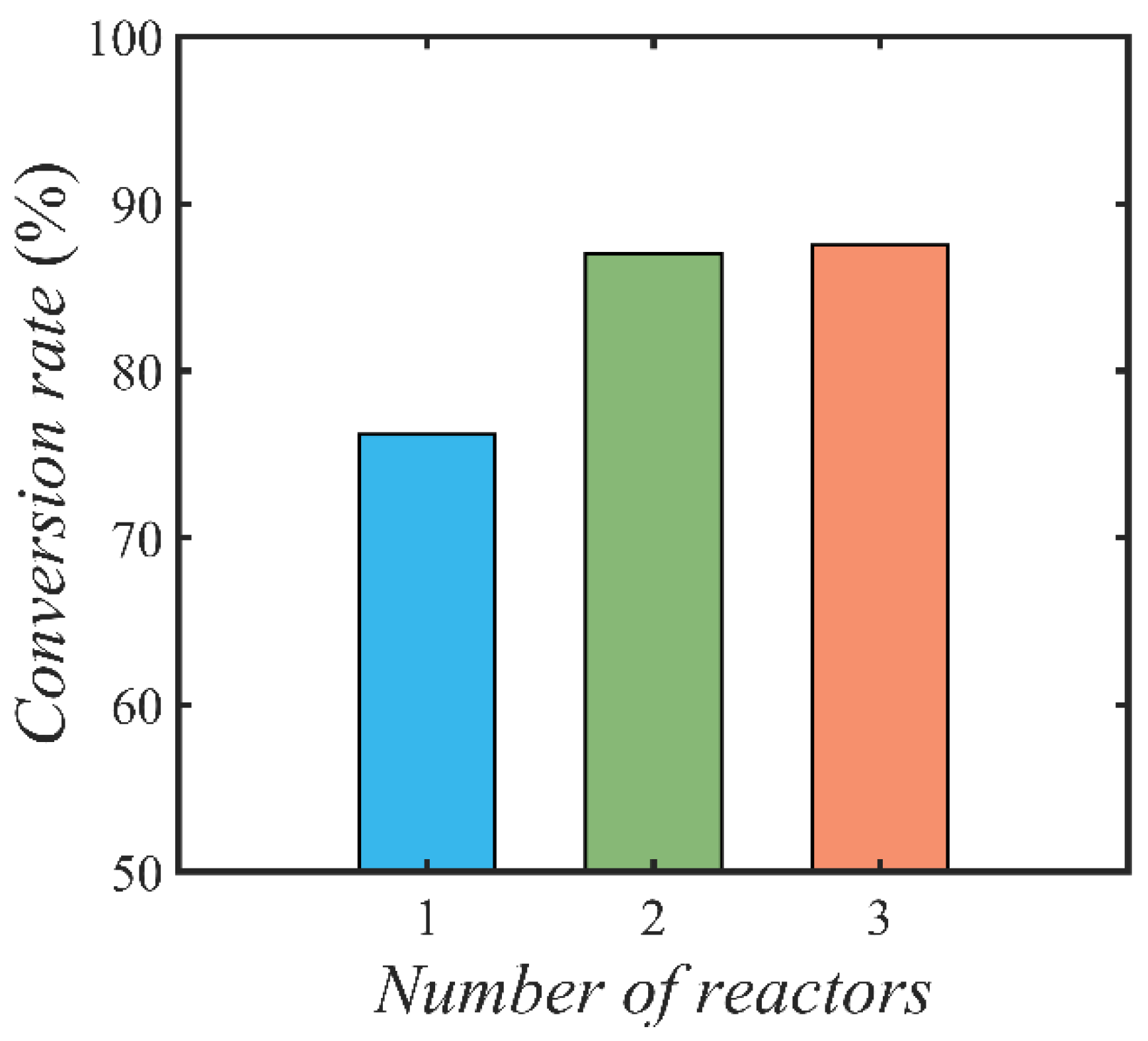
4.3. Effect of Flow Condition and Reactor Configuration on Conversion Rate

4.3.1. Effect of Temperature on Conversion Rate

In this section, we first investigated the relationship between reaction temperature and conversion rate within the PAO polymerization reactor. Figure 8 illustrates the conversion rate of 1-decene at various reaction temperatures ranging from 10 °C to 70 °C, with an impeller speed of 100 rpm and a space time of 4.2 h. As shown in the figure, the conversion rate of 1-decene increases monotonically with the rise in reaction temperature, which is consistent with our previous experimental findings [17]. In addition, the experimental results show that although increasing the reaction temperature effectively enhances the conversion rate of 1-decene, excessively high temperatures can reduce the selectivity of the target product.

4.3.2. Effect of Space Time on Conversion Rate

This section explores the relationship between space time and conversion rate within the PAO polymerization reactor. As indicated by Equation (11), when the reactor volume is held constant, we can manipulate the space time of the material in the reactor by adjusting the feed flow rate. Figure 9 illustrates the conversion of 1-decene over a range of space times from 2.1 h to 8.4 h, with the impeller speed set at 100 rpm and the reaction temperature at 30 °C. As shown in Figure 9, the conversion rate of 1-decene gradually increases as the space time is extended.

However, it can also be found that the rate of increase in conversion rate diminishes with a longer space time. In industrial applications, extending the space time can be achieved by reducing the throughput or enlarging the reactor volume, which is beneficial to the conversion rate of 1-decene. This approach is especially effective when the feed conversion rate is relatively low, as demonstrated by comparing the conversion rates when τ is 2.1 h and 4.2 h in Figure 9. However, when the conversion rate is already high, further extending the space time has a weak impact on the extra increase in conversion rate, as seen by comparing the conversion rates at 6.3 h and 8.4 h in Figure 9.

4.3.3. Effect of Reactor Number on Conversion Rate

In this section, we investigated the relationship between the number of PAO polymerization reactors and the conversion rate of 1-decene. As mentioned in Section 4.3.2, when the conversion rate of reaction is already high, it is not an effective way to increase the reactor size, which may lead to an unexpected scale-up effect, such as non-ideal mixing and heat transfer. Specifically, under the same conditions of reaction temperature, impeller speed, and total space time, we examined the conversion rate of 1-decene under conditions with single-reactor, two-reactor series, and three-reactor series configurations.

Figure 10 illustrates the conversion rates of 1-decene for these three configurations at an impeller speed of 100 rpm, a reaction temperature of 30 °C, and a total space time of 4.2 h. As shown in Figure 10, the conversion rate of 1-decene increases with the number of reactors in series. The conversion rates for single-reactor, two-reactor series, and three-reactor series configurations are 0.7089, 0.8702, and 0.8749, respectively. It is important to note that the conversion rate of 1-decene does not increase linearly with the number of reactors in series. As depicted in Figure 10, the rate of increase in the conversion rate of 1-decene gradually decreases as the number of reactors in series increases. When the total space time is held constant, the conversion rate for the two-reactor series configuration is 14.2% higher than that of the single-reactor configuration, while the conversion rate for the three-reactor series configuration increases by only 0.5% compared to the two-reactor series. According to the reaction kinetics, in the later stages of the reaction, the concentration of the reactant 1-decene decreases, leading to an extremely low reaction rate. As a result, further increasing the number of reactors has a limited effect on improving the conversion rate.

In practical industrial applications, for processes with a fixed production rate, the number of reactors in series should be appropriately increased to enhance the conversion rate of the feedstock. At the same time, a balance should be sought between equipment costs and production efficiency.

5. Conclusions

In this study, the flow and chemical reaction characteristics within a PAO polymerization reactor were investigated through numerical simulation, employing the Eulerian-–Eulerian multiphase flow model and species transport model. Additionally, based on the macroscopic kinetics of PAO polymerization, a mathematical model was developed to elucidate the relationship between the conversion rate of 1-decene in a continuous stirred tank reactor (CSTR) and the operating conditions as well as structural parameters.

Within the PAO polymerization reactor, the fluid exhibits an overall axial circulation flow pattern from the top to the bottom of the reactor under the action of the combined impellers. The single-layer coil inside the reactor not only facilitates the heat exchange but also serves as a flow guide, which is conducive to the rapid mixing of materials within the reactor. The gaseous catalyst is introduced into the reactor below the bottom turbine impeller and is then rapidly dispersed and mixed, resulting in a low overall gas holdup within the reactor.

The conversion rate of 1-decene in the PAO polymerization reactor is insensitive to changes in impeller speed in such a fully turbulent and well mixed stirred reactor. Analysis of the mixing time reveals that within the range of impeller speeds examined in this study, the mixing time is less than 0.15% of the space time of the material. Further increasing the impeller speed does not significantly enhance mass transfer within the reactor.

The conversion rate of 1-decene in the PAO polymerization reactor is positively correlated with reaction temperature and space time. Moreover, as the space time increases, the rate of increase in the conversion rate of 1-decene slows down. In actual production, a balance should be struck between the target conversion rate and production costs.

Finally, this study examined the effect of the number of reactors in series on the conversion rate of 1-decene under the same space time conditions. The results show that the conversion rate of 1-decene increases with the number of reactors in series. It is also worth noting that the rate of increase in conversion rate decreases as the number of reactors increases. In the design of industrial reactors, the number of reactors in series can be appropriately increased to achieve higher target conversion rates while also considering the balance between target conversion rate and equipment investment.