Seismic Response Characteristics and Characterization Parameter Prediction of Thin Interbedded Coal Seam Fracture System

Abstract

Fracture systems critically govern coal seam permeability, influencing hydrocarbon migration pathways and well placement strategies. We established a predictive framework for fracture characterization in thin-interbedded coal reservoirs by integrating seismic response analysis with multi-domain validation. Utilizing borehole log statistics and staggered-grid wave equation modeling, we first decode azimuthal amplitude anisotropy patterns in fractured coal seams under varying lithological contexts. Key findings reveal that (1) isotropic thick surrounding rocks yield distinct fracture symmetry axis alignment (ellipse long-axis orientation shifts with layer velocity), while (2) anisotropic thin-interbedded host strata amplify azimuthal anisotropy ratios at mid–far offsets but induce prediction ambiguity under comparable fracture intensities. By applying azimuthally partitioned OVT data with optimized mid–long offset stacking, our amplitude ellipse fitting method demonstrates unique fracture solutions validated against structural, logging, and production data. This workflow resolves the multi-solution challenges in thin-layered systems, enabling precise fracture parameter prediction to optimize coalbed methane development in geologically complex basins.

1. Introduction

The connectivity between coal seams and aquifers, as well as the development degree and orientation of fracture systems in surrounding rocks and coal, significantly impacts coalbed methane (CBM) development strategies, including well-type selection, horizontal well trajectory design, fracturing optimization, and reservoir management [1,2]. In coal-bearing formations, fracture networks are typically well-developed, with key parameters including spatial distribution, orientation, and density exerting critical controls on hydrocarbon migration pathways, accumulation patterns, and ultimately reservoir potential [1,2].

The development of fractures is particularly evident in Carboniferous rocks, which are exposed to equivalent stresses caused by water and high temperatures [3]. Vertically dominant fracture systems are commonly modeled as horizontally transversely isotropic media in coal-bearing strata. These fracture networks induce significant seismic anisotropy, manifesting as directionally dependent wave propagation characteristics. The diagnostic anisotropic signatures observable in seismic responses provide critical physical constraints for fracture characterization. Current methodologies for modeling this anisotropic behavior employ advanced numerical techniques: (1) T-matrix formulation for frequency-dependent stiffness tensor modeling, (2) high-order finite-difference schemes for viscoelastic anisotropic wavefield simulations, and (3) coupled T-matrix/staggered-grid finite-difference implementations to resolve 3D3C seismic responses in fractured media [4,5]. These computational approaches enable systematic investigation of fracture-induced seismic dispersion and attenuation patterns essential for quantitative fracture parameter inversion.

Chinese researchers have pioneered transformative methodologies in fractured media seismic analysis through dual advancements in anisotropic wavefield simulation and multi-physics AVO inversion. Their innovations encompass: (1) Development of hybrid computational frameworks combining finite-difference, reflectivity, and discontinuous Galerkin finite-element methods, enhanced by adaptive grid optimization and perfectly matched layer (PML) boundary conditions to achieve high-fidelity modeling of complex fracture networks; (2) Establishment of a fracture-sensitive AVO theory incorporating viscoelastic Biot-Gassmann models that quantify relationships between azimuthal reflection coefficients and fracture parameters (density, orientation, infill saturation). These breakthroughs enable decimeter-scale fracture characterization through machine learning-assisted inversion of frequency-dependent anisotropy signatures, fundamentally advancing coalbed methane reservoir assessment and production prediction capabilities.

Contemporary fracture characterization methodologies span geological analysis, geomechanical modeling, and seismic inversion techniques [6,7,8,9,10,11,12,13,14,15]. While conventional approaches predominantly rely on t anisotropic Zoeppritz formulations and their linearized approximations under single-interface assumptions to derive compliance tensors and crack weakness parameters through AVO/AVAZ inversion, these frameworks prove inadequate for thin-bedded reservoirs. Unlike single-interface reflections, thin interbedded reflections are actually composite wavefields superimposed by top and bottom reflections, interlayer multiples, and converted waves. Therefore, AVO/AVAZ inversion based on single-interface reflection prediction methods for coal seam fractures in thin interbeds is no longer applicable.

Fracture prediction methodologies encompass diverse approaches, including geological analysis, well logging, structural stress field numerical simulations, and seismic techniques [16,17]. Current methods predominantly rely on single-interface assumptions, employing anisotropic Zoeppritz equations and their approximations to compute AVO responses and invert fracture parameters such as compliance, weakness, and anisotropy coefficients. However, thin interbedded coal seams contrast sharply with single-interface reflection models. The seismic reflections observed in thin layers represent composite wavefields resulting from the superposition of multiple wave components: primary reflections from layer boundaries, interlayer multiples, and mode-converted waves. Consequently, conventional AVO/AVAZ inversion frameworks, designed under single-interface theoretical constraints, prove inadequate for characterizing fractures in thin interbedded coal seams [18,19].

Extensive analysis of field data reveals that coal seams exhibit pronounced seismic anisotropy, characterized by elliptical distributions in key seismic attributes. The application of Offset Vector Tile (OVT) technology to wide-azimuth seismic datasets effectively preserves azimuth-dependent offset information while capturing directional anisotropy patterns inherent to coal formations, thereby establishing a robust foundation for fracture characterization. Building upon this framework, this study develops a dual-methodology approach: (1) a wave-equation-based forward modeling system integrating well-log and acoustic array data to simulate anisotropic wave propagation in fractured coal seams, and (2) quantitative relationships between elliptical anisotropy signatures and fracture network parameters (density, orientation). Forward modeling demonstrates two critical insights: the major axis of anisotropy ellipses aligns with fracture symmetry directions, and anisotropic amplitude variations reach maximum sensitivity at mid–far offsets (20–45° incidence angles). To overcome the limitations of conventional AVAZ inversion constrained by single-interface assumptions, the proposed workflow employs azimuthally partitioned substacks of mid–far offset data optimized for noise suppression. Validation through structural interpretation, borehole fracture analysis, and production metrics confirms decimeter-scale accuracy in predicting fracture density and orientation [20,21,22].

2. Method and Principles

2.1. Seismic Forward Modeling of Fractures in Thin Interbeds

When the symmetry axis of fractures in the medium is horizontal, it is referred to as an HTI medium, used to approximate the transverse isotropy caused by vertically aligned fractures due to structural stress. The constitutive equation in HTI media is as follows:

$$\left[\begin{array}{l}{\sigma }_{xx}\\ {\sigma }_{yy}\\ {\sigma }_{zz}\\ {\sigma }_{yz}\\ {\sigma }_{xz}\\ {\sigma }_{xy}\end{array}\right]=\left[\begin{array}{cccccc}{c}_{11}& c_{13}& c_{13}& 0& 0& 0\\ c_{13}& c_{33}& c_{23}& 0& 0& 0\\ c_{13}& c_{23}& c_{33}& 0& 0& 0\\ 0& 0& 0& c_{44}& 0& 0\\ 0& 0& 0& 0& c_{66}& 0\\ 0& 0& 0& 0& 0& c_{66}\end{array}\right]\left[\begin{array}{l}{e}_{xx}\\ e_{yy}\\ e_{zz}\\ e_{yz}\\ e_{xz}\\ e_{xy}\end{array}\right]$$

(1)

Numerical simulation is performed using the first-order velocity–stress elastic wave equation. In a Cartesian coordinate system, the first-order velocity–stress elastic wave equation can be described as follows:

$$\left\{\begin{array}{l}\rho {\displaystyle \frac{\partial v_x}{\partial t}}={\displaystyle \frac{\partial {\sigma }_{xx}}{\partial x}}+{\displaystyle \frac{\partial {\sigma }_{xz}}{\partial z}}\\ \rho {\displaystyle \frac{\partial v_z}{\partial t}}={\displaystyle \frac{\partial {\sigma }_{xz}}{\partial x}}+{\displaystyle \frac{\partial {\sigma }_{zz}}{\partial z}}\\ {\displaystyle \frac{\partial {\sigma }_{xx}}{\partial t}}=c_{11}{\displaystyle \frac{\partial v_x}{\partial x}}+c_{13}{\displaystyle \frac{\partial v_z}{\partial z}}\\ {\displaystyle \frac{\partial {\sigma }_{zz}}{\partial t}}=c_{13}{\displaystyle \frac{\partial v_x}{\partial x}}+c_{33}{\displaystyle \frac{\partial v_z}{\partial z}}\\ {\displaystyle \frac{\partial {\sigma }_{xz}}{\partial t}}=c_{66}{\displaystyle \frac{\partial v_z}{\partial x}}+c_{66}{\displaystyle \frac{\partial v_x}{\partial z}}\end{array}\right.$$

(2)

where ${\sigma }_{ij}(i,j=x,y,z)$ represents stress variables, including normal and shear stresses, and $e_{ij}(i,j=x,y,z)$ represents the corresponding strain components. $v_x$, $v_y$, and $v_z$ are the particle velocity components. The matrix parameter $c_{ij}(i,j=1,\dots ,6)$ is related to the elastic parameters of the medium, such as velocity and density, where $c_{12}=c_{13}$, $c_{22}=c_{33}$, $c_{55}=c_{66}$, etc. To describe a fractured formation as an HTI anisotropic model, the anisotropy matrix needs to be calculated. For a model with a vertical symmetry axis and transverse isotropy, anisotropy coefficients ε ≤ 0.2, σ ≤ 0.2, and γ ≤ 0.2 indicate that coal is a weakly anisotropic medium [23]. Therefore, under the weak anisotropy assumption, Thomsen anisotropy parameters provide clearer meanings for describing HTI media. The relationship between the elastic parameters of an HTI medium and Thomsen parameters is as follows:

$$\left\{\begin{array}{l}\epsilon ={\displaystyle \frac{c_{11}-c_{33}}{2c_{33}}}\\ \delta ={\displaystyle \frac{{(c_{13}+c_{55})}^2-{(c_{13}-c_{55})}^2}{2c_{33}(c_{33}-c_{55})}}\\ \gamma ={\displaystyle \frac{c_{66}-c_{44}}{2c_{66}}}\\ c_{11}=\epsilon \times 2c_{33}+c_{33},c_{66}=\gamma \times 2c_{44}+c_{44}\\ c_{13}=\sqrt{\sigma \times 2c_{33}\times (c_{33}-c_{55})+(c_{33}-c_{55})\times (c_{33}-c_{55})}-c_{55}\\ c_{23}=c_{33}-2c_{44},c_{33}=\rho \times V_p^2,c_{44}=\rho \times V_s^2\end{array}\right.$$

(3)

where $\rho$ is the density, $V_p$ is the P-wave velocity in the background medium, $V_s$ is the S-wave velocity in the background medium, and $\epsilon ,\sigma ,\gamma$ are dimensionless anisotropy parameters for the HTI medium. In a fracture medium model, the relationship between Thomsen parameters and fracture density is given as follows:

$$\begin{array}{l}\epsilon =-{\displaystyle \frac{8}{3}}e,\gamma =-{\displaystyle \frac{8}{3}}\times {\displaystyle \frac{e}{3-2g}}\\ \delta =-{\displaystyle \frac{8}{3}}e\times (1+{\displaystyle \frac{g\times (1-2g)}{(3-2g)\times (1-g)}})\end{array}$$

(4)

After establishing the wave equation for the HTI medium, the high-order staggered-grid finite difference method is used to solve the wave equation. The calculation equation for the 2N-order accuracy finite difference of the first-order spatial derivative in a staggered grid is as follows:

$${\displaystyle \frac{\partial f}{\partial x}}={\displaystyle \frac{1}{\mathrm{\Delta }x}}{\displaystyle \sum _{n=1}^N{C}_n^{(N)}}\{f[x+{\displaystyle \frac{\mathrm{\Delta }x}{2}}(2n-1)]-f[x-2{\displaystyle \frac{\mathrm{\Delta }x}{2}}(2n-1)]\}$$

(5)

Using Equation (5), the recursion equation for wave Equation (2) is calculated as follows:

$$\begin{array}{ll}\hfill {\sigma }_{xx}^{n+}(i,j)=& {\sigma }_{xx}^{n-}(i,j)+c_{11}(i,j)\mathrm{\Delta }t{L}_x^{-}[v_x^n(i^{+},j)]\hfill \\ & +c_{13}(i,j)\mathrm{\Delta }t{L}_z^{-}[v_z^n(i,j^{+})]\\ \hfill {\sigma }_{zz}^{n+}(i,j)=& {\sigma }_{zz}^{n-}(i,j)+c_{13}(i,j)\mathrm{\Delta }t{L}_x^{-}[v_x^n(i^{+},j)]\hfill \\ & +c_{33}(i,j)\mathrm{\Delta }t{L}_z^{-}[v_z^n(i,j^{+})]\\ \hfill {\sigma }_{xz}^{n+}(i^{+},j^{+})=& {\sigma }_{xz}^{n-}(i^{+},j^{+})+c_{33}(i,j)\mathrm{\Delta }t\{L_x^{+}[v_z^n(i,j^{+})]\hfill \\ & +L_z^{+}[v_x^n(i^{+},j)]\}\\ \hfill v_x^n(i^{+},j)=& v_x^n(i^{+},j)+{\displaystyle \frac{\mathrm{\Delta }t}{\rho (i,j)}}\{L_x^{+}[{\sigma }_{xx}^{n-}(i,j)]\hfill \\ & +L_z^{-}[{\sigma }_{xz}^{n-}(i^{+},j^{+})]\}\\ \hfill v_z^n(i,j^{+})=& v_z^n(i,j^{+})+{\displaystyle \frac{\mathrm{\Delta }t}{\rho (i,j,k)}}\{L_x^{-}[{\sigma }_{xz}^{n-}(i^{+},j^{+})]\hfill \\ & +L_z^{+}[{\sigma }_{zz}^{n-}(i,j)]\}\end{array}$$

where $\mathrm{\Delta }t$ is the time difference interval; the superscript $n$ denotes the moment of $n\mathrm{\Delta }t$; $n^{+}$ denotes $n+1/2$; $n^{-}$ denotes $n-1/2$; i, j, denotes the location of the spatial difference lattice point; $i^{+}$ denotes $i+1/2$; $i^{-}$ denotes $i-1/2$; and $L_x^{+}$, $L_x^{-}$, $L_z^{+}$, $L_z^{-}$ are the difference operators. For the function $f$, the forward difference $L_x^{+}$ and the backward difference operator $L_x^{-}$ along the x direction are as follows, respectively:

$$\begin{array}{l}{L}_x^{+}[u(x)]={\displaystyle \frac{1}{\mathrm{\Delta }x}}{\displaystyle \sum _{i=1}^L{C}_i^{(L)}\{u(x+i\mathrm{\Delta }x)-u[x-(i-1)\mathrm{\Delta }x]\}}\\ L_x^{-}[u(x)]={\displaystyle \frac{1}{\mathrm{\Delta }x}}{\displaystyle \sum _{i=1}^L{C}_i^{(L)}\{u[x+(i-1)\mathrm{\Delta }x]-u(x-i\mathrm{\Delta }x)\}}\end{array}$$

The values of the corresponding differential weighting coefficients $C_n^{(L)}$ for different spatial differential accuracies are as follows:

$$\left[\begin{array}{ccccc}1& 3& 5& \dots & 2L-1\\ 1^3& 3^3& 5^3& \dots & {(2L-1)}^3\\ 1^5& 3^5& 5^5& \dots & {(2L-1)}^5\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1^{2L-1}& 3^{2L-1}& 5^{2L-1}& \dots & {(2L-1)}^{2N-1}\end{array}\right]\left[\begin{array}{c}{C}_1^{(L)}\\ C_2^{(L)}\\ C_3^{(L)}\\ ⋮\\ C_1^{(L)}\end{array}\right]=\left[\begin{array}{c}1\\ 0\\ 0\\ ⋮\\ 0\end{array}\right]$$

(6)

Based on the established wave equation and fracture parameter calculation equation, average data from multiple wells in the work area are used to calculate the P-wave and S-wave velocities and densities of the coal seam and its upper and lower layers. This establishes a seismic–geological model, conducting numerical simulation of the coal seam fracture seismic wavefield in a thin interbed background, providing theoretical support for predicting fracture characterization parameters.

2.2. Seismic Prediction of Fracture Characterization Parameters in Thin Interbeds

Under a strike-slip stress mechanism, nearly vertical shear fractures and tensile fractures are mainly formed [24]. Nearly vertical fractures in reservoirs can be approximated as HTI media, having two mutually perpendicular symmetry planes. The plane formed by the symmetry axis and the vertical line is called the symmetry axis plane, and the plane perpendicular to the symmetry axis is called isotropy. Figure 1 shows a schematic of azimuthal anisotropy in HTI media [25,26,27,28,29,30]. Due to the difference in the absorption degree of the fracture to the amplitude in different directions, the amplitude attenuation is the largest in the direction perpendicular to the fracture and the smallest in the direction parallel to the fracture, and the amplitude shows obvious azimuthal anisotropy and elliptical characteristics in plane space.

Based on the Thomsen coefficients in HTI media and under the weak anisotropy assumption, Rüger derived the equation for the variation in the P-wave reflection coefficient with azimuth and incident angle:

$$\begin{array}{l}{R}_{PP}\left(\theta ,\phi \right)={\displaystyle \frac{\mathrm{\Delta }Z}{2\overline{Z}}}+\\ {\displaystyle \frac{1}{2}}\left\{{\displaystyle \frac{\mathrm{\Delta }\alpha }{\overline{\alpha }}}-{\left({\displaystyle \frac{2\overline{\beta }}{\overline{\alpha }}}\right)}^2{\displaystyle \frac{\mathrm{\Delta }G}{\overline{G}}}+\left[\mathrm{\Delta }\delta +2{\left({\displaystyle \frac{2\overline{\beta }}{\overline{\alpha }}}\right)}^2\mathrm{\Delta }\gamma \right]{\cos }^2\phi \right\}{\sin }^2\theta \\ +{\displaystyle \frac{1}{2}}\left\{{\displaystyle \frac{\mathrm{\Delta }\alpha }{\overline{\alpha }}}+\mathrm{\Delta }\epsilon {\cos }^2\phi +\mathrm{\Delta }\delta {\sin }^2\phi {\cos }^2\phi \right\}{\sin }^2\theta {\tan }^2\theta \end{array}$$

(7)

where R_pp is the longitudinal wave reflection coefficient; α is the longitudinal wave velocity; β is the transverse wave velocity; Z is the wave impedance; ρ is the density; G = ρβ² denotes the transverse tangential modulus; Δ denotes the parameter difference between the upper and lower interfaces; and the upper line denotes the mean value of the upper and lower interface parameters.

Under a fixed incident angle, the equation can be further simplified as follows:

$$R_{pp}\left(\phi \right)=A+B{\cos }^2\left(\phi -{\phi }_{sym}\right)$$

(8)

In the equation, A, B, φ_sym are three fracture-related parameters, A can reflect the change in amplitude related to the gun checking distance, B reflects the change in amplitude with the orientation of the gun checking distance, φ_sym indicates the direction of the fracture, and B/A, i.e., the ratio of the long and short axes of the amplitude ellipse, can be used as a relative measure of the density of the fracture.

3. Simulation of Seismic Response of Fractured Coal Seams in Thin Interbeds

Based on the thin interbed characteristics of coal-bearing strata, we constructed three representative seismic geological models as shown in Figure 2: isotropic thick layers clamping HTI thin layers (Figure 2a), isotropic thin interlayers clamping HTI thin layers (Figure 2b), and HTI thin interlayers clamping HTI thin layers (Figure 2c). Each model has a horizontal size of 1000 m and a vertical size of 750 m.

To clarify the indicative effect of the intermediate layer’s velocity on the fracture orientation, the intermediate layer was designed as either a low-velocity layer (e.g., coal seam) or a high-velocity layer (e.g., carbonate rock). The elastic parameters of the models are shown in

Table 1. Parameters of isotropic thick layer clamped HTI thin layer model.

Layer No.	Type	Vp (m/s)	Vs (m/s)	ρ (g/cm3)	Fracture Density	Thickness
1	Isotropic medium	4031	2085	2.155	0	400
2	Low-velocity HTI	2727	1205	1.403	0:0.01:0.1	10
3	High-velocity HTI	5000	2650	2.45	0:0.01:0.1	10

, and all elastic parameters are from logging data. We used a second-order temporal and eighth-order spatial staggered grid finite difference forward simulation. The spatial grid size was set to 2 m, and the source wavelet was a Ricker wavelet with a dominant frequency of 35 Hz. The source was excited on the left side, and 501 geophones received the seismic signals. Forward simulations were conducted for different fracture densities, ranging from 0 (equivalent to isotropic) to 0.1, with intervals of 0.01. Simulations were performed for different azimuth angles (from 0° to 360°, with intervals of 5°) to study the seismic wavefield characteristics of HTI media under different observation systems. The azimuth angle perpendicular to the fracture strike was set to 0°.

The seismic forward modeling results for the HTI thin layer clamped by isotropic thick layers indicate that the greater the fracture density, the more significant the differences in seismic records at different azimuths (Figure 3). Figure 4 shows the pre-stack seismic gathers with a shot-receiver offset of 1000 m for different fracture densities (0, 0.02, 0.06, 0.10). The horizontal axis represents different azimuths, and the reflection P-wave appears at approximately 0.33 s in the 90° azimuth (isotropic plane). Figure 4a shows the data for a fracture density of 0 (isotropic medium), with no differences in reflection P-wave energy across different azimuths. From Figure 4b–d, as the fracture density increases from 0.02 to 0.10, significant differences in reflection P-wave energy appear at different azimuths. The higher the fracture density, the stronger the azimuthal anisotropy. The reflection wave energy is strongest at 0° and 180° azimuths (fracture symmetry axis direction) and weakest at 90° and 270° azimuths (fracture strike). Figure 5 shows the seismic gathers for a fracture density of 0.1 at offsets of 100 m, 400 m, 700 m, and 1000 m. The greater the offset, the stronger the azimuthal anisotropy. Combining the azimuthal gathers for different fracture densities and offsets, we observe that in the case of isotropic thick layers clamping low-velocity HTI thin layers, the amplitude azimuthal anisotropy is more pronounced, while the travel-time azimuthal anisotropy is weaker.

By extracting the amplitudes at the top surface of the intermediate layer at different azimuths and fitting them into ellipses, we found that regardless of whether the intermediate layer is high or low velocity, the greater the shot-receiver offset and fracture density, the stronger the azimuthal anisotropy of the reflected P-wave amplitude (Figure 6a). For low-velocity intermediate layers, the greater the fracture density and offset, the greater the ratio of the major to minor axis of the amplitude ellipse, with the reflection wave energy being strongest in the direction of the fracture symmetry axis (0°/180°) and weakest in the fracture strike direction (90°/270°). For high-velocity intermediate layers, the greater the fracture density and offset, the greater the ratio of the major to minor axis of the amplitude ellipse, but the major axis of the ellipse points in the direction of the fracture strike (Figure 6b).

The elastic and physical parameters of Model 2 are shown in

Table 2. Parameters of HTI thin layer model clamped in thin interlayer isotropic media.

Layer No.	Type	Vp (m/s)	Vs (m/s)	ρ (g/cm3)	Fracture Density	Thickness
1	Isotropic	3439	1793	1915	None	250
2	Isotropic	3717	1814	2043	None	8
3	Isotropic	4031	2085	2155	None	10
4	Isotropic	4916	2600	2375	None	10
5	Isotropic	4592	2520	2203	None	9
6	Low-velocity HTI	2727	1205	1403	0:0.01:0.1	10
7	Isotropic	4916	2600	2375	None	10
8	Isotropic	5166	2737	2520	None	7
9	Isotropic	4592	2520	2203	None	10
10	Isotropic	4916	2600	2375	None	8
11	Isotropic	5355	2790	2800	None	418

. The forward modeling parameters are consistent with those of Model 1, and all elastic parameters are from logging data. The fracture density of the low-velocity HTI layer in the sixth intermediate layer varies from 0 to 0.1, with intervals of 0.01. Forward simulations were performed at different azimuth angles (from 0° to 360°, with intervals of 5°). By extracting the amplitudes at the top surface of the intermediate layer at different azimuths and fitting them into ellipses, the forward results are shown in Figure 7. Compared to the results in Figure 6a, it can be observed that under the same conditions, the anisotropic characteristics are more pronounced when the HTI thin coal seam is clamped in isotropic thin interbeds, still showing the strongest reflection wave energy in the fracture symmetry axis direction and the weakest reflection wave energy in the fracture strike direction (90°/270°). Under the same fracture density and offset conditions, the azimuthal difference in amplitude is greater than that of a single HTI thin layer.

The parameters of Model 2 are shown in

Table 3. Parameters of HTI thin layer model clamped in thin interlayer HTI anisotropic media.

Layer No.	Type	Vp (m/s)	Vs (m/s)	ρ (g/cm3)	Fracture Density	Thickness
1	Isotropic	3439	1793	1915	None	300
2	HTI	3717	1814	2043	0:0.01:0.1	8
3	HTI	4031	2085	2155	0:0.01:0.1	10
4	HTI	4500	2485	2198	0:0.01:0.1	60
5	HTI	4916	2600	2375	0:0.01:0.1	10
6	HTI	4592	2520	2203	0:0.01:0.1	9
7	Low-velocity HTI	2727	1205	1403	0:0.01:0.1	10
8	HTI	5166	2737	2520	0:0.01:0.1	7
9	HTI	4592	2520	2203	0:0.01:0.1	10
10	HTI	4916	2600	2375	0:0.01:0.1	8
11	Isotropic	5355	2790	2800	None	308

, and all elastic parameters are from logging data. This model consists of an 11-layer horizontal stratified structure, where the first and eleventh layers are isotropic homogeneous media, the seventh layer is a low-velocity layer containing vertical fractures, and the remaining layers are high-velocity layers containing vertical fractures. By extracting the amplitude at the top surface of the intermediate layer at different azimuths and performing elliptical fitting, we can compare the results of a single HTI thin layer clamped by isotropic thin interbeds (Figure 8). It can be observed that when a single HTI thin layer is clamped by anisotropic thin interbeds, the amplitude azimuthal anisotropy of the thin layer is not significant, with the ratio of the major to minor axes of the fitted ellipse being nearly 1. This also indicates that when the fracture development characteristics of the target layer and the surrounding rock are similar, it is difficult to predict the fractures in the target layer through the elliptical characteristics of amplitude or travel time.

4. Prediction of Coal Seam Fracture System Based on Field Pre-Stack OVT Data

The elliptical fitting method is currently an effective approach for predicting fracture density and orientation using OVT data. This method is not constrained by the single-interface assumption related to fracture parameter inversion but instead utilizes the attribute information of different azimuths and offsets at each sampling point in the seismic data volume, which is more consistent with the characteristics of coal-bearing thin interbeds.

The elliptical fitting method requires pre-processed gather or stack data to be evenly divided by azimuth, and the attributes of data in each azimuth are then fitted. With sufficient fold coverage, the more azimuth divisions there are, the more finely the fracture orientation can be depicted. However, when the fold coverage is limited, too many azimuth divisions can compromise the signal-to-noise ratio of the data in each azimuth, thus affecting the prediction results. Based on the forward simulation and well-point elliptical fitting results from the previous section (Figure 9), we selected offsets ranging from 750–800 to 2800–2850 for elliptical fitting. To improve the stability of the calculation results, the azimuth angles were divided into 12 directions for stacking, and the stacked data volume was used for fracture parameter calculation.

Figure 10 shows the amplitude comparison results of stacked data volumes from different azimuths over the study area well. The ellipse position corresponds to the 8 + 9 coal seam. It can be observed that on azimuth-stacked data volumes centered at 0°, 45°, 90°, and 135°, there are certain amplitude differences, indicating significant azimuthal anisotropy (the red dashed circles). This suggests that predicting fracture development using the azimuthal anisotropy of seismic wave propagation is feasible.

Figure 11 presents the fracture development density profiles based on different data volumes over the well. It can be seen that the vertical fracture development characteristics predicted from OVT gathers and azimuth-stacked data are similar. However, the fracture development details predicted from OVT gathers are richer. In areas without significant structural changes, the anisotropy strength attributes predicted from partial offset stacking of OVT gathers can detect more microfaults and fractures compared to azimuth-stacked predictions.

Figure 12 shows the plane distribution of fracture development degree and orientation in the main coal seam 8 + 9 in the SF block on the eastern edge of Ordos, predicted using the method proposed in this paper. The colors represent the degree of fracture development, and the white short lines indicate the fracture orientation. It can be seen that fractures are generally more developed in the central and southern parts, with the main body in the central part showing near north–south and northeast trends, while north–south trending strip-shaped fracture zones are also developed in the eastern part.

5. Discussion and Conclusions

Currently, there are many methods for fracture prediction, mainly using different types of prestack data (azimuth stack data, prestack OVT gather data). The main difference is whether the offset information is fully utilized. Figure 13 shows the plane distribution of fractures calculated based on different data volumes. It can be seen from the figure that the fractures predicted based on the azimuth stack gather have obvious splicing footprints, but the plane distribution of fracture development calculated based on the OVT gather data has no obvious acquisition footprint characteristics. More microfaults and fractures can be predicted based on the anisotropic strength attributes of OVT gathers than the azimuthal stack attributes. Therefore, the prestack attribute prediction method based on OVT gather is selected for fracture prediction.

The left part of Figure 14 shows the horizontal stress difference results of the 8 + 9 coal seam, where compressive–torsional strike-slip faults are marked in red, extensional-torsional strike-slip faults in blue, normal faults in magenta, and reverse faults in green. The right part of Figure 14 shows the superposition of the strength of fracture development and the horizontal stress difference of the 8 + 9 coal seam. Analysis reveals a good correlation between fracture development and the distribution of horizontal stress difference, with fractures mainly developing between two sets of compressive–torsional strike-slip zones. The seismic fracture prediction results are consistent with regional geological understanding.

The reliability of the fracture prediction results was verified by analyzing the intersection of gas production results and fractures. The seismic predicted fracture strength at well points in the 8 + 9 coal seam was extracted, and an intersection analysis was performed with peak gas production and average gas production results of the 8 + 9 coal seam. The intersection results, shown in Figure 15, indicate a good correlation between the strength of fracture development and both average and peak gas production, with a correlation coefficient of approximately 0.7. This demonstrates that the pre-stack seismic fracture prediction results based on OVT gathers are reliable.

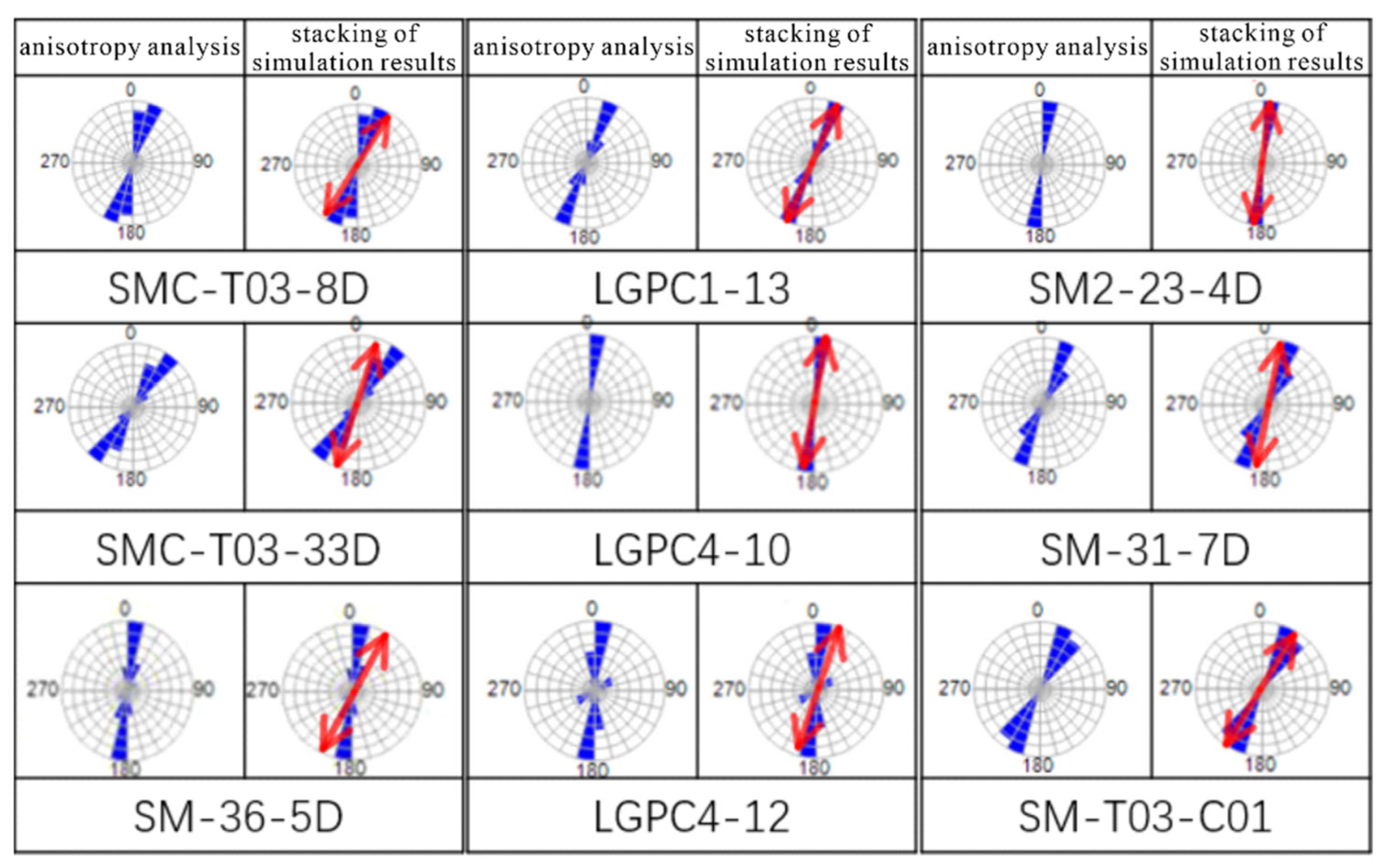
Generally, anisotropy analysis results at well points can accurately represent the fracture development direction. Therefore, the anisotropy analysis results at well points were compared with the seismic predicted fracture development directions at the same well points to verify the reliability of the prediction results. Figure 16 shows the comparison between the seismic predicted fracture orientations and the measured orientations at well points for the 8 + 9 coal seam. The main characteristics of both are consistent, predominantly showing northeast and north–south orientations. Fractures are more developed near fault zones, and the fracture orientations are consistent with the measured well point orientations, showing good correlation with gas production data. This indicates that the fracture prediction results obtained using the method proposed in this paper are consistent with regional geology, well logging predictions, and gas production performance, demonstrating that the pre-stack seismic fracture prediction results based on OVT gathers are reliable and have certain guiding significance for coalbed methane development.

For the first time, we have elucidated the seismic response characteristics of HTI (horizontally transversely isotropic) fracture systems in coal seams under coal-bearing formation conditions. The forward simulation results of fracture wave equations under the background of thin interbeds show that when the thin layer is low-velocity, the major axis of the fitted ellipse points in the direction of the fracture symmetry axis; when the thin layer is high-velocity, the major axis points in the direction of the fracture strike. This is also the main difference between coal seams and conventional high-velocity reservoirs.

When the top and bottom plates of a single-fracture-type coal seam are anisotropic thin interbeds, the amplitude azimuthal anisotropy of the coal seam is stronger, and the ratio of the major to minor axes of the fitted ellipse is greater compared to when the top and bottom plates are thick layers. As the offset increases, the elliptical characteristics become more evident. When the top and bottom plates of thin coal seams are anisotropic thin interbeds, the amplitude azimuthal anisotropy of the coal seam is not strong. When the fracture density of the coal seam is similar to that of the surrounding rock, the ratio of the major to minor axes of the fitted ellipse approaches, making it difficult to predict fracture development characteristics.

Based on the forward simulation results, the elliptical fitting of amplitude was performed using the azimuthal mid-to-far offset stacked data volumes of the OVT data body to predict the fracture development characteristics in the actual work area. The reliability of the proposed method was verified through multidimensional comparison with geological, well logging, and production data. However, because seismic data stacking is not carried out to suppress noise, fracture prediction based on OVT gathers requires a high signal-to-noise ratio of OVT gathers; otherwise, a large number of false anomalies will be produced [31,32].

The ellipse fitting result based on forward modeling optimization of azimuth-medium and long offset gather data is more consistent with the actual fracture development in the work area. Seismic data in the OVT domain retain the azimuth information better. Compared with the sub-azimuth stack data, the anisotropic characteristics of far offset are more obvious, which is conducive to the study of reservoir anisotropy and fracture prediction. The velocity of seismic data in the OVT domain shows the anisotropic characteristics related to fractures, which can be effectively used to predict the fracture system. The fracture density predicted by prestack seismic data can delineate the fracture development area, and the fracture direction can guide the drilling direction of the horizontal well.