Innovative Surrogate Combustion Model for Efficient Design of Small-Scale Waste Mono-Incineration Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Sewage Sludge Composition and Thermal Decomposition Properties
2.2. Innovative Sewage Sludge Surrogate-Based Combustion Model with Tailored Surrogates for Small-Scale System Conditions
2.3. The Pilot Small-Scale System for Model Validation
2.4. Numerical Setup
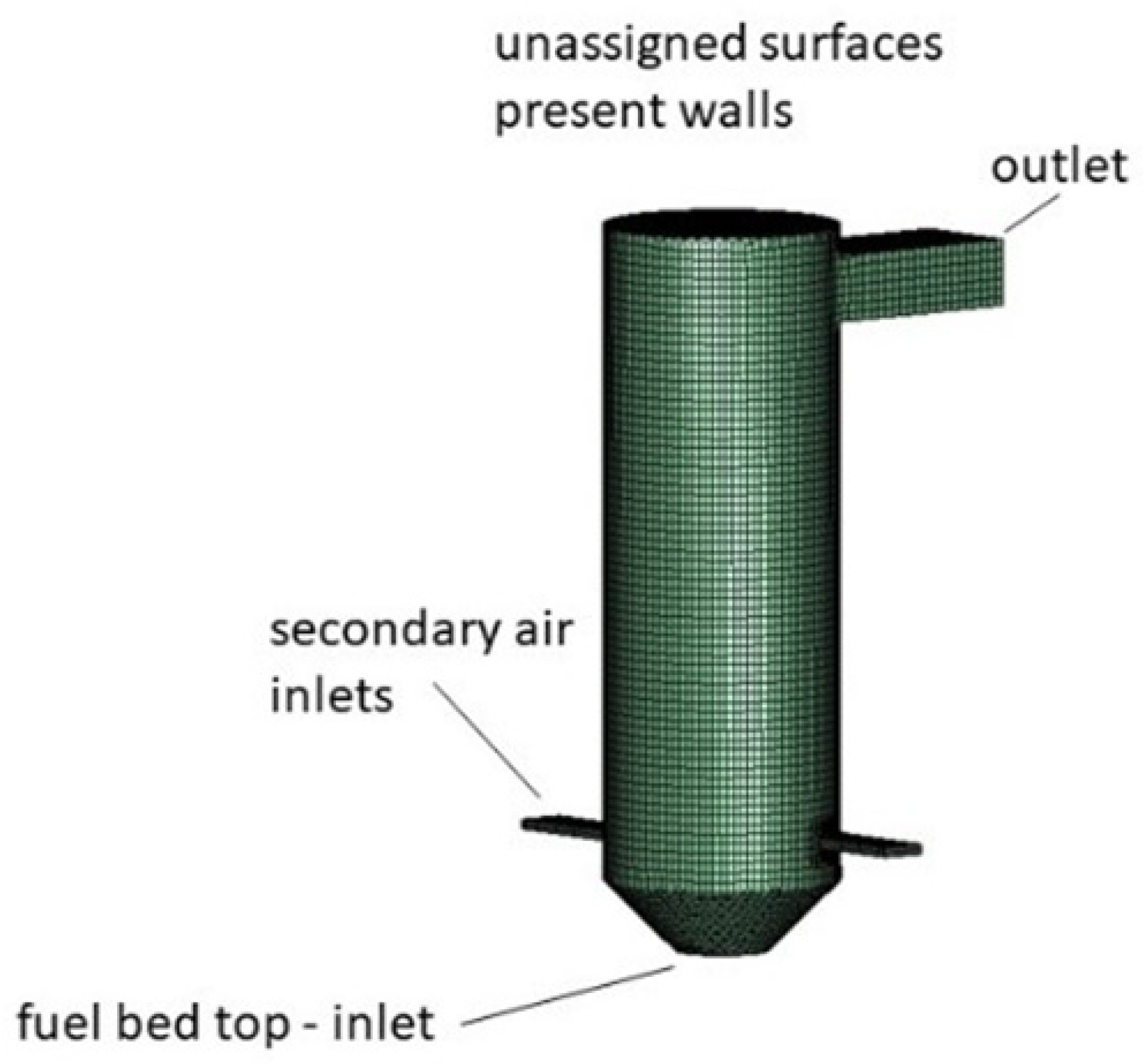
2.4.1. Computational Domain, Boundary Conditions, and Applied Mesh
2.4.2. Applied Flow Models and Discretization Schemes
2.4.3. Mesh Independence Study Setup
3. Results and Discussion
3.1. Experimental Measurements of the Pilot Small-Scale System Performance
3.2. The Applied Computational Mesh
3.3. Surrogate-Based Combustion Model Validation
3.3.1. The Inlet Temperature
3.3.2. Surrogate Composition Tailoring
3.3.3. Results and Validation of 3D CFD Simulations
3.4. Parametric Analysis for Definition of System Operation Control Strategies
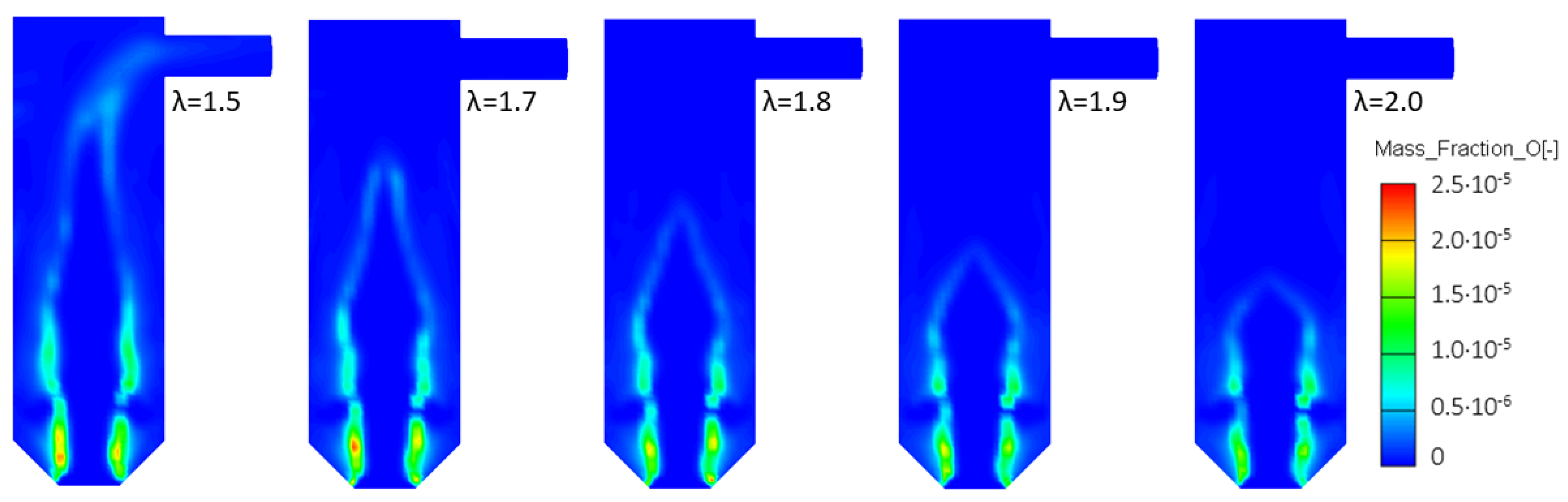
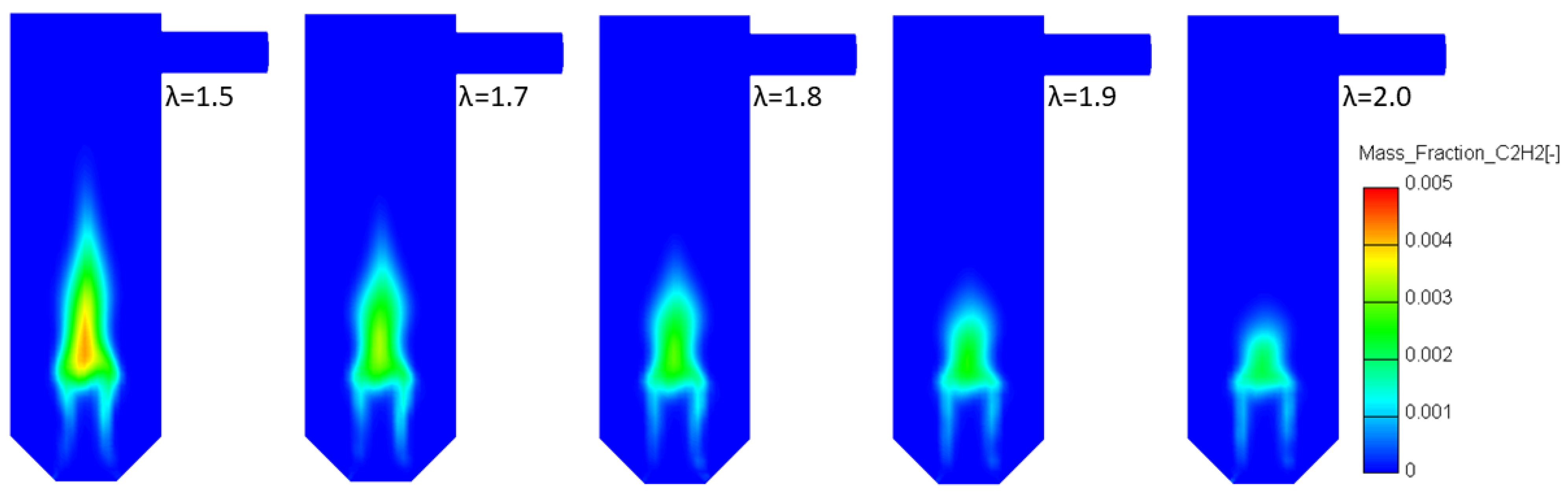
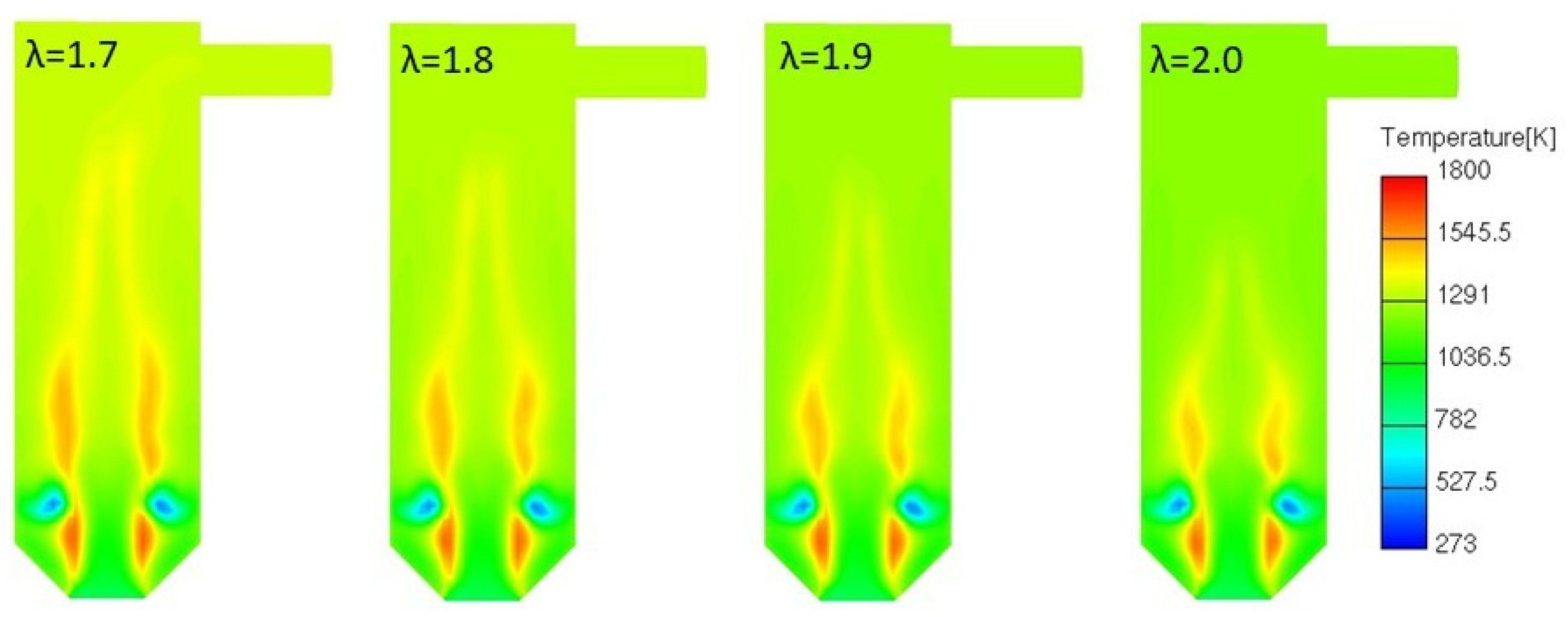
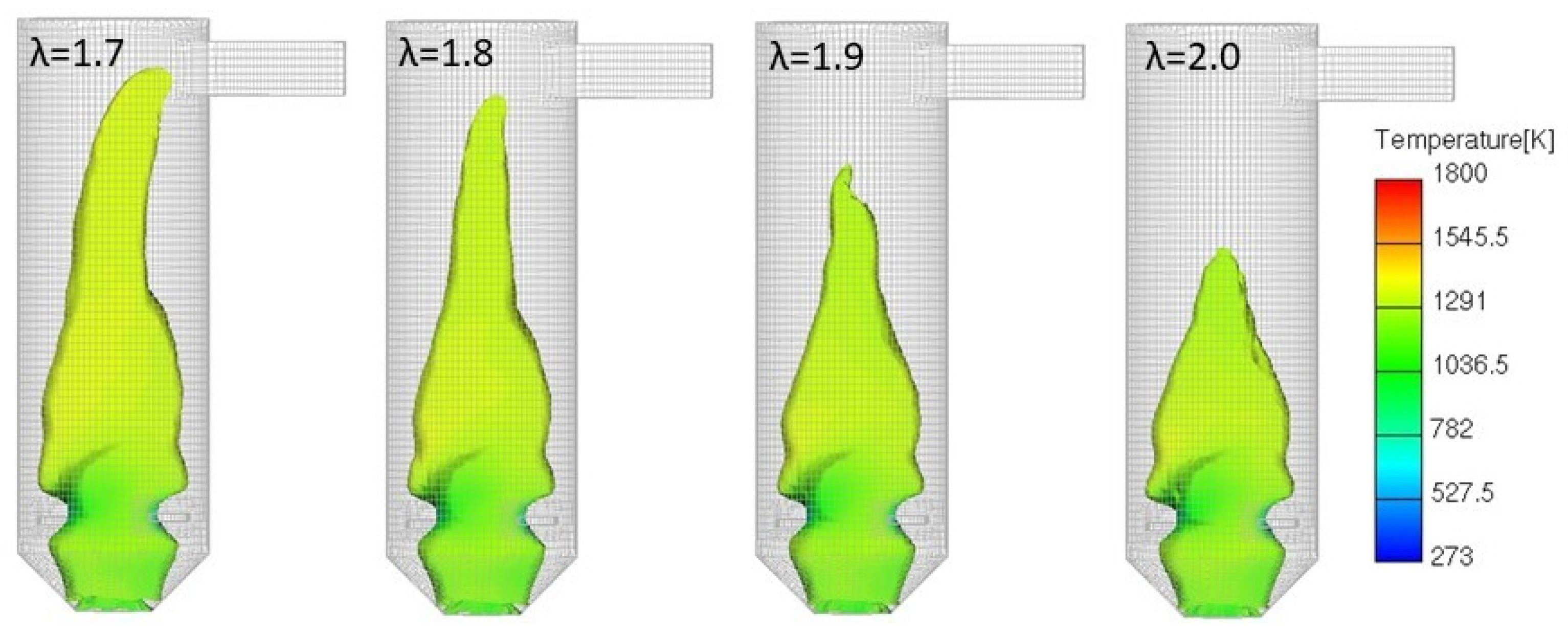
3.4.1. Variable Secondary Combustion Air Mass Flow
3.4.2. Impact of Higher SS Moisture Fraction
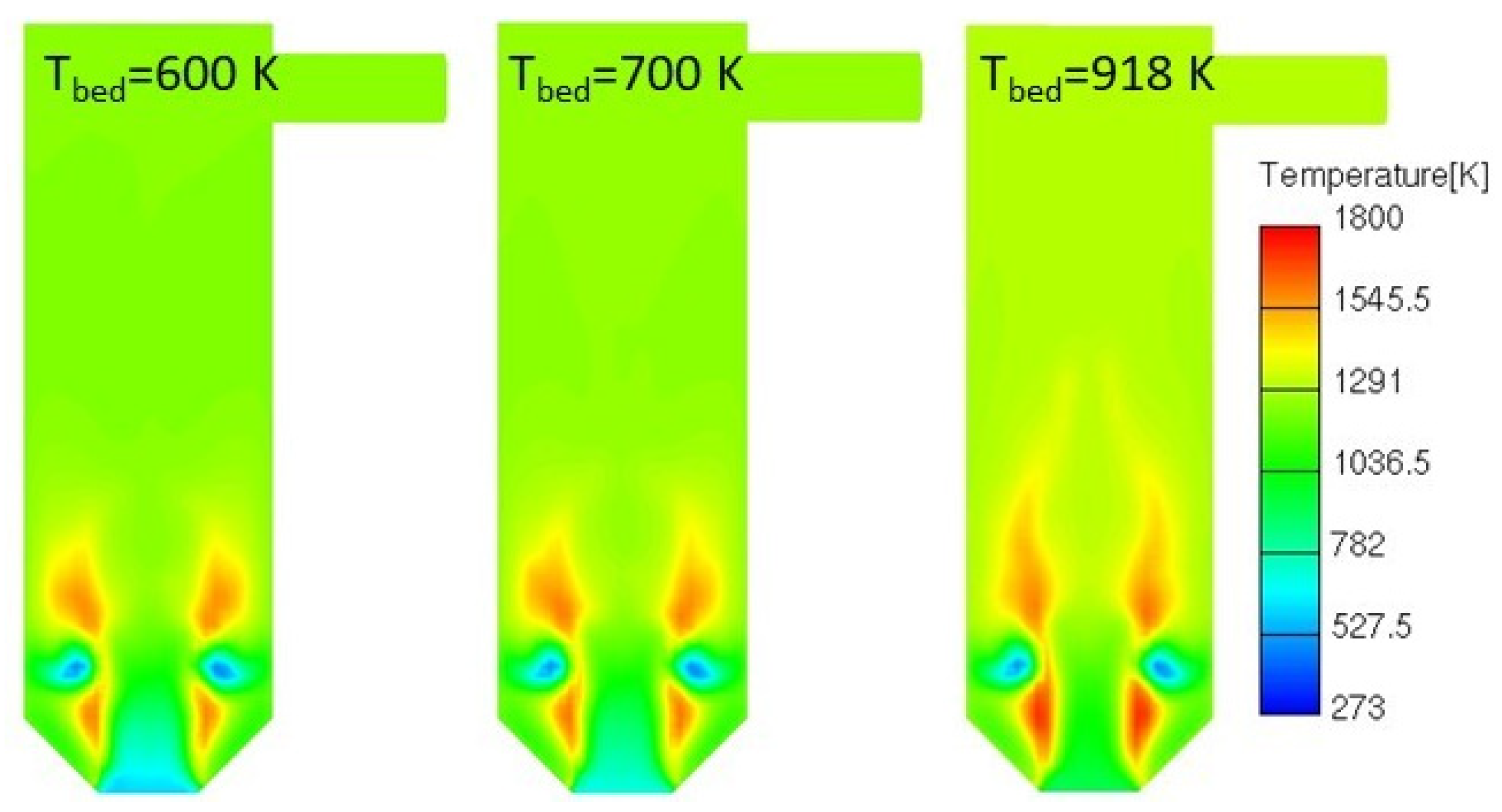
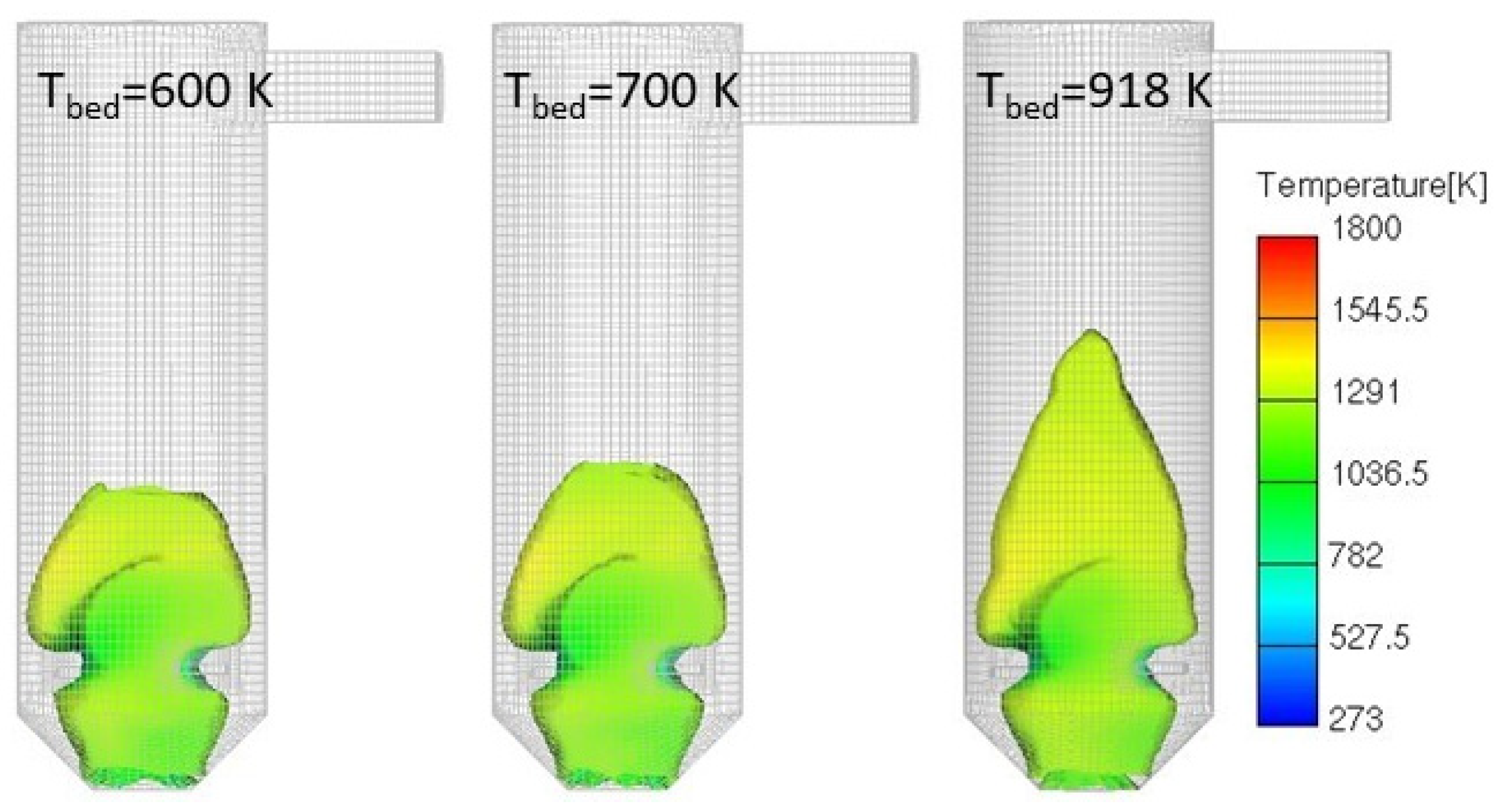
3.4.3. Lower Fuel Bed Temperature
3.4.4. Variable Thermal Power
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations and Nomenclature
| Abbreviations | |
| SS | Sewage sludge |
| AD | Anaerobic digestion |
| HTC | Hydrothermal carbonization |
| HHV | Higher heating value |
| MSW | Municipal solid waste |
| HC | Hydrocarbon |
| SEM | Simulation error minimization |
| CM | Connectivity method |
| Variables | |
| T | Temperature [K] |
| t | Time [s] |
| m’ | Mass flow [kg/s] |
| λ | Air-fuel ratio as lambda value [-] |
| Turbulent kinetic energy [m2/s2] | |
| Turbulent kinetic energy dissipation rate [m2/s3] | |
| Velocity scale ratio [-] | |
| Wall normal velocity fluctuation [m2/s2] | |
| Kinematic eddy viscosity [m2/s] | |
| Rate of production of species [mole/(cm3s)] | |
| Stoichiometric coefficient of species in reaction [-] | |
| Reaction rate [mole/(cm3s)] | |
| Molar concentration of species [mole/cm3] | |
| Forward reaction rate constant [depends on reaction] | |
| Backward reaction rate constant [depends on reaction] | |
| Pre-exponential factor in Arrhenius equation of reaction [depends on reaction] | |
| Temperature exponent in the Arrhenius equation of reaction [-] | |
| Activation energy in the Arrhenius equation of reaction [J/mol] | |
| Equilibrium constant of reaction [depends on reaction] | |
| Fuel consumption rate [kg/(m3s)] | |
| Reaction rate constant in SCM [-] | |
| Fuel mass fraction [-] | |
| Oxygen mass fraction [-] | |
| Superscripts | |
| i | i-th measuring position |
| , | Reaction order |
| Compounds and chemical elements | |
| H2 | Hydrogen |
| H2O | Water vapor |
| O2 | Oxygen |
| N2 | Nitrogen |
| CO | Carbon monoxide |
| CO2 | Carbon dioxide |
| CH4 | Methane |
| C2H5OH | Ethanol |
| C3H6 | Propene |
| C | Carbon (element) |
| H | Hydrogen (element) |
| O | Oxygen (element) |
Appendix A
Appendix A.1. Numerical Setup of Preliminary Small-Scale System Simulation
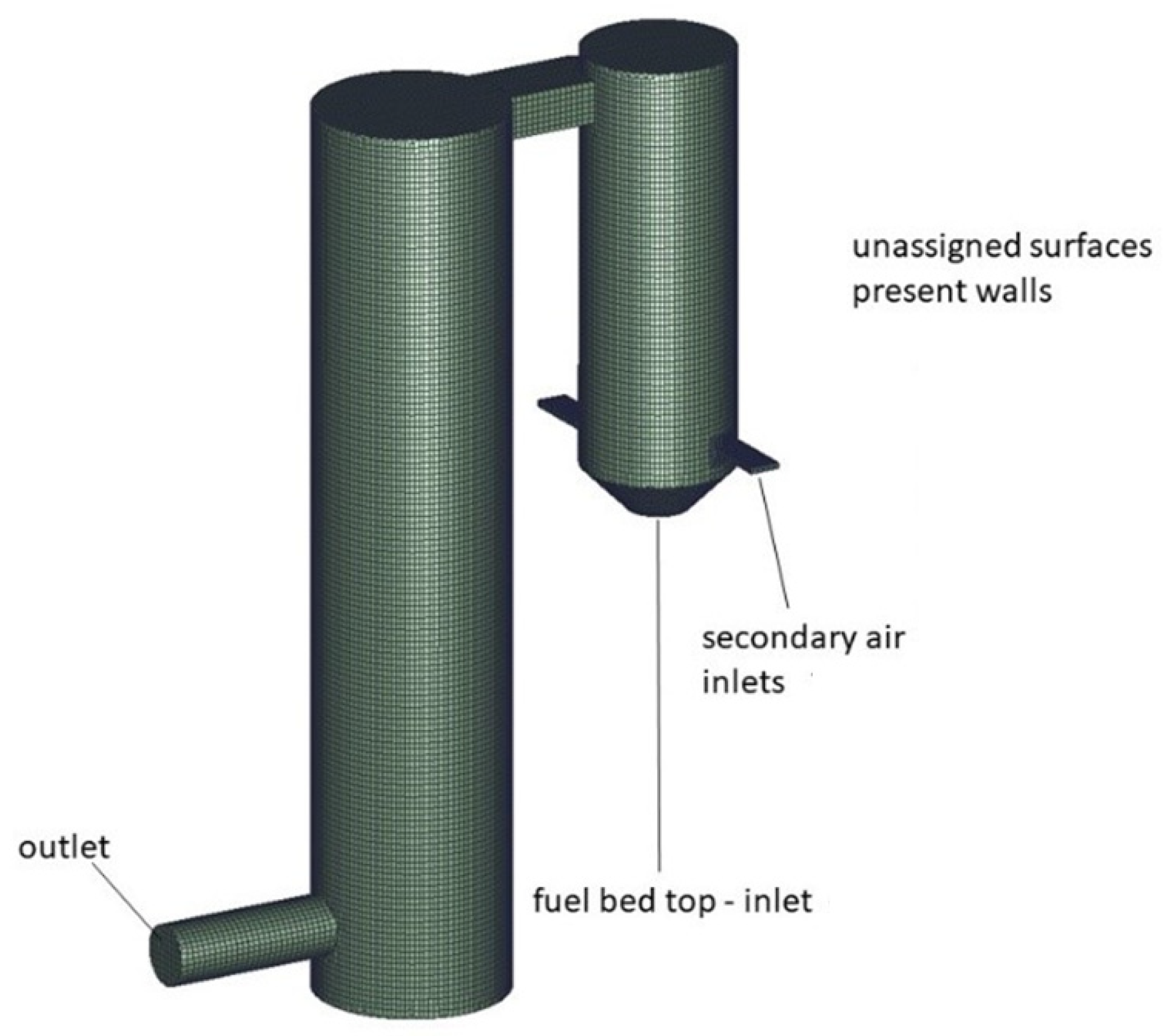
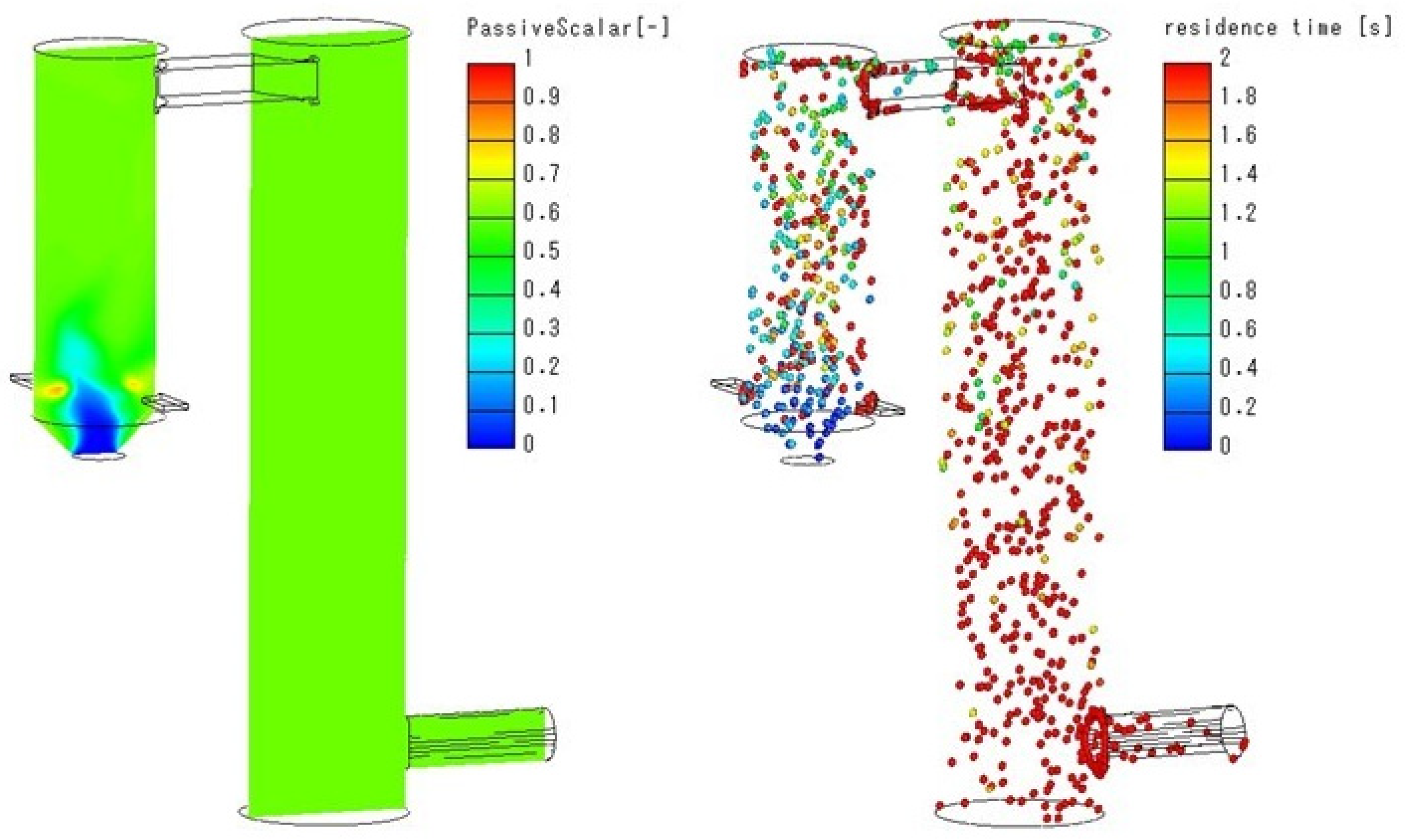
Appendix A.2. Results of Preliminary Small-Scale System Simulations

References
- Fonts, I.; Gea, G.; Azuara, M.; Ábrego, J.; Arauzo, J. Sewage sludge pyrolysis for liquid production: A review. Renew. Sustain. Energy Rev. 2012, 16, 2781–2805. [Google Scholar] [CrossRef]
- European Commission. Closing the Loop—An EU Action Plan for the Circular Economy; European Commission: Brussels, Belgium, 2015.
- European Commission. The European Green Deal; European Commission: Brussels, Belgium, 2019.
- Zhang, Y.; Wang, Y.; Chen, Z.; Hu, C.; Qu, J. Recovering nutrients and unblocking the cake layer of an electrochemical anaerobic membrane bioreactor. Nat. Commun. 2024, 15, 9111. [Google Scholar] [CrossRef] [PubMed]
- Krylova, A.Y.; Zaitchenko, V.M. Hydrothermal Carbonization of Biomass: A Review. Solid Fuel Chem. 2018, 52, 91–103. [Google Scholar] [CrossRef]
- Lima, D.; Li, L.; Appleby, G. A Review of Renewable Energy Technologies in Municipal Wastewater Treatment Plants (WWTPs). Energies 2024, 17, 6084. [Google Scholar] [CrossRef]
- Magdziarz, A.; Werle, S. Analysis of the combustion and pyrolysis of dried sewage sludge by TGA and MS. Waste Manag. 2014, 34, 174–179. [Google Scholar] [CrossRef]
- Fijalkowski, K.; Rorat, A.; Grobelak, A.; Kacprzak, M.J. The presence of contaminations in sewage sludge—The current situation. J. Environ. Manag. 2017, 203, 1126–1136. [Google Scholar] [CrossRef]
- Lin, H.; Ma, X. Simulation of co-incineration of sewage sludge with municipal solid waste in a grate furnace incinerator. Waste Manag. 2012, 32, 561–567. [Google Scholar] [CrossRef]
- Atienza-Martínez, M.; Gea, G.; Arauzo, J.; Kersten, S.R.A.; Kootstra, A.M.J. Phosphorus recovery from sewage sludge char ash. Biomass Bioenergy 2014, 65, 42–50. [Google Scholar] [CrossRef]
- Žnidarčič, A.; Seljak, T.; Katrašnik, T. Surrogate model for improved simulations of small-scale sludge incineration plants. Fuel 2020, 280, 118422. [Google Scholar] [CrossRef]
- Romano, P.; Zuffranieri, A.; Di Giacomo, G. Energy Valorization and Resource Recovery from Municipal Sewage Sludge: Evolution, Recent Advances, and Future Prospects. Energies 2025, 18, 3442. [Google Scholar] [CrossRef]
- GEMCO Energy. GEMCO Small Waste Incinerator. Available online: https://gasificationplant.com/pyrolysis-equipment/small-waste-incinerator/ (accessed on 4 July 2025).
- GEI Works. Small-Batch Incinerators. Available online: https://erosionpollution.com/wp-content/uploads/2023/08/GEI-Incinerator-Spec-Sheet.pdf (accessed on 4 July 2025).
- EMPYRIO. Sustainable Sewage Sludge Utilization in Small Cities. 2023. Available online: https://platform.cleantechscandinavia.com/wp-content/uploads/2023/12/EMPYRIO-pitch-deck-2023-12-07-2.pdf (accessed on 4 July 2025).
- Janković, B.; Manić, N.; Stojiljković, D. The gaseous products characterization of the pyrolysis process of various agricultural residues using TGA–DSC–MS techniques. J. Therm. Anal. Calorim. 2020, 139, 3091–3106. [Google Scholar] [CrossRef]
- Nowicki, L.; Ledakowicz, S. Comprehensive characterization of thermal decomposition of sewage sludge by TG-MS. J. Anal. Appl. Pyrolysis 2014, 110, 220–228. [Google Scholar] [CrossRef]
- Costa, M.; Massarotti, N.; Mauro, A.; Arpino, F.; Rocco, V. CFD modelling of a RDF incineration plant. Appl. Therm. Eng. 2016, 101, 710–719. [Google Scholar] [CrossRef]
- Murer, M.J.; Spliethoff, H.; de Waal, C.M.; Wilpshaar, S.; Berkhout, B.; Berlo, M.A.V.; Gohlke, O.; Martin, J.J. High efficient waste-to-energy in Amsterdam: Getting ready for the next steps. Waste Manag. Res. 2011, 29, S20–S29. [Google Scholar] [CrossRef]
- Frank, A.; Castaldi, M.J. CFD analysis of municipal solid waste combustion using detailed chemical kinetic modelling. Waste Manag. Res. 2014, 32, 745–754. [Google Scholar] [CrossRef]
- Mikulčić, H.; Von Berg, E.; Vujanović, M.; Duić, N. Numerical study of co-firing pulverized coal and biomass inside a cement calciner. Waste Manag. Res. 2014, 32, 661–669. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.B.; Yamauchi, H.; Nasserzadeh, V.; Swithenbank, J. Effects of fuel devolatilisation on the combustion of wood chips and incineration of simulated municipal solid wastes in a packed bed. Fuel 2003, 82, 2205–2221. [Google Scholar] [CrossRef]
- Costa, M.; Indrizzi, V.; Massarotti, N.; Mauro, A. Modeling and optimization of an incinerator plant for the reduction of the environmental impact. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 1463–1487. [Google Scholar] [CrossRef]
- Rajh, B.; Yin, C.; Samec, N.; Hriberšek, M.; Zadravec, M. Advanced modelling and testing of a 13 MWth waste wood-fired grate boiler with recycled flue gas. Energy Convers. Manag. 2016, 125, 230–241. [Google Scholar] [CrossRef]
- Rajh, B.; Yin, C.; Samec, N.; Hriberšek, M.; Kokalj, F.; Zadravec, M. Advanced CFD modelling of air and recycled flue gas staging in a waste wood-fired grate boiler for higher combustion efficiency and greater environmental benefits. J. Environ. Manag. 2018, 218, 200–208. [Google Scholar] [CrossRef]
- Mikulčić, H.; von Berg, E.; Vujanović, M.; Wang, X.; Tan, H.; Duić, N. Numerical evaluation of different pulverized coal and solid recovered fuel co-firing modes inside a large-scale cement calciner. Appl. Energy 2016, 184, 1292–1305. [Google Scholar] [CrossRef]
- Netzer, C.; Løvås, T. Chemical Model for Thermal Treatment of Sewage Sludge. ChemEngineering 2022, 6, 16. [Google Scholar] [CrossRef]
- Ortner, B.; Schmidberger, C.; Gerhardter, H.; Prieler, R.; Schröttner, H.; Hochenauer, C. Computationally Inexpensive CFD Approach for the Combustion of Sewage Sludge Powder, Including the Consideration of Water Content and Limestone Additive Variations. Energies 2023, 16, 1798. [Google Scholar] [CrossRef]
- Ortner, B.; Peham, L.; Schmidberger, C.; Prieler, R.; Hochenauer, C. CFD modeling of sewage sludge combustion in an experimental entrained flow reactor with integrated slag flow dynamics. Appl. Therm. Eng. 2025, 267, 125779. [Google Scholar] [CrossRef]
- Ortner, B.; Schmidberger, C.; Prieler, R.; Hochenauer, C. Computationally inexpensive CFD modeling of sewage sludge and waste additive combustion experiments in an entrained flow reactor. Fuel 2025, 389, 134797. [Google Scholar] [CrossRef]
- Žnidarčič, A.; Katrašnik, T.; Zsély, I.G.; Nagy, T.; Seljak, T. Sewage sludge combustion model with reduced chemical kinetics mechanisms. Energy Convers. Manag. 2021, 236, 114073. [Google Scholar] [CrossRef]
- Yao, H.; Naruse, I. Combustion characteristics of dried sewage sludge and control of trace-metal emission. Energy Fuels 2005, 19, 2298–2303. [Google Scholar] [CrossRef]
- Ninomiya, Y.; Zhang, L.; Sakano, T.; Kanaoka, C.; Masui, M. Transformation of mineral and emission of particulate matters during co-combustion of coal with sewage sludge. Fuel 2004, 83, 751–764. [Google Scholar] [CrossRef]
- Zhang, L.; Ito, M.; Sato, A.; Ninomiya, Y.; Sakano, T.; Kanaoka, C.; Masui, M. Combustibility of dried sewage sludge and its mineral transformation at different oxygen content in drop tube furnace. Fuel Process. Technol. 2004, 85, 983–1011. [Google Scholar] [CrossRef]
- Nyakuma, B.B.; Magdziarz, A.; Werle, S. Physicochemical, Thermal and Kinetic Analysis of Sewage Sludge. In Proceedings of the ECOpole’16 Conference, Zakopane, Poland, 5–8 October 2016; Volume 10. Available online: https://bibliotekanauki.pl/articles/126178 (accessed on 4 July 2025).
- Shao, J.; Yan, R.; Chen, H.; Wang, B.; Lee, D.H.; Liang, D.T. Pyrolysis Characteristics and Kinetics of Sewage Sludge by Thermogravimetry Fourier Transform Infrared Analysis. Energy Fuels 2008, 22, 38–45. [Google Scholar] [CrossRef]
- Conesa, J.A.; Marcilla, A.; Moral, R.; Moreno-Caselles, J.; Perez-Espinosa, A. Evolution of gases in the primary pyrolysis of different sewage sludges. Thermochim. Acta 1998, 313, 63–73. [Google Scholar] [CrossRef]
- Calvo, L.F.; Sánchez, M.E.; Morán, A.; García, A.I. TG-MS as a technique for a better monitoring of the pyrolysis, gasification and combustion of two kinds of sewage sludge. J. Therm. Anal. Calorim. 2004, 78, 587–598. [Google Scholar] [CrossRef]
- Thipkhunthod, P.; Meeyoo, V.; Rangsunvigit, P.; Kitiyanan, B.; Siemanond, K.; Rirksomboon, T. Pyrolytic characteristics of sewage sludge. Chemosphere 2006, 64, 955–962. [Google Scholar] [CrossRef] [PubMed]
- Urych, B.; Smoliński, A. Kinetics of Sewage Sludge Pyrolysis and Air Gasification of Its Chars. Energy Fuels 2016, 30, 4869–4878. [Google Scholar] [CrossRef]
- Gao, N.; Li, J.; Qi, B.; Li, A.; Duan, Y.; Wang, Z. Thermal analysis and products distribution of dried sewage sludge pyrolysis. J. Anal. Appl. Pyrolysis 2014, 105, 43–48. [Google Scholar] [CrossRef]
- Huang, Q.; Yu, B.; Qiu, K.; Zhou, G.; Wang, S.; Chi, Y.; Yan, J. Effect of moisture on sewage sludge combustion temperature profile and heavy metal leaching. Dry. Technol. 2016, 34, 1810–1819. [Google Scholar] [CrossRef]
- Deng, S.; Wang, X.; Tan, H.; Mikulčić, H.; Li, Z.; Cao, R.; Wang, Z.; Vujanović, M. Experimental and modeling study of the long cylindrical oily sludge drying process. Appl. Therm. Eng. 2015, 91, 354–362. [Google Scholar] [CrossRef]
- Rosec, Ž.; Katrašnik, T.; Žvar Baškovič, U.; Seljak, T. Exhaust gas recirculation with highly oxygenated fuels in gas turbines. Fuel 2020, 278, 118285. [Google Scholar] [CrossRef]
- Agwu, O.; Valera-Medina, A.; Katrašnik, T.; Seljak, T. Flame characteristics of glycerol/methanol blends in a swirl-stabilised gas turbine burner. Fuel 2021, 290, 119968. [Google Scholar] [CrossRef]
- Ischia, M.; Perazzolli, C.; Dal Maschio, R.; Campostrini, R. Pyrolysis study of sewage sludge by TG-MS and TG-GC-MS coupled analyses. J. Therm. Anal. Calorim. 2007, 87, 567–574. [Google Scholar] [CrossRef]
- Yang, Y.B.; Goh, Y.R.; Zakaria, R.; Nasserzadeh, V.; Swithenbank, J. Mathematical modelling of MSW incineration on a travelling bed. Waste Manag. 2002, 22, 369–380. [Google Scholar] [CrossRef]
- Nagy, T.; Turányi, T. Reduction of very large reaction mechanisms using methods based on simulation error minimization. Combust. Flame 2009, 156, 417–428. [Google Scholar] [CrossRef]
- Zsély, I.G.; Nagy, T.; Simmie, J.M.; Curran, H.J. Reduction of a detailed kinetic model for the ignition of methane/propane mixtures at gas turbine conditions using simulation error minimization methods. Combust. Flame 2011, 158, 1469–1479. [Google Scholar] [CrossRef]
- Zsély, I.G.; Nagy, T.; Simmie, J.M.; Curran, H.J. Reduction of a detailed kinetic model for the ignition of natural gas mixtures at gas turbine conditions. In Proceedings of the 4th European Combustion Meeting (ECM 2009), Vienna, Austria, 11–17 April 2009. [Google Scholar]
- Olm, C.; Varga, T.; Valkó, É.; Hartl, S.; Hasse, C.; Turányi, T. Development of an Ethanol Combustion Mechanism Based on a Hierarchical Optimization Approach. Int. J. Chem. Kinet. 2016, 48, 423–441. [Google Scholar] [CrossRef]
- European Council. Directive 2010/75/EU of the European Parliament and of the Council of 24 November 2010 on industrial emissions (integrated pollution prevention and control). Off. J. Eur. Union 2010, 53, 17–119. [Google Scholar] [CrossRef]
- AVL. AVL FIRETM-avl.com. 2021. Available online: https://www.avl.com/en/simulation-solutions/software-offering/simulation-tools-a-z/avl-fire-m (accessed on 3 June 2025).
- Seljak, T.; Katrašnik, T.; Žnidarčič, A. Sludge to energy in sub-Megawatt incineration plants. In Proceedings of the International Conference on Technologies and Business Models for Circular Economy (TBMCE 2018), Portorož, Slovenia, 5–7 September 2018. [Google Scholar]
- Popovac, M.; Hanjalic, K. Compound Wall Treatment for RANS Computation of Complex Turbulent Flows and Heat Transfer. Flow. Turbul. Combust. 2007, 78, 177. [Google Scholar] [CrossRef]
- Kong, S.-C.; Reitz, R.D. Use of Detailed Chemical Kinetics to Study HCCI Engine Combustion With Consideration of Turbulent Mixing Effects. J. Eng. Gas Turbines Power 2002, 124, 702–707. [Google Scholar] [CrossRef]













| System | Construction | Capacity | Flue Gas Cleaning | Source |
|---|---|---|---|---|
| Small-scale waste incinerator, GEMCO (Shanghai, China) | Pyrolysis and combustion in a dual-chamber system | 30 to 50 kg/h | Quenching and acid removal, cyclone and bag filters | [13] |
| HELIOS 0.3, GEI Works (Palm Bay, FL, USA) | Gasification and combustion in a dual-chamber system | 13 to 23 kg/h of waste with up to 9 MJ/kg higher heating value (HHV) | Not disclosed | [14] |
| Empyrio system, Empyrio (Riga, Latvia) | Incinerator and after-burner | 500 t/y of dry matter | Not disclosed | [15] |
| Variable | Mass Fraction [%] | Sources |
|---|---|---|
| Ash | Mostly 20–30, can reach 50 | [32,33,34,35,36,37,38,39] |
| Moisture | Mostly 4–20, can reach 80 | [7,32,35,36,40,41,42] |
| Volatiles | Approx. 50, can reach 70 | [7,32,33,35,36,38,40,41] |
| Carbon | Mainly around 30 | [7,35,36,39,40,41] |
| Oxygen | Mainly around 20 | [7,35,36,39,40,41] |
| Species | CO | H2O | H2 | CH4 | C2H5OH | CO2 |
|---|---|---|---|---|---|---|
| Mass fr. [%] | 69.27 | 9.83 | 0.34 | 10.29 | 10.27 | 0 |
| Chemical energy fraction [%] | 43.08 | 0 | 2.97 | 35.18 | 18.77 | 0 |
| Mechanism | Number of Species | Number of Reversible Reactions | Number of Irreversible Reactions |
|---|---|---|---|
| Reference | 47 | 249 | 2 |
| Reduced | 33 | 168 | 2 |
| Fuel bed inlet | Dispersed and separated positions of surrogates and remaining air inflows, with defined composition, mass flow, and temperature. Surface emissivity factor set as 1. |
| Secondary air inlets | Air mass flow and temperature definition. |
| Walls | No-slip boundary condition. Surface emissivity factor of 0.8 (estimated for rust iron with a film of carbon deposits). Thermal resistance value set at 1.25 m2K/W. Convective heat transfer to the environment with 25 W/m2K. Environment temperature set at 293 K. |
| Outlet | Static (atmospheric) pressure of 1 bar. |
| Governing equations and their solution algorithm | Unsteady compressible Navier–Stokes momentum, continuity, and energy equations, including the terms for gravity and pressure work. Coupled Navier–Stokes equations are solved via the SIMPLE algorithm. |
| Applied models | Turbulence k-ζ-f model. Hybrid wall functions for velocity profile solution at the wall. Standard wall function for wall heat transfer description. Ideal gas law for gas density. Discrete transfer radiation model with gas as a participating medium (Weighted-Sum-of-Gray-Gases model). |
| Discretization schemes | Second-order temporal discretization (Δt = 0.01 s). Blended upwind and central difference schemes for mom. Equations. Central difference scheme for the continuity equation. Upwind scheme for energy, turbulence, and scalar transport equations. Least squares fit method for the definition of derivatives. |
| Parameter | Setting |
|---|---|
| Sludge mass flow | 2.93 kg/h |
| Primary air mass flow | 3.045 kg/h |
| Secondary air mass flow | 19.79 kg/h |
| Primary air temperature | 413 K |
| Secondary air temperature | 273 K |
| Ambient temperature | 273 K |
| Measuring Position | Average Temperature and Standard Deviation [K] | Combined Measurement Uncertainty [K] |
|---|---|---|
| Fuel bed, T3 | 1423 ± 45 | 45.1 |
| 13 cm after secondary air injection, T1 | 1273 + 13.4 | 13.8 |
| 46 cm after secondary air injection (near cyclone top), T2 | 1213 + 6.5 | 7.2 |
| Inlet | Composition (% Mass Fraction) | Mass Flow [kg/h] | Temperature [K] |
|---|---|---|---|
| Fuel bed, combustible species | Methane (100%) | 0.648 | 918 |
| Fuel bed, inert species | Methane combustion products (15% CO2, 12% H2O, 73% N2) | 3.042 | 918 |
| Secondary air inlets | Air (23% O2, 77% N2) | 21.6 | 273 |
| Species | CO | H2O | H2 | CH4 | C2H5OH | CO2 |
|---|---|---|---|---|---|---|
| Mass fr. [%] | 59.05 | 18.5 | 0.36 | 8.47 | 8.35 | 5.27 |
| Chemical en. fraction [%] | 43.7 | 0 | 3.69 | 34.45 | 18.16 | 0 |
| Position | Measured Temperature [K] | Simulated Temperature [K] | Difference [K] |
|---|---|---|---|
| T1 | 1273 | 1294 | 21 |
| T2 | 1213 | 1243 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Žnidarčič, A.; Katrašnik, T.; Seljak, T. Innovative Surrogate Combustion Model for Efficient Design of Small-Scale Waste Mono-Incineration Systems. Processes 2025, 13, 3170. https://doi.org/10.3390/pr13103170
Žnidarčič A, Katrašnik T, Seljak T. Innovative Surrogate Combustion Model for Efficient Design of Small-Scale Waste Mono-Incineration Systems. Processes. 2025; 13(10):3170. https://doi.org/10.3390/pr13103170
Chicago/Turabian StyleŽnidarčič, Anton, Tomaž Katrašnik, and Tine Seljak. 2025. "Innovative Surrogate Combustion Model for Efficient Design of Small-Scale Waste Mono-Incineration Systems" Processes 13, no. 10: 3170. https://doi.org/10.3390/pr13103170
APA StyleŽnidarčič, A., Katrašnik, T., & Seljak, T. (2025). Innovative Surrogate Combustion Model for Efficient Design of Small-Scale Waste Mono-Incineration Systems. Processes, 13(10), 3170. https://doi.org/10.3390/pr13103170










