Service Restoration Strategy for Distribution Networks Considering Multi-Source Collaboration and Incomplete Fault Information
Abstract
1. Introduction
2. Mathematic Formulation of the Proposed Strategy
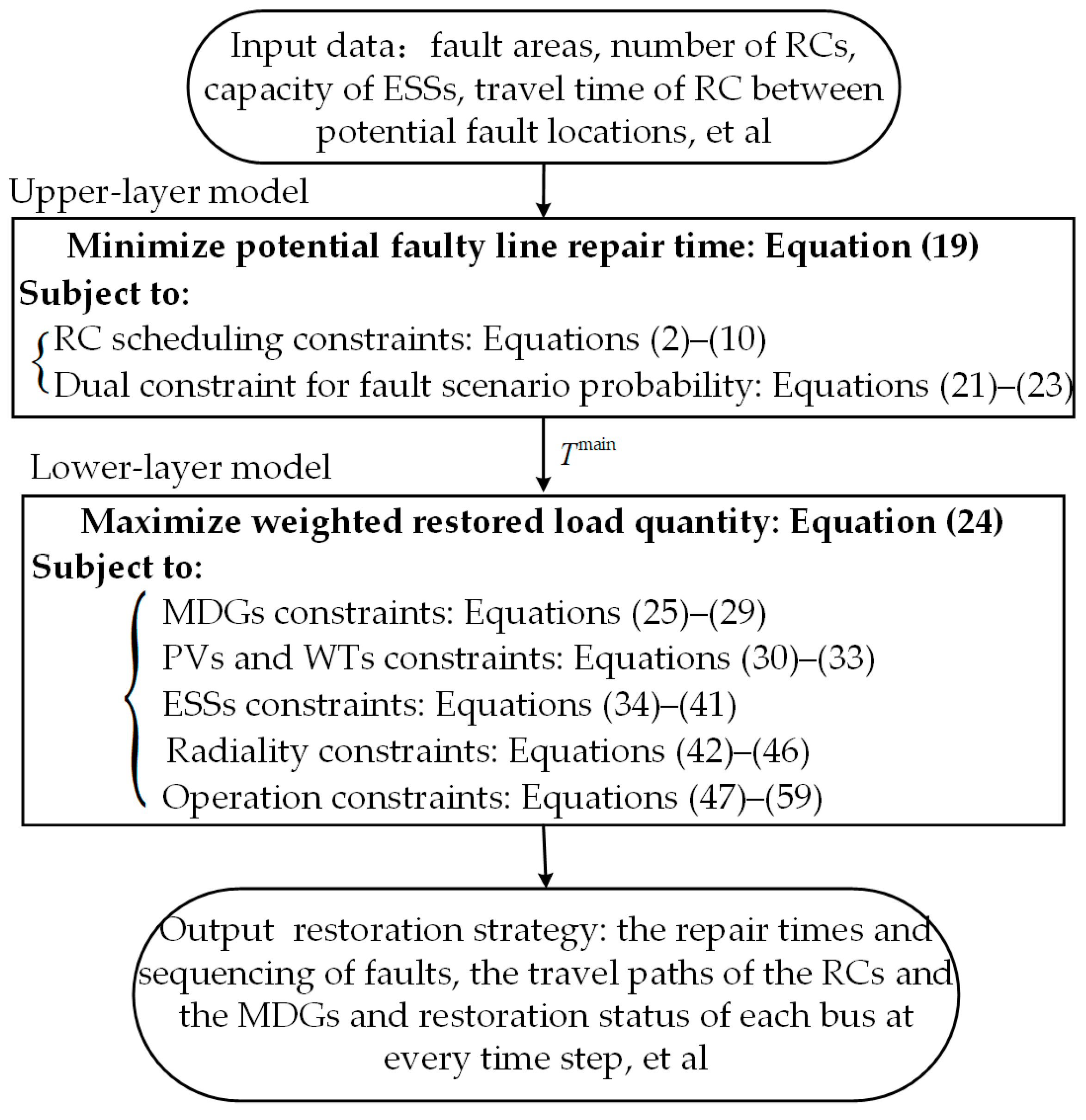
2.1. Framework of the Proposed Strategy
2.2. Upper-Layer Model
2.2.1. Master Problem of the Upper-Layer Model
2.2.2. Subproblem of the Upper-Layer Model
2.2.3. Dual Model of the Upper-Layer Model
2.3. Lower-Layer Model
2.3.1. Scheduling Model of MDGs
2.3.2. Scheduling Model of WTs and PVs
2.3.3. Scheduling Model of ESSs
2.3.4. Radiality Constraints [19]
2.3.5. Operation Constraints of the Distribution Networks
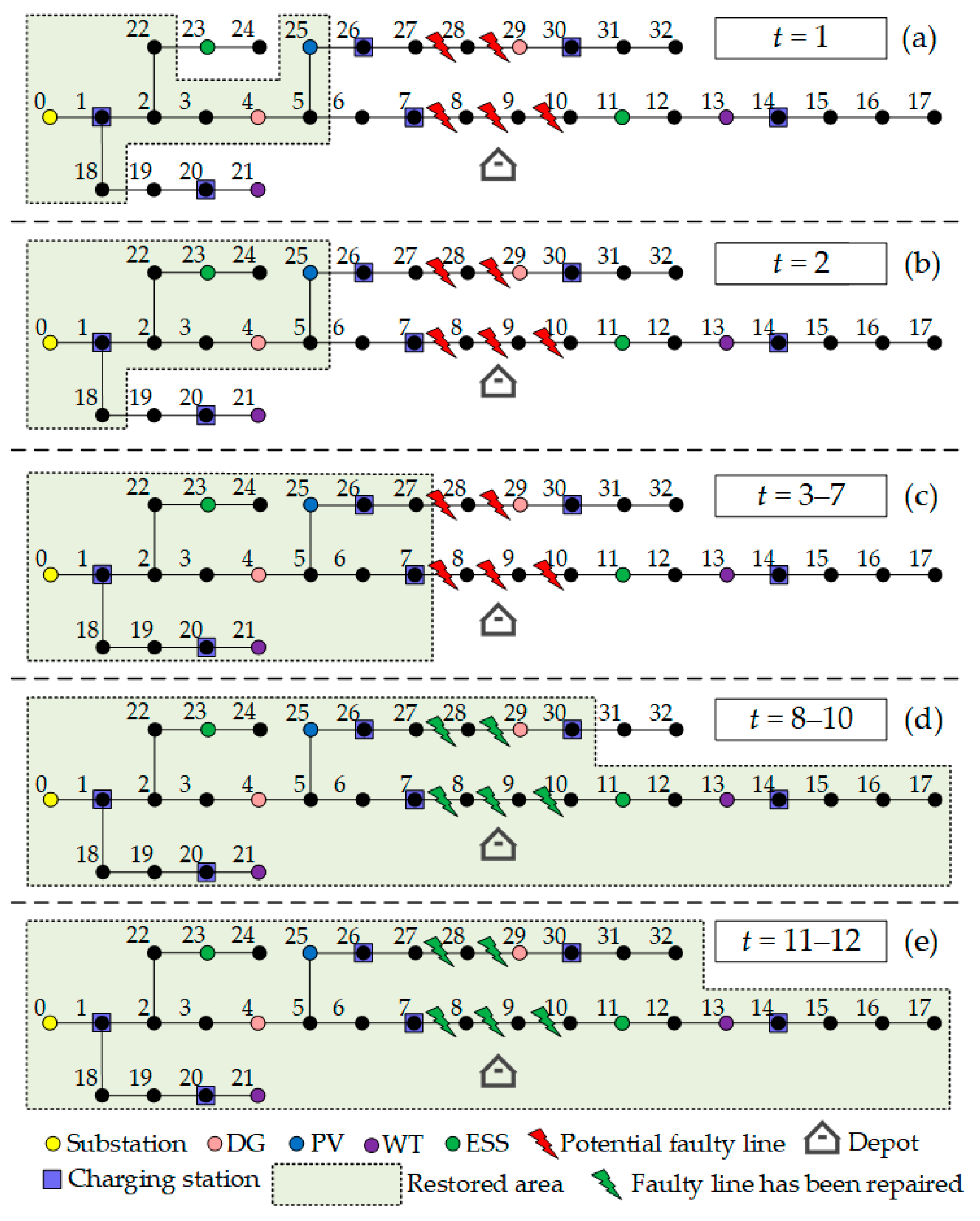
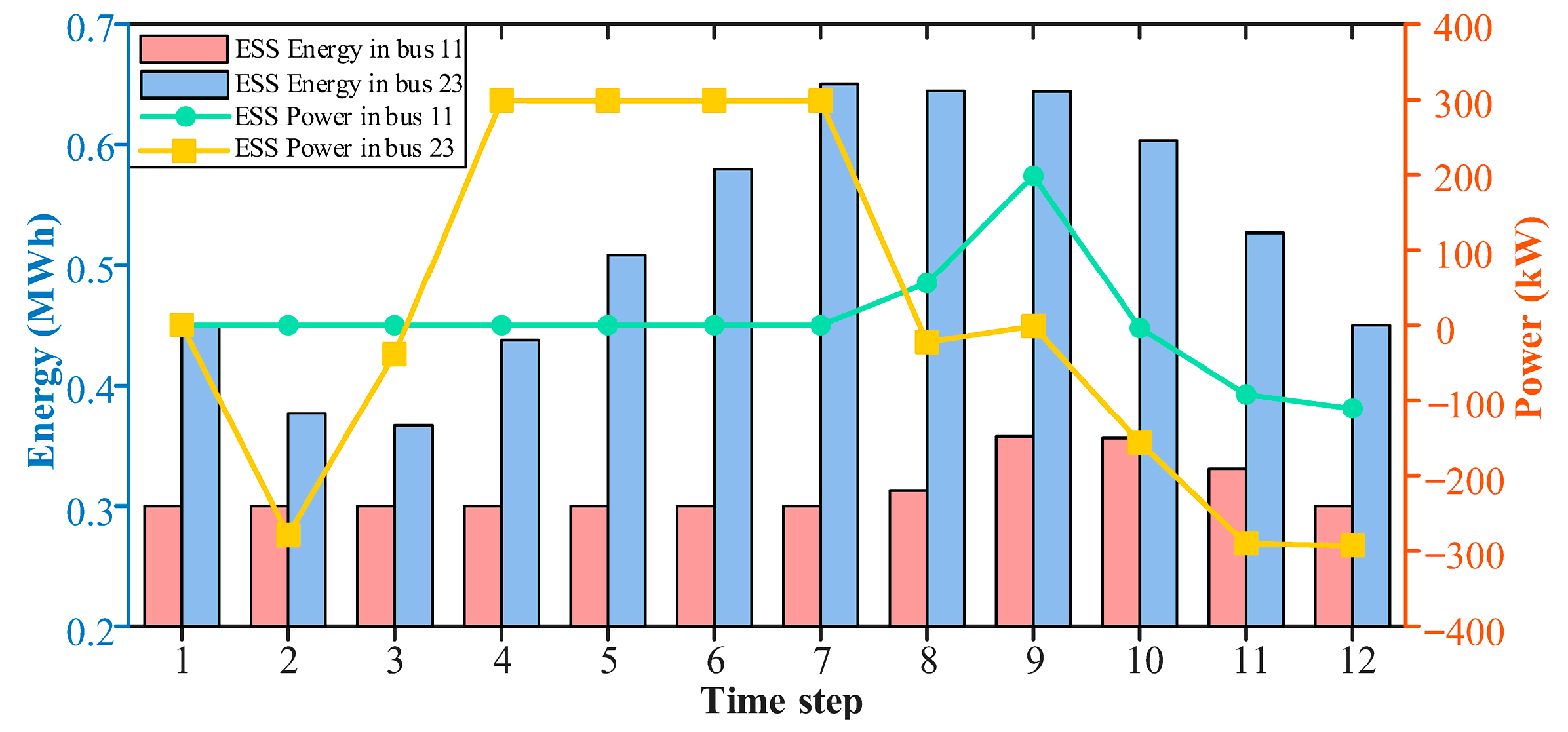
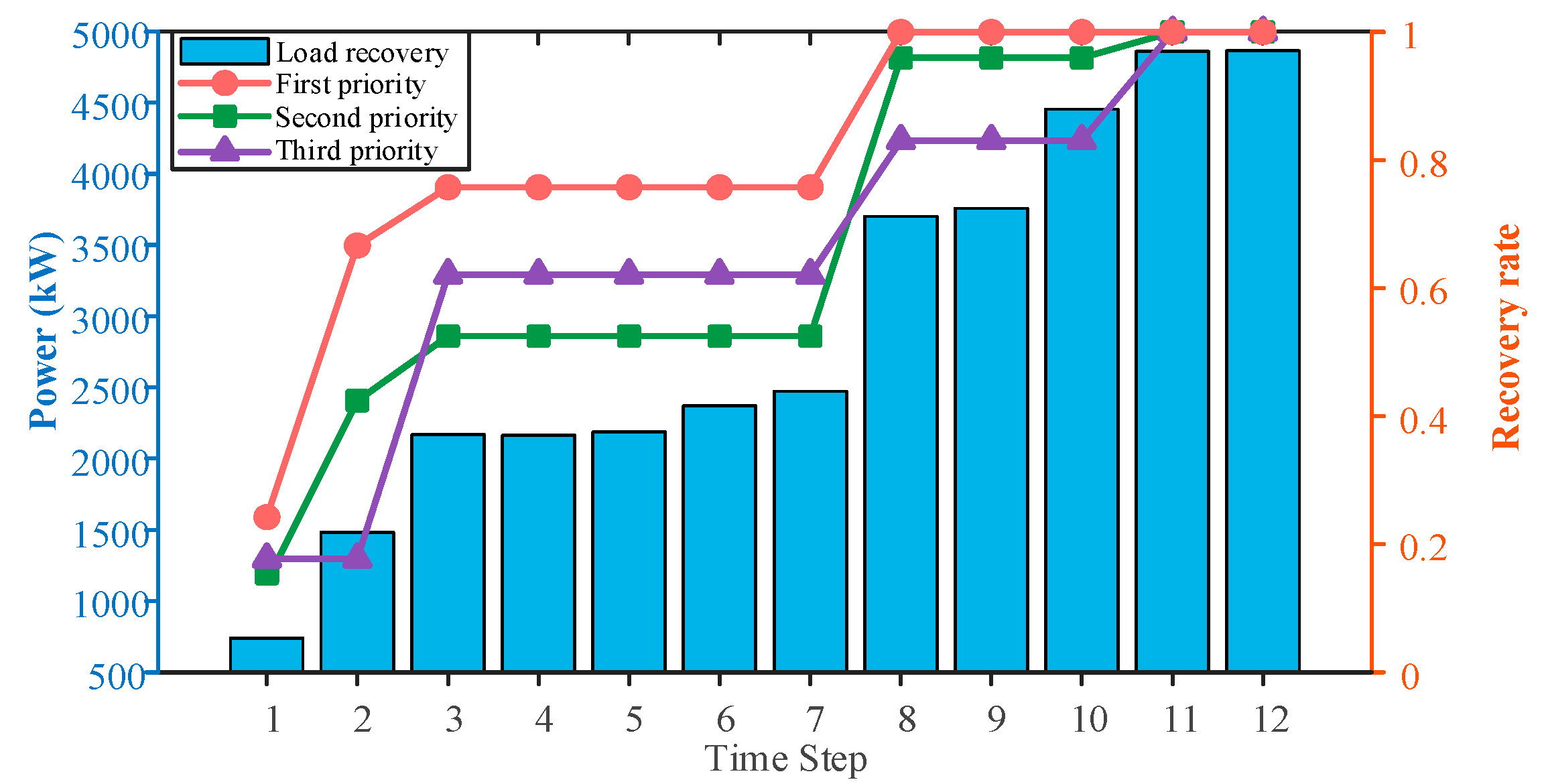
3. Results and Discussion
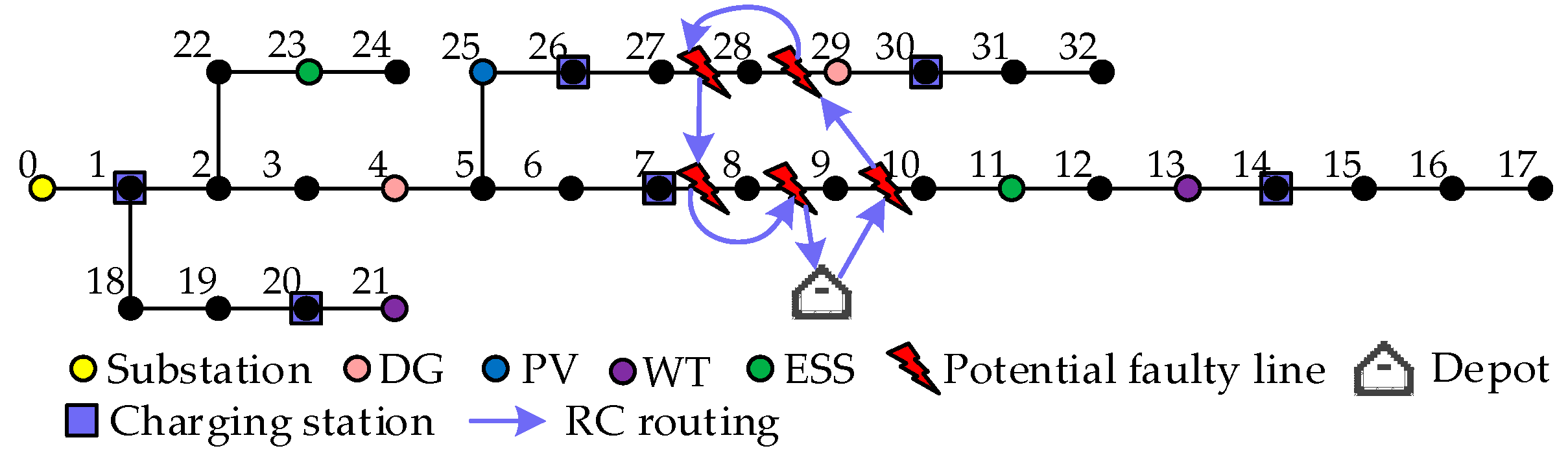
3.1. Simulation Parameters
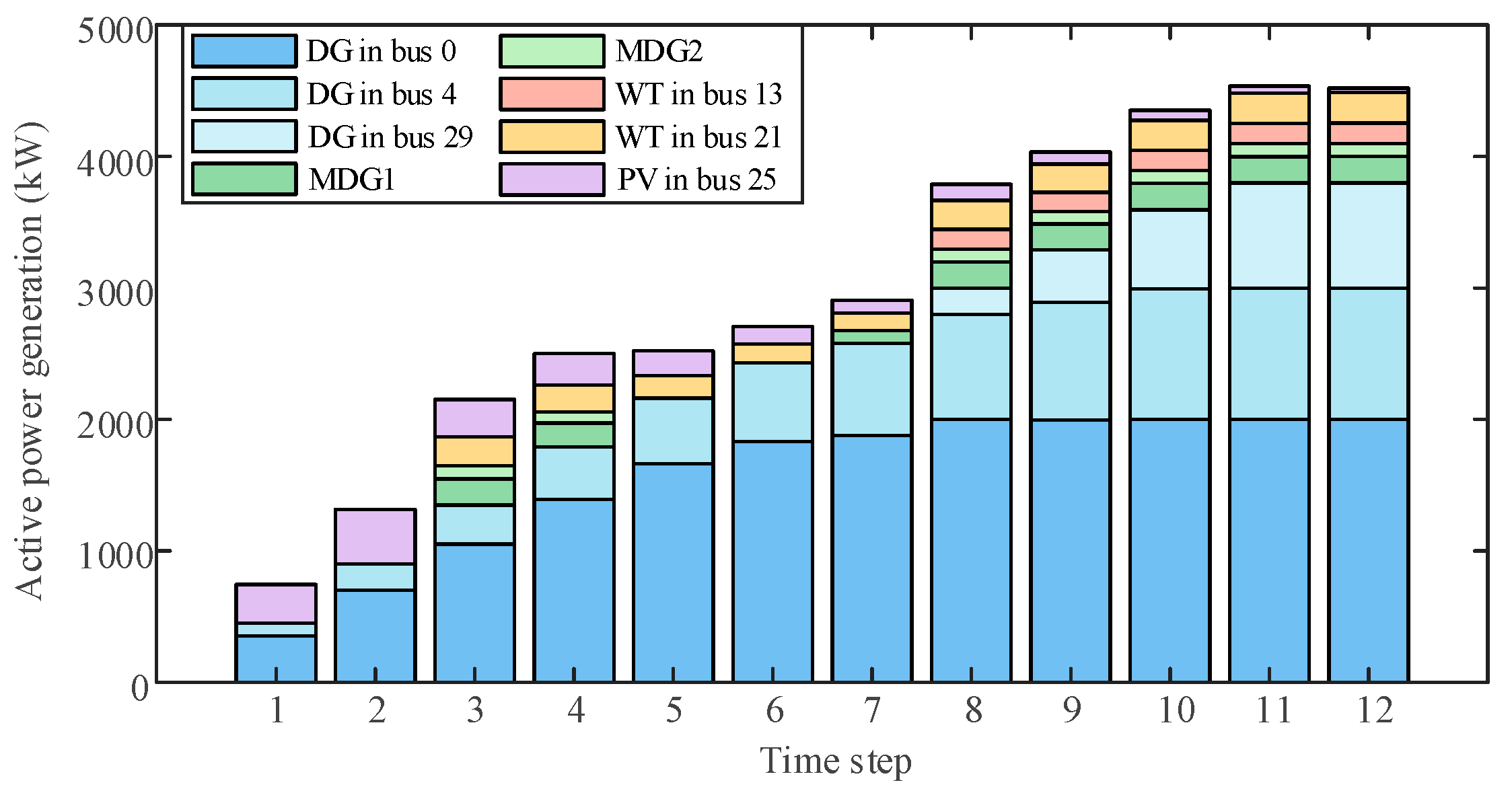
3.2. Result Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Sets and Indexes | |
| Set of positive real numbers for the scenario probability distribution. | |
| Feasible domain of subproblem of the upper-layer model, including Equation (11). | |
| Set of distribution network buses. | |
| Set of charging station buses. | |
| Set of depots. | |
| Set of ESSs. | |
| Set of fault areas. | |
| Set of generators. | |
| Set of potential fault locations. | |
| Set of distribution network lines. | |
| Set of MDGs. | |
| Set of PVs. | |
| Set of fault scenarios. | |
| Set of substation buses. | |
| Set of time steps. | |
| Feasible domain of master problem of the upper-layer model, including Equations (2)–(10). | |
| Set of WTs. | |
| Parameters | |
| Maximum number of connections for charging station bus i. | |
| Number of RCs in depot d. | |
| Capacity of ESS i. | |
| Initial state-of-charge level of ESS i. | |
| Minimum and maximum state-of-charge levels of ESS i, respectively. | |
| Square of the rated current of the line. | |
| A large parameter. | |
| Minimum and maximum active charging power of ESS i, respectively. | |
| Minimum and maximum active discharging power of ESS i, respectively. | |
| Minimum and maximum active power of the generator at bus i, respectively. | |
| Predicted power of the new energy source at bus i at time t. | |
| Upper limit of the active power output of MDG m. | |
| Ramp rate upper and lower limits of the generator at bus i, respectively. | |
| Actual power of the new energy source at bus i. | |
| Rated active and reactive power transmitted by the line, respectively. | |
| Minimum and maximum reactive charging power of ESS i, respectively. | |
| Minimum and maximum reactive discharging power of ESS i, respectively. | |
| Minimum and maximum reactive power of the generator at bus i, respectively. | |
| Reactive power demand of bus i at time t. | |
| Upper limit of the reactive power output of MDG m. | |
| Resistance line ij. | |
| Time for RC to inspect potential fault location k to check for a fault. | |
| Time required for RC to repair potential fault location k. | |
| Travel time of RC between potential fault locations k′ and k. | |
| Travel time of an MDG between charging station buses i and j. | |
| Square of the lower and upper limits of the bus voltage, respectively. | |
| Weight of buses. | |
| Reactance of line ij. | |
| A positive number approaching zero. | |
| Maximum values of the first-order norm and infinite norm of the scenario probability deviation, respectively. | |
| Robustness parameter of new energy source. | |
| Maximum prediction error of the new energy output. | |
| Charging and discharging loss coefficients of ESS i, respectively. | |
| Time duration of one step. | |
| Variables | |
| Binary variable indicating whether potential fault location k belongs to scenario s, where 1 means it belongs to scenario s and 0 otherwise. | |
| Remaining energy of ESS i at time t. | |
| Binary variable, where 1 indicates that a RC travels from a potential fault location k′ to k, and 0 otherwise. | |
| Square of the current transmitted by line ij at time t. | |
| Probability of scenario s. | |
| Charging and discharging power of ESS i, respectively. | |
| Active and reactive power of the generator at bus i at time t, respectively. | |
| Active power demand of bus i at time t. | |
| Active power output of MDG m at charging station bus i at time t. | |
| Active power of the PVs at bus i at time t. | |
| Active power of the WTs at bus i at time t | |
| Active and reactive power transmitted by the line, respectively. | |
| Charging and discharging reactive power of ESS i, respectively. | |
| Reactive power output of MDG m at charging station bus i at time t. | |
| Time for an RC to arrive at potential fault location k in scenario s. | |
| Robust fault repair time of the upper-layer model. | |
| Repair completion time for potential fault location k in scenario s, which is an integer variable. | |
| Binary variable for the energized status of bus i at time step t, where 1 indicates the bus is energized and 0 otherwise. | |
| Square of the bus voltage. | |
| Binary variable indicating charging and discharging status of ESS i, respectively, where 1 indicates that ESS i is in a charging or discharging state. | |
| Binary variable for the energized status of line ij at time t, where 1 means it is energized and 0 otherwise. | |
| Binary variable indicating whether bus i is the parent bus of bus j at time t, where 1 means bus i is the parent bus of bus j, and 0 otherwise. | |
| Binary variable indicating whether MDG m is connected to charging station bus i at time t. | |
| Repair completion time of all faults under scenario s. | |
| Auxiliary variable introduced for the linearized absolute value calculation. | |
| Dual variables. | |
References
- Yang, X.; Xu, C.; Wen, J.; Zhang, Y.; Wu, Q.; Zuo, W. Cooperative repair scheduling and service restoration for distribution systems with soft open points. IEEE Trans. Smart Grid 2023, 14, 1827–1842. [Google Scholar] [CrossRef]
- Hou, H.; Wang, Y.; Bai, X.; Lv, J.; Cui, R.; Zhang, L.; Li, S.; Li, Z. Modelling icing growth on overhead transmission lines: Current advances and future directions. Energy Convers. Econ. 2024, 6, 343–357. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Ju, Y.; Li, K.; Zhang, B.; Vazquez, S. A multi-timescale stability analysis framework for isolated DC microgrids. Chin. J. Elect. Eng. 2025; early access. [Google Scholar] [CrossRef]
- Sun, L.; Wang, H.; Huang, Z.; Wen, F.; Ding, M. Coordinated islanding partition and scheduling strategy for service restoration of active distribution networks considering minimum sustainable duration. IEEE Trans. Smart Grid 2024, 15, 5539–5554. [Google Scholar] [CrossRef]
- Lan, L.; Liu, G.; Zhu, S.; Hou, M.; Liu, X. Fault recovery strategy for urban distribution networks using soft open points. Energy Convers. Econ. 2024, 5, 42–53. [Google Scholar] [CrossRef]
- Lu, M.; Liu, Y.; Yan, Y.; Bian, R.; Du, Y.; Jiang, X. Distribution network repair scheduling with multiple types of cooperation using dynamic programming after disasters. IEEE Trans. Power Del. 2023, 38, 631–641. [Google Scholar] [CrossRef]
- Peng, Y.; Yang, Y.; Chen, M.; Wang, X.; Xiong, Y.; Wang, M. Value evaluation method for pumped storage in the new power system. Chin. J. Elect. Eng. 2023, 9, 26–38. [Google Scholar] [CrossRef]
- Taheri, B.; Safdarian, A.; Moeini-Aghtaie, M.; Lehtonen, M. Distribution system resilience enhancement via mobile emergency generators. IEEE Trans. Power Del. 2021, 36, 2308–2319. [Google Scholar] [CrossRef]
- Liu, F.; Chen, C.; Lin, C.; Li, G.; Xie, H.; Bie, Z. Utilizing aggregated distributed renewable energy sources with control coordination for resilient distribution system restoration. IEEE Trans. Sustain. Energy 2023, 14, 1043–1056. [Google Scholar] [CrossRef]
- Maji, A.; Croella, A.L.; Dose, V.; D’ Agostino, G.; Palagi, L.; Tofani, A. OPT-RecSIM: An optimization-simulation integrated system for the repair sequence optimization problem. Electr. Power Syst. Res. 2025, 249, 111995. [Google Scholar] [CrossRef]
- Lei, S.; Wang, J.; Chen, C.; Hou, Y. Mobile emergency generator pre-positioning and real-time allocation for resilient response to natural disasters. IEEE Trans. Smart Grid 2018, 9, 2030–2041. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, J.; Song, Y.; Xie, Y. Resilience-oriented valuation for energy storage amidst extreme events. Chin. J. Elect. Eng. 2023, 9, 15–25. [Google Scholar] [CrossRef]
- Shen, F.; Wu, Q.; Huang, S.; López, J.C.; Li, C.; Zhou, B. Review of Service Restoration Methods in Distribution Networks. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Sarajevo, Bosnia and Herzegovina, 21–25 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, J.; Song, Y.; Xu, Y. A robust microgrid formation strategy for resilience enhancement of hydrogen penetrated active distribution networks. IEEE Trans. Power Syst. 2024, 39, 2735–2748. [Google Scholar] [CrossRef]
- Liu, J.; Qin, C.; Yu, Y. Enhancing distribution system resilience with proactive islanding and RCS-based fast fault isolation and service restoration. IEEE Trans. Smart Grid 2020, 11, 2381–2395. [Google Scholar] [CrossRef]
- Cai, S.; Xie, Y.; Wu, Q.; Zhang, M.; Jin, X.; Xiang, Z. Distributionally robust microgrid formation approach for service restoration under random contingency. IEEE Trans. Smart Grid 2021, 12, 4926–4937. [Google Scholar] [CrossRef]
- Sedzro, K.S.A.; Shi, X.; Lamadrid, A.J.; Zuluaga, L.F. A heuristic approach to the post-disturbance and stochastic pre-disturbance microgrid formation problem. IEEE Trans. Smart Grid 2019, 10, 5574–5586. [Google Scholar] [CrossRef]
- Cai, S.; Zhang, M.; Xie, Y.; Wu, Q.; Jin, X.; Xiang, Z. Hybrid stochastic-robust service restoration for wind power penetrated distribution systems considering subsequent random contingencies. IEEE Trans. Smart Grid 2022, 13, 2859–2872. [Google Scholar] [CrossRef]
- Xu, R.; Zhang, C.; Zhang, D.; Dong, Z.; Yip, C. Adaptive robust load restoration via coordinating distribution network reconfiguration and mobile energy storage. IEEE Trans. Smart Grid 2024, 15, 5485–5499. [Google Scholar] [CrossRef]
- Arif, A.; Wang, Z.; Chen, C.; Wang, J. Repair and resource scheduling in unbalanced distribution systems using neighborhood search. IEEE Trans. Smart Grid 2020, 11, 673–685. [Google Scholar] [CrossRef]
- Pang, K.; Wang, C.; Hatziargyriou, N.D.; Wen, F. Microgrid formation and real-time scheduling of active distribution networks considering source-load stochasticity. IEEE Trans. Power Syst. 2024, 39, 2801–2813. [Google Scholar] [CrossRef]
- Arif, A.; Ma, S.; Wang, Z.; Wang, J.; Ryan, S.M.; Chen, C. Optimizing service restoration in distribution systems with uncertain repair time and demand. IEEE Trans. Power Syst. 2018, 33, 6828–6838. [Google Scholar] [CrossRef]
- Pang, K.; Wang, C.; Hatziargyriou, N.D.; Wen, F. Dynamic restoration of active distribution networks by coordinated repair crew dispatch and cold load pickup. IEEE Trans. Power Syst. 2024, 39, 4699–4713. [Google Scholar] [CrossRef]
- Zhang, M.; Cai, S.; Xie, Y.; Zhou, B.; Zheng, W.; Wu, Q. Supply resilience constrained scheduling of megs for distribution system restoration: A stochastic model and FW-PH algorithm. IEEE Trans. Smart Grid 2025, 16, 194–208. [Google Scholar] [CrossRef]
- Zhu, X.; Si, Y. Multi-period dynamic power supply recovery strategy for distribution networks considering cyber-physical-traffic network coupling. IEEE Trans. Power Del. 2023, 38, 4454–4464. [Google Scholar] [CrossRef]
- Chen, B.; Chen, C.; Wang, J.; Butler-Purry, K.L. Multi-time step service restoration for advanced distribution systems and microgrids. IEEE Trans. Smart Grid 2018, 9, 6793–6805. [Google Scholar] [CrossRef]
- Zheng, X.; Khodayar, M.E.; Wang, J.; Yue, M.; Zhou, A. Distributionally robust multistage dispatch with discrete recourse of energy storage systems. IEEE Trans. Power Syst. 2024, 39, 6960–6973. [Google Scholar] [CrossRef]
- Yin, C.; Wu, X.; Wang, X. Two-stage resilient recovery of unbalanced distribution system considering intelligent zoning and merging of microgrids. IEEE Trans. Smart Grid 2024, 15, 5555–5567. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge Univ. Press: New York, NY, USA, 2004. [Google Scholar]
- Sun, L.; Wei, Y.; Lin, Z.; Yang, X.; Li, M.; Wen, F.; Ding, M. Determining optimal generator start-up sequence in bulk power system restoration considering uncertainties: A confidence gap decision theory based robust optimization approach. Int. J. Elect. Power Energy Syst. 2023, 153, 109365. [Google Scholar] [CrossRef]
- Kumar, V.; Kumar, H.C.R.; Gupta, I.; Gupta, H.O. DG integrated approach for service restoration under cold load pickup. IEEE Trans. Power Deliv. 2010, 25, 398–406. [Google Scholar] [CrossRef]
- Huang, Y.; Lin, Z.; Liu, X.; Yang, L.; Dan, Y.; Zhu, Y.; Ding, Y.; Wang, Q. Bi-level coordinated planning of active distribution network considering demand response resources and severely restricted scenarios. J. Mod. Power Syst. Clean Energy 2021, 9, 1088–1100. [Google Scholar] [CrossRef]
- Wang, T.; Wu, C.; Sui, Q.; Chen, C.; Ma, Y.; Lin, X.; Li, Z.; Wei, F. Integrated dispatching strategy for post-disaster distribution networks with fault repair and network reconfiguration. Proc. CSEE 2024, 44, 1764–1776. [Google Scholar]
- Ghasemkhani, A.; Yang, L.; Zhang, J. Learning-based demand response for privacy-preserving users. IEEE Trans. Ind. Inform. 2019, 15, 4988–4998. [Google Scholar] [CrossRef]

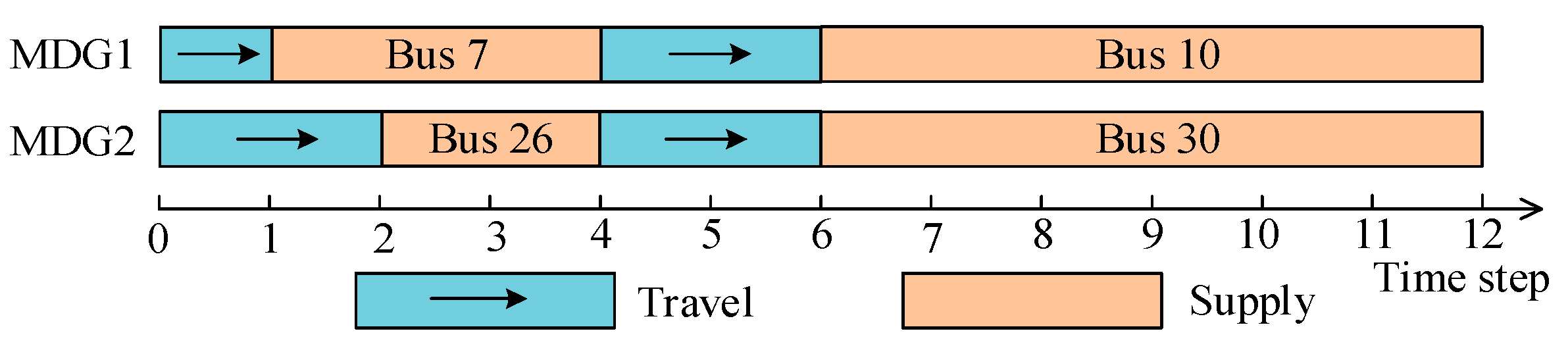
| [8] | [10] | [19] | [23] | [25] | [26] | [27] | [28] | This Work | |
|---|---|---|---|---|---|---|---|---|---|
| RC | √ | √ | √ | √ | × | × | × | √ | √ |
| ESS | × | √ | √ | × | √ | √ | √ | √ | √ |
| MDG | √ | × | × | × | × | × | × | √ | √ |
| Incomplete Fault Information | × | × | × | × | × | × | × | × | √ |
| Uncertainty of fault scenario | √ | × | √ | × | × | × | × | × | √ |
| Robust optimization | × | × | √ | × | × | × | √ | × | √ |
| Type | Bus No. | Maximum and Minimum Power Outputs | Other Parameters |
|---|---|---|---|
| Substation and DG | 0/4/29 | = 2000/1000/800 kW = 0/0/0 kW = 1500/600/600 kVar = −(1500/600/600) kVar | = 350/100/100) kW/15 min = −(350/100/100) kW/15 min |
| MDG | / | = 200/100 kW = 150/100 kVar | / |
| Bus No. | Parameters | |
|---|---|---|
| 11/23 | = 200/300 kW = 200/300 kW = 100/200 kVar = 100/200 kVar = 600/900 kWh | = 0.1/0.1 = 0.9/0.9 = 0.5/0.5 = 0.9/0.95 = 0.9/0.95 |
| Priority | Bus No. | Weight |
|---|---|---|
| Priority 1 | 2, 4, 12, 16, 20, 22, 24, 28 | 100 |
| Priority 2 | 0, 3, 8–10, 13–15, 17, 18, 21, 23, 26, 30, 32 | 10 |
| Priority 3 | 1, 5–7, 11, 19, 25, 27, 29, 31 | 1 |
| = 0.2 | = 0.4 | = 0.6 | = 0.8 | = 1 | |
|---|---|---|---|---|---|
| μ = 0.1 | 8.718 | 8.718 | 8.759 | 8.792 | 8.806 |
| μ = 0.2 | 8.718 | 8.759 | 8.803 | 8.947 | 8.997 |
| μ = 0.4 | 8.759 | 8.947 | 9.013 | 9.087 | 9.196 |
| μ = 0.6 | 8.803 | 9.013 | 9.150 | 9.231 | 9.342 |
| μ = 0.8 | 8.947 | 9.087 | 9.231 | 9.342 | 9.359 |
| μ = 1 | 8.997 | 9.196 | 9.342 | 9.359 | 9.457 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Xie, C.; Xia, L.; Li, J.; Wang, H.; Sun, L. Service Restoration Strategy for Distribution Networks Considering Multi-Source Collaboration and Incomplete Fault Information. Processes 2025, 13, 3075. https://doi.org/10.3390/pr13103075
Wang X, Xie C, Xia L, Li J, Wang H, Sun L. Service Restoration Strategy for Distribution Networks Considering Multi-Source Collaboration and Incomplete Fault Information. Processes. 2025; 13(10):3075. https://doi.org/10.3390/pr13103075
Chicago/Turabian StyleWang, Xunting, Cheng Xie, Lingzhi Xia, Jianlin Li, Han Wang, and Lei Sun. 2025. "Service Restoration Strategy for Distribution Networks Considering Multi-Source Collaboration and Incomplete Fault Information" Processes 13, no. 10: 3075. https://doi.org/10.3390/pr13103075
APA StyleWang, X., Xie, C., Xia, L., Li, J., Wang, H., & Sun, L. (2025). Service Restoration Strategy for Distribution Networks Considering Multi-Source Collaboration and Incomplete Fault Information. Processes, 13(10), 3075. https://doi.org/10.3390/pr13103075






