The Behavior of Fluid Flow and Solute Transport in 3D Crossed Rock Fractures
Abstract
1. Introduction
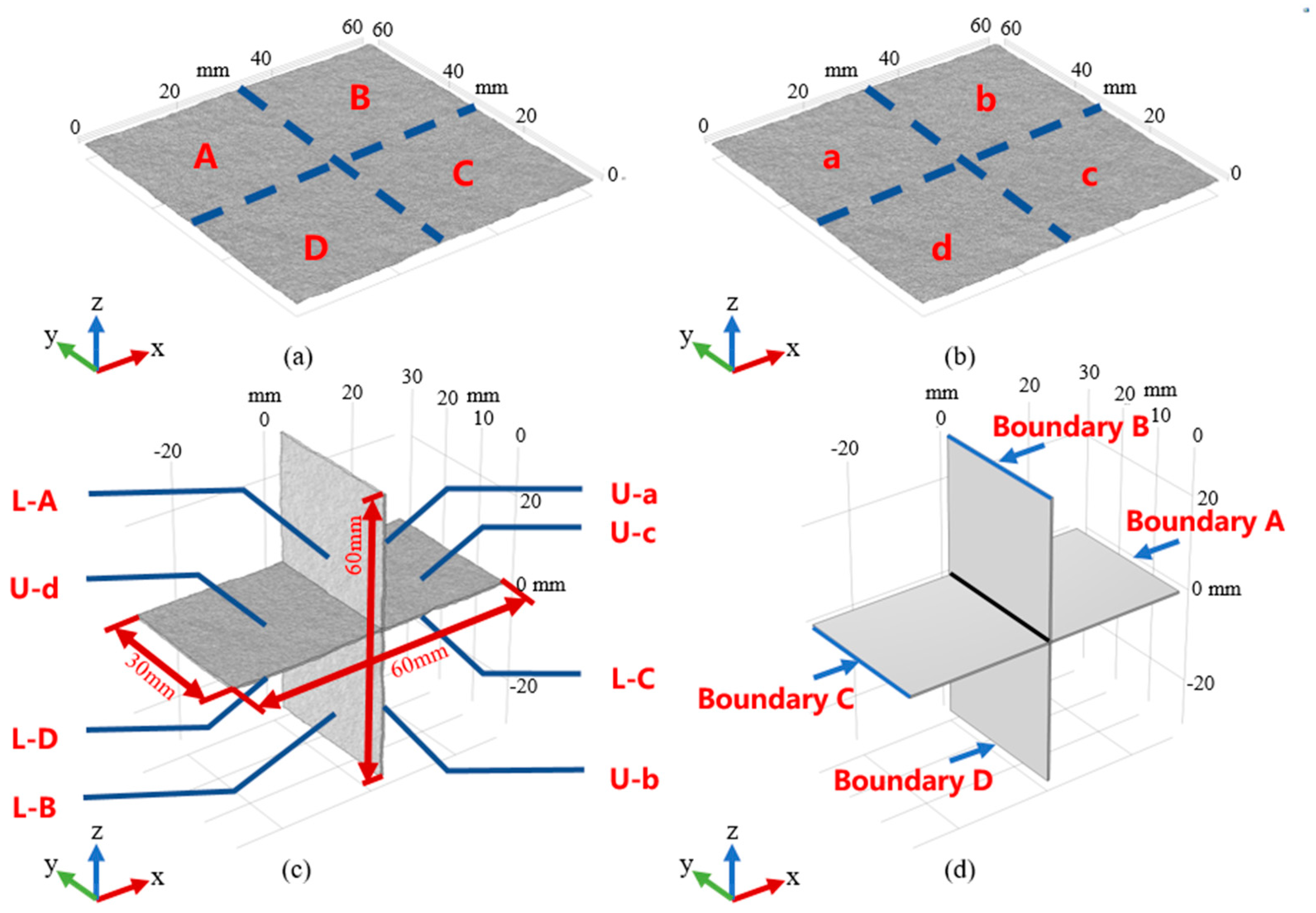
2. Geometric Model Construction and Characterization
2.1. Crossed Fractures Construction
2.2. Fracture Surface Roughness Characteristic
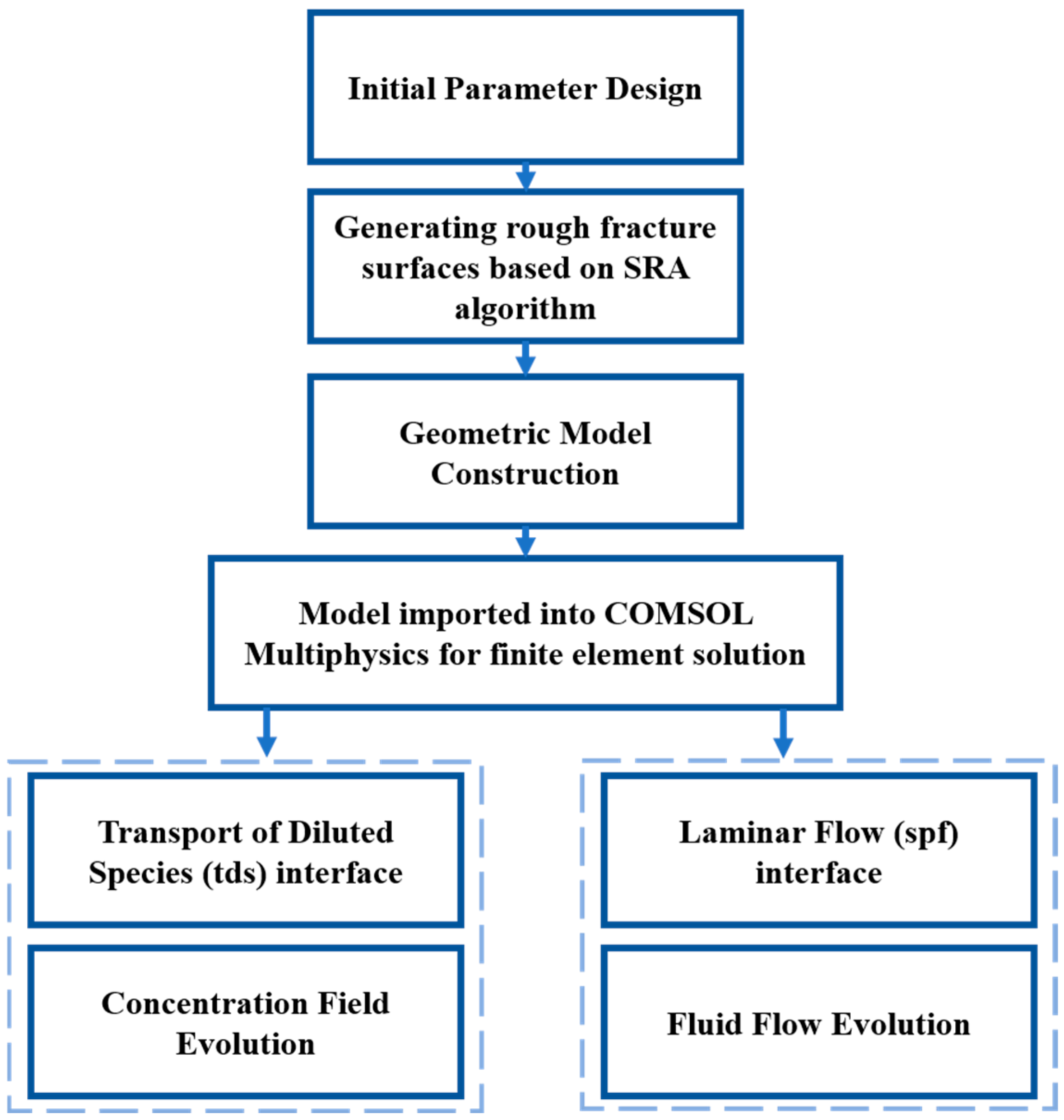
3. Crossed Fracture Seepage and Solute Transport Numerical Modeling
3.1. Method and Governing Equation for Fluid Flow and Solute Transport
3.1.1. Material and Method
3.1.2. Governing Equations for Fluid Flow
3.1.3. Governing Equations for Solute Transport
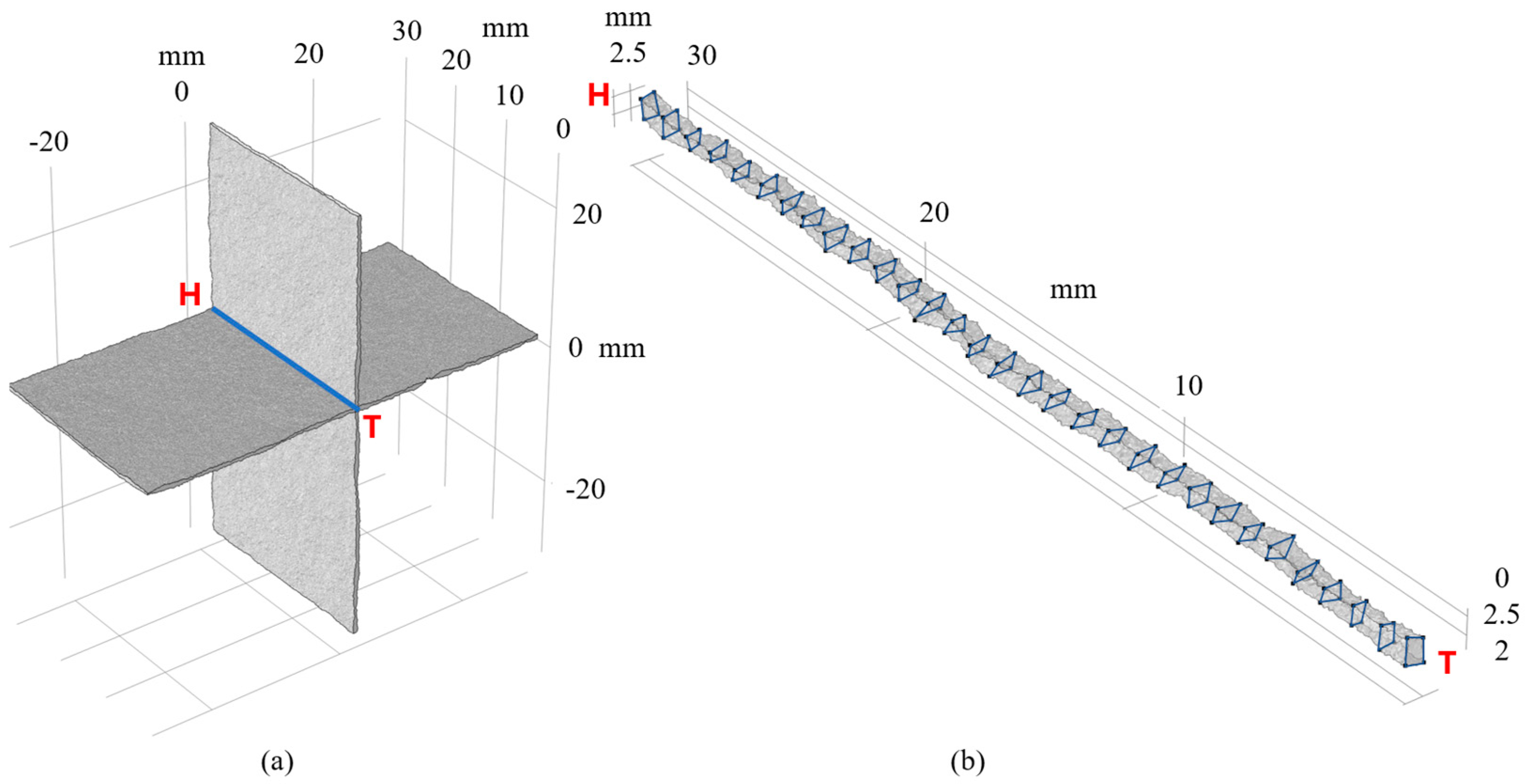
3.2. Boundary and Initial Condition
3.2.1. Boundary Condition
3.2.2. Initial Condition
3.2.3. Mesh Independence Check
4. Results and Discussions
4.1. Channeling Flow Variations in the Flow Field
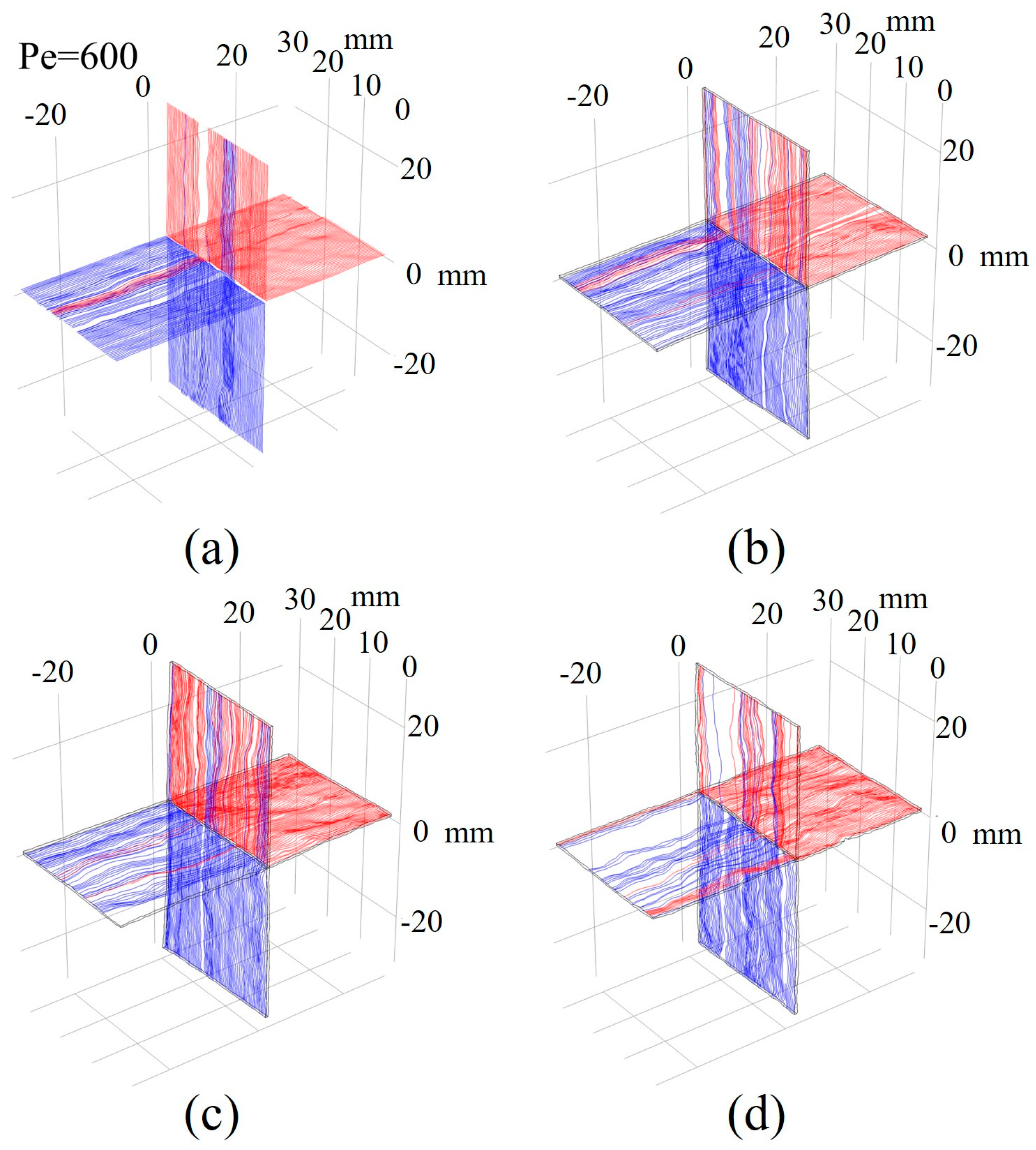
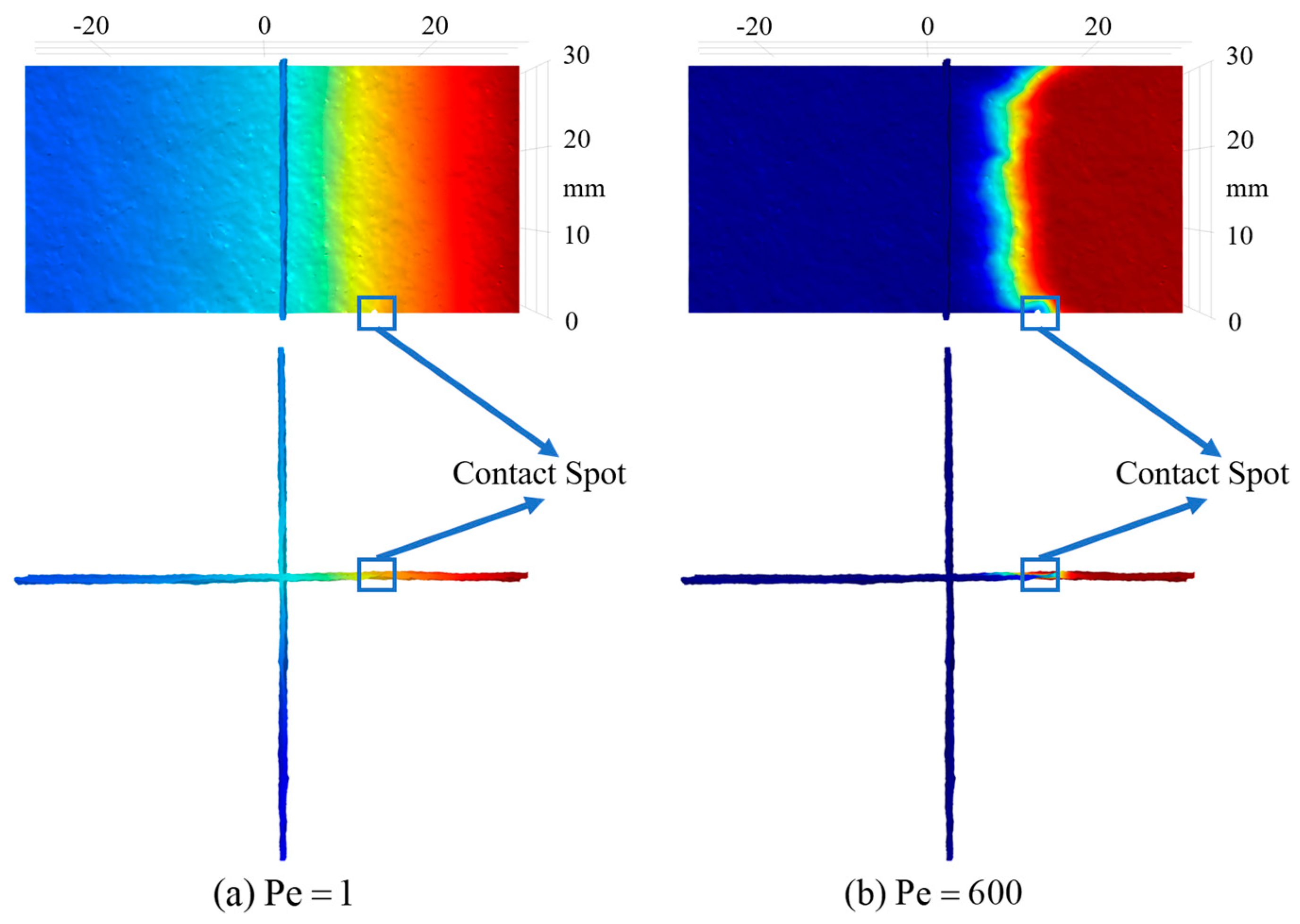
4.1.1. Effect of Pe
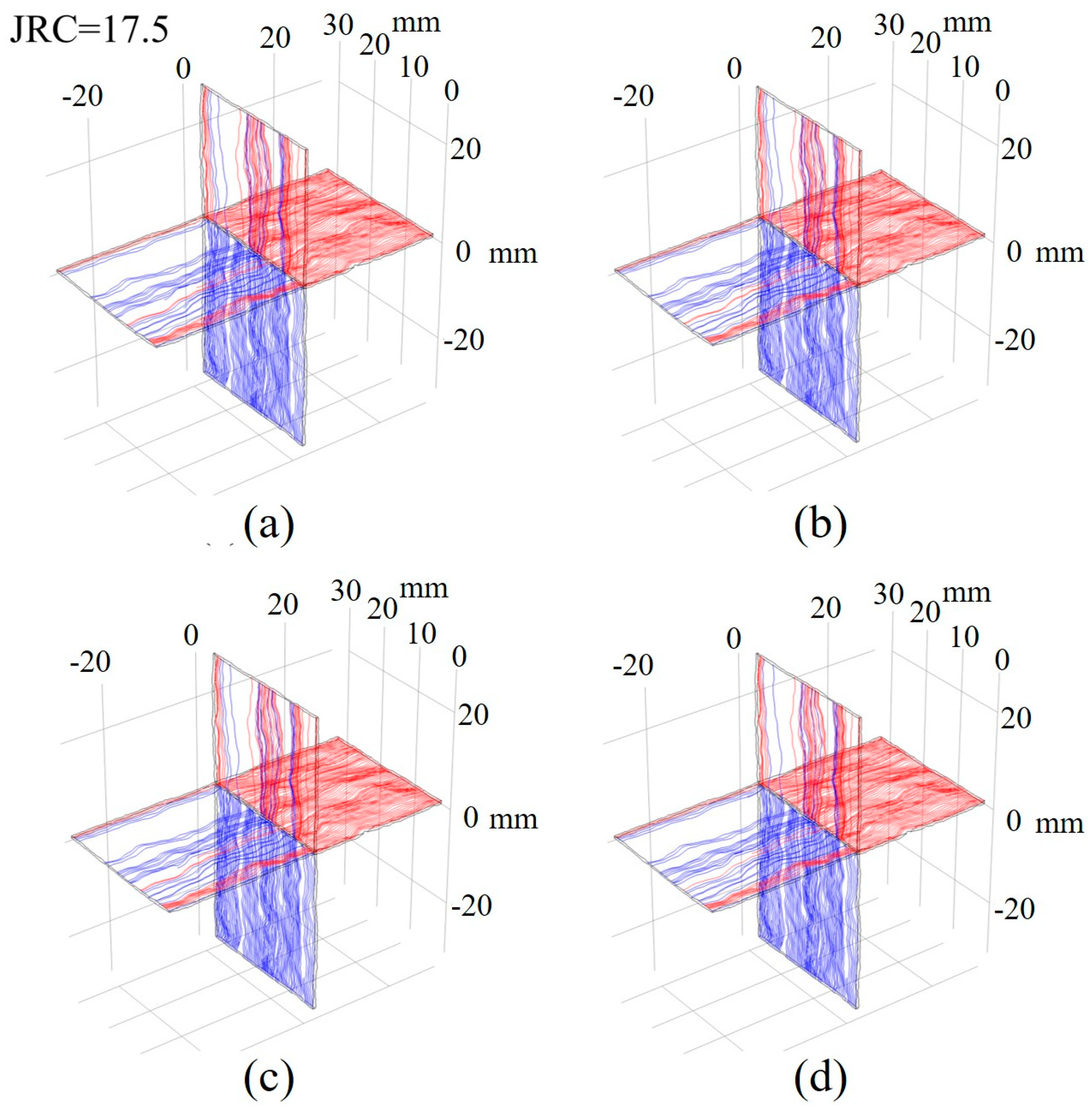
4.1.2. Effect of JRC
4.2. Evolution of Concentration Fields
4.2.1. Effect of Pe
4.2.2. Effect of JRC
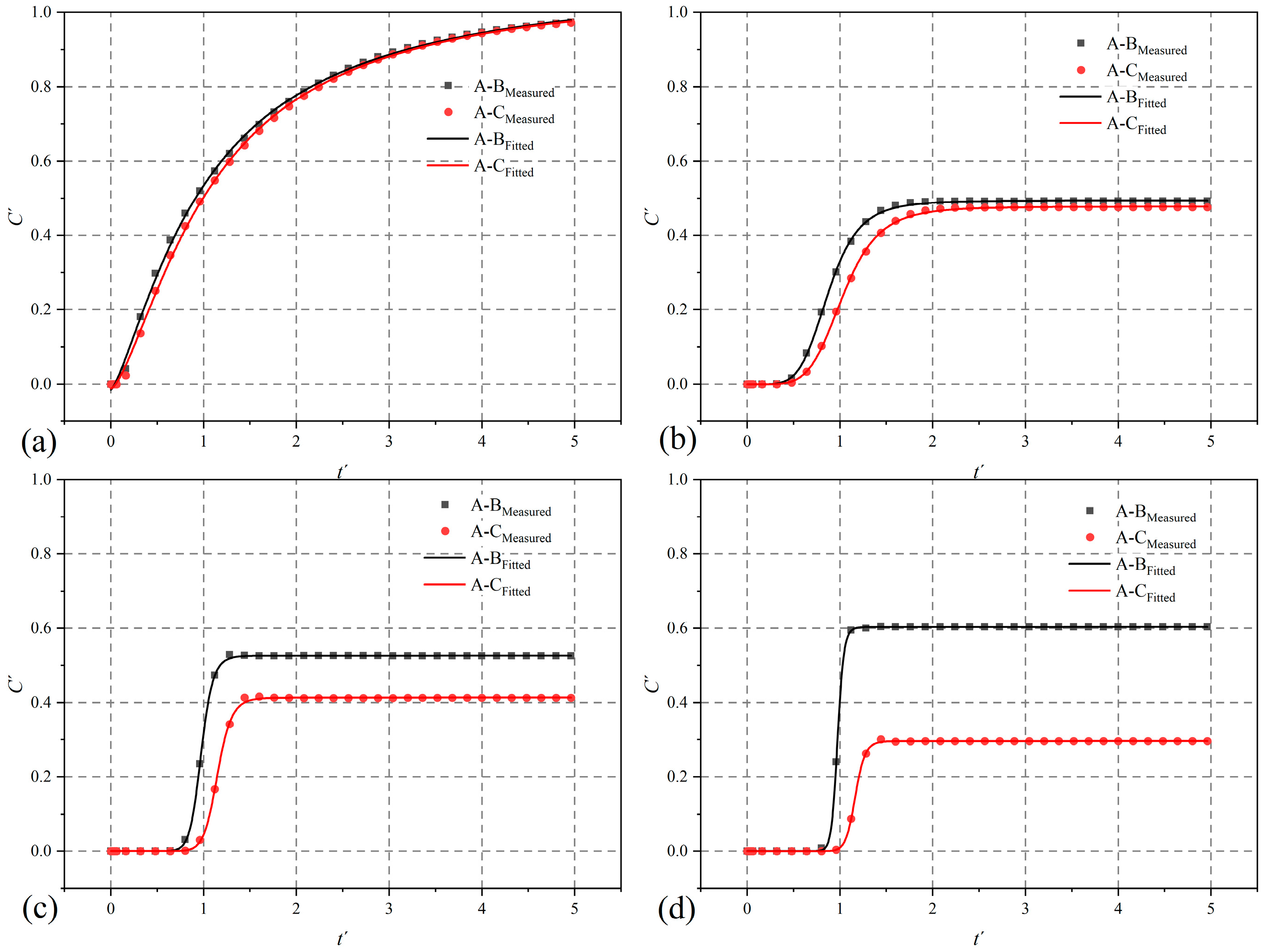
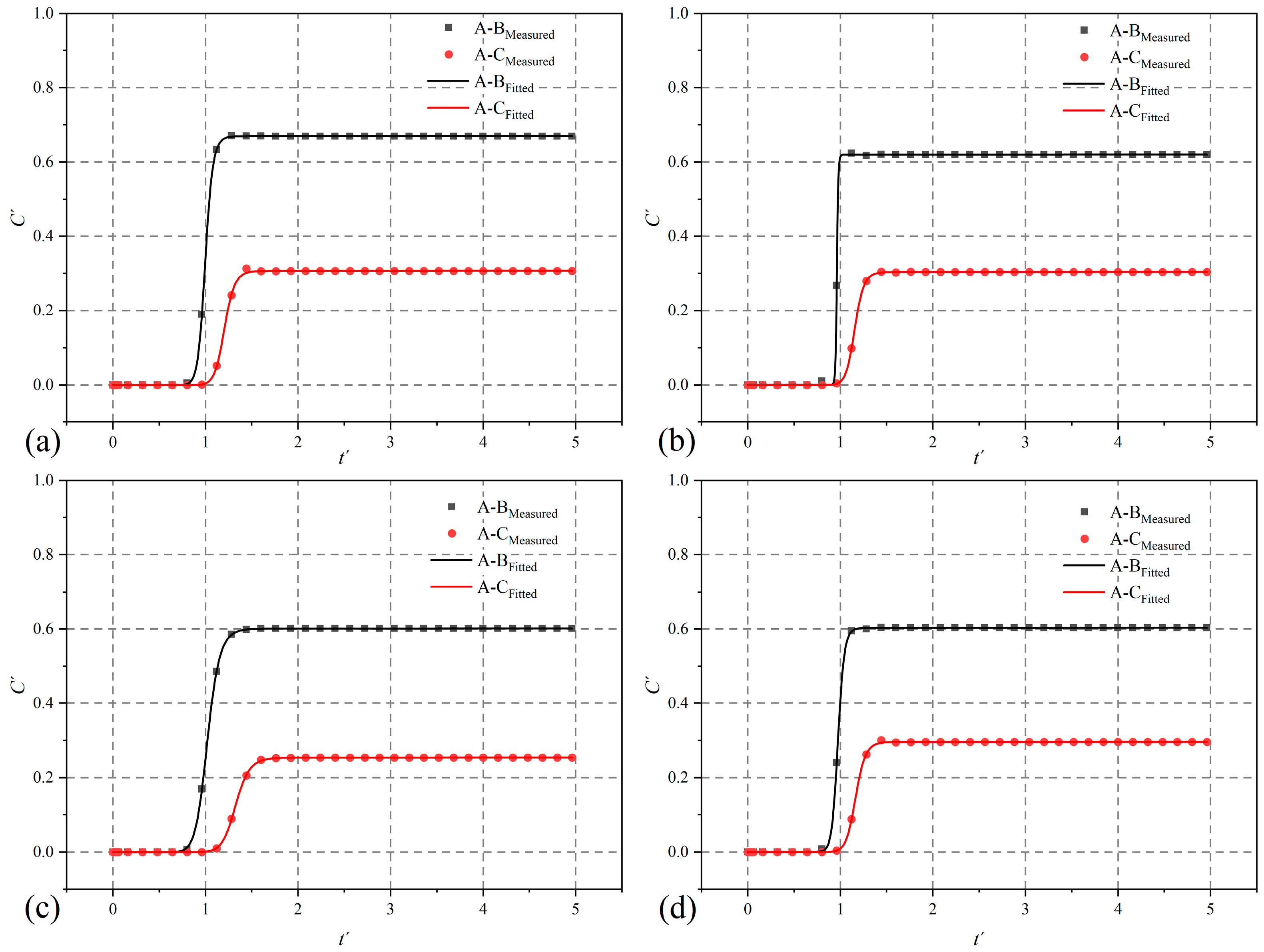
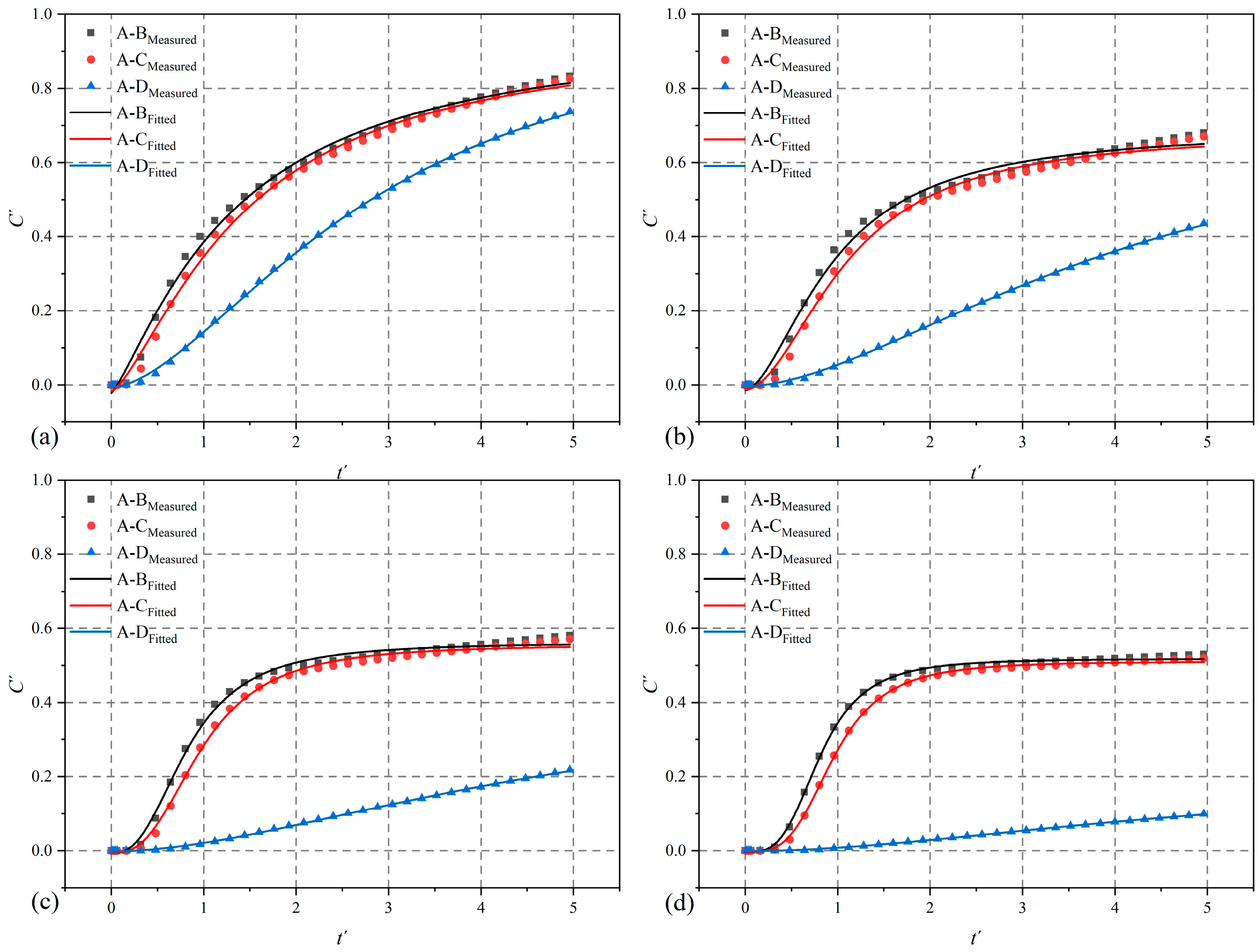
4.3. Solute Breakthrough
4.3.1. Effect of Pe
4.3.2. Effect of JRC
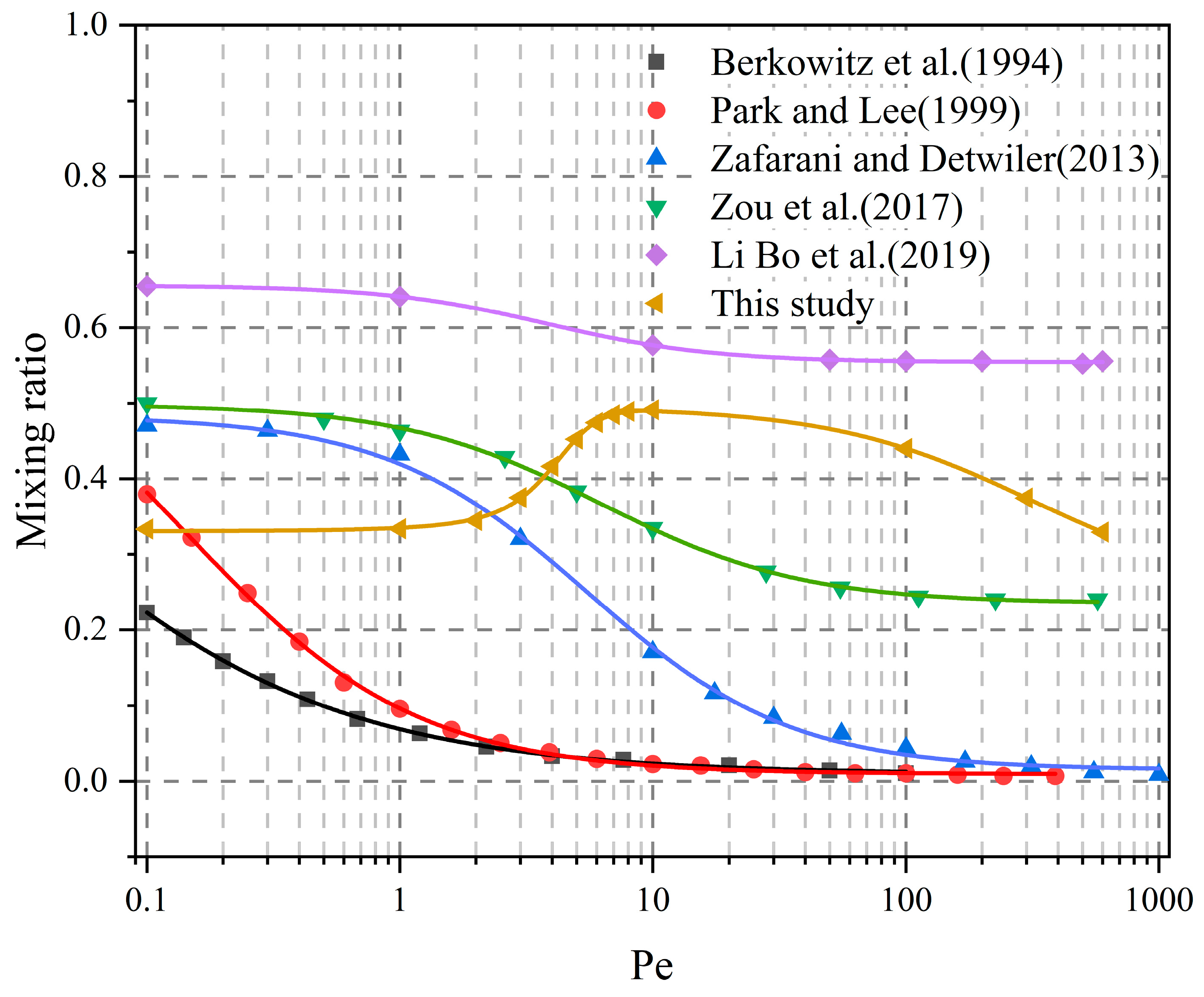
4.4. Solute Mixing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Neuman, S.P. Trends, prospects and challenges in quantifying flow and transport through fractured rocks. Hydrogeol. J. 2005, 13, 124–147. [Google Scholar] [CrossRef]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Chang, C.M.; Ni, C.F.; Li, W.C.; Lin, C.P.; Lee, I.H. Quantitation of the uncertainty in the prediction of flow fields in-duced by the spatial variation of the fracture aperture. Eng. Geol. 2022, 299, 106568. [Google Scholar] [CrossRef]
- Viswanathan, H.S.; Ajo-Franklin, J.; Birkholzer, J.T.; Carey, J.W.; Guglielmi, Y.; Hyman, J.D.; Karra, S.; Pyrak-Nolte, L.J.; Rajaram, H.; Srinivasan, G.; et al. From fluid flow to coupled processes in fractured rock: Recent advances and new frontiers. Rev. Geophys. 2022, 60, e2021RG000744. [Google Scholar] [CrossRef]
- Birdsell, D.T.; Rajaram, H.; Dempsey, D.; Viswanathan, H.S. Hydraulic fracturing fluid migration in the subsurface: A review and expanded modeling results. Water Resour. Res. 2015, 51, 7159–7188. [Google Scholar] [CrossRef]
- Pan, J.-B.; Lee, C.-C.; Yeh, H.-F.; Lin, H.-I. Application of fracture network model with crack permeability tensor on flow and transport in fractured rock. Eng. Geol. 2010, 116, 166–177. [Google Scholar] [CrossRef]
- Nong, R.; Wan, Y.; Ding, Y.; Chai, M.; Zhu, L. Effects of root systems on crack formation: Experiments, modeling, and analyses. Soil Tillage Res. 2023, 233, 105784. [Google Scholar] [CrossRef]
- Klyuev, R.V.; Brigida, V.S.; Lobkov, K.Y.; Stupina, A.A.; Tynchenko, V.V. On the issue of monitoring crack formation in natu-ral-technical systems during earth surface displacements. MIAB. Min. Inf. Anal. Bull. 2023, 11, 292–304. [Google Scholar]
- Berkowitz, B. Analysis of fracture network connectivity using percolation theory. J. Int. Assoc. Math. Geol. 1995, 27, 467–483. [Google Scholar] [CrossRef]
- Kosakowski, G.; Berkowitz, B. Flow pattern variability in natural fracture intersections. Geophys. Res. Lett. 1999, 26, 1765–1768. [Google Scholar] [CrossRef]
- Philip, J.R. The fluid mechanics of fracture and other junctions. Water Resour. Res. 1988, 24, 239–246. [Google Scholar] [CrossRef]
- Wilson, C.R.; Witherspoon, P.A. Flow interference effects at fracture intersections. Water Resour. Res. 1976, 12, 102–104. [Google Scholar] [CrossRef]
- Xu, C.; Dowd, P. A new computer code for discrete fracture network modelling. Comput. Geosci. 2010, 36, 292–301. [Google Scholar] [CrossRef]
- Berkowitz, B.; Naumann, C.; Smith, L. Mass transfer at fracture intersections: An evaluation of mixing models. Water Resour. Res. 1994, 30, 1765–1773. [Google Scholar] [CrossRef]
- Johnson, J.; Brown, S. Experimental mixing variability in intersecting natural fractures. Geophys. Res. Lett. 2001, 28, 4303–4306. [Google Scholar] [CrossRef]
- Park, Y.; Lee, K. Analytical solutions for solute transfer characteristics at continuous fracture junctions. Water Resour. Res. 1999, 35, 1531–1537. [Google Scholar] [CrossRef]
- Stockman, H.W.; Johnson, J.; Brown, S.R. Mixing at fracture intersections: Influence of channel geometry and the Reynolds and Peclet Numbers. Geophys. Res. Lett. 2001, 28, 4299–4302. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, H.; Li, C.; Wen, X. Examining fluid flow and solute transport through intersected rock fractures with stress-induced void heterogeneity. Eng. Geol. 2022, 311, 106897. [Google Scholar] [CrossRef]
- Zafarani, A.; Detwiler, R.L. An efficient time-domain approach for simulating Pe-dependent transport through frac-ture intersections. Adv. Water Resour. 2013, 53, 198–207. [Google Scholar] [CrossRef]
- Zou, L.; Jing, L.; Cvetkovic, V. Modeling of flow and mixing in 3D rough-walled rock fracture intersections. Adv. Water Resour. 2017, 107, 1–9. [Google Scholar] [CrossRef]
- Mourzenko, V.V.; Yousefian, F.; Kolbah, B.; Thovert, J.F.; Adler, P.M. Solute transport at fracture intersections. Water Resour. Res. 2002, 38, 1–14. [Google Scholar] [CrossRef]
- Hull, L.C.; Koslow, K.N. Streamline routing through fracture junctions. Water Resour. Res. 1986, 22, 1731–1734. [Google Scholar] [CrossRef]
- Berkowitz, B.; Braester, C. Solute transport in fracture channel and parallel plate models. Geophys. Res. Lett. 1991, 18, 227–230. [Google Scholar] [CrossRef]
- Robinson, J.W.; Gale, J.E. A laboratory and numerical investigation of solute transport in discontinuous fracture systems. Groundwater 1990, 28, 25–36. [Google Scholar] [CrossRef]
- Wendland, E.; Himmelsbach, T. Transport simulation with stochastic aperture for a single fracture—Comparison with a laboratory experiment. Adv. Water Resour. 2002, 25, 19–32. [Google Scholar] [CrossRef]
- Stockman, H.W.; Li, C.; Wilson, J.L. A lattice-gas and lattice Boltzmann study of mixing at continuous fracture Junc-tions: Importance of boundary conditions. Geophys. Res. Lett. 1997, 24, 1515–1518. [Google Scholar] [CrossRef]
- Grubert, D. Effective dispersivities for a two-dimensional periodic fracture network by a continuous time random walk analysis of single-intersection simulations. Water Resour. Res. 2001, 37, 41–49. [Google Scholar] [CrossRef]
- Li, B.; Liu, R.; Jiang, Y. Influences of hydraulic gradient, surface roughness, intersecting angle, and scale effect on nonlinear flow behavior at single fracture intersections. J. Hydrol. 2016, 538, 440–453. [Google Scholar] [CrossRef]
- Moreno, L.; Tsang, Y.W.; Tsang, C.F.; Hale, F.V.; Neretnieks, I. Flow and tracer transport in a single fracture: A stochastic model and its relation to some field observations. Water Resour. Res. 1988, 24, 2033–2048. [Google Scholar] [CrossRef]
- Thompson, M.E.; Brown, S.R. The effect of anisotropic surface roughness on flow and transport in fractures. J. Geophys. Res. 1991, 96, 21923–21932. [Google Scholar] [CrossRef]
- Jia, C.; Huang, T.; Yao, J.; Xing, H.; Zhang, H. Effect of isolated fracture on the carbonate acidizing process. Front. Earth Sci. 2021, 9, 2296–6463. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, W.; Zhan, L.; Ye, Z.; Chen, Y. Non-fickian solute transport in rough-walled fractures: The effect of contact area. Water 2020, 12, 2049. [Google Scholar] [CrossRef]
- Zou, L.; Cvetkovic, V. Impact of normal stress-induced closure on laboratory-scale solute transport in a natural rock fracture. J. Rock Mech. Geotech. Eng. 2020, 12, 732–741. [Google Scholar] [CrossRef]
- Brown, S.R. Fluid-Flow through Rock Joints—The Effect of Surface-Roughness. J. Geophys. Res.-Solid. 1987, 92, 1337–1347. [Google Scholar] [CrossRef]
- Mandelbrot, B. How long is the coast of britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef]
- Barnsley, M.F.; Devaney, R.L.; Mandelbrot, B.B.; Peitgen, H.O.; Saupe, D.; Voss, R.F.; Saupe, D. Algorithms for random fractals. In The Science of Fractal Images; Springer New York Inc.: New York, NY, USA, 1988; pp. 71–136. [Google Scholar] [CrossRef]
- Liu, R.; He, M.; Huang, N.; Jiang, Y.; Yu, L. Three-dimensional double-rough-walled modeling of fluid flow through self-affine shear fractures. J. Rock Mech. Geotech. Eng. 2020, 12, 41–49. [Google Scholar] [CrossRef]
- Liu, H.-H.; Bodvarsson, G.S.; Lu, S.; Molz, F.J. A corrected and generalized successive random additions algorithm for simulating fractional levy motions. J. Int. Assoc. Math. Geol. 2004, 36, 361–378. [Google Scholar] [CrossRef]
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. Rock Eng. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Ranjith, P.G.; Luo, Y. Water-gas flow in rough rock fractures: Insights from coupled triaxial compression experiments. Hydrogeol. J. 2022, 30, 1569–1581. [Google Scholar] [CrossRef]
- Karmakar, S.; Tatomir, A.; Oehlmann, S.; Giese, M.; Sauter, M. Numerical benchmark studies on flow and solute transport in geological reservoirs. Water 2022, 14, 1310. [Google Scholar] [CrossRef]
- De Dreuzy, J.R.; Méheust, Y.; Pichot, G. Influence of fracture scale heterogeneity on the flow properties of three-dimensional discrete fracture networks (DFN). J. Geophys. Res. Solid Earth 2012, 117, B11207. [Google Scholar] [CrossRef]
- Huang, N.; Liu, R.; Jiang, Y.; Li, B.; Yu, L. Effects of fracture surface roughness and shear displacement on geo-metrical and hydraulic properties of three-dimensional crossed rock fracture models. Adv. Water Resour. 2018, 113, 30–41. [Google Scholar] [CrossRef]
- Bodin, J.; Delay, F.; de Marsily, G. Solute transport in a single fracture with negligible matrix permeability: 2. mathematical formalism. Hydrogeol. J. 2003, 11, 434–454. [Google Scholar] [CrossRef]
- Bodin, J.; Delay, F.; de Marsily, G. Solute transport in a single fracture with negligible matrix permeability: 1. fundamental mechanisms. Hydrogeol. J. 2003, 11, 418–433. [Google Scholar] [CrossRef]
- Lee, S.H.; Kang, P.K. Three-Dimensional Vortex-Induced Reaction Hot Spots at Flow Intersections. Phys. Rev. Lett. 2020, 124, 144501. [Google Scholar] [CrossRef] [PubMed]
- Li, G. Tracer mixing at fracture intersections. Environ. Geol. 2002, 42, 137–144. [Google Scholar] [CrossRef]




| Parameter | Note (unit) | Value |
|---|---|---|
| Injection concentration | C0 (kg/m3) | 1 |
| Diffusion coefficient | Dc (m2/s) | 2.03 × 10−9 |
| Gravitational acceleration | g (m/s2) | 9.81 |
| Inlet flow rate | Q (m3/s) | 1.015 × 10−13 and 1.0155 × 10−12, 1.015 × 10−11 and 1.015 × 10−10, 3.045 × 10−10 and 6.09 × 10−10 |
| Péclet number | Pe (−) | 0.1, 1, 10, 100, 300, and600 |
| Reynolds number | Re (−) | 0.00016, 0.0016, 0.0155, 0.1553, 0.4658, and 0.9316 |
| Width of fracture | W (m) | 5 × 10−4 |
| Water viscosity | µ (Pa·s) | 1.307 × 10−3 |
| Water density | (kg/m3) | 9.997 × 102 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Xue, K.; Zhang, S. The Behavior of Fluid Flow and Solute Transport in 3D Crossed Rock Fractures. Processes 2025, 13, 67. https://doi.org/10.3390/pr13010067
Han X, Xue K, Zhang S. The Behavior of Fluid Flow and Solute Transport in 3D Crossed Rock Fractures. Processes. 2025; 13(1):67. https://doi.org/10.3390/pr13010067
Chicago/Turabian StyleHan, Xuefeng, Kangsheng Xue, and Shaojie Zhang. 2025. "The Behavior of Fluid Flow and Solute Transport in 3D Crossed Rock Fractures" Processes 13, no. 1: 67. https://doi.org/10.3390/pr13010067
APA StyleHan, X., Xue, K., & Zhang, S. (2025). The Behavior of Fluid Flow and Solute Transport in 3D Crossed Rock Fractures. Processes, 13(1), 67. https://doi.org/10.3390/pr13010067