Abstract
The study of bubble growth and collapse is of great significance in the context of sustainability due to its influence on numerous energy-related processes and technologies. Understanding the dynamics of bubble behavior is vital for optimising heat transfer efficiency, which has an energetic role in improving the performance of sustainable systems such as nuclear reactors, thermal inkjet printing, and nucleate boiling. Indeed, researchers can progress strategies to enhance the efficiency of these technologies by analysing the parameters influencing bubble growth and collapse, which can lead to reduced energy consumption and environmental impact. Although several theoretical models and experimental investigations have been achieved in the past to inspect bubble growth and collapse, a thorough review and critical assessment of the studies conducted have not yet been achieved. This review aims to provide a comprehensive understanding of the relationship between bubble dynamics and sustainability, highlighting the potential for further research and development in this area. Specifically, the scope and limitations of past research on bubble growth and collapse is conducted to fill this gap in the open literature. The review covers both numerical and experimental studies of bubble growth and collapse in a wide set of innovative industrial applications including nuclear reactors, thermal inkjet printing, nucleate boiling, hydrodynamic erosion, and ultrasonic and medicinal therapy. The current review also attempts to illustrate and evaluate the numerical methods used and underlines the most relevant results from the studies that were looked at in order to provide researchers with a clear picture of the growth and collapse of bubbles in different applications. The results give a precise understanding of the dynamics of bubble growth and collapse and the related temperature change and cumulative heat transmission from the thermal boundary layer. Additionally, it has been demonstrated that simulation-based models can effectively predict transport coefficients. However, the review observes a number of limitations of the past research on bubble growth and collapse. Due to numerical instability, very little work with respect to dynamic modelling has been carried out on the mechanisms of bubble collapse. Accordingly, a number of recommendations are made for the improvement of heat transmission during bubble growth and collapse. Specifically, future criteria for the highest heat transmission will demand more precise experimental and numerical approaches.
1. Introduction
The growth and collapse of bubbles in fluids can have significant impacts on a variety of physical processes and engineering applications, including subcooled nucleate boiling, bubble condensation, and liquid cavitation. In particular, as the liquid is being boiled, the bubbles will rise and promote the mixing of the liquid’s molecules and heat transmission. The procedures are intrinsically complicated due to the occurrence of phase-change heat transfer in a moving interface, which is characterised by the variable radius of the bubble. This makes the operations more difficult [1].
It is crucial to have a thorough appreciation of the bubble dynamics that take place throughout nucleate boiling in order to accomplish operative and reliable heat transfer in several industrial processes, such as distillation columns and refrigeration [2]. Specifically, bubbles are created on a surface immersed in a liquid that is below its boiling point during the subcooled nucleate boiling process. Due to the heat transfer from the surface, the liquid boils at the bubble site with the expansion of the bubbles. The bubble separates from the surface as the bubble reaches a sufficient size, rises to the surface, and then bursts. High-speed liquid jets may be created when the bubble bursts, which could recover heat transmission from the surface [3]. Throughout the boiling process, it is well acknowledged that changes in the shape of the bubbles and the dynamics of the contact lines can have a noteworthy influence on heat transmission. Due to the controlling role that they play in heat transmission and hydrodynamics, the bubble departure frequency, departure diameter, and growth rate are the subjects of a significant amount of research [4].
As the phenomenon of bubble condensation happens, a bubble may condense and collapse when it touches the boundary between a liquid’s surface and a gas phase. A fast-moving liquid jet is created when a bubble bursts, which can erode or damage surrounding surfaces. The collapse of bubbles is required in some applications, such as inkjet printing, since it can facilitate the production of tiny liquid droplets that are extruded from nozzles [5].
Cavitation, a physical phenomenon in liquids, is the act of rupturing a liquid by lessening the pressure at a relatively fixed liquid temperature. As the liquid pressure drops below its vapor pressure, bubbles start to develop and eventually collapse, which is known as liquid cavitation. These bubbles have the potential to expand and then burst, sending high velocity liquid jets and shockwaves toward nearby objects. Pumps, turbines, and propellers may experience cavitation in engineering applications, resulting in decreased performance or even failure [6,7]. Cavitation methods are specifically ultrasonic or ultrasound cavitation techniques. Under high-intensity sound wave irradiation (in industrial processes between 20 and 50 kHz), acoustic cavitation happens in liquids. Yet, the passageway of a liquid through a constriction, such as an orifice plate, throttling valve, venturi, etc., produces hydrodynamic cavitation [8]. The cavitation process is very attractive because it produces large amounts of local energy in the bulk liquid at a low cost, has a great degree of flexibility, and minimises environmental damage [9]. In nucleate boiling, bubble condensation, and liquid cavitation processes, the growth and collapse of bubbles play a substantial role in the overall behavior of systems. Understanding the dynamics of bubble growth and collapse can help engineers to design more efficient and reliable systems and improve our understanding of fundamental physical processes.
Both numerical and experimental studies were carried out concerning the growth and collapse of bubbles in different industrial applications. The ability of numerical modelling to forecast dynamic behavior and comprehend the mechanisms of heat transfer involved in nucleate boiling heat transfer has proven to be very promising. This potential can be ascribed to the rapid advancement of computational resources and the enhancement of various multi-phase models.
Both direct and indirect measurements of the bubble-induced pressure pulses have resulted in the development of a number of different methods over the years. Acoustic transients, such as shockwaves, micro-jets, turbulence, shear forces, etc., released during the collapse of a bubble are collected utilising a hydrophone at a distance from the centre of the collapse. These transients are then utilised to estimate the pressure that was exerted during the collapse [10,11]. During the collapsing bubble-driven pumping, the following effects are caused by a rise in the viscosity of the fluid: (1) an upsurge in the stability of the bubble oscillations, which restricts the creation of a jet that is vital in the operation of the pump; and (2) an upsurge in the viscous pressure head that has to be confronted in order to push the liquid through the hole [12].
The authors believe that the body of published research does not offer a thorough analysis of the advancements made in bubble growth and collapse. In this area of research, the drive of this review is to judgmentally evaluate the conducted studies of bubble growth and collapse illustrating the scope and limitations, innovative configurations, numerical methods, in addition to drawing some of the foremost findings from the existing open literature and identifying a number of unresolved questions for future studies. The scope of this review encompasses a broad diversity of subject areas, one of which is the configuration of experimental or numerical studies on bubble growth and collapse. This article goes into considerable detail about technology strategies for bubble growth and collapse, covering research, application, and development techniques. The consequences of this review may deliver a map for further investigations as they would make it easier for scientists to understand the numerous advancements made in bubble growth and collapse. On top of this, this review attempts to offer a comprehensive understanding of the link between bubble dynamics and sustainability, emphasizing the potential for further research and development in this region.
2. Review Method
The current review is presented to deliver an outline of research that has examined the scope and limitations of recent innovations and developments concerning the growth and collapse of bubbles. This overview facilitates a comprehensive understanding of the topic. The review is further augmented by a detailed examination of existing published studies. Different databases, including ScienceDirect, SpringerLink, Scopus, ResearchGate, and Google Scholar, were used to find related studies and peer reviewed content. The keywords designed to filter and catch related papers included: bubble growth, collapse, cavitation, hydrodynamics, bubble dynamics, and phase change. Although there were no restrictions on the publication dates of the articles, priority was given to the inclusion of the most successful current published studies between 2004 and 2023 to discourse the most innovative investigations.
3. Bubble Growth Studies
Indeed, it is essential to have a proper knowledge of the bubble dynamics that occur during boiling to achieve successful heat transfer in a wide set of applications. It is widely known that during boiling operations, variations in the bubble form and the dynamics of the contact lines may significantly affect the transport of bubbles [13]. Ebullition factors, including the bubble departure diameter, bubble departure frequency, and growth rate are the focus of a plethora of studies because of the controlling impact they have in heat transmission and hydrodynamics. In most situations where heterogeneous bubble nucleation happens on a solid surface, it is well known that the wettability of the surface will control the bubble shape during the whole ebullition cycle. This section focuses on presenting the associated studies of bubble growth and their influences on heat transmission within a wide set of applications with a critical evaluation. The next sections discuss the relative bubble growth studies that are classified as the liquid–gas and solid–gas studies.
3.1. Liquid–Gas Studies
Agarwal et al. [14] utilised a Volume of Fluid (VOF) based interface approach to model the film boiling and bubble production in water at 219 bars and 373 °C, while satisfying an isothermal horizontal surface. Together with an interface mass transfer model, the Navier–Stokes and thermal energy correlations were resolved. The models account for the impacts of interface mass transfer, surface tension, and conforming latent heat as well as the impact of temperature on the conveyed thermal characteristics (specific heat and thermal conductivity) of vapor. The findings provided a clear understanding of film boiling and yielded quantitative data on irregular periodic bubble release forms as well as on temporal and spatial variable film thickness. In comparison to simulations with constant fluid characteristics, the calculations also accurately anticipated the transport coefficients on the horizontal surface, which were strongly affected by the fluctuations in fluid characteristics.
Mukherjee and Dhir [15] numerically examined the heat transfer and bubble dynamics related to lateral bubble merger when nucleate boiling transitions from partial to fully developed. The 3-dimensional Navier/Stokes equation, the continuity equation, and the energy equation are all resolved by the SIMPLE approach. The Level-Set Method (LSM) was employed, and the liquid vapor interface was captured. The LSM involves solving a partial differential equation (PDE) that tracks the growth of the interface corresponding to time. Numerous bubble mergers in a line and in a plane were calculated, and the wall heat transfer and bubble dynamics were contrasted to the case study of a single bubble. The outcomes demonstrated that the total wall heat transmission is greatly increased by the merger of several bubbles. This improved wall heat transfer results from colder liquid being drawn toward the wall throughout contraction after bubble merger, which traps a layer of liquid between the bubble bases.
In 2005, a connected Level-Set and VOF technique for the simulation of incompressible two-phase flows with surface tension was presented by Tomar et al. [16]. The paired algorithm saves bulk while accurately capturing the intricate interfaces. For various superheat levels, a planar simulation of bubble development in water at a critical pressure was conducted. Analysis has been done on how superheat affects the frequency of bubble formation. Additionally, simulations of bubble formation and film boiling in the refrigerant R134a are carried out at pressures close to and far from the critical pressure points. The ways in which saturation pressure affects frequently bubble development have been investigated. When water is heated to over 15 K, a divergence from the sporadic bubble release is seen. Additionally, the impact of heat flow on instability was studied. For water in close-to-critical state, it has been discovered that a drop in super-heat between 15 K and 10 K causes fluctuations that affect the length of the ebullition cycle.
In 2010, a computer simulation of a vapor bubble boiling in a sub-cooled pool was achieved by Wu and Dhir [17]. By contrasting the findings of the bubble growth domain, while considering bubble departure diameter, the numerical process combining level-set function with moving mesh technique was proven to be effective. For various sub-cooling and varied gravity levels, the estimates of bubble dynamics and heat transmission are shown. The drop in gravity for a certain sub-cooling reduced the heat transfer around the bubble.
In 2016, the progression dynamics of a bubble population were studied by Marchal et al. [18] in a yield stress fluid matrix (a liquid medium (bitumen). A uniform generation of gas was used to drive the bubble population. The situation involves the gradual expansion of bitumen barrels over an extended period of time, inside of which radioactive salts were distributed. Radioactivity results in the creation of hydrogen in a consistent volume throughout the radiolysis of bitumen chains. The results ascertained that the utilised fluids can deform indefinitely if they are subjected to stress over a specific value. Furthermore, it has been demonstrated that, in the event that the population is stationary, yield stress interrupts the classic paradigm of nucleation, bubble formation, and Ostwald ripening in a Newtonian fluid. The study by Marchal et al. [18] was characterised by the use of two different nucleation models (threshold nucleation, continuous nucleation) to explore the impact of the yield stress on the most important metrics of the settling time to the steady state, the max. swelling, and the stationary swelling, as represented in Figure 1, Figure 2 and Figure 3, respectively. These figures indicate that the two nucleation models produce the same steady state swelling of up to 6 Pa of the yield stress (Figure 2).
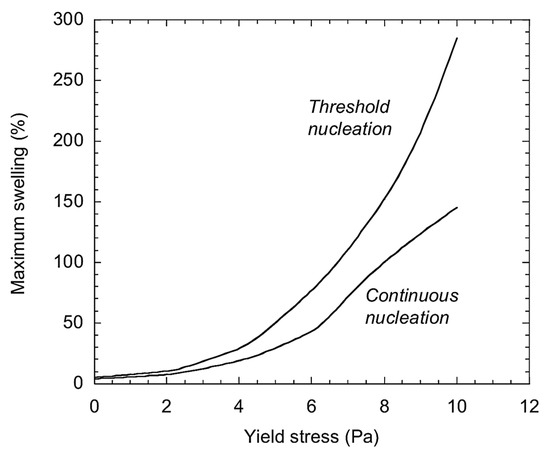
Figure 1.
Maximum swelling vs. yield stress [18] “(Reproduced with permission from Journal of Non-Newtonian Fluid Mechanics by Elsevier, 2024; Order Number: 5858171492020)”.

Figure 2.
Steady state swelling vs. yield stress [18] “(Reproduced with permission from Journal of Non-Newtonian Fluid Mechanics by Elsevier, 2024; Order Number: 5858171492020)”.
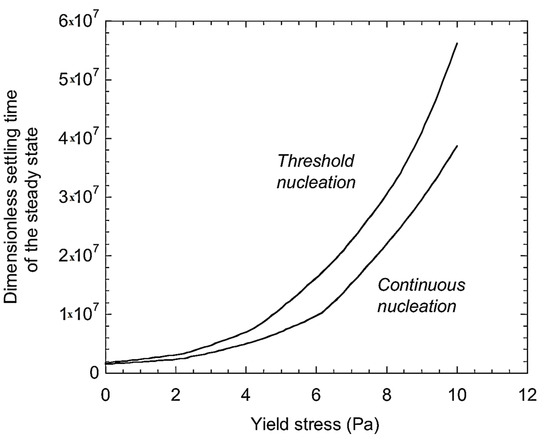
Figure 3.
Settling time of the steady state vs. yield stress [18] “(Reproduced with permission from Journal of Non-Newtonian Fluid Mechanics by Elsevier, 2024; Order Number: 5858171492020)”.
Goel et al. [19] used high-speed vision tests with sub-cooled de-mineralized water at 1 atm under nucleate pool boiling conditions to evaluate the bubble departure features such as the bubble departure frequency and diameters. To achieve the parametric examinations of bubble departure behavior, the water pool was designed with dimensions of 300 × 135 × 250 mm and four distinct heating components. The results indicated that the degree of sub-cooling (Tsub = 520 K), super-heat (Tsat = 110 K), as well as heat flux, parameters of heater configuration, heater inclination, and heater surface roughness were studied. It was revealed that the heater size, inclination angle, and wall super-heat all increased the departure diameter while liquid sub-cooling and surface roughness dampened it. It was also exposed that the departure rate reduced with an upsurge in heater size but enlarged wall superheat and inclination angle.
Thermal cavitating flows in liquid nitrogen surrounding a 2D hydrofoil were inspected by Zhang et al. [20]. The mass transfer homogeneous cavitation model connected to the energy equation and the RNG k-ε turbulence model with an adapted turbulent eddy viscosity were utilised to account for thermal effects. The Clausius-Clapeyron equation was utilised to enhance the saturated vapour pressure in the cavitation model process. Particularly in the thermal area, the enhanced Zwart–Gerber–Belamri model comes to an agreement with the experimental data of Hord et al. of NASA, as established by the expected pressure and temperature within the cavity under cryogenic circumstances. The cavitation dynamics during the phase-change process were significantly affected by the temperature effect, which may cause a delay or suppression in the onset and development of cavitation behavior.
Pahk et al. [21] invented the creation and dynamic performance of a boiling vapor-bubble that happens under boiling histotripsy insolation. Unambiguously, the researchers observed how the bubble expands and contracts over time. Numerical and experimental studies were attained using a high-speed camera to examine the dynamic of bubbles that were created in optically transparent tissue imitating gel phantoms and subjected to 2.0 MHz of the field of a High Intensity Focused Ultrasound (HIFU) transducer. The results indicated that the shockwave’s asymmetry and water vapor transport can cause incorrect bubble formation, that might be accountable for HIFU-tempted tissue decellularization.
Using in situ synchrotron radiography, Lu et al. [22] studied bubble development, intermetallic compounds (IMCs) dissolution, and their connections throughout heating of an Al-5 wt.% Mn alloy. As the melt was heated, the pores underwent a slow transition from an irregular shape to a subglobose shape, and then eventually a transformation into spherical bubbles. The radii (r) of bubbles 1 and 3 become smaller as time (t) progresses, and the connection between r and t may be effectively described by a Gaussian function in terms of its shape (Figure 4a). Bubbles 2, 4, and 5 all exhibit a rise in their radii with time, with bubble 5 exhibiting the most rapid expansion rate among the three (Figure 4b). With a rise in temperature, the hydrogen should become more soluble in the aluminum melt, causing the bubble size to diminish throughout the course of the heating process and eventually vanish altogether.

Figure 4.
(a,b) Bubble radii changes against operational time for the five representative bubbles [22]. The correlation of bubble 5 starts after 510 seconds as represented in blue background “(Reproduced with permission from Journal of Alloys and Compounds by Elsevier, 2024; Order Number: 5858181017625)”.
In 2020, Zeng et al. [23] exhibited concrete proof for the development of growth styles, shape, mass transfer channels, and lateral growth rate when thickening hydrates on gas (CH4-C3H8) bubbles are suspended in water with inhibitors. These findings were found during the process of thickening growth. During the thickening growth process, an identical and dense-hydrate coating was detected on the bubble as well as at the gas-liquid planar contact. This happened when an inhibitor was not present. The heterogeneous nature of the film instigated a number of circular and cross-shaped craters to perform on its surface. These craters represented as a new conduit for the transfer of mass and sped up the initial thickening and expansion of the hydrate. The hydrate’s viscosity was created in the reaction setup and the capacity of the aqueous solution to spread over the reactor wall was instituted to be connected with the enlargement of the morphology of the hydrate.
Allred et al. [24] created a conceptual framework for the wetting and de-wetting processes that occur throughout bubble generation relying on dynamic contact angles. To accurately illustrate the impact of surface wettability on contact angle dynamics and contact lines throughout bubble development and departure, this structure is integrated into VOF simulation. Computers were used to conduct these simulations. It has been established that the early stages of bubble formation are controlled by the declining contact angle. This happens as the contact line becomes farther and farther from a bubble’s centre. The primary wetting parameter that controls the greatest departure size and contact diameter is the receding contact angle. Better reduced-order models were then constructed, which resulted in correlations between the greatest departure diameter and contact diameter as functions of the dynamic contact angles, independent of fluid properties.
Zhao et al. [25] employed a phase change lattice Boltzmann to assess the impacts of 2-computational fields with constrained space and a free outlet boundary while observing conjugate heat transfer on the whole nucleate boiling. The model introduced was tested, notably in the enhanced convective outlet boundary for multi-phase flow in detailed information, using Laplace’s law and the droplet wetting process. A thorough investigation was carried out into the dynamic behaviors of the whole nucleate boiling process, considering the nucleation, growth, coalescence, departure, ascent, and ultimate rupture. Although growth and departure were significantly assisted when more isolated bubbles coalesced, the dynamic flow behaviors of bubbles’ coalescence are essentially similar. Additionally, the researchers demonstrated that the volume of escalating bubbles in the free outlet field increased over time. It was found that the pressure impact between the inside of the bubble and its surroundings was the main cause of this.
Winder et al. [26] used a stainless-steel framework called the SNS target module which is designed to hold mercury. In order to lessen stresses and prevent cavitation, bubbles of helium are inserted into the mercury. This gas makes it more challenging to precisely guesstimate the physical reaction of the target module. It is essential to have the skill to simulate the reaction of the target vessel before endeavoring to estimate its life. A forceful model for mercury with injected gas bubbles has been offered with the intention of delivering a high-accuracy mercury–vessel reply behavior without the obligatory level of processing expenditures to screen individual bubbles.
Li et al. [27] appraised the influence of thermodynamic effects on the cavitation flow in a liquid oxygen turbo-pump. To couple the physical parameters with temperature, the thermodynamic model based on the Zwart–Gerber–Belamri cavitation model and the shear stress transport k–ω turbulence model were utilised to numerically simulate the entire flow passage. Referring to numerical studies, cavitation mostly occurs at the head of the impeller inlet’s central blades and at the leading edge of the inducer inlet’s suction surface. At low cavitation numbers (σ = 0.07), thermodynamic impacts meaningfully lessen the vapor-phase volume fraction of the cavitation zone; yet, at high cavitation numbers, they increase it.
In 2022, the pool boiling tests were employed on vertical surfaces by Zhou et al. [28] in sub-cooled and nearly saturated conditions. Deploying a high-speed camera with great time-based and latitudinal resolution, the behavior of bubbles on micro-pin-finned surfaces was considered. Plentiful forms of bubble growth on many surfaces were created as a result of this research, which observed the impacts of the micro-pin-fins on the bubble creation and collapse. When scheming the bubble development rate, the influences of heat transfer from the micro-pin-fins and thermal boundary layer were considered. Further investigation was done to see how surface tension, reaction forces, and inertia affected the movement of bubbles. Following these components, a model for the growth and motion of bubbles was shaped. In this aspect, the micro-pin-fins used three key mechanisms to withstand bubble collapse. These include the inertia deduced by the variation in bubble growth rate, the pin influence on the contact radius, and the response force caused by the local differential pressure.
Lai et al. [29] formed a model for the construction of a single bubble in liquid hydrogen, while bearing in mind how temperature is disseminated throughout the bubble. By simultaneously resolving the Rayleigh Plesset equation, the thermal equilibrium correlation, the thermal diffusion correlation, and the heat conduction correlation in semi-infinite space, one may define and forecast the formation of a single bubble in liquid hydrogen. The model investigates the growth pattern of the bubble radius, the bubble radius growth rate, the vapor pressure, the thickness of the thermal boundary layer, and the temperature differential between the boundary and the centre; it inspects how variables like the liquid’s temperature and the surrounding pressure affected the growth of a single bubble in liquid hydrogen. It was possible to examine if a single bubble may transit from experiencing dynamic expansion to facing thermal growth by comparing the important moments of the numerous physical metrics described above.
Cheng et al. [30] built an examination setup with an observable flow channel in order to study bubble generation in vertical rectangular narrow channels. At the Onset of Nucleate Boiling location, bubbles were discovered at one atmosphere in sub-cooled flow boiling water. Two different common bubble development schemes were chosen to be simulated using numerical methods. During the experiment, thermocouples and a high-speed camera were utilised to capture the bubble shapes as well as the wall temperatures. Approximately 30% of the total amount of evaporation is attributed to the microlayer evaporation that takes place close to the base of the bubble.
3.2. Solid–Gas Studies
Hu et al. [31] outlined the Phase Field Model (PFM) of gas bubble growth that comprises micro-structure dependent cluster dynamics to discover the performance of gas bubble swelling in the recrystallization zone of a solid matrix Uranium Monolithic (UMo) fuel. The PFM is an influential numerical approach for simulating multi-phase flows with complex interface dynamics. It can precisely capture the interface between various fluids, handle complex geometries, and allow for easy implementation of boundary conditions. The PFM includes solving the model’s equations that recognize the progress of the scalar field representing the interface, along with the motion’s equations for the fluid-phases. This model was then utilised to discover gas bubble growth. The phase field coupled model permits the systematic simulation of the effect that the rate of defect creation, the rate of clustering, the rate of interstitial emission, and the rate of sink rates on grain boundaries have on the advance of gas bubbles. The findings specified that interstitial clustering is the prominent key physical process that leads to rapid gas bubble swelling kinetics in the recrystallization zone.
Zhou et al. [32] utilised molecular dynamic simulation to search for the dynamic progress features of a helium (He) bubble throughout spallation in single crystal aluminum (a solid matrix) and its consequences on void nucleation growth and thermomechanical features. Before and after the bubbles merge, the connection between bubble radius and time is nearly linear, and the expansion rates that are parallel to those rates were instituted. The expansion towards adjoining bubbles sources an overlap of plastic deformation zones, which endorses local melting. This happens due to the bubbles’ proximity to one another. The bubble avoids the nucleation and development of voids in the surrounding area, and when the expanding bubble comes into contact with developed voids, it absorbs them. This suppression becomes more operative as the bubble size or density is bigger, but it becomes less operative as the shock force grows stronger. When compared to the sample without He bubbles in solid state, this one has a much lower number of nucleated voids and a meaningfully smaller average radius of voids. Following the melting process, there is a destruction of the continued nucleation of voids, which grounds the radius to rise somewhat, while concurrently causing a lesser drop in quantity.
In 2020, the growth process of nano-solid structured cobalt foams was investigated by Arévalo-Cid et al. [33]. These nanostructured cobalt foams were generated via hydrogen bubble template electrodeposition. In order to accomplish this goal, cobalt foams have been created utilising a diversity of electro-deposition periods and inspected using a variability of characterization approaches, namely confocal microscopy in reflection mode and scanning electron microscopy (SEM). Throughout the creation of the foam, agar-agar was mixed into the electrolytic bath to examine the significance of the chemical additives on the growth process and concluding qualities of the foams. Figure 5 introduces the combination of agar occasioned in a successful adjustment of the micro-structure of the final foams. This resulted in a denser, more porous structure that had a lesser pore area and a slower rate of growth, which decoded into improved mechanical features.
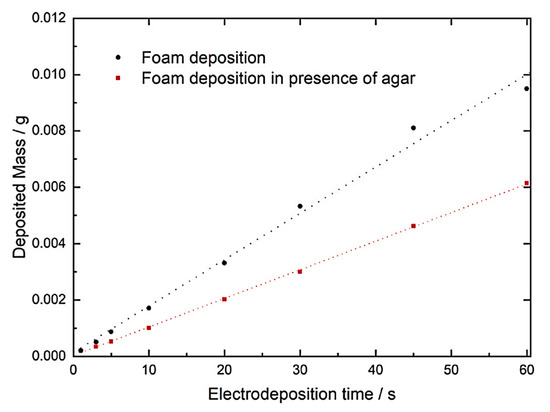
Figure 5.
Obtainable electrodeposited foam mass at various times [33] “(Reproduced with permission from Materials Characterization by Elsevier, 2024; Order Number: 5858181471771)”.
In 2022, the time evolution of an inter-granular bubble was reconstructed by Prudil et al. [34] utilising the Included Phase Model (IPM). The IPM involves resolving a number of partial differential equations that define the dynamics of the dispersed phase, including transport, diffusion, and reaction processes. The model incorporated complicated interface morphology while accounting for the creation and associated transit of gas atoms and vacancies. Interfacial energy, internal energy, and elasticity are the driving forces behind these two processes. The four processes that the model predicts ultimately resulted in the generation of linked high-aspect ratio bubbles on the grain face are over-pressure, bubble development, coarsening, and coalescence. The results compared favorably with both the CAGR/UOX/SWELL SEM data and the current SIFGRS model when sets of 250 bubbles were simulated over time using the model’s computing efficiency. Analysis of the simulation’s results revealed that the two-point autocorrelation function captured the development of an inter-connected network, perhaps leading to improved release thresholds. The findings of this investigation further showed the significance of bubble density as a measure of the bubble structure created by coalescence within a solid matrix. Furthermore, this study ascertained that the IPM is a powerful numerical technique for simulating multi-phase flows. It can accurately capture the dynamics of the dispersed phase, and its impacts on the continuous phase, while handling high volume fractions and complex physical phenomena.
Table 1 depicts the summarization of the associated research on bubble growth studies while distinguishing the most interesting results.

Table 1.
Outline of research on bubble growth indifferent applications.
According to the studies that were previously addressed, the creation of corrected bubbles may be the source of HIFU-induced tissue decellularization due to the potential imbalance in shockwaves and the transfer of water vapor. One may have a better understanding of the procedure by which a single bubble converts from dynamic development to thermal growth by linking the critical moments of the aforementioned physical indications. Furthermore, a cluster dynamics and phase field model can be stretched to train the accompanying growth of defect and second phase precipitates often detected in treated materials.
4. Bubble Collapse Studies
Plentiful academics have, over the past few decades, attempted to recognize the fluid dynamical mechanisms in charge of the impulses connected to the cavitation collapse of bubbles. However, it has been proved that at the three distinct processes—including the shockwave, the splashing properties, and the impinging liquid jet—are at work here. This section proposes conducting a critical assessment of the associated studies on bubble collapse in a wide range of industrial applications.
In 2013, Gong and Cheng [35] conducted numerical simulations in two dimensions using the novel phase-change lattice Boltzmann method (LBM) to study the nucleation of water on a micro-heater with constant heat flux and constant wall temperature, respectively. Under conditions of constant wall temperature, the effects of gravity, contact angle, and superheat on bubble departure diameter and release duration were tested. The analysis included the three-phase movement of the vapor bubble’s contact line, as well as the flow fields and temperature profiles both within and outside the bubble during the boiling process.
In 2015, using wavelets and Fourier transforms to analyse the piezoelectric waveforms, Navarrete et al. [36] investigated the dissipation of acoustic energy. The main experimental findings show that as compression progresses: (1) the liquid meniscus attains the conical zone in cavitation conditions; (2) the liquid meniscus undertakes a symmetrical alteration from two dimensions to three dimensions, becoming a “bulb with a nozzle”, where the instabilities are drawn and controlled; (3) the nozzle is maintained as part of the new meniscus that persists in pushing the gas pocket; and (4) furthermore, as the collapse process proceeds, the bulb eventually changes into a cloud of bubbles, and the bubble structures display their distinct expansion–contraction rate. The authors arrived at the conclusion that the breaking of a conical bubble activates a variety of distinct processes for the emission of light after looking at the dynamics and acoustics.
In 2016, Gong and Klaseboer [37] developed a fluid–solid integrated algorithmic scheme to consider the relationship between a deformable viscoelastic solid and a collapsing bubble. A Zener type viscoelastic model was utilised using the linked Boundary Element (BE) and Finite Element Method (FEM) to achieve this. The FEM was utilised to determine the viscoelastic solid response to the spontaneous pressure brought on by the bubble’s collapse, whereas the boundary element method was utilised to mimic bubble growth, contraction, and collapse. The Zener type viscoelastic model was employed to appropriately accommodate for the change in a viscoelastic solid’s stiffness over time as a result of pressure. The study indicated how variables, including the solid’s viscoelastic properties, the range of max. bubble sizes, and the locations of the bubbles affect the viscoelastic dynamic response of a solid.
In 2016, Tang et al. [38] conducted a study on the impact of an ultrasonic field on the deflation and condensation of vapor bubbles in a sub-cooled pool that was at rest. The effects of the ultrasonic field were examined in this study. When outcomes were introduced at liquid sub-cooling temperatures of 15–30 K, the vapor bubbles progressively disintegrated, but at temperatures over 40 K, they collapsed into a significant number of smaller bubbles. The limit of liquid sub-cooling for bubble break was lowered to 20–26 K while utilising ultrasonic vibration, causing capillary waves to appear on the bubble surface. The enhanced sensitivity of bubbles to the ultrasonic vibration made this possible. Additionally, the region of the bubble that was in touch with the cold bulk liquid was extended due to the capillary wave’s existence. The temperature boundary layer close to the vapor–liquid interface was also disturbed by the capillary wave’s presence, which augmented the condensation process. Accordingly, at the same amount of liquid sub-cooling, the liquid’s inertial shock to the vapor bubble with ultrasonic vibration was a bit more robust than what would have been detected in the absence of ultrasonic vibration, as proved in Figure 6.
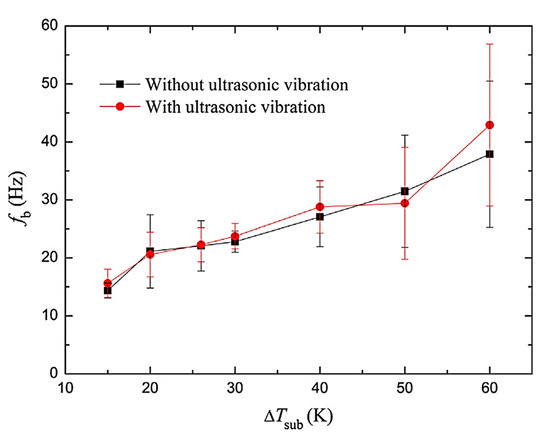
Figure 6.
Frequency of bubble collapse at various sub-cooling without and with ultrasonic vibration [38] “(Reproduced with permission from Experimental Thermal and Fluid Science by Elsevier, 2024; Order Number: 5858190317013)”.
In an underwater launching test, Wang et al. [39] testified to a distinct internal collapse mechanism that happens from the tail to the head of an axisymmetric projectile. This collapse phenomenon was discrete from other collapse scenarios and is on occasion seen in water tunnel experiments. The cavities swiftly contract upstream, which results in high-impact pressure. Moreover, fast re-entry jets occur, which causes substantial instability. Referring to the findings of the analysis, this phenomenon is associated with sudden changes in the cavitation number and vehicle speed. The quick acceleration of the vehicle causes the creation of thin cavitation bubbles, and the consequent rapid condensation of vapor during the deceleration phase results in the formation of an extra body force at the point where the cavity is closed. Hence, a major amount of velocity that is engaged toward the wall is created, and the layer of liquid water that is moving toward the wall remains to travel toward it and collide with it as an interior collapse. Additionally, numerical calculations were achieved with the effect of slowing down the development of the cavity. Referring to the findings, an enlargement in pressure was a crucial component, which brought about a nonlinear shift in the cavity’s overall length.
Qin and Alehossein [40] introduced a model of heat transfer allowing for the use of the Rayleigh/Plesset (RP) correlation and Computational Fluid Dynamics (CFD) with the aim of precisely forecasting the change of temperature and heat transfer that happens throughout a bubble’s collapse. CFD comprises solving a number of equations that outlines the dynamics of the fluid phases and their collaborations, while utilising numerical approaches. A two-phase compressible CFD model was formed to correctly mimic the bubble collapse to establish the changes in velocity, temperature, and pressure distribution between the liquid and the bubble. After being revised to take into account the impacts of radiation and conduction, the RP equation’s conclusions mostly settled with those of the numerical CFD. Further investigation was achieved on the temperature rise and collapse of bubbles, the rate of heat transmission by radiation and conduction, and the cumulative heat transfer of bubbles of altered sizes. It was detected that the bubble burst more violently as the initial max. bubble size was increased. The max. temperature was extended inside the bubble, which quickly enlarged, as depicted in Figure 7, along with the amount of heat that was accumulated and stored. The authors also confirmed the superiority of CFD as an influential instrument for appreciating and predicting the behaviour of complex multi-phase flows. The simulations are carefully validated against experimental data.
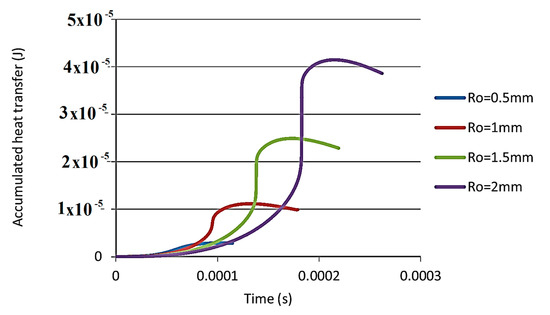
Figure 7.
Accumulation of heat transfer throughout different bubble collapse (Ro is the bubble radius) [40] “(Reproduced with permission from Heat transfer during cavitation bubble collapse by Elsevier, 2024; Order Number: 5858191386212)”.
Li et al. [41] calculated the dynamic bubble pressure using the Potential Flow Theory (PFT) and BEM. PFT is an analytical technique that describes fluid flow as an irrational and inviscid fluid motion. This technique assumes that the fluid particles move in such a way that the velocity vector at each point is the gradient of a scalar potential function. The pressure was specifically estimated using the Bernoulli equation and the auxiliary function approach. The potential function satisfying Laplace’s equation is defined such that the fluid velocity and pressure at any point in the flow can be obtained from the potential function. The BEM involves discretizing the boundary of the domain into a set of components and approximating the solution to the governing equations within each element. Bubble-induced pressure had two sources, and dynamic pressure had two portions. The first component, g, monitored the uneven pressure between bubble gas and ambient flow, which contributes to dynamic pressure. The second term of decomposed pressure, pm, is created via bubble motion, which evaluates jet impact. g fluctuation mirrored gas pressure. After the jet impact, pm at the wall centre peaks and subsequently drops owing to jet velocity and may increase when the toroidal bubble migrates into the wall.
Rowlatt and Lind [42] prolonged the Spectral Element Marker Particle (SEMP) technique to integrate a third fluid phase to investigate the bubble collapse problems in a fluid–fluid interface. The method is thought to be validated when a two-phase bubble explodes close to a stiff barrier. SEMP involves resolving a number of partial differential correlations that define the dynamics of the fluid and solid phases, including momentum conservation, mass conservation, and energy conservation. A wide set of fluid parameters and geometric arrangements were considered for understanding the impact of bubble collapse in bioengineering applications. In an effort to gain visions into the flow dynamics behind sono-poration and microbubble improved targeted drug administration, the authors considered a straightforward model of collaboration between the bubbles and cells. The bubbles deflated into spherical shapes at higher interface heights away from the rigid wall as a direct outcome of the compact contact that existed between the stiff wall and the bubbles. Indeed, SEMP has allowed for accurate modelling of the dynamics of the fluid–solid phases and can handle complex geometries.
Ye and Zhu [43] suggested the effect of a near wall acoustic bubble collapse micro-jet on an aluminum 1060 sheet, the cavitation threshold formula, and micro-jet velocity formulation. The Johnson Cook rate equation was used to create a 3-dimensional fluid–solid coupling model of the micro-jet effect on a wall. The utilised ultrasonic pressure amplitude was far higher than the liquid cavitation threshold, causing cavitation in the liquid. Micro-jets caused surface micro-pits. Clearly, micro-jet velocity affected the wall pressure. Ultrasonic cavitation examination evaluated tiny pits generated by micro-jet on aluminum 1060. Inversion analysis showed that pit diameter-to-depth ratio affected equivalent stress, equivalent strain, impact strength, and micro-jet velocity.
In 2017, calculations were made by Pavlov [44] to acquire the kinetics of a bubble’s collapse under the influence of an abruptly utilised external pressure. The bubble was initially in a state of thermal and mechanical balance with the nearby liquid. The condensation of vapor inside the bubble correlates to the bubble’s compression creating a pressure of saturated vapor inside the bubble at the interface temperature. Adiabatic processes are likely to cause a temperature increase in the main body of the bubble. Both the heat fluxes field and the temperature in the instant area of contact were deliberated. The mass flow coming from the bubble was calculated from the thermal balance. The assumption used in the calculation of the liquid’s pressure field was that the liquid is both incompressible and non-viscous. Several equations associated with the radius of bubble, compression rate, and internal vapor pressure were developed.
In 2017, a numerical simulation of the collapse of a cavitation bubble enclosed inside a diesel droplet was performed by Ming et al. [45] using the volume of fluid (VOF) method of the open source CFD toolbox OpenFOAM. The outcome exhibited that the collapse process was composed of several phases of rebound and collapse, which is alike to the vibration process of a damping spring oscillator. Figure 8 depicts that the pace of collapse accelerates as the pressure of the environment around it rises, whereas Figure 9 depicts that the collapse’s rate accelerates as the pressure of the saturated vapor falls. The impact of the surrounding pressure on the collapse process is far greater than the impact of the saturation vapor pressure.
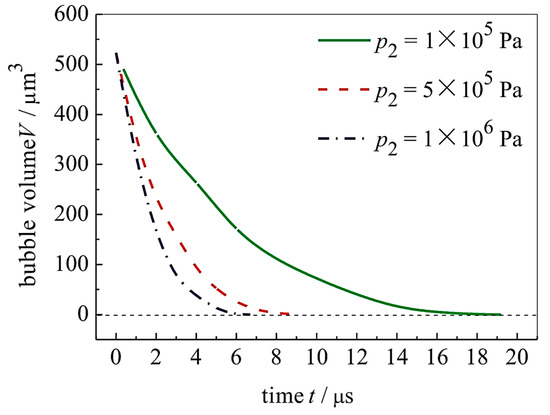
Figure 8.
Characteristics of collapse under different pressures [45] “(Reproduced with permission from Computers & Fluids by Elsevier, 2024; Order Number: 5858200400261)”.
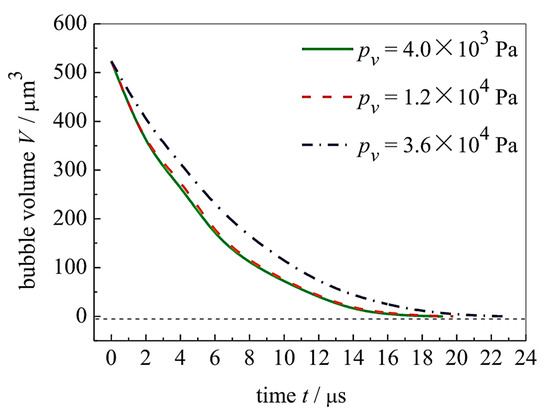
Figure 9.
Characteristics of collapse under different saturation vapor pressures [45] “(Reproduced with permission from Computers & Fluids by Elsevier, 2024; Order Number: 5858200400261)”.
Rosselló et al. [46] created a water hammer to achieve managed bubble collapses. A laser-generated bubble is enlarged and then squeezed utilising an electro-mechanical piston. It permits high energy concentrations in collapses and autonomous regulation of system parameters. To expand experimental findings, simulations of prototype bubble dynamics were conducted. The expansion ratio, consisting of the increased bubble radius over the equilibrium bubble radius, was the most important metric for collapse strength.
Phan et al. [47] developed an algorithm for compressible interface flows with and without mass transfers. The mathematical technique was built upon dual time fully compressible multi-phase homogeneous mixture flow modelling. The authors measured the boundaries that showed a substantial change in velocity, density, pressure, and temperature while deploying a compressive high-resolution interface capturing technique. It was possible to observe the formation of the wave-like boundary between the liquid and vapor around the sphere as the film boiled. The average heat fluxes generated by the simulation were contrasted against forecasted ones using analytical correlations and numerical data. Also considered were the impacts of the superheated wall on the heat fluxes. A pattern similar to the one seen in the previously published data was discovered as a result of a bigger heat flux on the sphere caused by a rise in the superheated wall’s temperature (Figure 10).
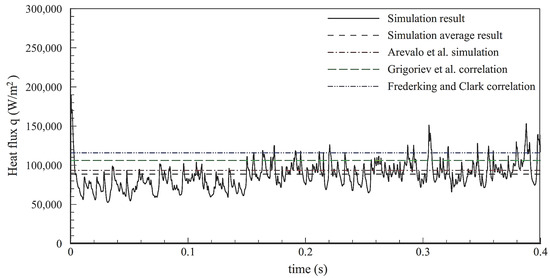
Figure 10.
Wall heat fluxes against operational time [47,48,49,50] “(Reproduced with permission from International Journal of Heat and Mass Transfer by Elsevier, 2024; Order Number: 5858200884075)”.
Kerabchi et al. [51] introduced computational results while considering the impact of depths between 0 and 10 m on acoustic cavitation. The study provided particular attention to the impact of the ultrasonic wave’s attenuation in regard to the dramatic conditions that emerged inside the bubbles as they burst. The liquid’s surface tension, compressibility, viscosity, depth, and attenuation of the ultrasonic wave are all reflected by the mathematical model that was utilised. The greatest pressure (pmax) and bubble temperature (Tmax) at the bubble collapse were instituted to meaningfully decrease when the depth of the water was increased up to 10 m, with the ultrasonic wave attenuation significantly contributing to the overall reduction event. However, when the bubbles were under the same pressure, this was the case. Lower temperature (10 °C) and higher frequency (1000 kHz) caused the decrease in Tmax and pmax with depth to be more dramatic; in these conditions, losses beyond 72% in Tmax and up to 94% in pmax (as opposed to values at z = 0) were achieved at z = 10 m. When the temperature and frequency were lower (10 °C) and higher (1000 kHz), the decrease in Tmax and pmax with depth was more dramatic.
In 2019, a Smoothed Particle Hydrodynamics (SPH) solver was established by Joshi et al. [52] to model the deflation of a single cavitation bubble near an elastic plastic material and examine the origins of plasticity which resulted in material degradation. The results highlighted the significance of the material deformation caused by the micro-impact jets and the shockwave produced during the collapse. An event dominated by shockwaves has the potential to degrade material at a far faster rate than a micro-jet hit. It was found that, in the case of the strain rate of stainless steel A2205, there is a significant impact on plastic deformation that, if ignored, may cause an over-estimation of the plastic deformation by as much as 60%. Additionally, they demonstrated that the biggest plastic strain happens at a radial offset from the symmetry axis, even though the impact pressure is the strongest below the collapsed bubble. This is due to the effects of inertia, which signify an influence on the position and the size of the plastic domain inside the material.
Brujan et al. [53] examined the dynamic of a laser-prompted cavitation bubble utilising 100,000 frame per second high-speed photography. A bubble near a vertical solid wall collapsed into a flat jet. Both radial and planar jets were created in the transition zone. The planar jet penetration and secondary cavitation construction creation were seen throughout bubble oscillation when the bubble diameter at max. expansion was lower than the distance between parallel solid walls. Planar jet height grew with bubble size relative to stiff wall distance. The jet velocity decreased as the bubble size and distance from the vertical wall increased.
In 2019, a unique experimental setup was reported by Hopfes et al. [54]. This novel experimental setup made use of a shock tube and applied a jellylike mixture as a water-like carrier medium. The effects of an instantaneous pressure rise on air bubbles of mm size that were injected in gelatin were investigated from two distinct angles. First, they demonstrated that individual bubbles in the gelatin behaved correspondingly to bubbles in water throughout the collapse of the structure, and that the concentration of the gelatin did not greatly impact the behavior of the bubbles. They also investigated four primary forms of bubble interactions that may also be defined by non-dimensional factors. It was observed that if there was a big size ratio between two bubbles, the interaction between them would either be controlled by the larger bubble if the bubbles were separated or would result in a prominent liquid jet if the bubbles were near to each other.
Bardia and Trujillo [55] offered a mathematical study of the intermediary bubble collapse. In contrast to thermally generated or inertia controlled collapse, intermediary bubble collapse was influenced by both liquid/vapor interfacial heat transfer and surrounding liquid advection. The bubble pressure and interfacial temperature were constantly shifting all the way through the process of this particular kind of collapse, which was one of the most identifying characteristics of this form of collapse. To be more specific, the work demonstrated in a quantitative manner that the collapse behavior shifted, when the process was happening, by a regular rate of pressurization in the adjacent liquid phase, rather than the commonly deployed approximated method of a step change. This was in contrast to the previous approximation, which assumed that the change would occur all at once.
Gan et al. [56] investigated a hull girder constructed to mimic a real warship and subsequently exposed to underwater explosion loads to see how it deformed. Experimental and computational techniques were both used in this study. The study also considered how a non-spherical underwater explosion bubble might affect things. The numerical computation was carried out by Coupled Eulerian–Lagrangian (CEL) method of CFD, and the experiment was carried out in an underwater environment with explosions that occurred in a swimming pool. Analysis of the associated results led to the conclusion that when detonation distances increase, the hull girder’s deformation form shifts from rigid-body motion to whipping, leading to the creation of a plastic hinge. The dynamic reactions of the hull girder will be the same for a range of charge weights when measured at the same dimensionless distance if the charge weights are within a given range.
Chudnovskii et al. [57] directed an examination of the boiling of a substantially sub-cooled liquid in which they explained how the liquid’s local heating by concentrated laser radiation via a thin optical fibre caused the boiling to begin. They investigated the growth of a vapor–gas bubble established at the surface of an optical fibre tip extensively. They presented estimations of these jets’ velocities, which appear to be in perfect agreement with the experiment.
Using a tank of water inside a cold room, Yuan et al. [58] studied the dynamics of a collapsed bubble close to a floating ice cake and its potential to be harmed by a high-speed jet and shockwave. A cryostat produced an ice cake from clean water, which was subsequently managed and positioned in a water tank inside a frigid room. The bubble was simultaneously created at a distance underneath the floating ice-cake by an electric spark that was produced at the same time. The two of them were interacting while being observed and captured by a fast camera. After seizing the bubble’s dynamics, which comprise the bubble jet and the shockwave, the authors calculated the negative impacts of bubble loads on the ice, counting fractures, breakage, and movement. Relying on the level of damage and the propagation of fractures, it was detected that crevasse patterns, radial and circumferential crack patterns, and radial crack patterns were produced on the ice. However, the most distinctive type of damage pattern was crevasse patterns.
Han et al. [59] deliberated the association between two bubbles of diverse sizes as well as the consequence of a wall on the process of bubble collapse using the Volumetric Optical Force (VOFE) microscopy method. VOFE microscopy is a prevailing experimental procedure used to train complex multi-phase flows in three dimensions. VOF microscopy contains and presents particles into the fluid and illuminates them with a laser beam. The laser light exerts optical forces on the particles, which can be utilised to operate their motion and track their trajectories. Thus, VOFE permits the quantification of the velocity, acceleration, and trajectory of individual particles or droplets within the flow. The authors observed connections between two bubbles of diverse sizes in free water without a wall in between. The authors guaranteed that these bubbles would move close to the wall and close to each other as they collapsed when there was a wall nearby. This has specifically occurred concurrently. They revealed that, in both a single bubble system and a double bubble system, the presence of a wall would increase the time necessary for the bubble to rupture. However, the wall’s existence can result in a more powerful process of the bubble collapsing and then rebounding. By inspecting the bubble’s centre of displacement, they revealed that the double bubble system may upsurge the dislocation of both bubbles. The VOFE technique is restricted to studying small-scale flows and requires careful calibration and validation against other experimental procedures to guarantee accurateness and reliability of the results.
Fursenko et al. [60] delivered a simulation of vapor bubble collapse close to a micro/fiber submerged in a sub-cooled liquid to suggest the process of high velocity liquid jet creation. Numerical simulations showed that jet generation is driven by bubble surface dynamics, not bubble shrinkage. The jet’s ideal fibre thickness was discovered.
Tan and Yeo [61] introduced a particle velocity estimate model relying on mass loss. Micro-abrasive particles measuring 5–50 μm were subjected to 20 kHz ultrasonic irradiation in deionized water for 10 min. In a well-controlled experiment, targets positioned 0.5 mm from the ultrasonic horn surface captured pushed particles. A reverse solid particle erosion model may estimate particle impact velocity from specimen mass loss. The results revealed particle velocity was 8–40 m/s and depended on the particle size and ultrasonic amplitude.
Orthaber et al. [62] conducted a number of tests in which they inspected the behavior of a single cavitation bubble on two sides of an oil–water interface. They looked at the specifics of the interaction between bubbles and surfaces (deformation, penetration). The anisotropy (the property of being directionally dependent) parameter makes the correct prediction that the bubble would permanently shoot to the interface if it was formed in low-density liquid. On the other hand, the bubble will continually shoot away from the interface if it was formed within high-density liquid. They expanded the scope of the study to include the correlations between a variety of bubble features and the anisotropy parameter.
Zhang et al. [63] performed an experiment to investigate the dynamics of a laser-prompted cavitation bubble that was near to the edge of a solid wall. The authors used high-speed photography equipment. Three typical scenarios were identified for the purpose of categorizing the phenomenon, relying on the deformation of the bubble interface that happened throughout the process of the bubble collapsing. The movements of the bubble centroid and interface in various directions were identified using a numerical analysis of the captured high-speed photographs. There was visible neck development in the middle of the bubble when it was extremely near to the edge. The drive of the bubble interface at the edge was hampered by this clear neck. In this case, the edge increased the time needed for the bubble to burst by up to 22% over Rayleigh’s entire time requirement (Rayleigh number is large, somewhere around 106 to 108).
Ezzatneshan and Vaseghnia [64] appraised the collapse dynamics of cavitation bubbles of various liquids in the vicinity of the solid surface with variable wettability conditions using a computational methodology based on the pseudo-potential multiphase lattice Boltzmann method (LBM). The simulation of the Redlich–Kwong–Soave equation of state (EoS) with an acentric factor was used to address the physical features of water (H2O), liquid nitrogen (LN2), and liquid hydrogen (LH2). The H2O, LN2, and LH2 fluids were considered while evaluating the cavitation bubble collapse close to the solid wall. Also, the effect of the surface’s wettability on the dynamics of the collapse was tested. The findings showed that the water’s cavitation bubble collapses faster when it comes across a strong liquid jet, but the LN2 bubble collapses more gently because of its bigger bubble radius at the rebound.
Huang et al. [65] explored the acoustic waves caused by the collapse and oscillation of a single bubble. The Schlieren Method was employed throughout the trials to document both the temporal growth of the bubble formations and the equivalent acoustic waves. A three-dimensional (3D) model was employed throughout the computational simulation to train the dynamics of a single bubble. The acoustic waves were the main topics of this study. The results showed that compression waves were produced as a result of the bubble’s rapid growth. These waves progressively steepened into a single shockwave that propagated outward through the liquid, and during the final phase of the collapse of the bubble, another strong shockwave was produced. The liquid field’s pressure and velocity increased following the shockwave. The liquid’s pressure dropped as a result of the rarefaction wave, and its spatial distribution became dispersive. As the distance over which the acoustic waves travel increased, the pressure that they exert and the effect they have on the liquid’s speed were observed to increase.
In 2021, to better understand the method of air entrainment used in the hydraulic aspect to lessen cavitation, Xu et al. [66] examined the influence of a single air bubble on the volume of noise produced by the collapse of a cavitation bubble. When a rising air bubble interacted with an underwater low-voltage electric discharge unit, it resulted in the formation of a cavitation bubble. For this analysis, only circumstances where the hydrophone probe, cavitation bubble centroid, and air bubble centroid were all almost on the identical horizontal line were taken into account. Referring to the findings, an air bubble’s size, roundness, and distance all considerably impacted the cavitation bubble’s direction of collapse and the sound generated pressure. The results also revealed a strong correlation between the direction of collapse and the associated pressure that the collapse produced.
Peng et al. [67] outlined the concept of the collapse of a single and a dual cavitation bubble while utilising the Thermal Lattice Boltzmann (TLBM) and double distribution function (DDF) approach. This approach uses a lattice-based model to simulate the movement of fluid particles and their interactions with solid particles and interfaces. Despite LBM including a thermal lattice model that defines the transfer of heat between fluid and solid phases, LBM affords an exceptional density-to-viscosity ratio. The approach also involves solving a number of partial differential correlations that define the dynamics of the fluid–solid phases, including mass conservation, momentum conservation, energy conservation, and temperature evolution. The correlations were solved using mathematical approaches such as the lattice Boltzmann method, and the simulation findings were authorized against experimental data. The outcomes of the simulation were in decent consistency with those of the theoretical analysis and the experiments. Peng et al. [67] dignified the max. collapse pressure, the lifetime of the cavitation bubble, the maximum collapse temperature, and the max. collapse velocity as corresponding to the distance between the cavitation bubble and the rigid barrier. Moreover, investigations were achieved to determine how the viscosity of the fluid and the starting pressure differential affect the max. temperature at which a system can collapse. The outcomes of the LBM simulation completely reproduced the slowing influence of a hard boundary on the cavitation bubble, the distance between the cavitation bubble, and the hard barrier growth; this resulted in the growth of the max. collapse pressure, max. collapse temperature, and max. collapse velocity.
In 2021, the behavior of cavitation bubbles when they collapse close to walls under conditions of high ambient pressure was highlighted by Trummler et al. [68]. Generic setups with various stand-off lengths were analysed using mathematical simulation with a solver that incorporates phase change. The findings showed that the stand-off distance and the collapse dynamics, the production of micro-jets, the rebound, and the maximum wall pressure were significantly related. The pressure impact data gathered at the wall may be used to establish a connection between cavitation-related material damage and the corresponding collapse processes. The findings on six different grid resolutions were contrasted, and it was exposed that, while the peak pressures were meaningfully dependent on the resolution, the key collapse characteristics were already documented on the coarsest resolution.
Long et al. [69] observed and investigated the collapse and formation of cavitation bubbles created throughout the pulsed-laser ablation of submerged targets in three different liquid environments: water, ethanol, and n-butanol, utilising a stroboscopic shadowgraph system. These bubbles were produced when submerged targets were being ablated by a pulsed laser. The images of collapsed bubble transitory phases were obtained. The bubble volume was at its lowest at this phase. Both ethanol and n-butanol might undergo cavitation-induced reactions, which generated gaseous molecules that prevented the bubbles from collapsing explosively. In contrast, the penultimate step of collapse was when cavitation bubbles produced by a laser in water acquired their lowest radii, leading to a higher upsurge in localized pressure and temperature that might cause a second round of etching.
Wang et al. [70] investigated the association between the various physical factors and the max. dimensionless radius of the bubbles by employing single factor analysis in addition to multiple regression analysis. Only a very weak linear relationship exists between the following quantities, for example, between density and viscosity, and between sound velocity and surface tension. Additionally, the regression models developed based on the random forest and neural network types of machine learning algorithms were utilised to forecast how the combined physical factors affect the severity of the bubble collapse. The outcomes confirmed that each of these models was workable and efficient. Additionally, the strength of the collapse was clearly influenced by the viscosity and surface tension, whereas density and sound velocity had the least effect.
Gai et al. [71] adapted the Conventional Lattice Boltzmann Method (CLBM) to allow for the statistical analysis of ice nucleation resulting from the collapse of a cavitation bubble. To examine cavitation bubble dynamics, including growth and collapse, the authors examined two distinct real-world ice nucleation application scenarios: scenario I used a solid barrier, while scenario II involved a pressured environment. Some of the significant system variables whose impacts on the max. collapse pressure (pmax) were inspected included the stand-off distance (λ), initial bubble size (R0), and differential pressure (Δp). The findings showed that scenario II yields a substantially higher pmax than scenario I, leading to more direct initiation of ice nucleation.
In 2021, a three-dimensional computational tool based on the multiphase lattice Boltzmann method (LBM) with multiple relaxation time (MRT) was used by Ezzatneshan and Vaseghnia [72] to study the dynamics of cavitation bubble clusters produced by sound near a solid wall under various wetting circumstances. To correctly impose the physical features of real fluids, the Peng–Robinson–Stryjek–Vera equation of state with an acentric component was integrated into the LBM. The obtained findings for the cavitation bubble cluster dynamics driven by sound showed that the pressure pulse cannot reach the lower bubbles due to the shielding effect of top bubbles. As such, the destruction of the top layer bubbles has a greater impact on the cluster core and the bubbles close to the solid surface than it does on the acoustic field.
In 2022, to better perceive the association between the cavitation bubble’s proximity to the wall and the collapse features, Xu et al. [73] created models with various distances from the benzamide wall to the cavitation bubble. The bubble placed exactly in the middle of two parallel walls experienced a major rate of volume change at the beginning of the collapse, according to the research. The bubble’s rate of volume change during the acceleration phase is proportional to its proximity to the wall and, thus, the pressure at its peak is higher. The initial spherical bubble regularly changed into an ellipsoid shape, and the surface of the bubble closest to the wall had a rather smooth texture. The wall penetrated the area with the strongest pressure field created by the collapse of the bubble when d was smaller than 1.59 R0.
In 2022, the dynamic behavior of bubble collapses, pressure loads, and water jets throughout the collapse of the bubble between walls and a free surface was mathematically inspected by Nguyen et al. [74] using a VOF-based simulation approach. This was done by mathematically analysing the pressure loads, water jets, and bubble collapses that occurred when the bubble collapsed close to the walls. The mathematical approach was relying on the compressible Navier–Stokes correlations, which were represented in a conservative formula. These equations explain how compressible viscous fluids flow. Investigations of spherical and non-spherical bubbles, as well as grid dependence studies of a spark-generated bubble were conducted. This study modelled the burst of a bubble. The outcomes indicated that the dynamics of the bubble during its collapse were highly consistent between the experiments and simulation’s results. The inspection of a single bubble that was situated near to a wall was done utilising a range of standoff distances. The pressure loads caused by the jets interacting with the walls were evaluated and analysed. A more difficult situation of bubble collapse along an inclined wall and free surface was also developed and experienced.
Yang et al. [75] evaluated the influences of wall temperature on the collapse of a bubble and formed a robust model for a cavitation bubble close to a cooled or heated wall. The process of the micro-jet and the cavitation bubble itself affecting the solid wall heat transfer, as well as the thermodynamic behavior traits of the cavitation bubble collapse close to the wall, were resolved by the researchers. This makes it possible to better realize how the micro-jet affects the cavitation bubble. By modifying the wall’s temperature, Tw, the cavitation’s thermal effects could also be influenced. To further explore the heat transfer intensity, a dimensionless temperature parameter was added. Research and analysis were conducted on the impact that p, and R0 have on the heat transfer. The outcomes showed that the ideal values of p, R0, and Tw could be utilised to recover heat conduction and device cooling or heating treatments on several surfaces.
He et al. [76] looked into the thermodynamics of bubble interactions using the double distribution function thermal lattice Boltzmann technique. Strong and weak interaction regimes of double cavitation bubbles were methodically explored, and the whole development and collapse processes during an interaction were effectively replicated. Also, the essential lengths between two equal-sized bubbles that allow for the distinction of various interaction types were proposed. When there are two unequal-sized bubbles in a liquid film, imbalanced forces operate on them, making the film harder to rupture than when the bubbles are equal in size. This means that the coalescence regime requires a smaller starting distance between the bubbles.
Ezzatneshan et al. [77] used a multiphase lattice Boltzmann method (LBM) to investigate the beginning of the boiling phenomena and the bubble dynamics that resulted. The researchers used two equations of state (EoS), the Peng–Robinson (P–R) and the Redlich–Kwong–Soave (R–K–S). Their predictive power for the nucleation, growth, and departure of bubbles was measured in comparison to the existing literature data. The influence of the wettability and form of the micro-heater surface, namely the grooved and cavity areas, was appraised in relation to the detached bubble’s separation time and velocity under various flow conditions. The region with larger temperature gradients—the groove and cavity’s sharply angled edges—were where the boiling phenomena originated, according to the results. The bubble continues to develop on the hydrophilic heated surface’s sharp edges where there are not many dry spots.
The implication of a dual distribution function multiphase lattice Boltzmann technique (DDF-MLBM) to examine the collapse of cavitation bubbles in cryogenic liquids was addressed by Ezzatneshan et al. [78]. The exact difference method (EDM) was used in the scheme to apply fluid–solid adhesion forces and interparticle interactions, while counting the energy equation. The Peng–Robinson (PR) equation of state was utilised in conjunction with an acentric factor to properly simulate phase shifts and the molecular complexity of cryogenic fluids such as liquid nitrogen (LN2) and hydrogen (LH2). The research observed the impacts of pressure, temperature, collapse duration, and the separation between a cavitation bubble and a nearby solid wall. The results indicated how vital the distances between the cavitation bubbles in the cluster and between the bubbles and the surrounding solid surface are in defining micro-jet velocity.
Table 2 shows a summary of the accompanying research of bubble collapse while demonstrating the most important conclusions.

Table 2.
Summary of studies on bubble collapse in different applications.
Despite the fact that it has a very tiny influence on the contour of the bubble, the analysis of a large number of previous studies revealed that the viscosity of the fluid may lower the pressure that is created by the bubble right before it bursts. The bubble deflated into a spherical shape as it moved further from the rigid wall’s interface heights as a further effect of the reduced contact between the bubble and the hard wall. Although nonlinear, the relationship between the max. bubble size and power is connected to the radiation power absorbed. In addition, the max. bubble size is proportionate to the absorbed radiation power.
5. Bubble Growth and Collapse Studies
This section develops the evaluation of the bubble growth and collapse studies that were encountered to enhance the heat transmission of specific set of industries.
In 2017, a Sharp-Interface Level-Set (SILS) approach was addressed by Lee and Son [79] for modelling the development and contraction of a compressible vapor bubble. This method utilises a level set function to characterize the interface and a number of partial differential correlations to express the dynamics of the fluid and solid phases. Referring to the findings, it was revealed that the temperature of the surrounding environment was an extensive factor in describing the pattern of bubble development and collapse. Throughout the phase of bubble expansion, it was also detected that the bubble’s pressure does not fall to a level lesser than the saturation pressure corresponding to the phase. The impacts of ambient temperature and phase change on the temporal discrepancies of the mathematical outcomes for the bubble growth and burst close to a wall, considering the radius of bubble and pressure of wall against time, are exhibited in Figure 11. Figure 11 shows that the bubble growth and collapse in close vicinity to a wall established that a re-entrant liquid jet was designed as a result of irregular liquid inertia and was influenced by the phase change and ambient liquid temperature. This phenomenon was observed when the bubbles formed near the wall. Furthermore, it was determined that the SILS Approach is a prevailing numerical technique for simulating complex multi-phase flows that involve fluid–solid interactions. It permits accurate modelling of the sharp interface between the fluid and solid phases and can handle complex geometries.
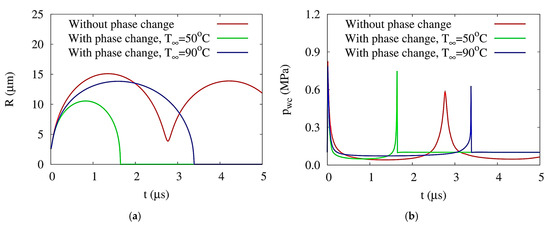
Figure 11.
The consequences of ambient temperature and phase change on the temporal variations of numerical results for the bubble growth and shrinkage near the wall: (a) radius of bubble vs. time and (b) pressure of wall vs. time [79] “(Reproduced with permission from International Communications in Heat and Mass Transfer by Elsevier, 2024; Order Number: 5858201250142)”.
Wang et al. [80] utilised a comprehensive set of ordinary differential equations to observe bubble production and collapse in micro-gravity situations. A dimensionless fitting constantly considers both the area changes of the moving vapor/liquid interface and the diffusive nature of the interface layer was added. By comparing predicted temporal fluctuations of bubble radii with actual data, one may define the fitting coefficients for bubble production and collapse in water and ethanol. The original conditions of a sharp lessening in temperature caused some “fluctuations” in the simulated bubble radii during the initial phase of bubble collapse. The “re-bound influence” of pressure equilibrium in the bubble, which occurred due to the original state, was linked to these “fluctuations”.
In 2019, to power micro-synthetic jets, Sourtiji and Peles [81] calculated the viability of using bubble growth and collapse over a wide set of operational frequencies between 0.1 and 2.5 Hz and a heating rate between 3 and 4.5 W. A primary micro-channel was linked to a micro heater that was placed inside a chamber with dimensions of 3.5 mm in radius and 220 μm in height. The nozzle’s aperture was 300 μm. The artificial jet was formed by switching the micro-heater on and off at regular intervals, which led to the implosion and explosion of bubbles inside the container. The authors captured successive images of bubble nucleation, growth, and eventual collapse using high speed DSLR photography and a microscope. The characterization of the synthetic jet comprised the use of a momentum coefficient. It was indicated that the synthetic jet’s average value was more than unity over a wide set of operational frequencies, which recommends that it could progress the performance of a number of micro-systems, including the micro-mixing that takes place in microfluidic devices.
In 2019, continued visual observations were prepared by Sun et al. [82] of the morphological development of a hydrate shell on suspended methane bubbles in super-saturated water. Referring to recently discovered information and results, the hydrate shell’s dynamic growth progressively went through three phases: rapid development, ongoing collapse, and growing stasis. These stages can be further separated into their individual sub-stages. A novel mechanistic model for the development of hydrate shells on bubble surfaces was established. This model measured the mechanical features of hydrate collapse as well as the inter-coupling of several hydrate-forming mechanisms and multi-phase mass transfer processes. This model was created based on the surface properties of hydrated bubbles at various phases. The model not only described the growth of hydrates on each side of the hydrate shell, it also provided the first quantifiable account of the capillary holes within the hydration shell.
Zimnyakov et al. [83] employed image analysis to pinpoint when foam samples started to form at various temperatures. The transition divided the collaborative of surface film cells into sub-ensembles that are developing and depopulating. With the depopulation of unstable sub-ensembles, a specific rate of cell rearrangements exponentially dropped and got closer to a fixed value during the growth. The association between the temperature dependent “macroscopic” growth collapse rate for average cell size, a “microscopic” rate parameter for individual cell growth–collapse, and the probability density function for cell size distribution was established for growth.
In 2020, a cavitation bubble produced by the nanosecond pulsed laser ablation of a solid at shallow liquid depths was explored by Nguyen et al. [84]. When the bubble radius was between 0.4 and 9 times the max. the liquid was presented. Photo-elasticity laser stroboscopic videography was utilised to track bubble dynamics. The bubble breaks through liquid when the liquid depth is slighter than the bubble radius. The duration of the bubbles is shortened but no further shock was felt. The bubbles expanded during contraction and flattened during expansion at liquid depths that are half or less of the max. bubble radius. The bubbles became toroidal at the lowest contraction, emitting more shockwaves.
Puncochar et al. [85] proposed a simple and straightforward physical model for the description of the bubble formation process. This concept covered bubble expansion, bubble ascent, bubble separation, and bubble deformation. Buoyancy, inertia, and elasticity are the three effects that were considered. The relationship between the final form of the bubble and its Weber number was assessed during the detachment procedure using the energy conservation concept. For this investigation, the bubble shapes, including oblate spheroid, prolate spheroid, spherical cap, and lens shape were taken into account. The data that were gathered are examined and contrasted with earlier studies. Table 3 shows different applications of the accompanying studies that delineated the bubble growth and collapse.

Table 3.
Outline of studies on bubble growth and collapse in different applications.
In the publications that were analysed above, it was found that ambient temperature was a key aspect in defining the pattern of bubble development and collapse. A re-entrant liquid jet arises as a result to the irregular liquid inertia and is substantially influenced by the phase shift and ambient liquid temperature, as seen by the bubble expansion and collapse close to the wall. The fact that the bubbles became larger before collapsing close to the wall served as evidence for this. Additionally, the secondary shockwaves become enlarged as the liquid depth increases, and a durable impulse is generated into the solid target.
6. Evaluation of the Numerical Methods Used in Bubble Growth and Collapse Studies
Many industrial and environmental activities involve binary and multi-phase flow phenomena. These procedures entail the simultaneous flow of multiple phases (gas, liquid, and solid) in varied arrangements. To accurately represent the complicated physical interactions between the phases in the numerical simulation of these processes, specialized models and techniques are needed. The current review recognizes the utilization of different numerical methods to mimic multi-phase flow phenomena. Each method has its advantages and shortcomings, depending on the specific presentation and the level of accurateness needed. Some of the commonly used numerical techniques for multi-phase flow simulation are discussed below:
The Finite Volume Method (FVM) is a generally utilised mathematical method for resolving complex multi-phase flow problems. It is a conventional approach that can handle complex geometries and irregular boundaries. FVM can also handle non-uniform grids and is computationally effective. However, FVM needs careful selection of numerical schemes to avoid numerical instability [86]. Specifically, FVM is an adaptable method that can be used in both liquid–gas and solid–gas systems as a result of its capacity to handle complicated geometries, non-uniform grids, and multi-phase interactions. However, the careful selection of numerical patterns is important in both cases to guarantee stability and precision in the simulations.
The Level-Set Method (LSM) is a general numerical method for pursuing the development of a free surface or interface between two fluids in a multi-phase flow. It indicates the interface as a level set of a higher dimension corresponding to the computational domain. The LSM delivers a number of benefits, including the ability to handle complex interface topologies and geometries, and making it simple to apply boundary conditions. The dynamics of the interface, such as merging and splitting events, can also be precisely captured [87].
The numerical method known as the Phase-Field Model (PFM) is utilised to mimic multiphase flows that entail the progress of a diffuse interface between various fluids. The interface between the two fluids is characterised by a non-conserved scalar field in the model’s mathematical foundation. The PEM delivers a number of benefits, including the ability to handle complex interface topologies and geometries and make boundary conditions simple to implement. Furthermore, it may faithfully depict the dynamics of the interface, such as coalescence and break-up processes [88].
A numerical technique known as the Included Phase Model (IPM) is utilized to simulate multiphase flows involving the presence of bubbles in a fluid. Instead of representing the dispersed phase as discrete particles, it signifies it as a continuum and uses a series of transport equations to chart its behavior. The IPM offers many benefits, including the ability to handle high volume fractions of the dispersed phase and the ability to consider the impacts of the dispersed phase on the continuous phase. Moreover, it can record intricate physical processes like turbulence modulation [89].
A powerful tool for modelling complicated multi-phase flows in which the collaboration between distinct phases is important is CFD. Multi-phase flows can be simulated using a variety of CFD techniques, counting the Eulerian–Eulerian, Eulerian–Lagrangian, and Eulerian–Granular approaches. The specific parameters of the multi-phase flow being simulated determine the CFD that should be used [90].
The complex multi-phase flow phenomenon can be accomplished using two analytical and numerical methods called the Potential Flow Theory (PFT) and the Boundary Element Method (BEM). Understanding the underlying notions regulating fluid dynamics is made easier by PFT. The BEM is a mathematical approach to solve partial differential equations that contain discretization within the domain of interest’s borders. When dealing with complex geometries, where more standard numerical tactics like the Finite Element or Finite Difference approaches can become computationally expensive, BEM is particularly helpful. It is crucial to remember that both PFT and BEM methods include restrictions and presumptions that might not always hold true in practical settings. Thus, suspicious validation of the results against experimental data is necessary to safeguard the accurateness and reliability of the simulation results [91].
Spectral Element Marker Particle (SEMP) is a mathematical method used in general to simulate complex multi-phase flows that include the interaction between fluid and solid phases to accurately model fluid and solid dynamics. SEMP discretizes the fluid and solid domains, which permits a high order of accuracy and efficient computation of the solution. SEMP has several benefits over other numerical techniques, such as its ability to accurately capture the dynamics of the fluid–solid interface and the interaction between the particles [92].
The Finite Element Method (FEM) is a mathematical approach that can solve complicated multi-phase flow problems by dividing the domain into small subdomains. The FEM can handle complex geometries and asymmetrical boundaries and can provide accurate results. However, the FEM is computationally expensive, particularly for large-scale problems [93].
A numerical method called the Thermal Lattice Boltzmann Method (TLBM) is utilised to model intricate multiphase flows involving heat transfer. This technique is based on a mesoscopic approach that simulates the behavior of individual particles within a lattice to address fluid flow problems. In comparison to other numerical methods, LBM provides a number of benefits, including the ability to precisely model the dynamics of multi-phase flows and heat transfer events. Also, it is computationally active and enables the simulation of intricate geometries. To settle the correctness of the results, it is essential to compare the simulation results to experimental data [94].
Smoothed Particle Hydrodynamics (SPH) is a meshless numerical method that can simulate multi-phase flow phenomena with complicated geometries and boundaries. SPH is computationally efficient and can handle large deformations and complex free-surface flows. However, SPH requires a large number of particles to achieve accurate results, which can raise computational cost [95].
A prevalent numerical approach to simulate free-surface flows is Volume of Fluid (VOF). It is capable of handling complicated geometries and boundaries as well as properly capturing the interface between several phases. To accurately capture the contact, VOF may need a fine grid resolution, which can be computationally expensive, especially for large-scale problems [96].
A numerical method known as Sharp-Interface Level-Set (SILS) is also used to model complex multi-phase flows that incorporate the collaboration of the fluid and solid phases. The approach relies on the Level-Set Technique, which numerically tracks the boundary between two fluids in a flow. In comparison to other numerical methods, the SILS Approach has several benefits, such as the ability to accurately represent the sharp boundary between fluid and solid phases. Moreover, complex multi-phase flows incorporating surface tension and other interfacial phenomena can be simulated using this method. To ensure the correctness of the simulation outcomes, the outcomes should be contrasted with experimental data [97].
The various discussed numerical methods, including the Finite Volume Method (FVM), Level-Set Method (LSM), Phase-Field Model (PFM), Included Phase Model (IPM), Computational Fluid Dynamics (CFD), Potential Flow Theory (PFT), Boundary Element Method (BEM), Spectral Element Marker Particle (SEMP), Thermal Lattice Boltzmann Method (TLBM), Smoothed Particle Hydrodynamics (SPH), Volume of Fluid (VOF), and Sharp-Interface Level-Set (SILS) are all useful tools to simulate both liquid–gas and solid–gas systems. Each method affords exceptional strengths, particularly when capturing the complexities of multiphase flows. These include an accurate modeling of fluid–solid interactions, managing complex geometries, and efficiently tracking phase interfaces. Despite some numerical methods being prominent in specific cases—like SPH for large deformations or VOF for free-surface flows—others can provide detailed contexts for perceiving the dynamics in both types of systems, such as CFD and IPM. This flexibility can highlight the prosperity of these numerical methods to be used in a wide sector of applications in fluid dynamics and materials science.
7. Recommendations for Further Research
The following are some suggestions that may be derived from the thermal performance analysis of each research study conducted, as well as from a careful examination of the information shown in Table 1, Table 2 and Table 3. In other words, the review came up with the limitations of past research on bubble growth and collapse that should be resolved following these suggestions:
There is a necessity to utilise the Bayesian approach to modelling bubble growth and collapse because it is still extremely pertinent today.
As the use of high-speed underwater acoustic communications shifts from military to commercial applications, it has absorbed a lot of attention. The implementation of these vehicles necessitates a speed variation in the cavitation flow, which introduces a significant challenge. Furthermore, deceleration may contribute to the worsening of cavitation instability, making it an important factor that has to be researched further. Thus, more exact experimental and numerical methodologies are necessary in the future to quantify the necessities of the maximum heat transfer.
The creation of bubbles with variable amounts of gas within them and the subsequent investigation of how this affects the behavior of the bubbles, as well as the investigation of how a bursting bubble interacts with a flexible substance, are both interesting possibilities for future research.
8. Conclusions
These are the most important conclusions that can be made:
The interaction between the ultimate form of the bubble and its Weber number is assessed throughout the detachment process using the energy conservation concept.
Throughout the splitting process, the average specific rate of local rearrangements in surface film cells and bulk bubble clusters decreases rapidly until it achieves a fixed value. This occurs as the intensity of rearrangements in the bulk bubbles and clusters of surface film cells declines.
A key element in deciding whether continuous collapse takes place is the degree of competitiveness between the critical collapse pressure of the hydrate shell and the bubble differential pressure.
It was found that the pattern of bubble formation and collapse was significantly influenced by the ambient temperature.
Collapse strength is most strongly influenced by viscosity, followed by surface tension, and then by density and sound velocity, in that order of diminishing importance.
Inside the bubble of ethanol and n-butanol, cavitation-induced reactions result in the production of gaseous by-products that prevent the bubble from collapsing.
The dynamics of the collapse, the growth of the micro-jet, the rebound, and the maximum wall pressure are all significantly influenced by the stand-off distance.
The shockwave sources a growth in the velocity and pressure of the liquid field. The rarefaction waves trigger a reduction in the liquid’s pressure, which causes a dispersive change in the liquid’s spatial distribution.
A visible neck will form in the middle of the bubble when the bubble is near the edge. This apparent neck will restrict the bubble interface’s mobility close to the edge.
Bubble density, a metric of bubble structure created by coalescence, and the two/point autocorrelation function show the expansion of a linked network, that may result in lower release thresholds.
The micro-layer that forms at the bubble bottom is responsible for around thirty percent of the entire quantity of evaporation.
Numerical methods can accurately simulate complex physical interactions between different phases while providing detailed information on the flow field and phase distribution.
Careful selection of numerical schemes is important to avoid numerical instability.
Author Contributions
F.L.R.: Conceptualization, Formal analysis, Writing—original draft, Project administration. M.A.A.-O.: Formal analysis, Investigation, Writing—review & editing, Visualization, Project administration. A.K.H.: Formal analysis, Investigation, Visualization. S.A.: Formal analysis, Visualization. M.S.A.: Formal analysis. I.M.M.: Investigation, Writing—review & editing, Visualization, Project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Nomenclature
| ANOVA | analysis of variance |
| BE | boundary-element |
| BEM | boundary-element method |
| CEL | Coupled Eulerian–Lagrangian |
| CFD | Computational Fluid Dynamics |
| CLBM | Conventional Lattice Boltzmann Method |
| DDF | double distribution function |
| FEM | Finite Element Method |
| HIFU | High Intensity Focused Ultrasound |
| IMCs | intermetallic compounds |
| IPM | Included Phase Model |
| LBM | Lattice Boltzmann method |
| LSM | Level-Set Method |
| MRT-LBM | multi-relaxation-time lattice Boltzmann method |
| ONB | Onset of Nucleate Boiling |
| PDE | partial differential equation |
| PFM | Phase-Field Model |
| PFT | Potential Flow Theory |
| RP | Rayleigh-Plesset |
| SEM | scanning electron microscopy |
| SEMP | Spectral Element Marker Particle |
| SILS | Sharp-Interface Level-Set |
| SPH | Smoothed Particle Hydrodynamics |
| TLBM | Thermal Lattice Boltzmann method |
| UMo | Uranium Monolithic |
| VOF | Volume of Fluid |
| VOFE | Volumetric Optical Force |
References
- Wang, H.; Zhang, C.; Xiong, H. Growth and collapse dynamics of a vapor bubble near or at a wall. Water 2020, 13, 12. [Google Scholar] [CrossRef]
- Mehralizadeh, A.; Shabanian, S.R.; Bakeri, G. Effect of modified surfaces on bubble dynamics and pool boiling heat transfer enhancement: A review. Therm. Sci. Eng. Prog. 2020, 15, 100451. [Google Scholar] [CrossRef]
- Hussein, E.Q.; Rashid, F.L.; Hussein, A.K.; Younis, O. Hydrodynamics of single bubble rising through water column using volume of fluid (VOF) method. J. Therm. Eng. 2021, 7, 2107–2114. [Google Scholar] [CrossRef]
- Mohanty, R.L.; Das, M.K. A critical review on bubble dynamics parameters influencing boiling heat transfer. Renew. Sustain. Energy. Rev. 2017, 78, 466–494. [Google Scholar] [CrossRef]
- Hong, Y.; Ashgriz, N.; Andrews, J.; Parizi, H. Numerical simulation of growth and collapse of a bubble induced by a pulsed microheater. J. Microelectromech. Syst. 2004, 13, 857–869. [Google Scholar] [CrossRef]
- Al-Obaidi, M.A.; Rasn, K.H.; Aladwani, S.H.; Kadhom, M.; Mujtaba, I.M. Flexible design and operation of multi-stage reverse osmosis desalination process for producing different grades of water with maintenance and cleaning opportunity. Chem. Eng. Res. Des. 2022, 182, 525–543. [Google Scholar] [CrossRef]
- Al-Obaidi, M.A.; Alsarayreh, A.A.; Mujtaba, I.M. Reduction of energy consumption of brackish water reverse osmosis desalination system via model based optimisation. J. Tech. 2023, 5, 1–7. [Google Scholar] [CrossRef]
- Avvaru, B.; Venkateswaran, N.; Uppara, P.; Iyengar, S.B.; Katti, S.S. Current knowledge potential applications of cavitation technologies for the petroleum industry. Ultrason. Sonochem. 2018, 42, 493–507. [Google Scholar] [CrossRef]
- Rajoriya, S.; Carpenter, J.; Saharan, V.K.; Pandit, A.B. Hydrodynamic cavitation: An advanced oxidation process for the degradation of bio-refractory pollutants. Rev. Chem. Eng. 2016, 32, 379–411. [Google Scholar] [CrossRef]
- Edwards, D.H.; Jones, I.R. An experimental study of the forces generated by the collapse of transient cavities in water. J. Fluid Mech. 1960, 7, 596–609. [Google Scholar]
- Fujikawa, S.; Akamatsu, T. Experimental investigations of cavitation bubble collapse by a water shock tube. Bull. JSME 1978, 21, 223–230. [Google Scholar] [CrossRef]
- Karri, B.; Pillai, K.S.; Klaseboer, E.; Ohl, S.W.; Khoo, B.C. Collapsing bubble induced pumping in a viscous fluid. Sens. Actuators A Phys. 2011, 169, 151–163. [Google Scholar] [CrossRef]
- Koynov, A.; Khinast, J.G.; Tryggvason, G. Mass transfer and chemical reactions in bubble swarms with dynamic interfaces. AIChE J. 2005, 51, 2786–2800. [Google Scholar] [CrossRef]
- Agarwal, D.K.; Welch, S.W.J.; Biswas, G.; Durst, F. Planar Simulation of Bubble Growth in Film Boiling in Near-Critical Water Using a Variant of the VOF Method. J. Heat Transf. 2004, 126, 329–338. [Google Scholar] [CrossRef]
- Mukherjee, A.; Dhir, V.K. Study of Lateral Merger of Vapor Bubbles During Nucleate Pool Boiling. J. Heat Transf. 2005, 126, 1023–1039. [Google Scholar] [CrossRef]
- Tomar, G.; Biswas, G.; Sharma, A.; Agrawal, A. Numerical simulation of bubble growth in film boiling using a coupled level-set and volume-of-fluid method. Phys. Fluids 2005, 17, 112103. [Google Scholar] [CrossRef]
- Wu, J.; Dhir, V.K. Numerical simulations of the dynamics and heat transfer associated with a single bubble in subcooled pool boiling. J. Heat Transf. 2010, 132, 1–15. [Google Scholar] [CrossRef]
- Marchal, A.; Vergnes, B.; Poulesquen, A.; Valette, R. Competitive growth and rising of bubbles in a yield stress fluid. Consequences on the macroscopic swelling of bitumen drums. J. Nonnewton Fluid Mech. 2016, 234, 162–169. [Google Scholar] [CrossRef]
- Goel, P.; Nayak, A.K.; Kulkarni, P.P.; Joshi, J.B. Experimental study on bubble departure characteristics in subcooled nucleate pool boiling. Int. J. Multiph. Flow 2017, 89, 163–176. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zhu, Z. Numerical simulation of cryogenic cavitating flow by an extended transport-based cavitation model with thermal effects. J. Cryog. 2018, 92, 98–104. [Google Scholar] [CrossRef]
- Pahk, K.J.; de Andrade, M.O.; Gélat, P.; Kim, H.; Saffari, N. Mechanical damage induced by the appearance of rectified bubble growth in a viscoelastic medium during boiling histotripsy exposure. Ultrason. Sonochem. 2019, 53, 164–177. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.; Zhang, N.; Ding, Z.; Yang, F.; Hu, Q.; Zeng, L.; Li, J. Bubble growth, intermetallic compounds dissolution and their interactions during heating of an Al-5wt.%Mn alloy by in-situ synchrotron radiography. J. Alloys Compd. 2020, 822, 153554. [Google Scholar] [CrossRef]
- Zeng, X.; Wu, G.; Wang, J.; Yang, C.; Meng, Q.; Chen, G.; Chen, D. Effects of inhibitors on the morphology and kinetics of hydrate growth on surface of bubble. J. Nat. Gas. Sci. Eng. 2020, 74, 103096. [Google Scholar] [CrossRef]
- Allred, T.P.; Weibel, J.A.; Garimella, S.V. The Role of Dynamic Wetting Behavior during Bubble Growth and Departure from a Solid Surface. Int. J. Heat Mass Transf. 2021, 172, 121167. [Google Scholar] [CrossRef]
- Zhao, W.; Liang, J.; Sun, M.; Wang, Z. Investigation on the effect of convective outflow boundary condition on the bubbles growth, rising and breakup dynamics of nucleate boiling. Int. J. Therm. Sci. 2021, 167, 106877. [Google Scholar] [CrossRef]
- Winder, D.; Lin, L.; Mach, J. Incorporating bubble growth volume feedback to improve simulation of the response of a structure containing liquid and gas to sudden energy input. Nucl. Instrum. Methods. Phys. Res. A 2021, 1005, 165371. [Google Scholar] [CrossRef]
- Li, D.; Ren, Z.; Li, Y.; Gong, R.; Wang, H. Thermodynamic effects on the cavitation flow of a liquid oxygen turbopump. Cryogenics 2021, 116, 103302. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, P.; Qi, B.; Zhang, Y.; Wei, J. Effects of micro-pin-fins on the bubble growth and movement of nucleate pool boiling on vertical surfaces. Int. J. Therm. Sci. 2022, 171, 107186. [Google Scholar] [CrossRef]
- Lai, T.; Yan, S.; Zhao, Q.; Zhang, Z.; Ding, W.; Liu, Y.; Hou, Y. Numerical study on thermodynamic growth of single hydrogen bubble in an infinite space. Int. J. Hydrogen Energy 2022, 47, 24406–24420. [Google Scholar] [CrossRef]
- Cheng, N.; Yu, S.; Xiao, J.; Peng, C. Numerical simulation of single bubble growth in vertical rectangular narrow flow channels. Nucl. Eng. Des. 2022, 391, 111749. [Google Scholar] [CrossRef]
- Hu, S.; Setyawan, W.; Beeler, B.W.; Gan, J.; Burkes, D.E. Defect cluster and nonequilibrium gas bubble associated growth in irradiated UMo fuels-A cluster dynamics and phase field model. J. Nucl. Mater. 2020, 542, 152441. [Google Scholar] [CrossRef]
- Zhou, T.T.; He, A.M.; Wang, P. Dynamic evolution of He bubble and its effects on void nucleation-growth and thermomechanical properties in the spallation of aluminum. J. Nucl. Mater. 2020, 542, 152496. [Google Scholar] [CrossRef]
- Arévalo-Cid, P.; Adán-Más, A.; Silva, T.M.; Rodrigues, J.A.; Maçôas, E.; Vaz, M.F.; Montemor, M.F. On the growth mechanical properties of nanostructured cobalt foams by dynamic hydrogen bubble template electrodeposition. Mater. Charact. 2020, 169, 110598. [Google Scholar] [CrossRef]
- Prudil, A.A.; Welland, M.J.; Ofori-Opoku, N. Modelling the growth and evolution of statistically significant populations of intergranular fission gas bubbles by IPM. J. Nucl. Mater. 2022, 566, 153777. [Google Scholar] [CrossRef]
- Gong, S.; Cheng, P. Lattice Boltzmann simulation of periodic bubble nucleation, growth and departure from a heated surface in pool boiling. Int. J. Heat Mass Transf. 2013, 64, 122–132. [Google Scholar] [CrossRef]
- Navarrete, M.; Godínez, F.A.; Castellanos, F.; Mejía-Uriarte, E.V.; Naude, J.L.; Méndez, F. Dynamics and acoustic energy dissipation in conical bubble collapse. Int. J. Multiph. Flow 2015, 76, 86–100. [Google Scholar] [CrossRef]
- Gong, S.W.; Klaseboer, E. Interaction between collapsing bubble and viscoelastic solid: Numerical modelling and simulation. Appl. Math. Model. 2016, 40, 122–132. [Google Scholar] [CrossRef]
- Tang, J.; Yan, C.; Sun, L. Enhanced vapor bubble condensation and collapse with ultrasonic vibration. Exp. Therm. Fluid Sci. 2016, 70, 115–124. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, C.; Fang, X.; Wu, X.; Du, T. On the internal collapse phenomenon at the closure of cavitation bubbles in a deceleration process of underwater vertical launching. Appl. Ocean. Res. 2016, 56, 157–165. [Google Scholar] [CrossRef]
- Qin, Z.; Alehossein, H. Heat transfer during cavitation bubble collapse. Appl. Therm. Eng. 2016, 105, 1067–1075. [Google Scholar] [CrossRef]
- Li, S.; Han, R.; Zhang, A.M.; Wang, Q.X. Analysis of pressure field generated by a collapsing bubble. Ocean. Eng. 2016, 117, 22–38. [Google Scholar] [CrossRef]
- Rowlatt, C.F.; Lind, S.J. Bubble collapse near a fluid-fluid interface using the spectral element marker particle method with applications in bioengineering. Int. J. Multiph. Flow 2017, 90, 118–143. [Google Scholar] [CrossRef]
- Ye, L.; Zhu, X. Analysis of the effect of impact of near-wall acoustic bubble collapse micro-jet on Al 1060. Ultrason. Sonochem. 2017, 36, 507–516. [Google Scholar] [CrossRef] [PubMed]
- Pavlov, P.A. Fast collapse of a vapor bubble. Int. J. Heat Mass Transf. 2017, 104, 627–633. [Google Scholar] [CrossRef]
- Ming, L.; Zhi, N.; Chunhua, S. Numerical simulation of cavitation bubble collapse within a droplet. Comput. Fluids 2017, 152, 157–163. [Google Scholar] [CrossRef]
- Rosselló, J.M.; Urteaga, R.; Bonetto, F.J. A novel water hammer device designed to produce controlled bubble collapses. Exp. Therm. Fluid Sci. 2018, 92, 46–55. [Google Scholar] [CrossRef]
- Phan, T.H.; Ha, C.T.; Park, W.G. Numerical simulation of bubble collapse between two parallel walls and saturated film boiling on a sphere. Int. J. Heat Mass Transf. 2018, 127, 116–125. [Google Scholar] [CrossRef]
- Arévalo, R.; Antúnez, D.; Rebollo, L.; Abánades, A. Estimation of radiation coupling factors in film boiling around spheres by mean of Computational Fluid Dynamics (CFD) tools. Int. J. Heat Mass Transf. 2014, 78, 84–89. [Google Scholar] [CrossRef]
- Grigoriev, V.A.; Klimenko, V.V.; Shelepen, A.G. Pool film toiling from submerged spheres. In Proceedings of the International Heat Transfer Conference Digital Library, Munich, Germany, 6–10 September 1982; Begel House Inc.: Danbury, CT, USA, 1982. [Google Scholar]
- Frederking, T.H.; Clark, J.A. Natural convection film boiling on a sphere. In Advances in Cryogenic Engineering: Proceedings of the 1962 Cryogenic Engineering Conference University of California Los Angeles, CA, USA, 14–16 August 1962; Springer: New York, NY, USA, 1963; pp. 501–506. [Google Scholar]
- Kerabchi, N.; Merouani, S.; Hamdaoui, O. Depth effect on the inertial collapse of cavitation bubble under ultrasound: Special emphasis on the role of the wave attenuation. Ultrason. Sonochem. 2018, 48, 136–150. [Google Scholar] [CrossRef]
- Joshi, S.; Franc, J.P.; Ghigliotti, G.; Fivel, M. SPH modelling of a cavitation bubble collapse near an elasto-visco-plastic material. J. Mech. Phys. Solids 2019, 125, 420–439. [Google Scholar] [CrossRef]
- Brujan, E.A.; Takahira, H.; Ogasawara, T. Planar jets in collapsing cavitation bubbles. Exp. Therm. Fluid Sci. 2019, 101, 48–61. [Google Scholar] [CrossRef]
- Hopfes, T.; Wang, Z.; Giglmaier, M.; Adams, N.A. Collapse dynamics of bubble pairs in gelatinous fluids. Exp. Therm. Fluid Sci. 2019, 108, 104–114. [Google Scholar] [CrossRef]
- Bardia, R.; Trujillo, M.F. An improved categorization of vapor bubble collapse: Explaining the coupled nature of hydrodynamic thermal mechanisms. Int. J. Heat Mass Transf. 2019, 145, 118754. [Google Scholar] [CrossRef]
- Gan, N.; Yao, X.L.; Liu, L.T.; Xiao, W.; Wang, X.L. Research on overall damage characteristics of a hull girder under explosion bubble collapse. Ocean. Eng. 2019, 188, 106315. [Google Scholar] [CrossRef]
- Chudnovskii, V.M.; Levin, A.A.; Yusupov, V.I.; Guzev, M.A.; Chernov, A.A. The formation of a cumulative jet during the collapse of a vapor bubble in a subcooled liquid formed as a result of laser heating. Int. J. Heat Mass Transf. 2020, 150, 119286. [Google Scholar] [CrossRef]
- Yuan, G.Y.; Ni, B.Y.; Wu, Q.G.; Xue, Y.Z.; Zhang, A.M. An experimental study on the dynamics and damage capabilities of a bubble collapsing in the neighborhood of a floating ice cake. J. Fluids Struct. 2020, 92, 102833. [Google Scholar] [CrossRef]
- Han, S.; Li, Y.; Zhu, H. The similarities and differences between the bubble collapse near a solid wall and in free water. Eur. J. Mech.-B/Fluids 2020, 84, 553–561. [Google Scholar] [CrossRef]
- Fursenko, R.V.; Chudnovskii, V.M.; Minaev, S.S.; Okajima, J. Mechanism of high velocity jet formation after a gas bubble collapse near the micro fiber immersed in a liquid. Int. J. Heat Mass Transf. 2020, 163, 120420. [Google Scholar] [CrossRef]
- Tan, K.L.; Yeo, S.H. Velocity estimation of micro-particles driven by cavitation bubble collapses through controlled erosion experiments. Int. J. Multiph. Flow 2020, 127, 103271. [Google Scholar] [CrossRef]
- Orthaber, U.; Zevnik, J.; Petkovšek, R.; Dular, M. Cavitation bubble collapse in a vicinity of a liquid-liquid interface—Basic research into emulsification process. Ultrason. Sonochem. 2020, 68, 105224. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiu, X.; Zhang, X.; Tang, N. Collapsing dynamics of a laser-induced cavitation bubble near the edge of a rigid wall. Ultrason. Sonochem. 2020, 67, 105157. [Google Scholar] [CrossRef] [PubMed]
- Ezzatneshan, E.; Vaseghnia, H. Simulation of collapsing cavitation bubbles in various liquids by lattice Boltzmann model coupled with the Redlich-Kwong-Soave equation of state. Phys. Rev. E 2020, 102, 053309. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Zhang, M.; Han, L.; Ma, X.; Huang, B. Physical investigation of acoustic waves induced by the oscillation and collapse of the single bubble. Ultrason. Sonochem. 2021, 72, 105440. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Zhu, R.; Wang, J.; Fu, Q.; Wang, X.; Zhao, Y.; Zhao, G. Molecular dynamics simulations of the distance between the cavitation bubble and benzamide wall impacting collapse characteristics. J. Clean. Prod. 2022, 352, 131633. [Google Scholar] [CrossRef]
- Peng, H.; Zhang, J.; He, X.; Wang, Y. Thermal pseudo-potential lattice Boltzmann method for simulating cavitation bubbles collapse near a rigid boundary. Comput. Fluids 2021, 217, 104817. [Google Scholar] [CrossRef]
- Trummler, T.; Schmidt, S.J.; Adams, N.A. Effect of stand-off distance and spatial resolution on the pressure impact of near-wall vapor bubble collapses. Int. J. Multiph. Flow 2021, 141, 103618. [Google Scholar] [CrossRef]
- Long, J.; Eliceiri, M.H.; Wang, L.; Vangelatos, Z.; Ouyang, Y.; Xie, X.; Zhang, Y.; Grigoropoulos, C.P. Capturing the final stage of the collapse of cavitation bubbles generated during nanosecond laser ablation of submerged targets. Opt. Laser Technol. 2021, 134, 106647. [Google Scholar] [CrossRef]
- Wang, X.; Ning, Z.; Lv, M.; Sun, C. Machine learning for predicting the bubble-collapse strength as affected by physical conditions. Results Phys. 2021, 25, 104226. [Google Scholar] [CrossRef]
- Gai, S.; Peng, Z.; Moghtaderi, B.; Yu, J.; Doroodchi, E. LBM study of ice nucleation induced by the collapse of cavitation bubbles. Comput. Fluids 2022, 246, 105616. [Google Scholar] [CrossRef]
- Ezzatneshan, E.; Vaseghnia, H. Dynamics of an acoustically driven cavitation bubble cluster in the vicinity of a solid surface. Phys. Fluids 2021, 33, 1075290. [Google Scholar] [CrossRef]
- Xu, W.L.; Li, J.B.; Luo, J.; Zhai, Y.W. Effect of a single air bubble on the collapse direction and collapse noise of a cavitation bubble. Exp. Therm. Fluid Sci. 2021, 120, 110218. [Google Scholar] [CrossRef]
- Nguyen, T.T.P.; Tanabe-Yamagishi, R.; Ito, Y. Effects of liquid depth on the expansion and collapse of a hemispherical cavitation bubble induced in nanosecond pulsed laser ablation of a solid in liquid. Opt. Lasers Eng. 2020, 126, 105937. [Google Scholar] [CrossRef]
- Yang, Y.; Shan, M.; Su, N.; Kan, X.; Shangguan, Y.; Han, Q. Role of wall temperature on cavitation bubble collapse near a wall investigated using thermal lattice Boltzmann method. Int. Commun. Heat Mass Transf. 2022, 134, 105988. [Google Scholar] [CrossRef]
- He, X.; Peng, H.; Zhang, J.; Yuan, H. Multiple vapor cavitation bubble interactions with a thermal lattice Boltzmann method. Ocean. Eng. 2022, 266, 113058. [Google Scholar] [CrossRef]
- Ezzatneshan, E.; Salehi, A.; Vaseghnia, H. Study of micro-heater shape and wettability effects on inception of boiling phenomenon using a multiphase lattice Boltzmann method. Int. J. Therm. Sci. 2023, 184, 107913. [Google Scholar] [CrossRef]
- Ezzatneshan, E.; Salehi, A.; Vaseghnia, H. Numerical study on collapsing cavitation bubble dynamics in cryogenic fluids. Cryogenics 2024, 141, 103879. [Google Scholar] [CrossRef]
- Lee, J.; Son, G. A sharp-interface level-set method for compressible bubble growth with phase change. Int. Commun. Heat Mass Transf. 2017, 86, 1–11. [Google Scholar] [CrossRef]
- Wang, Q.; Yao, W.; Quan, X.; Cheng, P. Validation of a dynamic model for vapor bubble growth and collapse under microgravity conditions. Int. Commun. Heat Mass Transf. 2018, 95, 63–73. [Google Scholar] [CrossRef]
- Sourtiji, E.; Peles, Y. A micro-synthetic jet in a microchannel using bubble growth and collapse. Appl. Therm. Eng. 2019, 160, 114084. [Google Scholar] [CrossRef]
- Sun, B.; Liu, Z.; Wang, Z.; Chen, L.; Li, H.; Duan, W. Experimental and modeling investigations into hydrate shell growth on suspended bubbles considering pore updating and surface collapse. Chem. Eng. Sci. 2019, 207, 1–16. [Google Scholar] [CrossRef]
- Zimnyakov, D.A.; Yuvchenko, S.A.; Isaeva, A.A.; Isaeva, E.A.; Tsypin, D.V. Growth/collapse kinetics of the surface bubbles in fresh constrained foams: Transition to self-similar evolution. Colloids Surf. A Physicochem. Eng. Asp. 2019, 579, 123693. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Phan, T.H.; Duy, T.N.; Kim, D.H.; Park, W.G. Modeling of the bubble collapse with water jets and pressure loads using a geometrical volume of fluid based simulation method. Int. J. Multiph. Flow 2022, 152, 104103. [Google Scholar] [CrossRef]
- Puncochar, M.; Ruzicka, M.C.; Simcik, M. Bubble formation and deformation. Chem. Eng. Sci. 2022, 260, 117729. [Google Scholar] [CrossRef]
- Castro, J.M. Modelling and Numerical Simulation of Combustion and Multi-Phase Flows Using Finite Volume Methods on Unstructured Meshes; Universitat Politècnica de Catalunya: Barcelona, Spain, 2018. [Google Scholar]
- Van der Pijl, S.P.; Segal, A.; Vuik, C.; Wesseling, P. A mass-conserving Level-Set method for modelling of multi-phase flows. Int. J. Numer. Methods Fluids 2005, 47, 339–361. [Google Scholar] [CrossRef]
- Alpak, F.O.; Riviere, B.; Frank, F. A phase-field method for the direct simulation of two-phase flows in pore-scale media using a non-equilibrium wetting boundary condition. Comput. Geosci. 2016, 20, 881–908. [Google Scholar] [CrossRef]
- Kono, K.; Ishizuka, T.; Tsuda, H.; Kurosawa, A. Application of lattice Boltzmann model to multiphase flows with phase transition. Comput. Phys. Commun. 2000, 129, 110–120. [Google Scholar] [CrossRef]
- Afzali, S.; Rezaei, N.; Zendehboudi, S.; Chatzis, I. Computational fluid dynamic simulation of multi-phase flow in fractured porous media during water-alternating-gas injection process. J. Hydrol. 2022, 610, 127852. [Google Scholar] [CrossRef]
- Sichani, A.B.; Mehring, C. Generalized pressure-correction for viscous potential flow simulations of multiphase flows using boundary element method. Int. J. Multiph. Flow 2021, 141, 103646. [Google Scholar] [CrossRef]
- Pei, C.; Vahab, M.; Sussman, M.; Hussaini, M.Y. A Hierarchical Space-Time Spectral Element and Moment-of-Fluid Method for Improved Capturing of Vortical Structures in Incompressible Multi-phase/Multi-material Flows. J. Sci. Comput. 2019, 81, 1527–1566. [Google Scholar] [CrossRef]
- Efendiev, Y.; Ginting, V.; Hou, T.; Ewing, R. Accurate multiscale finite element methods for two-phase flow simulations. J. Comput. Phys. 2006, 220, 155–174. [Google Scholar] [CrossRef]
- Sahu, A.; Bhowmick, S. Applications of Lattice Boltzmann in method in multi-component and multi-phase flow: A review. In Proceedings of the AIP, Woodbury, Long Island, NY, USA, 6–7 December 2019. [Google Scholar]
- Szewc, K.; Tanière, A.; Pozorski, J.; Minier, J.-P.A. Study on Application of Smoothed Particle Hydrodynamics to Multi-Phase Flows. Int. J. Nonlinear. Sci. Numer. Simul. 2012, 13, 383–395. [Google Scholar] [CrossRef]
- Kim, M.S.; Lee, W.I.L. A new VOF-based numerical scheme for the simulation of fluid flow with free surface. Part I: New free surface-tracking algorithm and its verification. Int. J. Numer. Methods Fluids 2003, 42, 765–790. [Google Scholar] [CrossRef]
- Han, L.H.; Hu, X.Y.; Adams, N.A. Scale separation for multi-scale modeling of free-surface and two-phase flows with the conservative sharp interface method. J. Comput. Phys. 2015, 280, 387–403. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).