Measuring Domain Shift in Vibration Signals to Improve Cross-Domain Diagnosis of Piston Aero Engine Faults

Abstract

Transfer learning is an effective approach to address the decline in generalizability of intelligent fault diagnosis methods. However, there has been a persistent lack of comprehensive and effective metrics for assessing the transferability of cross-domain data, making it challenging to answer the fundamental question in transfer learning: “When to transfer”. This study proposes a novel hybrid transferability metric (HTM) based on weighted correlation-diversity shift. The metric introduces a correlation shift measurement based on sparse principal component analysis, effectively quantifying distribution differences in domain-invariant features based on the sparse representation theory. It also designs a diversity shift measurement based on label space differences, addressing the previously overlooked impact of label variation on transferability. The proposed transferability metric is validated on four types of cross-domain diagnosis tasks involving piston aero engines. The results show that in diagnostic scenarios involving both supervised transfer learning and extreme class imbalance problems, HTM accurately predicted the transferability of the target tasks, which aligned with the actual diagnostic accuracy trends. It provides a feasible method for predicting and evaluating the applicability of transfer learning methods in real-world scenarios.

1. Introduction

Machine learning and artificial intelligence technologies have achieved tremendous breakthroughs in recent years, greatly promoting the intelligent development of signal processing and condition monitoring for low-carbon energy systems [1,2,3]. High generalizability is one of the core objectives of machine learning, emphasizing the ability of a model or algorithm to make accurate predictions when facing unseen data [4,5]. In the discussion of domain shift and transfer learning, generalizability refers more specifically to the applicability to out-of-distribution (OOD) data scenarios [6,7]. In contrast to generalizability, transferability is a consideration for evaluating whether data from different domains have similar characteristics, emphasizing the ability of machine learning algorithms to maintain their performance at the data level. Generalizability and transferability are closely related [8,9]. When a machine learning model is applied to a mechanical fault cross-domain diagnosis task, the stronger the model’s generalizability, the higher the inter-domain or inter-task transferability, and the better the transfer learning task is accomplished.

According to the relevant reviews and studies on transfer learning [10,11], transfer learning research mainly consists of three foundational issues:

• What to transfer; that is, which cross-domain knowledge to transfer to improve the generalization performance of the target domain. The knowledge includes neural network parameters, feature transformation matrices, components of signal decomposition, and other data information, as well as the logic of sample selection involved in transfer learning.
• How to transfer; that is the methods and forms of transfer learning. The goal is to design a reasonable transfer learning process that accomplishes the preset knowledge transfer tasks with minimal resource consumption.
• When to transfer; that is, under what circumstances should transfer learning be conducted, or can safely be conducted? Specifically, it involves resolving how to measure the distance between different domains or tasks. Subsequently, it requires determining the logical distance threshold for recommending transfer learning operations based on the distance measurements between domains or tasks.

Compared to the first two methodology-related issues, ‘when to transfer’ is a prerequisite question in determining whether a transfer learning method should be implemented. Transferability measurement is the essential means to address this question. Transferability measurement involves quantitatively estimating the difficulty of knowledge transfer from a source task to a target task [12,13]. Specifically, the goal of transferability measurement is to design a score that can clearly indicate the extent to which knowledge learned from the source task contributes to the target task without any training on the target task. It is crucial for predicting the effectiveness of transfer learning and holds significant value in engineering applications.

Currently, research on transferability measurement primarily focuses on distance measurement between different datasets. These metrics refer to statistical methods for measuring the distance between data probability distributions. The most widely used metric is the maximum mean discrepancy (MMD) [14]. Yang [15] proposed a novel distance metric known as polynomial kernel-induced MMD (PK-MMD). It overcomes the inaccuracies and low computational efficiency associated with traditional Gaussian kernel-induced MMD (GK-MMD) and has been successfully applied to the transfer learning-based health state recognition of motor bearings and gearbox bearings. Qian [16] proposed a novel discrepancy representation metric based on the mean square statistic, known as maximum mean square discrepancy (MMSD). It can comprehensively reflect the mean and variance information of data samples in the reproducing kernel Hilbert space (RKHS). The MMSD has been successfully applied to the end-to-end fault diagnosis of the planetary gearbox in wind turbines. Wan [17] proposed a novel deep convolutional multi-adversarial domain adaptation (DCMADA) model for rolling bearing fault diagnosis. The domain adaptation module of this model utilizes multi-kernel MMD (MK-MMD) to simultaneously adjust the marginal and conditional distributions.

In addition to MMD, there are also Kullback–Leibler divergence (KL divergence) [18], Jensen–Shannon divergence (JS divergence) [19], Bhattacharyya distance [20], Wasserstein-1 distance [21], and Chebyshev distance [22]. These measurement methods assume that the source domain (or source task) and the target domain (or target task) share the same feature space and label space, applying existing statistical distance measures for probability distributions to measure the distance between domains or tasks. Qin [23] utilizes the singular value decomposition (SVD) of the Jacobian matrix to provide a more precise mathematical description of the transferability of adversarial samples between models. A corresponding metric is proposed for the performance evaluation of adversarial generation models. Tian [24] proposed a complementary transferability metric based on multiple classifiers. It quantifies the similarity between target samples and known samples by comparing the consistency, confidence, and entropy of multiple classification results. The complementary transferability metric assists with open-set domain adaptation problems across multiple source domains. Tran [25] proposed a conditional entropy (CE) approach to estimate the hardness and transferability of supervised classification tasks. This method does not rely on specific solutions or assume a particular training model. Instead, it uses information-theoretic techniques to assess the statistical properties of training labels, offering valuable insights and tools for model transfer and multi-task learning. Nguyen [26] proposed a new metric called log expected empirical prediction (LEEP) to evaluate the transferability of deep networks. The LEEP score is obtained through a single forward pass, without requiring any training on the target task. Research on transferability metrics has directly advanced the development and application of transfer learning, and it has also played a significant role in areas such as joint training [27] and multi-source feature fusion [28].

However, transferability metrics based on statistical distance measurement have several limitations. First, statistical distance measurement methods are calculated based on the general data distribution. They cannot accurately capture all distribution differences between the source and target domains. Even if the statistical distance of distribution differences between the two domains is small, the differences in key features may still be significant. This severely affects the accuracy of evaluating the domain’s transferability. Secondly, transferability metrics should include not only the measurement of data feature distribution shift but also the measurement of label space shift. Because the label space in mechanical fault diagnosis is highly likely to be mismatched. Statistical distance measurement overlooks the impact of label space shift on transferability. Finally, existing statistical distance measurements are disconnected from the performance of machine learning models. In machine learning, data diversity is crucial for improving the model’s generalizability. Machine learning-driven fault diagnosis models need to learn the feature distribution patterns of data through a complex learning process. However, statistical distance measurement methods fail to utilize the feature distribution representation capabilities. More importantly, the stronger the data diversity, the worse the transferability predicted by traditional statistical distance measurements. This results in prediction outcomes that are contrary to the actual transferability trend.

To address the above limitations, this paper conducts a study on quantifying the transferability between cross-domain datasets. Focusing on vibration signals that characterize the operational state of machinery, we innovatively propose a new hybrid transferability metric that combines the weighted correlation-diversity shift. This metric includes a correlation shift measurement strategy based on sparse principal component analysis (sparse PCA) and a diversity shift measurement strategy based on label space differences. The study provides a valuable benchmark for assessing the generalizability of transfer learning models. The main innovations of this research are:

• A novel correlation shift metric for measuring feature shifts between domains has been innovatively introduced. It utilizes sparse PCA to assess distribution differences in classification-relevant features. This approach effectively filters out noise and irrelevant features, addressing the measurement inaccuracies associated with general statistical methods.
• The concept of diversity shift metric was introduced to measure the difference between domains. It is achieved through the differences in label space and provides an effective formula for measurement. This approach addresses the previous oversight of the impact of label space differences on transferability measurement.
• A novel hybrid transferability metric, based on the weighted correlation-diversity shift, has been proposed. It comprehensively and accurately assesses the transferability of specific target domains relative to source domains. This metric successfully achieves transferability prediction for various types of cross-domain fault diagnosis tasks in piston aero engines.

The rest of this paper is organized as follows: Section 2 defines the concept of transferability metrics and outlines the basic assumptions followed in this study. It also introduces the methodological principles and computational procedures for the proposed correlation shift metric, diversity shift metric, and hybrid transferability metric. Section 3 describes the cross-domain diagnostic experiments and datasets used for validation, which are based on piston aero engines. Section 4 presents the validation results of the transferability metrics, with a multifaceted analysis and discussion of the results. Section 5 states the conclusions of this study.

2. Hybrid Transferability Metric Based on Weighted Correlation-Diversity Shift

2.1. Problem Discussion

Assume there exists a supervised source domain ${\mathcal{D}}_s=\{{\chi }_s,{\gamma }_s,P\left({\overrightarrow{x}}_s,y_s\right)\}$ and a target domain ${\mathcal{D}}_t=\{{\chi }_t,{\gamma }_t,P\left({\overrightarrow{x}}_t,y_t\right)\}$. Then a transferability metric function can be defined as follows: $M:{\mathcal{D}}_s\times {\mathcal{D}}_t\to \mathbb{R}$. It accepts the datasets of the source and target domains as input and outputs a real number, representing the transferability from the source domain to the target domain.

When designing the transferability metric function M, the following basic assumptions should be followed:

• There are differences between the source and target domains. Among the three elements of feature space, label space, and feature distribution of the source and target domains, at least one of them differs. This is a prerequisite for conducting transfer learning.
• There is still some similarity between the source and target domains. Despite the differences, the source and target domains are usually considered to share common features or patterns, which provides the possibility of transfer learning.
• The differences between the source and target domains are measurable. It is assumed that the differences between the source and target domains can be quantified by certain methods.
• The model’s generalizability is limited. For any transfer learning model, its generalizability is finite. The performance of the model will vary when applied to target domain datasets with different transferability. Only under this assumption is it meaningful to evaluate the transferability of datasets.
• The labels in the source domain are fully available, while the data in the target domain may be partially or completely unlabeled. Unsupervised transfer learning is more challenging than supervised transfer learning and requires higher generalization performance from the diagnostic model. Consequently, the transferability of the target domain corresponding to unsupervised datasets is lower.
• The sample amount and label categories of the source domain are both greater than those of the target domain. Transfer learning requires the source domain to contain abundant knowledge for learning and transferring. Therefore, the source domain generally has a larger dataset. The number of samples there is sufficient, and the diversity of samples is rich.
• The generalizability of the model and the transferability of the domain (or task) are independent of each other. For a specific model, the better the performance metrics in the target domain, the better the transferability of the domain. For a specific target domain, the better the performance metrics of the model, the better the generalization capability of the model.

2.2. Proposed Transferability Metric

According to the definition and basic assumptions of transfer learning and transferability, a domain is composed of three fundamental elements. They are data samples, labels, and joint probability distributions. These correspond to the three types of transfer learning tasks: feature space difference, label space difference, and feature distribution difference.

• The feature space differences are mathematically represented as ${\chi }_s\ne {\chi }_t$. This situation refers to the scenario where the nature of the data used for learning has changed compared to the data where the knowledge is applied. For example, transfer learning between images, text, sound, and vibration.
• The label space differences are mathematically represented as ${\gamma }_s\ne {\gamma }_t$. This situation refers to the scenarios in classification tasks where the diversity of data has changed, leading to differences in the types of labels. For instance, in cross-domain diagnostics of mechanical faults, the source domain contains various types of bearing fault data, while the target domain includes various types of gear system fault data.
• The feature distribution differences are mathematically represented as $P\left({\overrightarrow{x}}_s,y_s\right)\ne P\left({\overrightarrow{x}}_t,y_t\right)$. This situation refers to the scenario where the joint probability distribution of data and labels has changed between the source and target domains. For example, when the rotational speed and load of rotating machinery change, the corresponding vibration signal feature distribution will vary due to changes in the energy of the vibration source.

For the cross-domain diagnosis task, the feature spaces of the data are consistent across multiple domains. However, there generally be differences in the label space and feature distribution. Therefore, it is necessary to consider both the domain shift of the data samples and the shift in the label space simultaneously when measuring transferability.

In this section, a study of transferability metrics applied to cross-domain diagnosis of vibration signals is conducted. Two new metrics are proposed: the correlation shift metric (CSM) to measure the degree of shift in the distribution of sample features of cross-domain data, and the diversity shift metric (DSM) to measure the degree of difference in the corresponding label space of cross-domain data. Finally, a hybrid transferability metric (HTM) based on weighted correlation-diversity shifts is proposed. It is successfully applied to predict the transferability of cross-domain diagnostic datasets for piston aero engines.

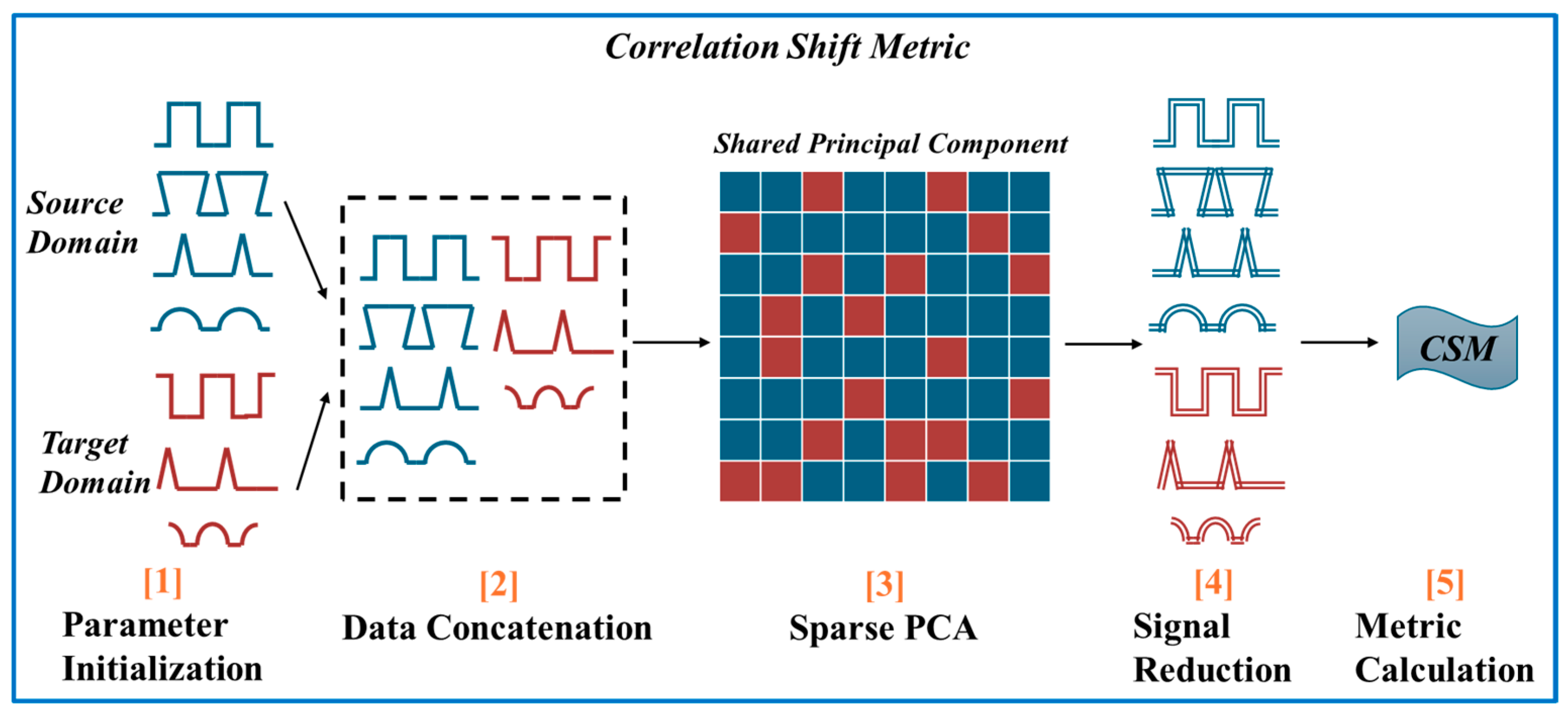
2.2.1. Correlation Shift Metric

The difference in the joint probability distributions that data and labels follow between different domains is represented as the correlation shift. Correlation shift is one of the fundamental components of domain difference. The degree of correlation or correlation shift between two probability density functions can be quantified using certain statistical methods. As shown in Figure 1, the correlation measure can be represented by the area of the gray region in the diagram, while the correlation shift measure can be represented by the area of the colored region (to facilitate understanding, conditional probability density functions are used in the image to represent joint probability distributions, due to the dependency relationship between the sample x and label y). However, the collected raw vibration signals are often discrete time series. The joint probability distribution of the sample and label is implicit. How to accurately mine the probability distributions from the original signals, and which kind of appropriate function to measure their correlation shift, is an important task in the research on transferability measurement of mechanical fault cross-domain diagnosis.

Previous studies have extensively explored correlation shift measures based on statistical methods, which are convenient and effective. However, the main issue with simple statistical measurement methods is that they overlook the varying contributions of different feature components to the transferability. As shown in Figure 2, existing research on signal feature extraction and pattern recognition indicates that the mapping between signals and labels is often nonlinear. It is necessary to use specific feature extractors to perform complex high-dimensional feature extraction on the original signals to obtain the mapping relationship from features to labels. Moreover, the different features (such as the multi-channel features extracted by convolutional neural networks, or the dictionary atoms obtained from sparse representation) have different contribution weights to label prediction. When evaluating the generalizability of models and the transferability of datasets, some features have little impact on the assessment index. Therefore, when measuring the correlation shift for transferability, it is necessary to screen and judge the features, which can make the metrics more accurately aligned with the actual transferability performance.

According to previous studies [29,30], sparse representation methods can obtain a sparse dictionary containing redundant features through the dictionary learning process. The sparse dictionary can help extract domain-invariant features. Cross-domain data can be mapped to the sparse space through a shared sparse dictionary and feature alignment can be performed. These have a certain resistance to the shift in feature distribution of cross-domain data. This section researches the measurement of feature distribution differences between domains based on the sparse representation theory. A correlation shift metric (CSM) based on sparse PCA is proposed.

Sparse PCA [31,32] is a high-dimensional extension of the conventional principal component analysis (PCA) method. Analyzed from the perspective of dimensionality reduction, the principle of PCA is to transform the original variables into a set of orthogonal linear transformations (principal components) so that the transformed variables retain as much information as possible from the original variables. Sparse PCA introduces sparsity constraints while maintaining the main features of the data. Sparsity requires that each order of principal components contains only a finite number of non-zero coefficient variables. The solution problem of sparse PCA is formally described as follows:

$$\underset{u}{\max }{u}^T{X}^{T}Xu \mathrm{s}.\mathrm{t}. {‖u‖}_2=1 \mathrm{and} {‖u‖}_1\le t$$

(1)

where u represents the sparse principal component vector. ${‖u‖}_2=1$ indicates that the principal component vector is constrained to be a unit vector. ${‖u‖}_1\le t$ is a sparsity constraint, where t is the sparsity control parameter. The solution is solved by the greedy algorithm of orthogonal matching tracking (OMP). The detailed principles, proofs, and algorithm implementation of sparse PCA can be found in the literature [31].

Sparse PCA can be seen as a simplified process of sparse representation. Compared with sparse representation methods [33], the sparse principal component vectors in sparse PCA are similar to dictionary atoms and can be represented as a type of signal feature extracted. By concatenating cross-domain data as a set of training inputs for sparse PCA, the sharing of sparse principal components can be achieved. In addition to the ability to extract domain-invariant features, sparse PCA also offers the following advantages for measuring correlation shift:

• Greater stability: In high-dimensional datasets, sparse PCA introduces sparsity to reduce computational complexity, thereby enhancing the consistency of estimation in high-dimensional scenarios [34].
• Higher computational efficiency: Sparse PCA can speed up computation by reducing the number of non-zero elements in the sparse principal components. This feature is particularly suitable for processing large datasets, which is often encountered in transferability measurement.
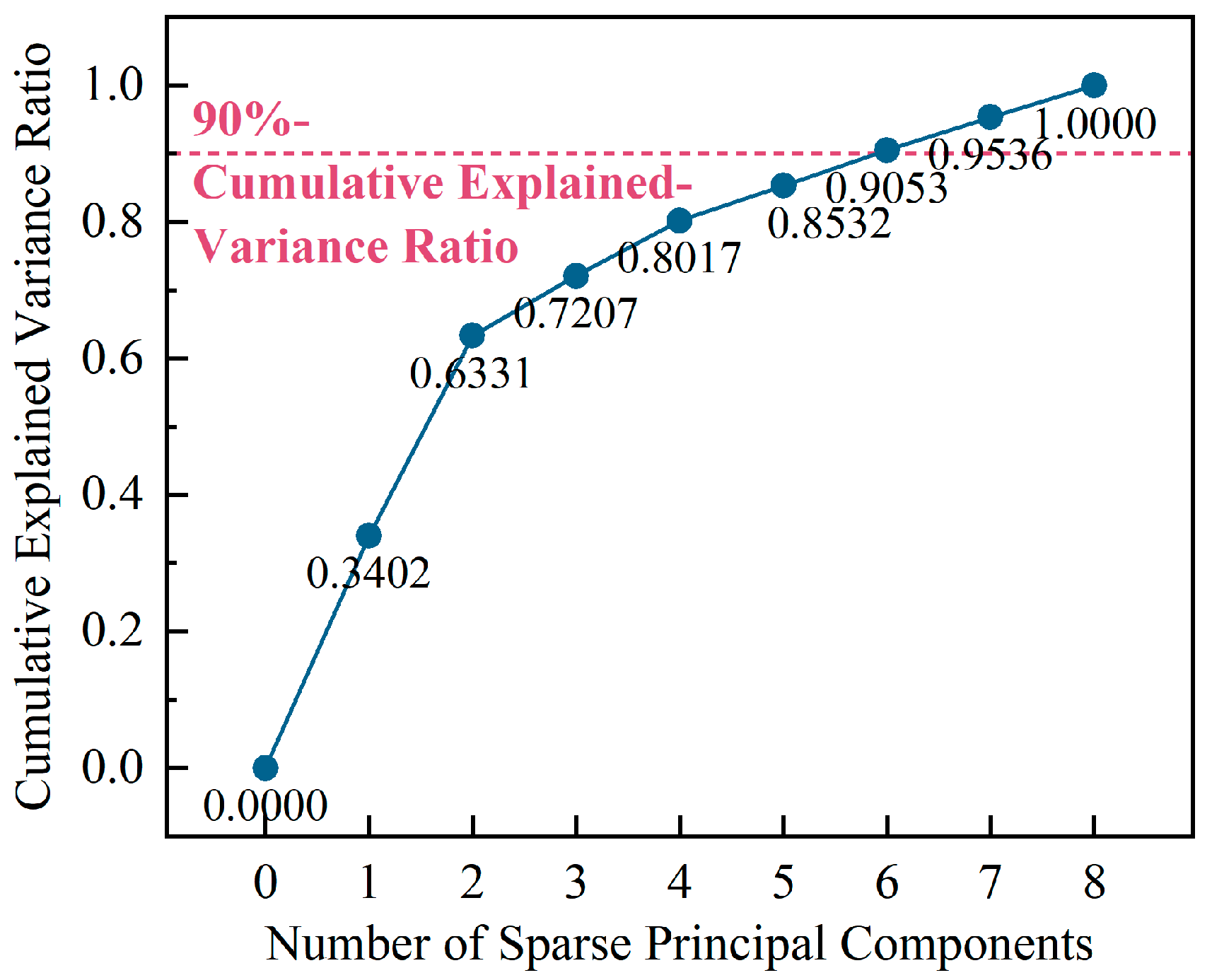
• Providing conditions for the interpretability study of transferability measurement: Sparse PCA tends to produce sparse vectors, which means that each principal component is related to only a few original variables. This sparse structure can help to explain the data patterns better, especially when the variables have specific physical or practical significance. So it lays the foundation for the interpretability of transferability metrics.

The sparse PCA method maps the original signal to a sparse space, thereby yielding a set of sparse principal components and a projected data set after dimensionality reduction. This process extracts the domain-invariant features of the cross-domain data. Moreover, the sparse principal components obtained are ordered, and they are sorted according to the magnitude of the variance of the explained data. In the sparse PCA method, the variance refers to the degree of dispersion of the data after projection onto the principal component directions. It reflects the extent to which each order of principal components accounts for the total variability or information content of the original data. The formula for the variance of the i-th order sparse principal component is as follows:

$${\tau }_i={\displaystyle \frac{{\lambda }_i}{{\displaystyle {\sum }_{j=1}^k{\lambda }_j}}}$$

(2)

where ${\lambda }_i$ is the eigenvalue of the i-th order sparse principal component, and k is the total number of sparse principal components.

The cumulative variance explained ratio is a term that shows the cumulative percentage of the original data variance accounted for by the first few principal components. It helps to understand how many principal components are needed to approximate the original dataset effectively, thus preventing the loss of important information. The formula for calculating the cumulative variance explained ratio of the first m sparse principal components is as follows:

$${{\rm T}}_m={\displaystyle {\sum }_{i=1}^m{\tau }_i}={\displaystyle \frac{{{\displaystyle {\sum }_{i=1}^m\lambda }}_i}{{\displaystyle {\sum }_{j=1}^k{\lambda }_j}}}$$

(3)

Figure 3 displays the cumulative variance explained ratio curve after performing sparse PCA on the cross-domain diagnostic dataset of piston aero engines. The number of sparse principal components to be extracted is set to 8, and the sparsity regularization parameter is set to 1. The following can be observed: (1) The first principal component has the largest variance explained ratio, at 34.02%. This indicates that the projection of the data in this direction captures the most variability of the original data. The second principal component has the next highest ratio, with the rest following in sequence. (2) The cumulative variance explained by the first 6 sparse principal components has reached 90%, which means that the main cross-domain feature data in the original data were captured. The cumulative variance explained by the first 8 sparse principal components reached 100%. This indicates that the number of sparse principal components set is redundant, as the seventh and eighth principal components contribute less to the explanation of the original signal. However, appropriate redundancy is necessary to obtain sufficient domain-invariant features.

Based on the domain-invariant feature extraction and selection capabilities of sparse PCA, this study proposes a new correlation shift metric (CSM). The calculation process is shown in Figure 4 and described as follows:

(1)

Parameter initialization.

There are two sets of key parameters for sparse PCA: the number of principal components and the sparsity regularization parameter. The number of principal components parameter mainly affects the proportion of total variance explained by the principal components of sparse PCA. The lower the number of principal components, the more information is lost in the explanation. The number of principal component parameters can be determined according to the cumulative variance explained ratio curve analysis and the needs of the actual problem. The sparse regularization parameter mainly controls the sparsity of the principal components. The larger the parameter indicates the stronger the sparsity and the better the model interpretability. However, an excessively large size may cause information loss. The sparsity regularization parameter can be selected according to cross-validation and specific domain background to choose the most appropriate value, striking a balance between sparsity and model performance.

(2)

Data concatenation.

Concatenate the source domain data $X_s$ and the target domain data $X_t$ and then form a unified dataset. Randomly shuffle the dataset to enhance robustness. Additionally, if the number of samples in the source domain is too large, a certain proportion of random sampling can be performed to reduce computational time.

(3)

Sparse PCA.

Sparse PCA is performed using the above dataset to obtain the shared sparse principal component P and the dimensionality reduction data $Z_s$ and $Z_t$ projected to the sparse space.

(4)

Selection of sparse principal components and signal reduction.

Taking the 90% cumulative variance explained ratio as a criterion, the first m orders of sparse principal components $P^m$ are selected for signal reduction. The calculation is shown as Equation (4):

$$\begin{array}{l}{X}_s^{\prime }=Z_s^m·P^m\\ X_t^{\prime }=Z_t^m·P^m\end{array}$$

(4)

where $X_s^{\prime }$ and $X_t^{\prime }$ are the reconstructed signals in the source and target domains, respectively. $Z_s^m$ and $Z_t^m$ are the column vectors corresponding to the first m orders of sparse principal components in the sparse space.

(5)

Metrics calculation.

Calculate the difference in distribution between the reconstructed signals of source and target domains, denoted as follows:

$$M_C(P_s\parallel P_t)=\sigma f_W(X_s^{\prime },X_t^{\prime })$$

(5)

where the constant σ is a scaling factor that controls the output CSM values within a specific range. Its recommended setting is the inverse of the variance of the source domain dataset. $f_W$ is the Wasserstein-1 distance function for any two discrete variables corresponding to the probability distributions µ and ν. Its calculation formula is as follows:

$$\begin{array}{c}{f}_W(\mu ,\nu )={\inf }_{p\in \Pi (\mu ,\nu )}{E}_{(x^1,x^2)\sim p}[‖x^1-x^2‖]\\ \hspace{1em}\hspace{1em}\hspace{1em}={\inf }_{p\in \Pi (\mu ,\nu )}{\displaystyle \sum _i{\displaystyle \sum _j{p}_{i,j}‖x_i^1-x_j^2‖}}\end{array}$$

(6)

Through the above process, CSM achieves the measurement of correlation shift between different domain datasets, with a value range between 0 and 1.

2.2.2. Diversity Shift Metric

The diversity shift caused by the difference in label space between domains is an important component affecting the transferability of datasets, but it is often overlooked by previous transferability measurement studies. Due to the limitations of data collection conditions, it is difficult for the label space of the target domain in mechanical fault diagnosis to be consistent with the source domain. Therefore, diversity shift occurs more frequently in cross-domain diagnosis of mechanical faults. Moreover, compared to the difference in data feature distribution, the difference in label space has a greater impact on the transferability. This is mainly because data under new labels often have new feature patterns. The joint probability distribution information of data features and labels under new labels is poorly learned or not learned at all by the source-domain model. The above two factors pose more serious obstacles to transfer learning.

The distribution of the label space in the source and target domains and the illustration of their diversity shift is shown in Figure 5. Assuming that the union of the label spaces of the source and target domains is $\{C_1,C_2,C_3,\dots ,C_n\}$, it represents that there are n types of labels common to both the source and target domains. Among them, the source domain contains $K_s$ types of label categories; the target domain contains $K_t$ types of label categories. Their intersection represents the shared label space, which contains $K_p$ types of label categories. Then, their relationship is as follows:

$$K_s+K_t-K_p=n$$

(7)

This section proposes a diversity shift metric (DSM) based on the difference in label space. Its mathematical form is as follows:

$$M_D({\gamma }_s,{\gamma }_t)={\displaystyle \frac{K_t-K_p}{K_s}}={\displaystyle \frac{n-K_s}{K_s}}={\displaystyle \frac{n}{K_s}}-1$$

(8)

Furthermore, the discussion on the distribution of DSM results under different target domain label space scenarios is as follows:

• ${\gamma }_t\subseteq {\gamma }_s$: That is, the target domain label space is contained within or equal to the source domain label space. Thus, $K_p=K_t$. And the diversity shift metric for the target domain is the lowest, $M_D=0$;
• ${\gamma }_t\cap {\gamma }_s=\varnothing$: That is, the label spaces of the target domain and the source domain are completely different. Thus, $K_p=0$. And the diversity shift metric for the target domain is the highest, $M_D=K_t/K_s$.
• ${\gamma }_t\cap {\gamma }_s\ne \varnothing$: That is, the label spaces of the target domain and the source domain partially overlap. Thus, $0<K_p<K_t$. The diversity shift metric for the target domain is in an intermediate state, $0<M_D<K_t/K_s$ The larger the DSM value, the greater the degree of diversity shift, and the worse the transferability of the target domain; the smaller the DSM value, the opposite is true.
• The target domain label space is unknown: That is, some or all the target domain data is unlabeled, belonging to semi-supervised or unsupervised transfer learning. In this case, $M_D=1$ is defined to reflect the difficulty level of transferability.

From the above analysis, it can be concluded that DSM achieves the measurement of diversity shift between different domain datasets, with a value range between 0 and 1. The scope of the application covers all target domain label space conditions in cross-domain fault diagnosis and is also applicable to supervised, unsupervised, or semi-supervised transfer learning.

2.2.3. Hybrid Transferability Metric

The transferability metric function for cross-domain diagnostic datasets can be expressed as follows:

$$M(D_s,D_t)=\alpha M_C(P_s\parallel P_t)+\beta M_D({\gamma }_s,{\gamma }_t)+\eta M_S({\chi }_s,{\chi }_t)$$

(9)

where $M({\mathcal{D}}_s,{\mathcal{D}}_t)$ represents the composite transferability measurement function from the source domain to the target domain. $M_C\left(P_s\parallel P_t\right)$ denotes the correlation shift metric. $M_D\left({\gamma }_s,{\gamma }_t\right)$ denotes the diversity shift metric. $M_S\left({\chi }_s,{\chi }_t\right)$ denotes the shift measurement for the feature space. α, β, η are the weighting coefficients for each measurement metric, respectively. Since this study focuses on mechanical fault cross-domain diagnosis with the same feature space in the datasets, $M_S\left({\chi }_s,{\chi }_t\right)$ is constant and equal to 0.

As a result, the hybrid transferability metric function based on weighted correlation-diversity shift degenerates to the following:

$$M(D_s,D_t)=\alpha M_C(P_s\parallel P_t)+\beta M_D({\gamma }_s,{\gamma }_t)$$

(10)

Equation (10) is the HTM for quantifying the transferability of datasets based on domain differences. The higher the HTM value indicated by this measurement, the greater the differences between domains, and the worse the transferability from a specific source domain to the target domain.

The weighted coefficients in Equation (10) are set based on different tendencies of transferability measurement. In the cross-domain diagnosis task of piston aero engine datasets, balanced weighting coefficients are set as follows: α = 0.5, β = 0.5.

Figure 6 presents the overall process of applying HTM to assess the transferability of a specific target domain relative to a particular source domain. The entire process can generally be divided into four main steps:

• Data preparation: Organize the source domain dataset and the target domain dataset to be evaluated. On the one hand, use methods such as resampling to segment the samples to ensure that the sample lengths of the source and target domains are consistent. If the number of samples in the source domain dataset is excessively large, random sampling of the dataset can also be performed to reduce computational load. On the other hand, organize the label space. Apply the same label encoding to both the source and target domains to facilitate the counting of common label types and unique label types.
• Correlation shift measurement: Following the CSM calculation process, sequentially complete: parameter initialization—data concatenation—sparse principal component analysis—selection of sparse principal components and signal reduction—metric calculation, ultimately obtaining the CSM assessment result.
• Diversity shift measurement: According to the DSM calculation process, successively tally the source domain label category count $K_s$, the target domain label category count $K_t$, and the count of shared label categories $K_p$. Then calculate the DSM assessment result based on Equation (8).
• Hybrid weighting: Based on the nature of the transfer task and the requirements for transferability assessment, select the weighting coefficients. Utilize the above results to calculate the HTM by weighted correlation-diversity shift and evaluate the transferability of the target domain based on the magnitude of the HTM results.

3. Cross-Domain Experiment and Dataset

The proposed transferability metrics are validated through the classification tasks of a designed cross-domain diagnostic dataset for piston aero engines. This cross-domain dataset is acquired through a series of bench fault simulation experiments. The engine test bench is set up in a dedicated simulation environment laboratory. The data acquisition system relies on the SCADAS-XS acquisition front-end from Siemens and the 621B40 vibration acceleration sensors from PCB Company. The sensors PCB-621B40 have a sensitivity of 10 mV/g, a resolution of 0.0012 g rms, and a frequency response range (±5%) of 1.6 Hz to 30 kHz. According to the Nyquist sampling theorem, the sampling frequency is set at 25.6 kHz. These experimental conditions above ensure the credibility of the collected dataset.

The dataset contains a total of 27 types of engine operating status data (vibration acceleration signals), corresponding to 27 categories of manually annotated labels. Fault diagnosis falls under the classification task, which requires predicting the labels corresponding to new, unknown data based on the mapping pattern of existing data and labels. In the dataset, label 0 represents the vibration signals of the engine under normal operating conditions; labels 1–13 represent the vibration signals for ignition system fault states; labels 14–23 represent the vibration signals for fuel supply system fault states; labels 24–26 represent the vibration signals for mechanical body fault states.

Table 1. Index of labels and fault types for piston aero engine cross-domain dataset.

Label	Fault Type	Fault Contribute	Simulation Operation
0	Normal	Health condition	Healthy mechanical components and standard-calibrated ECU patterns
1	Ignition Advance −8°	Ignition system faults, belonging to electronic control unit (ECU) failure	Change the ECU setting of the ignition advance angle pulse spectrum deviation from the calibration state
2	Ignition Advance −6°
3	Ignition Advance −4°
4	Ignition Advance −2°
5	Ignition Advance +1°
6	Ignition Advance +2°
7	Ignition Advance +2.5°
8	Ignition Advance +4°
9	Ignition Advance +5°
10	Ignition Advance +6°
11	Ignition Advance +8°
12	Random Misfire		Control via misfire generator
13	Fully Misfire
14	Fuel Charge −15%	Fuel supply system faults, belonging to electronic control unit (ECU) failure	Change the ECU setting of the fuel injection quantity deviating from the calibration state
15	Fuel Charge −10%
16	Fuel Charge −5%
17	Fuel Charge +5%
18	Fuel Charge +10%
19	Fuel Charge +15%
20	Fuel Pressure −20%		Change the injection pump pressure
21	Fuel Pressure −10%
22	Fuel Pressure +10%
23	Fuel Pressure +20%
24	Piston Ablation	Body faults, belonging to mechanical system failure	Replace the corresponding failed parts
25	Piston Pin Failure
26	Pin-Bearing Roller Loss

provides a detailed description of the correspondence between these labels and the engine states, as well as the simulated operations for the faults. The design of these fault types mainly depends on (1) the high-frequency types of fault historical data provided by the engine manufacturer; and (2) the high correlation between fault manifestations and the vibration signals. Additionally, it can be observed that different severities of the same fault condition are also distinctly labeled. Such dataset design increases the difficulty of the classification task and is more meaningful for practical engineering applications.

Before conducting the formal vibration signal acquisition experiments, the test engine needs to undergo necessary warm-up operations. The experiment begins after confirming the correct installation of both the engine system and the signal acquisition system. The engine is then brought to the designated operating conditions using the electronic control system. Once the engine speed and load have stabilized, the signal acquisition system starts collecting vibration signal data. Ultimately, the experiment yields vibration signals that reflect the engine’s operating state under the specified conditions and corresponding fault labels.

Cross-domain fault diagnosis is a typical OOD data scenario. The datasets of the source and target domains have both similarities and differences. They exhibit shifts in two aspects: label space and feature distribution. To simulate different domains, the experiments were conducted on three different benches. As shown in Figure 7, they are Figure 7a: Engine-I on an air-cooled bench; Figure 7b: Engine-II on an air-cooled bench; and Figure 7c: Engine-I on a water-cooled bench. Multiple vibration acceleration sensors were installed on each set of benches. The experimental data were collected in three different operating conditions (different speeds and loads).

As shown in

Table 2. Information on cross-domain diagnosis tasks.

Task		Cross- Engine		Cross- Platform		Cross- Condition			Cross- Sensor
Domain Description		E1: Engine-I E2: Engine-II		P1: air-cooled bench P2: water-cooled bench		C1: 4000 rpm C2: 4500 rpm C3: 5000 rpm			S1: Cylinder ① S2: Cylinder ② S3: Crankcase
Mark		E1	E2	P1	P2	C1	C2	C3	S1	S2	S3
Label Space	0	√	√	√	√	√	√	√	√	√	√
	1		√
	2		√
	3		√
	4		√
	5	√		√	√	√	√	√	√	√	√
	6		√
	7	√		√	√	√	√	√	√	√	√
	8		√
	9				√
	10		√
	11		√
	12	√		√	√	√	√	√	√	√	√
	13	√		√		√	√	√	√	√	√
	14	√		√		√	√	√	√	√	√
	15	√	√	√		√	√	√	√	√	√
	16	√	√	√	√	√	√	√	√	√	√
	17	√	√	√	√	√	√	√	√	√	√
	18		√		√
	19		√		√
	20	√		√		√	√	√	√	√	√
	21	√		√	√	√	√	√	√	√	√
	22				√
	23				√
	24	√		√		√	√	√	√	√	√
	25	√		√		√	√	√	√	√	√
	26	√		√		√	√	√	√	√	√
Total		14	14	14	12	14	14	14	14	14	14

, the piston aero engine dataset can be designed for four cross-domain diagnosis tasks. The collected vibration signals can be categorized into different domains according to the varying tasks. Based on the “source-path-receiver” principle of vibration propagation, the feature distribution of the vibration signals across different domains will experience shifts.

• Cross-engine task: As shown in Figure 7a,b, Engine-I is a horizontally opposed two-cylinder engine, and Engine-II is a single-cylinder engine. Both are naturally aspirated two-stroke engines that use aviation kerosene as fuel. They also use as many identical parts as possible. Due to the differences in the number and size of the cylinders, Engine-I has a total displacement of 0.288 L, while Engine-II has a total displacement of 0.085 L. Consequently, there is a shift in both the power and the number of vibration sources. Simultaneously, due to differences in mechanical construction, the propagation path of the vibrations has also shifted. The combined shift in the source and path results in the feature shift of the received vibration signals. The other main structural and performance parameters of the two engines are displayed in

  Table 3. Structure and Performance Parameters of Engine-I and Engine-II.

  Parameter Term	Engine-I	Engine-II
  Stroke	2	1
  Overall dimensions	0.46 ∗ 0.27 ∗ 0.19 m3	0.31 ∗ 0.21 ∗ 0.32 m3
  Layout	Horizontal opposed	Inline
  Number of cylinders	2	1
  Bore diameter	56 mm	52 mm
  Piston stroke	58 mm	40 mm
  Total displacement	0.288 L	0.085 L
  Compression ratio	13.5:1	9:1
  Cooling type	Air/water-cooled	Air-cooled
  Typical RPM range	3500–5500 rpm	3000–6000 rpm

  .
• Cross-platform task: Comparing Figure 7a,c, the same Engine-I was subjected to external system modifications for air-cooling and water-cooling and was installed on different experimental platforms. At low speeds, the cooling efficiency of the air-cooled platform is lower than that of the water-cooled platform. It is only at high speeds that the cooling conditions of the two become consistent. The difference in cooling conditions affects the following: (1) the pre-mixing condition of fuel and air; (2) the combustion condition of the mixture; (3) the properties of the lubricant and the friction of moving parts. All of these can cause a shift in the vibration source, which leads to a feature shift in the vibration signals.
• Cross-condition task: As shown in Figure 7a, the signals collected from the Engine-I air-cooled platform are used as the dataset. Vibration signals collected at different rotational speeds are categorized into different domains. Since the engine uses a propeller as the output form, the engine’s rotational speed and output power are directly proportional. Therefore, when the rotational speeds differ, the power output from engine combustion is also different. The differences in combustion lead to differences in the vibration sources, which is the main reason for the feature shift in the vibration signals.
• Cross-sensor task: As shown in Figure 7a, the signals collected from the Engine-I air-cooled platform are used as the dataset. Vibration signals collected by sensors placed at different locations on the engine surface are categorized into different domains. Due to changes in the propagation path from the vibration source to the sensors, the feature distribution of the collected vibration signals will exhibit shifts.

Due to the limitations of the experimental benches and engine properties, there are differences in the types of engine faults simulated on different benches. It results in a shift in the label space for cross-domain diagnosis, which is also widespread in real-world cross-domain diagnosis of mechanical faults. The situation of the labeling space for each domain is shown in Table 2.

The proposed transferability metrics will be predicted across all domains of the four cross-domain diagnosis tasks. To ensure the comparability of the results, a common domain is selected as the public source domain; that is, the shared data of the E1/P1/C1/S1 domains is used as the starting point for transfer.

4. Results

To verify the applicability of the proposed hybrid transferability measurement based on the weighted correlation-diversity shift in practical mechanical fault cross-domain diagnosis, the piston aero engine cross-domain diagnostic dataset was taken as the research object, and the CSM, DSM, and HTM for different tasks were calculated, as shown in

Table 4. Transferability metrics for cross-domain diagnosis datasets of piston aero engines.

Cross-Domain Task	CSM	DSM	HTM
E1/P1/C1/S1→E2	0.244	0.714	0.4790
E1/P1/C1/S1→P2	0.062	0.286	0.1740
E1/P1/C1/S1→C2	0.131	0	0.0655
E1/P1/C1/S1→C3	0.173	0	0.0865
E1/P1/C1/S1→S2	0.020	0	0.0100
E1/P1/C1/S1→S3	0.035	0	0.0175

. The CSM values were obtained by extracting data samples from different domains. The DSM values were calculated based on the types of label spaces recorded in Table 2 for each domain. Finally, the overall transferability measurement HTM for each cross-domain diagnosis task was obtained through weighted calculation.

The results show that a larger HTM indicates lower transferability of the domain. Therefore, under this transferability measurement evaluation index, the transferability ranking of each target domain is as follows: E2 < P2 < C3 < C2 < S3 < S2. For different cross-domain diagnosis tasks, the transferability ranking is as follows: cross-machine < cross-platform < cross-condition < cross-sensor.

The transferability ranking results are consistent with the design expectations of the cross-domain diagnostic simulation experiments. According to the experimental design and the “Source-Path-Receiver” theory, the cross-engine diagnosis task is the most challenging due to significant differences between the two engines. The cross-platform diagnosis task is the next most difficult because of the considerable impact of different cooling systems on combustion. Cross-condition diagnosis tasks are the most common in actual engineering, where speed variations cause shifts in the frequency characteristics of the vibration signals. The cross-sensor diagnosis task is the simplest because the vibration signals from different sensors are collected simultaneously, resulting in paired data with minimal feature shift.

If the label spaces of the source and target domains are the same, the DSM value equals 0. For example, the cross-condition and cross-sensor diagnosis tasks are shown in Table 4. In this case, the domain transferability index HTM follows the trend of the CSM. However, if the label space of the target domain changes, the diversity shift will have a greater effect on transferability. For example, as shown in Table 4 for cross-machine and cross-platform diagnosis tasks, it can be analyzed from the results that their transferability index HTM is significantly higher than other cross-domain diagnosis tasks. In particular, when comparing cross-platform and cross-condition diagnosis tasks, it can be found that the CSM of the P2 target domain is lower than that of the C2/C3 target domains. This indicates that the degree of feature distribution shift of the P2 dataset is smaller. However, due to the greater impact caused by the difference in label space, the overall transferability of P2 becomes worse, which is reflected in the HTM of the P2 target domain being higher than that of the C2/C3 target domains. Overall, the proposed CSM, DSM, and HTM metrics effectively demonstrate the degree of transferability of each target domain dataset relative to the source domain. These transferability metrics provide guidance and reference for applying transfer learning methods to solve cross-domain diagnostic problems.

When measuring the degree of correlation shift between cross-domain data through the CSM, sparse principal components that account for more than 90% of the cumulative variance explained ratio are used to reconstruct the signal. The remaining sparse principal components are discarded. This mechanism facilitates the extraction and selection of domain-invariant features. As shown in Figure 3, the first six sparse principal components were selected to reconstruct the signal, which accounted for 90.53% of the cumulative variance explained ratio. The remaining two principal components and their corresponding original signal components were omitted. To visually assess the representational effect of sparse PCA on signals and to substantiate the rationale behind the selection of sparse principal components, the dimensionality reduction mapping of the original signal in the sparse space was visualized. Given the ordered nature of the sparse principal components derived from sparse PCA, the first and second-order components, as well as the discarded seventh and eighth-order components, were specifically selected. The dimensionality reduction projection of the original signal in the sparse space was presented in a two-dimensional distribution format, as depicted in Figure 8. Each dot in the figure represents a data sample from a particular domain. A random selection of 1000 samples was made from each domain. The color and shape of the dots can distinguish the domain they represent.

Figure 8a displays the visualization of the first two sparse principal components for data from seven domains. It can be observed that the sample points from each domain are generally distributed in a ring-like pattern, with relatively clear boundaries between domains. The red sample points in the figure represent the distribution of the source domain data in the sparse space, clustered at the center of the image. The larger the distribution radius of the sample points from other domains, and the farther away from the center of the image, the greater the difference in distribution from the source domain samples in the sparse space. From the distribution in the figure, the cross-machine task domain E2 is at the outermost edge of the image, showing the greatest difference from the source domain sample distribution. The remaining domains, from the outermost to the inner, are in the following order: cross-condition task domains C3 and C2, cross-platform task domain P2, and cross-sensor task domains S3 and S2. This order is consistent with the transferability trend measured by the HTM indicator. This suggests that in this application case, there are significant differences in the original signals from different domains in the direction of the first two shared sparse principal components. If the shared sparse principal components are defined as domain-invariant features, the differences in the projection of the signals in the direction of the sparse principal components can be defined as the correlation shift of the signals.

The visualization of the projection of the last two sparse principal components is shown in Figure 8b. Compared with Figure 8a, it can be observed that the distribution of sample points from each domain appears chaotic. The data from various domains are intermingled in the visualization. Our analysis suggests that the last sparse principal components account for the smallest proportion of the variance explained, and the corresponding signal features are more likely to be noise and interference components. Although these sparse principal components originate from different domains, the distribution of noise and interference features is random. Therefore, domains cannot be distinguished from each other based on the distribution of these components. Through the above analysis and comparison, it can be proven that the sparse PCA method achieves the extraction of domain-invariant features through shared sparse principal components. The principle of the 90% cumulative variance explained ratio can effectively filter out the main domain-invariant feature components, thereby aiding in the calculation of the CSM to measure the degree of correlation shift between domains.

The following discussion addresses the transferability measurement under the extreme class imbalance problem. The extreme class imbalance problem [35,36,37] refers to a situation where the target domain has training data with only one label, and this label is included in the label space of the source domain. The extreme class imbalance problem falls within the category of unsupervised transfer learning. In mechanical fault diagnosis, the target domain typically assumes a large amount of normally operating state data, while the fault state data remains unlabeled. This scenario is closer to the actual data condition of cross-domain diagnosis. The difficulty of solving it is also greater compared to supervised transfer learning.

Compared to the supervised scenario, the DSM and HTM values of the piston aero engine cross-domain diagnostic dataset under extreme class imbalance problems have changed. The calculation results are shown in

Table 5. Transferability metrics for cross-domain diagnosis datasets in extreme class imbalance problems.

Cross-Domain Task	CSM	DSM	HTM
E1/P1/C1/S1→E2	0.244	0.929	0.5865
E1/P1/C1/S1→P2	0.062	0.786	0.4240
E1/P1/C1/S1→C2	0.131	0.929	0.5300
E1/P1/C1/S1→C3	0.173	0.929	0.5510
E1/P1/C1/S1→S2	0.020	0.929	0.4745
E1/P1/C1/S1→S3	0.035	0.929	0.482

. It can be observed that due to the increased difference in label space, the DSM values for various tasks have increased, leading to a corresponding increase in the weighted HTM values. According to the HTM assessment, the transferability ranking of each target domain under extreme class imbalance problem is as follows: E2 < C3 < C2 < P2 < S3 < S2. For different cross-domain diagnosis tasks, the transferability ranking is as follows: cross-machine < cross-condition < cross-platform < cross-sensor. Compared to supervised transfer learning tasks, the gap in transferability metrics among tasks under extreme class imbalance is reduced. This is primarily because the label space in the target domain for all tasks deteriorates, and its impact on transferability becomes dominant. This also indicates that the previous approach of focusing solely on correlation shift while neglecting diversity shift in transferability metrics is flawed.

Based on the relative relationship between model generalizability and dataset transferability, the transferability metric can also be based on model generalization performance. The relationship between them can be expressed as follows:

$$\begin{array}{c}{M}^{\prime }(D_s,D_t)=1-Accuracy(f_{D_s}({\overrightarrow{x}}_t),y_t)\\ \hspace{1em} =Error(f_{D_s}({\overrightarrow{x}}_t),y_t)\end{array}$$

(11)

where $M^{\prime }({\mathcal{D}}_s,{\mathcal{D}}_t)$ is a transferability metric function based on the generalization performance of the model. Accuracy denotes the accuracy of the model f trained in the source domain applied in the target domain. Error denotes the misclassification rate of the model f applied in the target domain.

Due to the lack of a universally accepted standard model, transferability measurement methods based on model generalization performance are difficult to apply practically to specific problems. In addition, model performance is highly dependent on the training process and the number of samples in the target domain, leading to an inaccurate assessment of transferability. However, accuracy is the most important performance indicator in cross-domain diagnosis and is directly related to practical application goals. Therefore, this study conducted a comparison between the transferability measurement based on the accuracy (which is actually the misclassification rate) and the hybrid transferability metric based on the weighted correlation-diversity shift proposed in this study, thereby verifying the consistency and effectiveness of the transferability measurement. Due to the different measurement principles, there may not be a strict linear relationship between the two measurement methods. They are influenced by various factors, including the nonlinear mapping relationship between data and labels, model complexity, and others. However, the trends in transferability changes should consistently reflect these influences.

Figure 9a shows the transferability measurement results in supervised transfer learning problems. Two transfer learning methods were selected and applied to the corresponding target domains to demonstrate their respective misclassification rates. These methods are as follows: (1) the original long short-term memory (LSTM) method [38]; and (2) the pre-training and fine-tuning method [29]. LSTM is currently the most effective neural network model for processing time series data. The pre-training and fine-tuning method is one of the most common and effective means of transfer learning. The diagnostic accuracy of the above two methods represents the level of generalizability of current cross-domain diagnosis intelligent methods.

In various cross-domain fault diagnosis tasks for piston aero engines, the misdiagnosis rate of the pre-training-fine-tuning method is on average about 25% lower compared to LSTM. This is mainly because the pre-training-fine-tuning model is trained with target domain data, enhancing its generalization ability in the target domain. Nevertheless, Figure 9a demonstrates that the transferability trend predicted by HTM is consistent with the misclassification rate trends of the two methods. It indicates that HTM makes an accurate prediction of transferability for supervised transfer learning problems and has a guiding significance in actual supervised cross-domain fault diagnosis. Additionally, the misdiagnosis rates indicate that cross-engine and cross-platform diagnosis tasks are significantly more challenging than cross-condition and cross-sensor tasks. HTM effectively predicted this as well.

Figure 9b presents the transferability measurement results under extreme class imbalance problems. Two generative transfer learning methods were used to calculate the misclassification rates for the corresponding target domains. The generative transfer learning methods are as follows: (1) cycle generative adversarial network (Cycle GAN) [39]; and (2) fast neural style (FNS) [35]. These methods are typical representatives of generative models solving the extreme class imbalance problem. They have all undergone a one-dimensional transformation in this study to adapt to the classification task of vibration signals.

It can be observed from Figure 9b that the transferability predicted by HTM is consistent with the misclassification rate trends shown by Cycle GAN and FNS in most tasks. However, there is a deviation between the performance of FNS in the target domain C2 and the transferability predicted by HTM. HTM indicates that the transferability of the target domain C2 should be lower than that of the target domain P2 and higher than that of the target domain E2. But the actual diagnostic results of FNS suggest that the transferability of the target domain C2 is higher than both P2 and E2. The diagnostic results of FNS in the target domains C2 and C3 also reveal a significant fluctuation. After ruling out human and systematic errors, this study speculates that the above errors are caused by the instability of generative neural networks. The results of generative algorithms are sensitive to model hyperparameters and network inputs, leading to a fluctuation in the performance of generative transfer learning.

In summary, HTM provides valuable transferability predictions for both supervised transfer learning and extreme class imbalance problems. These results demonstrate its potential to guide real-world cross-domain diagnosis, especially in scenarios with small samples and unsupervised learning.

5. Conclusions

To address the fundamental transfer learning question of “when to transfer”, a novel transferability measurement is proposed in this study to determine the degree of shift between the target domain and the source domain. It can help predict the difficulty of transfer learning for tasks in different target domains, as well as guide the application strategy of transfer learning methods. This study proposes a hybrid transferability metric based on the weighted correlation-diversity shift, suitable for evaluating the transferability between mechanical fault cross-domain diagnostic datasets. The main results and conclusions are summarized as follows:

(1)

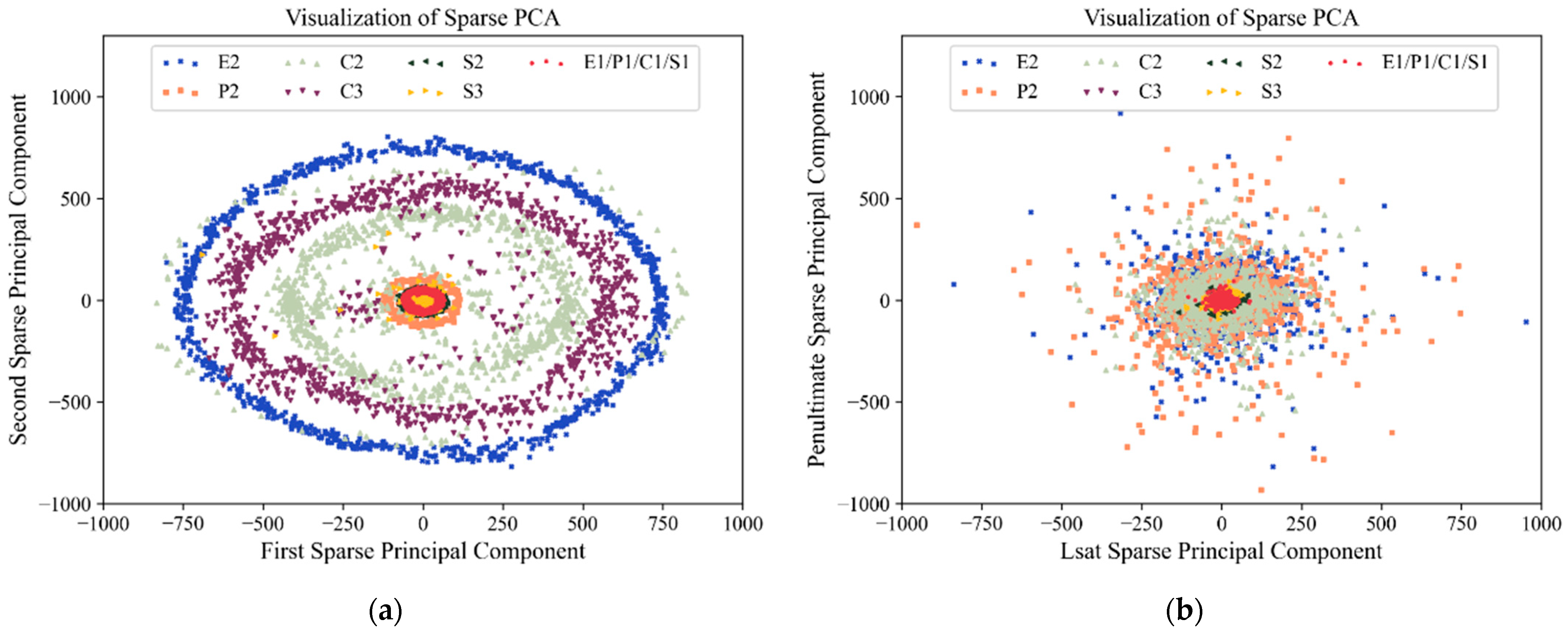
To measure the correlation shift between domains, this study proposes a correlation shift metric (CSM) based on the sparse PCA, which overcomes the issue of common statistical methods being insensitive to signal features. The method first extracts domain-invariant features across domains by utilizing shared sparse principal components. Next, it selects sparse principal components based on the criterion of the 90% cumulative variance explained ratio, thereby discarding interference and noise components. Lastly, it calculates the Wasserstein-1 distance based on the projection of sparse principal components to determine the CSM value for the target domain.

(2)

To measure the diversity shift between domains, this study introduces a diversity shift metric (DSM) based on the differences in label spaces, addressing the neglect of label space differences in traditional transferability measurements. A DSM calculation method is designed based on the label types of the source and target domains, which is widely applicable to supervised, semi-supervised, or unsupervised transfer learning problems.

(3)

By combining the correlation shift measurement and the diversity shift measurement, this study proposes a hybrid transferability metric (HTM), which achieves the prediction of transferability for target domains in cross-domain mechanical fault diagnosis.

(4)

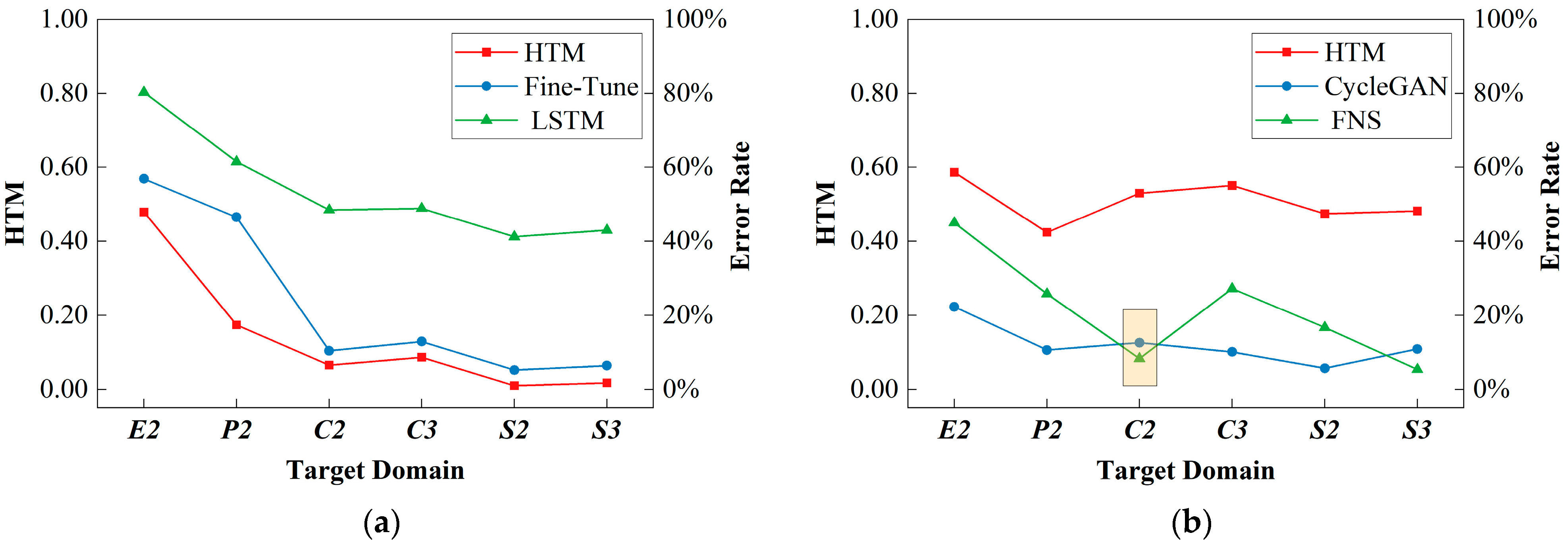
Applying the proposed HTM metric, transferability predictions were made for different tasks and domains in the piston aero engine cross-domain diagnostic dataset. Transferability prediction results were provided under both the supervised transfer learning conditions and the extreme class imbalance problem. Based on the connection between model generalizability and domain transferability, transferability metrics based on model generalization performance were obtained using the misdiagnosis rates of different models for comparison and verification with the HTM prediction results. It is demonstrated that HTM achieved accurate transferability predictions across multiple transfer learning tasks in two different data scenarios, aligning with the diagnostic accuracy trends of the intelligent diagnosis models. These results indicate the significant potential and value of HTM in practical applications of transfer learning.

In future research, the weighted correlation-diversity shift-based hybrid transferability metric proposed in this study could serve as a general transferability measurement framework applicable to a broader range of transfer learning tasks. Due to the limitations of the datasets, this study focused on transferability metrics in vibration signal-driven mechanical fault cross-domain diagnosis and provided clear quantitative evaluation metrics for transferability. Additionally, exploring the interpretability of the correlation shift metric based on sparse PCA presents a promising direction for further research.