Dynamic Evolution Law of Production Stress Field in Fractured Tight Sandstone Horizontal Wells Considering Stress Sensitivity of Multiple Media
Abstract
1. Introduction
2. Model Establishment
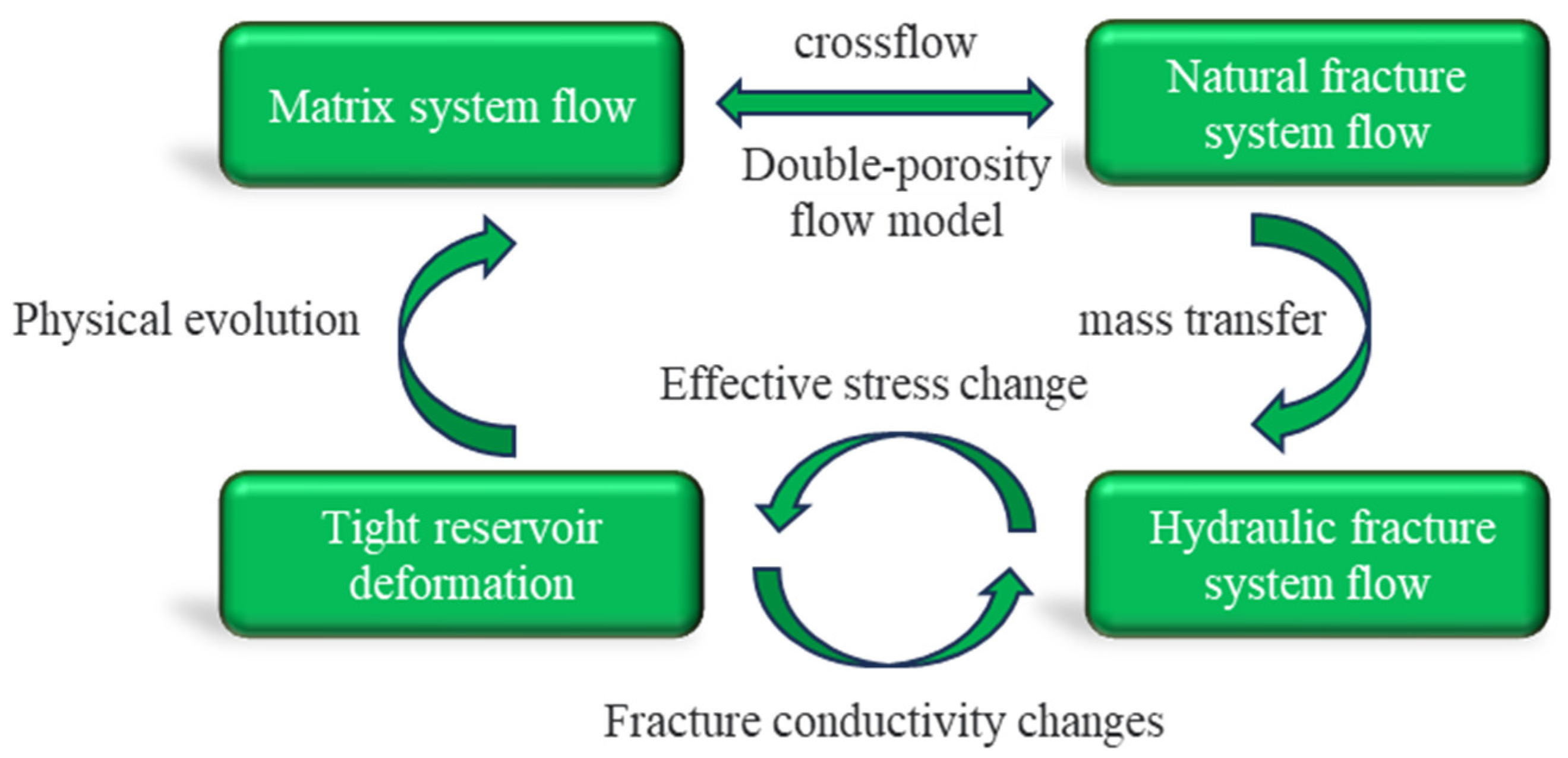
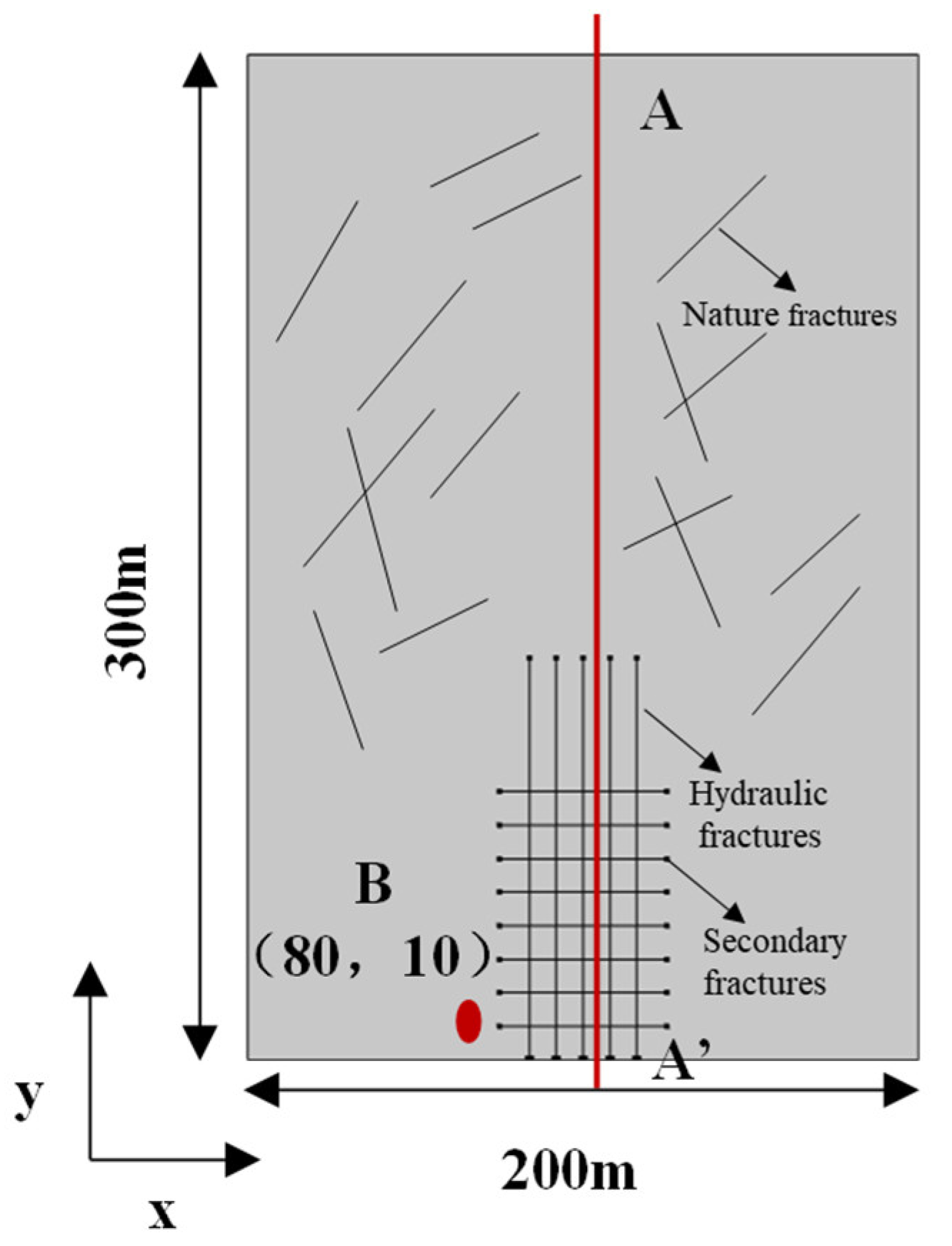
2.1. Physical Model
2.2. Mathematical Models
2.3. Finite Element Numerical Model
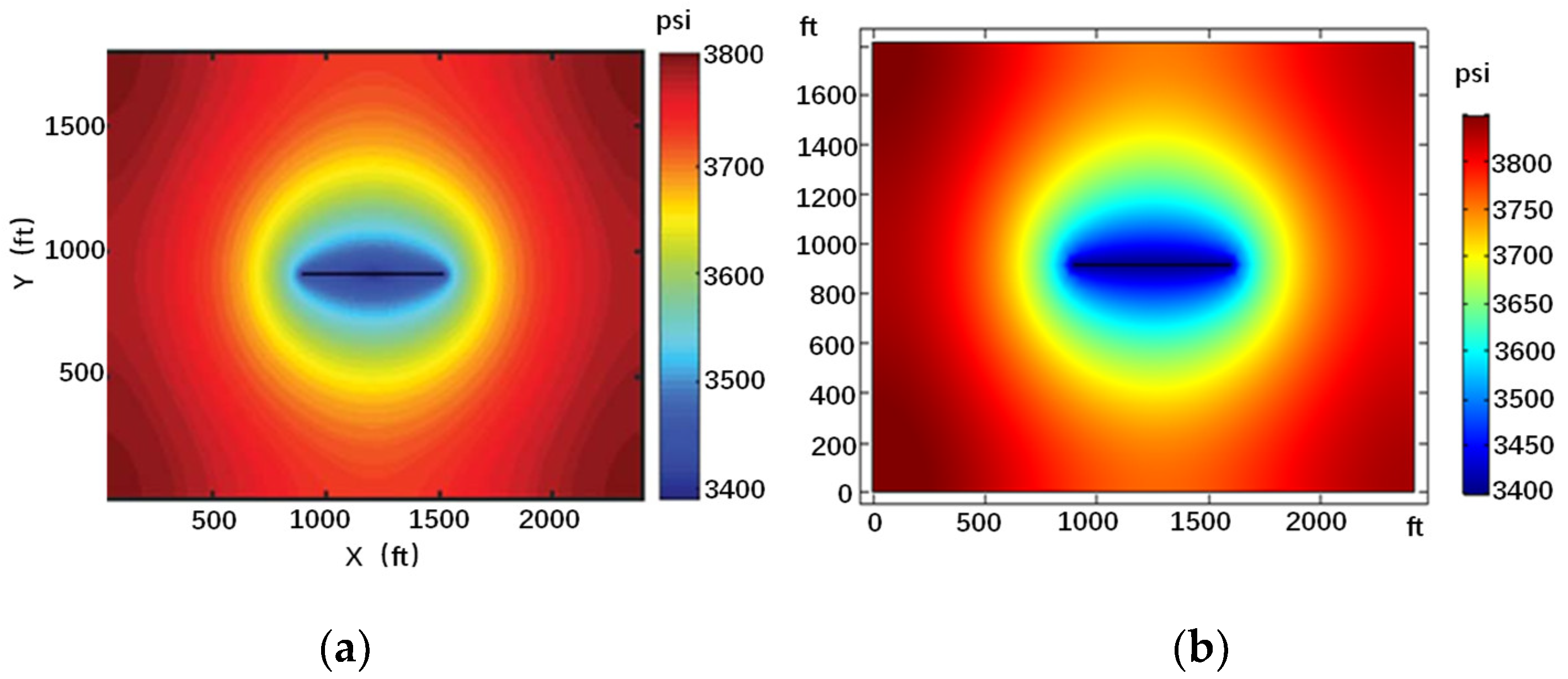
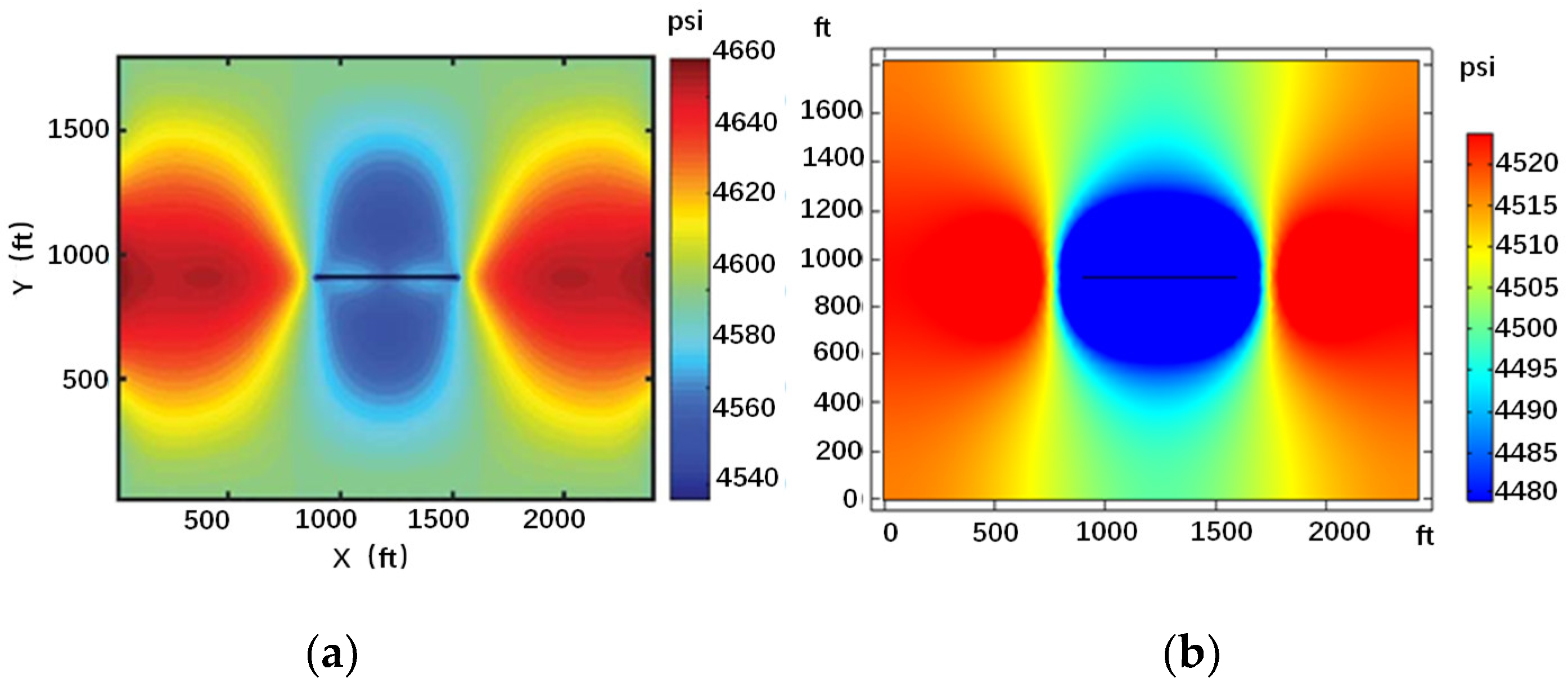
3. Model Validation
4. Analysis of Impact Patterns
4.1. Stress Sensitivity Coefficient of Matrix Porosity
4.2. Matrix Permeability Stress Sensitivity Coefficient
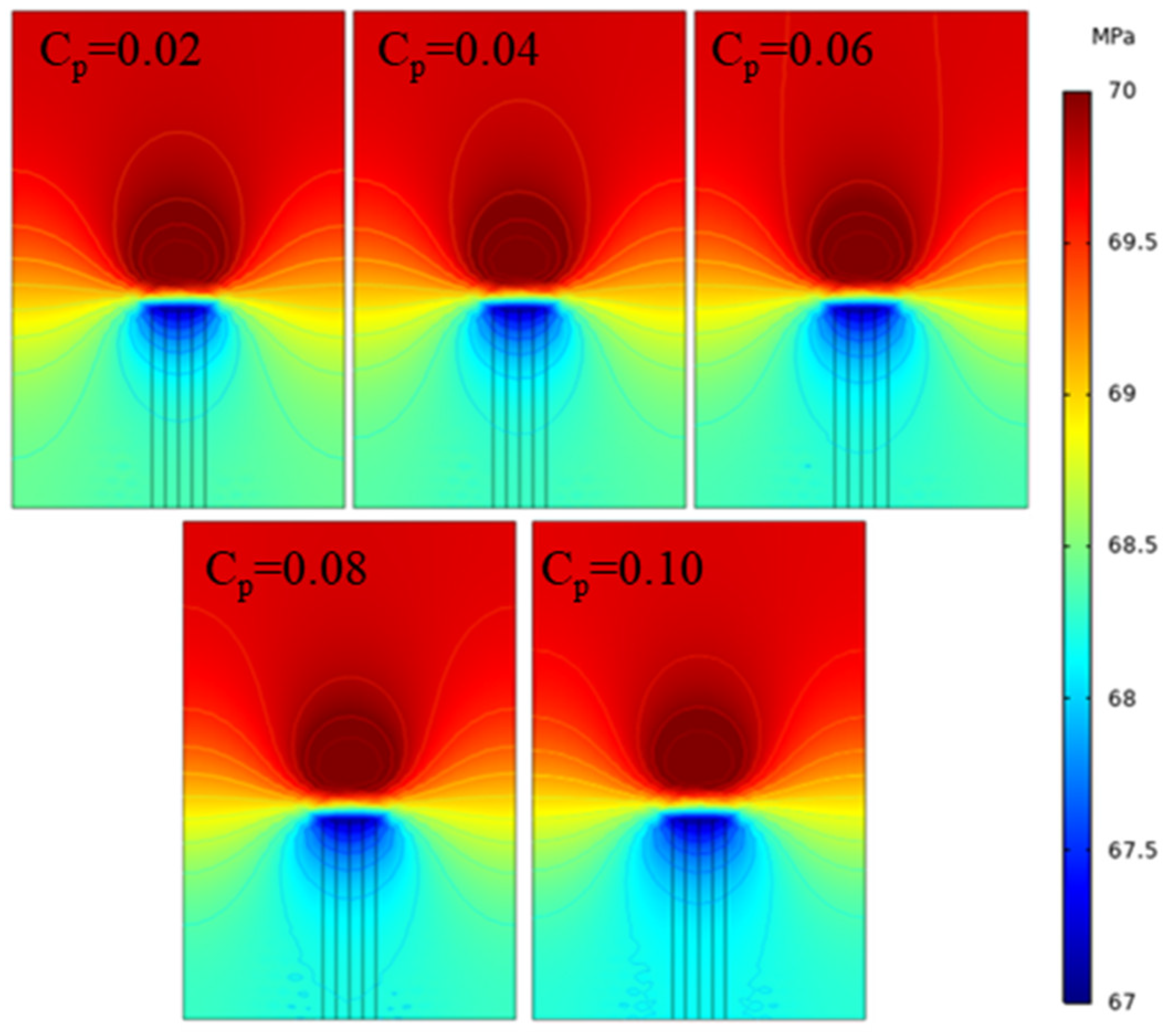
4.3. Compression Coefficient of Main and Secondary Fracture
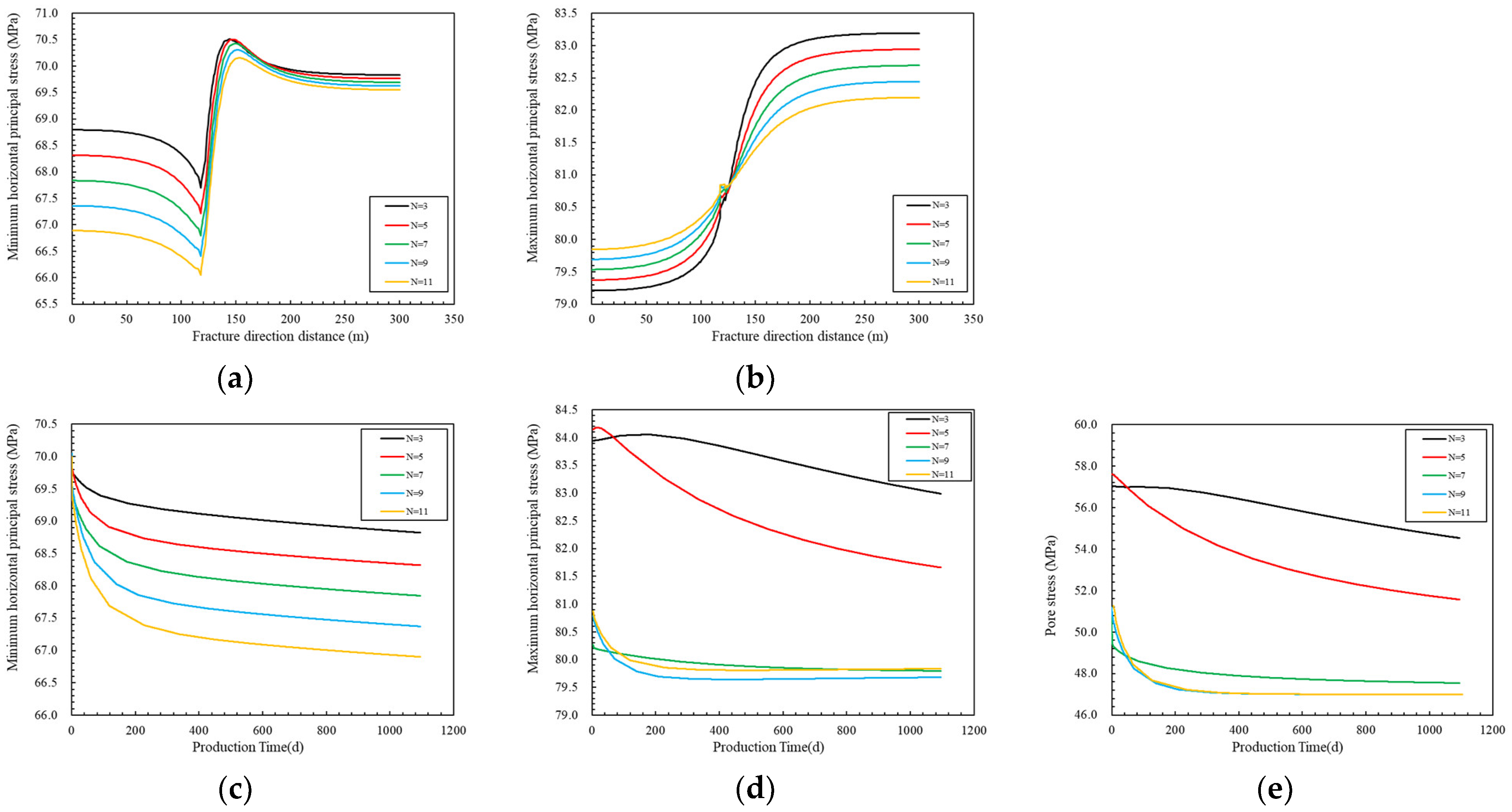
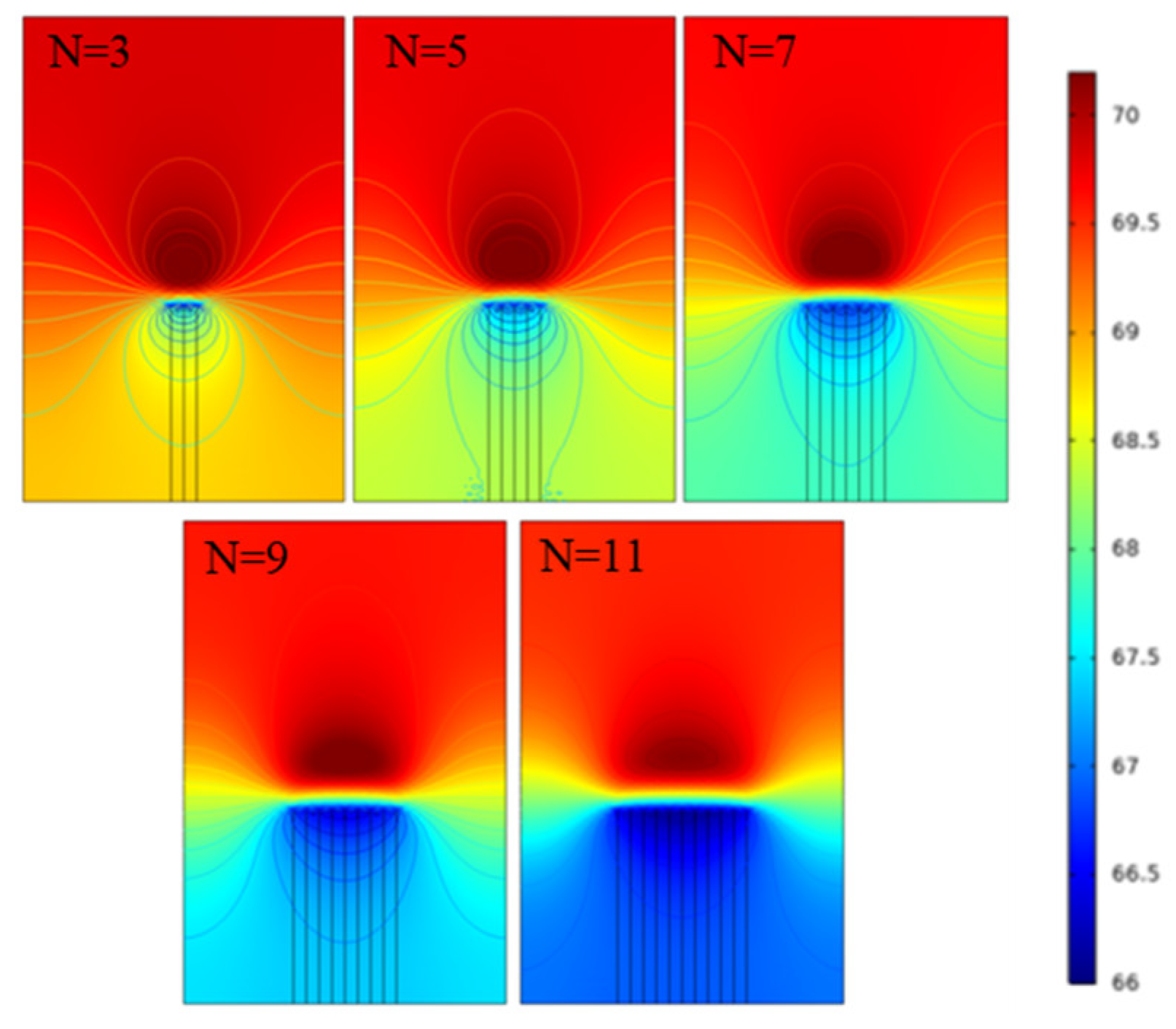
4.4. Number of Main Fracture
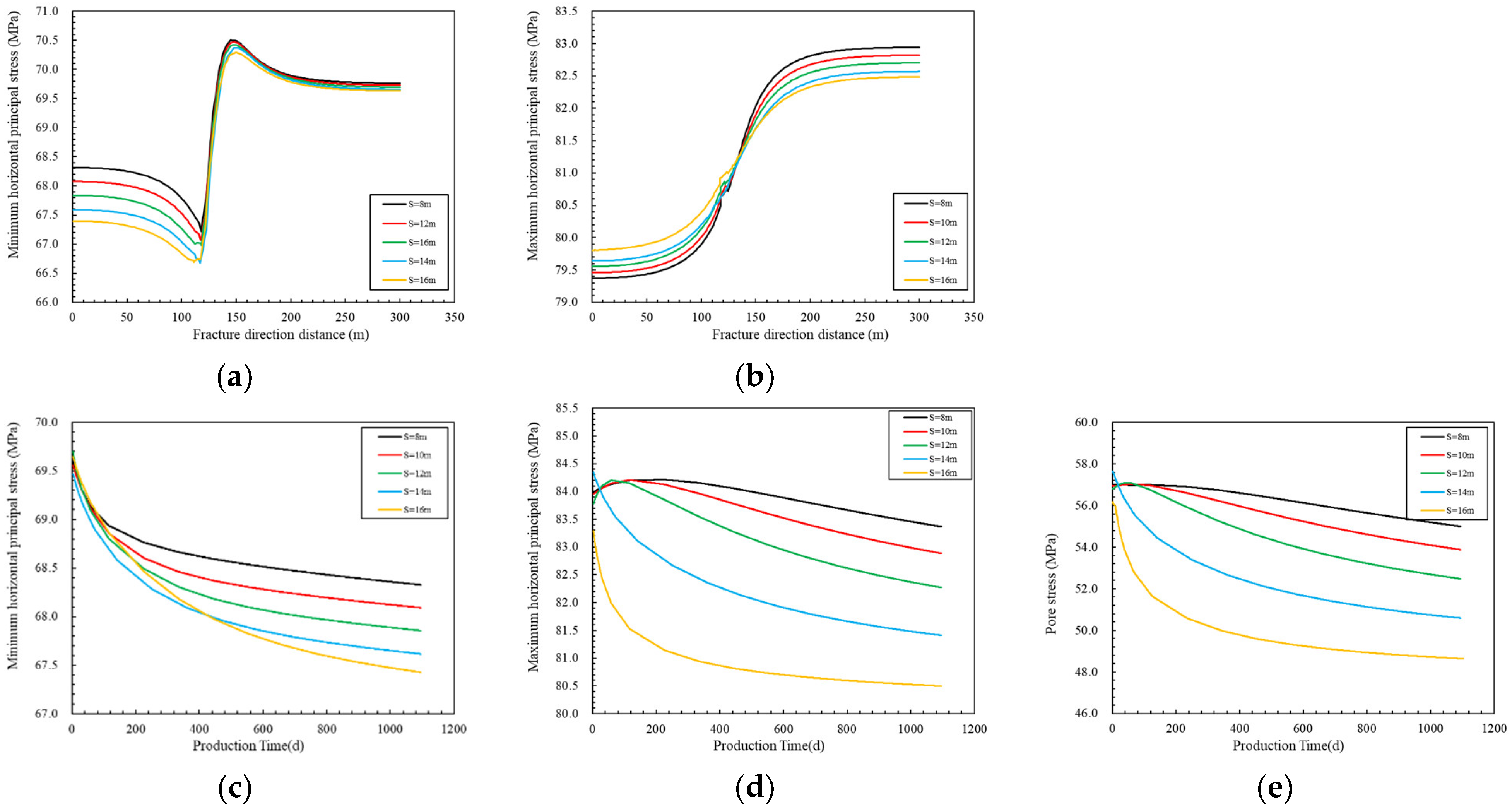
4.5. Main Fracture Spacing
4.6. Main Fracture Length
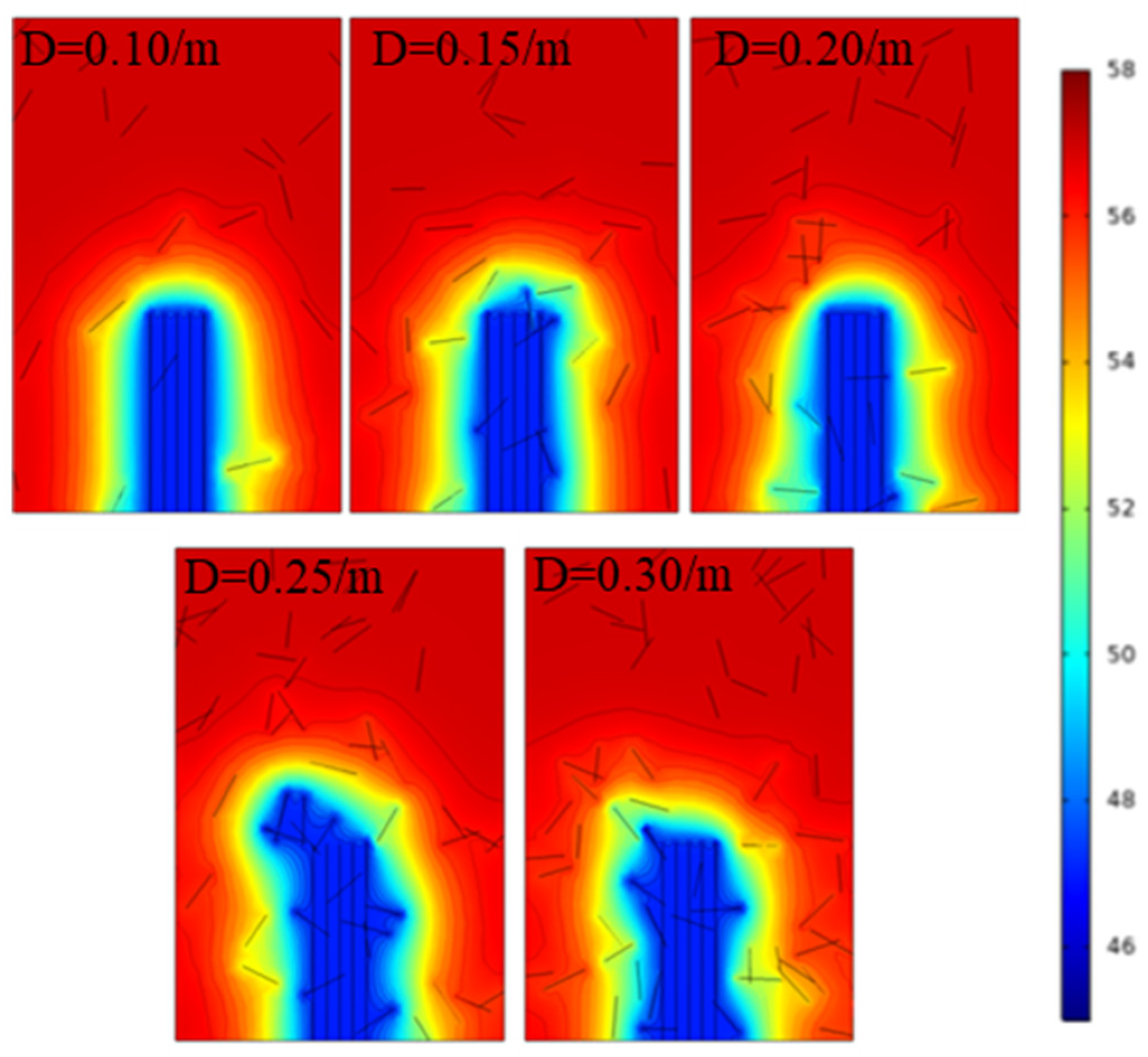
4.7. Natural Fracture Density
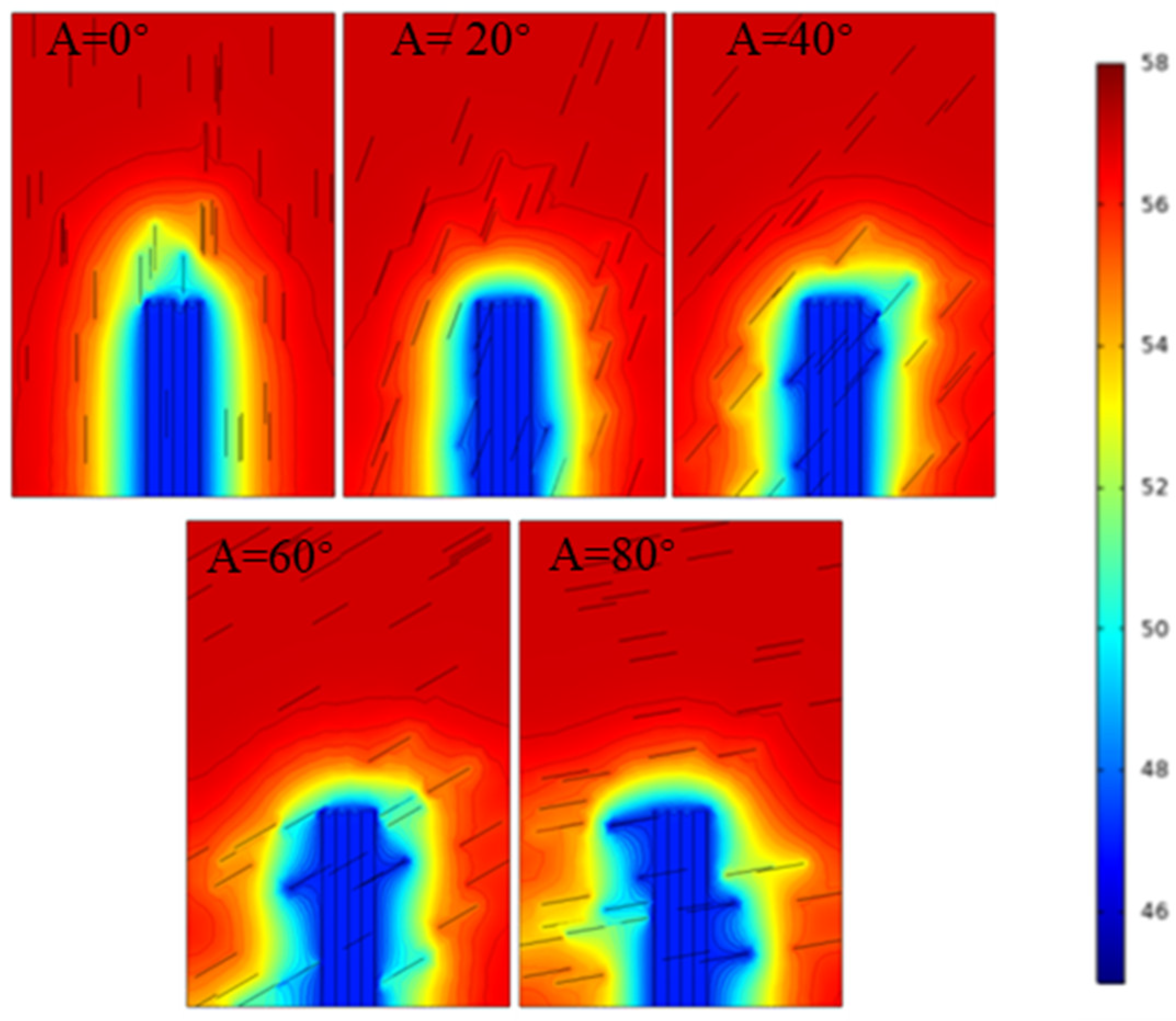
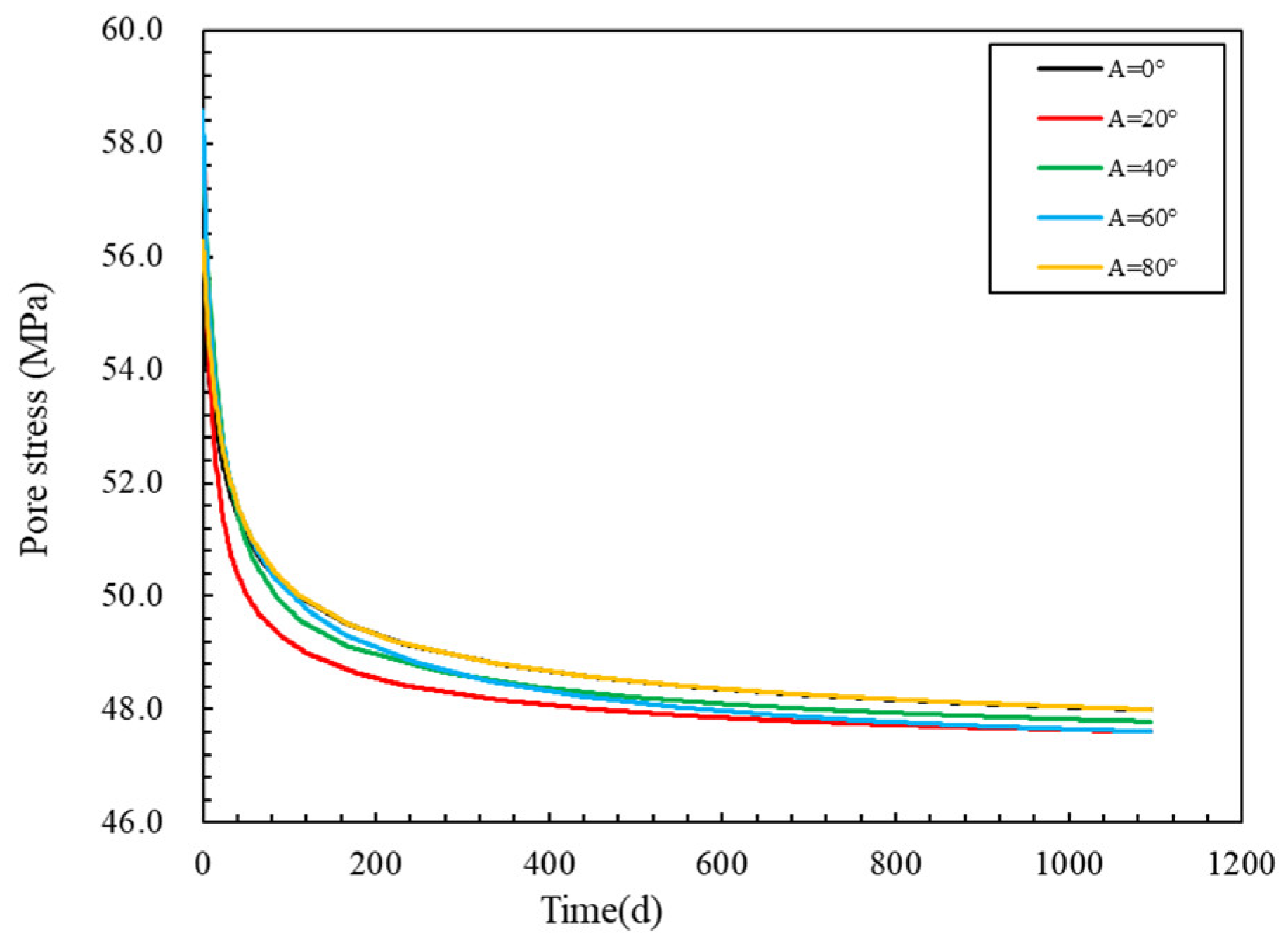
4.8. Natural Fracture Angle
5. Conclusions and Recommendations
- For low-permeability reservoirs, multi-stage stress sensitivity has a relatively low impact on reservoir stress. As the stress sensitivity coefficients of matrix porosity and matrix permeability increase, the minimum horizontal principal stress value in the entire fracture length direction decreases within the range of 0.27%, the low stress area increases, and the high stress area decreases. With the change of the fracture compression coefficient, the principal stress changes within 0.001 MPa, and the stress distribution pattern does not significantly change.
- The main fracture parameters have a significant impact on the stress field. As the number, spacing, and length of the main fractures change, the main stress varies within the range of 2.85%, 1.36%, and 0.83%, respectively. The number, spacing, and size of the main fractures show a negative correlation, while the length of the main fractures shows a negative correlation.
- Random natural fractures have a significant impact on pore pressure, with the density of natural fractures increasing from 0.1 to 0.3, resulting in a decrease of 3.32% in pore pressure and a significant increase in the diffusion area of pore pressure. As the angle between natural fractures increases, it is easier to communicate with the reservoir on both sides of the fracture.
- This type of reservoir should pay more attention to the impact of perforation spacing, perforation cluster number, construction displacement, and natural fracture conditions on the stress field.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jia, A.; Wei, Y.; Guo, Z.; Wang, G.; Meng, D.; Huang, S. Development status and prospect of tight sandstone gas in China. Nat. Gas Ind. B 2022, 9, 467–476. [Google Scholar] [CrossRef]
- Gakhar, K.; Shan, D.; Rodionov, Y.; Malpani, R.; Ejofodomi, E.A.; Xu, J.; Fisher, K.; Fischer, K.; Morales, A.; Pope, T.L. Engineered Approach for Multi-Well Pad Development in Eagle Ford Shale. In Proceedings of the Unconventional Resources Technology Conference, San Antonio, TX, USA, 1–3 August 2016. [Google Scholar]
- Niu, G.; Sun, J.; Parsegov, S.; Schechter, D. Integration of Core Analysis, Pumping Schedule and Microseismicity to Reduce Uncertainties of Production Performance of Complex Fracture Networks for Multi-Stage Hydraulically Fractured Reservoirs. In Proceedings of the SPE Eastern Regional Meeting, Lexington, KY, USA, 4–6 October 2017. [Google Scholar]
- Miller, G.; Lindsay, G.; Baihly, J.; Xu, T. Parent Well Refracturing: Economic Safety Nets in an Uneconomic Market. In Proceedings of the SPE Low Perm Symposium, Denver, CO, USA, 5–6 May 2016. [Google Scholar]
- He, Y.; Guo, J.; Tang, Y.; Xu, J.; Li, Y.; Wang, Y.; Lu, Q.; Patil, S.; Rui, Z.; Sepehrnoori, K. Interwell Fracturing Interference Evaluation of Multi-Well Pads in Shale Gas Reservoirs: A Case Study in WY Basin. In Proceedings of the SPE Annual Technical Conference and Exhibition, Virtual, 26–29 October 2020. [Google Scholar]
- Liu, H.; Lan, Z.; Zhang, G. Evaluation of Refracure Reorientation in Both Laboratory and Field Scales. In Proceedings of the 2008 SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, USA, 13–15 February 2008. [Google Scholar]
- Zhang, G.Z.G.; Chen, M.C.M. Dynamic fracture propagation in hydraulic re-fracturing. J. Petrol. Sci. Eng. 2010, 70, 266–272. [Google Scholar] [CrossRef]
- Mortazavi, A.; Atapour, H. An experimental study of stress changes induced by reservoir depletion under true triaxial stress loading conditions. J. Petrol. Sci. Eng. 2018, 171, 1366–1377. [Google Scholar] [CrossRef]
- Elliott, I.N.S.A. The opening of a Griffith Crack under internal pressure. Quart. Appl. Math. 1946, 262–267. [Google Scholar]
- Sneddon, I.N. The Distribution of Stress in the Neighbourhood of a Crack in an Elastic Solid. Proc. R. Soc. A Math. Phys. Eng. Sci. 1946, 229–260. [Google Scholar]
- Palmer, I.D. Induced Stresses Due to Propped Hydraulic Fracture in Coalbed Methane Wells. In Proceedings of the Low Permeability Reservoirs Symposium, Denver, CO, USA, 26–28 April 1993. [Google Scholar]
- Zhai, Z.; Sharma, M.M. Estimatina Fracture Reorientation due to Fluid Injection/Production. In Proceedings of the SPE Production and Operations Symposium 2007, Oklahoma City, OK, USA, 31 March–3 April 2007. [Google Scholar]
- Guan, B.A.S.C.; Li, S.A.; Liu, J.A.; Zhang, L.A.; Chen, S.A. Analysis and optimization of multiple factors influencing fracturing induced stress field. J. Pet. Explor. Prod. Technol. 2020, 10, 171–181. [Google Scholar] [CrossRef]
- Jia, L.; Peng, S.; Wu, B.; Xu, J.; Yan, F.; Li, Q.; Chen, Y. Research on Quantitative Characterization of 3D Fractures Induced by Hydraulic Fracturing: Insights from Experimental Analysis and Mathematical Models. Rock Mech. Rock Eng. 2023, 57, 1997–2016. [Google Scholar] [CrossRef]
- Liu, E.; Yao, T.; Qiao, L.; Li, J.; Wang, H.; Gao, Q. Research on the propagation mechanism of hydraulic fractures in infill horizontal wells. Front. Earth Sci. 2022, 10, 1026551. [Google Scholar] [CrossRef]
- Bajestani, B.M.; Osouli, A. Effect of Hydraulic Fracture and Natural Fractures Interaction in Fracture Propagation. In Proceedings of the 13th ISRM International Congress of Rock Mechanics, Montreal, QC, Canada, 10–13 May 2015. [Google Scholar]
- Hu, Y.; Gan, Q.; Hurst, A.; Elsworth, D. Hydraulic fracture propagation and interaction with natural fractures by coupled hydro-mechanical modeling. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 1–26. [Google Scholar] [CrossRef]
- Shakib, J.T. RETRACTED: Numerical modeling of hydraulic fracture propagation: Accounting for the effect of stresses on the interaction between hydraulic and parallel natural fractures. Egypt. J. Pet. 2015, 231, 557–563. [Google Scholar] [CrossRef]
- Li, X.L.X.; Wang, J.W.J.; Elsworth, D.E.D. Stress redistribution and fracture propagation during restimulation of gas shale reservoirs. J. Petrol. Sci. Eng. 2017, 154, 150–160. [Google Scholar] [CrossRef]
- Saberhosseini, S.E.E.S. Optimization of the horizontal-well multiple hydraulic fracturing operation in a low-permeability carbonate reservoir using fully coupled XFEM model. Int. J. Rock Mech. Min. Sci. 2019, 114, 33–45. [Google Scholar] [CrossRef]
- Mu, S.; Liu, Y.; Lu, Q.; Guo, J.; Yu, H. Numerical simulation of fracture propagation in child wells considering dual-stress field. Eur. J. Environ. Civ. Eng. 2024, 28, 1–17. [Google Scholar] [CrossRef]
- Mu, S.; Liu, Y.; Wen, Z.; Liu, H.; Guo, J.; Yu, H. Analysis on refracturing of deep fractured sandstone gas well with set production in Tarim Basin. Pet. Sci. Technol. 2023, 42, 1–27. [Google Scholar] [CrossRef]









| Basic Parameter | Value |
|---|---|
| Initial matrix permeability (mD) | 50 |
| Poisson’s ratio | 0.22 |
| Bottom-hole pressure (MPa) | 47 |
| Original formation pressure (MPa) | 57 |
| Cluster count | 5 |
| Primary fracture length (m) | 120 |
| Primary fracture initial conductivity (Dc.cm) | 1 |
| Primary fracture compressibility coefficient (1/Pa) | 8.00 × 10−9 |
| Number of secondary fractures | 8 |
| Secondary fractures initial conductivity (Dc.cm) | 0.1 |
| Secondary fractures compressibility coefficient (1/Pa) | 3.00 × 10−8 |
| Compressibility coefficient (GPa) | 21 |
| Biot coefficient | 0.7 |
| Maximum horizontal principal stress (MPa) | 83.8 |
| Minimum horizontal principal stress (MPa) | 70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, M.; Zhao, Q.; Qi, J.; Zhou, J.; Fan, G.; Liu, Y. Dynamic Evolution Law of Production Stress Field in Fractured Tight Sandstone Horizontal Wells Considering Stress Sensitivity of Multiple Media. Processes 2024, 12, 1652. https://doi.org/10.3390/pr12081652
Yao M, Zhao Q, Qi J, Zhou J, Fan G, Liu Y. Dynamic Evolution Law of Production Stress Field in Fractured Tight Sandstone Horizontal Wells Considering Stress Sensitivity of Multiple Media. Processes. 2024; 12(8):1652. https://doi.org/10.3390/pr12081652
Chicago/Turabian StyleYao, Maotang, Qiangqiang Zhao, Jun Qi, Jianping Zhou, Gaojie Fan, and Yuxuan Liu. 2024. "Dynamic Evolution Law of Production Stress Field in Fractured Tight Sandstone Horizontal Wells Considering Stress Sensitivity of Multiple Media" Processes 12, no. 8: 1652. https://doi.org/10.3390/pr12081652
APA StyleYao, M., Zhao, Q., Qi, J., Zhou, J., Fan, G., & Liu, Y. (2024). Dynamic Evolution Law of Production Stress Field in Fractured Tight Sandstone Horizontal Wells Considering Stress Sensitivity of Multiple Media. Processes, 12(8), 1652. https://doi.org/10.3390/pr12081652







