Abstract
Accurate identification of lithology in petroleum engineering is very important for oil and gas reservoir evaluation, drilling decisions, and petroleum geological exploration. Using a cross-plot to identify lithology only considers two logging parameters, causing the accuracy of lithology identification to be insufficient. With the continuous development of artificial intelligence technology, machine learning has become an important means to identify lithology. In this study, the cutting logging data of the Junggar Basin were collected as lithologic samples, and the identification of argillaceous siltstone, mudstone, gravel mudstone, silty mudstone, and siltstone was established by logging and logging parameters at corresponding depths. Aiming at the non-equilibrium problem of lithologic data, this paper proposes using equilibrium accuracy to evaluate the model. In this study, manifold learning is used to reduce logging and logging parameters to three dimensions. Based on balance accuracy, four dimensionality reductions including isometric feature mapping (ISOMAP), principal component (PCA), independent component (ICA), and non-negative matrix factorization (NMF) are compared. It is found that ISOMAP improves the balance accuracy of the LightGBM model to 0.829, which can effectively deal with unbalanced lithologic data. In addition, the particle swarm optimization (PSO) algorithm is used to automatically optimize the super-parameters of the lightweight gradient hoist (LightGBM) model, which effectively improves the balance accuracy and generalization ability of the lithology identification model and provides strong support for fast and accurate lithology identification.
1. Introduction
In the process of petroleum exploration, lithology identification plays a key role in decision-making and risk management in the petroleum engineering industry [1]. Accurate identification of rock properties helps engineers evaluate the quality of a reservoir and reservoir capacity determination, select well locations and drilling design schemes, optimize reservoirs and production, and assess geological risks [2]. In addition, lithologic identification also reveals that the change in and evolution of the sedimentary environment are of great significance to the study and prediction of the oil and gas accumulation mechanism.
Traditional lithology identification methods mainly rely on cutting logging, drilling coring, and logging data interpretation. Cutting logging is a method of collecting cutting samples during drilling and conducting on-site or laboratory analysis. The identification effect of this technology is highly dependent on the experience and quality of the logging personnel; it is easily affected by subjective factors, and the reliability and consistency of the identification results may be questioned. On the other hand, although drilling coring can provide direct petrophysical and chemical properties, it is time-consuming and expensive, can only sample a limited number of wells during the drilling process, and has difficulty reflecting the full lithologic changes in the entire well.
In contrast, log data interpretation is the most commonly used lithology identification technique in traditional methods, which distinguishes different lithologies by drawing a cross-plot and other diagrams among log parameters [3]. This method mainly uses data collected by acoustic logging, resistivity logging, gamma ray logging, and other techniques. However, although this method is widely used in lithology analysis, its accuracy and speed are not satisfactory. Especially when dealing with complex geological structures, traditional logging data interpretation has difficulties in identifying lithology accurately because it usually ignores the complex nonlinear relationship between logging parameters and lithology, resulting in a lack of accuracy in interpretation results.
Machine learning, as a data-driven model, can handle large-scale logging and logging data and effectively integrate different types of multi-source data [4]. These data are massive and complex, and traditional manual interpretation methods are often inefficient. A data-driven model can process and analyze these data efficiently, extract the potential lithology information, and find the patterns and correlations in logging and logging data more easily for lithology identification. In addition, compared with traditional manual interpretation methods, data-driven models have the advantages of automation and efficiency. New logging and logging data can be processed and analyzed quickly, and the efficiency of lithology identification can be improved [5]. Therefore, data-driven models have important applications and advantages in lithology identification, and many researchers have applied machine learning algorithms in lithology identification [6]. Sun et al. improved the Extreme Gradient Boosting model using a Bayesian optimization algorithm, which enhanced the accuracy of the model in lithology identification [7]. Singh et al. propose an algorithm that combines unsupervised and supervised learning to automate traditional workflows for logging processing and classification, increasing the accuracy of lithology identification from 70% to 90% [8]. Xie et al. compared the predictive performance of various algorithms including Naive Bayes, Support Vector Machine (SVM), Artificial Neural Network (ANN), Random Forest (RF), and Gradient Boosting Decision Tree (GBDT) in lithology identification, and they found that ensemble learning algorithms such as GBDT and RF outperformed the other algorithms [9]. Liang et al. developed a lithology identification model based on mechanical energy ratio parameters and improved the accuracy of lithology identification by optimizing the Support Vector Machine (SVM) algorithm using simulated annealing. The algorithm achieved a prediction accuracy of over 90% for lithology samples [10].
Because noise data are present in logging and logging data, each characteristic datum itself has a collinear relationship. Therefore, the data preprocessing stage helps eliminate noise, redundancy, and outliers in the data. ISOMAP, a manifold learning method, filters out noise points by mapping the data into a low-dimensional manifold space [11]. In addition, ISOMAP can achieve nonlinear dimensionality reduction. Four dimensionality reduction methods are compared in Table 1. Based on the nonlinear characteristics of logging and logging data, ISOMAP is preliminarily judged to be a suitable dimensionality reduction method. This feature extraction method reduces redundant information, retains important data structures and trends, and maps high-dimensional data to low-dimensional space, thus facilitating visualization and understanding of the structure of datasets.

Table 1.
Comparison of four dimensionality reduction methods.
Particle swarm optimization (PSO) is a global optimization technique widely used in various optimization problems, especially for hyperparameter adjustment of machine learning models. The performance of machine learning models, especially advanced models such as LightGBM, relies heavily on precise hyperparameter settings. The traditional method of manually adjusting hyperparameters is not only time-consuming and inefficient, but it also has difficulty in achieving global optimization. The PSO algorithm simulates the social behavior of birds in nature and seeks the optimal solution through group cooperation, which greatly improves the efficiency and effect of the parameter search.
To sum up, ISOMAP was used in this study to reduce the dimension of logging and logging data, extract 3D features, and visualize the spatial relationship with different lithologies. Then, a combined method of ISOMAP with the particle swarm optimization (PSO) algorithm and LightGBM, a lightweight gradient boosting machine, was established. It was compared with linear dimensionality reduction methods such as principal component analysis (PCA), independent component analysis (ICA), and non-negative matrix factorization (NMF) to select the optimal intelligent lithology identification model. In addition, to address the issue of imbalanced lithology samples, this study proposes using balanced accuracy as the evaluation metric for the lithology model. Compared with the accuracy metric, the balanced accuracy metric enables fast and accurate classification of imbalanced lithology data.
2. Research Technique
2.1. Equal Metric Mapping
The Isometric Mapping (ISOMAP) algorithm is an improved feature extraction method based on Multidimensional Scaling (MDS), which maps high-dimensional data on a nonlinear surface to a lower-dimensional space [12]. Unlike MDS, which uses Euclidean distance to compute the distance matrix of inputs, ISOMAP is based on geodesic distance calculation for the distance matrix. Calculating the distance among data points in high-dimensional space cannot be simply achieved through Euclidean distance. Instead, using geodesic distance can better reflect the intrinsic relationships among data points and uncover low-dimensional information [13].
Let the high-dimensional dataset be ; after dimensionality reduction, it is The basic flow of the ISOMAP algorithm is as follows:
- (1)
- Construct the neighborhood graph G for high-dimensional data points using the k-nearest neighbor method.
- (2)
- Calculate the geodesic distance matrix DG between high-dimensional data points, represent the geodesic distance dG (xi, xj) by the shortest path between xi and xj on the graph G, and obtain the geodesic distance matrix DG as follows:
- (3)
- Compute the low-dimensional embedding of high-dimensional data. Substitute the geodesic distance matrix DG into the MDS algorithm, and calculate the centered inner product matrix of the constructed original matrix X using Equation (2):where I is the n-order identity matrix and l is the n-dimensional unit column vector.
- (4)
- Compute the reduced-dimensional data Y. Let Λ be a diagonal matrix constructed from the d largest eigenvalues of matrix B, and let a = (a1, a2, ..., ad), where a1, a2, ..., ad are the corresponding eigenvectors of the eigenvalues. The output Y after dimensionality reduction is given by:
2.2. Particle Swarm Optimization Algorithm
Particle swarm optimization (PSO) algorithm is an optimization algorithm based on population search, inspired by the foraging behavior of birds [14]. When foraging, bird flocks compare their own positions and flight speeds with those of their companions to find the optimal flight route to obtain food [15]. The search principle of the algorithm is illustrated in Figure 1. This algorithm has the advantages of fast convergence speed, few parameters, and easy implementation, allowing it to obtain the optimal solution of the model in a relatively small number of attempts.
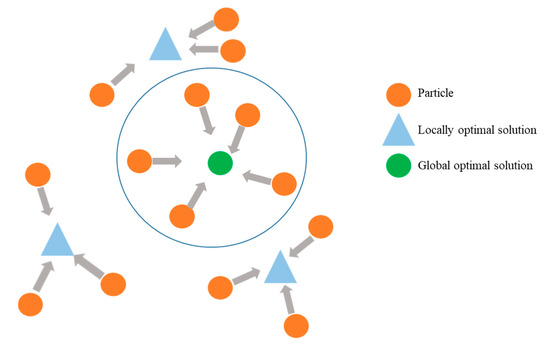
Figure 1.
Search principle of the particle swarm optimization algorithm.
The basic idea of the particle swarm optimization (PSO) algorithm is to treat a problem as a search problem in a multi-dimensional space, where each solution can be seen as a particle in the space. Each particle has a position and velocity, and the algorithm continuously updates the position and velocity of particles to search for the optimal solution [16]. Each swarm consists of N particles randomly initialized in a D-dimensional search space. During the search process, each particle i is represented by a velocity vector v and a position vector X. The update of Vi is given by Equation (4), and the update of Xi is given by Equation (5):
where and represent the velocity and position of the ith particle in the dth dimension at the tth iteration. represents the best position found by the ith particle in the dth dimension at the tth iteration, and represents the best position found by the entire swarm at the tth iteration. is the inertia weight, c1 and c2 are acceleration coefficients, and r1 and r2 are random numbers between 0 and 1.
The update of each particle’s personal best position and the global best position in each iteration is given by Equations (6) and (7), respectively:
where f represents the objective function to be optimized, and for the purpose of minimizing the function, the personal best position and global best position of each particle are updated.
2.3. Lightweight Gradient Hoist
LightGBM is an integrated learning method based on decision trees. Its workflow is shown in Figure 2. It adopts gradient lifting technology to combine multiple decision trees into a powerful integrated model [17]. LightGBM supports efficient parallel training and has the advantages of faster training speed, lower memory consumption, better accuracy, distributed support, and fast processing of massive data [18]. In order to speed up training without compromising accuracy, LightGBM has the following specific improvements:
- (1)
- LightGBM incorporates a histogram-based decision tree algorithm. When traversing the data, it accumulates statistical quantities in histograms based on the discretized values, and after one pass of data, it searches for the optimal split point based on the discrete values in the histograms.
- (2)
- LightGBM incorporates histogram differencing acceleration. The histogram of a leaf node can be obtained by subtracting the histograms of its parent node and its sibling node, which can double the speed of computation.
- (3)
- LightGBM incorporates a Leaf-wise algorithm with a depth constraint. It discards the commonly used level-wise growth strategy in most gradient boosting algorithms, which is relatively inefficient as it searches and splits the nodes in the same level without distinction [19]. Instead, LightGBM uses a Leaf-wise growth algorithm with a depth constraint, which accelerates the computation speed and prevents overfitting.
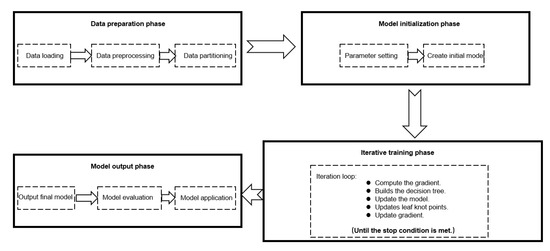
Figure 2.
Lightweight gradient elevator workflow.
3. Experimental Data and Processing
3.1. Data Collection
The lithology data for this study were sourced from the cutting logging data of Well DaFeng-1 in the Junggar Basin. The collected lithologies include siltstone, mudstone, conglomerate mudstone, silty mudstone, and sandstone. In addition, eight logging data features, including weight on bit (WOB), revolutions per minute (RPM), input density (ID), input temperature (IT), input conductivity (IC), acoustic travel time (AC), natural gamma (GR), and well diameter (CAL), were collected at depths corresponding to each lithology label. Outliers in some lithology samples were removed using box plots, resulting in a final dataset of 1278 lithology samples. The sample counts for different lithologies are shown in Figure 3. Additionally, 80% of the samples were randomly selected as the training set, while the remaining 20% were used as the test set.
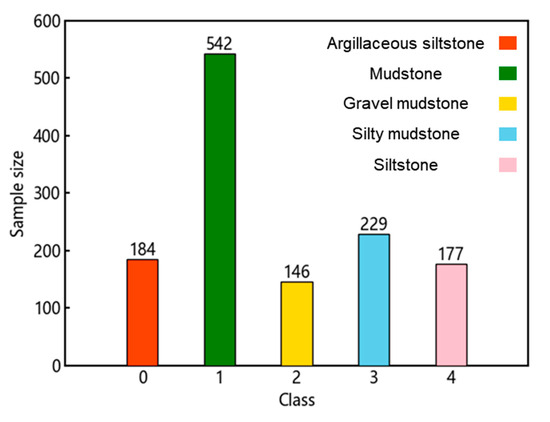
Figure 3.
Comparison of the sample numbers of different lithologies.
Before building the lithology recognition model, it was necessary to convert the rock categories into numerical values for machine learning identification and training. Conventional machine learning models typically require one-hot encoding to ensure spatial distance consistency in all categories before processing classification tasks, but this can lead to computationally complex models. However, since LightGBM uses decision trees as base models, the decision tree algorithm treats numerical values as categorical symbols without any ordinal relationship, thus eliminating the need for one-hot encoding. Therefore, in this study, the labels for argillaceous siltstone, mudstone, gravel mudstone, silty mudstone, and siltstone were set as 0, 1, 2, 3, and 4, respectively.
The cross-plot method reflects the distribution and morphology of different lithologies in the attribute variable space by intersecting the logging and logging data on a plane and can visually demonstrate the discriminative ability of different attribute combinations in the lithology [20]. The two-dimensional cross-plots of logging and logging parameters are shown in Figure 4. It can be observed that only a few lithologies have clear distinctions in the two-dimensional cross-plots, while most lithologies still exhibit significant overlap. Therefore, traditional methods relying on cross-plots are less efficient in distinguishing different lithologies, and further exploration of the nonlinear relationship between multidimensional features and lithology is needed through machine learning algorithms.
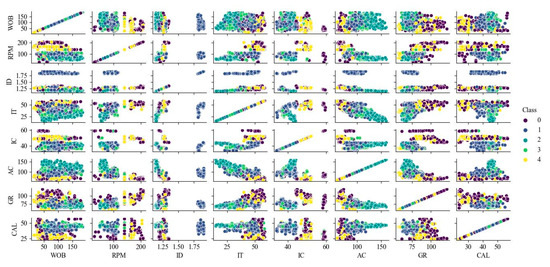
Figure 4.
Two-dimensional cross-plot of logging and logging parameters.
3.2. Feature Extraction
When training machine learning algorithms, attributes with smaller values are easily overshadowed by attributes with larger values. Therefore, it is necessary to normalize the data to unify the scales of the attributes. Additionally, normalizing the data before dimensionality reduction ensures that the feature values are scaled to a similar range, preventing the scale differences among different features from interfering with the dimensionality reduction process. This ensures more reliable and accurate comparisons among features [21]. In this study, the maximum–minimum normalization method was used to scale all features between 0 and 1. The normalization formula is as follows:
where xmin represents the minimum value in the feature samples and xmax represents the maximum value in the feature samples.
In order to map high-dimensional data to a low-dimensional space for visualizing the data while reducing computational complexity, this study set the dimensionality reduction target to three dimensions. By visualizing in a low-dimensional space, more information can be retained compared with one-dimensional and two-dimensional representations. The dimensionality reduction results of ISOMAP, PCA, ICA, and NMF on the training set samples in three-dimensional space are shown in Figure 5. In Figure 4, it can be observed that ISOMAP has distinct differences compared with the other three linear dimensionality reduction methods. PCA, ICA, NMF, and the other methods exhibit a linear distribution in three-dimensional space, where lithology categories are reduced to clustered distributions that surround each other. On the other hand, the dimensionality reduction results of ISOMAP exhibit a nonlinear structure, with an irregular distribution in three-dimensional space, better preserving the local structure and similarity in the data. However, this spatial distribution alone does not directly reflect the effectiveness of dimensionality reduction. It is necessary to compare the classification performance on lithology through training machine learning models.
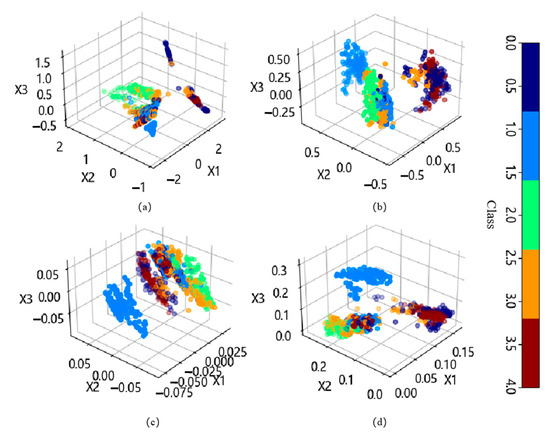
Figure 5.
Three-dimensional visualization of the training set after dimensionality reduction. (a) ISOMAP; (b) PCA; (c) ICA; and (d) NMF.
3.3. Algorithm Parameter Setting
In the PSO algorithm, the parameter ω plays a significant role in the convergence of the algorithm. A higher value of ω leads to a wider range of particle leaps, making it easier to find the global optimum, but it may also result in a loss of local search capability [22]. Typically, the value of ω is set between 0.9 and 1.2, and in this study, it was set to 0.9. The parameters c1 and c2, representing the individual learning factor and social learning factor, are commonly set to 2. Additionally, the maximum number of iterations for the PSO algorithm in this study was set to 100, with a particle count of 10.
The main hyperparameters that affect the performance of the LightGBM algorithm are the number of trees, tree depth, and learning rate. Generally, increasing the number of trees can improve the model’s accuracy. However, increasing the number of decision trees also increases computation time and memory usage. On the other hand, deeper decision trees can capture more complex relationships but may also lead to overfitting. The learning rate controls the impact of each base learner on the final prediction. A smaller learning rate can make the model converge slower but may result in better model performance, while a larger learning rate may prevent the model from converging or lead to overfitting. To ensure a wider range of hyperparameter exploration during model training, this study set the search range for the number of trees, tree depth, and learning rate as [1, 100], [1, 100], and [0, 1], respectively.
The optimization goal of this model is balanced accuracy. The calculation formula of balanced accuracy is as follows:
where xni represents the i-th sample of the n-th class, and xnm represents the m-th correctly recognized sample of the n-th class. The balanced accuracy calculation formula avoids overestimating the performance on imbalanced datasets. Balanced accuracy is equivalent to the macro-average of recall for each class, which is calculated by weighting the original accuracy based on the ratio of true classes for each sample. Therefore, for balanced datasets, the balanced accuracy score is the same as accuracy.
Experimental Flow
The overall workflow of lithology identification is shown in Figure 6. Firstly, logging and cutting data are collected for different lithologies and corresponding depths. Outliers are removed using data processing techniques such as box plots. The entire dataset is then divided into training and testing data, and the input features are normalized before applying ISOMAP for dimensionality reduction. Finally, the PSO algorithm is used to automatically optimize the hyperparameters of the LGBM model during the training process, and the best lithology identification model is selected based on balanced accuracy.
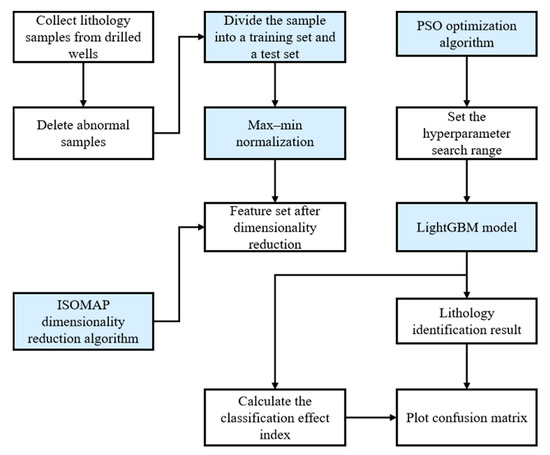
Figure 6.
The whole process of lithology identification.
4. Results and Discussion
4.1. Parameter Optimization
The paper utilized a computer operating system of Windows 10,64-bit, and the development tool used was Python 3.9.7. Since ISOMAP has a parameter k that determines the connectivity among data points, it is important to choose an appropriate value for k. A smaller value of k preserves more local structure but may ignore the global structure, while a larger value of k may introduce noise or unrelated data points into the manifold. This study compared the balanced accuracy of ISOMAP with different values of k within the range of [1, 20]. The balanced accuracy after dimensionality reduction with ISOMAP for different values of k is shown in Figure 7. The highest balanced accuracy is achieved when k = 8 in the ISOMAP algorithm for dimensionality reduction. As the value of k increases further, the balanced accuracy starts to decrease. Therefore, this study set k = 8 as the default parameter for ISOMAP. The optimal hyperparameter combination for the LightGBM model, optimized by the PSO algorithm, is 55, 98, and 0.052 in sequential order.
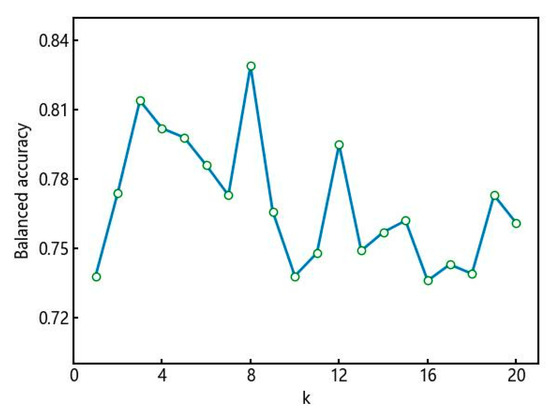
Figure 7.
Balanced accuracy of ISOMAP after dimensionality reduction under different k values.
In addition, this study also tested the balanced accuracy results of three other algorithms including the following: PCA, ICA, and NMF. The iterative optimization process and balanced accuracy comparison of the LightGBM models after dimensionality reduction using these four algorithms are shown in Figure 8 and Figure 9. Among them, ISOMAP and PCA achieved higher balanced accuracies, with values of 0.829 and 0.823, respectively. On the other hand, ICA and NMF had lower balanced accuracies, with values of 0.797 and 0.801, respectively. Therefore, in terms of balanced accuracy, the non-linear dimensionality reduction method ISOMAP outperformed the linear dimensionality reduction methods PCA, ICA, and NMF.
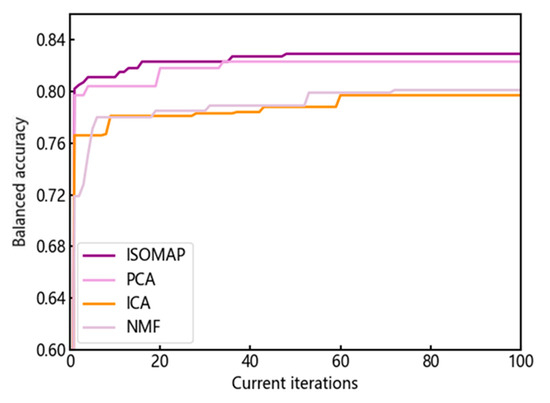
Figure 8.
Iterative optimization of four dimension-reduced LightGBM models by PSO.
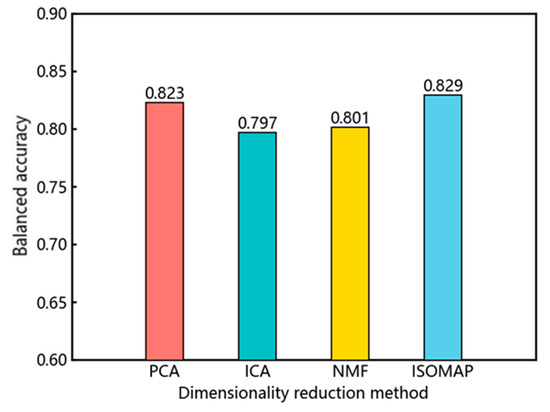
Figure 9.
Balanced accuracy of four dimension-reduced LightGBM models.
4.2. Results
The confusion matrix can provide detailed information about the prediction results of a classification model, including true positives, false negatives, false positives, and true negatives, to evaluate the performance of the model in multi-class tasks. Figure 10 shows the confusion matrix of the LightGBM model based on balanced accuracy. The horizontal axis represents the predicted labels, and the vertical axis represents the actual labels. Each row represents the number of predicted rock types for that specific rock type by the LightGBM model. When optimized based on balanced accuracy, the LightGBM model shows a balanced recognition performance for all rock types in the test set, without significantly low accuracy for any specific rock type.
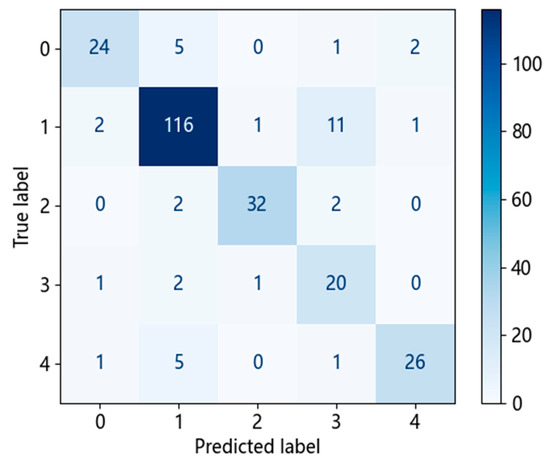
Figure 10.
Confusion matrix based on balanced accuracy in the LightGBM model.
To compare the recognition performance of balanced accuracy and accuracy, this study also optimized the LightGBM model based on accuracy. Figure 11 shows the confusion matrix of the LightGBM model based on accuracy. It can be observed that when optimized based on accuracy, the LightGBM model focuses on recognizing the dominant rock type, which is mudstone with an accuracy of 0.969. However, this model exhibits severe overfitting, with an accuracy of only 0.625 for siltstone, which is a less-represented rock type. Additionally, the error identification samples of this model are also concentrated on mudstone, and the balanced accuracy rate is only 0.805, while the balanced accuracy rate of the above model based on balanced accuracy is 0.829, which is stronger than the comprehensive identification ability of lithology based on balanced accuracy. Therefore, in practical applications, the LightGBM model optimized based on balanced accuracy demonstrates better generalization compared with the model optimized based on accuracy, effectively reducing overfitting on underrepresented rock types.
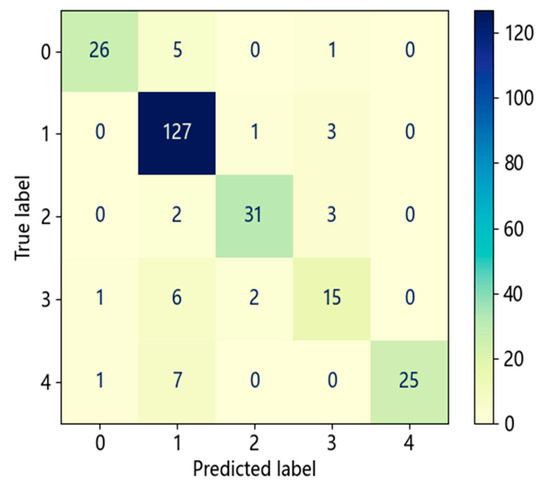
Figure 11.
Confusion matrix based on accuracy in the LightGBM model.
5. Conclusions
- (1)
- Manifold learning methods can map high-dimensional data to a lower-dimensional space, allowing for visualization of well logging and cutting logging data while reducing the complexity of model construction. ISOMAP, as a non-linear dimensionality reduction method, is better able to preserve the local structure and similarity of the data compared with linear dimensionality reduction methods such as PCA, ICA, and NMF. Additionally, when the number of neighbors for ISOMAP is set to eight, the LightGBM model achieves the highest balanced accuracy of 0.829.
- (2)
- Balanced accuracy can handle imbalanced rock type datasets, and the LightGBM model optimized based on balanced accuracy demonstrates more balanced recognition performance across all rock types compared with the model optimized based on accuracy. Balanced accuracy avoids overfitting the LightGBM model towards the majority of mudstone samples, effectively improving the recognition accuracy of minority classes in imbalanced rock-type data.
- (3)
- The PSO algorithm can help the LightGBM model automatically search the hyperparameter space and find the optimal hyperparameter configuration, thereby improving the model’s performance and generalization ability. Future research could explore more efficient optimization strategies or introduce other metaheuristic algorithms, such as genetic algorithms or ant colony optimization, to further enhance parameter tuning efficiency and effectiveness. Additionally, considering ensemble learning techniques such as improved random forests or boosting tree algorithms could enhance the model’s generalization ability to handle complex or noisy datasets. Furthermore, by comparing with advanced machine learning models like deep learning networks, the effectiveness of the methods can be validated and the strengths and weaknesses in processing geological data can be investigated. Moreover, extensive testing of the model on various geological datasets and in actual oil field projects is essential to assess its real-world performance and applicability, thus transforming these technologies into practical geological analysis tools.
Author Contributions
Conceptualization, C.L. (Chaowei Li); Methodology, W.G.; Validation, W.W., C.L. (Changsheng Li) and W.G.; Investigation, H.P.; Resources, G.W. and S.D.; Data curation, G.W. and S.X.; Writing—original draft, S.D.; Writing—review & editing, S.D.; Visualization, S.D.; Supervision, S.D. and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to (signing of confidentiality agreement).
Conflicts of Interest
Authors Guo Wang, Shuguo Xu, Wan Wei, Haolin Zhang and Changsheng Li were employed by the company SINOPEC Research Institute of Petroleum Engineering Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Fu, G.; Yan, J.; Zhang, K.; Hu, H.; Luo, F. Current status and progress of lithology identification technology. Prog. Geophys. 2017, 32, 26–40. [Google Scholar]
- Ren, Q.; Zhang, H.; Zhang, D.; Zhao, X.; Yan, L.; Rui, J.; Zeng, F.; Zhu, X. A framework of active learning and semi-supervised learning for lithology identification based on improved naive Bayes. Expert Syst. Appl. 2022, 202, 117278. [Google Scholar] [CrossRef]
- Xu, T.; Chang, J.; Feng, D.; Lv, W.; Kang, Y.; Liu, H.; Li, J.; Li, Z. Evaluation of active learning algorithms for formation lithology identification. J. Pet. Sci. Eng. 2021, 206, 108999. [Google Scholar] [CrossRef]
- Lin, S.; Han, Z.; Li, D.; Zeng, J.; Yang, X.; Liu, X.; Liu, F. Integrating model-and data-driven methods for synchronous adaptive multi-band image fusion. Inf. Fusion 2020, 54, 145–160. [Google Scholar] [CrossRef]
- Ren, Q.; Zhang, H.; Zhang, D.; Zhao, X. Lithology identification using principal component analysis and particle swarm optimization fuzzy decision tree. J. Pet. Sci. Eng. 2023, 220, 111233. [Google Scholar] [CrossRef]
- Xu, Z.; Ma, W.; Lin, P.; Shi, H.; Pan, D.; Liu, T. Deep learning of rock images for intelligent lithology identification. Comput. Geosci. 2021, 154, 104799. [Google Scholar] [CrossRef]
- Sun, Z.; Jiang, B.; Li, X.; Li, J.; Xiao, K. A data-driven approach for lithology identification based on parameter-optimized ens14emble learning. Energies 2020, 13, 3903. [Google Scholar] [CrossRef]
- Singh, H.; Seol, Y.; Myshakin, E.M. Automated well-log processing and lithology classification by identifying optimal features through unsupervised and supervised machine-learning algorithms. SPE J. 2020, 25, 2778–2800. [Google Scholar] [CrossRef]
- Xie, Y.; Zhu, C.; Zhou, W.; Li, Z.; Liu, X.; Tu, M. Evaluation of machine learning methods for formation lithology identification: A comparison of tuning processes and model performances. J. Pet. Sci. Eng. 2018, 160, 182–193. [Google Scholar] [CrossRef]
- Liang, H.; Chen, H.; Guo, J.; Bai, J.; Jiang, Y. Research on lithology identification method based on mechanical specific energy principle and machine learning theory. Expert Syst. Appl. 2022, 189, 116142. [Google Scholar] [CrossRef]
- Han, X.; Su, J.; Hong, Y.; Gong, P.; Zhu, D. Mid-to Long-Term Electric Load Forecasting Based on the EMD–Isomap–Adaboost Model. Sustainability 2022, 14, 7608. [Google Scholar] [CrossRef]
- Samko, O.; Marshall, A.D.; Rosin, P.L. Selection of the optimal parameter value for the Isomap algorithm. Pattern Recognit. Lett. 2006, 27, 968–979. [Google Scholar] [CrossRef]
- Anowar, F.; Sadaoui, S.; Selim, B. Conceptual and empirical comparison of dimensionality reduction algorithms (pca, kpca, lda, mds, svd, lle, isomap, le, ica, t-sne). Comput. Sci. Rev. 2021, 40, 100378. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Jain, M.; Saihjpal, V.; Singh, N.; Singh, S.B. An overview of variants and advancements of PSO algorithm. Appl. Sci. 2022, 12, 8392. [Google Scholar] [CrossRef]
- Xing, Z.; Zhu, J.; Zhang, Z.; Qin, Y.; Jia, L. Energy consumption optimization of tramway operation based on improved PSO algorithm. Energy 2022, 258, 124848. [Google Scholar] [CrossRef]
- Wang, D.; Li, L.; Zhao, D. Corporate finance risk prediction based on LightGBM. Inf. Sci. 2022, 602, 259–268. [Google Scholar] [CrossRef]
- Liang, W.; Luo, S.; Zhao, G.; Wu, H. Predicting hard rock pillar stability using GBDT, XGBoost, and LightGBM algorithms. Mathematics 2020, 8, 765. [Google Scholar] [CrossRef]
- Li, L.; Liu, Z.; Shen, J.; Wang, F.; Qi, W.; Jeon, S. A LightGBM-based strategy to predict tunnel rockmass class from TBM construction data for building control. Adv. Eng. Inform. 2023, 58, 102130. [Google Scholar] [CrossRef]
- Liu, Z.; Li, D.; Liu, Y.; Yang, B.; Zhang, Z.-X. Prediction of uniaxial compressive strength of rock based on lithology using stacking models. Rock Mech. Bull. 2023, 2, 100081. [Google Scholar] [CrossRef]
- Vafaei, N.; Ribeiro, R.A.; Camarinha-Matos, L.M. Comparison of normalization techniques on data sets with outliers. Int. J. Decis. Support Syst. Technol. (IJDSST) 2022, 14, 1–17. [Google Scholar] [CrossRef]
- Deng, S.; Pan, H.; Wang, H.; Xu, S.-K.; Yan, X.-P.; Li, C.-W.; Peng, M.-G.; Peng, H.-P.; Shi, L.; Cui, M.; et al. A hybrid machine learning optimization algorithm for multivariable pore pressure prediction. Pet. Sci. 2024, 21, 535–550. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).