Pressure Interpolation in Water Distribution Networks by Using Gaussian Processes: Application to Leak Diagnosis
Abstract
1. Introduction
2. Material and Methods
2.1. Foundation of Gaussian Processes
2.2. Pressure Interpolation Using GPR
2.3. Leak Localization
| Algorithm 1: Water Leak Localization in a Distribution Network | |
| Part | 1: Pressure Estimation Using Gaussian Process Regression |
| Inputs: Pressure measurements at specific instrumented nodes, and pipe lengths. Outputs: Estimated pressures at all nodes. | |
| |
| Part | 2: Leak Localization Using Decision Tree Classification |
| Inputs: Estimated node pressures from Part 1. Outputs: Probable locations of leaks. | |
| |
3. Results
3.1. Examples of Leak Isolation under Noise-Free Conditions
3.1.1. Case 1: Leak at Node 24
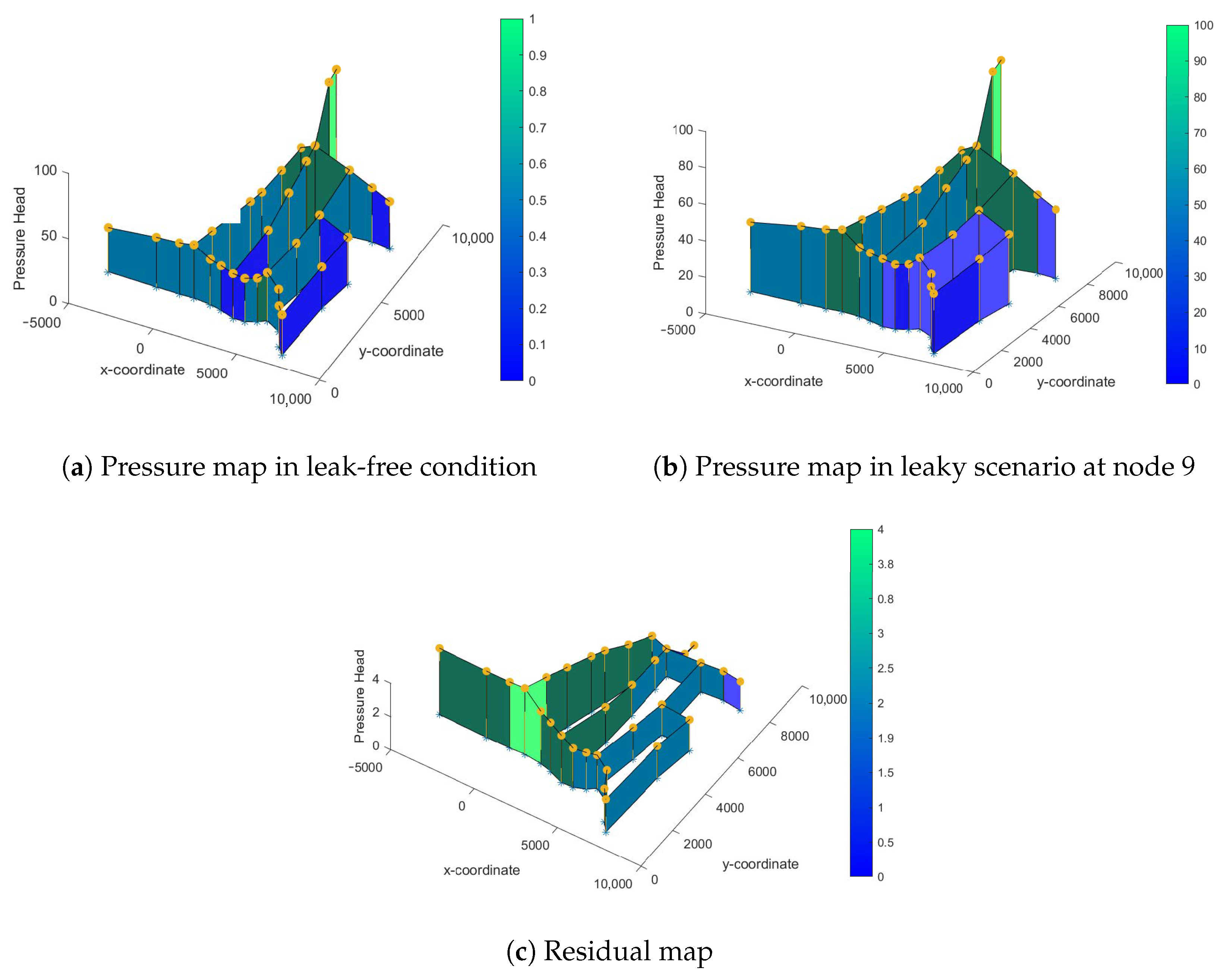
3.1.2. Case 2: Leak at Node 9
3.2. Examples of Leak Diagnosis by Using the Classification Tree Algorithm
3.2.1. Case 1: Leak at Node 4
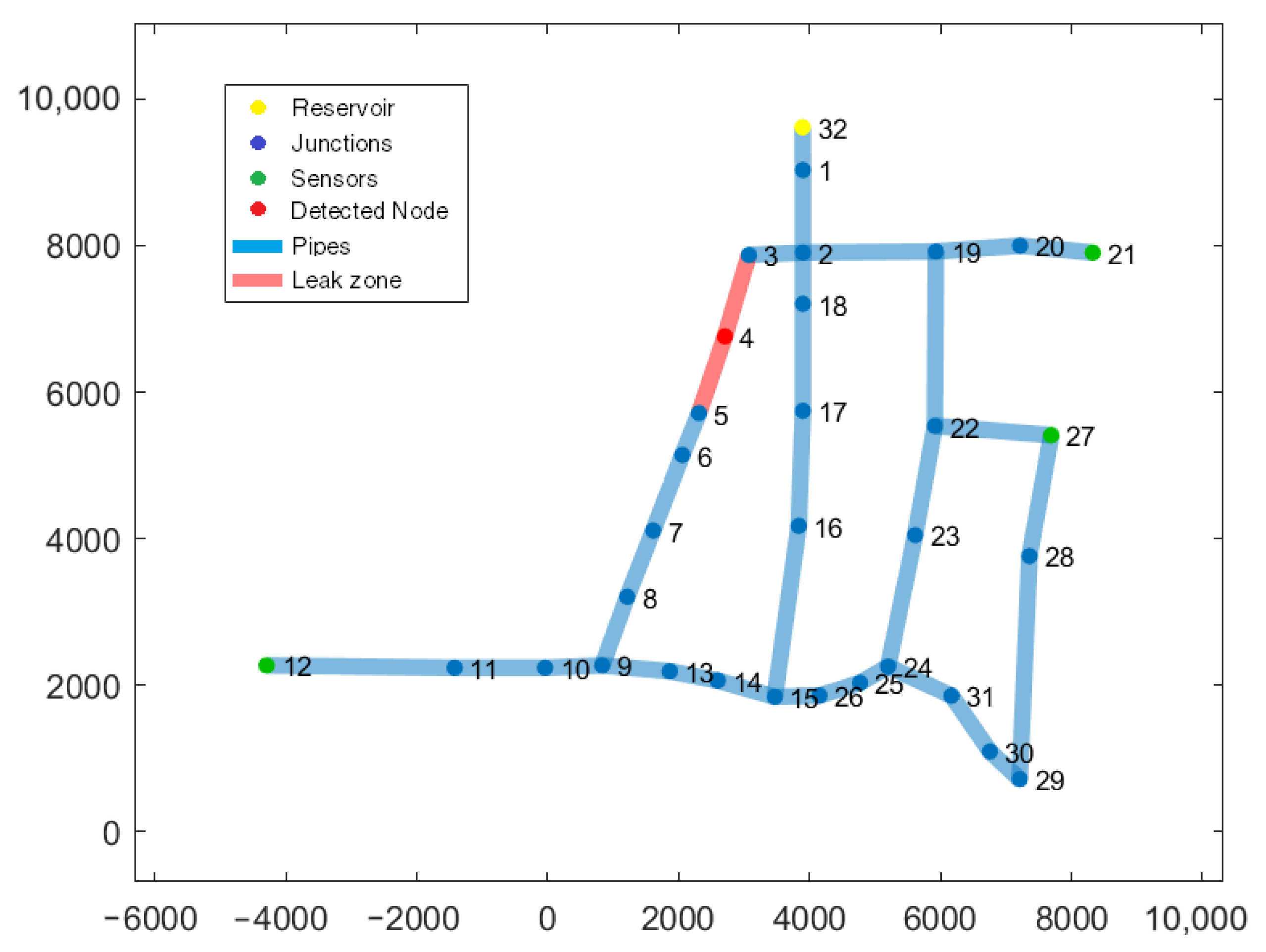
3.2.2. Case 2: Leak at Node 13

3.3. Discussion of the Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reda, A.; Mahmoud, R.M.A.; Shahin, M.A.; Amaechi, C.V.; Sultan, I.A. Roadmap for Recommended Guidelines of Leak Detection of Subsea Pipelines. J. Mar. Sci. Eng. 2024, 12, 675. [Google Scholar] [CrossRef]
- Morales-González, I.; Santos-Ruiz, I.; López-Estrada, F.; Puig, V. Pressure Sensor Placement for Leak Localization Using Simulated Annealing with Hyperparameter Optimization. In Proceedings of the 2021 5th International Conference on Control and Fault-Tolerant Systems (SysTol), Saint-Raphael, France, 9 November 2021; pp. 205–210. [Google Scholar] [CrossRef]
- Santos-Ruiz, I.; López-Estrada, F.R.; Puig, V.; Valencia-Palomo, G.; Hernández, H.R. Pressure Sensor Placement for Leak Localization in Water Distribution Networks Using Information Theory. Sensors 2022, 22, 443. [Google Scholar] [CrossRef]
- Soldevila, A.; Jensen, T.N.; Blesa, J.; Tornil-Sin, S.; Femandez-Canti, R.; Puig, V. Leak localization in water distribution networks using a kriging data-based approach. In Proceedings of the 2018 IEEE Conference on Control Technology and Applications (CCTA), Copenhagen, Denmark, 21–24 August 2018; pp. 577–582. [Google Scholar]
- Javadiha, M.; Blesa, J.; Soldevila, A.; Puig, V. Leak localization in water distribution networks using deep learning. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 1426–1431. [Google Scholar]
- Mankad, J.; Natarajan, B.; Srinivasan, B. Integrated approach for optimal sensor placement and state estimation: A case study on water distribution networks. ISA Trans. 2021, 123, 272–285. [Google Scholar] [CrossRef]
- Wang, S.; Taha, A.F.; Gatsis, N.; Sela, L.; Giacomoni, M.H. Probabilistic state estimation in water networks. IEEE Trans. Control. Syst. Technol. 2021, 30, 507–519. [Google Scholar] [CrossRef]
- Fusco, F.; Arandia, E. State estimation for water distribution networks in the presence of control devices with switching behavior. Procedia Eng. 2017, 186, 592–600. [Google Scholar] [CrossRef]
- Do, N.C.; Simpson, A.R.; Deuerlein, J.W.; Piller, O. Calibration of water demand multipliers in water distribution systems using genetic algorithms. J. Water Resour. Plan. Manag. 2016, 142, 04016044. [Google Scholar] [CrossRef]
- Do, N.; Simpson, A.; Deuerlein, J.; Piller, O. Demand estimation in water distribution systems: Solving underdetermined problems using genetic algorithms. Procedia Eng. 2017, 186, 193–201. [Google Scholar] [CrossRef]
- Meirelles, G.; Manzi, D.; Brentan, B.; Goulart, T.; Luvizotto, E. Calibration model for water distribution network using pressures estimated by artificial neural networks. Water Resour. Manag. 2017, 31, 4339–4351. [Google Scholar] [CrossRef]
- Vrachimis, S.G.; Timotheou, S.; Eliades, D.G.; Polycarpou, M.M. Interval State Estimation of Hydraulics in Water Distribution Networks. In Proceedings of the 2018 European Control Conference (ECC), Limassol, Cyprus, 12–15 June 2018; pp. 2641–2646. [Google Scholar]
- Tshehla, K.S.; Hamam, Y.; Abu-Mahfouz, A.M. State estimation in water distribution network: A review. In Proceedings of the 2017 IEEE 15th International Conference on Industrial Informatics (INDIN), Emden, Germany, 24–26 July 2017; pp. 1247–1252. [Google Scholar]
- Zanfei, A.; Menapace, A.; Santopietro, S.; Righetti, M. Calibration procedure for water distribution systems: Comparison among hydraulic models. Water 2020, 12, 1421. [Google Scholar] [CrossRef]
- Nicolini, M.; Falcomer, L. Genetic Algorithm for Calibration and Leakage Identification in Water Distribution System. In Proceedings of the 2020 3rd IEEE International Conference on Knowledge Innovation and Invention (ICKII), Kaohsiung, Taiwan, 21–23 August 2020; pp. 273–276. [Google Scholar]
- Lučin, I.; Čarija, Z.; Družeta, S.; Lučin, B. Detailed Leak Localization in Water Distribution Networks Using Random Forest Classifier and Pipe Segmentation. IEEE Access 2021, 9, 155113–155122. [Google Scholar] [CrossRef]
- Alves, D.; Blesa, J.; Duviella, E.; Rajaoarisoa, L. Robust Data-Driven Leak Localization in Water Distribution Networks Using Pressure Measurements and Topological Information. Sensors 2021, 21, 7551. [Google Scholar] [CrossRef]
- Predescu, A.; Mocanu, M.; Lupu, C. A modern approach for leak detection in water distribution systems. In Proceedings of the 2018 22nd International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 10–12 October 2018; pp. 486–491. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, X.; Li, Y.; Tie, Y.; Zhang, Y.; Gao, J. Water Pipeline Leakage Detection Based on Machine Learning and Wireless Sensor Networks. Sensors 2019, 19, 5086. [Google Scholar] [CrossRef]
- Ramotsoela, D.T.; Hancke, G.P.; Abu-Mahfouz, A.M. Attack detection in water distribution systems using machine learning. Hum.-Centric Comput. Inf. Sci. 2019, 9, 13. [Google Scholar] [CrossRef]
- Fuentes, V.C.; Pedrasa, J.R.I. Leak detection in water distribution networks via pressure analysis using a machine learning ensemble. In Proceedings of the International Conference on Society with Future: Smart and Liveable Cities, Braga, Portugal, 4–6 December 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 31–44. [Google Scholar]
- Alizadeh, Z.; Yazdi, J.; Mohammadiun, S.; Hewage, K.; Sadiq, R. Evaluation of data driven models for pipe burst prediction in urban water distribution systems. Urban Water J. 2019, 16, 136–145. [Google Scholar] [CrossRef]
- Pasolli, L.; Melgani, F.; Blanzieri, E. Gaussian process regression for estimating chlorophyll concentration in subsurface waters from remote sensing data. IEEE Geosci. Remote Sens. Lett. 2010, 7, 464–468. [Google Scholar] [CrossRef]
- Alghamdi, A.S.; Polat, K.; Alghoson, A.; Alshdadi, A.A.; Abd El-Latif, A.A. Gaussian process regression (GPR) based non-invasive continuous blood pressure prediction method from cuff oscillometric signals. Appl. Acoust. 2020, 164, 107256. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K. Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning); MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Lio, W.H.; Li, A.; Meng, F. Real-time rotor effective wind speed estimation using Gaussian process regression and Kalman filtering. Renew. Energy 2021, 169, 670–686. [Google Scholar] [CrossRef]
- Santos-Ruiz, I.; López-Estrada, F.R.; Puig, V.; Blesa, J. Estimation of Node Pressures in Water Distribution Networks by Gaussian Process Regression. In Proceedings of the 2019 4th Conference on Control and Fault Tolerant Systems (SysTol), Casablanca, Morocco, 18–20 September 2019; pp. 50–55. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Yuan, H.; Hu, J.; Song, Y.; Li, Y.; Du, J. A new exact algorithm for the shortest path problem: An optimized shortest distance matrix. Comput. Ind. Eng. 2021, 158, 107407. [Google Scholar] [CrossRef]
- Bort, C.G.; Righetti, M.; Bertola, P. Methodology for leakage isolation using pressure sensitivity and correlation analysis in water distribution systems. Procedia Eng. 2014, 89, 1561–1568. [Google Scholar] [CrossRef]
- Santos-Ruiz, I.; Blesa, J.; Puig, V.; López-Estrada, F. Leak localization in water distribution networks using classifiers with cosenoidal features. IFAC-PapersOnLine 2020, 53, 16697–16702. [Google Scholar] [CrossRef]
- Loh, W.Y. Regression tress with unbiased variable selection and interaction detection. Stat. Sin. 2002, 12, 361–386. [Google Scholar]
- Coppersmith, D.; Hong, S.J.; Hosking, J.R. Partitioning nominal attributes in decision trees. Data Min. Knowl. Discov. 1999, 3, 197–217. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: London, UK, 2017. [Google Scholar]
- Savic, D.A.; Walters, G.A. Genetic algorithms for least-cost design of water distribution networks. J. Water Resour. Plan. Manag. 1997, 123, 67–77. [Google Scholar] [CrossRef]
- Ayad, A.; Khalifa, A.; Fawy, M.; Moawad, A. An integrated approach for non-revenue water reduction in water distribution networks based on field activities, optimisation, and GIS applications. Ain Shams Eng. J. 2021, 12, 3509–3520. [Google Scholar] [CrossRef]
- Eliades, D.G.; Kyriakou, M.; Vrachimis, S.; Polycarpou, M.M. EPANET-MATLAB Toolkit: An Open-Source Software for Interfacing EPANET with MATLAB. In Proceedings of the 14th International Conference on Computing and Control for the Water Industry (CCWI), Amsterdam, The Netherlands, 7–9 November 2016; p. 8. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET Users Manual; U.S. Environmental Protection Agency: Cincinnati, OH, USA, 1994.
- Paluszek, M.; Thomas, S. MATLAB Machine Learning Toolboxes. In Practical MATLAB Deep Learning; Springer: Berlin/Heidelberg, Germany, 2020; pp. 25–41. [Google Scholar]
- Liu, M.; Chowdhary, G.; Da Silva, B.C.; Liu, S.Y.; How, J.P. Gaussian processes for learning and control: A tutorial with examples. IEEE Control Syst. Mag. 2018, 38, 53–86. [Google Scholar] [CrossRef]
- Santos-Ruiz, I.; Bermúdez, J.; López-Estrada, F.; Puig, V.; Torres, L.; Delgado-Aguiñaga, J. Online leak diagnosis in pipelines using an EKF-based and steady-state mixed approach. Control Eng. Pract. 2018, 81, 55–64. [Google Scholar] [CrossRef]




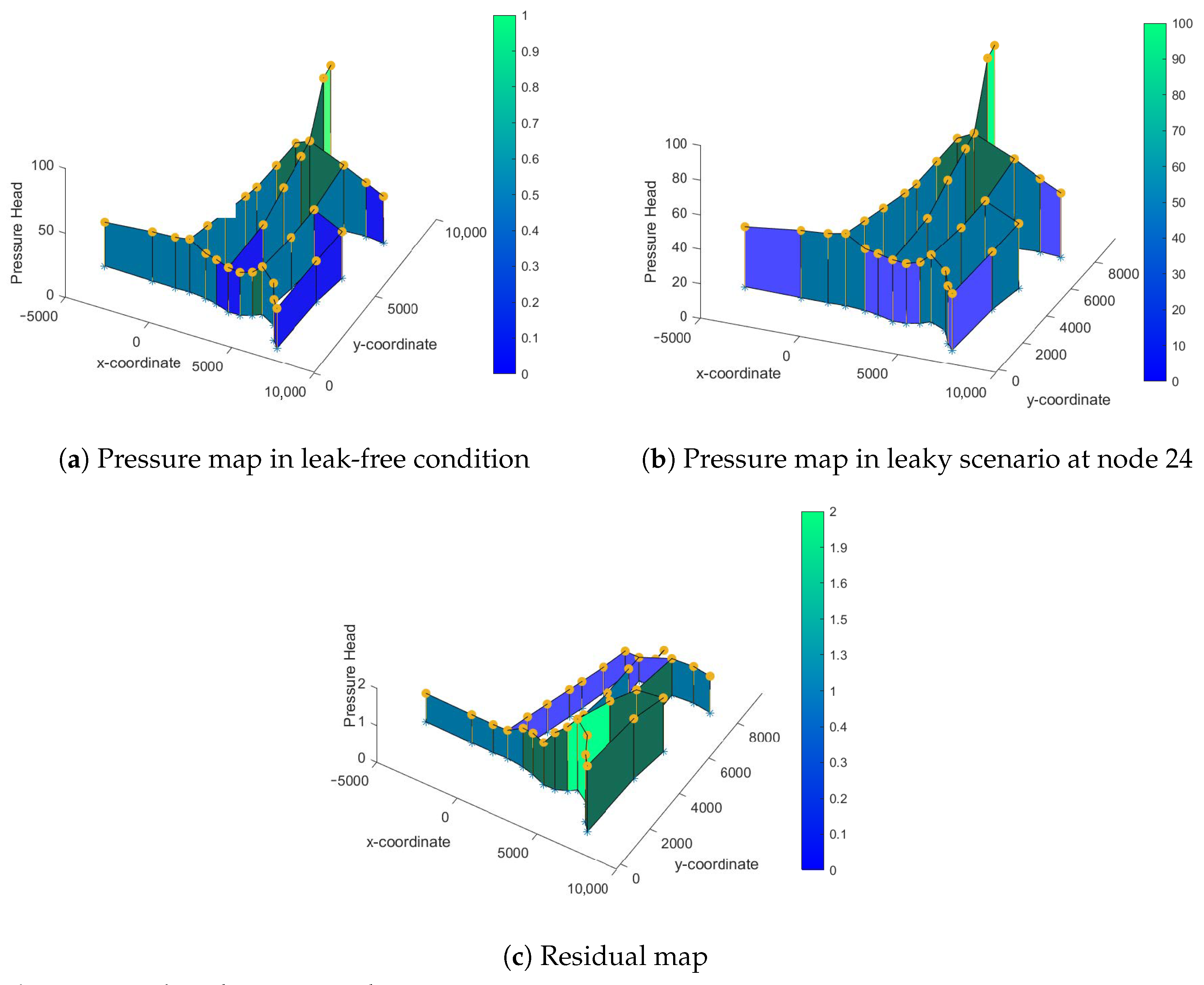

| Hour | Candidate Node | Pressure | Residual |
|---|---|---|---|
| 4:00 | 24 | 38.7372 | 1.9205 |
| 8:00 | 24 | 38.8332 | 2.0165 |
| 12:00 | 24 | 38.8271 | 2.0104 |
| 16:00 | 24 | 38.7944 | 1.9777 |
| 20:00 | 24 | 38.8301 | 2.0134 |
| 24:00 | 24 | 38.8598 | 2.0431 |
| Hour | Candidate Node | Pressure | Residual |
|---|---|---|---|
| 4:00 | 9 | 45.0551 | 3.9741 |
| 8:00 | 9 | 45.0409 | 3.9599 |
| 12:00 | 9 | 44.8347 | 3.7537 |
| 16:00 | 9 | 44.9123 | 3.8313 |
| 20:00 | 9 | 45.0352 | 3.9542 |
| 24:00 | 9 | 44.1563 | 3.0753 |
| Classification Method | Classification Loss |
|---|---|
| k-NN with 50 neighbours, using cosine distance | 0.9280 |
| k-NN with 50 neighbours, using correlation distance | 0.7066 |
| Classification tree with default hyperparameters | 0.1967 |
| Classification tree with optimized hyperparameters | 0.0260 |
| SNR (dB) | Using 3 Sensors | Sensing All Nodes |
|---|---|---|
| 40 | 0.9067 | 0.0253 |
| 45 | 0.8540 | 0.0253 |
| 50 | 0.7427 | 0.0280 |
| 55 | 0.6300 | 0.0273 |
| 60 | 0.4820 | 0.0273 |
| ∞ | 0.1920 | 0.0267 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liy-González, P.-A.; Santos-Ruiz, I.; Delgado-Aguiñaga, J.-A.; Navarro-Díaz, A.; López-Estrada, F.-R.; Gómez-Peñate, S. Pressure Interpolation in Water Distribution Networks by Using Gaussian Processes: Application to Leak Diagnosis. Processes 2024, 12, 1147. https://doi.org/10.3390/pr12061147
Liy-González P-A, Santos-Ruiz I, Delgado-Aguiñaga J-A, Navarro-Díaz A, López-Estrada F-R, Gómez-Peñate S. Pressure Interpolation in Water Distribution Networks by Using Gaussian Processes: Application to Leak Diagnosis. Processes. 2024; 12(6):1147. https://doi.org/10.3390/pr12061147
Chicago/Turabian StyleLiy-González, Pedro-Antonio, Ildeberto Santos-Ruiz, Jorge-Alejandro Delgado-Aguiñaga, Adrián Navarro-Díaz, Francisco-Ronay López-Estrada, and Samuel Gómez-Peñate. 2024. "Pressure Interpolation in Water Distribution Networks by Using Gaussian Processes: Application to Leak Diagnosis" Processes 12, no. 6: 1147. https://doi.org/10.3390/pr12061147
APA StyleLiy-González, P.-A., Santos-Ruiz, I., Delgado-Aguiñaga, J.-A., Navarro-Díaz, A., López-Estrada, F.-R., & Gómez-Peñate, S. (2024). Pressure Interpolation in Water Distribution Networks by Using Gaussian Processes: Application to Leak Diagnosis. Processes, 12(6), 1147. https://doi.org/10.3390/pr12061147








