Study of Methane Solubility Calculation Based on Modified Henry’s Law and BP Neural Network
Abstract
1. Introduction
2. CH4 Solubility Data Collection and Processing
2.1. CH4 Solubility Data Collection
2.2. Data Processing
- 1.
- Outlier Removal [28]
- 2.
- Data Standardization [29]
- 3.
- Processing Data Under Identical Conditions
3. Prediction of CH4 Solubility Based on Revised Henry’s Law
3.1. Henry’s Law
3.2. Effect of Hydrate Formation on Solubility
3.3. Modification of Henry’s Coefficient of CH4
- P ≤ 40 MPa
- 2.
- P > 40 MPa
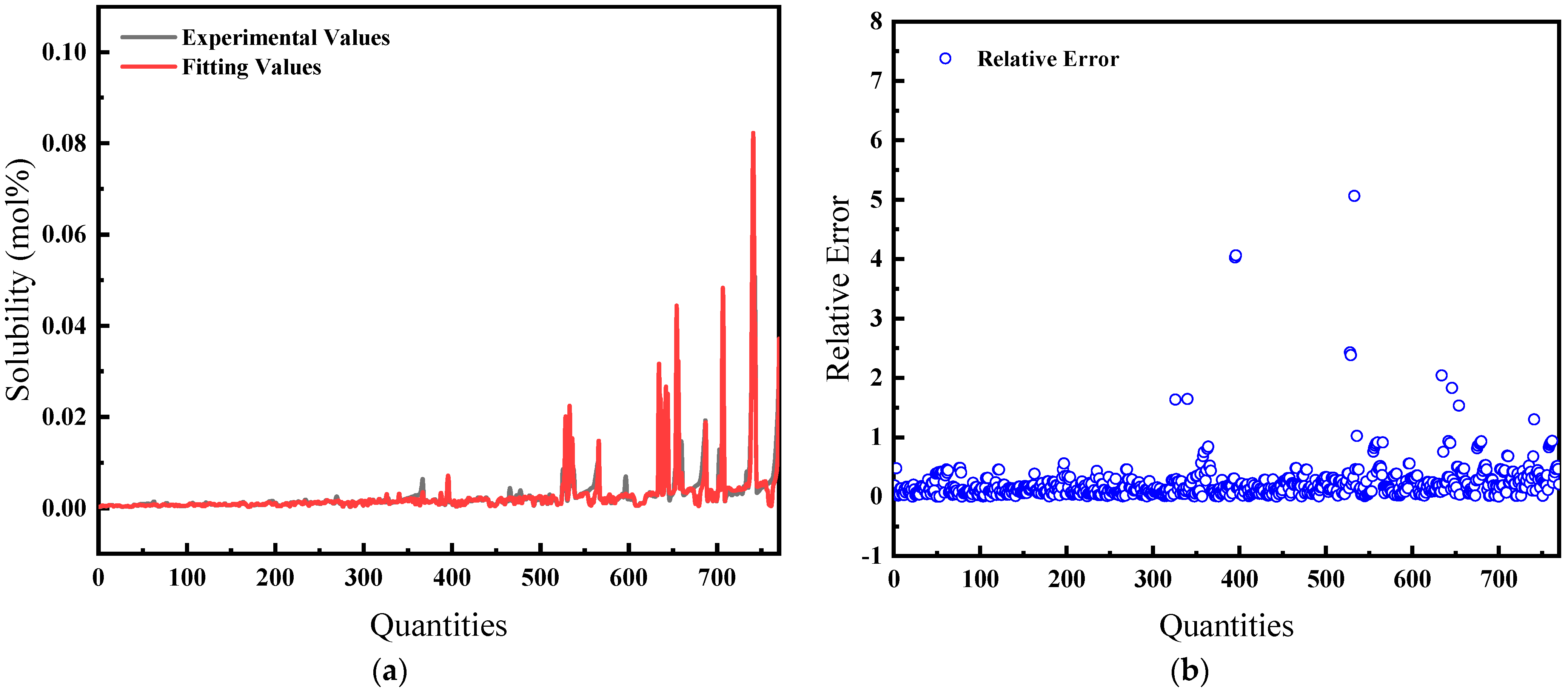
3.4. Prediction of CH4 Gas Solubility
4. Prediction of CH4 Gas Solubility Based on BP Neural Network
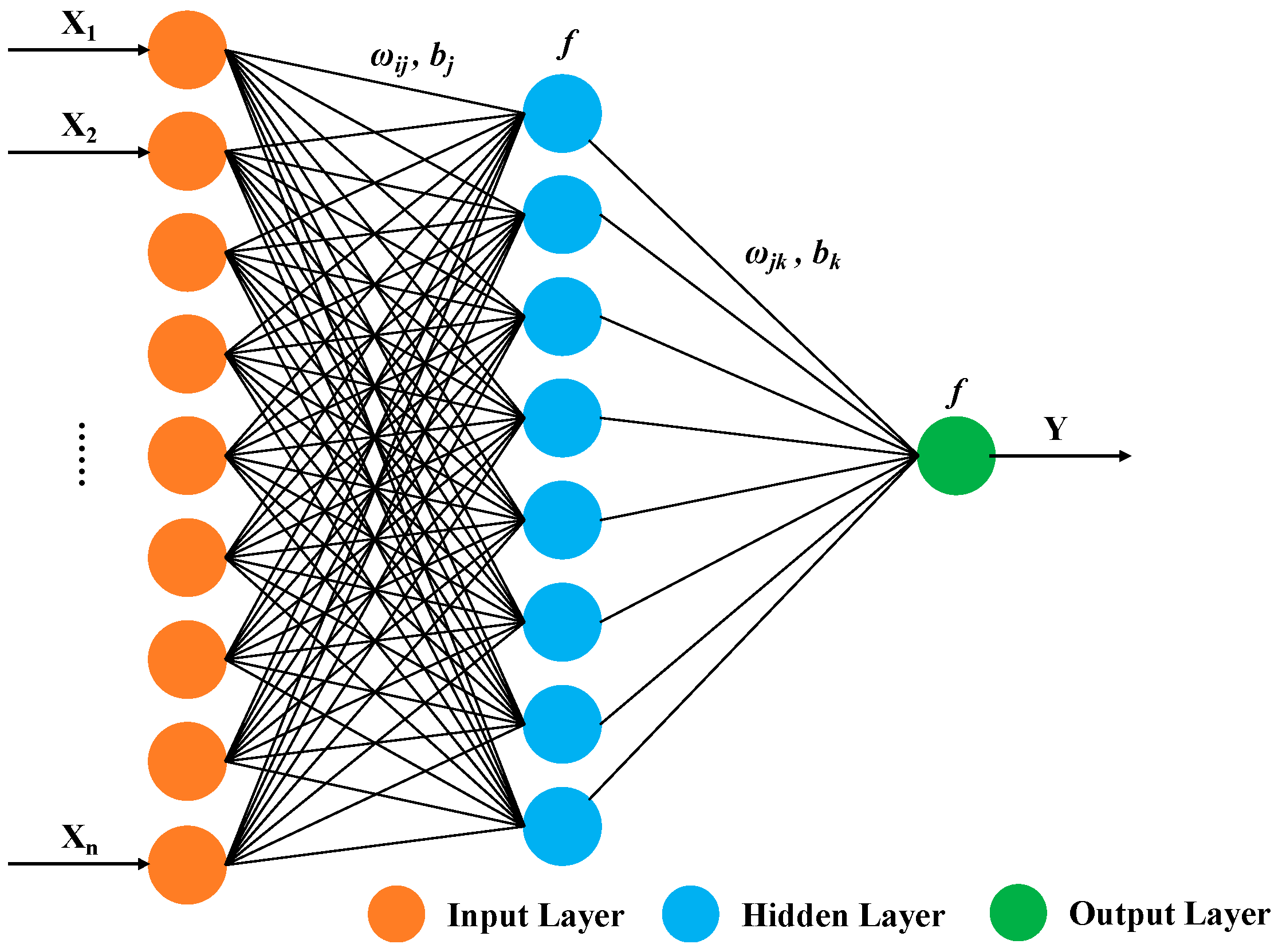
4.1. Principle of BP Neural Network
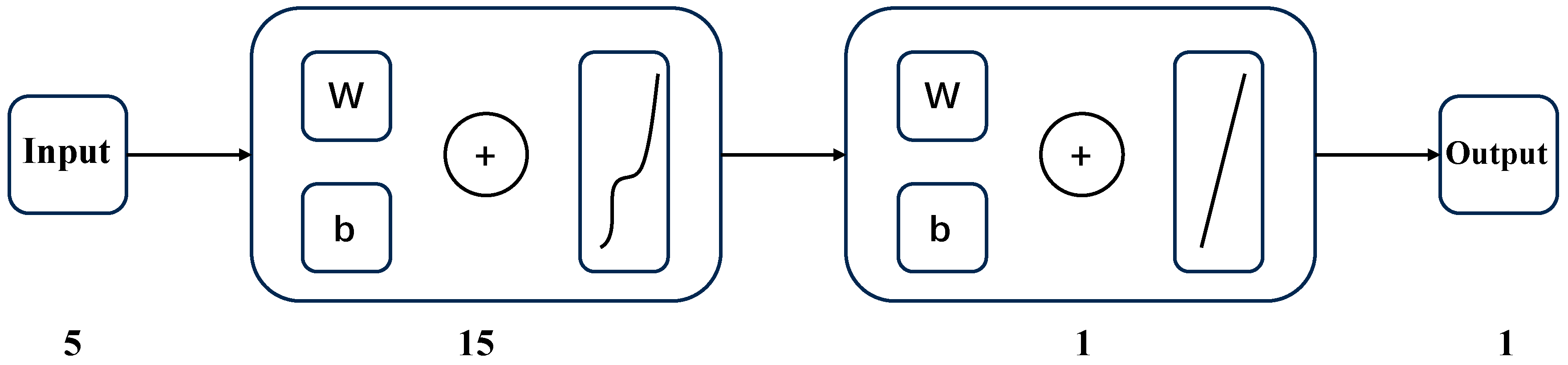
4.2. Establishment of BP Neural Network Model
4.2.1. Input Variables and Output Variables
4.2.2. Neural Network Training Parameters
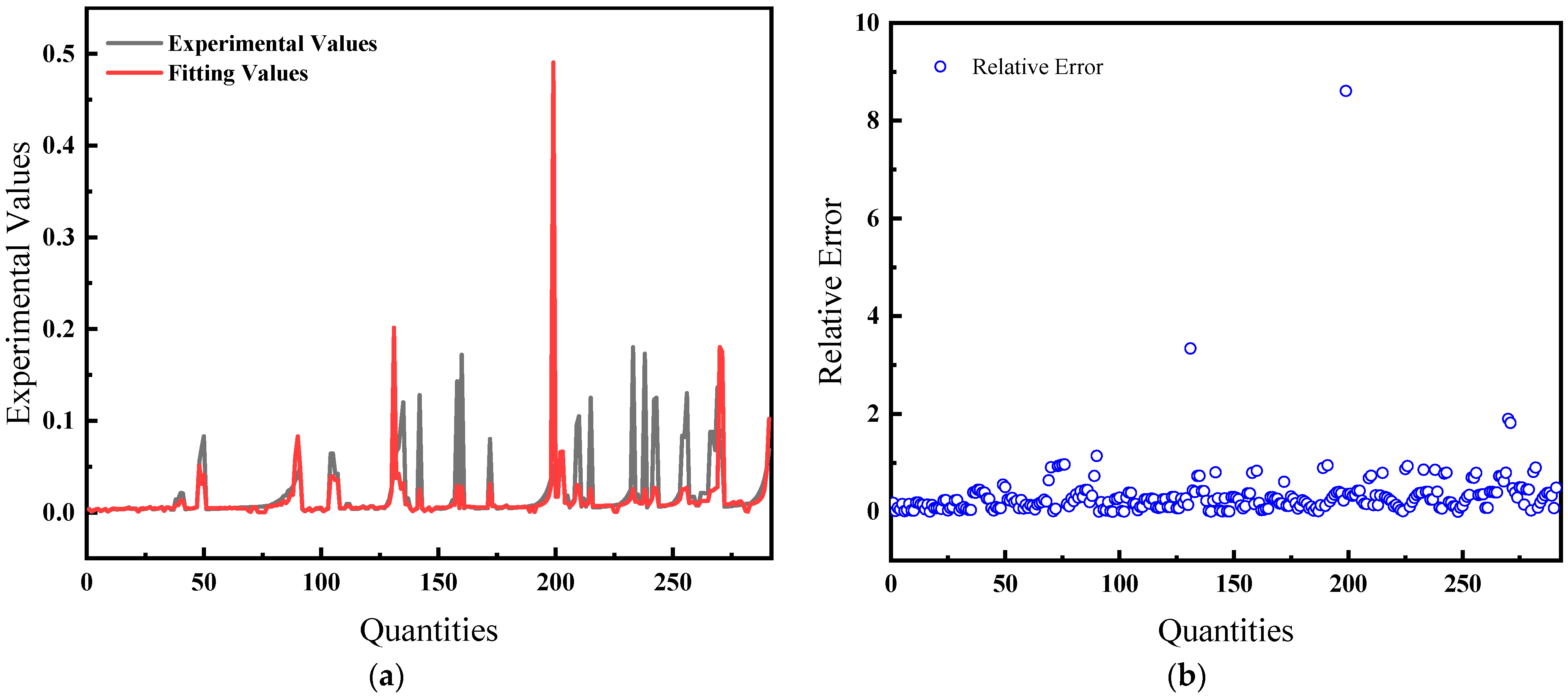
4.3. BP Neural Network Prediction
4.3.1. Training Prediction Results for Multiple Combinations of Input Variables
- Temperature, pressure, and salinity (combination 1)
- 2.
- Temperature, pressure, salinity, and compressibility factor (combination 2)
- 3.
- Temperature, pressure, salinity, and fugacity (combination 3)
- 4.
- Temperature, pressure, fugacity, and compressibility factor (combination 4)
- 5.
- Temperature, pressure, salinity, fugacity, and compressibility factor (combination 5)
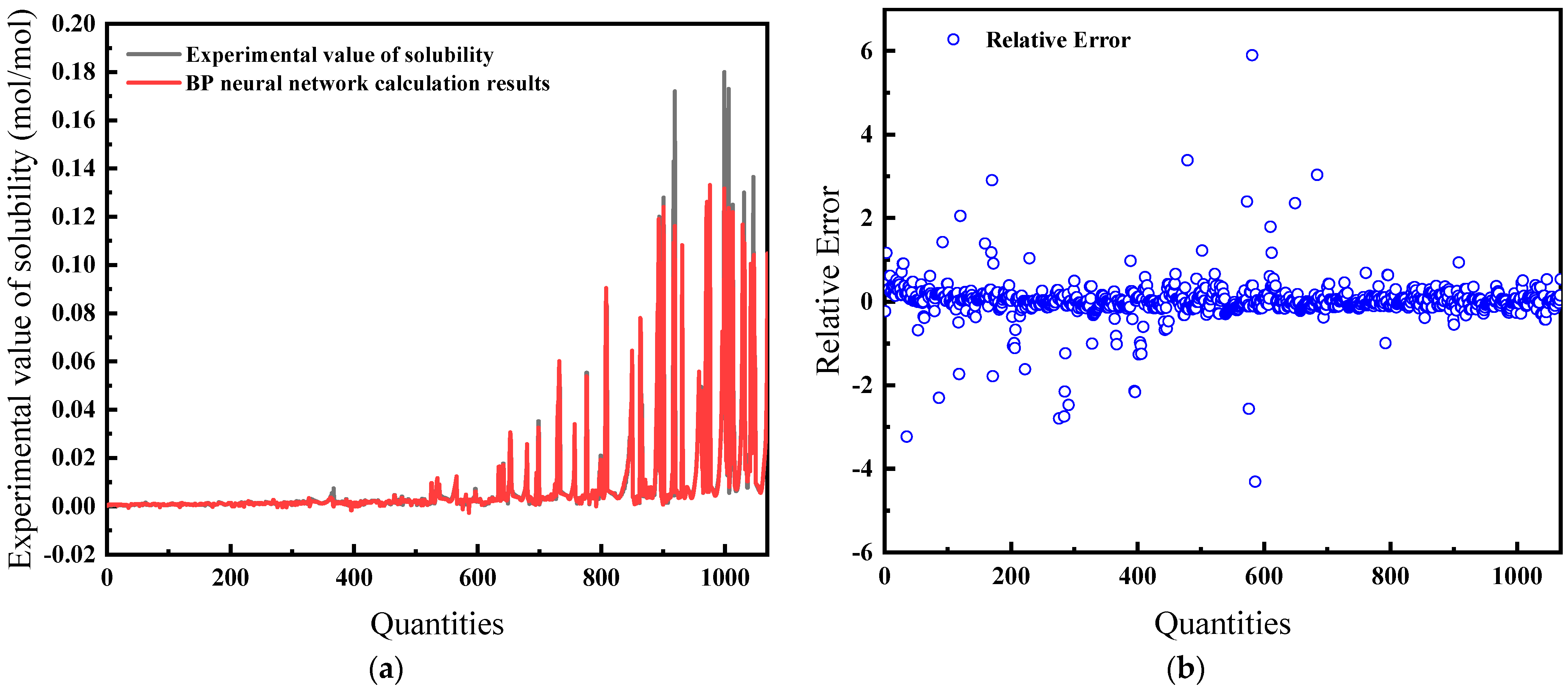
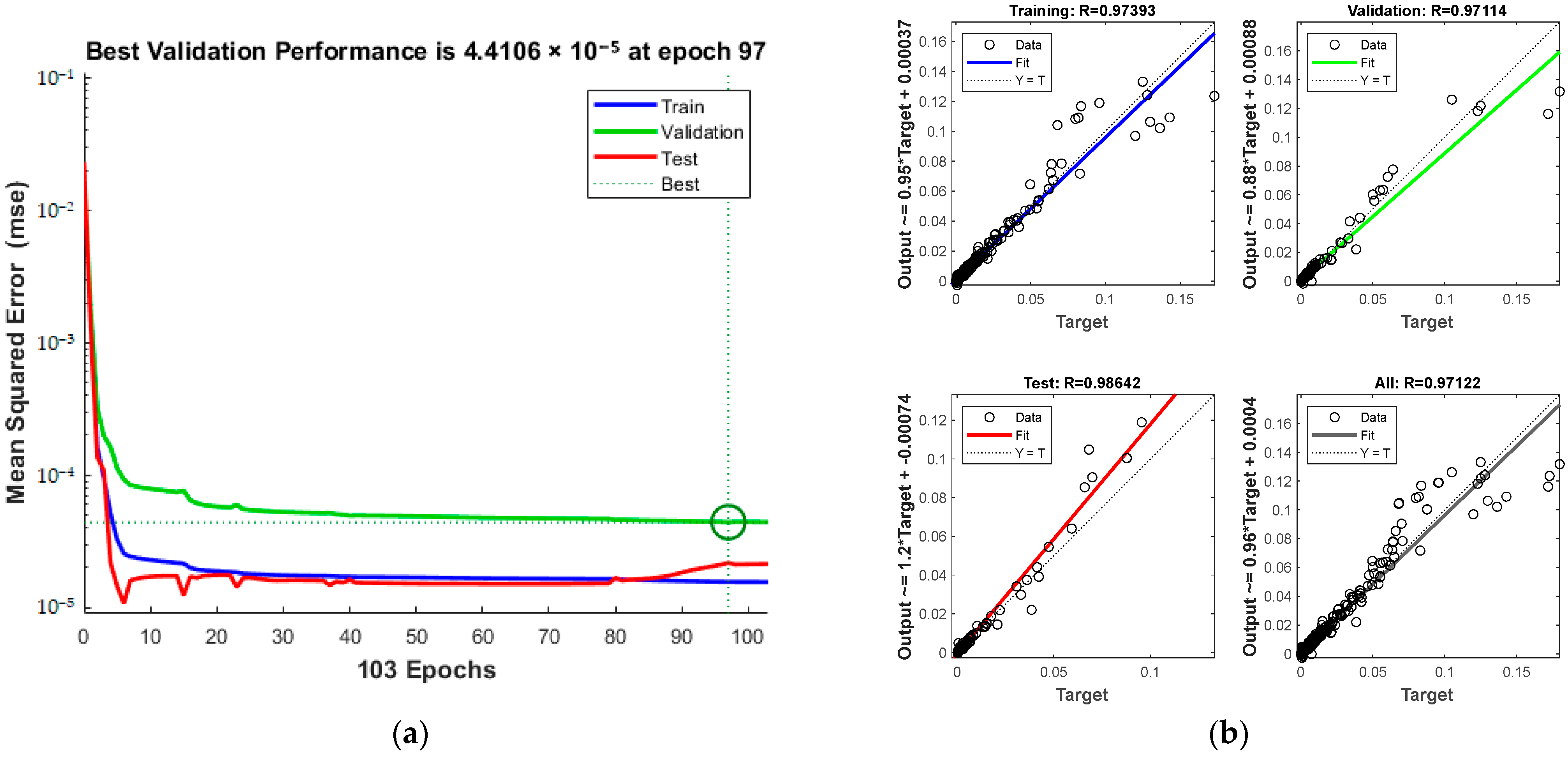
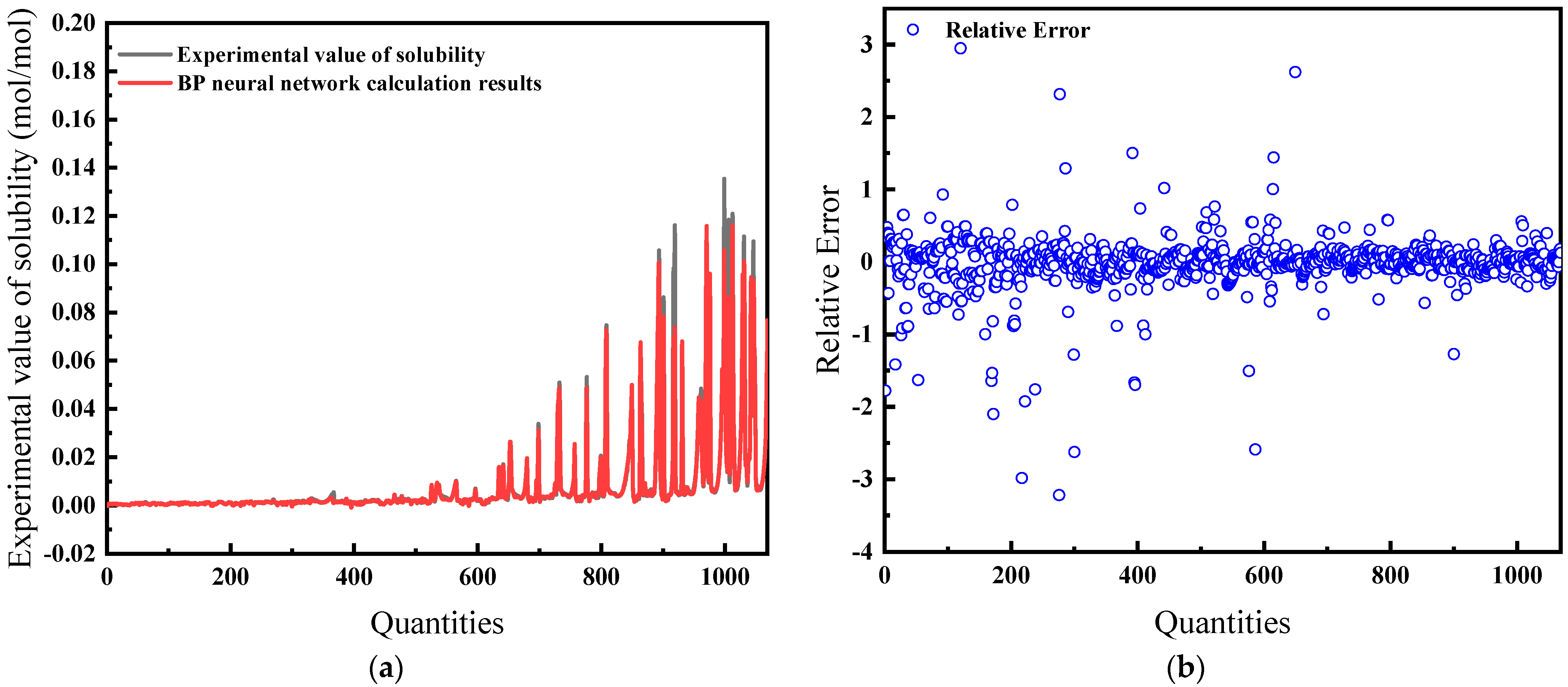
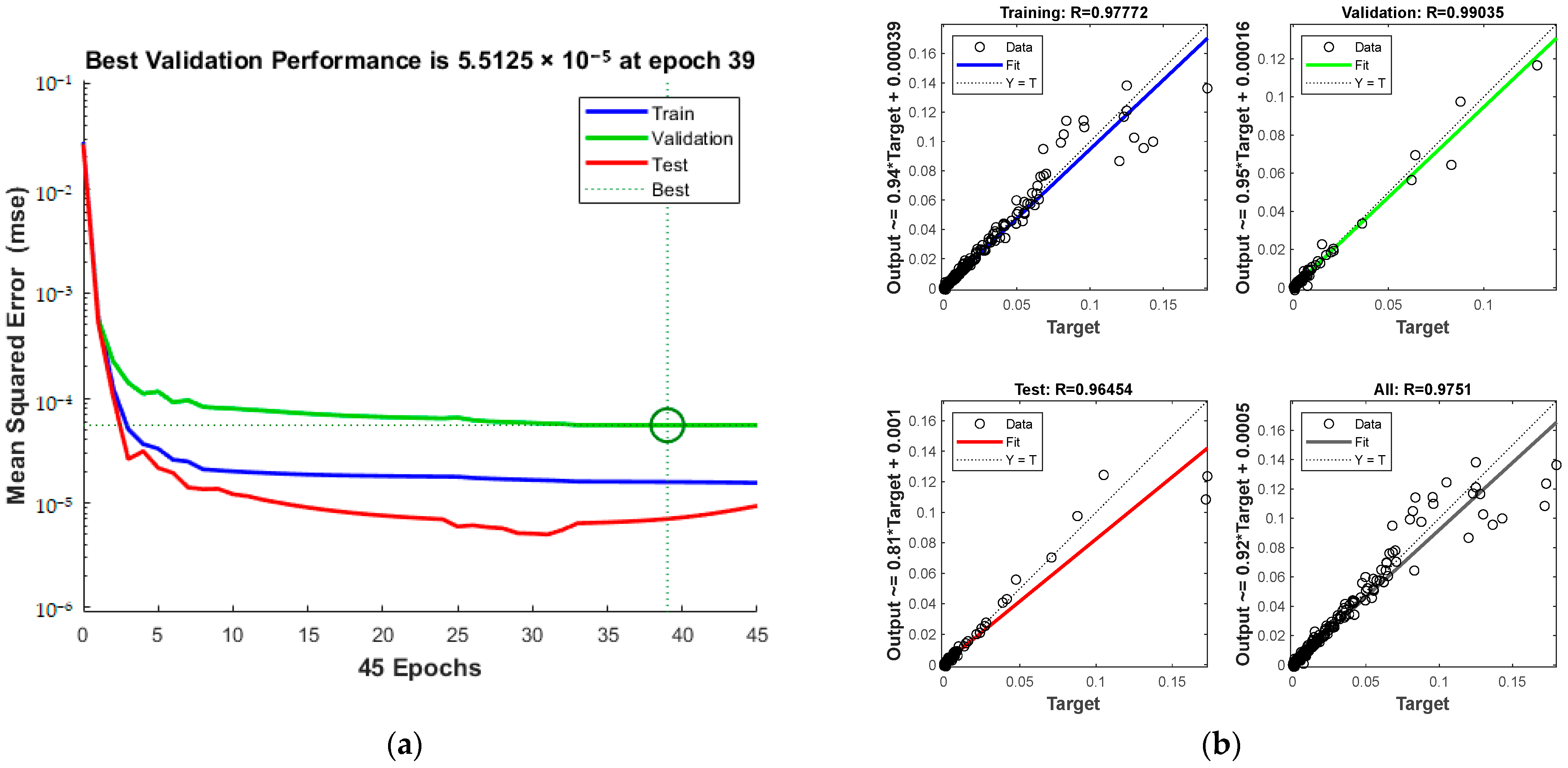
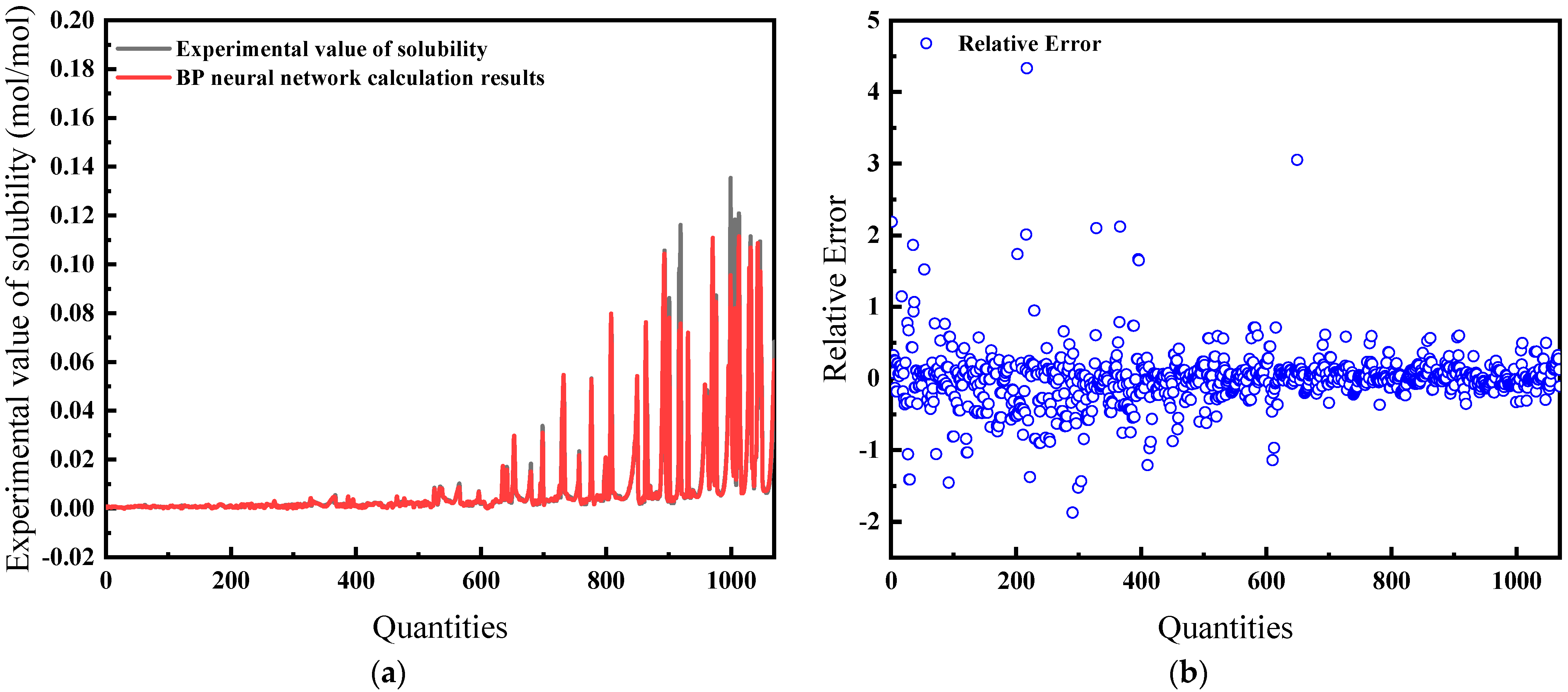
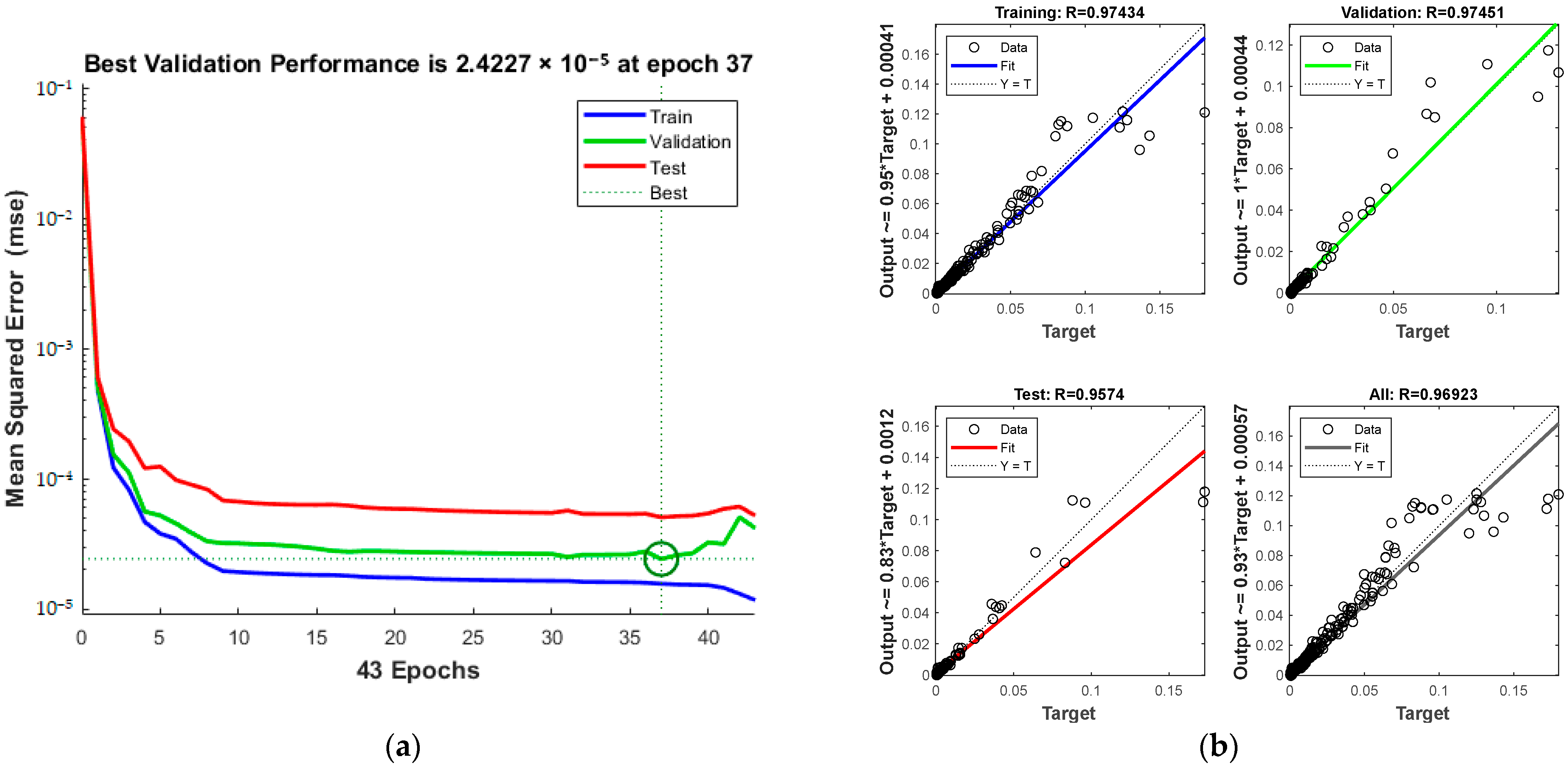
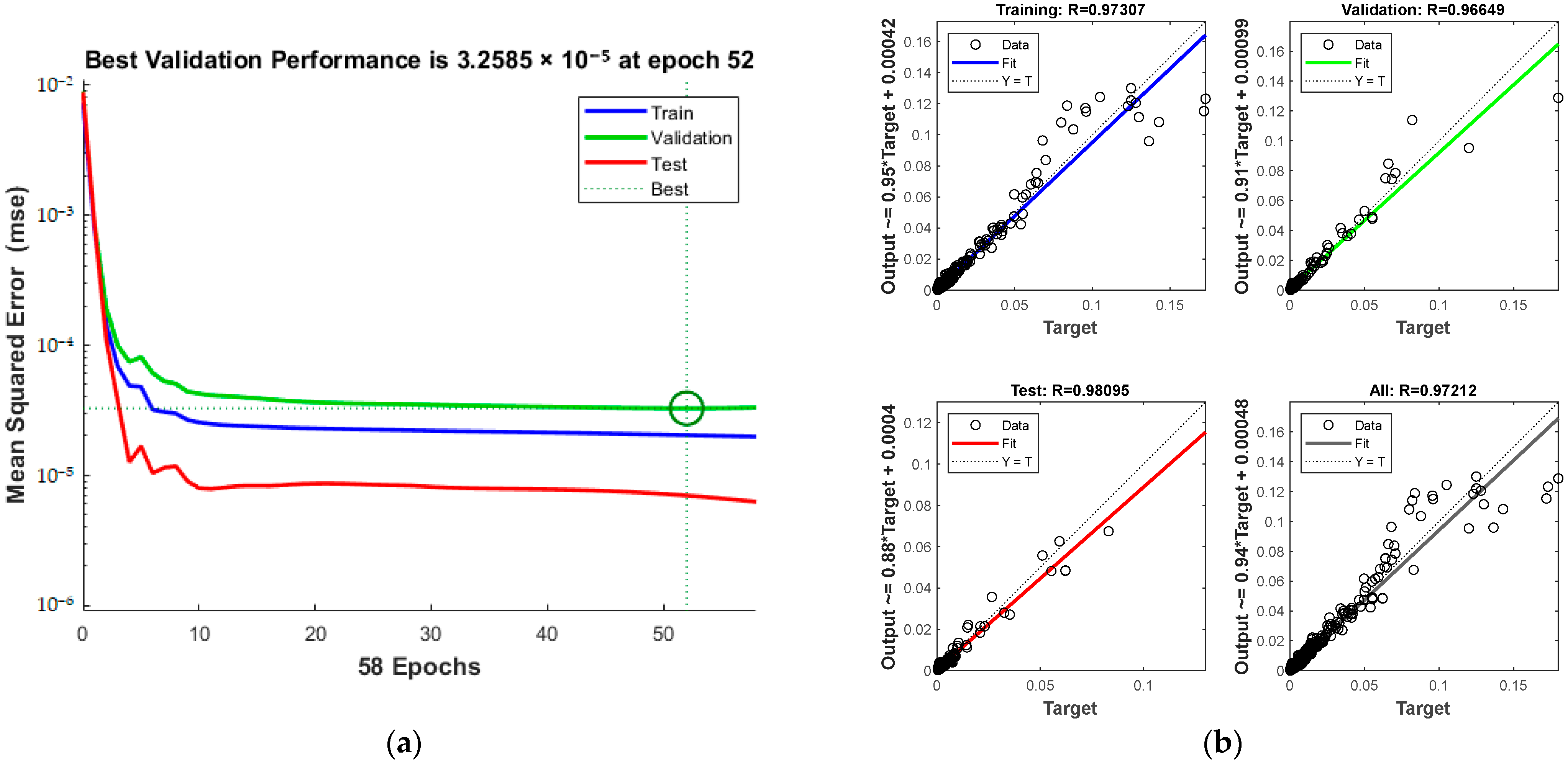
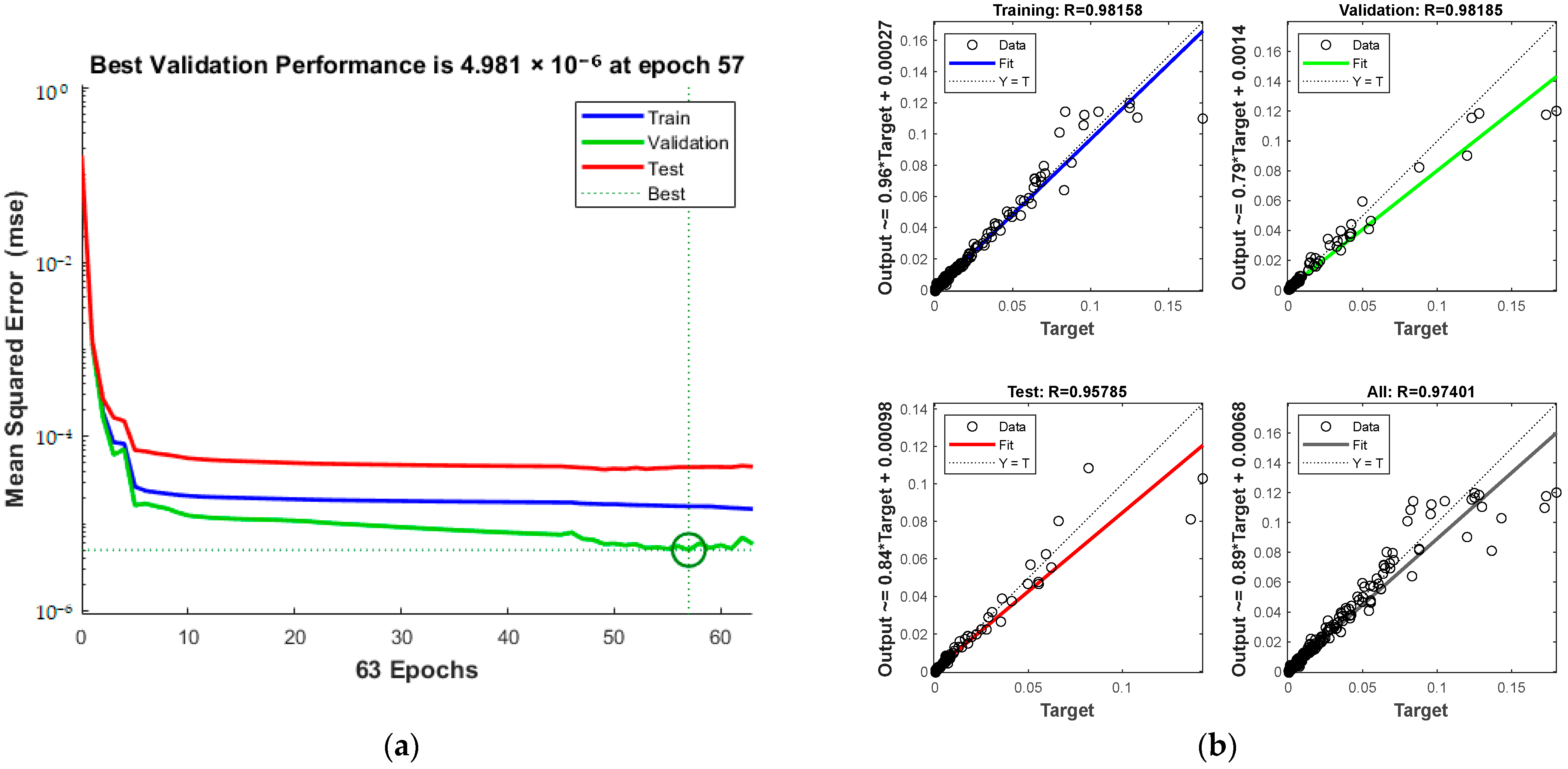
4.3.2. Selection of the Best CH4 Gas Solubility Prediction Model
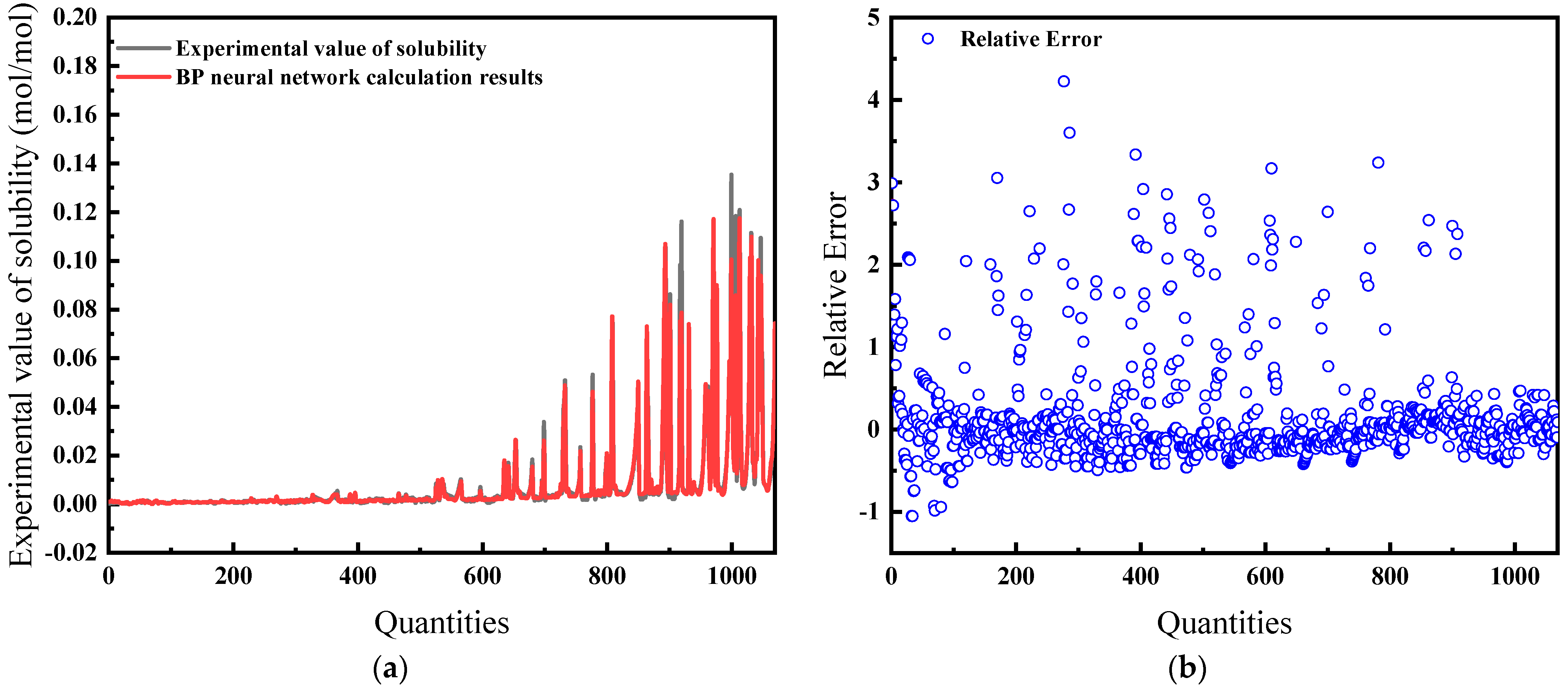
4.3.3. Comparative Analysis of Traditional Methods and Big Data Methods
5. Conclusions
- (1)
- We used Henry’s law and a BP neural network model to predict CH4 solubility, taking into account the effect of hydrates on CH4 solubility. At the temperature of hydrate formation, the pressure was updated to improve the prediction accuracy of Henry’s law and BP model.
- (2)
- Henry’s coefficient was adjusted, and the solubility of CH4 gas in water was subsequently calculated using the modified Henry’s Law. The results showed that the model’s predictions were more accurate at lower pressures, with the prediction error increasing at higher pressure states.
- (3)
- A BP artificial neural network model was developed using solubility data of CH4 gas in water. By adjusting different input variables for comparison and error analysis, it was ultimately determined that the model with temperature, pressure, salinity, enrichment, and compression factor as input variables was the most effective, with the least error and the best fit.
- (4)
- We compared the prediction results of Henry’s law and the BP neural network, and the results showed that the neural network model was more accurate for the prediction of CH4 solubility.
- (5)
- Despite the progress made, there are still some limitations in this study. First, although the neural network model employed can effectively handle a large range of input variables, its performance and stability under extreme conditions (e.g., very high- or very low-pressure and -temperature conditions) still need to be further verified. In addition, the generalizability and performance of the models in real industrial applications need to be tested more extensively. Secondly, although the model selected in this study has a minimum error of 16.32% in all tests, compared with the models of other scholars, there is still room for further optimization, and attempts can be made to reduce the error in the future by introducing more advanced training algorithms or adjusting the network structure. Finally, the pressure interval selected in this paper is from 1.482 MPa to 120 MPa, and data beyond this range need to be collected to extend the application range of the model and improve its prediction accuracy.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Neurons | Input Layer-Hidden Layer Weight P | Input Layer-Hidden Layer Weight T | Input Layer-Hidden Layer Weight S | Input Layer-Hidden Layer Weight Z | Input Layer-Hidden Layer Weight F | Input Layer-Hidden Layer Bias | Output Layer Weights | Output Layer Bias |
|---|---|---|---|---|---|---|---|---|
| Neuron 1 | −1.13968 | −1.76479 | −3.45330 | 1.73109 | −3.24137 | 2.85507 | −0.12289 | −1.0186 |
| Neuron 2 | −0.45666 | −7.88603 | 0.96231 | 9.97330 | 0.59206 | 4.61570 | 4.61349 | −1.0186 |
| Neuron 3 | −1.60336 | −3.28937 | 0.26834 | 3.27836 | 0.94896 | 1.70066 | −1.23907 | −1.0186 |
| Neuron 4 | 1.01862 | 1.62973 | 1.22274 | −1.60368 | 1.00475 | −3.64760 | 3.39638 | −1.0186 |
| Neuron 5 | 0.03258 | 0.08096 | −1.31394 | −2.67360 | −0.87854 | 2.14356 | 1.42482 | −1.0186 |
| Neuron 6 | −0.17362 | −3.31162 | −0.56108 | 0.67030 | 1.36350 | 0.53858 | −0.55372 | −1.0186 |
| Neuron 7 | 2.97357 | 1.17050 | −0.59135 | 1.08239 | −0.25718 | −0.74667 | −0.09509 | −1.0186 |
| Neuron 8 | −1.41132 | 1.29744 | 0.77452 | 1.45754 | 0.70243 | 0.91928 | −0.01336 | −1.0186 |
| Neuron 9 | −1.19623 | 1.18812 | −1.38642 | 0.25159 | 1.07455 | −0.72375 | −0.00381 | −1.0186 |
| Neuron 10 | −1.62494 | −1.16618 | 0.99793 | 0.21276 | 1.33450 | −1.00104 | 0.36620 | −1.0186 |
| Neuron 11 | −0.82606 | 2.69633 | 0.31178 | −0.70906 | −0.86557 | −1.89572 | −1.21750 | −1.0186 |
| Neuron 12 | 0.86384 | 1.36316 | −1.05806 | 0.20601 | −1.59463 | 0.36616 | 0.74156 | −1.0186 |
| Neuron 13 | 1.00624 | −0.96938 | 1.30182 | −0.49245 | 1.47591 | 1.64634 | 1.65459 | −1.0186 |
| Neuron 14 | −1.33706 | 0.75793 | −1.35121 | 0.47029 | −1.37207 | −2.08971 | 1.27833 | −1.0186 |
| Neuron 15 | 0.02949 | −1.01606 | 0.58556 | −0.65841 | 0.42895 | 2.65211 | −2.01326 | −1.0186 |
References
- Li, L. Solubility and Exsolution Study of CO2 and CH4. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2018. [Google Scholar]
- Changquan, G. Study of Solubility of Methane in Water Combined With Mechanism of Hydrate Formation. Master’s Thesis, Zhejiang University of Technology, Hangzhou, Zhejiang, 2002. [Google Scholar]
- Price, L.C. Aqueous Solubility of Methane at Elevated Pressures and Temperatures. AAPG Bull. 1979, 63, 1527–1533. [Google Scholar] [CrossRef]
- Ou, W.; Geng, L.; Lu, W.; Guo, H.; Qu, K.; Mao, P. Quantitative Raman spectroscopic investigation of geo-fluids high-pressure phase equilibria: Part II. Accurate determination of CH4 solubility in water from 273 to 603 K and from 5 to 140 MPa and refining the parameters of the thermodynamic model. Fluid Phase Equilibria 2015, 391, 18–30. [Google Scholar] [CrossRef]
- Duffy, J.R.; Smith, N.O.; Nagy, B. Solubility of natural gases in aqueous salt solutions—I: Liquidus surfaces in the system CH4-H2O-NaCl2-CaCl2 at room temperatures and at pressures below 1000 psia. Geochim. Cosmochim. Acta 1961, 24, 23–31. [Google Scholar] [CrossRef]
- Krader, T.; Franck, E.U. The Ternary Systems H2O-CH4-NaCl and H2O-CH4-CaCl2 to 800 K and 250 MPa. Ber. Bunsenges. Phys. Chem. 1987, 91, 627–634. [Google Scholar] [CrossRef]
- Hongche, F.; Zhilong, H.; Jian, Y.; Gang, G.; Chuanxin, T.; Chong, F. Methane and carbon dioxide solubility tests under high temperature and pressure conditions. J. China Univ. Pet. (Nat. Sci. Ed.) 2011, 35, 6–11+19. [Google Scholar]
- Duan, Z.; Møller, N.; Greenberg, J.; Weare, J.H. The prediction of methane solubility in natural waters to high ionic strength from 0 to 250 °C and from 0 to 1600 bar. Geochim. Cosmochim. Acta 1992, 56, 1451–1460. [Google Scholar] [CrossRef]
- Liang, Y.; Nie, Y. The development of artificial neural network research from the perspective of scientific research methodology. J. Jilin Univ. (Inf. Sci. Ed.) 2002, 1, 59–62. [Google Scholar]
- Li, M.; Huang, X.; Liu, H.; Liu, B.; Wu, Y.; Xiong, A.; Dong, T. Prediction of gas solubility in polymers by back propagation artificial neural network based on self-adaptive particle swarm optimization algorithm and chaos theory. Fluid Phase Equilibria 2013, 356, 11–17. [Google Scholar] [CrossRef]
- Mohammadi, M.-R.; Hadavimoghaddam, F.; Atashrouz, S.; Abedi, A.; Hemmati-Sarapardeh, A.; Mohaddespour, A. Modeling the solubility of light hydrocarbon gases and their mixture in brine with machine learning and equations of state. Sci. Rep. 2022, 12, 14943. [Google Scholar] [CrossRef]
- Taherdangkoo, R.; Liu, Q.; Xing, Y.; Yang, H.; Cao, V.; Sauter, M.; Butscher, C. Predicting methane solubility in water and seawater by machine learning algorithms: Application to methane transport modeling. J. Contam. Hydrol. 2021, 242, 103844. [Google Scholar] [CrossRef]
- Deng, H.; Guo, Y. Artificial Neural Network Model for the Prediction of Methane Bi-Reforming Products Using CO2 and Steam. Processes 2022, 10, 1052. [Google Scholar] [CrossRef]
- Li, T.; Tantikhajorngosol, P.; Yang, C.; Tontiwachwuthikul, P. Experimental investigations and developing multilayer neural network models for prediction of CO2 solubility in aqueous MDEA/PZ and MEA/MDEA/PZ blends. Greenh. Gases Sci. Technol. 2021, 11, 712–733. [Google Scholar] [CrossRef]
- Hamzehie, M.E.; Mazinani, S.; Davardoost, F.; Mokhtare, A.; Najibi, H.; Van der Bruggen, B.; Darvishmanesh, S. Developing a feed forward multilayer neural network model for prediction of CO2 solubility in blended aqueous amine solutions. J. Nat. Gas Sci. Eng. 2014, 21, 19–25. [Google Scholar] [CrossRef]
- Mokarizadeh, H.; Atashrouz, S.; Mirshekar, H.; Hemmati-Sarapardeh, A.; Mohaddes Pour, A. Comparison of LSSVM model results with artificial neural network model for determination of the solubility of SO2 in ionic liquids. J. Mol. Liq. 2020, 304, 112771. [Google Scholar] [CrossRef]
- Mohammadi, M.-R.; Hadavimoghaddam, F.; Atashrouz, S.; Abedi, A.; Hemmati-Sarapardeh, A.; Mohaddespour, A. Toward predicting SO2 solubility in ionic liquids utilizing soft computing approaches and equations of state. J. Taiwan Inst. Chem. Eng. 2022, 133, 104220. [Google Scholar] [CrossRef]
- Prausnitz, J.M.; Lichtenthaler, R.N.; Azevedo, E.G.D. Molecular Thermodynamics of Fluid-Phase Equilibria; Prentice-Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Böttger, A.; Pérez-Salado Kamps, Á.; Maurer, G. An experimental investigation of the phase equilibrium of the binary system (methane+water) at low temperatures: Solubility of methane in water and three-phase (vapour + liquid + hydrate) equilibrium. Fluid Phase Equilibria 2016, 407, 209–216. [Google Scholar] [CrossRef]
- Rahmati-Abkenar, M.; Manteghian, M. Effect of silver nanoparticles on the solubility of methane and ethane in water. J. Nat. Gas Sci. Eng. 2020, 82, 103505. [Google Scholar] [CrossRef]
- Wang, L.-K.; Chen, G.-J.; Han, G.-H.; Guo, X.-Q.; Guo, T.-M. Experimental study on the solubility of natural gas components in water with or without hydrate inhibitor. Fluid Phase Equilibria 2003, 207, 143–154. [Google Scholar] [CrossRef]
- Kiepe, J.; Horstmann, S.; Fischer, K.; Gmehling, J. Experimental Determination and Prediction of Gas Solubility Data for Methane + Water Solutions Containing Different Monovalent Electrolytes. Ind. Eng. Chem. Res. 2004, 43, 3216. [Google Scholar] [CrossRef]
- Zhao, G.; Gong, G.; Sun, H.; Chen, B.; Zheng, J.-N.; Yang, M. Effect of Methane Solubility on Hydrate Formation and Dissociation: Review and Perspectives. Energy Fuels 2022, 36, 7269–7283. [Google Scholar] [CrossRef]
- Michels, A.; Gerver, J.; Bijl, A. The influence of pressure on the solubility of gases. Physica 1936, 3, 797–808. [Google Scholar] [CrossRef]
- O’sullivan, T.D.; Smith, N.O. Solubility and partial molar volume of nitrogen and methane in water and in aqueous sodium chloride from 50 to 125.deg. and 100 to 600 atm. J. Phys. Chem. 1970, 74, 1460–1466. [Google Scholar] [CrossRef]
- Amirijafari, B.; Campbell, J.M. Solubility of Gaseous Hydrocarbon Mixtures in Water. Soc. Pet. Eng. J. 1972, 12, 21–27. [Google Scholar] [CrossRef]
- Crovetto, R.; Fernández-Prini, R.; Japas, M.L. Solubilities of inert gases and methane in H2O and in D2O in the temperature range of 300 to 600 K. J. Chem. Phys. 1982, 76, 1077–1086. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Outlier Analysis; Springer: New York, NY, USA, 2013. [Google Scholar]
- Pyle, D. Data Preparation for Data Mining; Elsevier Science: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Vul’fson, A.N.; Borodin, O.O. A thermodynamic analysis of the solubility of gases in water at high pressures and supercritical temperatures. Russ. J. Phys. Chem. A 2007, 81, 510–514. [Google Scholar] [CrossRef]
- Englezos, P.; Bishnoi, P.R. Gibbs free energy analysis for the supersaturation limits of methane in liquid water and the hydrate-gas-liquid water phase behavior. Fluid Phase Equilibria 1988, 42, 129–140. [Google Scholar] [CrossRef]
- Song, K.Y.; Feneyrou, G.; Fleyfel, F.; Martin, R.; Lievois, J.; Kobayashi, R. Solubility measurements of methane and ethane in water at and near hydrate conditions. Fluid Phase Equilibria 1997, 128, 249–259. [Google Scholar] [CrossRef]
- Carroll, J.J.; Mather, A.E. A model for the solubility of light hydrocarbons in water and aqueous solutions of alkanolamines. Chem. Eng. Sci. 1997, 52, 545–552. [Google Scholar] [CrossRef]
- Sander, R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics; CRC press: Boca Raton, FL, USA, 2004; Volume 85. [Google Scholar]
- Duan, Z.; Sun, R. An improved model calculating CO2 solubility in pure water and aqueous NaCl solutions from 273 to 533 K and from 0 to 2000 bar. Chem. Geol. 2003, 193, 257–271. [Google Scholar] [CrossRef]
- Peng, D.-Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Sloan, E.; Koh, C. Clathrate Hydrates of Natural Gases; Marcel Decker. Inc.: New York, NY, USA, 1998. [Google Scholar]
- Hashemi, S.; Macchi, A.; Bergeron, S.; Servio, P. Prediction of methane and carbon dioxide solubility in water in the presence of hydrate. Fluid Phase Equilibria 2006, 246, 131–136. [Google Scholar] [CrossRef]
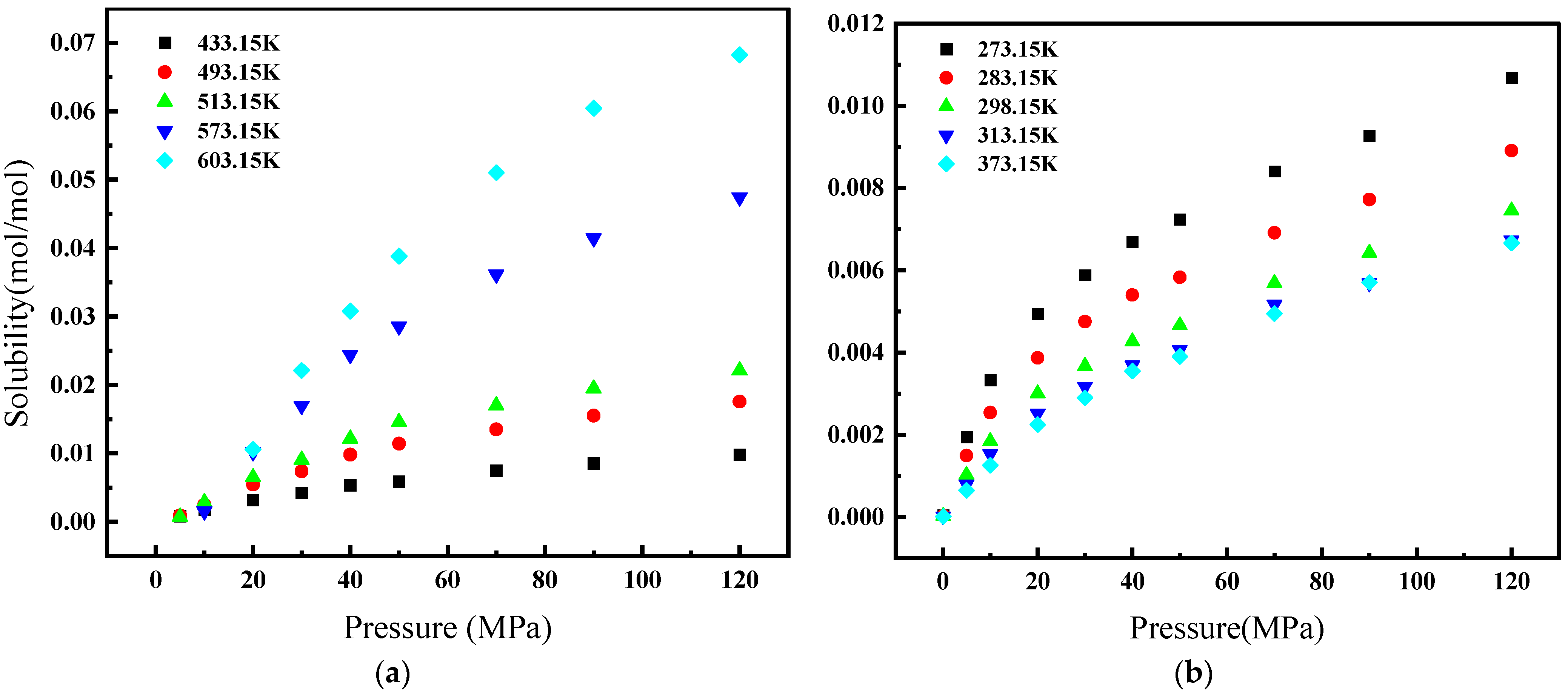



| References | Pressure MPa | Temperature K | Salinity g/L | Solubility mol/mol |
|---|---|---|---|---|
| [4] | 5~140 | 273.15~603.15 | 0 | 0.00065~0.073 |
| [2] | 0.567~9.08 | 274~285.68 | 0 | 0.00026~0.002 |
| [19] | 1.151~10.36 | 283.14~298.15 | 0 | 0.00038~0.0021 |
| [20] | 1~2.7 | 274.15~284.65 | 0 | 0.00033~0.0015 |
| [21] | 2~40.03 | 283.2~303.2 | 0 | 0.00056~0.0041 |
| [22] | 0.34~9.26 | 313.35~373.29 | 0 | 0.00005~0.0015 |
| [23] | 0.567~9.08 | 274.2~285.6 | 0 | 0.00025~0.0022 |
| [24] | 4.06~46.91 | 298.15~423.15 | 0~315.9 | 0.00017~0.003 |
| [5] | 0.317~6.52 | 298.15~303.15 | 0~315.9 | 0.00007~0.00113 |
| [3] | 0.101325~200 | 273.15~633.20 | 0 | 0.000016~0.18 |
| [25] | 10.1325~61.61 | 298.15~398.15 | 0~234 | 0.00081~0.0043 |
| [26] | 4.137~34.47 | 310.93~344.26 | 0 | 0.000602~0.00335 |
| [27] | 1.327~6.451 | 297.50~518.30 | 0 | 0.00021~0.00103 |
| Coefficients | Values |
|---|---|
| a | −30,352,612,628.3169 |
| b1 | 117,170,471.025335 |
| b2 | −1,833,088.19361018 |
| b3 | 175,581,561.321355 |
| b4 | −209,307.407123789 |
| b5 | 24,472,236.0289736 |
| b6 | 4,156,153.62314121 |
| Coefficients | Values |
|---|---|
| a | −5,311,667,915.66811 |
| b1 | 1603.92554912757 |
| b2 | −1,033,012.08072614 |
| b3 | −102,060.909835676 |
| b4 | 9,677,746.84501353 |
| b5 | 1727.13635637011 |
| b6 | −157,130.38162931 |
| b7 | 109,837,329.146691 |
| b8 | 396,002.273542842 |
| b9 | −185,624,382.240331 |
| b10 | 169,960.110823592 |
| Input Variables | MSE | Average Relative Error | Correlation Coefficient R |
|---|---|---|---|
| PTS | 4.4106 × 10−5 | 20.86% | 0.97122 |
| PTZF | 5.5125 × 10−5 | 19.26% | 0.9751 |
| PTSF | 2.4227 × 10−5 | 21.38% | 0.96923 |
| PTZF | 3.2585 × 10−5 | 35.31% | 0.97212 |
| PTSZF | 4.981 × 10−6 | 16.32% | 0.97401 |
| P | T | S | Z | F | Input Layer-Hidden Layer Bias | |
|---|---|---|---|---|---|---|
| average value | 1.05 | 1.97 | 1.08 | 1.70 | 1.14 | 1.84 |
| standard deviation | 0.75 | 1.87 | 0.76 | 2.46 | 0.70 | 1.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Yu, J.; Shi, H.; Guo, J.; Liu, D.; Lin, J.; Song, S.; Wu, H.; Gong, J. Study of Methane Solubility Calculation Based on Modified Henry’s Law and BP Neural Network. Processes 2024, 12, 1091. https://doi.org/10.3390/pr12061091
Zhao Y, Yu J, Shi H, Guo J, Liu D, Lin J, Song S, Wu H, Gong J. Study of Methane Solubility Calculation Based on Modified Henry’s Law and BP Neural Network. Processes. 2024; 12(6):1091. https://doi.org/10.3390/pr12061091
Chicago/Turabian StyleZhao, Ying, Jiahao Yu, Hailei Shi, Junyao Guo, Daqian Liu, Ju Lin, Shangfei Song, Haihao Wu, and Jing Gong. 2024. "Study of Methane Solubility Calculation Based on Modified Henry’s Law and BP Neural Network" Processes 12, no. 6: 1091. https://doi.org/10.3390/pr12061091
APA StyleZhao, Y., Yu, J., Shi, H., Guo, J., Liu, D., Lin, J., Song, S., Wu, H., & Gong, J. (2024). Study of Methane Solubility Calculation Based on Modified Henry’s Law and BP Neural Network. Processes, 12(6), 1091. https://doi.org/10.3390/pr12061091





