A Study on the Man-Hour Prediction in Structural Steel Fabrication

Abstract

Longitudinal cutting is the most common process in steel structure manufacturing, and the man-hours of the process provide an important basis for enterprises to generate production schedules. However, currently, the man-hours in factories are mainly estimated by experts, and the accuracy of this method is relatively low. In this study, we propose a system that predicts man-hours with history data in the manufacturing process and that can be applied in practical structural steel fabrication. The system addresses the data inconsistency problem by one-hot encoding and data normalization techniques, Pearson correlation coefficient for feature selection, and the Random Forest Regression (RFR) for prediction. Compared with the other three Machine-Learning (ML) algorithms, the Random Forest algorithm has the best performance. The results demonstrate that the proposed system outperforms the conventional approach and has better forecast accuracy so it is suitable for man-hours prediction.

1. Introduction

The production planning and scheduling of steel structure manufacturing enterprises is an important task, and the processing time of components is an important reference for enterprises to arrange overall production plans and determine production nodes for components. The accuracy of man-hour prediction greatly affects production planning and full process scheduling of enterprises. Taking the longitudinal cutting steel coil processing of steel structure manufacturing enterprises as an example, the man-hour of processing generally includes dozens of process times, such as loading time, tailing time, unloading time, separation plate replacement time, material return time, and slitting tailing time. The current workshop scheduling mainly revolves around processing time and is based on the premise of determined processing time. That is, the same components and processing procedures are processed using the same model of machine, and the processing time remains unchanged. However, in the actual production process, due to the influence of worker proficiency, workshop environment, lighting, and physical parameters of steel in the process flow, the cutting process of steel coils is greatly affected by factors such as raw material specifications, width, and thickness of the workpieces, resulting in an uncontrollable fluctuation in production hours, which leads to a certain deviation between the used processing hours and the actual processing hours. With the continuous progress of production and the accumulation of man-hour deviations, the production plan executed on the production line deviates from the pre-arranged production plan. This estimation of production tasks and operation time based on inaccurate man-hours parameters can lead to significant deviations between the plan and actual production, which can easily lead to implementation gaps [1,2]. Even through rescheduling and resource rearrangement, it is difficult to compensate for the impact of man-hour deviations. Moreover, rescheduling and resource rearrangement consume a lot of manpower and time, thereby reducing the feasibility of the entire production plan, which makes it difficult for production plans to effectively guide the actual production operations of enterprises.

At present, the prediction of the man-hours is carried out by an expert based on the historical production data in most structural steel fabrication enterprises. The expert uses various factors to predict the man-hours, but such a process carries some problems:

• First of all, and most importantly, the prediction is not objective. A human ultimately carries out the expert prediction, and therefore there is no guarantee of a consistent prediction. Further, there is the concern that factors that are difficult to objectify may lower the accuracy of predictions [3].
• There is a complex relationship between man-hours and these subjective factors, where a significant amount of effort and time are required to make predictions.
• It is difficult to share the implicit know-how of experts over prediction, and this know-how is also difficult to quantify. Therefore, any person other than the applicable expert needs to assign significant prior experience.

Such problems could be overcome by using the man-hour prediction model. In manufacturing production, the man-hour parameter is an important basis for production planning and scheduling [4], and is used to determine the amount of work tasks and the time interval for each task, which is a key parameter in planned production. Some related studies in recent years, such as data-based scheduling models [5] and data-based methods for predicting key parameters [6] have proved that mining relevant information and knowledge from underlying data and applying it to production decisions can reduce uncertainty in decision-making, enable rapid analysis, and reduce the number of erroneous decisions [7]. If the factors that affect man-hours are identified and quantified, and a prediction model is established based on these factors, then a low-cost, objective and efficient prediction can be performed.

The remainder of the paper is organized as follows: In Section 2, theoretical background related to predicting man-hours and applications of Random Forest (RF) in different industries are analyzed. The data used in this study, the method of data preprocessing and the man-hour prediction system are discussed in Section 3. Section 4 and Section 5 discusses the prediction model and its performance. Finally, Section 6 provides the significance and the limitations of this study.

2. Related Works

In recent years, thanks to widespread adoption such as big data, artificial intelligence, the Internet of Things, and general information technology infrastructure in manufacturing, scholars have conducted extensive research on the application of these technologies to man-hour prediction. Hur et al. [3] constructed a man-hour prediction system based on multiple linear regression and classification regression trees for the shipbuilding industry, and the results showed that the prediction system has strong reliability. Based on this study, three types of plans have been established in man-hour prediction, they are quarter plan, month plan and day plan, respectively. Yu et al. [8] conducted a study on the ML-based quantitative prediction of the process’ man-hour during aircraft’s assembly. The study proposed a forecasting model based on a Support Vector Machine (SVM), which was optimized by particle swarm optimization. The authors showed that the improved model could effectively predict man-hours of assembly work in a short time while maintaining sufficient accuracy. Mohsenijam et al. [9] proposed a framework for labour-hour prediction in structural steel fabrication. The research explored a data-driven approach that used Multiple Linear Regression (MLR) and available historical data from Building Information Models (BIM) to associate project labour hours and project design features. IşıkS et al. [10] explored the use of machine-learning techniques such as Support Vector Regression (SVR), Gaussian Process Regression (GPR) and Adaptive Neuro-Fuzzy Inference System (ANFIS) for predicting man-hours in Power Transformer manufacturing. The authors reported that these techniques, especially GPR are useful in the prediction of man-hours in the Power Transformer production industry. The results showed that the predictive model based on GPR attained good performance in terms of effectiveness and usability and could be effectively used in an acceptable error range, especially when compared to pure expert forecast. Aiming at a kind of key equipment in the metal machining and weld machining, namely the multi-station and multi-fixture machining centre. Dong et al. [11] designed a man-hour calculation system for a motorcar manufacturing company, which was based on the practical production situation, manual time and parallel time between man and machine. Hu [12] proposed a man-hour prediction model based on optimizing the back propagation neural network with a genetic algorithm (AG_BP) for the management process of chemical equipment design. The results showed that the model could be a good solution for predicting the man-hours required for chemical equipment design and improving the prediction accuracy.

In recent years, there has been a growing interest in using ML algorithms to solve both linear and non-linear problems in regression analysis. The RF algorithm, as an ensemble learning algorithm based on CART decision trees, is widely used in classification or regression problems [13,14]. Fraiwan et al. [15] proposed an automated sleep stage identification system based on time-frequency analysis of a single EEG channel and an RF classifier. The results demonstrate that the system achieves an accuracy of 83% in classifying the five sleep stages. Yanni Dong [16] proposed an efficient metric learning detector based on RF, which was applied to the classification of HSI data. Experimental results demonstrated that the proposed method outperformed state-of-the-art target detection algorithms and other classical metric learning methods. Berecibar et al. [17] presented a novel machine-learning approach for online battery capacity estimation. By establishing an RFR model to approximate the relationships between features, it accurately estimated the capacity of aged batteries under various cycling conditions. Liu et al. [18] proposed a classification framework utilizing RF, integrating Out-of-Bag (OOB) prediction, Gini variation, and Predictive Measure of Association (PMOA). The approach aimed to accurately evaluate the significance and correlation of battery manufacturing features and their influence on the classification of electrode properties. Tarchoune et al. [19] proposed a hybrid model named 3FS-CBR-IRF (Three feature selection–Case-based reasoning–Improved random forest) to apply for the evaluation of medical databases. The model was evaluated on 13 medical databases, and the results indicated an improvement in the performance of the CBR system. Li et al. [20] utilized a GIS platform to assess the sensitivity of slope-type geological hazards in the study area using the information value model and the RF-weighted information value model. The approach addressed the issue of negative impacts caused by sensitivity zoning results. The results indicated that the proposed models exhibited high ROC accuracy. Moin Uddin et al. [21] presented a novel hybrid framework combining feature selection, oversampling, and hybrid RF classifier to predict the adoption of vehicle insurance. The framework could benefit insurance companies by reducing their financial risk and helping them reach out to potential customers who are likely to take vehicle insurance.

ML has also been widely applied in the field of steel structure manufacturing. Dai et al. [22] proposed a steel plate cold straightening auxiliary decision-making algorithm based on multiple machine-learning competition strategies. The authors reported that the algorithm effectively improved the product quality of steel plates in practical production applications. In the study of Cho et al. [23], reinforcement learning was applied to the development of a real-time stacking algorithm for steel plates considering the fabrication schedule in the steel stockyard of the shipyard. The test results indicated that the proposed method was effective in minimizing the use of cranes for stacking problems. Korotaev et al. [24] applied two methods, the physics-based Calphad method and the data-driven machine-learning method to predict steel class, based on the composition and heat treatment parameters. Cemernek et al. [25] presented a scientific survey of machine-learning techniques for the analysis of the continuous casting process of steel. The authors demonstrated that the development, extension and integration of ML techniques provided a variety of future work for the steel industry. He et al. [26] proposed a novel steel plate defect inspection system based on deep learning and set up a steel plate defect detection dataset NEU-DET. The proposed method could achieve the specific class and precise location of each defect in an image. Similarly, a study was conducted by Luo et al. [27] who presented a survey on visual surface defect detection technologies for three typical flat steel products of con-casting slabs and hot- and cold-rolled steel strips. Cha et al. [28] developed a database for five types of damages—concrete crack, steel corrosion with two levels (medium and high), bolt corrosion, and steel delamination. An improved FasterRCNN architecture was proposed for defect detection and achieved good results. Extreme Learning Machines (ELMs) were optimized by Shariati et al. [29] to estimate the moment and rotation in steel rack connection based on variable input characteristics such as beam depth, column thickness, connector depth, moment and loading. Madhushan et al. [30] presented the application of four popular machine-learning algorithms in the prediction of the shear resistance of steel channel sections. The results indicated that the implemented machine-learning models exceeded the prediction accuracy of the available design equations.

Against this backdrop, the above studies show that ML algorithms and data-mining techniques have been wildly used in man-hours prediction and a variety of industries. However, different ML algorithms have different advantages and disadvantages, and the algorithms suitable for different specific fields are also different. Different specific requirements require different algorithms or the integration of multiple technologies to improve the accuracy and stability of the model.

On the basis of an extensive study of man-hour prediction methods and the present project-based production environments, we listed various related variables. Then we utilized the Pearson correlation coefficient to perform variable selection to identify the essential features for enhancing accuracy. A prediction system based on the RFR model was developed in this study for the prediction of the man-hour. Moreover, the predictive performance was also compared with three other machine-learning models.

3. Methodology

3.1. Data Descriptions

To build the man-hour prediction system, we collected processing data from the production lines of a steel structure enterprise for a total of two years, including 2022, and 2023. There are over 5000 rows of data in this dataset, each with 11 attributes. Two of these attributes (production schedule number and production bundle number) are attributes that uniquely represent the data and the other one is a textual description of the data. These three attributes are not relevant to the man-hour prediction, so we directly removed them prior to data preprocessing. One of the remaining nine attributes is the man-hour, which is the dependent variable to be predicted, and the remaining 7 attributes are independent variables. Attributes are mostly of numeric and character types.

Table 1. Variables and their descriptions.

Variables	Variable Type	Unit	Description	Labels
Man-hour (MH)	Interval	min	Dependent Variable	Y
Raw material thickness	Interval	mm	The thickness of raw material steel	X1
Raw material width	Interval	m	The width of raw material steel	X2
Raw material weight	Interval	kg	The weight of raw material steel	X3
Business type	Nominal	—	Including two values: processing, distribution	X4
Allocated length	Interval	m	The length of finished product	X5
Allocated weight	Interval	kg	The weight of finished product	X6
Finished product thickness	Interval	mm	The thickness of finished product	X7
Finished product width	Interval	m	The width of finished product	X8

shows further specific descriptions for the dataset.

3.2. Data Preprocessing

Data preprocessing is important to improve the usability and accuracy of the model. For a given dataset, certain missing, unusual and redundant values were found after exploring all the data by analyzing and visualizing the distribution of each variable. This type of data cannot be directly used for model training, or the training results are unsatisfactory. In order to improve the accuracy of model predictions, data preprocessing techniques have emerged. There are various methods for data preprocessing: data cleaning, data integration, data transformation, data normalization, etc. These data processing techniques used before machine learning can greatly improve the quality of model predictions and reduce the time required to train the model.

In the steel structure manufacturing enterprise, each steel plate to be processed had been labelled with a QR code, which would be scanned to record the starting time of steel plate processing when the workers fed the plate into the machine for processing, and then scanned again to record the end time of processing after the end of processing, so that the actual man-hours could be calculated through the processing starting time and the end time. The start time and end time would be uploaded to the enterprise’s Manufacturing Execution System (MES) and the man-hours could be calculated from the start and end times in the MES. Figure 1 shows the process in which the start and end times of processing were recorded by workers in the plant, as well as the man-hours calculated by MES. However, in the actual operation process, workers might forget to scan the code at the beginning or end of processing, and instead scan and record the time after a certain period of processing, thus resulting in a significant error between the actual processing time and the processing time recorded by the scan. These kinds of data that deviate significantly from the actual real data are called noise. Noise can cause deviations in the prediction model, which seriously affects the accuracy of the model, so it is necessary to remove the noisy data before modelling. After analysis, it was found that workers forgetting to scan the code would result in either very small or very large recorded processing time values. In response to this situation, this paper adopts an outlier detection based on the box graph method to remove nearly 2000 noisy data. Finally, 3000 pieces of data were left to form the dataset, which was divided in an 8–2 ratio, 2400 pieces of data were placed in the training set, and 600 pieces of data were placed in the testing set.

Discrete data, such as business type (X4), are divided into two types: incoming material processing and delivery, and this article uses one-hot encoding for conversion. One-hot encoding is a common method for converting character data into discrete integer encoding. After using one-hot encoding, 1 represents incoming processing and 0 represents incoming delivery. This can convert character features into numerical features that can be recognized by machine-learning models.

The units of X1, X2, …, X8 are different and the magnitude of them differs tremendously. For example, the unit of raw material weight is kilogram, while the unit of allocated length is meter, and data from different units cannot be compared. If the original data are directly used for model training, they will enhance the impact of features with larger numerical scales on the model, weaken or even ignore the effect of features with smaller numerical scales. Therefore, in order to significantly reduce the interference of features in terms of different value scales and ensure the effectiveness of the model training and fitting process, it is necessary to standardize the feature variables of the original sample data, so that the features of each dimension have the same weight impact on the model objective function. In this paper, Equation (1) is used to min–max normalize the sample by scaling the range of values of each variable to between [0, 1]. In Equation (1), x* represents the normalized new value, x_min represents the minimum value of the sample, and x_max represents the maximum value of the sample.

$${\mathrm{x}}^{*}=\frac{\mathrm{x}-{\mathrm{x}}_{\min }}{{\mathrm{x}}_{\max }-{\mathrm{x}}_{\min }}$$

(1)

3.3. Input Variable Selection

Minimizing the number of input variables significantly reduces the likelihood of over-fitting, collinearity (high correlation between input variables), and transferring noise from data to the calibrated model (Ivanescu et al. 2016) [31]. Having too many input variables, the regression model tends to fit itself to the noise hidden in the training set instead of generalizing underlying patterns and hidden relationships. A proper method for variable selection removes those insignificant or redundant input variables from the regression model (Akinwande et al. 2015) [32].

In the field of natural sciences, the Pearson correlation coefficient is widely used to measure the degree of correlation between two variables. The Pearson correlation coefficient between two variables is defined as the quotient of the covariance and standard deviation between the two variables, as shown in Equation (2), where cov(X,Y) represents the covariance between X and Y, δ_X represents the standard deviation of X, and E[X] represents the expected value of X.

$${\mathsf{\rho }}_{\mathrm{X},\mathrm{Y}}=\frac{\mathrm{cov}(\mathrm{X},\mathrm{Y})}{{\mathsf{\delta }}_{\mathrm{X}}{\mathsf{\delta }}_{\mathrm{Y}}}=\frac{\mathrm{E}\left[\right(\mathrm{X}-\mathsf{\mu }\mathrm{X}\left)\right(\mathrm{Y}-\mathsf{\mu }\mathrm{Y}\left)\right]}{{\mathsf{\delta }}_{\mathrm{X}}{\mathsf{\delta }}_{\mathrm{Y}}}$$

(2)

For discrete random variables, the Pearson correlation coefficient is calculated as shown in Equation (3).

$${\mathrm{r}}_{\mathrm{xy}}=\frac{\mathrm{n}{\displaystyle \sum {\mathrm{x}}_{\mathrm{i}}{\mathrm{y}}_{\mathrm{i}}-{\displaystyle \sum {\mathrm{x}}_{\mathrm{i}}{\displaystyle \sum {\mathrm{y}}_{\mathrm{i}}}}}}{\sqrt{\mathrm{n}{\displaystyle \sum {\mathrm{x}}_{\mathrm{i}}^2-{\left({\displaystyle \sum {\mathrm{x}}_{\mathrm{i}}}\right)}^2}}\sqrt{\mathrm{n}{\displaystyle \sum {\mathrm{y}}_{\mathrm{i}}^2-{\left({\displaystyle \sum {\mathrm{y}}_{\mathrm{i}}}\right)}^2}}}$$

(3)

Pearson correlation coefficient varies from −1 to 1. The value of the coefficient is 1, which means that X and Y can be well described by the linear equation, and all data points fall well on the same line, and Y increases with the increase in X. −1 means that all data points fall on a straight line, and Y decreases as X increases. In addition, 0 means that there is no linear relationship between the two variables.

This paper analyzed the Pearson correlation coefficients between man-hours (Y) and variables X1~X11, respectively, and the results are demonstrated in

Table 2. Correlation comparison of different variables.

	X1	X2	X3	X4	X5	X6	X7	X8
Pearson correlation coefficients	0.0132	0.5009	0.2104	0.3281	0.7410	0.7326	0.0132	0.5116

. Pearson correlation coefficients bigger than 0.4 mean good correlation, bigger than 0.5 mean strong correlation and bigger than 0.6 represent very strong correlation. We selected variables with a correlation greater than 0.4 with man-hours (Y), which are raw material width (X2), allocated length (X5), allocated weight (X6), and finished product width (X8).

Table 3. Characteristic and Man-hour Data of Samples.

No.	X2 (m)	X5 (m)	X6 (kg)	X8 (m)	Man-Hour (min)
1	1.514	939.848	11170	0.755	17.48
2	1.072	720.422	9700	1.072	23.02
3	1.434	528.945	10420	0.715	23.98
4	1.218	1133.040	9750	1.210	30.50
5	1.114	1109.891	8250	0.370	35.50
…	…	…	…	…	…
26	1.386	1077.119	7172	0.460	39.00
27	1.278	1670.853	13410	1.270	43.00
28	1.514	1168.710	13890	0.755	48.00
29	1.278	1680.821	13490	1.270	51.00
30	1.534	1782.664	12880	0.765	55.00

shows some samples which were randomly collected after variable selection.

Table 4. Samples after normalization.

No.	X2	X5	X6	X8	Man-Hour
1	0.72	0.30	0.57	0.46	17.48
2	0.06	0.15	0.48	0.70	23.02
3	0.60	0.03	0.52	0.43	23.98
4	0.27	0.42	0.47	0.80	30.50
5	0.12	0.41	0.38	0.17	35.50
…	…	…	…	…	…
26	0.53	0.39	0.76	0.23	39.00
27	0.36	0.78	0.72	0.85	43.00
28	0.72	0.45	0.75	0.46	48.00
29	0.36	0.79	0.72	0.85	51.00
30	0.75	0.85	0.68	0.46	55.00

shows the product characteristics and man-hours of some samples, which were randomly collected after variable selection and min–max normalization.

3.4. Man-Hour Prediction System

In this study, a man-hour prediction system which consists of data preprocessing, input variable selection and model prediction was established. Data preprocessing and input variable selection are discussed in detail above. After data preprocessing and input variable selection, an ML model is applied to forecast the target outputs. After training the ML model, separate predictions are conducted on test data to check the progress of the ML model. Figure 2 shows the overall work flow of the man-hour prediction system which includes data preprocessing and prediction.

Historical data are a comprehensive reflection of the internal mechanism of a system’s changes. The amount of historical data shows the mechanism of the changes to an extent (Bing, 2014) [33]. We obtained historical processing data from the partner companies, and then used data cleaning methods to remove the noisy data; used one-hot coding to convert the text data into discrete data, and then normalized the data using min–max normalization; used Pearson correlation coefficient for variable selection, and then used machine-learning regression models for man-hour prediction.

Machine learning is now widely used in man-hour prediction and workshop production, such as SVM [34], Back Propagation Neural Network (BPNN) [35], and Decision Tree (DT) [36]. In order to obtain the optimal prediction results, this paper selected four models: SVM, BPNN, RF and Logistic Regression (LR) [37] for experiments. In order to obtain optimal model prediction performance, appropriate model parameters need to be used. For the above four models, we used network search methods to optimize the parameters of the four models and selected the best model parameters for model prediction.

3.5. Random Forest Regression

RF is a combination of decision tree classifiers such that each tree depends on the values of an independently sampled vector with the same distribution for all trees in the forest.

An RF consists of a set of decision trees h(X, θ_k) where X is an input vector, θ_k is an independent and identically distributed random vector. θ_k is generated for the k-th tree independently of the previous random vectors θ₁, …, θ_k−1, but with the same distribution. The reason for introducing θ_k is to control the growth of each tree. After many decision trees are generated, the most popular class is voted on. The k-th tree which is grown by a training set and θ_k, is equivalent to generating a classifier h(X, θ_k). In this sense, given a set of classifiers h(X, θ₁), h(X, θ₂), …, h(X, θ_k), and with the training set randomly presented from the distribution of the random vector Y, X where X is the sample vector and Y is the correctly classified classification label vector, the margin function is defined by Equation (4).

$${\mathrm{m}}_{\mathrm{g}}(\mathrm{X},\mathrm{Y})={\mathrm{av}}_{\mathrm{k}}{\mathrm{I}(\mathrm{h}}_{\mathrm{k}}\left(\mathrm{X}\right)=\mathrm{Y})-{\max }_{\mathrm{j}\ne \mathrm{Y}}{\mathrm{av}}_{\mathrm{k}}{\mathrm{I}(\mathrm{h}}_{\mathrm{k}}\left(\mathrm{X}\right)=\mathrm{j})$$

(4)

where I(x) is the indicator function. The margin function measures the extent to which the number of votes X, Y for the right class exceeds the maximum vote for any other error class—the larger the value, the higher the confidence of the classification. The generalization error is provided by Equation (5) [38]:

$${\mathrm{PE}}^{*}={\mathrm{P}}_{\mathrm{X},\mathrm{Y}}{(\mathrm{m}}_{\mathrm{g}}(\mathrm{X},\mathrm{Y})<0)$$

(5)

where X and Y represent the definition space of probability.

According to the law of large numbers [39], as the number of decision trees increases, all sequences θ_k and PE will converge to Equation (6), corresponding to the frequency converging to probability in the law of large numbers. It explains why random forests do not overfit with the increase in decision trees and have a limited generalization error value.

$${\mathrm{P}}_{\mathrm{X},\mathrm{Y}}{(\mathrm{P}}_{\mathsf{\theta }}\left(\mathrm{h}\right(\mathrm{X},\mathsf{\theta })=\mathrm{Y})-{\max }_{\mathrm{j}\ne \mathrm{Y}}{\mathrm{P}}_{\mathsf{\theta }}\left(\mathrm{h}\right(\mathrm{X},\mathsf{\theta })=\mathrm{j})<0)$$

(6)

The working flow of the random forest algorithm is as follows (also illustrated in Figure 3):

Step 1—The n sub-data sets D1, D2, …, Dn are randomly selected from the whole data set D.

Step 2—A decision is generated for each sub-data, i.e., n decision trees are generated according to n sub-data sets, and a prediction result is obtained for every single decision tree.

Step 3—The third step votes for each decision tree based on their prediction results, and then summarize the voting results.

Step 4—Based on the summarized voting results, the algorithm selects the predicted result with the most votes as the final algorithm’s prediction result.

3.6. Performance Evaluation Metrics

To assess models, we employed the root mean square error (RMSE), mean absolute percentage error (MAPE), population stability index (PSI) which were very widely used for assessment in prediction. The formula are as follows:

$$\mathrm{RMSE}=\sqrt{\frac{1}{\mathrm{n}}\times {{\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{n}}{(\mathrm{y}}_{\mathrm{i}}-{\hat{\mathrm{y}}}_{\mathrm{i}})}}^2}$$

(7)

$$\mathrm{MAPE}=\frac{100\%}{\mathrm{n}}{\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left|\frac{{\hat{\mathrm{y}}}_{\mathrm{i}}-{\mathrm{y}}_{\mathrm{i}}}{{\mathrm{y}}_{\mathrm{i}}}\right|}$$

(8)

$${\mathrm{R}}^2=1-\frac{{{\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{n}}{(\mathrm{y}}_{\mathrm{i}}-{\hat{\mathrm{y}}}_{\mathrm{i}})}}^2}{{{\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{n}}{(\mathrm{y}}_{\mathrm{i}}-\overline{\mathrm{y}})}}^2}$$

(9)

$$\mathrm{PSI}={\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\left(\right(\mathrm{P}}_{\mathrm{a}}^{\mathrm{i}}-{\mathrm{P}}_{\mathrm{e}}^{\mathrm{i}})\times \ln (\frac{{\mathrm{P}}_{\mathrm{a}}^{\mathrm{i}}}{{\mathrm{P}}_{\mathrm{e}}^{\mathrm{i}}}\left)\right)}$$

(10)

In Formulas (7) and (8), n represents the number of evaluated samples, y_i represents the true value of the samples, i.e., actual man-hour, and ŷ_i represents the predicted value of the samples, i.e., estimated man-hour. The closer RMSE and MAPE are to 0, the better the predictive performance of the model. In Formula (9), $\overline{\mathrm{y}}$ represents the mean of the sample, the meanings of n and y_i are the same as those in Formulas (7) and (8). The closer R² is to 1, the better the model performance; the closer it is to 0, the worse the model performance. In Formula (10), ${\mathrm{P}}_{\mathrm{a}}^{\mathrm{i}}$ is the actual proportion of the sample within the partition boundaries, and ${\mathrm{P}}_{\mathrm{e}}^{\mathrm{i}}$ is the predicted proportion of each partition sample in the test dataset. PSI is used to measure the difference in data distribution between test samples and modelling samples and is a common indicator of model stability. It is generally believed that model stability is high when the PSI is less than 0.1, average when the PSI is between 0.1 and 0.25, and poor when the PSI is greater than 0.25.

4. Results

In this paper, experimentation has been carried out using Python 3.9.13, Scikit-Learn 1.0.2 and Pandas 1.4.4, the steel cutting hours were predicted using four models: (SVR), BPNN, LR, and RFR, respectively. A total of 600 data points were used in the test set for prediction, and the parameters of each model were optimized using network search. Finally, experimental comparisons are conducted on the four prediction schemes, and the four man-hours prediction schemes are shown in

Table 5. Prediction performance of the four models.

Model	RMSE	MAPE%	R2	PSI
SVR	3.65	8.03	0.91	0.0226
BPNN	3.94	8.69	0.90	0.0286
LR	4.14	9.12	0.89	0.0249
RFR	2.96	6.51	0.94	0.0072

.

Figure 4 shows a histogram comparing four prediction results, where Figure 4a shows RMSE and R², and Figure 4b shows MAPE. Due to the significant difference in magnitude between PSI and the other three metrics, in order to better demonstrate the comparative relationship of PSI, a separate comparison is made in Figure 4c. Table 5 and Figure 4 show that the RMSE, MAPE, R², and PSI of the RFR model are superior to the other three models. The RMSE of RFR is 0.69 lower than SVR, 0.98 lower than BPNN, and 1.18 lower than LR; The R² of RFR is 0.03 higher than SVR, 0.04 higher than BPNN, and 0.05 higher than LR, indicating that the predicted man-hours of the RFR model are closer to the actual man-hours and have the smallest error. For MAPE, RFR is 1.52% lower than SVR, 2.18% lower than BPNN, and 2.61% lower than LR, which indicates that the RFR model has the highest prediction accuracy. The PSI value of all four models is less than 0.1, indicating that the stability of all four models is high, among which the PSI value of the RFR model is significantly lower than that of the other three models by one order of magnitude, indicating that the RFR model has the highest stability.

Because PSI is a metric of model stability, in order to better analyze the stability of the RFR model, we divided the samples into 10 intervals.

Table 6. Interval distribution of PSI values.

Interval No.	Actual	Predict	Actual_Rate	Predict_Rate	PSI
1	76	69	12.83%	11.67%	0.001112
2	59	54	10.00%	9.17%	0.000725
3	47	58	8.00%	9.83%	0.003783
4	62	65	10.50%	11.00%	0.000233
5	45	42	7.67%	7.17%	0.000337
6	61	64	10.33%	10.83%	0.000236
7	65	63	11.00%	10.67%	0.000103
8	53	51	9.00%	8.67%	0.000126
9	64	68	10.83%	11.50%	0.000398
10	68	66	11.50%	11.17%	0.000098

shows the detailed data for each interval of the RFR model, where actual represents the number of real samples in the interval, predict represents the number of predicted samples in the interval, actual_rate represents the percentage of actual samples in the interval to the total sample, and predict_rate represents the percentage of predicted samples in the interval to the total sample. As can be seen from Table 6, except for the difference of 11 between the number of predicted samples and the actual number of samples in the 3rd interval, there is not much difference between the number of predicted samples and the actual number of samples in the other 9 intervals, such as interval 8 and interval 10, where the difference is only two samples. This indicates that the RFR model has high stability in the prediction of man-hours.

The prediction result of the test set by RFR is shown in Figure 5. The RFR model exhibited outstanding performance on the test set, achieving a coefficient of determination (R²) as high as 0.9447. This metric signifies the model’s capability to elucidate the variability in the target variable. The R² value of the RFR model underscores its considerable advantage in capturing the intricate relationship among steel processing hours. Furthermore, there exists a robust linear correlation between the model predictions and the actual observations, underscoring the RFR model’s high level of accuracy and reliability in predicting steel longitudinal cutting processing time.

In order to further validate the performance of the model, we also presented SVR, BPNN and LR to make a prediction experiment. The forecasting results are shown in Figure 6, Figure 7, Figure 8. Figure 6 shows the prediction result by SVR. The R² value of the SVR model stands at 0.9125, slightly lower than that of the RFR model but still within an acceptable range, indicating the effectiveness of SVR in addressing nonlinear problems. SVR efficiently captures the nonlinear features of the data by identifying the optimal hyperplane in the high-dimensional space. Despite its slightly inferior prediction accuracy compared to RFR, SVR’s robustness in handling small samples or high-dimensional data suggests its potential applicability in specific contexts.

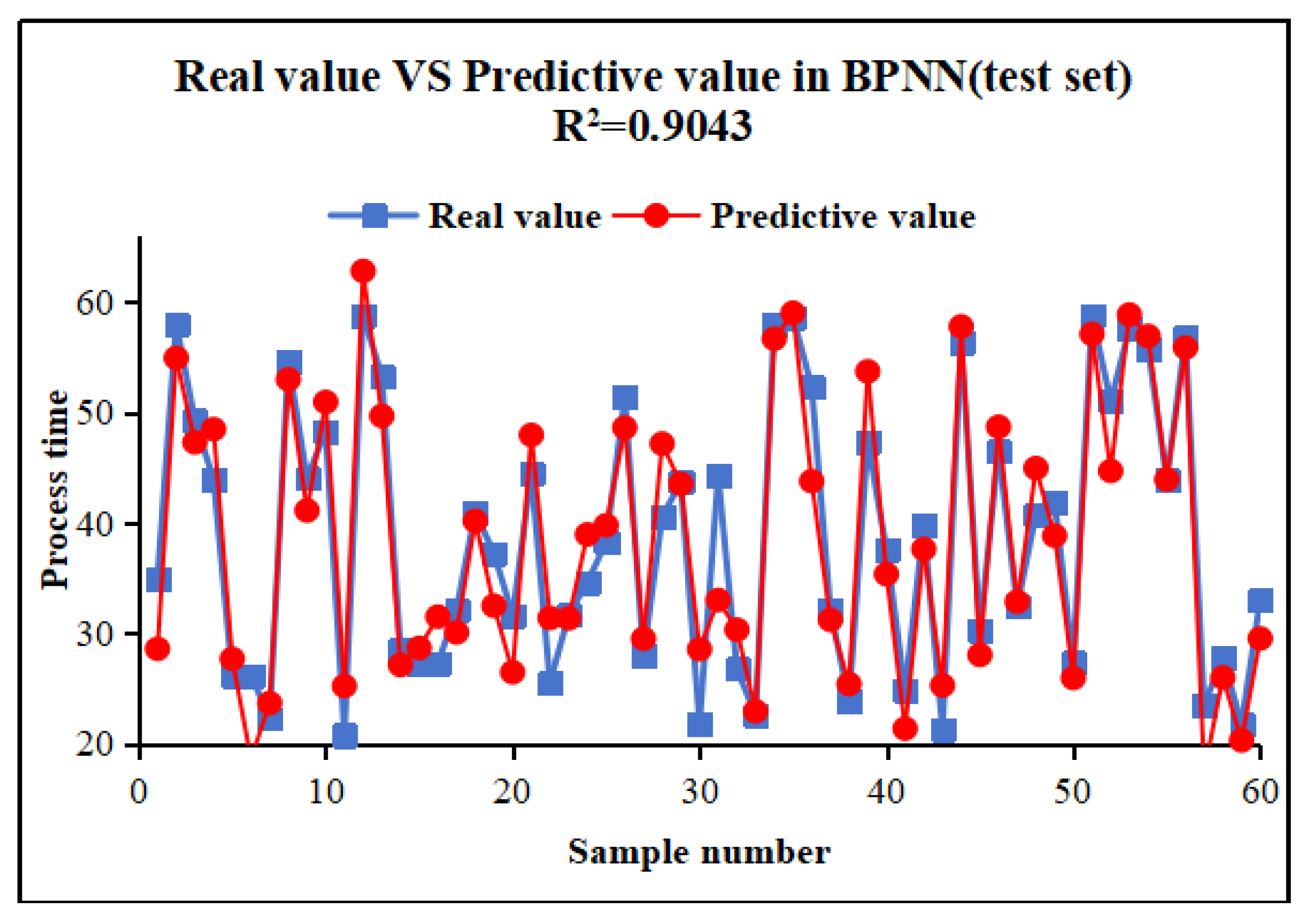
The forecasting result of BPNN can be seen in Figure 7. The R² value of the BPNN model stands at 0.9043, indicating a certain degree of accuracy in modelling the nonlinear relationship between the steel processing time. BPNN, as a deep learning model, can learn complex data mapping relationships through training with the back-propagation algorithm. Despite the potential requirement for more tuning parameters and computational resources, the BPNN’s robust capability in handling large-scale datasets should not be overlooked, particularly in scenarios where data features are rich and model complexity requirements are high.

Figure 8 shows the prediction result of LR. The LR model yields an R² value of 0.8914, representing the weakest performance among the four models. However, this does not diminish LR’s practical value. As a linear model, LR remains effective in handling simple linear relationships or serving as a benchmark model. Its simplicity and interpretability render it a reliable choice in certain scenarios, particularly in studies with limited datasets or stringent requirements for model interpretability.

The relative error of the RFR model is depicted in Figure 9, showcasing an average relative error of −1.7956%. This indicates that the model’s predicted values on the test set generally tend to be lower than the actual values, exhibiting a slight negative bias. This bias could stem from the model’s inadequate comprehension or overfitting of specific data features during the training process. However, given the high R² value of the RFR model, the influence of this bias on the overall prediction results may be constrained.

Figure 10 exhibits the scatter plots with actual man-hours in the x-axis and predicted man-hours in the y-axis from each model. The data for the prediction results come from the test set. The models predicted well as the points are located on or near the y = x line with similar actual and predicted values. However, the result of RFR in (a) shows that the R-square value is small compared to (b), (c) and (d). It indicates that the prediction result of RFR is much better than the other three models. It proves that RFR can be effectively applied to the prediction problem of man-hours while maintaining sufficient accuracy.

Table 7. The comparison of the forecasting results.

No.	Real Man-Hour (m)	RFR	SVR	BPNN	LR
1	20.82	24.23	25.05	25.26	21.80
2	26.24	27.37	27.65	27.72	18.13
3	31.65	27.70	26.74	31.38	35.22
4	34.98	30.10	28.92	38.97	39.27
5	38.24	39.44	39.73	39.80	36.82
6	43.95	47.43	48.28	43.54	32.25
7	49.28	47.76	47.39	47.30	51.14
8	51.41	49.28	48.76	48.63	44.27
9	54.65	53.38	53.07	56.67	52.87
10	58.78	57.49	57.18	59.02	56.98

assesses the comparison of the prediction results by RFR, SVR, BPNN and LR. From reviewing the model prediction results, it is deemed that the RFR model would be a good choice for predicting man-hours in steel plants.

In summary, the findings of this study reveal that the RFR model exhibits the most effective performance in predicting steel longitudinal cutting processing time, followed by the SVR, BPNN, and LR models. These results offer a valuable tool for enhancing production optimization within the steel processing industry, with potential benefits including increased productivity and cost reduction. Future research endeavours could delve into optimizing model strategies, such as employing feature selection and dimensionality reduction techniques to enhance prediction accuracy. Additionally, integrating learning methods could combine the strengths of various models, thereby further improving prediction accuracy and robustness.

5. Discussion

The study presented in this paper focuses on developing a system for predicting man-hours in structural steel fabrication, specifically in the longitudinal cutting process. This is a crucial aspect of production planning and scheduling in steel manufacturing enterprises, as accurate estimates directly impact the efficiency and profitability of the overall production process.

The proposed system utilizes historical data from the manufacturing process, coupled with machine-learning techniques, to predict man-hours with higher accuracy than traditional expert-based estimation methods. This approach addresses a problem in the industry, where the reliance on expert knowledge often leads to inconsistencies and inaccuracies in man-hour predictions.

The use of data preprocessing techniques like one-hot encoding and data normalization is crucial in handling the data inconsistency problem that is often encountered in real-world applications. These techniques help transform the raw data into a format that is more suitable for analysis by machine-learning algorithms. The paper also provides the correlation between independent variables and the dependent variable for the prediction of man-hours. After correlation analysis, the most relevant factors to the longitudinal cutting man-hour of steel coils are raw material width, allocated length, allocated weight, and finished product width, which is consistent with the conclusion drawn by experts in the field in their daily estimation of man-hours.

RFR’s ability to handle complex datasets and its inherent ensemble nature, which combines the predictions of multiple decision trees, makes it a robust choice for this task. The results demonstrated that RFR outperformed the other three ML algorithms considered, further validating its suitability for this application. Ensemble learning models like RF can perform effectively in a global regression when dealing with nonlinear systems which is consistent with previous studies [3,9,40]. Although RFR can effectively handle different nonlinear problems in regression analysis, it also has limitations, such as overfitting when the training set is small. To verify this conclusion, we trained the model with 100 samples and predicted with 50 samples in the dataset. We found that the RFR performed well in the training set, but poorly in the test set. Increasing the number of samples in the training set can prevent overfitting. Our training set has 2400 samples, which effectively prevents overfitting.

However, it is important to note that while the proposed system shows promising results, there are still limitations and areas for improvement. For instance, the system was designed and tested using data from a specific steel manufacturing enterprise. Its generalization ability to other contexts or industries remains to be investigated. Additionally, the system’s performance may be further enhanced by exploring more sophisticated feature engineering techniques or integrating additional data sources.

Future research could also focus on incorporating the system into a comprehensive production planning and scheduling framework. This would allow for a more holistic approach to optimizing production efficiency, taking into account not only man-hour predictions but also other factors like material availability, machine utilization, and workforce capabilities.

6. Conclusions

In the field of steel structure manufacturing, man-hour prediction has always been an indispensable part of production planning and scheduling. Accurate man-hour prediction is not only related to the production efficiency of enterprises but also a key factor affecting the overall production process arrangement and cost control. This article proposes a man-hour prediction system based on historical data, focusing on this core issue, and elaborates on the key technologies of the system in data processing, feature selection, and prediction model construction.

In response to the issue of data inconsistency in the manufacturing process, this article adopted one-hot coding and data normalization techniques. These technologies not only solved the problem of diversity in data formats but also improved the comparability of data and the stability of models. Through this step, we successfully transformed the raw data into effective inputs that the model can recognize. The Pearson correlation coefficient was used to filter out features highly correlated with man-hours. This step not only reduced the complexity of the model and improved computational efficiency but also identified the factors that have a decisive impact on man-hour prediction. After comparing multiple machine-learning algorithms, the random forest regression algorithm was chosen as the main prediction model. Through training and optimization, the model showed superior performance in predicting man-hours.

The man-hour prediction system proposed in this article has higher prediction accuracy and stronger practicality compared to traditional expert estimation methods. The introduction of this system not only improves the accuracy of production planning and scheduling for enterprises but also provides strong support for production cost control and efficiency improvement. The system has good scalability and flexibility. With the continuous accumulation of data in the manufacturing process and the emergence of new technologies, the system can be continuously optimized and upgraded to further improve the accuracy and efficiency of prediction. Meanwhile, the system can also be easily applied to other similar manufacturing fields, providing a solution for predicting man-hours for a wider range of production scenarios.

However, we must also recognize that any predictive model has its limitations and uncertainties. Although the system proposed in this article has greatly improved the accuracy of man-hour prediction, it may still be affected by some uncontrollable factors in practical applications, such as equipment failures and human operation errors. Therefore, when using this system, we need to consider the actual situation comprehensively and make timely adjustments and optimizations. In the future, we will consider more factors, such as the proficiency of workers, and the failure rate of machines, in order to provide more efficient and accurate man-hour prediction services for enterprises.