A Temperature Control Method of Lysozyme Fermentation Based on LRWOA-LSTM-PID

Abstract

In order to overcome the difficulty of parameter tuning caused by the large lag and time-varying nonlinearity of the tank for lysozyme fermentation, a temperature control method based on LRWOA-LSTM-PID is proposed in this paper. Firstly, according to the intrinsic mechanism of the fermenter, a temperature mechanism model based on a dynamic equation is designed, which can better reflect the temperature changes in the fermenter. Secondly, a Proportional Integral Derivative (PID) parameter tuning method based on a Long-Short Term Memory Network (LSTM) is proposed, which takes advantage of the ability of LSTM to learn time sequence information and obtains the variation trend between error sequences under continuous time sampling, thereby adjusting network weights more reasonably and accelerating PID parameter tuning. Finally, a Whale Optimization Algorithm (WOA) based on the Lévy flight and random walk strategy (LRWOA) is proposed for the initialization of LSTM parameters; this algorithm has excellent optimization capabilities and overcomes the problem of LSTM falling into local optimal solutions prematurely during parameter randomization. The results show that the method proposed in this paper can achieve rapid tuning of PID parameters, thereby improving the convergence speed of the system and reducing system overshoot.

1. Introduction

Lysozyme is a hydrolytic enzyme that possesses the function of decomposing microbial cell walls. It functions in bactericidal, anti-inflammatory, antiviral, hemostatic, and tissue regeneration acceleration [1]. As a non-toxic natural antimicrobial agent, lysozyme plays a vital role in biotechnology, food industry and pharmaceutical formulations. Currently, the main method for large-scale industrial production of lysozyme is through the fermentation of genetically modified microorganisms [2].

The process of lysozyme production has strict requirements for temperature control [3,4,5]. During the process, due to the lag issue in the refrigerant cooling method of the fermenter system, using traditional control algorithms to control the temperature will cause a large overshoot, which cannot be recovered in a short time. The temperature error will affect the quality of lysozyme. Therefore, researchers have tried many different control algorithms to improve the precision and stability of temperature control.

Among them, the PID control algorithm has been widely used in temperature control. It has been applied in various fields such as controlling the temperature of aircraft cabins, the temperature control areas of 3D bioprinting devices and the environmental temperature in military equipment development and production [6,7,8,9]. Satisfactory results have been obtained in PID temperature control.

Tuning the PID gain quickly and precisely is necessary to make it work in the control system. The traditional parameter tuning method is the Ziegler–Nichols tuning method [10,11,12], which adjusts the PID parameters based on the open-loop dynamic characteristics of the control system. This method is simple and operable, but it often produces a large overshoot and oscillates back and forth with the response of the controlled system. With the development of technology, some new parameter tuning methods continue to emerge. The Fuzzy PID control algorithm uses fuzzy logic to optimize and tune PID parameters in real time according to certain fuzzy rules [13,14,15,16]. However, this method relies on operators’ experience to establish fuzzy rules, making it unsuitable for systems that require frequent changes in conditions. The PID parameter tuning method based on the Particle Swarm Optimization (PSO) algorithm [17,18,19,20] combines bird foraging behavior, group organization, and optimization mechanisms to better optimize system performance, but it can fall into local optima and premature convergence. The PID parameter tuning method based on the Genetic Algorithm (GA), through a compilation mechanism [21,22,23,24,25], avoids the PID parameter optimization from falling into local optimal solutions. Although the aforementioned meta-heuristic algorithms have strong adaptability and high efficiency [26,27,28,29], their nature of work is still based on iteration, and they are usually based on one-time parameter optimization. When the system model changes, it is necessary to re-optimize the parameters. The ability to control temperature in real-time is poor. How to improve the dynamic characteristics and adaptability of the control system has gradually become an urgent engineering problem to be solved.

Artificial Neural Networks (ANN) [30,31,32,33] have advantages such as good fault tolerance, high non-linearity, unique associative memory function, and excellent adaptability. They can adaptively handle non-linear dynamic information and perform complex logical operations, and have been widely used in PID parameter tuning. The BP neural network can be used to optimize PID controller parameters [34]. It has been utilized to control camera stabilizers, achieving the precise control of the stable position of the camera. The Dynamic Neural Network (DNN) can be used to tune the gain of the PID controller online [35], which is applied to control pneumatic artificial muscles. This improves the speed and performance of the control process, and features a dynamically self-organizing structure. In [36], a Radial Basis Function (RBF) neural network is used to identify the information of a floating system, and adjust controller parameters in real time. This method exhibits good control effects when dealing with external disturbances and internal parameter changes in maglev systems. The Recurrent Neural Network (RNN) can be used to adapt the PID controller [37], which controls a single degree of freedom pendulum to track the desired reference position with a rapid response and minimal tracking error. This provides excellent position tracking results and robustness to changes in system parameters. In [38], the Diagonal Recurrent Neural Network (DRNN) is used to optimize PID controller parameters. In a multi-point mooring system, the network learns the dynamic changes in the mooring system, minimizing square positioning error, which enhances recognition ability and interference resistance. In order to further improve the optimization ability of neural networks, the PSO algorithm is used to optimize the initial values of the BP neural network, and then optimize the control parameters of PID to achieve the precise control of liquid fertilizer flow rate [39]. The Grey Wolf Optimization algorithm is used to optimize the initial parameters of fuzzy neural networks; then, the fuzzy neural network with the optimal parameters is used to adjust the PID parameters to achieve the smoothness and stability of vehicle control [40]. Although the aforementioned neural networks can quickly tune PID parameters and improve the system’s dynamic characteristics and adaptability, they have not effectively utilized target information, historical parameter information, and historical control information. Moreover, the backpropagation algorithm in neural networks has poor global optimization capability and is prone to falling into local optima, limiting the application of neural networks in PID controllers.

To improve the shortcomings of traditional neural network methods in optimizing PID controller parameters, a temperature control method of lysozyme fermentation based on the LRWOA-LSTM-PID method is proposed in this paper. The method first establishes a fermenter temperature mechanism model described using dynamic equations. Then, it utilizes the ability of LSTM to learn time sequence information to capture the trend of error sequences under continuous time sampling. Finally, it initializes LSTM parameters based on the LRWOA algorithm to enhance the stability of the initial parameters of the LSTM, thus endowing the controller with an excellent temperature control capability.

The contributions of the method proposed in this paper are as follows:

(1)

A temperature mechanism model based on a dynamic equation is designed, which can better reflect the temperature changes in the fermenter.

(2)

A Whale Optimization Algorithm based on the Lévy flight and random walk strategy is proposed. By introducing Levy flight and random walk strategies into the Whale Optimization Algorithm, the global and local optimization abilities of the algorithm are improved. It overcomes the problem of the original algorithm falling into local extrema prematurely when dealing with complex issues.

(3)

A PID parameter tuning method based on LSTM is proposed. This method has the ability to learn time sequences information and capture the trend of error sequences under continuous time sampling, so the network weight can be adjusted more reasonably. As a result, it achieves the rapid tuning of the PID parameters K_p, K_i, and K_d.

(4)

An LSTM parameter initialization method based on the LRWOA algorithm is proposed. The method takes advantage of the excellent optimization capability of the LRWOA algorithm, overcoming the problem of traditional random parameter initialization methods falling into local optimum solutions prematurely, thereby enhancing the stability of the initial parameters of the LSTM neural network.

The remainder of this paper is organized as follows: Section 2 introduces the modeling of the lysozyme fermenter temperature system. Section 3 introduces the improved LRWOA algorithm. Section 4 describes the overall network structure and the LRWOA-LSTM-PID algorithm. Section 5 analyzes the experimental results and draws conclusions. Finally, the conclusion is given in Section 6.

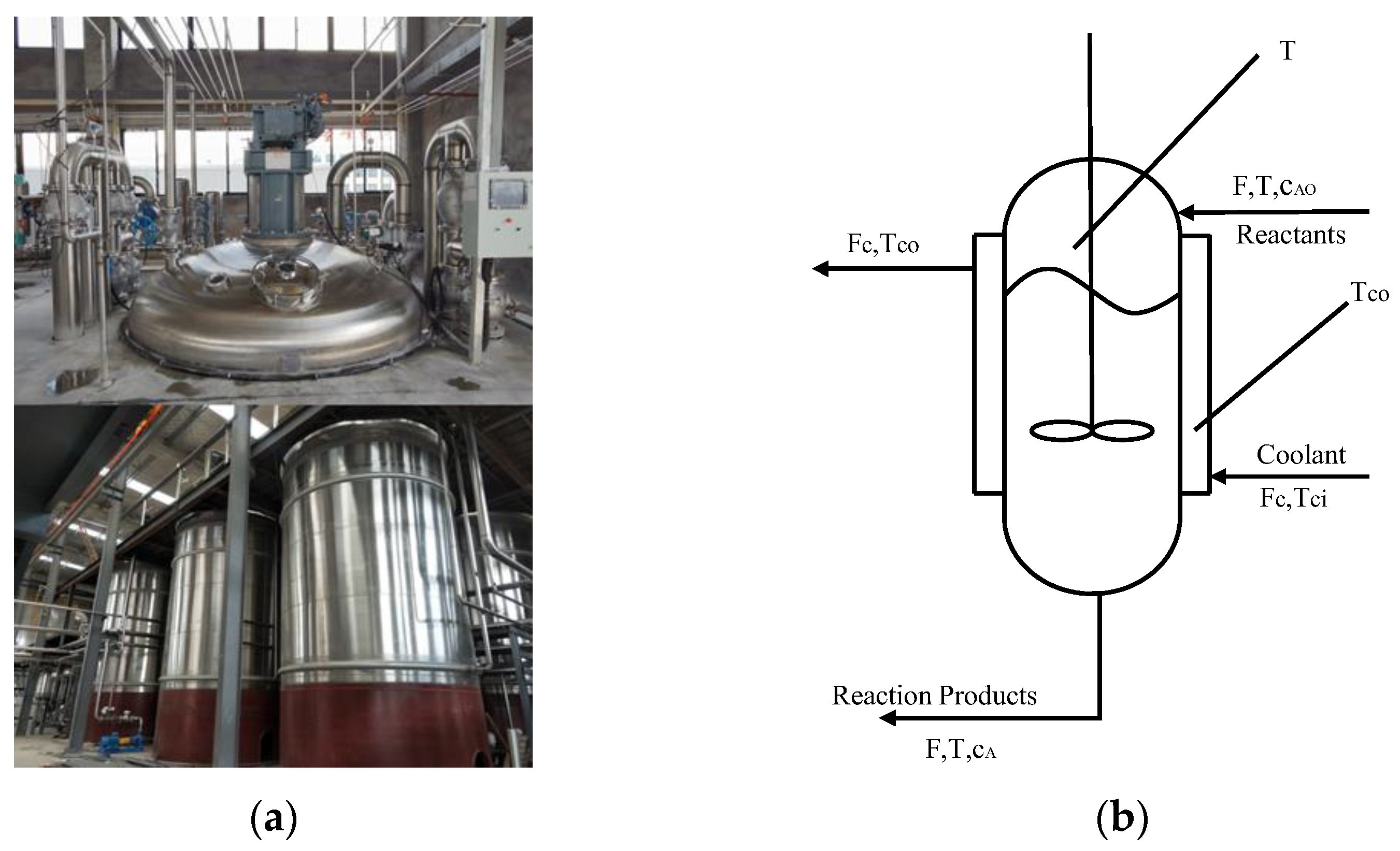
2. Modeling of Fermenter Temperature

An appropriate mathematical model can accurately describe the dynamic relationship between input and output variables over time, playing a crucial role in lysozyme fermentation temperature control.

Fermenter Temperature Mathematical Model

The lysozyme fermenter is shown in Figure 1a. The lysozyme fermenter is a non-adiabatic continuously stirred liquid-phase reaction vessel, as shown in Figure 1b.

According to the internal mechanism of the fermenter, the mathematical model of the lysozyme reaction vessel was established using mechanism modeling method in this paper.

(1)

Chemical reaction rate equation

The chemical reaction inside the fermenter is an irreversible exothermic reaction $A\stackrel{k_0}{\to }B$, and the concentration of yeast $C_A$ and temperature $T$ are essentially uniformly distributed inside the fermenter. From this, $r_A$ for the chemical reaction rate equation of $A$ can be obtained:

$$r_A=\frac{d{C}_A}{dt}=-k_0{c}_A{e}^{-\frac{E}{RT}}$$

(1)

In the equation, $A$ represents the seed of the microorganism; $B$ is lysozyme; $E$ is the activation energy of the reaction (J/mol); $k_0$ is the reaction frequency factor; $R$ is the gas constant; $C_A$ is the concentration of reactant $A$ (mol/m³).

(2)

Material balance equation

The changing rate of cumulant of materials in the fermenter should equal the amount of material entering the fermenter minus the amount leaving, plus or minus the amount consumed or produced using the chemical reaction of the yeast. Given that the stirrer in the fermenter can mix the yeast thoroughly, we can assume complete mixing within the fermenter, making the density, temperature, and yeast molecular concentration equal everywhere.

For the fermenter, the overall material balance equation is:

$$\frac{d\left(\rho V\right)}{dt}={\rho }_0{F}_0-\rho F$$

(2)

In (2), $F_0$ is the volume flow of yeast (m³/s); ${\rho }_0$ is the yeast density (kg/m³); $F$ is the volume flow of fermentation products (m³/s); $\rho$ is the fermentation product density (kg/m³); $V$ represents the effective volume of fermenter (m³).

The material balance equation for reactant $A$ is as follows:

$$\frac{d{V}_{C_A}}{dt}=F_0{C}_{A0}-F_{C_A}+V_{r_A}$$

(3)

In (3), $C_{A0}$ is the concentration of reactant in yeast (mol/m³); $F_{C_A}$ stands for the volumetric flow rate of reactant $A$ (m³/s); $V_{r_A}$ is the volume of reactant $A$ (m³).

(3)

The heat balance equation

From the heat balance relationship, we know:

$$\frac{d{H}_R}{dt}=Q_1-Q_2\pm Q_3\pm Q_4$$

(4)

In (4), $H_R$ represents the accumulated heat within the fermenter (J); $Q_1$ is the heat brought into the fermenter by the material per unit time (J/s); $Q_2$ is the heat taken away by the material leaving the fermenter per unit time (J/s); $Q_3$ refers to the heat effect brought about by the chemical reaction per unit time (J/s)—if it is an endothermic reaction, the minus sign is taken before $Q_3$, if it is exothermic, the plus sign is taken; $Q_4$ is the heat exchanged between the fermenter and the environment per unit time (J/s). If heat is dissipated, the minus sign is taken before $Q_4$, if heat is absorbed from the environment, the plus sign is taken. If the fermenter is adiabatic, $Q_4$ is zero.

Assuming that the temperature of the cooling liquid in the interlayer is consistent with its outlet temperature $T_{co}$, ignoring the thermal melt of the inner wall, and assuming that the specific heat capacity of the feed and the effluent always remain consistent, the heat balance equation can be derived as follows:

$$\frac{dV\rho C_{P}T}{dt}=F_0{\rho }_0{C}_P{T}_f-C_P{F}_{P}T+K_e{A}_e\left(T_{co}-T\right)-\left(∆H\right)V_{r_A}$$

(5)

In the (5), $T_f$ is the feed temperature during yeast fermentation (K); $C_P$ is the average specific heat capacity of the feed and effluent in the fermentation process (J/(kg·K)); F is the average volumetric flow rate of materials entering and exiting the fermenter (m³/s); ∆H is the reaction heat per unit time (J/s); $K_e$ is the total heat transfer coefficient between the fermenter wall and the material inside the tank (W/(m²·K)); $A_e$ is the heat transfer area (m²); $T_{co}$ is the outlet temperature of the condensate (K).

The heat balance equation for the condensate in the fermenter jacket can also be obtained as follows:

$$\frac{d{V}_c{\rho }_c{C}_{pc}}{dt}=F_c{\rho }_c{C}_{pc}\left(T_{ci}-T_{co}\right)+K_e{A}_e\left(T-T_{co}\right)$$

(6)

In the (6), $C_{pc}$ represents the average specific heat capacity of the condensate (J/(kg·K)); $V_c$ is the volume of the condensate in the jacket (m³); ${\rho }_c$ represents the density of the condensate (kg/m³); $F_c$ is the volume flow rate of the condensate (m³/s); $T_{ci}$ is the inlet temperature of the condensate (K).

As the volumes in the fermenter and jacket remain constant and the density of the inflowing and outflowing materials is identical, (1) indicates that $F=F_0$. Substituting Equations (1) and (2) into Equations (3), (5) and (6) yields:

$$\frac{d{c}_A}{dt}=\frac{F}{V}\left(c_{A0}{-c}_A\right)-k_0{c}_A{e}^{-\frac{E}{RT}}$$

(7)

$$\frac{dT}{dt}=\frac{F}{V}\left(T_f-T\right)+\frac{∆H}{\rho C_P}{c}_A{k}_0{e}^{-\frac{E}{RT}}+\frac{K_e{A}_e}{V\rho C_P}\left(T_{co}-T\right)$$

(8)

$$\frac{d{T}_{co}}{dt}=\frac{F_c}{V_c}\left(T_{ci}-T_{co}\right)+\frac{K_e{A}_e}{V_c{\rho }_c{C}_{Pc}}\left(T-T_{co}\right)$$

(9)

The mathematical Equations (7)–(9) established above are nonlinear dynamic equations. To use existing control theory to analyze the dynamic characteristics of the fermenter under small disturbances, the mathematical equations need to be linearized. The state variable of the fermenter temperature system is denoted by $\left\{c_{A}T{T}_{co}\right\}$, and the input variable, denoted by $\left\{F{c}_{A0}{T}_f{F}_c{T}_{ci}\right\}$, consists of control variables and external disturbances from the actual fermentation process.

The steady-state values of the state and input variables of the fermenter temperature system are $\left\{\overline{c_A}\overline{T}\overline{T_{co}}\overline{F}\overline{c_{A0}}\overline{T_f}\overline{F_c}\overline{T_{ci}}\right\}$ and the corresponding changes in the input variables are $\left\{∆c_A∆T∆T_{co}∆F∆c_{A0}∆T_f∆F_c∆T_{ci}\right\}$. By using differential operations, a linearized model can be obtained. According to (7), the equation is:

$$\frac{d∆c_A}{dt}=\frac{\overline{F}}{V}\left(∆c_{A0}-∆c_A\right)+\left(\frac{\overline{c_{A0}}}{V}-\frac{\overline{c_A}}{V}\right)∆F-K_T∆c_A-K_T\overline{c_A}\frac{E}{R{\overline{T}}^2}∆T$$

(10)

In (10), $K_T=K_0{e}^{-\frac{E}{RT}}$; $K_0$ is the total heat transfer coefficient, (W/(m²·K)); $E$ is the activation energy (J/mol); $R$ is the molar gas constant, ((Pa·m³)/(mol·K)); $T$ is the thermodynamic temperature (K); $\mathsf{\Delta }$ represents changes; the superscript indicates the vector of each variable.

Similarly, based on Equations (8) and (9), we have:

$$\frac{d∆T}{dt}=\frac{\overline{F}}{V}\left(∆T_f-∆T\right)+\left(\frac{\overline{T_f}}{V}-\frac{\overline{T}}{V}\right)∆F+\frac{∆H}{\rho C_P}{K}_T∆c_A+\frac{∆H}{\rho C_P}{K}_T\overline{c_A}\frac{E}{R{\overline{T}}^2}∆T+\frac{K_e{A}_e}{V\rho C_P}\left(∆T_{co}-∆T\right)$$

(11)

$$\frac{d∆T_{co}}{dt}=\frac{\overline{F_c}}{V_c}\left(∆T_{ci}-{∆T}_{co}\right)+\left(\frac{\overline{T_{ci}}}{V}-\frac{\overline{T_{co}}}{V}\right)∆F_c+\frac{K_e{A}_e}{V_c{\rho }_c{C}_{Pc}}\left(∆T-{∆T}_{co}\right)$$

(12)

If we set $Z={\left\{∆c_A∆T∆T_{co}\right\}}^T$ and $Z={\left\{∆F∆c_{A0}∆T_f∆F_c∆T_{ci}\right\}}^T$, we can obtain the following standard linear state equation:

$$\frac{dZ}{dt}=AZ+BU$$

(13a)

$$A=\left[\begin{array}{ccc}-\left(\frac{\overline{F}}{V}+K_T\right)& -\frac{E}{R_T^{-2}}{K}_T\overline{c_A}& 0\\ & & \\ K_T\frac{\Delta H}{\rho c_p}& K_T\overline{c_A}\frac{\Delta H}{\rho c_p}\frac{E}{R_T^{-2}}-\frac{\overline{F}}{V}-\frac{K{A}_e}{V\rho c_p}& \frac{K{A}_e}{V\rho c_p}\\ & & \\ 0& \frac{K{A}_e}{V_c{\rho }_c{c}_{pc}}& -\left(\frac{{\overline{F}}_c}{V_c}+\frac{K{A}_e}{V_c{\rho }_c{c}_{pc}}\right)\end{array}\right]$$

(13b)

$$\left.B=\left[\begin{array}{ccccc}\frac{\overline{c_{A0}}}{V}-\frac{\overline{c_A}}{V}& \frac{\overline{F}}{V}& 0& 0& 0\\ \frac{\overline{T_f}}{V}-\frac{\overline{T}}{V}& 0& \frac{\overline{F}}{V}& 0& 0\\ 0& 0& 0& \frac{\overline{T_{ci}}}{V_c}-\frac{\overline{T_{co}}}{V_c}& \frac{\overline{F_c}}{V_c}\end{array}\right.\right]$$

(13c)

The temperature state equation established using the above mathematical equation can reflect the dynamic impact of control variables and external disturbances on the output of the fermenter temperature system. This mathematical model can be used to analyze the stability of the fermenter temperature.

First, parameters such as the temperature, density, flow rate, volume of the lysozyme in the fermenter, the volume of the fermenter jacket, and the volume of the condensate must be collected; then, the heat transfer area, heat transfer coefficient, specific heat capacity, condensate density, reaction activation energy, gas constant, and reaction frequency factor based on the parameters of the fermenter and the lysozyme fermentation process is determined. The collected parameters are then analyzed and set, and brought into the established mathematical model to obtain the transfer function designed using the mechanistic modeling. The equation is as follows:

$$G\left(S\right)=\frac{4.6e^{-8.6s}}{8s^2+8.9s+2}$$

(14)

3. Algorithm

3.1. Whale Optimization Algorithm

WOA [41] is a new swarm intelligence optimization algorithm, which contains three parts: Encircling Prey, Bubble-net attacking and Search Predation.

(1)

Encircling Prey

Assume that in a D-dimensional space, the location of the whale individual with the best solution in the current whale population is ${\overrightarrow{X}}^{\ast }$(t), and the location of any other whale individual is $\overrightarrow{X}$(t). Then, the whale individual $\overrightarrow{X}$(t) will change its location under the influence of the best whale individual. The calculation equations for the next location $\overrightarrow{X}$(t + 1) is as follows:

$$\overrightarrow{D}=\left|\overrightarrow{C}·{\overrightarrow{X}}^{\ast }\left(t\right)-\overrightarrow{X}\left(t\right)\right|$$

(15)

$$\overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}^{\ast }\left(t\right)-\overrightarrow{A}\cdot \overrightarrow{D}$$

(16)

$$\overrightarrow{C}=2·\overrightarrow{r}$$

(17)

$$\overrightarrow{A}=2\overrightarrow{a}·\overrightarrow{r}-\overrightarrow{a}$$

(18)

In the calculation of $\overrightarrow{D}$, the meaning of | | is to find the absolute value; $a$ gradually decays from 2 to 0 as the number of iterations of the algorithm increases; $r$ is a random vector between [0, 1].

(2)

Bubble-net attacking

Bubble-net attacking is a unique hunting method of whales. To mathematically model the behavior of bubble-net behavior, the following two methods are designed:

• Contraction enveloping mechanism: This method is roughly the same as enveloping prey, the difference being that the original range of a is adjusted from 2 to 0 to a fixed value of 1. Since a determines the range of A, the range of A changes from the original [−a, a] to now [−1, 1]. At this time, the new position of the whale individual can appear at any position between the original position and the optimal solution position.
• Spiral updating position: This method first calculates the distance between the whale individual located at (X,Y) and the prey located at (X*,Y*). Then, a spiral equation is established between the two positions, thereby simulating the spiral movement pattern of the whale population. The equation is as follows:

$$\overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}^{\ast }\left(t\right)+{\overrightarrow{D}}^{\prime }·e^{bl}·\mathit{cos}\left(2\pi l\right)$$

(19)

$${\overrightarrow{D}}^{\prime }=\left|{\overrightarrow{X}}^{\ast }\left(t\right)-\overrightarrow{X}\left(t\right)\right|$$

(20)

In (19), $b$ is the constant for the shape of the logarithmic spiral; $l$ is a random number between −1 and 1. At this time, the whale will move around the prey in a spiral path within the previous circular area.

To simulate the synchronized behavior of whales, we assume that the probabilities of choosing the contraction enveloping mechanism and the spiral updating position are equal. This makes it convenient to update the position of the whales during the optimization process. The mathematical model is as follows:

$$\overrightarrow{X}\left(t+1\right)=\left\{\begin{array}{c}{\overrightarrow{X}}^{\ast }-\overrightarrow{A}·\overrightarrow{D}ifp<0.5\\ {\overrightarrow{X}}^{\ast }(t)+{\overrightarrow{D}}^{\prime }·e^{bl}·\mathit{cos}\left(2\pi l\right)ifp\ge 0.5\end{array}\right.$$

(21)

(3)

Search Predation

In the mathematical model of the contraction enveloping predation behavior, the range of $A_1$ is limited to [−1, 1]. If the range of $A_1$ is not within [−1, 1], any whale in the current swarm may not approach the currently optimal whale individual, but instead randomly select one individual from the current whale swarm to approach. Although search predation can cause a random individual in the current whale swarm to deviate from the target prey, it can enhance the global search ability of the whale swarm. $A$ and $C$ are coefficients. In the D-dimensional space, the position of a random individual in the current whale swarm is ${\overrightarrow{X}}_{rand}$. The mathematical model of search predation behavior can be described using the following equation:

$$\overrightarrow{D}=\left|\overrightarrow{C}·{\overrightarrow{X}}_{rand}-\overrightarrow{X}\right|$$

(22)

$$\overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}_{rand}-\overrightarrow{A}·\overrightarrow{D}$$

(23)

3.2. LRWOA Algorithm

The WOA tends to prematurely fall into local optimums when solving complex optimization problems. To solve this issue, this paper proposes a WOA based on Lévy flight and random walk strategies. The Lévy flight strategy is introduced to make individual whales exist widely in the search range and improve the global optimization ability of the algorithm. The random walk strategy is introduced to make individual whales search for the best value in a relatively concentrated range and improves the local optimization ability of the algorithm.

3.2.1. Lévy Flight Strategy

The Lévy flight [42] refers to a random walk where the probability distribution of the step length follows a heavy-tail distribution, which can maximize the search efficiency in uncertain environments. When the spatial dimension of the Lévy flight’s random movement is higher than one dimension, the step length distribution shows isotropy. The Lévy flight strategy exhibits excellent global search capability due to its high probability of performing a small area search and a low probability of long-distance flight. The position update equation in the Lévy flight strategy is as follows:

$$x_k^{new}\left(t\right)=x_k\left(t\right)+l\oplus levy\left(\lambda \right)$$

(24)

where $levy\left(\lambda \right)$ is the step length of the Lévy distribution, which satisfies $levy~u=t^{-\lambda }$, 1< λ ≤ 3; $\oplus$ denotes element-wise multiplication; $l$ represents the control step factor, $l=0.01(x_k\left(t\right)-x_b)$; $x_b$ is the optimal solution obtained after $t$ iterations; $x_k\left(t\right)$ is the k-th solution of the t-th generation.

The Mantegna method is commonly used to obtain the step length $s$ of the Lévy flight strategy, as shown in (25):

$$s=\frac{\mu }{{\left|v\right|}^{1/\gamma }}$$

(25)

where $\gamma$ is typically 1.5; $\mu$ and $\nu$ follow a normal distribution, $\mu ~N\left(0,{\sigma }_{\mu }^2\right),v~N\left(0,{\sigma }_v^2\right),{\sigma }_v=1$, defined as follows:

$${\sigma }_{\mu }={\left\{\frac{\Gamma \left(1+\gamma \right)\mathit{sin}\left(\pi \gamma /2\right)}{\gamma ·\Gamma \left[\left(\gamma +1\right)/2·2^{\left(\gamma -1\right)/2}\right]}\right\}}^{1/\gamma }$$

(26)

Figure 2 shows the walking trajectory of a two-dimensional random walk and a two-dimensional Levy flight. The difference between the two modes can be seen: the random walk provides roughly the same size for each step, while the Levy flight performs many small steps with the occasional large step.

3.2.2. Random Walk Strategy

The basic idea of random walk [43] is as follows: starting from any individual in a group, traverse the entire group. For any given individual, the probability of moving to an adjacent individual is 1 − a, and the probability of randomly jumping to any individual in the group is $a$. The $a$ mentioned above is the probability of the jump occurring. After each jump, the probability distribution can be obtained that reflects the probability of each individual in the group being found. This probability distribution is then used as an input for the next walk and the process is repeated. Under predetermined conditions, the probability distribution tends to converge, and the stable probability distribution is obtained after convergence.

Random walks utilize crossover and hybrid mutation to generate new solutions, which can enhance the diversity of the group and effectively avoid falling into local optimal solutions, thereby improving the local search ability of the target algorithm. Applying a random walk strategy in swarm intelligence algorithms can accelerate the speed of finding optimal solutions. The update equation for the random walk strategy is as follows:

$$x_k^{new}\left(t\right)=x_k\left(t\right)+\epsilon \left(x_j\left(t\right)-x_i\left(t\right)\right)$$

(27)

where, $\epsilon$ is the scale factor, ε~U(0, 1); $x_j\left(t\right)$ and $x_i\left(t\right)$ are two random solutions in the t-th generation.

3.2.3. LRWOA

While both the random walk strategy and Levy flight strategy can update individual positions, they cannot guarantee that the fitness of the new solution is greater than the fitness of the original solution. Therefore, we use a Greedy mechanism to ensure the selection of the optimal solution, as shown in the following equation:

$$x_k\left(t\right)=\left\{\begin{array}{c}{x}_k\left(t\right),fit\left({x_i}^{\prime }\right(t\left)\right)<fit\left(x_k\right(t\left)\right)\\ x_i^{\prime }\left(t\right),fit\left(x_i^{\prime }\left(t\right)\right)>fit\left(x_k\left(t\right)\right)\end{array}\right.$$

(28)

Once the random walk strategy and Levy flight strategy have been established, the Whale Optimization Algorithm (WOA) proceeds with its optimization process as follows: If a randomly selected individual’s value is equal to the best, second best, or third best individual value and is less than $0.5-0.5t/(\phi \ast max)$, the whale individual will use the Levy flight strategy to update its position. On the other hand, if the value of a randomly selected individual matches the best, second best, or third best individual value and is greater than or equal to $0.5-0.5t/(\phi \ast max)$, the whale individual will choose the random walk strategy to update its position. Otherwise, the whale individual will use the original WOA strategy to update its position. $t$ represents the current iteration within the process, $max$ denotes the maximum number of iterations, and $\phi$ refers to the exploration iteration ratio. The algorithm flow as shown in the Algorithm LRWOA (Algorithm 1).

Algorithm 1. LRWOA

Input: Number of whales $N$, maximum number of iterations $max$, iteration ratio $\phi$ Output: $X_{\alpha }$

Start:

1: Initialize the whale population $X_k$ (k = 1, 2,...,N) in the search space. 2: Calculate the fitness values of the whale population individuals and select the best individual $X_{\alpha }$, the second best individual $X_{\beta }$, and the third best individual $X_{\delta }$. 3: Select a random individual rand and record its position. 4: while $t < max$ 5:   for $k = 1$ to $N$ perform 6:    Calculate the values of parameters $C$ and $A$ according to $\overrightarrow{C}=2·\overrightarrow{r}$ and $\overrightarrow{A}=2\overrightarrow{a}·\overrightarrow{r}-\overrightarrow{a}$ 7:     if (X= =$X_{\alpha }$||X= =$X_{\beta }$||X= =$X_{\delta }$) perform 8:      if (rand < $0.5 - 0.5t/\left(\phi \ast max\right)$) perform 9:       Adjust the positions by $x_k^{new}\left(t\right)=x_k\left(t\right)+l\oplus levy\left(\lambda \right)$. 10:       else 11:       Adjust the positions by $x_k^{new}\left(t\right)=x_k\left(t\right)+\epsilon \left(x_j\left(t\right)-x_i\left(t\right)\right)$. 12:       end if 13:      Select the better positions based on $x_k\left(t\right)=\left\{\begin{array}{c}{x}_k\left(t\right), fit\left({x_i}^{\prime }\left(t\right)\right)<fit\left(x_k\left(t\right)\right)\\ {x_i}^{\prime }\left(t\right), fit\left({x_i}^{\prime }\left(t\right)\right)>fit\left(x_k\left(t\right)\right)\end{array}\right.$. 14:     end if 15:     Update the individuals’ positions based on Equations (15) to (23). 16:    end for 17:    Calculate the fitness of individuals, update whale positions, and record the positions. 18:    $t = t + 1$ 19: end while

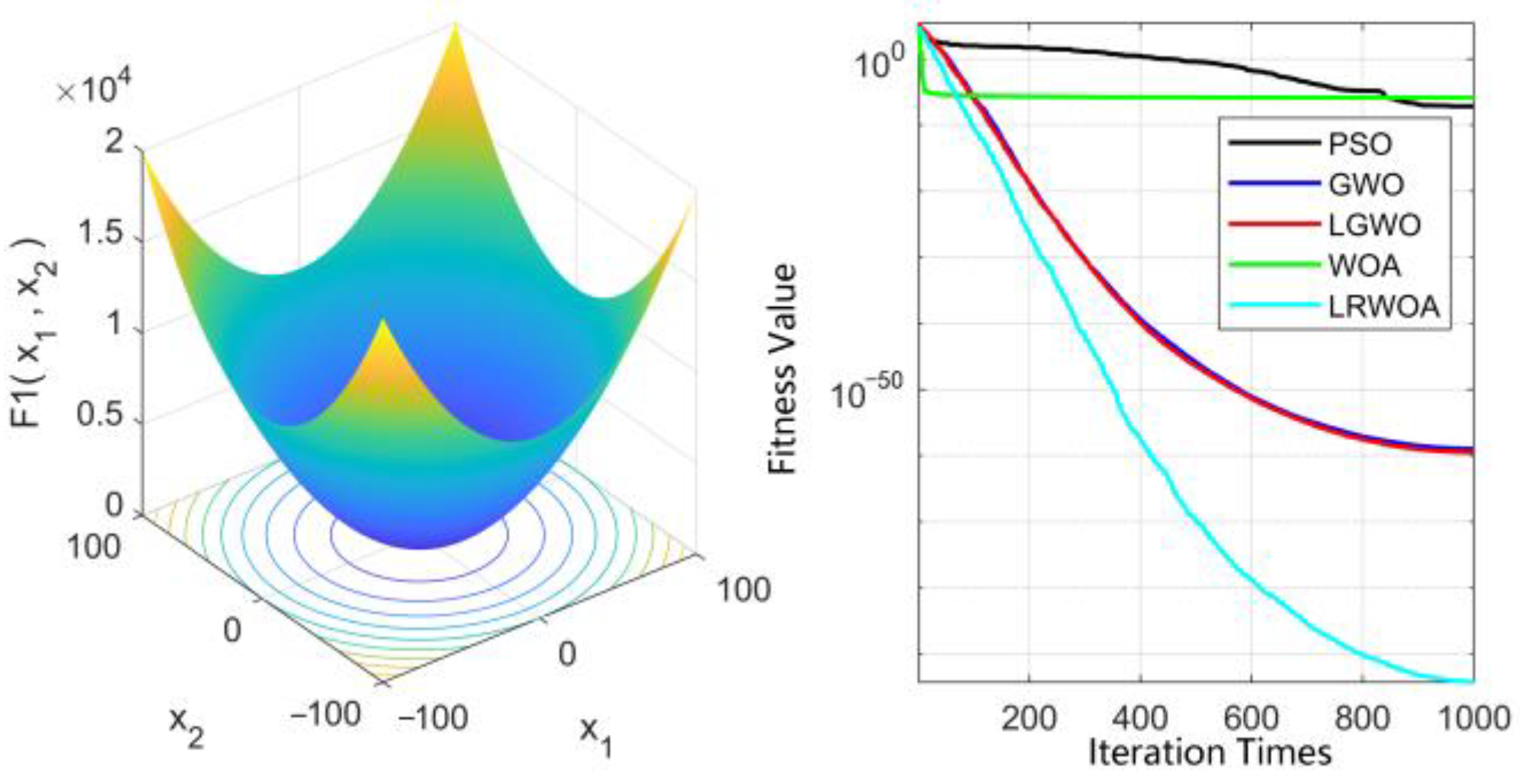
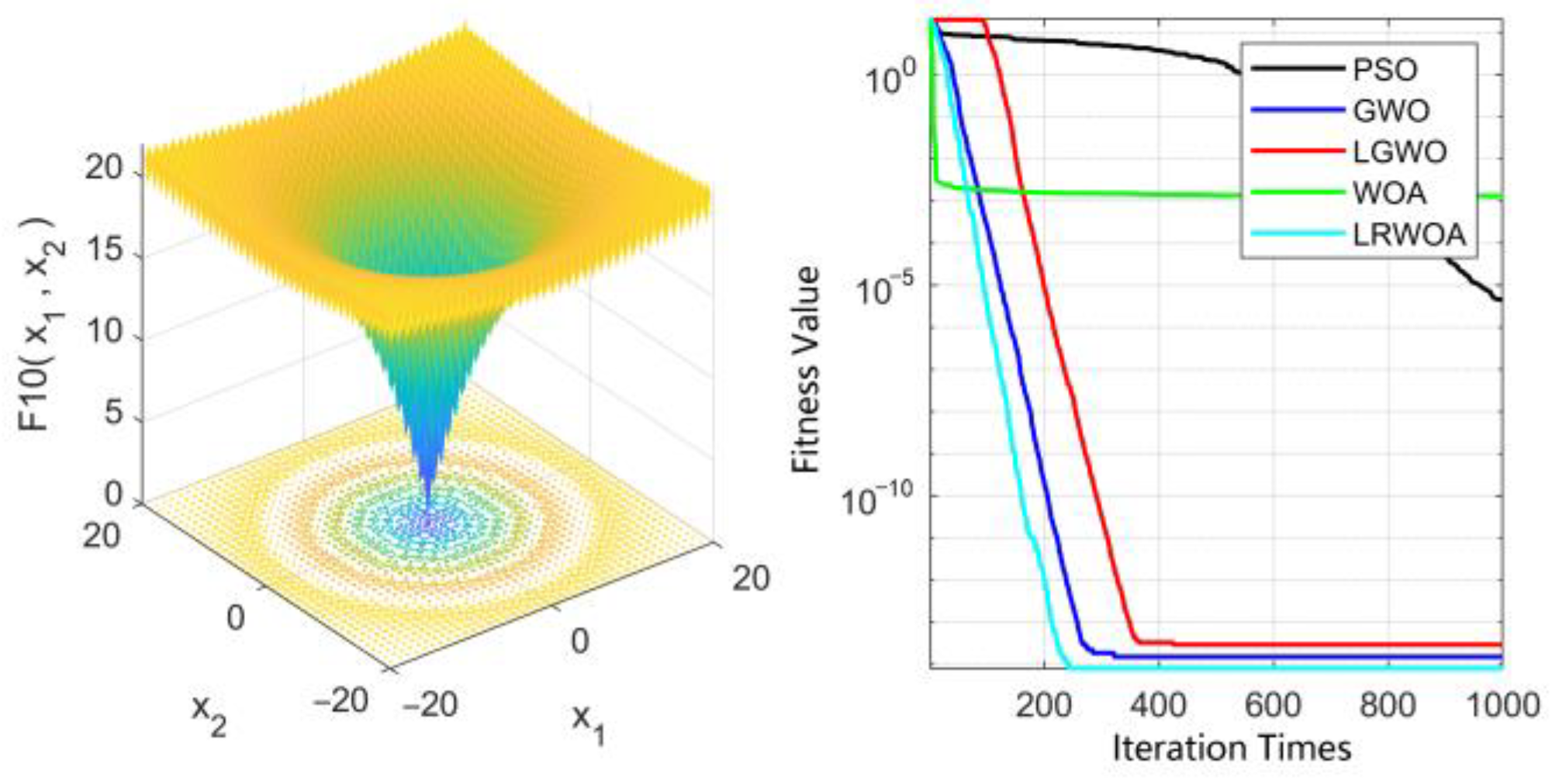
3.2.4. Results and Analysis

To evaluate the performance of the LRWOA algorithm, this study selects 15 internationally recognized benchmark functions as the basis for the experimental tests. These benchmark functions vary in size and complexity but are all designed for minimization problems. The benchmark functions can be classified into single-peak and multi-peak functions. The single-peak functions are used to assess the algorithm’s exploitation capability, while the multi-peak functions are used to assess the algorithm’s exploration capability.

Table 1. Types, names, ranges, and adaptive values of international test functions.

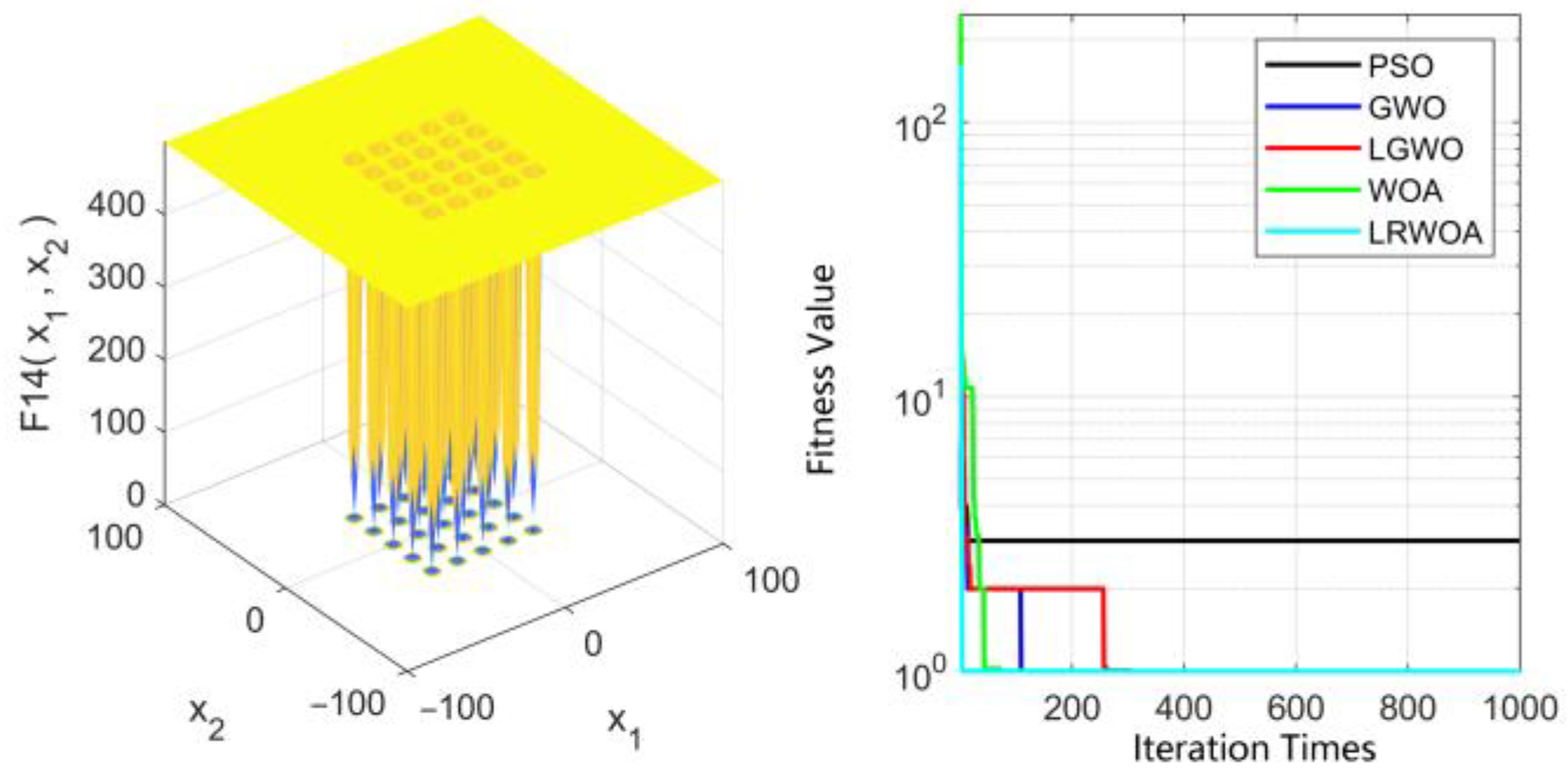
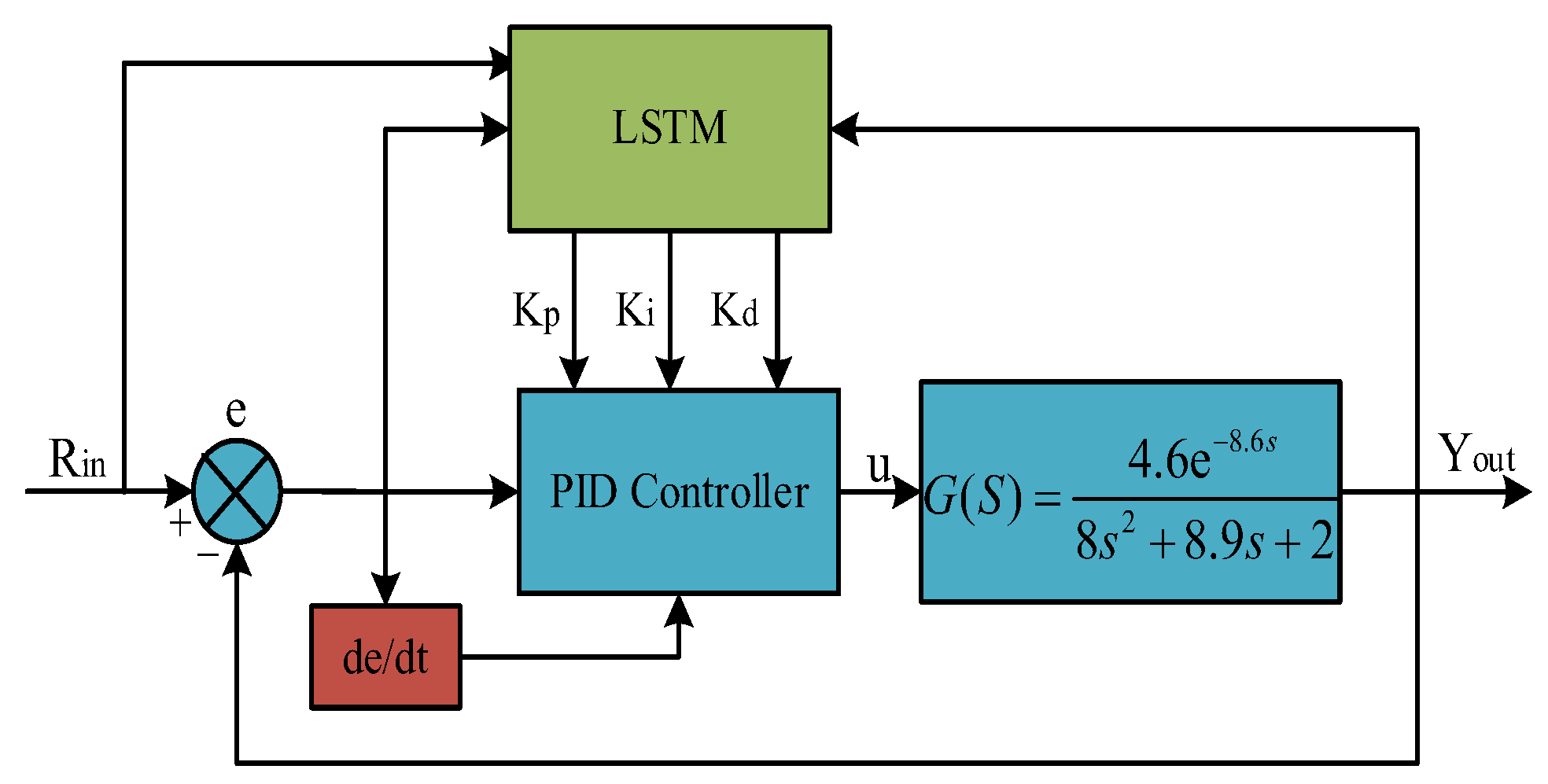
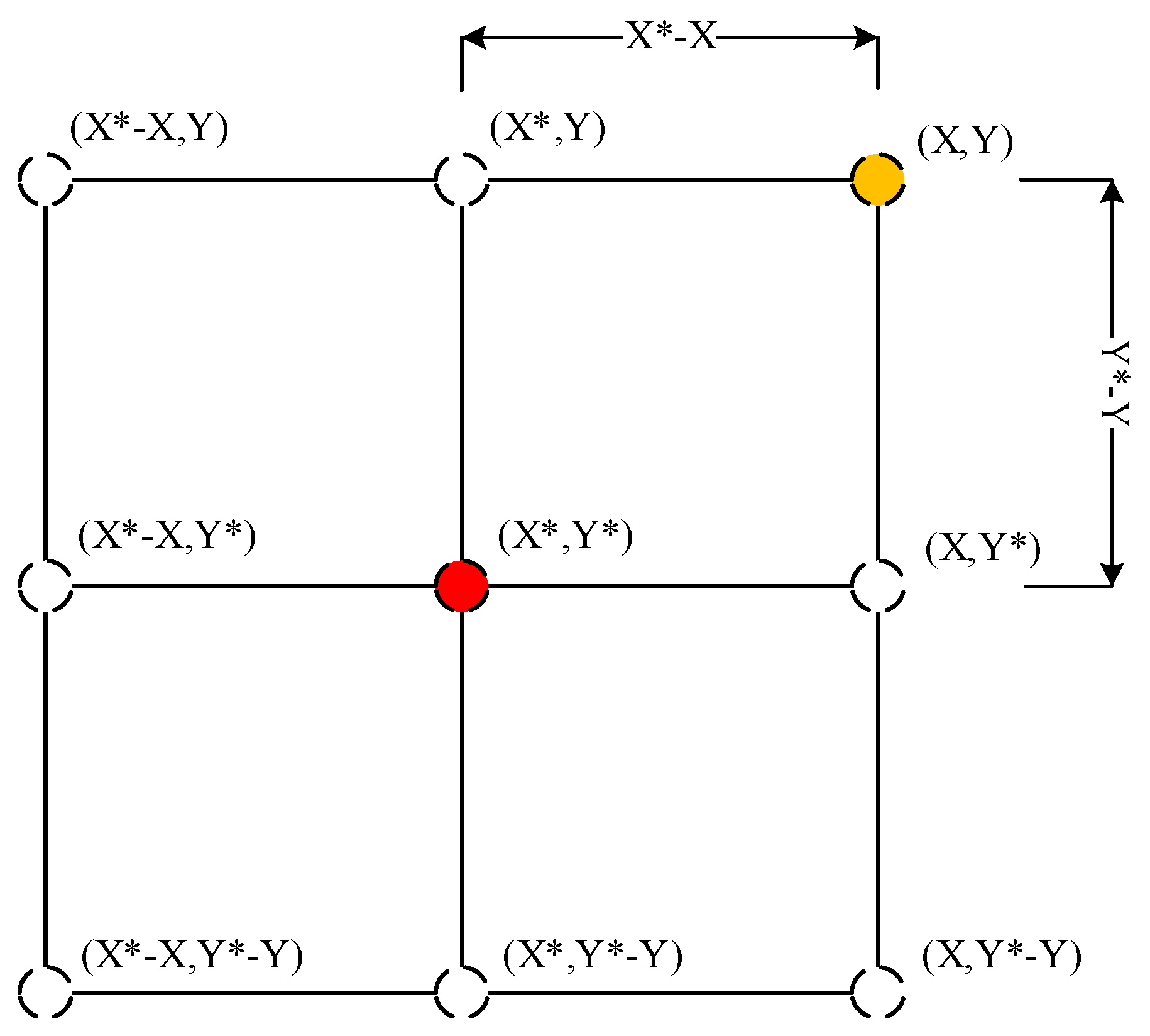
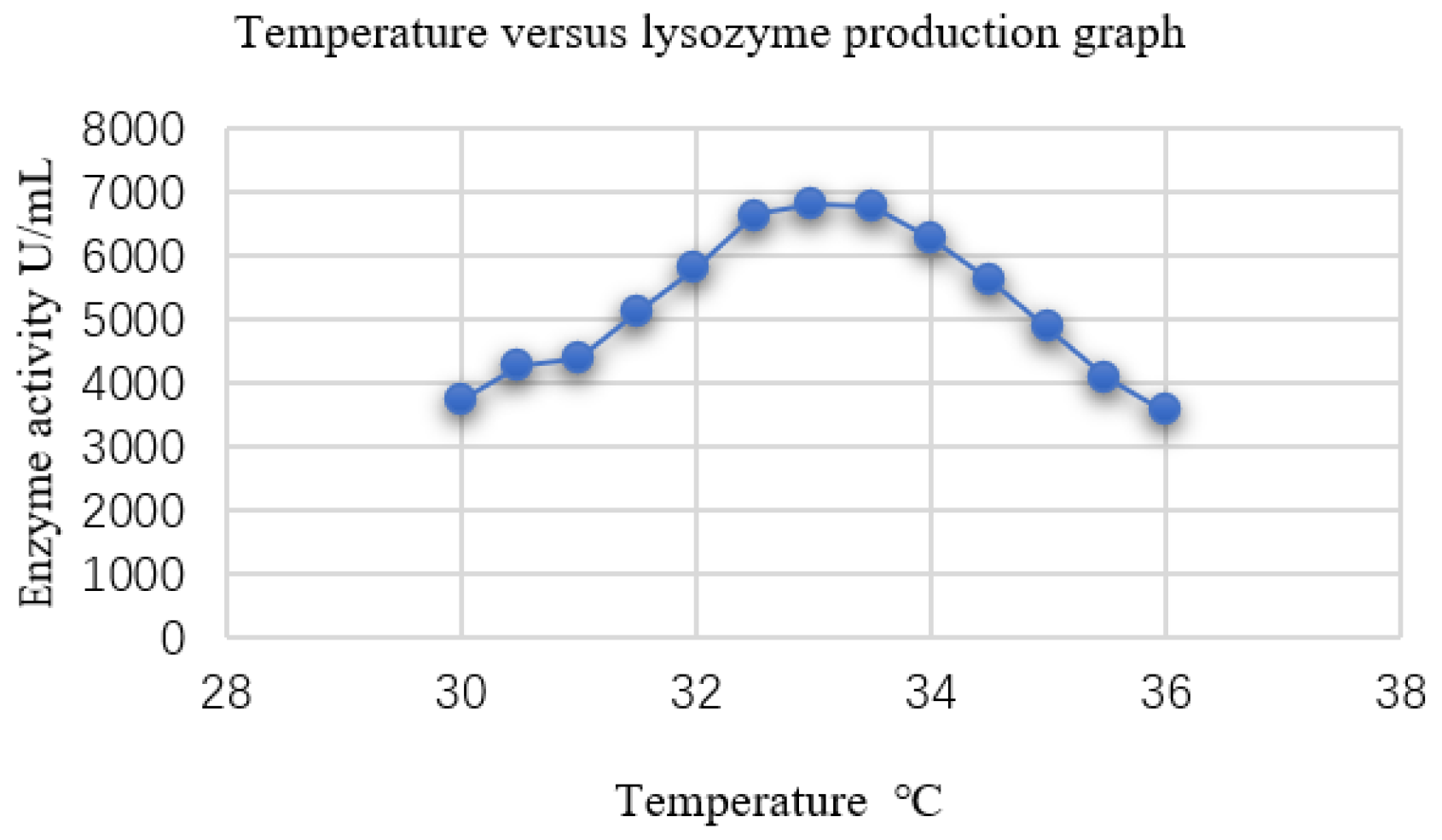
Function Type	Index	Function Name	Search Range	Adaptive Value
single-peak functions	F1	Sphere Function	[−100, 100]	0
	F2	Schwefel’s Problem 1.2	[−100, 100]	0
	F3	Schwefel’s Problem 1.2 With Noise	[−32, 32]	0
	F4	Schwefel’s Problem 2.21	[−5, 5]	0
	F5	Schwefel’s Problem 2.22	[−10, 10]	0
	F6	High Conditioned Elliptic Function	[−3, 1]	0
	F7	Step Function	[−10, 10]	0
multi-peak functions	F8	Schwefel Function	[−500, 500]	0
	F9	Rosenbrock’s Function	[−10, 10]	0
	F10	Quartic Function	[2, 5]	0
	F11	Griewank’s Function	[−600, 600]	0
	F12	Ackley’s Function	[−32, 32]	0
	F13	Rastrign’s Function	[−5.12, 5.12]	0
	F14	Rastrign’s Noncontinue Function	[−5.12, 5.12]	0
	F15	Weierstrass Function	[−100, 100]	0

provides the names, search ranges, function indices, and adaptive values of the 15 benchmark functions.

The LRWOA is compared with the WOA, PSO [44], Grey Wolf Optimizer (GWO) [45], and GWO enhanced using the Lévy-flight strategy (LGWO) [46] through experiments. To ensure fairness and impartiality, considering the instability of the algorithms, each algorithm experiment is run independently 10 times, and the average results are taken. In the comparative experiments of different algorithms, the population size is set to 50, and the dimension of the decision variables is set to 60. Figure 3, Figure 4, Figure 5 and Figure 6 shows the convergence curves of some functions, where F1 and F8 represent unimodal functions, and F10 and F14 represent multimodal functions.

Upon comprehensively analyzing the convergence curves in Figure 3, Figure 4, Figure 5 and Figure 6, it can be observed that the LRWOA converges rapidly on both unimodal and multimodal functions, and its convergence precision is also improved. On the unimodal functions F1 and F8, the PSO, GWO, LGWO, and WOA all fall into local optima in the early stages of the search process, indicating a weaker local search capability. Among these, the PSO performs less effectively in local search capabilities than the other four and does not exhibit a strong performance in global optimization. The LRWOA, aided by the random walk strategy, can ensure the rapid convergence and the capability of escaping local optima, manifested specifically in the steep declines on the convergence curves. On the multimodal functions F10 and F14, compared to the other four algorithms, the LRWOA demonstrates a faster drop and closer approach to the function’s adaptive values on the convergence curve graph, while also avoiding stagnation points that are easily entrapped.

This indicates that the LRWOA has better global exploration capabilities with the assistance of the Lévy flight strategy. The above analysis indicates that, compared with the other four algorithms, the LRWOA excels in comprehensive performance, efficiently solving various problems.

4. LRWOA-LSTM-PID Controller

This section sequentially introduces the PID controller, the LSTM-PID controller model, and the LSTM-PID controller based on the LRWOA.

Figure 7 illustrates the overall structure diagram of the control system, which contains four modules: the LRWOA module, the LSTM module, the PID controller module, and the fermenter temperature system module. The LRWOA provides optimized initial parameters for the LSTM, thereby reducing the possibility of the network falling into local optima to some extent. The LSTM online tunes parameters for the PID controller, strengthening the connection between control information and thus accelerating the temperature control speed and stability; the PID controller still plays a leading role in the control process. It controls the actuator by outputting control quantities, thereby controlling the fermenter temperature system. The model of the fermenter temperature system in this paper is shown in (14).

4.1. PID Controller

The control law for the PID controller as shown in (29). In (29): $t$ represents the sample number, $u\left(t\right)$ is the computed output value at the t-th sampling instant, and $e\left(t\right)$ is the deviation value input at the t-th sampling instant. The working principle of PID is to perform proportional calculation, differential calculation, and integral calculation on the difference value $e\left(t\right)$, and add these three calculation results to obtain the control quantity $u\left(t\right)$ of the PID controller.

$$u\left(t\right)=K_p\ast e\left(t\right)+K_i\sum _{j=0}^{t}e\left(j\right)+K_d\left[e\left(t\right)-e\left(t-1\right)\right]$$

(29)

After determining the expression of $u\left(t\right)$, using $u\left(t\right)-u(t-1)$ can obtain the increment of the control quantity. The resulting mathematical expression is as follows:

$$∆u\left(t\right)=\left(k_p+k_i+k_d\right)e\left(t\right)-\left(k_p+2k_d\right)e\left(t-1\right)+k_{d}e\left(t-2\right)$$

(30)

In (30), $k_p$, $k_i$, and $k_d$ are the proportional coefficient, integral coefficient, and derivative coefficient, respectively; $∆u\left(t\right)$ is the difference between the controller output at time t and the previous moment; $e\left(t\right)$ is the difference between the target value of lysozyme fermentation temperature $r\left(t\right)$ at time t and the output value of the fermenter temperature model $y\left(t\right)$.

4.2. LSTM-PID Controller

Control systems designed using neural network methods have stronger real-time performance, robustness, and adaptability. However, the BP-PID controller designed using the BP does not effectively utilize target information, previous parameter information, previous control information, etc. Additionally, the global optimization capability of the backpropagation learning algorithm is relatively poor, making it easy to fall into local optima, which fails to achieve good control effects and limits the application of neural networks in PID controllers.

To solve these issues, a PID controller based on the LSTM is designed. An ordinary RNN simply stacks past information, which can easily lead to problems with gradient explosion and gradient vanishing during training. In contrast, an LSTM can control the transmission state through a gating system, remembering information that needs to be stored long-term and ignoring less relevant information. The structure of the LSTM-PID controller designed in this paper is shown in Figure 8. The inputs to the LSTM are set as the target value of the current time point for lysozyme fermentation temperature, the output value of the current time point for the lysozyme fermentation temperature model, and the error values of these two factors for the three time points before and after; the output of the neural network is set as the three parameter values of the PID controller, $k_p$, $k_i$, and $k_d$.

The structure diagram of the LSTM-PID controller is shown in Figure 9, where:

$$\overrightarrow{x}=\left\{\begin{array}{c}h(t-1)\\ c(t-1)\\ x\left(t\right)\end{array}\right.$$

(31)

$h(t-1)$ represents the output value of the network at the previous moment; $c(t-1)$ denotes the memory unit at the previous moment. $x\left(t\right)$ is the current input as a one-dimensional vector.

$$\left\{\begin{array}{c}{x}_1\left(t\right)=r\left(t\right)\\ x_2\left(t\right)=y\left(t\right)\\ x_3\left(t\right)=e\left(t\right)\\ x_4\left(t\right)=e\left(t-1\right)\\ x_5\left(t\right)=e(t-2)\end{array}\right.$$

(32)

where $r\left(t\right)$ is the target temperature value for lysozyme fermentation; $y\left(t\right)$ is the output temperature value of the fermenter system; $e\left(t\right)$ is the difference between $r\left(t\right)$ and $y\left(t\right)$ at time $t$.

4.2.1. The Forward Propagation of LSTM

Neural network training is divided into forward propagation and backpropagation. Forward propagation starts from the input layer and continuously calculates the results obtained using each layer of the neural network and the output results through the activation function, finally obtaining the output process. The forward propagation of the LSTM involves the computation of output $h$ and cell state $c$. The gate system inputs a vector and outputs a value between 0 and 1, allowing useful information flow to pass and blocking useless information flow. Assuming that the weight vector and bias of the gate are represented by $W$ and $b$ respectively, then the gate can be represented by (33):

$$g\left(\overrightarrow{x}\right)=\sigma \left(W\overrightarrow{x}+b\right)$$

(33)

where, $\sigma$ is the sigmoid function $\sigma \left(z\right)=\frac{1}{1+e^{-z}}$.

The use of gates involves element-wise multiplication of the output vector by the vector to be controlled. Given that the output of the gate is a real vector between 0 and 1, when the gate output is 1, any vector multiplied by it will not change, meaning all information can pass through; when the output is 0, any vector multiplied by it will result in a zero vector, meaning no data can be passed through. As the value range of the sigmoid function is (0, 1), the state of the gate is always half-open and half-closed. The input gate and forget gate in the gating system can be represented by Equations (34) and (35), respectively.

$$i\left(t\right)=\sigma \left(W_i·\left[h\left(t-1\right),x\left(t\right)\right]+b_i\right)$$

(34)

$$f\left(t\right)=\sigma \left(W_f·\left[h\left(t-1\right),x\left(t\right)\right]+b_f\right)$$

(35)

where, $W_i$ is the weight matrix of the input gate, $\left[h\left(t-1\right),x\left(t\right)\right]$ represents concatenating two vectors into a longer vector, $b_i$ is the bias term of the input gate, $W_f$ is the weight matrix of the forget gate, and $b_f$ is the bias term of the forget gate.

The current time input cell state $\tilde{c}\left(t\right)$ is calculated from the previous moment’s output and the current moment’s input, as shown in (36).

$$\tilde{c}\left(t\right)=\mathit{tanh}\left(W_c·\left[h\left(t-1\right),x\left(t\right)\right]+b_c\right)$$

(36)

In the (36), $W_c$ is the weight matrix of the cell state, and $b_c$ is the bias term of the cell state. The current time cell state $c\left(t\right)$ can be obtained by multiplying the forget gate $f\left(t\right)$ and the cell state $c\left(t-1\right)$ of the last moment element by element, then multiplying the input gate $i\left(t\right)$ and the cell state $\tilde{c}\left(t\right)$ of the current moment input element by element, and finally adding the two results, the equation is as follows:

$$c\left(t\right)=f\left(t\right)\ast c\left(t-1\right)+i\left(t\right)\ast \tilde{c}\left(t\right)$$

(37)

In the (37), the symbol * indicates that the variables are multiplied element by element. It can be seen that the new cell state $c\left(t\right)$ is obtained by combining the memory $\tilde{c}\left(t\right)$ of the current moment of the LSTM and the memory $c\left(t-1\right)$ of the previous moment. Due to the control of the input gate and the forget gate, it can prevent unimportant information from entering the memory and can save previous information. Finally, the output gate is used to control the influence of the LSTM on the current moment output, and the output gate equation is as follows:

$$o\left(t\right)=\sigma \left(W_o·\left[h\left(t-1\right),x\left(t\right)\right]+b_o\right)$$

(38)

In (38), $W_o$ is the weight matrix of the output gate, and $b_o$ is the bias term of the output gate. The final output of the LSTM is determined using the cell state and the output gate. The output is shown in (39). In this paper, the output $h\left(t\right)$ of the LSTM neural network is the three parameters of PID: $k_p$, $k_i$, and $k_d$.

$$\left\{\begin{array}{c}{h}_1\left(t\right)=o_1\left(t\right)\ast \mathit{tanh}\left[c_1\left(t\right)\right]=k_p\\ h_2\left(t\right)=o_2\left(t\right)\ast \mathit{tanh}\left[c_2\left(t\right)\right]=k_i\\ h_3\left(t\right)=o_3\left(t\right)\ast \mathit{tanh}\left[c_3\left(t\right)\right]=k_d\end{array}\right.$$

(39)

4.2.2. The Backpropagation of the LSTM

The loss function is obtained based on the results of forward propagation and input into the backpropagation process to train the neural network. In this section, the backpropagation algorithm used to train the LSTM mainly consists of the following three steps: First, compute the output values of all neurons in the network, namely the five vectors $i\left(t\right)$, $f\left(t\right)$, $o\left(t\right)$, $c\left(t\right)$, and $h\left(t\right)$ Then, calculate the error values of all neurons in the network in reverse; the backpropagation of the error of the LSTM includes two directions, namely the propagation to the previous layer and the propagation along the time direction. Finally, calculate the gradients of each weight according to the relevant error values.

The error of the LSTM is backpropagated over time, which is a common method for training recursive neural networks. The central idea of this method is to constantly find suitable values along the negative gradient direction of the parameters to be optimized until the model converges. Before performing backpropagation, the error $\delta \left(t\right)$ at time $t$ is defined as follows:

$$\delta \left(t\right)=\frac{\partial E}{\partial h\left(t\right)}$$

(40)

To propagate the error back in time, it is necessary to calculate the error $\delta (t-1)$ at time $t-1$. This can be achieved using (40):

$${\delta }^T\left(t-1\right)=\frac{\partial E}{\partial h\left(t-1\right)}=\frac{\partial E}{\partial h\left(t\right)}·\frac{\partial h\left(t\right)}{\partial h\left(t-1\right)}={\delta }^T\left(t\right)\frac{\partial h\left(t\right)}{\partial h\left(t-1\right)}$$

(41)

By expanding (41) and utilizing the total derivative formula along with Equations (37) and (39), we can derive the formula for error propagation to any time $k$:

$${\delta }^T\left(k\right)=\prod _{j=k}^{t-1}{\delta }_o^T\left(j\right)W_{oh}+{\delta }_f^T\left(j\right)W_{fh}+{\delta }_i^T\left(j\right)W_{ih}+{\delta }_{\tilde{c}}^T\left(j\right)W_{ch}$$

(42)

In (42), ${\delta }_{\ast }\left(t\right)$ represents the error at moment $j$ for * (* stands for the input gate, output gate, forget gate, and cell state), and $W_{\alpha ,\beta }$ represents the weight between $\alpha$ and $\beta$.

In the backpropagation of error terms in the LSTM, it is assumed that the current layer is the lth layer. The error term of the $l-1st$ layer is defined as the derivative of the error function with respect to the weighted input of the $l-1st$ layer, which is:

$${\delta }_t^{l-1}=\frac{\partial E}{{net}_t^{l-1}}$$

(43)

When calculating the gradients of each weight, for the weight gradients of $W_{oh}$, $W_{fh}$, $W_{ih}$, and $W_{ch}$, they are actually the sum of the gradients at each moment. Therefore, it is first necessary to find out their gradients at the moment $t$, and then calculate their final gradients. The error terms ${\delta }_o,{\delta }_f,{\delta }_i$ and ${\delta }_{\tilde{c}}$ have been obtained in the previous (42), so the gradient values at the moment t can be obtained as follows:

$$\left\{\begin{array}{c}\frac{\partial E}{\partial W_{fh,t}}=\frac{\partial E}{\partial {net}_{f,t}}·\frac{\partial {net}_{f,t}}{\partial W_{fh,t}}={\delta }_{f,t}{h}_{t-1}^T\\ \frac{\partial E}{\partial W_{oh,t}}=\frac{\partial E}{\partial {net}_{o,t}}·\frac{\partial {net}_{o,t}}{\partial W_{oh,t}}={\delta }_{o,t}{h}_{t-1}^T\\ \frac{\partial E}{\partial W_{ih,t}}=\frac{\partial E}{\partial {net}_{i,t}}·\frac{\partial {net}_{i,t}}{\partial W_{ih,t}}={\delta }_{i,t}{h}_{t-1}^T\\ \frac{\partial E}{\partial W_{ch,t}}=\frac{\partial E}{\partial {net}_{\tilde{c},t}}·\frac{\partial {net}_{\tilde{c},t}}{\partial W_{\tilde{c}h,t}}={\delta }_{\tilde{c},t}{h}_{t-1}^T\end{array}\right.$$

(44)

By summing up the gradients at each moment, the final gradients can be obtained:

$$\left\{\begin{array}{c}\frac{\partial E}{\partial W_{oh}}={\displaystyle \sum _{j=1}^t}{\delta }_{o,j}{h}_{j-1}^T\\ \frac{\partial E}{\partial W_{fh}}={\displaystyle \sum _{j=1}^t}{\delta }_{f,j}{h}_{j-1}^T\\ \frac{\partial E}{\partial W_{ih}}={\displaystyle \sum _{j=1}^t}{\delta }_{i,j}{h}_{j-1}^T\\ \frac{\partial E}{\partial W_{ch}}={\displaystyle \sum _{j=1}^t}{\delta }_{\tilde{c},j}{h}_{j-1}^T\end{array}\right.$$

(45)

The following can be obtained based on the corresponding error terms:

$$\frac{\partial E}{\partial W_{ij}}=\frac{\partial E}{\partial net}·\frac{\partial net}{\partial W_{ij}}$$

(46)

In (46), $W_{ij}$ represents the weight of the $ith$ neuron in the hidden layer and the $jth$ neuron in the output layer; $net$ is the input to the output layer.

However, after setting the output of the neural network as the three parameters of the controller, since the desired PID controller target parameters are uncertain, the external environment cannot provide clear target values for the neural network to learn. Therefore, this paper redesigns the backpropagation algorithm of the LSTM in combination with the formula of the PID controller and sets the difference between the temperature to be controlled in the fermenter and the actual temperature in the fermenter as the new error value of the neural network. As shown in (47), a new factor is integrated when solving, which is:

$$\frac{\partial E}{\partial W_{ij}}=\frac{\partial E}{\partial y}·\frac{\partial y}{\partial ∆u}·\frac{\partial ∆u}{\partial h}·\frac{\partial h}{\partial net}·\frac{\partial net}{\partial W_{ij}}$$

(47)

In (47), $E$ is the mean square error function; $y$ is the actual measured value of the system; $∆u$ is the output of the controller; $h$ is the output of the neural network; since $\partial y/\partial ∆u$ is unknown, it can be approximately replaced by the sign function $sgn$ which leads to the inaccuracy of the calculation and can be compensated by adjusting the learning rate.

4.2.3. PID Parameter Tuning Based on LSTM

The design of the neural network includes the error calculation and the way of error backpropagation. It leverages the LSTM to optimize the $k_p$, $k_i$, and $k_d$ parameters of the PID controller.

The main process of this controller during control is as follows:

Step 1: Build the PID control algorithm and design the LSTM, combine the PID control algorithm and the LSTM, determine the learning rate $\eta$ and the inertia coefficient $\alpha$ of the LSTM, and set the initial time $t$ to 1.

Step 2: By setting the target temperature $r\left(t\right)$ and the actual temperature $y\left(t\right)$ calculated using the mathematical model, the error $e\left(t\right)$ at this moment is obtained. The calculation formula of $e\left(t\right)$ is $e\left(t\right)=r\left(t\right)-y\left(t\right)$.

Step 3: Take $r\left(t\right)$, $y\left(t\right)$, $e\left(t\right)$, $e(t-1)$, $e(t-2)$ as the inputs of the LSTM, and set the initial values $r\left(0\right)$, $y\left(0\right)$, $e\left(0\right)$, $e(-1)$, $e(-2)$ to 0.

Step 4: Set the output of the LSTM as the three adjustable parameters of the PID controller.

Step 5: Calculate the output $u\left(t\right)$ of the PID controller:

$$\left\{\begin{array}{c}u\left(t\right)=u\left(t-1\right)+∆u\left(t\right)\\ ∆u\left(t\right)=k_p\left(e\left(t\right)-e\left(t-1\right)\right)+k_{i}e\left(t\right)+k_d\left(e\left(t\right)-2e\left(t-1\right)+e\left(t-2\right)\right)\end{array}\right.$$

(48)

Step 6: Set the difference $e\left(t\right)$ between $y\left(t\right)$ and $r\left(t\right)$ as the error of the LSTM, carry out the learning of the LSTM, adjust the weight parameters of the neural network online, and realize the adaptive adjustment of the controller parameters.

Step 7: When $e\left(t\right)$ is less than the set threshold, stop adjusting the controller parameters, determine the final controller parameters and input them into the PID controller to obtain the control parameters, otherwise let $t=t+1$ and return to step 2.

4.3. LSTM-PID Controller Based on LRWOA Algorithm

Although the PID controller based on the LSTM has improved the shortcomings of the classical PID controller, there are still some shortcomings in the training process of the LSTM. For example, when using the backpropagation algorithm to optimize the neural network during training, there is a certain probability that the control system will diverge and not converge. In response to this situation, this article introduces inertia terms into the backpropagation algorithm to alleviate the oscillation problem. In addition, because the initial parameter values of the neural network are initialized in a randomized manner during training, this may cause the neural network to fall into a local optimal solution, resulting in poor results. If suitable parameters can be found for the neural network in the early stages of neural network training, the above problems can be effectively improved. Using the excellent optimization ability of the LRWOA algorithm can find more appropriate parameters in the early stages of neural network training, which can reduce the divergence and non-convergence problems of neural network training.

Using the LRWOA algorithm to solve the problem of initial weights in LSTM has the following two key points: First, the dimension values of the whales in the LRWOA algorithm should be equal to the number of connection weights in the LSTM. Each position of the whale in the LRWOA is set to an initial weight in the neural network. Second, the fitness function in the LRWOA algorithm needs to be replaced with the mean square error function in the LSTM.

Figure 10 provides an explanation in a two-dimensional space for (16). The position (X, Y) of the whale individual can be updated according to the position (X*, Y*) of the whale individual currently obtaining the best solution. By adjusting the values of A and C, the whale individual can be updated to different positions around the current best solution. The possible update positions in three-dimensional space are shown in Figure 11.

By defining a vector $r$, the individual can be updated to any position around the best solution in Figure 11, therefore, (16) can simulate the behavior of surrounding prey. The above knowledge can also be applied to the n-dimensional search space. Whale individuals will move around the currently obtained best solution in the n-dimensional space. Therefore, when applied to the optimization of initial parameters of LSTM, it is necessary to set the Whale Optimization Algorithm as a four-dimensional search space, corresponding to $W_i$, $W_f$, $W_c$ and $W_o$ of the LSTM network, respectively.

The workflow of the optimized controller is as follows:

Step 1: Firstly, determine the topology of the LSTM to find out the number of parameters in each layer of the network and the number of network hyperparameters;

Step 2: Set the dimension of the LRWOA algorithm to the number of parameters in step 1 and randomly initialize the position of the whale population;

Step 3: Use the error between the target value and the output value as the fitness function. According to the fitness function, judge whether the current position of the whale meets the conditions. If it meets the conditions, output the best position of the whale individual in the whale population and jump to step 7, otherwise, jump to step 4;

Step 4: Calculate the objective function value of the whale population;

Step 5: Update the positions of all whale individuals in the whale population;

Step 6: Update the objective function value of the whale population;

Step 7: Use the obtained output result as the optimal initial parameter of the neural network;

Step 8: Set the target temperature $r\left(t\right)$ and obtain the actual temperature $y\left(t\right)$ through measurement sampling to obtain the current error $e\left(t\right)$. The calculation equation of $e\left(t\right)$ is $e\left(t\right)=r\left(t\right)-y\left(t\right)$;

Step 9: Use $r\left(t\right)$, $y\left(t\right)$, $e\left(t\right)$, $e(t-1)$, $e(t-2)$ as the input of the LSTM neural network;

Step 10: Set the output of the LSTM as the three adjustable parameters of the PID controller;

Step 11: Calculate the output of the PID controller, set the difference $e\left(t\right)$ between $y\left(t\right)$ and $r\left(t\right)$ as the error of the LSTM, conduct LSTM learning, adjust the weight parameters of the neural network online, and realize the self-adaptive adjustment of the controller parameters;

Step 12: When $e\left(t\right)$ is less than the set threshold, stop adjusting the controller parameters, determine the final controller parameters, and obtain the control parameters into the PID controller, otherwise, let $t=t+1$ and return to step 8.

5. Experiment

5.1. Parameter Description

According to the parameters of the lysozyme fermentation process provided by the project cooperation unit, the relationship between temperature and lysozyme activity is shown in Figure 12. As can be seen from Figure 12, the yield of lysozyme shows a trend of first increasing and then decreasing with temperature. This is because the lysozyme is not active enough at low temperatures, while higher temperatures will cause the enzyme to lose activity. From the figure, it can be seen that the enzyme activity reaches the highest point when the temperature is 33 °C. Therefore, the best temperature in the process of lysozyme fermentation is set as 33 °C. The subsequent experiments will use this temperature as the control target of the control system.

The input data of the control system are different from the dataset of traditional neural networks. The input of the neural network in this paper is a time series sequence. The specific input is as follows: the output sequence of the control system at the current moment, the system target value, and the error sequence of the two in the previous three moments.

In [6,34], PID and BP-PID have been widely applied in the industry and are the two most representative controllers. In [17,18,19,20,21,22,39], heuristic algorithms are used to optimize the initial parameters of the BP neural network, among which PSO-BP-PID is the most representative. In [37], the method of using the RNN is employed to optimize the PID parameters, which demonstrates excellent position tracking results and robustness against variations in system parameters.

For this purpose, we chose PID [6], BP-PID [34], PSO-BP-PID [39] and RNN-BP-PID [37] as the comparison methods for the experiment.

The control system in this paper is the temperature control system of the fermenter, and its system function is shown in (14) in Chapter 2. The parameters analyzed in the comparative experiment are explained in Figure 13.

In Figure 13, $M_p$ represents the overshoot generated by the system; $T_s$ represents the system’s settling time; $T_d$ represents the system’s delay time; $T_r$ represents the system’s rise time; $T_p$ represents the system’s peak time; $Err$ represents the system’s error value.

5.2. Experimental Results and Analysis

Comparative experiments were conducted on the five controllers, and Figure 14 shows the control performance of the classic PID controller, BP-PID controller, PSO-BP-PID controller, RNN-BP-PID controller, and LSTM-PID controller. Rin represents the target temperature. These controllers can complete the control of the fermenter temperature in a short time; the control duration can be kept within 1 s and the overshoot size can be controlled within 2 °C. Among them, the classic PID controller, BP-PID, and PSO-BP-PID controllers have very similar responses, showing an upward and downward fluctuation and gradually stabilizing trend, while the RNN-BP-PID and LSTM-PID controllers stabilize slowly after continuously rising to the target temperature.

In terms of the $T_d$ parameter, the five controllers are basically consistent, thanks to the excellent performance of the PID controller itself. In terms of the $T_r$ and $T_p$ parameters, PID, BP-PID, and PSO-BP-PID show an increasing relationship in sequence, while RNN-BP-PID and LSTM-PID do not produce overshoot due to the addition of recurrent neural network, so that their rising time, peak time and stable time are consistent. In terms of the $T_s$ parameter, it can be observed that LSTM-PID performs best, reaching stability at 0.61 s. The control duration of the classic PID controller is significantly longer than the other four controllers, gradually stabilizing around 1 s. This is because the parameters of the classic PID are fixed and cannot change with the environment. The performances of the other three controllers are comparable, stabilizing the target temperature almost at the same time. In terms of the $M_p$ parameter, controllers with the recurrent neural network perform better than other controllers. Specifically, classic PID, BP-PID, and PSO-BP-PID all have an overshoot, which are 1.62 °C, 0.79 °C, and 0.1 °C, respectively. However, the recurrent neural network, thanks to its stronger fitting ability and unique associative memory ability, therefore has no overshoot in RNN-BP-PID and LSTM-PID in this system.

Table 2. Controller comparison table at 33 °C. Bold represents the best result.

CONTROLLER	PID	BP-PID	PSO-BP-PID	RNN-BP-PID	LSTM-PID
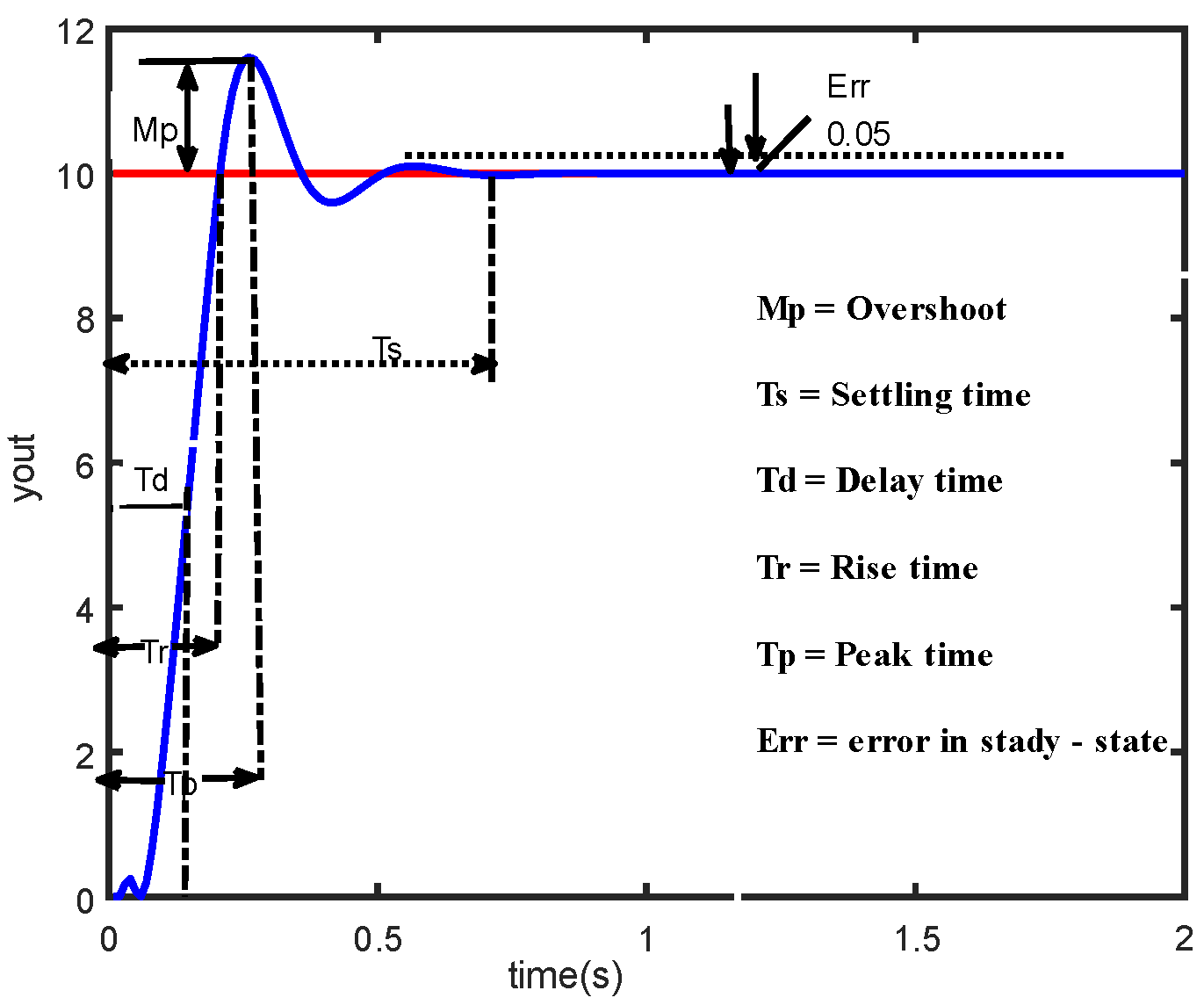
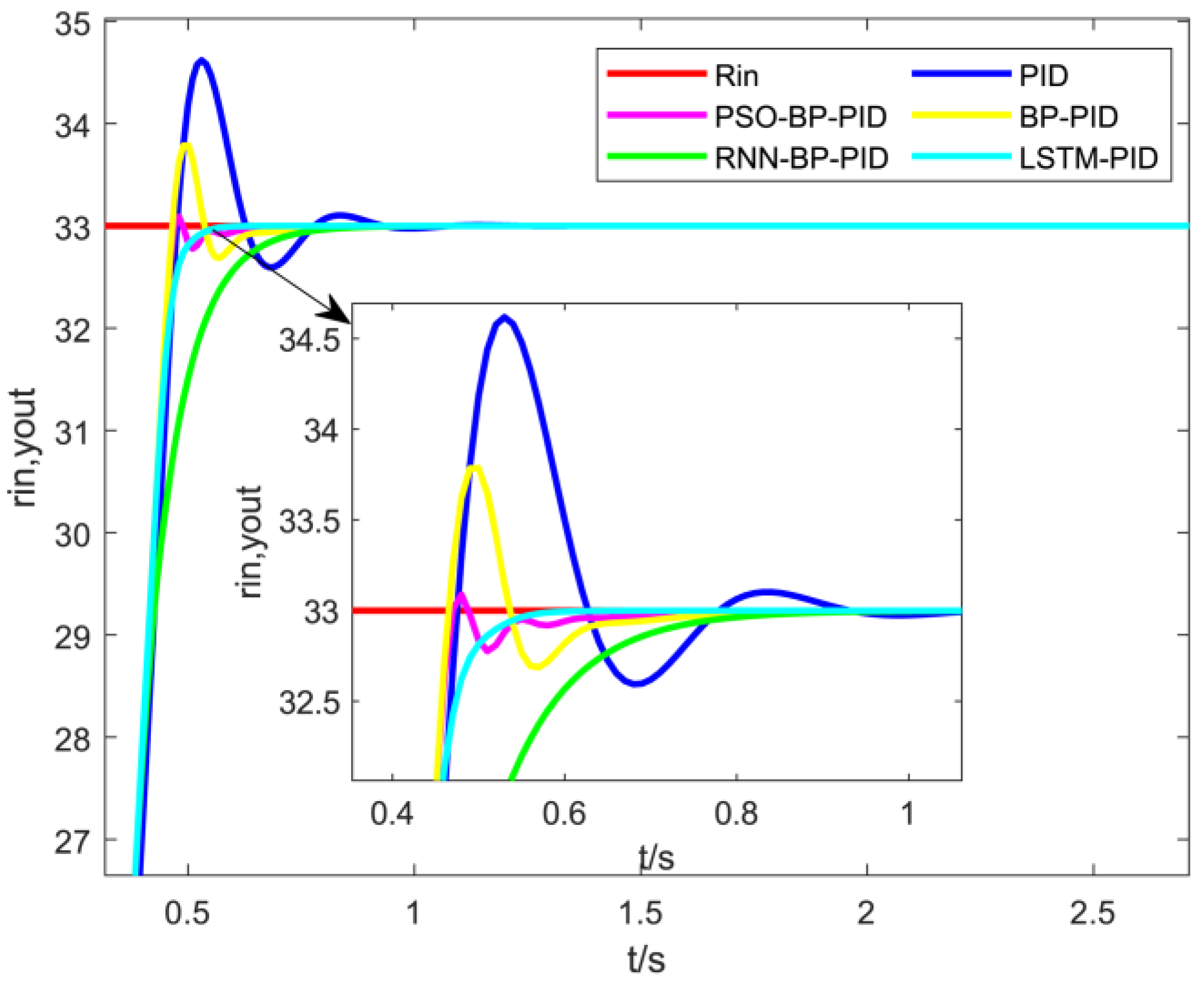
Rise time (s)	0.48	0.46	0.47	0.77	0.61
Settling time (s)	1.06	0.74	0.72	0.77	0.61
Overshoot (°C)	1.62	0.79	0.10	0.00	0.00
Peak (°C)	34.62	33.79	33.10	33.00	33.00
Peak time (s)	0.53	0.50	0.48	0.77	0.61
Kp	4.08	9.91	2.51	14.82	10.01
Ki	0.87	1.92	1.72	1.8	2.09
Kd	12.00	9.46	10.03	10.4	10.06
Error	0	0	0	0	0

shows the specific parameters of the five controllers during the control process. It can be seen that LSTM-PID and RNN-BP-PID have the most outstanding performance in terms of overshoot, with no overshoot observed. In terms of settling time, LSTM-PID performs best, reducing by 42.5% compared to the traditional PID, 17.6% compared to BP-PID, 15.3% compared to PSO-BP-PID, and 20.8% compared to RNN-BP-PID. However, in terms of rise time and peak time, since LSTM-PID does not produce overshoot, both of these times are equivalent to the settling time, so they have no comparative significance. From the above analysis, it is clear that LSTM-PID has the best performance.

To verify the effectiveness and optimization ability of the LRWOA algorithm, a comparative experiment was carried out between the LSTM-PID controller based on the LRWOA algorithm and the PID controller based on the LSTM. The results are shown in Figure 15.

From Figure 15, it can be seen that, compared to LSTM-PID, LRWOA-LSTM-PID can reach the target temperature more quickly during the control process. Overall, LRWOA-LSTM-PID shows stable improvements in rise time, peak time, and settling time compared to LSTM-PID. Specifically, in terms of rise time, peak time, and settling time, the controller designed in this section benefits from the inclusion of the strong optimization ability of the LRWOA algorithm, which can quickly find suitable initial parameter values for the LSTM, thus reducing by 9.8% compared to the LSTM-PID controller. In terms of overshoot, both LRWOA-LSTM-PID and LSTM-PID benefit from the cyclic neural information feedback mechanism, so both show excellent performance and do not produce overshoot in this system. In terms of controller parameters, both LRWOA-LSTM-PID and LSTM-PID can quickly find a reasonable parameter combination for the PID controller, enabling it to respond quickly to the control system. The specific parameters of the results are shown in

Table 3. Comparison result of LRWOA-LSTM-PID and LSTM-PID. Bold represents the best result.

CONTROLLER	LSTM-PID	LRWOA-LSTM-PID
Rise time (s)	0.61	0.55
Settling time (s)	0.61	0.55
Overshoot (%)	0.00	0.00
Peak (°C)	33.00	33.00
Peak time (s)	0.61	0.55
Kp	10.01	12.02
Ki	2.09	3.04
Kd	10.06	11.20
Error	0	0

.

In summary, the LRWOA-LSTM-PID controller has good performance, can achieve the rapid tuning of PID parameters, improves the convergence speed of the system, and reduces the overshoot of the system, which can meet the strict temperature control requirements in the lysozyme fermentation process, providing a guarantee for high-quality lysozyme production.

6. Conclusions

The paper designs a fermenter temperature mechanism model based on a dynamic equation description, which can reflect the temperature changes in the fermenter well. A method for PID parameter tuning based on LSTM is proposed, which can more reasonably adjust the network weights, speeding up the tuning of PID parameters. A Whale Optimization Algorithm (WOA) based on Levy flight and the random walk strategy (LRWOA) is proposed for the initialization of LSTM parameters, enhancing the global and local optimization capabilities of the neural network parameters. On this basis, a method of temperature control for lysosomal fermentation based on LRWOA-LSTM-PID is proposed. Experimental results show that the method proposed in this paper can achieve the rapid tuning of PID parameters $K_p$, $K_i$, and $K_d$, thus improving the convergence speed of the system and reducing the overshoot of the system.

Considering the further optimization of the proposed algorithm, the following future research is planned: (1) The verification of the LRWOA-LSTM-PID model on a hardware platform, and an attempt to implement this method in a real environment; (2) the enhancement of the real-time capabilities of LRWOA-LSTM-PID through offline parameter tuning; (3) the proposal of better controllers for a more accurate control of parameters such as dissolved oxygen in the lysosomal fermentation process.